1. Asseris te in varietate scribentium de circuli quadratura involutum et a me nunc otio dato exigis, ut scibilis illius sufficientiam tradam. Accipe per propositionem, quid sentiam. Hoc tamen me fecisse sic tui causa recipito, ut per huius assimilationem mathematicis relictis facilius ad theologiam te transferre queas.
Propositio
2. Si datae peripheriae trigoni est dabilis aequalis peripheria circuli, tunc illius circuli semidiameter in quinta sui parte excedit lineam ductam de centro trigoni ad punctum unum alicuius lateris ab angulo per quartam partem lateris distantis.
3. Sunt qui circuli quadraturam admittunt. Et hi habent necessario admittere circulorum peripherias aequari posse peripheriis polygoniarum figurarum, cum circulus aequetur quadrangulo, cuius minus latus est semidiameter et maius semicircumferentia. Quando igitur quadratum aequale circulo in tale quadrangulum resolveretur, haberetur recta linea curvae aequalis. Hinc deveniretur ad aequalitatem peripheriarum circuli et polygoniae, ut est de se notum.
4. Illi etiam hoc argumentum admittunt, sine quo nihil attingerent, scilicet: Ubi est dare magis et minus, est et dare aequale; quia, cum detur quadratum maius circulo, ut est circumscriptum, et minus, ut est inscriptum, igitur et aequale, quod erit nec circumscriptum nec inscriptum, sed pariter inscriptum et circumscriptum. Hoc idem argumentum admittunt in peripheriis: Quia est dabilis peripheria circuli maior peripheria trigoni, ut est peripheria circuli trigono circumscripti, et dabilis est peripheria circuli minor peripheria trigoni, ut est peripheria circuli inscripti, igitur est et dabilis peripheria circuli aequalis peripheriae trigoni, et hic circulus nec est circumscriptus nec inscriptus, sed pariter circumscriptus et inscriptus.
5. Sunt et qui circuli quadraturam negant, et hi omnia iam dicta negant. Aiunt enim argumentum in mathematicis non procedere: Ubi est dare magis et minus, quod ibi sit dare aequale. Nam dabilis est angulus incidentiae maior recto et alius minor recto, et tamen numquam aequalis. Unde in quantitatibus incommensurabilibus hoc non procedit. Si enim daretur angulus incidentiae maior recto parte aliquota recti et minor recto parte aliquota recti, daretur et aequalis. Sed cum angulus incidentiae non sit proportionalis recto, non potest esse aut maior aut minor parte aliquota recti, igitur neque umquam aequalis. Et cum inter superficiem circularem et rectilinealem non possit cadere proportio, sicut nec inter angulum incidentiae et angulum rectum, igitur argumentum etiam ibi non procedit.
6. Hoc sic patet: Omnis quantitas in aliam resolubilis necessario sic se habet, quod quaelibet eius pars possit esse pars alterius, cum totum non sit nisi suae partes. Sed lunula per rectam de circulo abscisa non est secundum angulos suos incidentiae, qui sunt partes quantitatis eius, in rectilineam resolubilis; igitur nec secundum eius totalitatem. Manifestum est autem, si circulus est resolubilis in quadratum, necessario sequi lunulas resolubiles in rectilineales; et cum hoc sit impossibile, igitur et illud, ex quo sequitur. Sic patet semicirculum non esse rectilineabilem, et per consequens nec circulum aut aliquam eius partem.
7. Omnis angulus incidentiae excedit alium aut exceditur ab alio per quantitatem anguli rectilinei, ad quem non potest habere proportionem. Hinc evenit, quod omnes abscisiones circuli per lineas rectas sunt ad illum penitus improportionales, et cum maior abscisio sit per [semi] diametrum, tunc omnes aliae abscisiones ad illam sunt improportionales. Non potest igitur aliqua pars circuli per tales lineas abscindi, quando nullam habet proportionem ad maiorem abscisionem, scilicet semicirculum. Sic non valet argumentum: Abscinditur lunula maior tertia circuli et lunula minor tertia parte circuli, ergo et aequalis. Ex quo evenit, quod abscisiones, quae fiunt per rectam lineam minorem diametro, non sunt ex eo nequaquam rectilineabiles, quia sunt partes aliquotae circuli, sed quia sequeretur circuli quadratura, si forent rectilineabiles.
8. Ex quo elice omne id impossibile, ex quo sequitur circuli quadratura. Habet igitur circulus hoc ex singularitate sua, quod sicut angulus incidentiae non est rectilineabilis, sic nec circulus est in figuram rectilinealem reducibilis. Sed sicut datur angulo incidentiae angulus rectilineus maior per angulum contingentiae, qui angulus contingentiae est quantitas in suo genere tantum divisibilis, quoniam omni angulo contingentiae est dabilis alius contingentiae maior ac minor, tamen, cum angulus contingentiae sit minor omni angulo rectilineo, sic dato incidentiae datur rectilineus maior, qui tamen non est maior aliqua parte aliquota rectilinei anguli; sic dato rectilineo datur incidentiae angulus minor, scilicet quantum est angulus contingentiae, qui tamen non est pars aliquota incidentiae, sed minor omni parte aliquota eius.
9. Tali quidem modo dici potest dato circulo posse dari quadratum, quod etsi fuerit maius circulo, non tamen aliqua parte aliquota eius, scilicet quadrati; et dato quadrato potest dari circulus minor eo, non tamen minor parte aliquota circuli. Et consequenter ex hoc habetur, quod licet dato circulo posset dari quadratum maius, non tamen parte aliquota eius maius; et quod quocumque quadrato tali dato adhuc possit dari aliud praecisius circulo, licet nullum praecisissimum, et nullum minus circulo parte aliquota eius, ita et e converso.
10. Et hanc partem puto veriorem. Nam cum figurae polygoniae non sint eiusdem generis quantitatis cum figura circulari, tunc, etsi reperiatur una polygonia dato circulo quoad quantitatem aequalior quam alia, habebit tamen regula locum: In recipientibus maius et minus non deveniri ad maximum simpliciter in esse et posse. Capacitas enim circularis est quod maximum simpliciter in comparatione ad capacitates polygoniarum, quae recipiunt maius et minus et ideo eam non attingunt, sicut numeri non attingunt capacitatem unitatis et multiplicitates non attingunt virtutem simplicis.
11. Sufficere autem videbatur primam opinionem tenentibus, quod dato circulo posset dari quadratum, quod non esset nec maius nec minus circulo. Omne enim maius aut est parte aliquota aut sui aut alterius, cui comparatur, maius; sic, si minus. Sed cum quadratum, quod datur, neque minima dabili parte aut quadrati aut circuli est circulo aut maius aut minus, hoc vocarunt aequale. Eo enim modo ceperunt aequale, ut scilicet id sit alteri aequale, quod nulla parte aliquota, quantumcumque minima, aliud excedit aut exceditur. Sic aequale capiendo puto verum esse, quod datae peripheriae polygoniae dabilis sit peripheria circuli aequalis et e converso. Capiendo vero aequalitatem absolute, prout respicit quantitatem, absque respectu ad partes aliquotas, tunc, quia circulari quantitati non potest non circularis praecise aequalis assignari, secundi verum dixerunt, et hoc per declarationem principii propositionis, scilicet: Si datae peripheriae trigoni etc. Sic dixisse sufficiat. Per quae intelligas ea, quae de hac re in certis aliis libellulis meis varie scripta reperies.
Declaratio propositionis
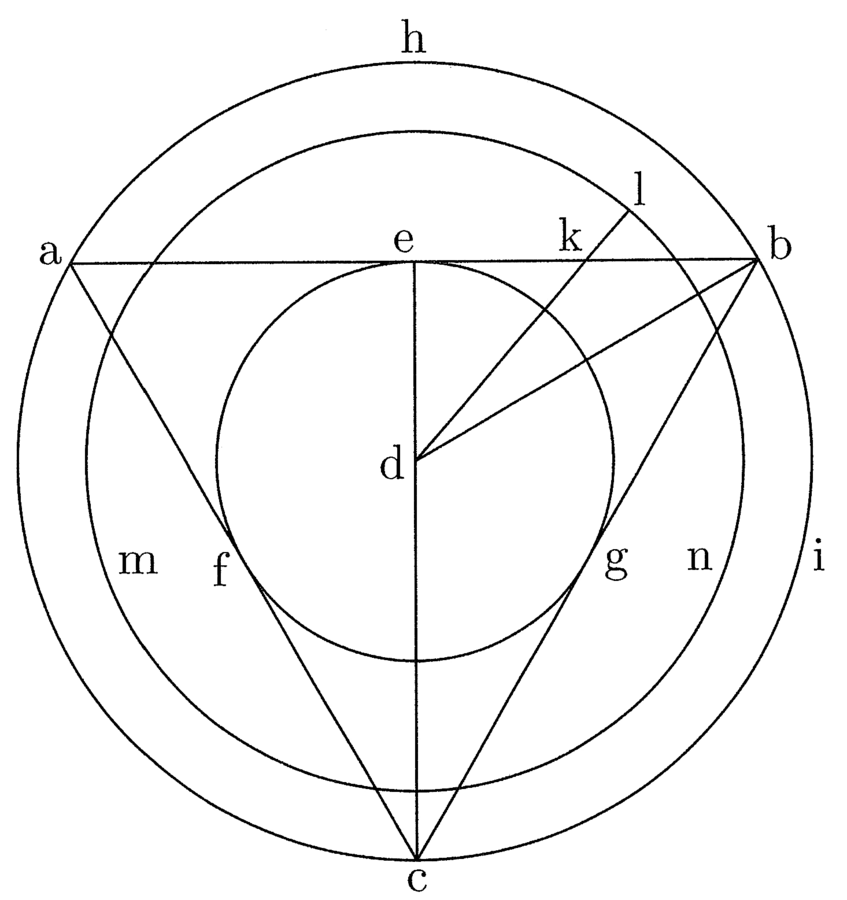
12. Ad declarandum autem propositionem fiat trigonus abc, cui inscribatur circulus super d centro, qui sit efg, et circumscribatur circulus hi; ducaturque linea de sic, quod e sit punctus medius inter a et b, et ducatur linea db. Ducaturque linea de d ad punctum medium inter e et b, quae sit dk. Dico dk esse minorem semidiametro circuli isoperimetri trigono, quantum est quarta ipsius dk (cfr. figura 1).
13. Addatur igitur quarta ad dk, et sit dl maior dk per quartam dk. Dico, quod dl est semidiameter circuli isoperimetri trigono. Describatur igitur circulus, qui sit lmn. Dico peripheriam lmn aequalem peripheriae abc, sic scilicet, quod lmn non est nec maior nec minor quacumque minima parte aliquota ipsius peripheriae abc.
14. Ad hoc ostendendum sic procedo et dico quod, si de d ad eb linea duci debet, quae sit semidiameter circuli isoperimetri trigono, oportet, quod illa se habeat ad omnia latera trigoni simul sumpta sicut semidiameter circuli ad circumferentiam. Sed cum semidiameter ad circumferentiam nullam penitus habeat proportionem, nec in quantitate nec in potentia, scilicet cum area quadrati semidiametri, quae est potentia semidiametri, nullam habeat proportionem ad aream circuli, neque etiam ad aream quadrati potentiae lineae aequalis circumferentiae, si dabilis foret, proportionem haberet. Patet, quod nec quaesitae lineae quantitas aut potentia esse potest proportionalis lineae de aut db, quarum potentiae sunt proportionales ad potentiam eb. Unde linea illa non potest duci de d ad partem aliquotam eb aut aliquotam db, sic quod punctus terminalis eius, qui distabit ab e versus b, non poterit distare per lineam ab e, quae sit proportionalis ad eb vel db; quia, si sic, semper esset potentia proportionalis eb, ut de se patet. Unde non est assignabilis punctus in eb, ad quem si duceretur, haberetur praecise quaesita. Sed bene est punctus in eb, ad quem si duceretur, linea illa non foret nec maior nec minor parte aliquota quacumque minima quaesita. Dico consequenter, quod, sicut nulla linea, quae de d ad eb duci potest ad partem aliquotam eb, potest esse quaesita, sic etiam nulla talis potest esse proportionalis ad quaesitam, ut de se patet, cum omnium illarum potentiae sint potentiae lineae eb proportionales.
15. Dico deinde, quod licet nulla talium sit praecise proportionalis quaesitae, una tamen erit magis proportionalis quam alia. Et hoc patet. Nam etsi omnes sint improportionales ad de et eb, tamen adhuc una est magis proportionalis ad eb et db quam alia, et ideo minus proportionalis ad quaesitam. Unde illa ex omnibus, quae est maxime improportionatis ad eb, de et db, illa est minime improportionalis ad quaesitam. Una igitur erit inter omnes ducibiles de d ad partes eb minus improportionalis quaesitae.
De adinvestigando proportionalem
16. Ad investigandum vero proportionalem est advertendum, quod inter lineas improportionales habent se aliquae ut costa et diameter, et numquam potest proportio adeo praecisa reperiri, quin sit excessus maior parte aliquota: ut una decima diametri minor est una septima costae, et excessus est maior parte aliquota diametri et costae, et ita in quibuscumque minimis partibus.
17. Alia est improportio ut angulorum incidentiae et rectilinei. Nam linea se habens ut angulus incidentiae est improportionalis ad lineam se habentem ut angulus rectilineus, et medietas rectilinei est maior medietate incidentiae per quantitatem medietatis contingentiae; quae tamen medietas minor est omni parte aliquota, tam rectilinei anguli quam incidentiae.
18. Quod autem talis habitudo sit reperibilis in lineis, ex hoc videtur: Nam cum angulus sit superficies et linea sit terminus superficiei, patet, quod eo modo, quo angulus contingentiae est superficies divisibilis, sic suo modo et eius terminus, scilicet linea angulum illum superficialem terminans. Similiter linea terminans anguli rectilinei superficiem linea est divisibilis secundum divisibilitatem superficiei. De linea igitur, quae terminat superficiem anguli rectilinei, potest abscindi linea terminans angulum contingentiae, et ideo linea terminans angulum incidentiae est improportionalis ad lineam terminantem angulum rectilineum per lineam terminantem angulum contingentiae. Unde cum haec linea terminans angulum contingentiae sit minor omni parte aliquota lineae rectilineum aut incidentiae angulum terminantis, patet propositum.
19. Et in hoc notare poteris, quomodo ante omnem divisibilitatem lineae rectae est linea inattingibilis per omnem divisibilitatem, qua linea recta rectam secare potest. Quae tamen etsi non sit divisibilis divisione, qua linea recta per rectam dividitur, in cuius respectu est ut punctus terminalis inattingibilis, est tamen suo modo per curvam divisibilis. Unde linea illa, quoniam est terminus superficiei, et divisibilis linea dicitur, licet in comparatione ad lineam, quam terminat punctus, indivisibilis appareat. Sicut enim divisibilitas superficiei terminatur in linea, quae in respectu ad superficiem est indivisibilis, quoniam non est superficialiter divisibilis, tamen linea ipsa terminalis superficiei in se considerata quantitas divisibilis est, ita divisibilitas rectae lineae per rectam terminatur in punctum, qui est terminus divisionis et lineae, et est rectilinealiter indivisibilis in quantum terminus lineae, in se tamen est quantitas divisibilis. Est igitur possibile unam lineam esse alia minorem aut maiorem, non tamen aliqua parte aliquota aut maiori aliquota, sed minori. Ex quo elicere potes, quid de lineis et punctis indivisibilibus sentiendum.
20. Dico igitur, quod etsi possit de d ad eb linea proportionalis ad quaesitam trahi, ita quod excessus non sit maior parte aliquota, non tamen potest trahi talis, quin excessus sit licet minor parte aliquota. Deinde dico, quod etsi innumerabiles tales trahi possent, tamen una praecisior alia, nulla vero praecisissima.
21. Videamus igitur, quam talium potest humanum ingenium de omnibus attingere. Manifestum est autem, quod si linea, quae debet esse proportionalis quaesitae, extenditur secundum quamcumque partem eius aliquotam, puta tertiam eius aut quartam aut aliam, semper manet proportionalis. Si igitur linea ipsa extenditur secundum habitudinem lineae, quae cadit inter terminum eius in eb et e, ad lineam ab aut secundum habitudinem lineae inter terminum eius in eb et b ad lineam ab, semper manet proportionalis. Aut igitur habitudines illae sunt tales, quod secundum aliquam ipsarum devenitur ad quaesitam, aut non. Si non, tunc per ipsam lineam, quam praesupponimus proportionalem ad quaesitam ignotam, nihil de quaesita scire poterimus. Nam cum quaesita sit ignota et extensio non ducat nos ad eam, sed ad maiorem vel minorem ea, quam ignoramus, non poterimus excessum scire quaesitae penitus ignotae.
22. Si dixeris per alteram extensionem ad quaesitam perveniri et non per ambas, idem erit, quia ignoramus, per quam et ubi linea illa cadat, cum de illis possint cadere infinitae inter e et b. Si dixeris aequales fore extensiones et tamen aut minores aut maiores quaesitae ignotae, iterum ad quaesitam numquam deveniretur.
23. Necesse est igitur proportionalem, per quam humanum ingenium hoc modo procedendi se iuvare potest, ut veniat ad quaesitam, eam esse, quae per ambas aequales extensiones sive unam sive aliam quaesitam ostendit; et haec est linea, quae ducitur de d ad medium inter e et b, puta f. Et haec est sola illa, quae per habitudinem unam, qua se habet altera linearum distantiae ab e vel b ad ab extensa, scilicet quartam sui, nos ducit ad quaesitam, modo quo sic procedendo est nobis possibile attingere, etiam si in aliis procedendi modis alia praecisior posset reperiri.
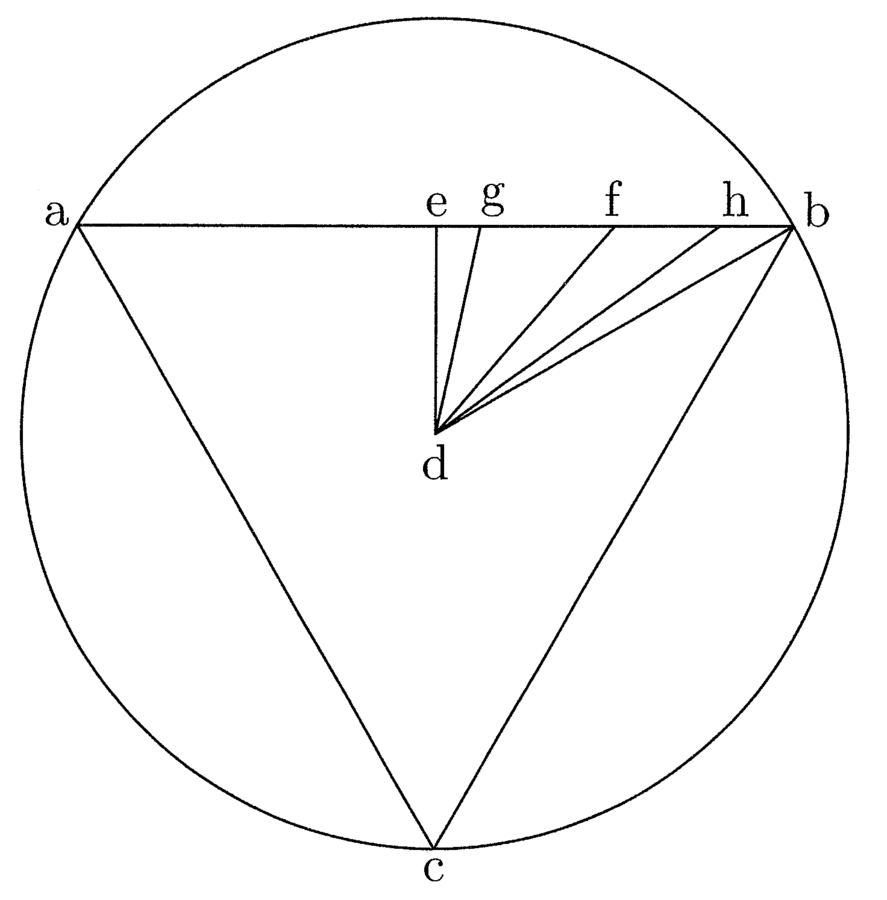
24. Verum ne penitus hanc putes puram esse coniecturam, ita quod humanum ingenium nulla ratione alia ad hanc assertionem ducatur, facere poteris syllogismum, qui hoc casu extra ultimam praecisionem et citra differentiam minimae partis aliquotae admittitur (cfr. figura 2). Nam cum de d prope e linea, puta ad g, tracta et extensa secundum habitudinem eg ad ab sit minor quaesita, et similiter extensa secundum habitudinem gb ad ab etiam sit minor quaesita; et alia linea de d prope b, puta h, tracta et secundum habitudinem eh ad ab extensa sit maior quaesita, et similiter secundum habitudinem hb ad ab extensa sit maior quaesita, ut est hinc inde notorium: igitur est alia de d ad eb trahibilis, quae secundum lineae inter terminum eius et e cadentis habitudinem ad ab extensa non est maior nec minor quaesita. Et est similiter linea de d trahibilis ad eb, quae extensa secundum habitudinem lineae inter terminum eius et b cadentis ad ab non est maior nec minor quaesita. Sed quia illae duae lineae, ex quarum extensionibus quaesita evenire debet, non possunt esse diversae, cum diversae lineae de d ad eb trahibiles non possint habere aeque praecisam proportionem ad quaesitam, sed una semper erit praecisior alia: ideo nec extensae secundum varias habitudines suarum partium ad eas ad eandem quaesitam aequaliter attingere possunt. Necesse igitur erit, quod sit una tantum linea et extensio eadem, quod extra f punctum non est possibile. Quare omnis sufficientia, quae in hoc procedendi modo sciri potest, est illa, quae ponitur in propositione sic declarata.
25. Quoniam autem nunc tibi id, quod est scibile de aequalitate peripheriarum curvilinealium et rectilinealium figurarum, patefeci – scilicet, quomodo verius quod in hoc scitur est, aequalitatem sciri non posse, atque etiam quod id, quod propinquissime sciri potest in hoc, est per propositionem brevem revelatum –, tunc desiderio tuo, quantum potui, satisfeci. Nam scito hoc: Habes modum omne mathematice scibile investigandi. Omnis enim propositio in mathematicis, per quam sequitur praecisa aequalitas circuli et quadrati, est impossibilis, et omnis propositio, per cuius contrarium inferretur praecisio, est necessaria. Immo assero, quod qui in mathematicis scit omnem inquisitionem ad hoc reducere, perfectionem adeptus est artis illius. Nam nihil penitus in ea verum est, ex cuius opposito non sequitur circuli et quadrati aequalitas, et haec est omnis mathematicae inquisitionis sufficientissima resolutio.
26. Id autem, quod sine praecisione citra tamen omnem sensibilem aut assignabilem errorem etiam minimae partis aliquotae sciri potest in transmutationibus figurarum et habitudinibus innumerabilibus, ex iam dictis etiam patefeci. Per quae habes, quomodo habitudo diametri circuli ad circumferentiam eius est ut duarum radicum numeri 1575 cum medietate unius radicis ad sex radices numeri 2700. Et licet non sit praecisissima, non tamen est nec maior nec minor per minutum aut minuti quamcumque dabilem partem. Unde sciri non potest, quantum a praecisione ultima deficiat, cum non sit communi numero attingibilis. Et hinc iste defectus non est reparabilis, cum non nisi alto intellectu et nequaquam sensibili experimento sit attingibilis. Scire ex solo isto nunc potes, quod in non scibili praecisius attingitur, quam scientiam hactenus traditam non repperi.
27. Attendere autem praeter hoc utile videtur, quod, uti hoc casu vides, per unum, puta quadratum, non attingi aliud, scilicet circulare, aut e converso adeo praecise, quin praecisius attingi possit, etiam si defectus nequaquam appareat. Ita in omni inquisitione veri, ubi per unum ad aliud sciendum pergimus, per notum scilicet ad ignotum, idem fore sentiendum, scilicet verum varie et differenter attingi citra praecisionem ultimam, quoniam per unum praecisius quam per alium, per nullum vero praecisissime, licet defectus non appareat; quoniam mensura, qua homo pergit ad veri inquisitionem, est vero improportionalis, et hinc ille, qui citra praecisionem quietatur, errorem non apprehendit. Et haec est differentia hominum, quoniam quidam se praecisionem attigisse iactant, quam sapientiores inattingibilem sciunt, ut hi sint doctiores, qui suae ignorantiae scientiam habent.
28. Admonebam in exordio, ut via assimilationis de his mathematicis ad theologiam te transferres, nam hic est convenientior modus ascendendi. Versantur enim mathematicae doctrinae in veris intelligentiis, quoniam figuras in sua veritate absque variabili materia considerant. Unde ad formam primam, quae est formarum forma penitus absoluta, illis figurarum multiplicitatibus inferius relictis quadam assimilatione facilius scanditur. Nam omnes theologi quandam quaerunt praecisionem, quomodo circularem aeternitatem, unissimam et simplicissimam, possint attingere. Sed vis infinita est incommensurabilis per omne non infinitum, sicut capacitas circularis per omnem non circulum incommensurabilis manet.
29. Sicut igitur circulus est perfectio figuralis omnem figurarum perfectionem in se complicans, sicut eius capacitas omnium figurarum capacitatem, et nihil commune habet cum omni figura alia, in se penitus simplex et una: sic aeternitas absoluta est forma omnium formarum in se complicans perfectionem, et eius vis omnipotens omnem vim formarum, omnem speciem ambiens, nihil tamen commune habens cum omni alia forma. Et quemadmodum circularis figura in eo, quia sine principio et fine, quandam habet assimilationem aeternitatis, et in sua capacitate, qua omnes omnium figurarum capacitates includit, quandam habet figuram omnipotentiae, et in sua connexione, qua circumferentia unitur capacitate, habet quandam figuram amorosissimi et infiniti nexus: ita quidem in essentia divina intuemur aeternitatem in se habentem omnipotentiam atque in his infinitum nexum. In aeternitate quidem intuemur principium sine principio, et hoc quidem principium paternum dicimus. In omnipotentia, quae est a principio sine principio, intuemur principium illimitatum a principio. In infinito nexu intuemur principii sine principio et principii a principio amorosissimum nexum. In hoc enim, quod in divina essentia intuemur aeternitatem, intuemur patrem. In hoc, quod in eadem essentia intuemur aeternitatis potentiam, quae non potest esse nisi infinita, cum sit potentia aeternitatis, principii scilicet sine principio, in hoc intuemur aequalitatem unitatis aeternae, scilicet filium patris. In hoc, quod intuemur aeternae unitatis et suae aequalitatis nexum amorosissimum utriusque, spiritum intuemur. In unitate igitur simplicissima aeternitatis vigorosissimam et omnipotentissimam aequalitatem intuemur, ac e converso in aequalitate unitatem, similiter et in nexu unitatem et aequalitatem. Sine aeternae entitatis unitate nihil esse potest. Sine illius unitatis aequalitate nihil sic esse uti est esse potest. Sine infinito nexu esse et simul sic esse uti est nihil esse potest. Sine unitrino igitur principio nihil esse potest.
30. Haec assimilantur in circulo, et eius capacitate atque strictissimo nexu, quo circulus est maxime sibi ipsi constrictus, cohaerens atque naturaliter unitus esse videmus. Post haec advertimus, quod cum omnes polygoniae figurae sint ex peripheria, capacitate et nexu ad imaginem circularis figurae, et omnis peripheria polygoniae sit cadens a peripheria circuli, et omnis capacitas polygoniae improportionabiliter deficiens a capacitate circuli, et similiter omnis nexus utriusque – quod sic etiam se habent species rerum sensibilium ad formam formarum, ut species harum sensibilium rerum sint in comparatione ad deum quasi ut trigoni, tetragoni, pentagoni et ita consequenter ad circulum comparati.
31. Quaelibet autem polygoniarum quandam habet diffinitam perfectionem, extra quam nec est nec esse potest. Trigoni enim esse extra triangularitatem nequaquam esse potest; ita de tetragono et ceteris. Quiescit igitur sic omnis species inter ambitum suum, qui sub sua clauditur peripheria, et extra ipsum nec esse potest nec appetit. Desineret enim omne esse trigonum, si in tetragonum pergeret, uti de se notissimum est. Unde ad interitum suum nulla species ex sua natura, qua habet esse et sic esse, moveri potest, quare in terminis suae specificae naturae quiescit. Et haec quies est sua, quia infra peripheriam suae perfectionis vim divinam suo habet modo, in qua amoroso nexu deliciatur.
32. Mensurat igitur omnis sensibilis species suo quodam modo aeternitatem, virtutem et nexum amoris infinitum, licet in mensurando nihil habeat proportionale, cum omnis polygonia multiangula sit diminutae virtutis et capacitatis, parvi nexus et unionis, quae ad circularem aeternitatis unitatem, capacitatem inexhauribilem ac infinitam connexionem nihil proportionis habere potest, etiam si omne id, quod habet, eo habeat modo, ut in triangulari aut tetragona natura virtus circularis potest participari. Haec est igitur habitudo specierum sensibilium ad formam formarum, quae est polygoniarum ad circulum. Deinde, cum multi sint modi essendi trigoni, quoniam alter est trigonus rectiangulus, alter acutiangulus, alter obtusiangulus, cadentque in singulis talibus varii essendi modi in variabili materia, et hi omnes modi sunt contractiones individuales. Species enim in se vere consideratae sic cadunt in variabili materia variabiliter. Nam trigonus verius figuratur et perfectius in auro quam aqua aut labili alia materia, et adhuc verius intelligitur quam figuretur in quacumque materia.
33. Unde ex hoc advertimus, quomodo omnes polygoniae possunt inscribi circulo ac quomodo in circulo sunt omnes meliori modo quam ut sunt in materia, quoniam ibi sunt circulus. Et in hoc videmus, si omnes polygoniae possunt inscribi circulo sensibili et circulus aeternitatis sit actus omnis possibilitatis, quod tunc, sicut omnes polygoniae possunt circulo sensibiliter inscribi, ita sunt actu omnes species in specie seu forma aeternitatis ipsa forma aeterna. Et sicut in nostra mente verius esse habet trigonalis forma quam in variabili materia, ita in aeterna mente seu verbo verius esse habent omnes rerum species, ubi sunt ipsa aeterna veritas, quam in individuali varietate.
34. Adhuc progredientes advertimus circulorum varietatem, quodque non potest esse nisi unus maximus, verissimus, in se subsistens, aeternus et infinitus circulus, ad quem per circulos quantos non ascenditur, quoniam in recipientibus magis et minus non devenitur ad maximum simpliciter. Et circa hunc infinitum circulum mira et indicibilia consideramus, quae alibi diffusius tacta sunt.
35. Unde dicimus esse naturas circulares, quae non possunt esse sui ipsius principium, quia non sunt ut circulus maximus simpliciter, qui solus est ipsa aeternitas. Alii autem circuli, licet non videantur habere principium et finem, prout considerantur via abstractionis a sensibili circulo, tamen, quia non sunt ipsa infinita aeternitas, tunc sunt circuli, quorum esse est ab ipso infinito primo aeterno circulo, et sunt circuli illi in comparatione ad polygonias eis inscriptibiles quasi aeternitas quaedam atque simplicitas perfecta. Habent enim capacitatem improportionabiliter excedentem capacitatem omnium polygoniarum, et sunt infiniti circuli primi prima imago, licet ob infinitatem primi sint ad ipsum incomparabiles. Et sunt naturae, quae habent motum quendam circularem et infinibilem circa essentiam infiniti circuli, in se vim omnium aliarum specierum complicantes et ex sua vi complicativa via assimilationis alias omnes species explicantes, et in se omnia intuentes atque se imaginem infiniti circuli contemplantes per ipsamque imaginem, hoc est se ipsas, ad veritatem aeternitatis seu exemplar ipsum elevantes. Hae sunt naturae intellectuales vi sua intellectuali cuncta ambientes.
36. Conantur autem omnes figurae, quantum possunt, capacitatem aeternae veritatis mensurare. Sed sicut finiti ad infinitum nulla est proportio, sic manet deus super omnem inquisitionem praecisio incognita, ut ipse sit non solum incognitus, sed ipsa praecisio incognita, quae in nullo cognoscibili cognoscitur. Nititur enim quaelibet creatura deum suum intra limites suae naturae definire; sicut si trigonus vellet circulum trigonare et tetragonus tetragonare, et ita de polygoniis, sic et natura intellectualis intelligere. Sed quamvis deus ipse, qui non habet partes, cum sit simplicitas infinita, non sit parte aliquota excedens omnem mensurandi modum specifice varium, tamen sic excedit omnem magnitudinis mensuram, quod est omni inquisibili modo maior. Et sic excedit omnem subtilium mensurarum, minutissimas fractiones, eo quod est omnium talium fractionum subtilior, ut neque in ascensu neque descensu praecisio eius attingi possit.
37. Sufficit autem omni naturae, quod in sua specie deum modo, quo potest, attingat. Tunc enim quiescit, quando extra speciem suam eum nec quaerit nec esse apprehendit. Sufficientia igitur, qua ipsum in sua specie modo, quo potest, attingit, est quies eius, quoniam est satietas motus suae naturae.
38. Quod nobis assimilatorie declarat investigatio, quam fecimus in trigono, quem ad aequalitatem peripheriae circuli elevare studuimus. Et quievimus in modo uno, quem solum praecisiorem, licet deficientem, repperimus in trigonali elevatione ad aequalitatem circularem. Qui modus speciei tetragonali non conveniret; tamen, si suo modo ad aequalitatem circuli ascenderet, etiam si non foret praecisio, dummodo in sua specie alius perfectior non foret tetragonus, se quietem attigisse gauderet. Ita de ceteris.
39. Sic quietatur omnis intellectus, si modo, quo suae speciei conceditur, se senserit ad aequalitatem infinitatis elevari divina praecisione semper inaccessa remanente. Talia quidem et alia infinita per te elicere poteris. Haec sic tetigisse sufficiat. Amen.