Chapter structure
- [LIBRO PRIMO]
- Prima proposizione
- Seconda proposizione
- Terza proposizione
- Quarta proposizione
- Quinta proposizione
- Sesta proposizione
- Settima proposizione
- Ottava proposizione
- Nona proposizione
- Decima proposizione
- Undicesima proposizione
- Dodicesima proposizione
- Tredicesima proposizione
- [LIBRO SECONDO]
- Note a piè pagina
1. È talmente grande la potenza del Tuo pontificato, Niccolò V, beatissimo padre1, che coloro che hanno considerato attentamente la sua forza l’hanno paragonata al potere di rendere quadrato ciò che è tondo e di rendere circolare ciò che è quadrato, quasi che non si potesse dare una [forza] più grande. E poiché tu non solo possiedi la chiave e la potenza del sapere e della suprema gerarchia ecclesiastica, ma, grazie alla tua acutissima intelligenza, sei un eccellente maestro di impareggiabile fama in tutti i campi del sapere, sarai tu a giudicare tra tutti. Grazie alla tua straordinaria diligenza hai fatto moltissimo affinché gli scritti di tutti gli autori che possono essere reperiti, sia latini sia greci, pervenissero a noi tutti con la massima cura, così come non hai trascurato le opere di geometria, che erano state considerate dai nostri antenati degne di ogni onore2.
2. E, infatti, nei giorni scorsi mi hai dato gli
scritti di geometria del grande Archimede
[LIBRO PRIMO]
3. Secondo tutti coloro che si sono dedicati allo
studio della geometria, nessuno più di Archimede
4. Innanzitutto bisogna dire che, in una figura
avente più angoli, cioè in un poligono che ha lati uguali7, il punto equidistante dalla metà e dall’estremità dei
lati si chiama centro, e la linea condotta da questo centro al
punto medio del lato è il semidiametro del cerchio ad esso
inscritto, ed è detta prima linea. E l’altra linea condotta dallo
stesso centro fino all’estremità di un lato, cioè, a un angolo
qualsiasi, è il semidiametro del cerchio circoscritto in essa ed è
detta seconda linea. In ogni poligono queste due linee sono di
diversa lunghezza e lo sono tanto più quanto più lungo è il lato.
Infatti, il quadrato8 della seconda linea include il quadrato della prima e
con ciò il quadrato della metà del secondo lato, e questo perché
il lato del triangolo rettangolo è opposto all’angolo retto, come
dimostra Euclide
5. E poiché la prima delle figure rettilinee10 è il triangolo, in esso la prima e la seconda linea hanno lunghezze massimamente diverse. Tuttavia nel cerchio coincidono, poiché qui il centro si trova a uguale distanza dalla circonferenza; e infatti, la metà e l’estremità del lato coincidono, e c’è un angolo ovunque11. Tuttavia, nel triangolo la prima linea è la più corta, la seconda la più lunga. Nel quadrato12 avente lo stesso perimetro13, la prima linea è la più corta dopo la prima del triangolo e la seconda è la più lunga dopo la seconda del triangolo e così via. E poiché in tale quadrato la prima è più lunga della prima nel triangolo, se si moltiplica la prima nel quadrato per la metà del perimetro e, similmente, la prima nel triangolo per la stessa metà [del perimetro], è evidente che si ottengono diverse superfici che sono uguali ai poligoni14(cfr. figura 1).
6. Perciò l’eccesso di quella superficie, che risulta dal prodotto della prima del quadrato per la metà del perimetro, sulla superficie che risulta dal prodotto della prima del triangolo per la stessa metà del perimetro, è [uguale] all’eccesso dell’ampiezza15 del quadrato sull’ampiezza del triangolo, e così, in tutti i poligoni, dall’eccesso della prima linea di un qualsiasi poligono sulla prima del triangolo isoperimetrico si trova l’eccesso dell’ampiezza di questo stesso poligono sull’ampiezza del triangolo. Inoltre, quanto minore è la differenza tra la prima e la seconda linea, tanto maggiore sarà l’eccesso della prima linea del poligono sulla prima del triangolo. E poiché nel cerchio la prima e la seconda coincidono, l’eccesso del semidiametro del cerchio isoperimetrico sulla prima del triangolo è massimo, e perciò l’ampiezza del cerchio è massima rispetto all’ampiezza del triangolo16. Perciò, la stessa linea retta, che nel triangolo è estesa lungo i tre lati per formare il perimetro di questa superficie, nel quadrato si estende lungo i quattro lati, formando il perimetro del quadrato, e [si estende] ancora di più nel pentagono. Se tuttavia si estende al massimo, tanto da non potersi estendersi ulteriormente, allora sarà la circonferenza del cerchio17.
7. Da quanto detto è chiaro che se il triangolo ha l’ampiezza minima, la prima linea si differenzia al massimo dalla seconda, e se il cerchio ha l’ampiezza massima, la prima e la seconda linea coincidono, e così sarà, con le debite proporzioni, nei poligoni intermedi18. Di conseguenza, se si pone che l’eccesso dell' ampliezza del cerchio sul triangolo è uguale alla differenza tra la prima e la seconda linea nel triangolo, l’eccesso dell'ampliezza del cerchio sul quadrato sarà uguale alla differenza tra la prima e la seconda linea nel quadrato e così via di conseguenza: a un maggiore eccesso della prima linea dell’uno sulla prima linea dell’altro consegue infatti nel [poligono] maggiore una differenza tra la prima e la seconda [che è] minore rispetto alla differenza tra la prima e la seconda nel [poligono] minore. Da ciò, dati l’eccesso della prima di un qualsiasi [poligono] sulla prima del triangolo e la differenza tra la differenza della prima e la seconda del [poligono] più ampio e quella della prima e la seconda del triangolo, si può facilmente ottenere il semidiametro del cerchio isoperimetrico, la cui circonferenza cioè è uguale alla somma dei tre lati del triangolo o a quella dei quattro lati del quadrato.
8. Compreso ciò, la quadratura del cerchio
risulta evidente. Infatti, se si moltiplica il semidiametro di
questo cerchio isoperimetrico per la metà della circonferenza
risulta un rettangolo19 che non può essere né maggiore né minore della
superficie del cerchio, come Archimede
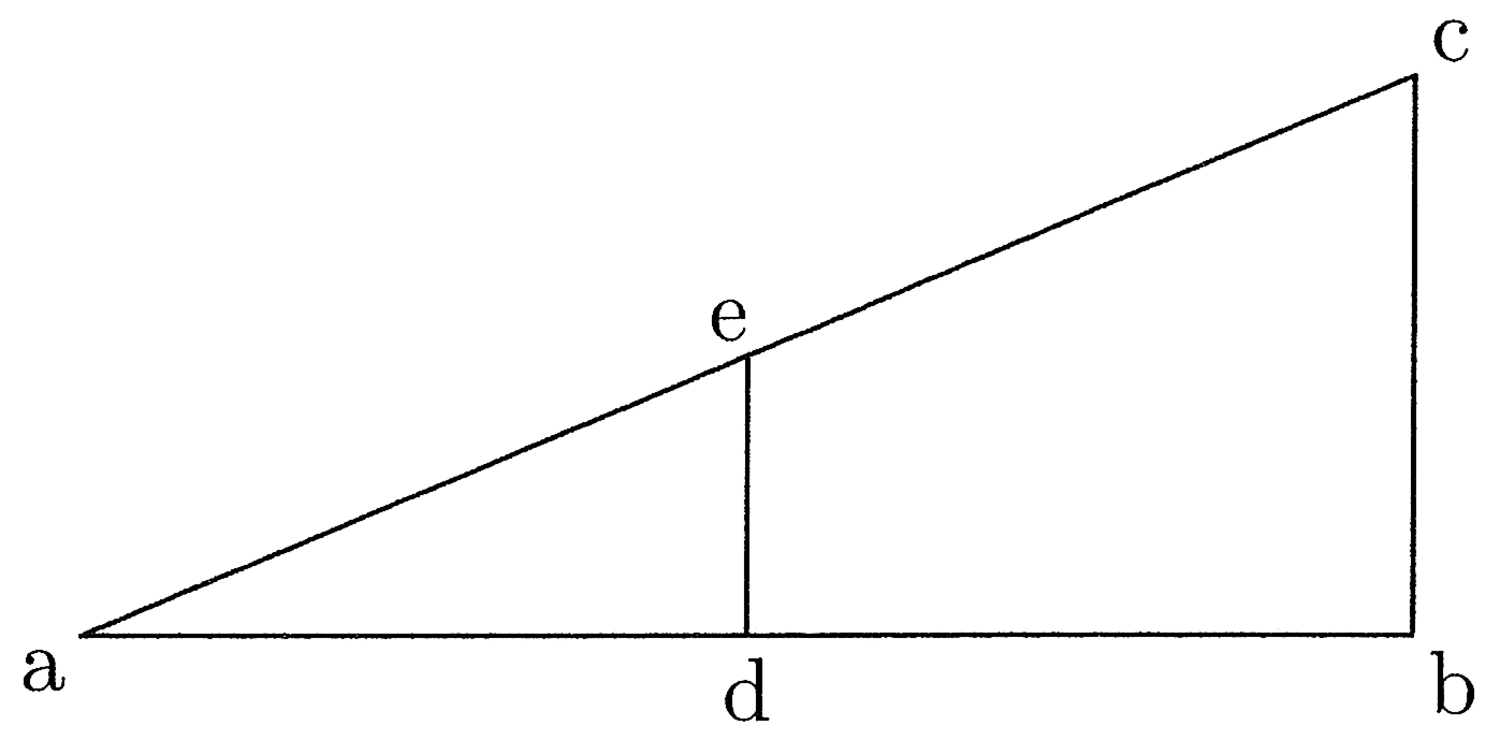
9. Se si moltiplica una linea retta per una linea retta, si ottiene una figura di quattro angoli retti e se la si moltiplica per una doppia linea, si ottiene una figura doppia, e così di seguito. Se si traccia una linea retta da un angolo all’altro, questa sarà la diagonale23 perché li divide in due (cfr. figura 2).
Se si moltiplica ab per bc, si ottiene il quadrato ABCD avente quattro angoli retti. Se si moltiplica ab per be, che è il doppio di bc, si ottiene il rettangolo ABEF che è il doppio di ABCD. E senza dubbio ac è la diagonale, così come lo è anche ae.
Prima proposizione
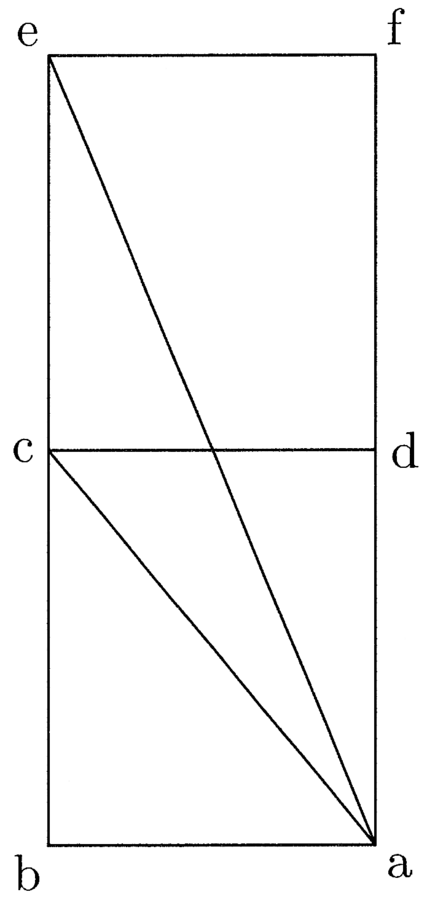
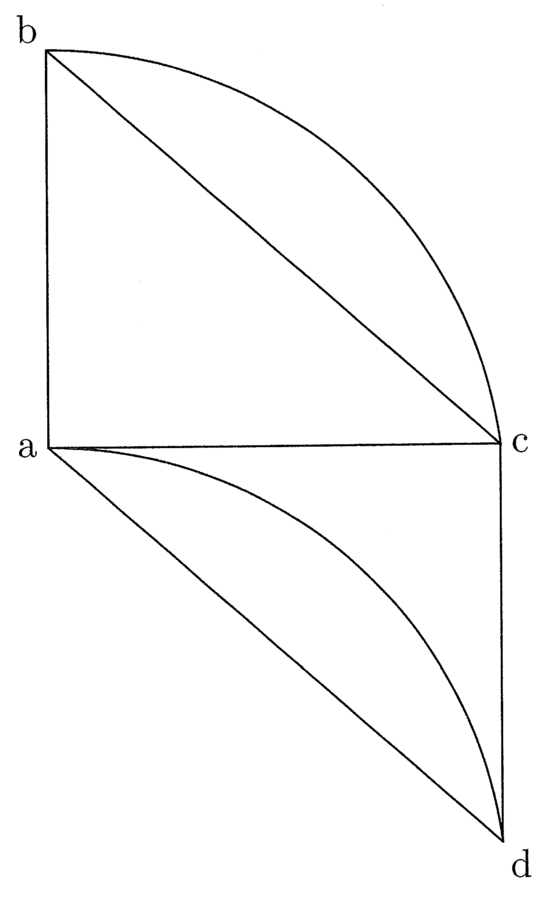
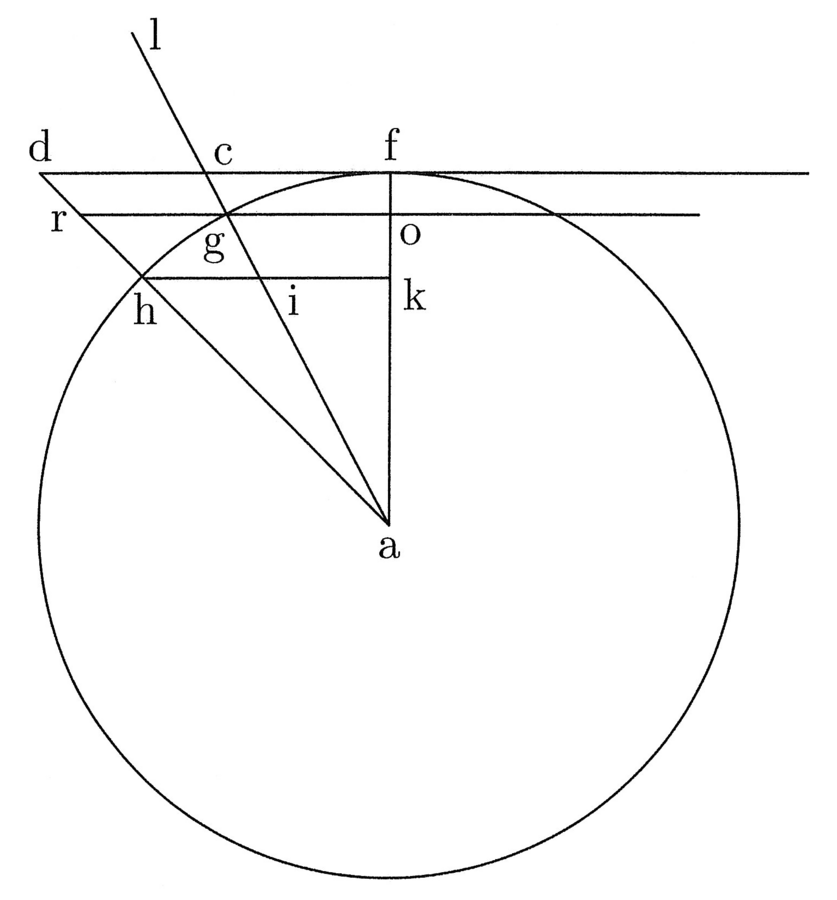
10. Il prodotto della prima linea per la metà del perimetro è uguale a due poligoni24.
Sia ABCD un quadrato di quattro angoli retti e quattro lati uguali. In esso è inscritto un cerchio attorno al centro e in modo che tocchi i quattro lati del quadrato nel punto medio. Si tracci da e fino al punto in cui il cerchio tocca ab la linea ef, che è la prima poiché è il semidiametro del [cerchio] inscritto, si tracci la linea eb e anche la linea da e fino al punto in cui il cerchio tocca il lato bd e sia questa eg. Si raddoppi fb in modo da ottenere fh, e, allo stesso modo, si raddoppi eg così da ottenere ei. Si chiuda il rettangolo con la linea hi e si tracci la diagonale eh. Da quanto premesso è chiaro che i triangoli EFB e EBH sono uguali. Il primo, infatti, è la metà del primo quadrato, poiché eb è la diagonale, e il triangolo EFH è la metà del secondo rettangolo – che è il doppio del primo [rettangolo] – poiché eh è la diagonale (cfr. figura 3).
11. Il triangolo EBH sarà, dunque, uguale a EFB. Si raddoppino le linee fh e ei, e sia fk il doppio di fh ed el il doppio di ei; si chiuda il rettangolo con la linea lk. Poiché il triangolo EFB è l’ottava parte del quadrato ABCD, il rettangolo EFKL sarà uguale al quadrato ABCD. Ma fk è uguale alla metà del perimetro del [quadrato] ABCD, ossia è uguale alla [somma di] due lati del quadrato, e la prima linea ef è moltiplicata per la metà del perimetro, di conseguenza la proposizione è valida. Come nel quadrato, ciò è evidente nello stesso modo in tutti i poligoni: tutti, infatti, si risolvono in tanti doppi triangoli rettangoli quanti sono i lati; e così si procede nello stesso modo come sopra detto.
Seconda proposizione
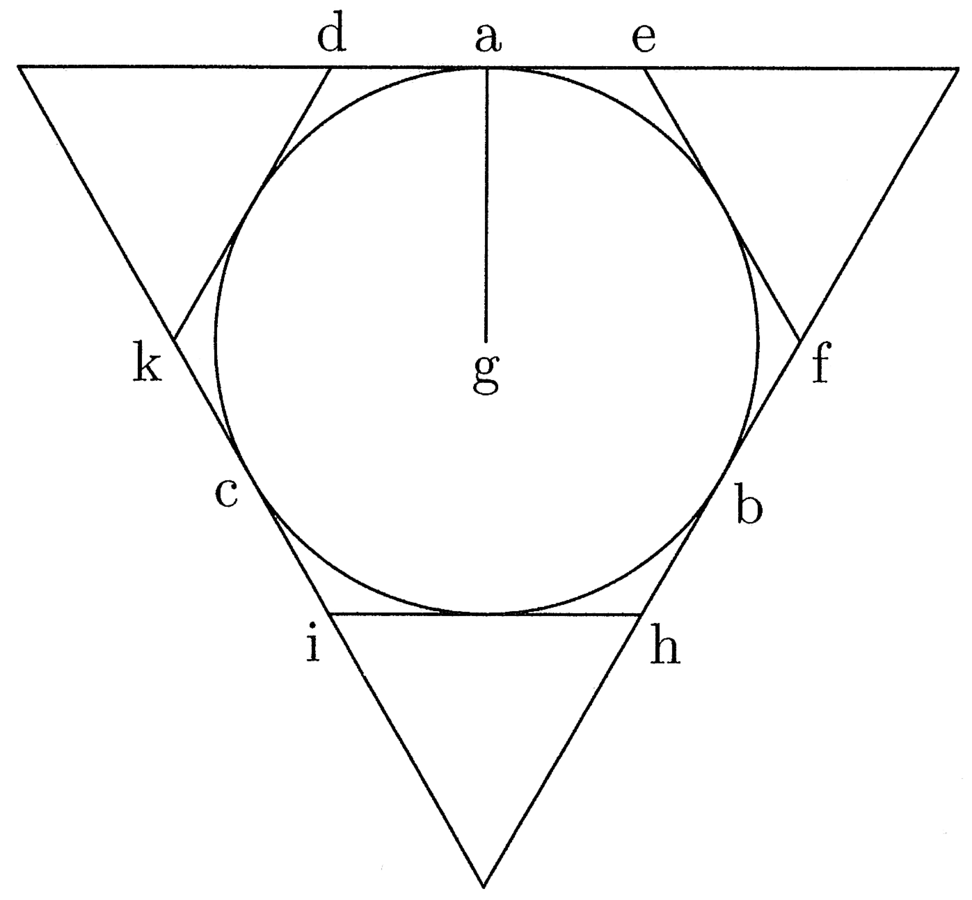
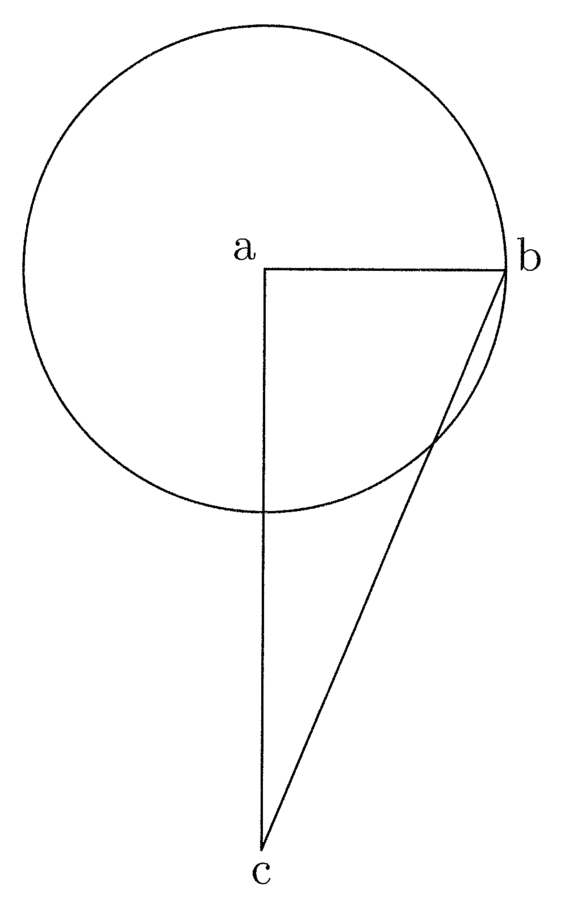
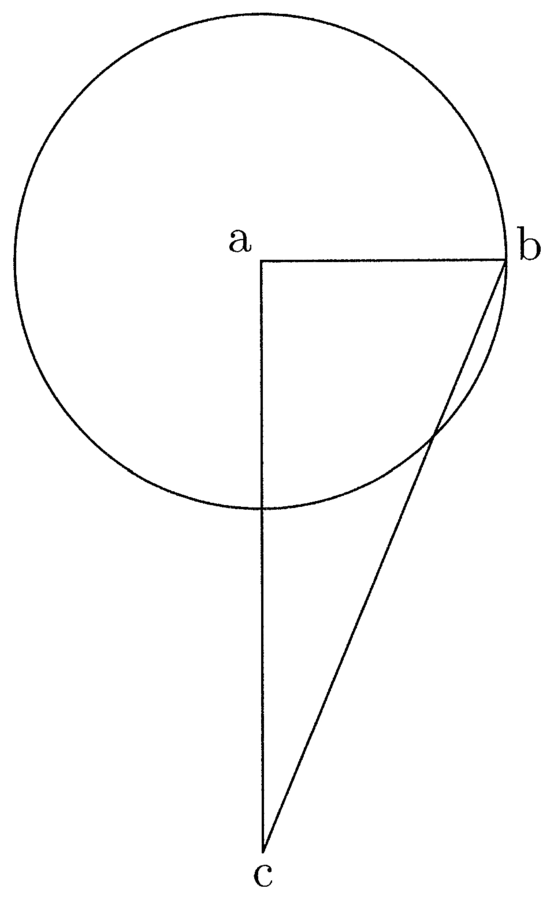
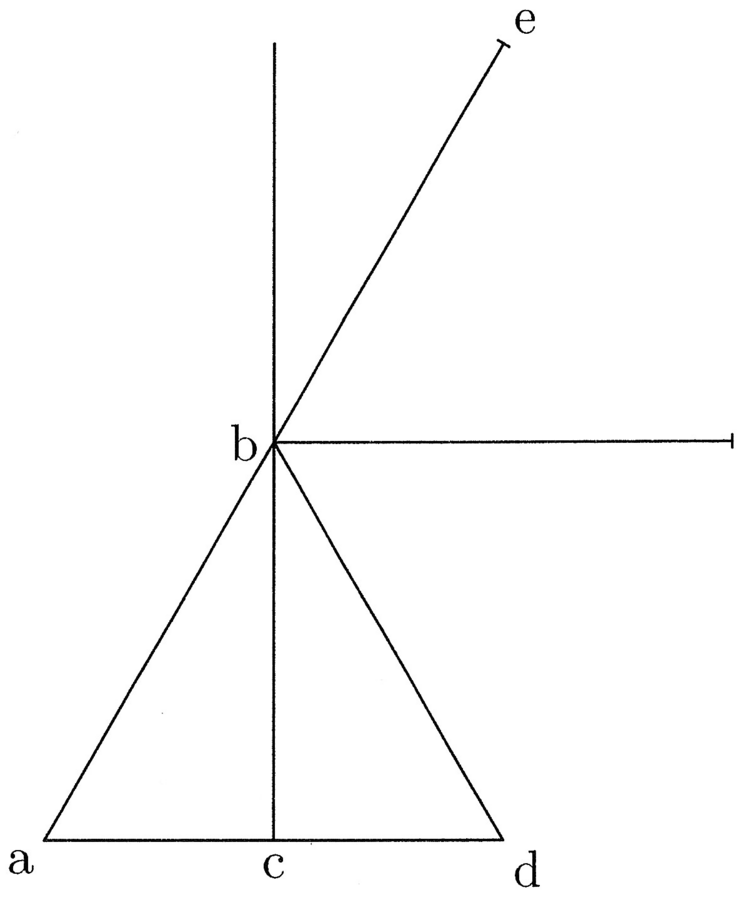
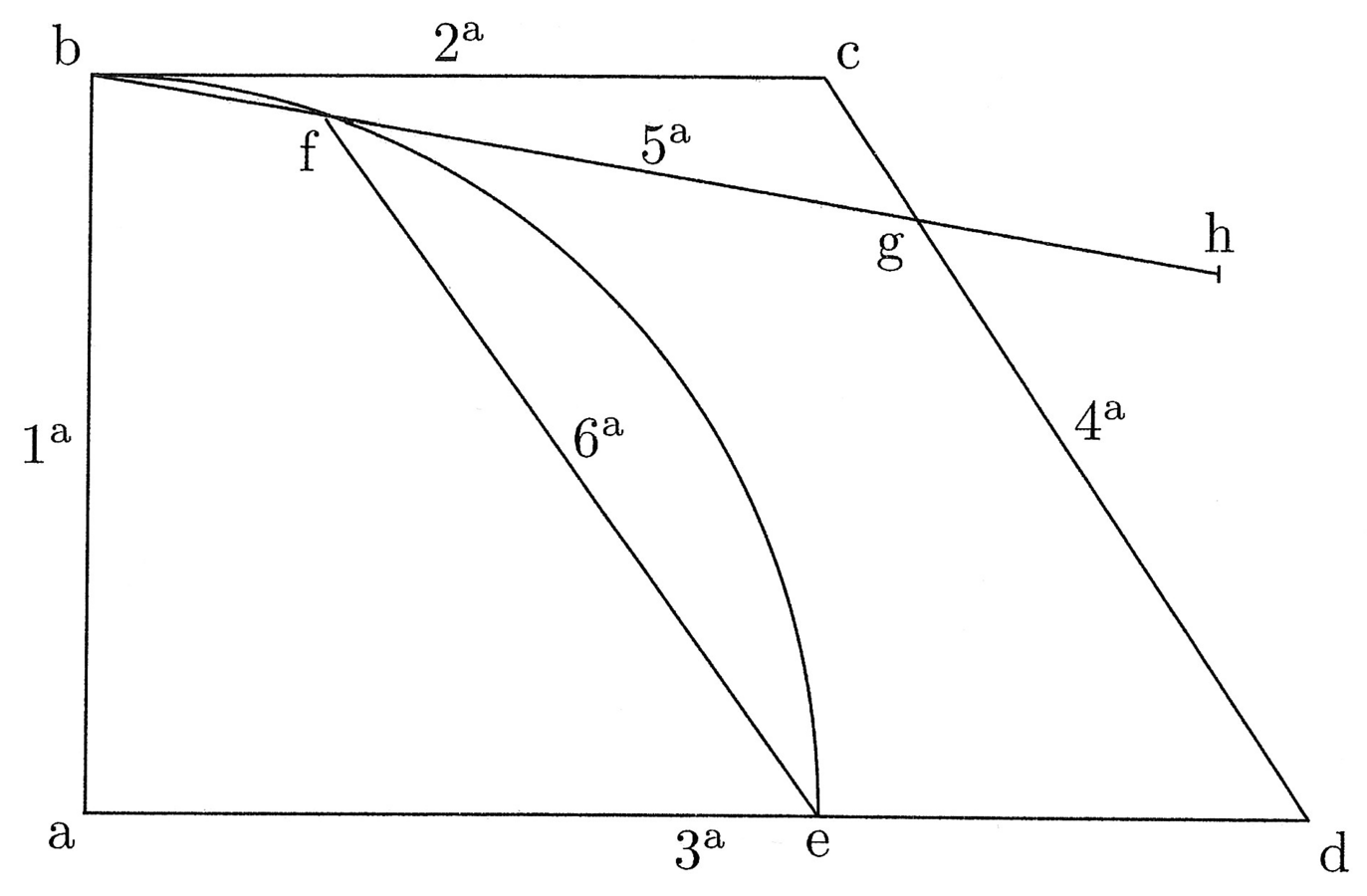
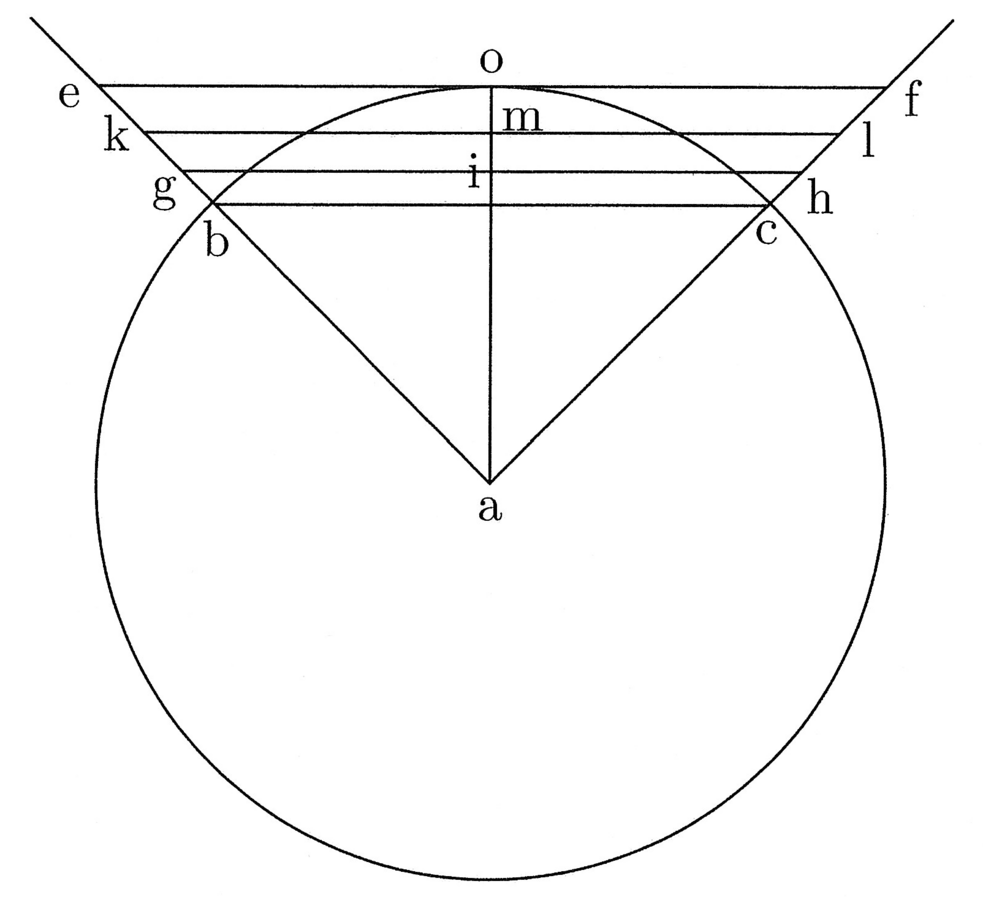
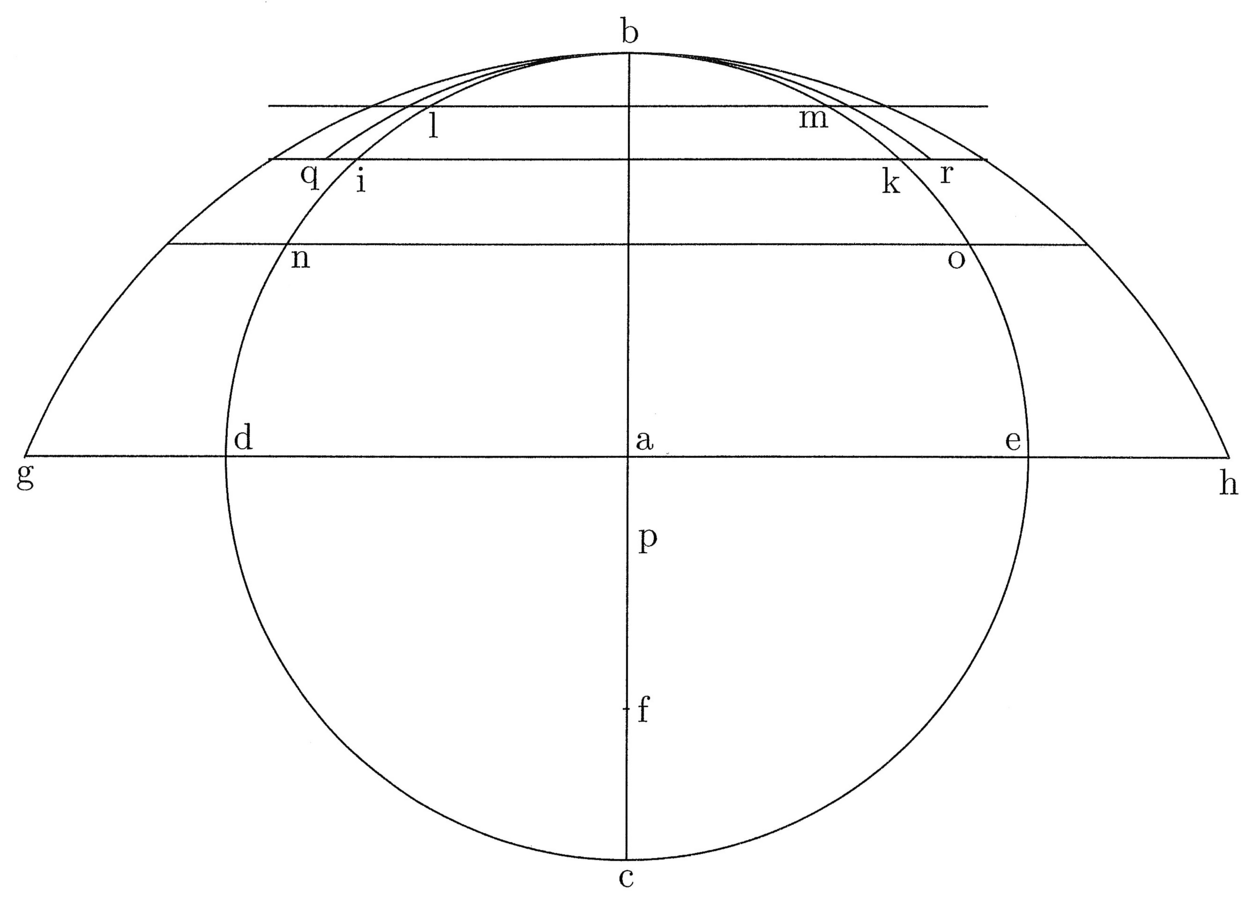
12. Il perimetro di un poligono circoscritto a un cerchio è maggiore della circonferenza del cerchio, e lo è tanto più quanto meno lati esso avrà; accadrà il contrario se [il poligono] sarà inscritto nel cerchio (cfr. figura 4).
Siano circoscritti al cerchio il triangolo ABC e l’esagono DEFHIK e dal centro g si tracci il semidiametro del cerchio ga che sarà la prima [linea] del triangolo e dell’esagono. Se dunque si moltiplica ag per la metà del perimetro del triangolo si ottiene un rettangolo uguale al triangolo. La superficie, ossia l’area25 del triangolo, include l’area del cerchio inscritto.
13. L’area del cerchio sarà quindi minore, perché la circonferenza del cerchio è minore del perimetro del triangolo, e così anche il perimetro dell’esagono è minore del perimetro del triangolo e la circonferenza del cerchio è minore del perimetro dell’esagono; di conseguenza la proposizione è valida. Nei poligoni inscritti accade il contrario, giacché l’area del cerchio è maggiore. Di conseguenza il rettangolo uguale26 ad esso si genera moltiplicando il semidiametro per una linea, che sarà più lunga della metà del perimetro di qualsiasi poligono inscrivibile. L’area del cerchio, quindi, include l’area dell’esagono inscritto e quella dell’esagono l’area del triangolo. La circonferenza del cerchio sarà dunque quella maggiore, poi verrà il perimetro dell’esagono, quindi quello del triangolo, e così via in tutti gli altri poligoni.
Terza proposizione
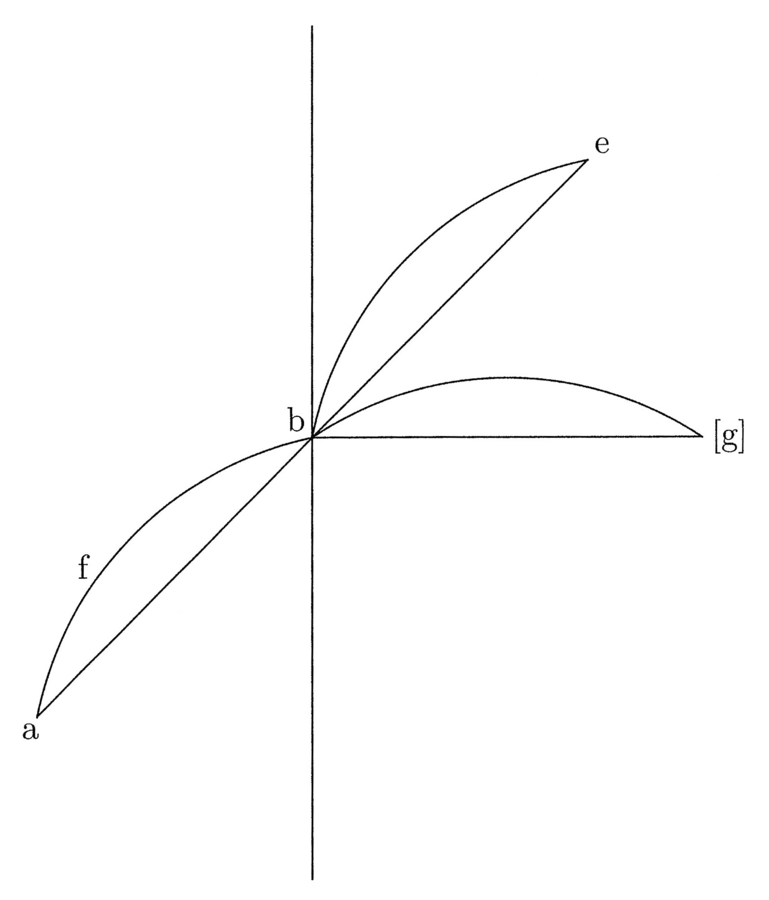
14. Tra linee rette e linee circolari la minore è quella che è sottesa all’altra, e tra linee diverse, la linea sottesa, che è minore, è quella che meno è superata da quella alla quale è sottesa27.
La terza parte della circonferenza del cerchio, che è sottesa al lato del triangolo, è minore del lato e, allo stesso modo, la sesta parte della stessa circonferenza che è sottesa al lato dell’esagono è minore [del lato]. Poiché in questo caso il perimetro dell’esagono è minore del perimetro del triangolo, di conseguenza la sesta parte della circonferenza del cerchio è superata, in proporzione, dal lato dell’esagono meno di quanto la terza parte [della circonferenza del cerchio] è superata dal lato del triangolo. Così, la terza parte della circonferenza del cerchio supera, in modo proporzionale, il lato del triangolo inscritto più di quanto la sesta parte superi il lato dell’esagono inscritto.
Quarta proposizione
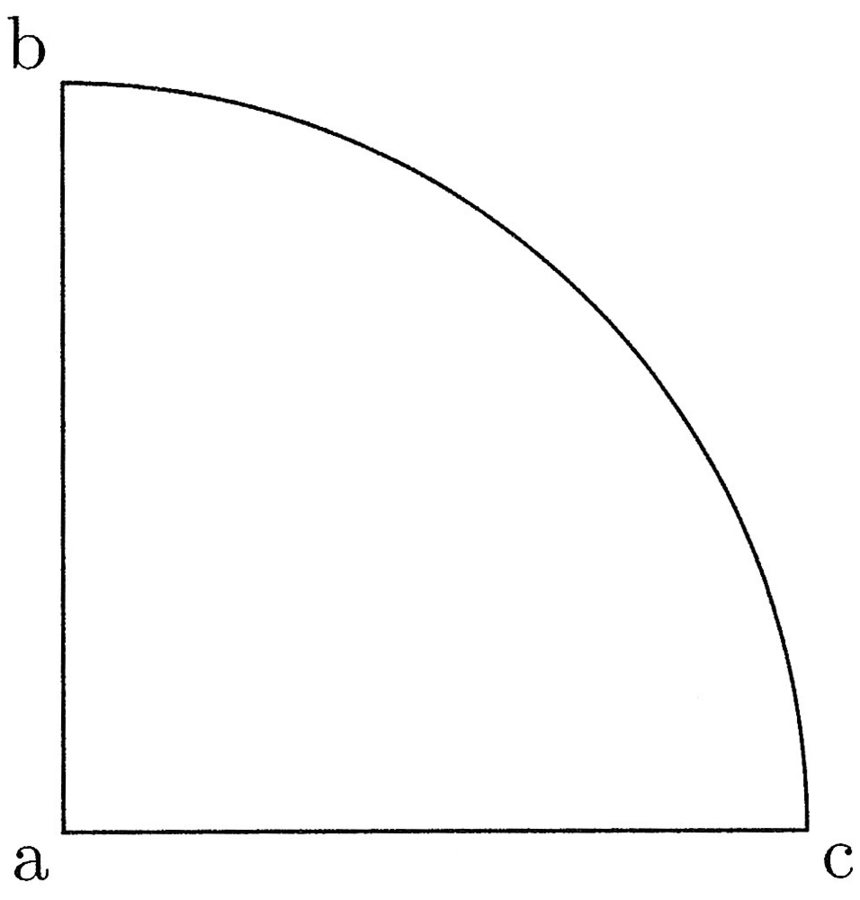
15. Il cerchio avente la circonferenza uguale al perimetro di un poligono è maggiore del cerchio inscritto in esso e minore di quello circoscritto, ed è tanto più simile28 ad essi quanto più sono i lati del poligono.
È evidente. Infatti, il lato del poligono è minore dell’arco al quale è sotteso, che è l’arco [della circonferenza] del cerchio circoscritto, e maggiore dell’arco che lo sottende, che è l’arco [della circonferenza] del cerchio inscritto. E poiché [il cerchio] inscritto e quello circoscritto sono tanto più simili quanto più sono i lati del poligono, allora saranno così anche più simili al cerchio isoperimetrico.
Quinta proposizione
16. Tra un qualsiasi poligono inscritto e un cerchio può cadere un numero infinito di poligoni maggiori del poligono [dato] e minori del cerchio. Allo stesso modo, tra un poligono circoscritto e un cerchio, [può cadere un numero infinito di poligoni] minori del poligono e maggiori del cerchio.
Ciò è evidente dalla divisione all’infinito di ciò che è continuo mediante parti proporzionali29. Data, infatti, la corda di un qualsiasi arco, la corda del semiarco sarà minore. Così all’infinito. Le corde sono i lati dei poligoni [inscritti]. Lo stesso vale per i lati dei poligoni circoscritti, perché, se si dà il lato di un poligono circoscritto a cui è sotteso l’arco, si darà il lato minore al quale è sotteso il semiarco e così all’infinito.
Sesta proposizione
17. [L’area del] rettangolo che si ottiene moltiplicando il semidiametro per la semicirconferenza del cerchio non è né maggiore né minore dell’area del cerchio30.
È evidente da quanto detto sopra. Infatti, il perimetro di un poligono circoscrivibile è maggiore della circonferenza del cerchio, così anche la sua area è maggiore dell’area del cerchio. Il perimetro di un poligono inscrivibile è minore della circonferenza del cerchio, e lo stesso accade per l’area. Quindi, il prodotto del semidiametro del cerchio per la metà della sua circonferenza è maggiore dell’area di ogni poligono inscrivibile e minore dell’area di ogni poligono circoscrivibile. E, poiché, data un’area maggiore di [quella di] un poligono inscritto e minore di [quella del] del cerchio, si può sempre dare un poligono inscrivibile [avente un’area] maggiore, allo stesso modo, data un’area maggiore di [quella del] cerchio, si può sempre dare un poligono circoscrivibile [avente un’area] minore. Quindi la proposizione è evidente.
Settima proposizione
18. L’ampiezza del cerchio supera quella di tutti i poligoni isoperimetrici31.
È evidente. Infatti, in tutti i poligoni la prima linea è minore della prima linea del cerchio e il perimetro è lo stesso in tutti. Quindi, moltiplicando la prima linea del cerchio per la metà del perimetro, risulterà [un’ampiezza] maggiore di quella di qualsiasi poligono isoperimetrico.
Ottava proposizione
19. L’ampiezza del triangolo isoperimetrico è l’ampiezza minima.
È evidente, dal momento che ha il lato maggiore. Dunque, esso supera la circonferenza [del cerchio] inscritto più di qualsiasi altro poligono. Di conseguenza, il cerchio inscritto in esso è minore di tutti gli inscritti; la sua prima linea è la linea minima e, quindi anche l’ampiezza è l’ampiezza minima.
Nona proposizione
20. Più lati ha un poligono, più esso è esteso32.
È evidente, perché, avendo i lati più corti ed essendo il quadrato della seconda linea uguale alla somma del quadrato della prima più quello della metà del suo lato, allora la prima e la seconda linea differiscono meno l’una dall’altra e sono più simili alla prima del cerchio isoperimetrico. Infatti, il lato corto è superato di meno dall’arco.
Decima proposizione
21. Nel poligono più esteso è necessario che la prima linea sia più lunga e la seconda più corta.
Si deduce da quanto premesso; infatti, essendo il cerchio inscritto in esso più simile al cerchio isoperimetrico, perché è più esteso e il cerchio isoperimetrico è il più esteso, allora la prima linea di quel poligono è più lunga e il suo lato è minore. Infatti, minore è il lato, meno è superato dall’arco, e, di conseguenza, più si avvicina al cerchio isoperimetrico. E poiché il lato è minore, allora la seconda linea differisce meno dalla prima e quindi è più simile alla prima linea del cerchio isoperimetrico; sarà, dunque, più corta [nel poligono] più esteso. Questa è la proposizione principale per scoprire ciò che cerchiamo.
Undicesima proposizione
22. Se si pone l’eccesso della superficie del cerchio sulla superficie del triangolo uguale alla differenza tra la prima e la seconda linea del triangolo, allora l’eccesso della superficie del cerchio sulla superficie del poligono intermedio tra il triangolo e il cerchio sarà uguale alla differenza tra la prima e la seconda linea di esso; e se si pone l’eccesso uguale alla metà (o a un’altra parte) della differenza tra la prima e la seconda linea nel triangolo, allora sarà così anche nei [poligoni] intermedi33.
Si ponga, per esempio, che l’eccesso della superficie del cerchio sulla superficie del triangolo sia uguale alla differenza tra la prima e la seconda [linea]34 e, numericamente parlando, siano la prima [linea] del triangolo [uguale a] 7, e la seconda [uguale a] 14. La differenza sarà 7. La prima [linea] del cerchio isoperimetrico sarà 14, dato che essa è maggiore della prima del triangolo della differenza, che è 7. Dico che la prima [linea] del cerchio sarà maggiore della prima [linea] di qualsiasi poligono intermedio di una quantità pari alla differenza tra la prima e la seconda [linea] di esso. Come nel quadrato, in cui la differenza è 4, la prima [linea] del cerchio eccede la prima del quadrato di 4. La prima [linea] del quadrato sarà, quindi, 10. Se dirai che il quadrato è più esteso del cerchio, allora la sua prima [linea] sarà più lunga. Sia essa uguale a 11; aggiungendo ad essa la differenza, otterrai 15. E poiché 15 supera 14, [il quadrato] sarà, da quanto premesso, meno ampio e dunque contemporaneamente più esteso e meno esteso. Accadrà la stessa cosa, se dirai che il quadrato è meno esteso. Se per esempio [la prima linea] è pari a 9, la seconda sarà 13, minore di 14, e di conseguenza, da quanto premesso, il quadrato sarà più esteso. Così risulterà contemporaneamente più esteso e meno esteso, il che è contraddittorio. Questa dimostrazione vale per tutti [i poligoni].
23. Considera che, se un poligono [alla prima linea] aggiunge una qualche parte35 di freccia, affinché risulti la prima [linea] del cerchio, tutti [i poligoni] aggiungono una [lunghezza] simile36. Per capirlo chiaramente, procedi così. È evidente, dalle premesse, che se la prima [linea] del poligono più esteso è maggiore di quella di uno meno esteso, essa sarà sempre minore della prima [linea] di qualche altro poligono, poiché tra un qualsiasi poligono, che è minore del cerchio, [e il cerchio], se ne possono dare infiniti altri più grandi. E così la prima [linea del poligono] è sempre minore della prima [linea] del cerchio. Allo stesso modo, se la prima [linea] di un poligono più esteso è minore della prima [linea] di uno meno esteso, essa sarà maggiore della seconda linea di qualche altro poligono e, in questo modo, maggiore della prima [linea] del cerchio. Dunque, se porrai che dalla somma di una parte di freccia con la prima [linea] del poligono risulta la prima [linea] del cerchio isoperimetrico, allora sarà necessario che ciò accada in qualsiasi poligono intermedio, aggiungendo alla prima [linea] la parte avente con la freccia un rapporto simile.
24. Per esempio, se aggiungendo due terzi della freccia del triangolo alla prima [linea] di questo si ottiene la prima [linea] del cerchio [isoperimetrico], lo stesso accadrà nel pentagono, nell’esagono e in tutti gli altri poligoni. Infatti, se dicessi che in qualche poligono la somma risultante è di più o di meno, ciò accadrà necessariamente perché è più esteso [rispetto al triangolo]. Quindi, se dicessi che è maggiore, ciò non è possibile; infatti, sarebbe necessario che fosse minore della prima [linea] del cerchio, e poiché la prima [linea] del cerchio è uguale alla somma della prima [linea] del triangolo e della suddetta parte di freccia, la somma sarebbe contemporaneamente maggiore e minore. Similmente, se dicessi che è meno esteso, sarebbe necessario dire che essa è contemporaneamente minore e maggiore.
25. Da ciò si evince pure chiaramente che, se due poligoni si rapportano in modo che la somma tra la parte simile di freccia e la prima [linea] di ciascuna dia lo stesso risultato, ciò accadrà necessariamente in tutti [i poligoni]37. Infatti, [poni il caso in cui] tra questi due poligoni ce ne siano altri, come tra il triangolo e il pentagono c’è il quadrato: in tal caso, è necessario che ciò che vale nel triangolo e nel pentagono valga anche nel quadrato. Infatti, se dicessi che la linea risultante [dalla somma] è maggiore [di quella nel triangolo] per la maggiore estensione del quadrato rispetto al triangolo, allora essa sarebbe anche minore [di quella nel pentagono], perché l’estensione del quadrato è minore di quella del pentagono. Dunque, se dicessi che, per la minore estensione [del quadrato rispetto al triangolo] la linea risultante [dalla somma] è minore, allora essa sarebbe anche maggiore e questo è impossibile. Lo stesso accadrebbe nel caso in cui i due poligoni si susseguissero senza che tra loro ci sia un poligono intermedio, come nel caso del triangolo e il quadrato, e nel caso in cui lo negassi nel pentagono. Allora, se dicessi che [la linea risultante] è maggiore a causa della maggiore estensione del pentagono, ciò non si potrebbe dire; infatti, il quadrato risulta più esteso dove [la linea risultante] non è maggiore; a maggior ragione, essa non sarà maggiore nel pentagono, ma piuttosto minore. Se dicessi che essa è minore sarebbe [ugualmente] sbagliato, dal momento che nel quadrato non è minore. È dunque evidente che ci sarebbe una contraddizione se negli altri poligoni non si ottenesse lo stesso risultato.
26. Da ciò segue che, se in due poligoni [dalla somma] tra una parte simile [di freccia] e la prima [linea] di ciascuno risulta la stessa linea nel suddetto modo, essa sarà il semidiametro del cerchio isoperimetrico. Infatti, poiché nel cerchio isoperimetrico la prima e la seconda linea sono un’unica linea, allora, se alle prime [linee] dei poligoni si aggiunge una qualche parte di freccia — sia che le linee aumentino sia che diminuiscano, sia che restino le stesse — l’ultima sarà sempre la prima del cerchio isoperimetrico. Per esempio, se aggiungo alle prime un quarto di freccia, allora esse saranno sempre maggiori e la massima sarà l’ultima e la prima del cerchio. Se aggiungo i tre quarti, saranno sempre minori e l’ultima sarà la minima e la prima del cerchio. E se aggiungo una parte tale che in due poligoni risulti la stessa linea, allora sarà così in tutti gli altri. Così, essendo l’ultima uguale alla prima, sarà una prima [linea] qualsiasi del cerchio. Da qui, è anche evidente che la superficie del cerchio supera la superficie di un qualsiasi poligono di una [lunghezza pari alla] linea che in quel [poligono] mantiene lo stesso rapporto con la propria freccia. E così, un qualsiasi poligono più esteso supera tutti i poligoni meno estesi di una [lunghezza pari alla] linea che, in un qualsiasi poligono, ha lo stesso rapporto con la propria freccia.
27. Si potrebbe dimostrare anche in un altro modo (cfr. figura 5).
Sia ab la seconda linea del triangolo e sia essa divisa [in due] da c; traccia da a, b e c le perpendicolari uguali a bc e chiudi la figura con la linea def. Poiché la prima linea del triangolo è ac, la prima del cerchio isoperimetrico sarà maggiore di fe: sia essa uguale a fh e sia eh due terzi di ed. Da h traccia la parallela a bd e sia questa hi; traccia ora la linea ch. È chiaro che se fh è la prima [linea] del cerchio isoperimetrico, allora le prime [linee] dei poligoni intermedi saranno maggiori di ac e minori di fh e che la prima [linea] del poligono più esteso sarà più simile a fh. È anche chiaro che, come la somma di ai e ih è uguale alla somma della prima [linea] del triangolo più la differenza tra la prima e la seconda di esso, che è la freccia del suo lato, e i due terzi della freccia, così, nello stesso modo, nei poligoni intermedi possono essere tracciate linee parallele ad ai, che terminano su ih e af. Queste, unite alla linea restante ih, sono uguali alla [somma] tra la prima linea del poligono intermedio, la freccia e i due terzi della freccia di ognuna, come è stato detto nel triangolo. Ed è cosa nota che meno esteso è il poligono, più lunga sarà la linea risultante da queste linee prese insieme, dal momento che il [poligono] meno esteso ha il lato maggiore e, quindi, la freccia, maggiore. Così queste due linee saranno le più lunghe nel triangolo, e le più corte nel cerchio isoperimetrico, giacché il cerchio non ha lati e, quindi, neppure frecce, per cui le due linee nei poligoni saranno un’unica linea nel cerchio.
28. Pertanto, dico che se tracci da h verso i la freccia di un poligono intermedio e dall’estremità della freccia tiri la linea parallela ad ai, allora la linea ch la taglierà in due parti, di cui la minore sarà una parte della freccia, e la maggiore la prima [linea] del poligono. Per esempio, sia hk la freccia del quadrato, si tracci da k la linea parallela a hf, e sia questa kl, e, nel punto in cui ch la taglia, poni m. Dico che km sarà due terzi di hk, il che è cosa nota da sé: infatti mh sta a kh come ci a ih. E dico che ml sarà la prima linea del quadrato. Se lo negassi, dicendo che il quadrato è o più esteso o meno esteso, per esempio più esteso, allora la sua prima [linea] deve essere maggiore di lm e dunque la somma di lk e kh è minore della somma della prima linea del quadrato, della sua freccia e dei due terzi della freccia, il che implica contraddizione. Infatti, se il quadrato deve essere più esteso, come tu dici, è necessario che la somma di lk e hk superi la somma della prima [linea] del quadrato, della freccia e dei due terzi di essa. Sarebbe altrettanto contraddittorio se dicessi che il quadrato è meno esteso. Infatti, in tal caso, è necessario che lm sia minore e che la somma di lk e kh sia maggiore della somma della prima [linea] del quadrato, della freccia e dei due terzi di essa. Lo stesso accade negli altri poligoni. Di conseguenza, è evidente che, se la prima [linea] del cerchio isoperimetrico supera la prima del triangolo di una parte aliquota38 della freccia del triangolo, essa supera anche la prima linea di qualsiasi poligono intermedio della parte aliquota simile della freccia di questo poligono, e dire qualcosa di diverso implica contraddizione.
Dodicesima proposizione
29. Il rapporto tra l’eccesso della superficie di un cerchio sulla superficie di un triangolo isoperimetrico e l’eccesso della superficie di un poligono intermedio sulla superficie dello stesso triangolo è uguale a quello tra la freccia del triangolo e la linea risultante dalla differenza tra la freccia del triangolo e la freccia del poligono intermedio39.
Se si pone l’eccesso della superficie del cerchio sulla superficie del triangolo pari a 7, [l’eccesso del]la superficie del quadrato sulla superficie del triangolo corrisponderà alla linea risultante dalla differenza tra la freccia del triangolo e la freccia del quadrato. Per esempio, se la freccia fosse uguale a 4, la superficie del quadrato sarà pari a 3. Questo corollario è evidente da quanto detto.
Tredicesima proposizione
30. Conoscendo l’eccesso della superficie di un qualsiasi poligono intermedio sulla superficie del triangolo isoperimetrico si conosce la superficie del cerchio isoperimetrico.
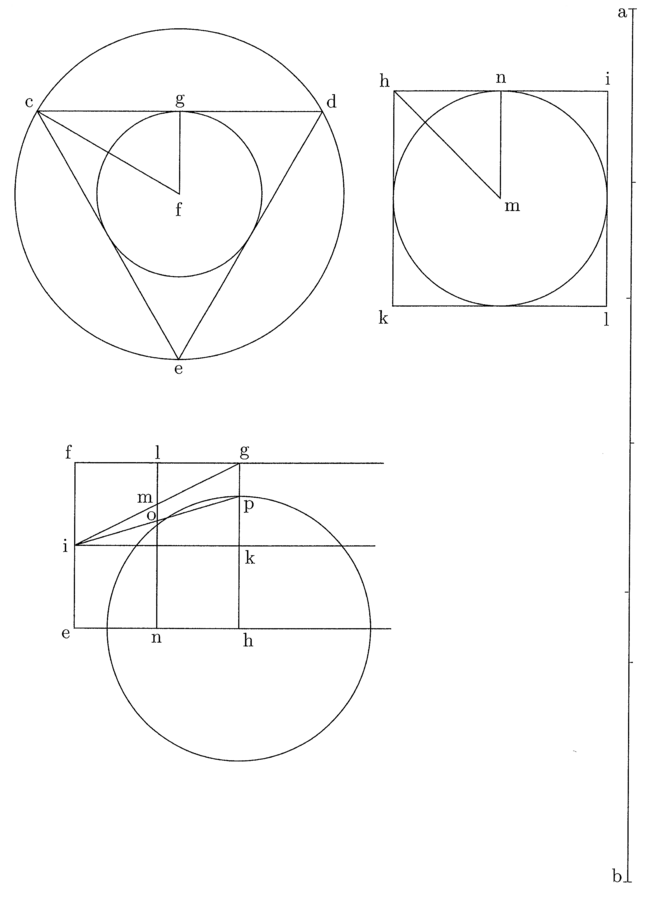
È chiaro che, se si conosce il rapporto, allora, una volta conosciuto un eccesso, si conoscerà anche l’altro. Ma poiché l’eccesso nel quadrato, nel pentagono, nell’esagono e in ogni altro poligono intermedio può essere conosciuto per mezzo della prima linea del triangolo e del poligono intermedio, allo stesso modo si conoscerà anche l’eccesso del cerchio isoperimetrico.
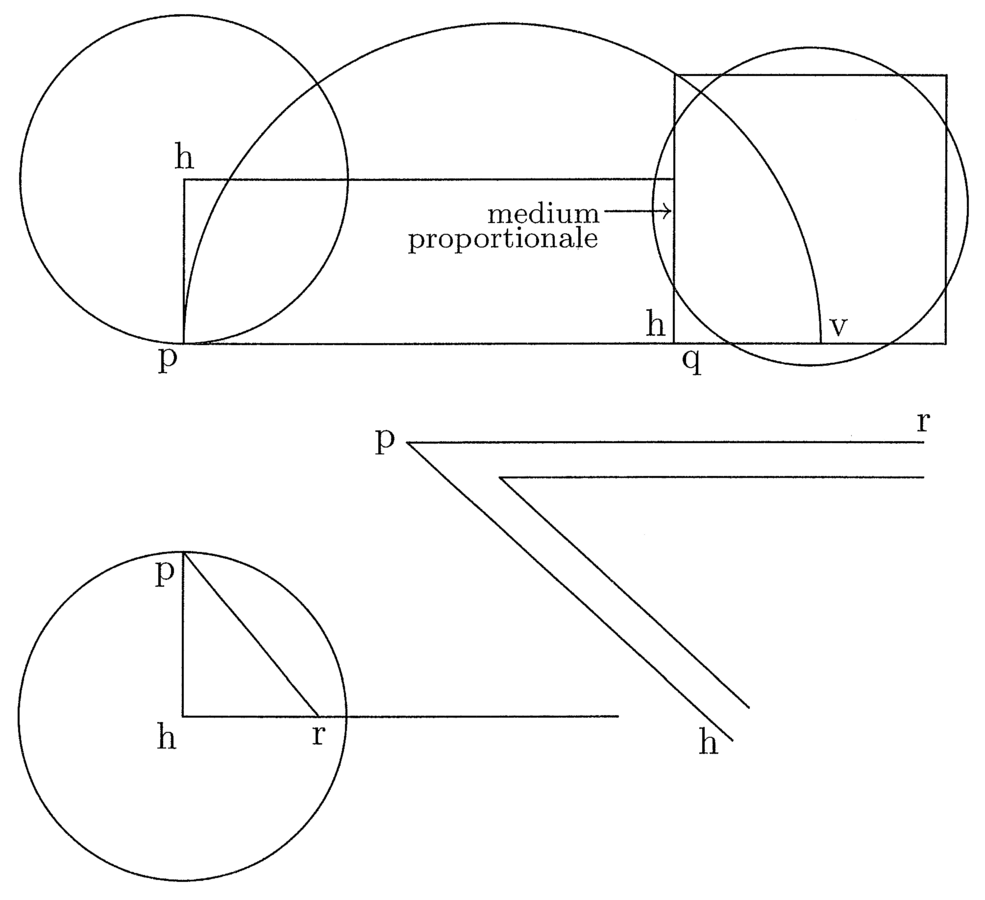
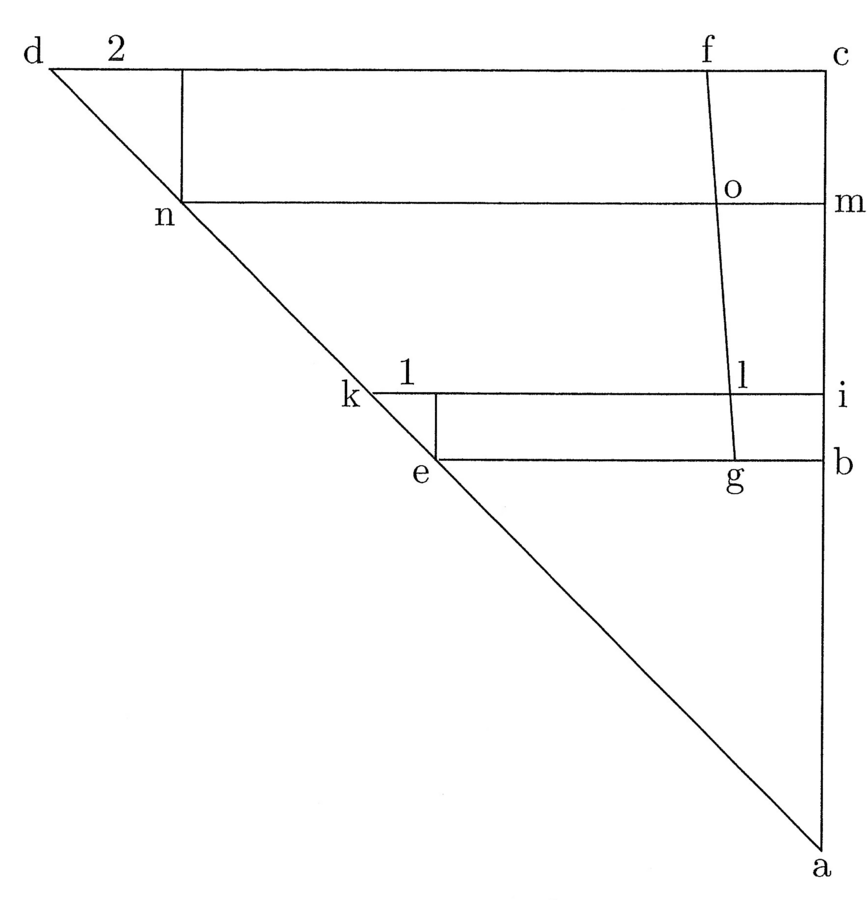
Sia ab la linea retta, e, a partire da essa, siano costruiti un triangolo e un quadrato, come premesso; sia ef la seconda linea del triangolo e il lato del quadrato EFGH. Dividi [ef] a metà attraverso la linea ik, traccia la linea ig e cerca il punto in cui ig e fg abbiano una distanza [l’una dall’altra] pari alla differenza tra la prima e la seconda [linea] del quadrato, e traccia [per questo punto] la linea parallela a ef, ossia ln e sia lm la suddetta differenza. Segna su nl la prima del quadrato, ossia no, traccia da i attraverso o la linea verso gh e, dove essa la taglia, poni p. È chiaro, da quanto detto prima, che hp è il semidiametro del cerchio la cui circonferenza è uguale al perimetro del triangolo e del quadrato, cioè, della linea retta ab, che è quanto si voleva trovare42.
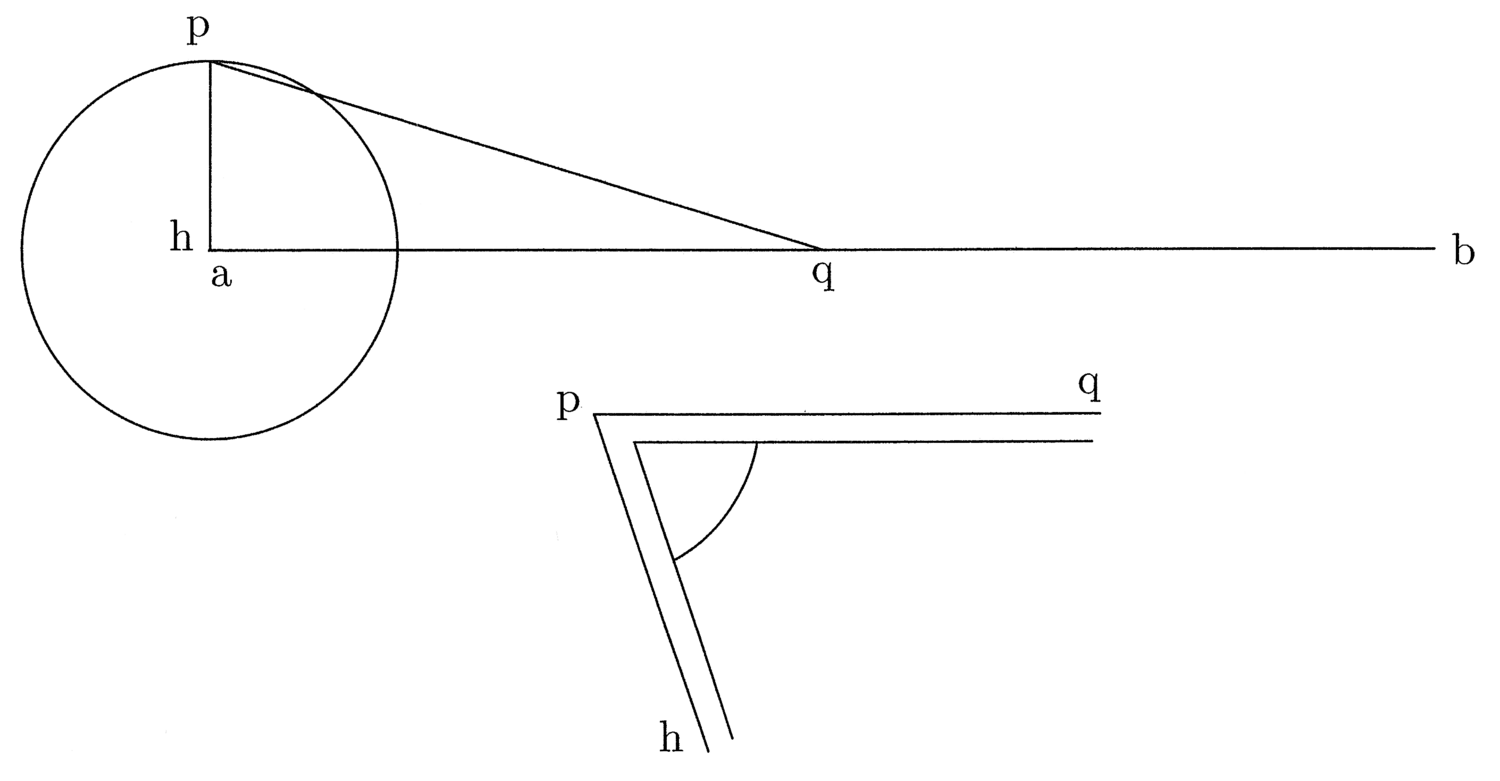
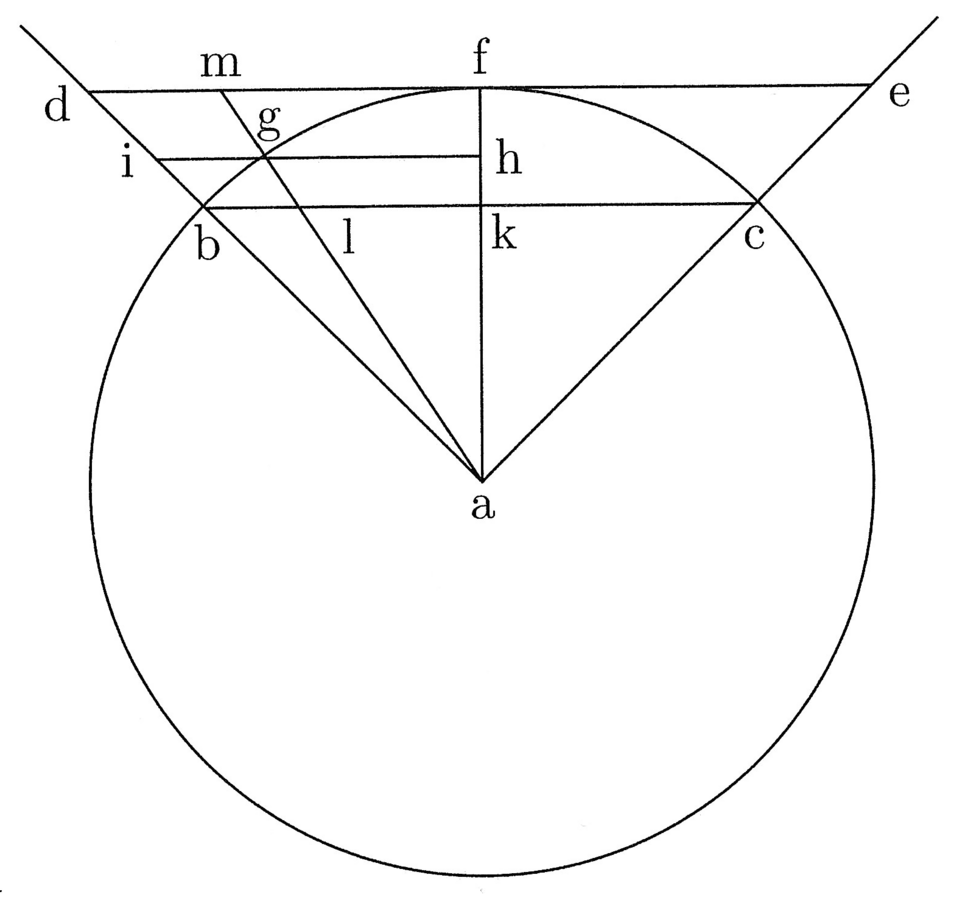
32. Trovare una linea retta uguale a una [linea] curva circolare data (cfr. figura 7).
Se vuoi ottenere ciò in breve tempo, disegna un angolo attraverso il quale troverai [ciò che cerchi] in questo modo: al semidiametro hp del suddetto cerchio unisci, al centro, la perpendicolare ab e, alla sua metà q, traccia pq. Otterrai così l’angolo hpq. Costruiscilo in metallo o in legno, e dal momento che vuoi risolvere una linea circolare in una linea retta, traccia una linea di lunghezza indefinita perpendicolare al semidiametro passante per il centro, e considera l’angolo compreso tra il semidiametro e la circonferenza, in modo che il lato minore si trovi sul semidiametro e il lato maggiore dell’angolo tagli sulla linea di lunghezza indefinita una parte uguale alla semicirconferenza.
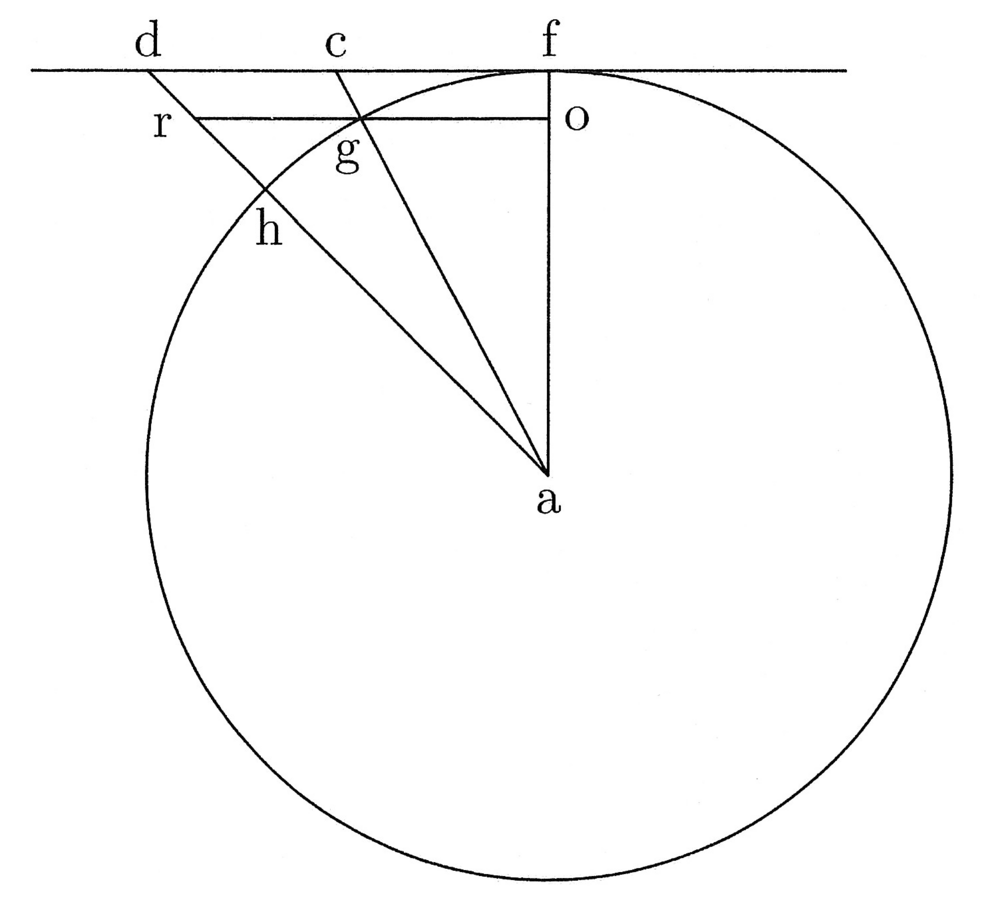
33. Trovare un quadrato uguale a un cerchio dato (cfr. figura 8).
Procedi nel seguente modo43: per mezzo di Euclide
34. Trovare un cerchio uguale a un quadrato dato.
Dalla metà del lato traccia la perpendicolare e riporta su di essa l’angolo appena descritto; alzala fino al punto in cui il lato più lungo dell’angolo cade sull’estremità del lato del quadrato; la linea tracciata [dal piede della perpendicolare] fino al vertice dell’angolo sarà il semidiametro del cerchio uguale al quadrato. Tutto ciò è evidente, perché in tutti i cerchi il rapporto tra i semidiametri e la circonferenza è lo stesso di quello [tra i semidiametri] e i lati del quadrato.
35. Senza questi due angoli, potrai [trovare un cerchio uguale a un quadrato dato] da quanto premesso, essendo il rapporto tra l’eccesso del semidiametro del cerchio sul semidiametro [dell’inscritto] nel triangolo uguale a quello. Per esempio, se vuoi trasformare la circonferenza di un cerchio dato S in una linea retta, prendi una linea qualsiasi, per esempio ab, e trova, in base a quanto premesso, una circonferenza della stessa lunghezza. Poi, traccia una linea, hp, perpendicolare a un’altra, tv, e sia hp il semidiametro del cerchio; riporta su di essa hk, il semidiametro del cerchio inscritto nel triangolo isoperimetrico, tracciando le linee rette da t attraverso h e k. Traccia, poi, il semidiametro del cerchio dato S parallelo a hp, compreso tra la linea tv e quella che da t r passa per p, e sia esso xy. Segna con z il punto in cui xy è tagliata dalla linea che parte da t e passa per k. È chiaro che yz è il semidiametro del cerchio inscritto nel triangolo isoperimetrico al cerchio S. In questo modo troverai la linea retta cercata (cfr. figura 9).
36. Da quanto stabilito sopra, si potrà indagare ciò che in geometria è rimasto finora sconosciuto. La perfezione dell’arte dei seni e delle corde non era conosciuta; nessuno poteva conoscere la corda di un arco di un grado, di due, di quattro e così via; adesso ciò è possibile44. È evidente che, per ottenere il semidiametro del cerchio isoperimetrico, ogni poligono regolare45 aggiunge alla prima [linea] una parte uguale alla differenza tra la prima e la seconda linea, e similmente, ogni eccesso, di cui la prima linea di un qualsiasi [poligono] supera la prima [linea] del triangolo, e l’eccesso di cui la seconda [linea] del triangolo supera la seconda [linea] di un altro [poligono], mantengono in tutti [i poligoni] sempre lo stesso rapporto. Da questi si determina l’arte generale dei seni e delle corde, senza la quale la geometria è rimasta sin qui incompleta. Ma [se ti domandi] come si possa realizzare praticamente quest’arte, mediante numeri approssimati, procederai in questo modo. In realtà ciò è impossibile perché la metà della doppia proporzione46 non può essere espressa numericamente, non essendo il risultato né pari, né dispari47.
37. Sia dunque il semidiametro del cerchio
circoscritto al triangolo pari a 14. Il semidiametro
dell’inscritto sarà 7 e il suo quadrato 49, il quadrato della metà
del lato del triangolo sarà tre volte di più, cioè 147, e il
quadrato del semidiametro del circoscritto quattro volte di più,
cioè 196. La metà del lato del quadrato sarà, dunque, la radice di
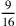 del
quadrato della metà del lato del triangolo, cioè la radice di 82
più
del
quadrato della metà del lato del triangolo, cioè la radice di 82
più 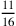 e tale sarà il semidiametro del suo inscritto. Il semidiametro del
circoscritto sarà anche la radice del numero doppio, cioè 165 più
e tale sarà il semidiametro del suo inscritto. Il semidiametro del
circoscritto sarà anche la radice del numero doppio, cioè 165 più
 . Se
ora sottrai la radice di 49 dalla radice di 82 più
. Se
ora sottrai la radice di 49 dalla radice di 82 più 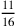 , la
differenza sarà l’eccesso del semidiametro dell’inscritto nel
quadrato sul semidiametro dell’inscritto nel triangolo, che sarà
qualcosa più di 2. Se sottrai la radice di 165 più
, la
differenza sarà l’eccesso del semidiametro dell’inscritto nel
quadrato sul semidiametro dell’inscritto nel triangolo, che sarà
qualcosa più di 2. Se sottrai la radice di 165 più 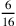 dalla radice
di 196 — differenza il cui risultato sarà poco più di 148—, ottieni gli eccessi [ossia le differenze delle prime
da un lato e delle seconde dall’altro], e dal loro rapporto può
essere trovato tutto il resto. Infatti, se sottrarrai questi
eccessi dalla freccia del lato del triangolo, cioè da 7, resterà
la freccia del quadrato. Se, dunque, ora tu dividerai per 7,
secondo il rapporto delle differenze sopra indicato, e aggiungerai
il maggiore al semidiametro dell’inscritto nel triangolo, otterrai
il semidiametro del cerchio isoperimetrico.
dalla radice
di 196 — differenza il cui risultato sarà poco più di 148—, ottieni gli eccessi [ossia le differenze delle prime
da un lato e delle seconde dall’altro], e dal loro rapporto può
essere trovato tutto il resto. Infatti, se sottrarrai questi
eccessi dalla freccia del lato del triangolo, cioè da 7, resterà
la freccia del quadrato. Se, dunque, ora tu dividerai per 7,
secondo il rapporto delle differenze sopra indicato, e aggiungerai
il maggiore al semidiametro dell’inscritto nel triangolo, otterrai
il semidiametro del cerchio isoperimetrico.
38. Dal quadrato del lato del triangolo o del quadrato, potrai anche conoscere il quadrato del lato di qualsiasi poligono dato; da ciò e dal rapporto degli eccessi si arriva alla freccia e al semidiametro dell'inscritto e si conosce così l’arco della corda. E questa è la massima perfezione della geometria, a cui gli antichi, per quanto io abbia letto, non sono pervenuti. Ora è completa anche l’arte delle trasformazioni geometriche che ho descritto precedentemente, in maniera rapida ma sufficiente, a proposito della quadratura del cerchio49.
39. Per trasformare ora velocemente il lato di un qualsiasi poligono in una linea curva, potrai costruire uno strumento di due angoli (cfr. figura 10). Sia ab il lato del triangolo, la cui freccia, ossia la differenza della prima e della seconda linea (che è la stessa cosa), è cd e sia ce l’eccesso del semidiametro del cerchio isoperimetrico sulla prima [linea] del triangolo. Ora, se tracci una linea che parte da a e passa per e, e un’altra che parte da a e passa per d, si formeranno due angoli intorno ad a. Riporta, quindi, [gli angoli] bae e bad su uno strumento di metallo, e applicali a tutti i poligoni in modo che, ora, nel triangolo, risulti che il lato di questi ab si trovi sul lato del poligono e il lato ad tocchi l’estremità della freccia. Così, il lato ae mostra quanto bisogna aggiungere alla prima [linea] di questo poligono per ottenere il semidiametro del cerchio isoperimetrico. Descritto, quindi, l’arco in questo modo e tracciati i raggi50 dal centro verso l’estremità del lato, l’arco che cade tra le linee risulterà uguale al lato dato. La verità di quanto detto consegue dall’uguaglianza del rapporto tra la parte che bisogna aggiungere alla prima del [poligono] affinché derivi il semidiametro del cerchio isoperimetrico, e l’intera differenza tra la prima e la seconda linea del suddetto [poligono], differenza che è chiamata freccia51.
40. Ora, da quanto detto, è palese che, poiché una qualsiasi linea retta può essere il lato di un triangolo, di un quadrato, di un pentagono e così via, allo stesso modo, data una linea retta, si potranno dare innumerevoli curve uguali e, grazie ad esse, si potranno trovare angoli che si rapportano tra di loro come le linee date, cioè come il lato e la diagonale di un quadrato o il diametro di un cerchio e la sua circonferenza e così in tutti i poligoni, [e si potranno trovare] anche superfici che si rapportano l’una con l’altra come le linee date. Da ciò, si potrà scoprire ciò che non solo era rimasto nascosto in geometria, ma anche ignorato nel campo della musica e degli strumenti musicali, e così, a colui che vorrà applicare ancor di più la propria mente, ciò che non era conoscibile né conosciuto in geometria si paleserà chiaramente. È per questa ragione che tale scoperta merita di portare il nome di complemento ed è degna di essere portata alla conoscenza di tutti, affinché possano ammirare la tua grandezza, Padre Santo, di cui tutti i cattolici si stupiscono a tal punto che, conformemente all’espressione d’ammirazione che si usa nei confronti di un padre, ti chiamano Papa52.
[LIBRO SECONDO]
42. A proposito delle trasformazioni delle superfici l’una nell’altra aggiungo ora alcune mie scoperte che, come le precedenti, dedico alla tua santità, a te che primeggi su tutti e che sei il solo ad essere degno che tutto ti sia rivelato.
43. Considero la linea come la figura del movimento di un punto. Ora, se essa fosse una [linea] retta e si muovesse tenendo fissa una delle estremità, questo movimento sarebbe rappresentato in modo adeguato da un triangolo rettangolo.
Così, se la linea ab si muove mentre a resta fisso, il movimento è rappresentato dal triangolo ABC. Infatti, se il movimento di b è uguale53 al lato bc, allora la stessa cosa si avrà in proporzione in tutti i punti che si possono dare [di ab]. Per esempio, se d è il centro [di ab], allora de è uguale al movimento di d e il lato de è la metà di bc (cfr. figura 11). D’altra parte, se la linea retta ab si muove con lo stesso moto tanto in a quanto in b, il movimento è rappresentato da un doppio triangolo rettangolo, ossia dal rettangolo ABCD (cfr. figura 12); infatti, tutti i punti che si possono dare [di ab] si muovono con lo stesso moto. Se invece a e b si muovono con moto simile, ma non uguale, questo [movimento] può avvenire in un’infinità di modi e non potrebbe essere rappresentato da un’unica figura54.
44. Dalla prima rappresentazione del movimento di una linea retta di cui un estremo resta fisso, consegue che la superficie, che è la misura del moto di una linea ed è generata dalla rotazione di questa, ha come linea di contorno una linea curva che si origina dal punto b, e una superficie circolare che deriva dalla linea ab (cfr. figura 13). E se prendi su ab un punto qualsiasi, per esempio al centro, e sia questo punto d, la curva generata dal moto di d starà alla curva generata da b come, nella figura55, il lato de sta al lato bc; le linee di contorno sono, infatti, le misure dei movimenti dei punti. Da ciò sarà necessario che la misura [del rapporto] tra ogni semidiametro e la circonferenza resti la stessa.
45. Inoltre, poiché la superficie è generata dal movimento del semidiametro attorno alla circonferenza e il rapporto tra ogni semidiametro e le circonferenze è lo stesso, il rapporto tra le superfici sarà uguale a quello tra i quadrati dei semidiametri. Di conseguenza, la superficie del cerchio che ha un semidiametro pari a 4 è quattro volte la superficie di quello che ha un semidiametro pari a 2. Da ciò, si avrà il rapporto delle superfici coniche tra di loro e con quelle di base. Infatti, poiché il semidiametro [della circonferenza] di base e il lato del triangolo che descrive la [superficie] conica si muovono intorno allo stesso punto fisso all’estremità di essi e sulla stessa circonferenza di base, il rapporto delle superfici [di base e conica] sarà uguale a quello delle linee dal cui movimento si generano quelle superfici56. Siano, per esempio, il semidiametro della circonferenza di base e il lato del triangolo che descrive la [superficie] conica uguali ad ab e bc57(cfr. figura 14).
46. Dalla seconda rappresentazione di una linea che si muove con lo stesso moto in tutti i punti consegue che la superficie originata da tale movimento è doppia rispetto a quella che si origina dal primo movimento. Di conseguenza, se il semidiametro si muove con [questo] secondo movimento sulla stessa circonferenza sulla quale si era mosso con il primo movimento, si avrà una superficie doppia della prima. Perciò, sarà necessario che il prodotto del semidiametro per la semicirconferenza sia uguale alla superficie del cerchio. Parlo tuttavia del caso in cui entrambi i punti estremi si muovono con lo stesso moto (cfr. figura 15). Infatti, se uno si muove sul lato concavo di un arco e l’altro sul lato convesso, la superficie non sarà il doppio di quella originata dal movimento della linea avente un’estremità fissa e l’altra in movimento sul lato concavo dell’arco, ammesso pure che gli archi siano uguali. Se l’arco bd è uguale all’arco ce, e se la linea bc si muove descrivendo la superficie compresa tra le rette bc e de e le curve bd e ce, ammesso pure che si muova su archi uguali, essa non descriverà tuttavia una superficie doppia rispetto a quella originata dal movimento di ab, uguale a bc, con a che resta fisso, mentre b si muove sull’arco uguale fino a d, perché b si muove sul lato concavo dell’arco bd, mentre c, della linea bc, sul lato convesso. Inoltre, la convessità diminuisce tanto quanto sono le porzioni FGCH e FIEK.
47. Da ciò, ogni sapere ricava tutto ciò che riguarda i rapporti tra le superfici [laterali] e le superfici di base dei cilindri ossia delle colonne rotonde, e tra cilindri, curve coniche e piani circolari. Infatti, è evidente che il cilindro, la cui altezza è uguale al semidiametro della base, ha la superficie [laterale] doppia rispetto a quella di base. Infatti, la linea che genera la [superficie di] base si muove avendo un punto fisso a una estremità e descrivendo una circonferenza con l’altro punto; la stessa linea genera la superficie laterale del cilindro attraverso lo stesso movimento di entrambi i due punti estremi sulla stessa circonferenza di base58, cosicché dall’angolo retto abc che ruota attorno ad a si descriveranno la [superficie di] base attraverso ab e una doppia superficie cilindrica attraverso bc, dato che bc, che è uguale ad ab, si muove con lo stesso moto nei punti estremi b e c (cfr. figura 16).
48. La stessa cosa accade nelle coniche. Se ABC è il triangolo il cui angolo retto bac ruota attorno ad a, e se il lato bc è doppio di ab, la superficie [laterale] sarà uguale alla superficie [laterale] del cilindro di prima, e, se disegni il cerchio il cui semidiametro è il doppio di ab, allora la sua superficie sarà uguale alla superficie [laterale] del cilindro59 e a quella del cono prese insieme (cfr. figura 17).
49. È chiaro che se la linea corrispondente alla circonferenza di un cerchio fosse ridotta a una [linea] retta e fosse moltiplicata per il semidiametro, allora la superficie del rettangolo che ne deriverebbe sarebbe il doppio della superficie del cerchio avente quella circonferenza. Infatti, questo movimento generatore60 sarebbe quello in cui entrambi i punti estremi si muovono con lo stesso moto, mentre il cerchio si origina dal movimento di una linea in cui un punto rimane fisso. Pertanto, da molti è stato detto giustamente che tale prodotto, cioè, la moltiplicazione del semidiametro per la linea uguale alla semicirconferenza, genera una superficie uguale a [quella] del cerchio.
50. Esiste un’altra modalità di movimento, quello composto, ossia di avanzamento e di arretramento61, come quello rappresentato nella figura62(cfr. figura 18). Infatti, come puoi notare, ab si muove con moto doppio su ac, avanzando e arretrando sempre con lo stesso moto. La misura dell’avanzamento sarà ac, quella dell’arretramento ab e quella di avanzamento e di arretramento prese insieme sarà bc. Infatti, il tempo di avanzamento di a verso c è lo stesso di quello di arretramento di b su bc fino a c, e il risultato è la figura ABCD. bc comprende in sé il doppio movimento di arretramento di ab e di avanzamento di ac perché il quadrato di bc è uguale a quello di ab più quello di ac. Da ciò, nota come dal movimento di una linea si originano contemporaneamente due triangoli e un quadrilatero.
51. Se tuttavia ab avanza su ac e arretra con moto differente e questa differenza è uguale all’arco [bc], allora si ha la figura ABCD, e poiché l’arco bc comprende in sé un movimento di avanzamento che non è uguale a quello di arretramento, allora l’arco cb è maggiore della linea retta cb (cfr. figura 19).
Dico che il movimento di arretramento non è uguale perché dopo che b raggiunge la metà dell’arco, non scende lungo la sua metà sotto ca, come quando b scende lungo la metà della linea bc. Considera come a descrive l’arco ad. a si muove sul lato convesso e b su quello concavo, e quanto più concava è la linea cb, meno essa è convessa. Di conseguenza, la figura curvilinea compresa tra l’arco concavo bc e l’arco convesso uguale ad è uguale al parallelogramma ABCD63, e così saprai come tra le linee curve più lunghe cade la stessa superficie di quella compresa tra linee rette più corte. Da ciò si possono considerare diversi altri modi di moto composto, su cui ora sorvolo, dal momento che chiunque potrà concepirli per sé.
52. Se fai attenzione a un terzo movimento che si verifica quando entrambe le estremità della linea si muovono, ma con moto differente, vedrai chiaramente che, facendo il rapporto dei moti, si perviene alla superficie. E, per rappresentartelo più facilmente, considera il doppio della linea ab, divisibile fino al punto b, che resta l’estremo indivisibile per entrambe le parti divise; si avrà dunque che, mentre b resta fermo, a si muove (cfr. figura 20). Se ora sposti il punto isolato a così che formi un angolo attorno a b, potrai conoscere il rapporto delle superfici facendo il rapporto tra la circonferenza, che descrive il punto mobile a, e la circonferenza che descrive b. Per esempio, sposta il punto mobile a in modo da formare un angolo tale che la linea ad, che va da a fino al punto della linea orizzontale, con il punto fisso a, sia metà di ab; quindi, la linea mobile ba descrive una superficie conica che sarà della metà maggiore della superficie della circonferenza di base che descrive ab, e così proporzionalmente in tutti i casi64. Di conseguenza è evidente che, quando il [punto] mobile a si sposta in modo tale che il suo movimento risulti il doppio del movimento di ab, vale a dire quando entrambe cadranno su un’unica linea, allora la linea mobile ba descriverà una superficie piana tripla della superficie che descrive ab. E questa è l’ultima e la massima [superficie], alla quale le intermedie si avvicinano in maniera proporzionale. Da ciò, sai come formare sezioni di cono che abbiano qualsiasi rapporto tu voglia con la base; e nello stesso tempo sai come ridurre le superfici dei solidi formati da due coni65 aventi un’unica [superficie di] base in altre figure. E quel che vuoi sapere di queste cose, puoi ottenerlo facilmente così.
53. Bisogna tuttavia fare attenzione, da quanto detto, a come procedere nelle coniche. Se ABC66 è il triangolo, ab il lato che descrive il cono e cb il semidiametro della [circonferenza di] base, prolunga la linea ac e conduci da b una linea in modo da ottenere il triangolo uguale BDC (cfr. figura 21).
È evidente che, se ad resta fisso e si fa ruotare il triangolo ABD attorno a sé, si ottiene un solido67 formato da due coni uguali. Prolunga, quindi, la linea ab e sia be uguale ad ab. È chiaro che, se si compie la rotazione come prima [attorno a ad], la linea be genera una superficie tripla rispetto alla superficie che genera ab, e ae una superficie conica quadrupla rispetto a quella generata da ab. Così, se sposti bd in modo che si trovi a metà tra bd e be, risulterà una superficie doppia, con bd una uguale e be una tripla, e si giungerà sempre a metà quando si forma un angolo retto con il semidiametro della [circonferenza di] base. Se invece si sposta [bd] più in là [della metà] o di qua [della metà], si genererà una [superficie] maggiore o minore, il che è noto da quanto detto in precedenza. Sai, dunque, che, quando il cono e il cilindro hanno la stessa base e il lato del cono è uguale all’altezza del cilindro, la superficie del cilindro è sempre doppia rispetto a quella del cono, e se è maggiore [dell’altezza del cilindro], [la superficie] sarà maggiore, e se è minore [dell’altezza del cilindro], [la superficie] sarà minore, in maniera proporzionale.
54. Se prendi come lato del cono la corda di un arco68 e descrivi su di esso l’arco, come sul lato ab l’arco afb e su be lo stesso arco, allora la superficie che si genera dalla curva afb sarà un terzo della superficie che si genera dalla curva be. Così, se vuoi ottenere una superficie doppia, fa’ com’è stato detto per le coniche. Pertanto, se afb è un quadrante, è chiaro che dalla sua rotazione si origina una superficie semisferica e dalla curva bg una doppia rispetto a quella, ossia una superficie curva uguale a quella ‹della sfera› di cui cb è il semidiametro del cerchio maggiore; e dalla curva bc una superficie tripla (cfr. figura 22).
Da ciò saprai come effettuare qualsiasi moltiplicazione tu voglia in queste superfici curve.
55. Se trasformi un arco in una linea curva avente la curvatura di una qualsiasi sezione di parabola o di una sezione obliqua di cilindro — sezioni che non sono archi di circonferenza, ma curve di diversa curvatura69 —, procedendo nello stesso modo il rapporto delle superfici sarà uguale.
56. Tenendo fisso a, descrivi una superficie circolare piana facendo ruotare ab, e fai ruotare su ac il quadrante del cerchio che si ottiene unendo un punto estremo b a un altro c, fisso come a, allora la superficie risultante dal quadrante sarà doppia rispetto a quella generata dalla linea ab (cfr. figura 23).
È evidente, infatti, che da bc si genera
una superficie semisferica e da ab il
cerchio massimo la cui superficie, moltiplicata per quattro, è
uguale alla superficie della sfera, come dimostra Archimede
57. Se vorrai descrivere una superficie cilindrica, una sferica e una conica e infinite sezioni coniche della stessa superficie, procederai così (cfr. figura 24):
sia ab il semidiametro di un cerchio a cui unisci bc, uguale ad ab, in modo che si formi un angolo retto; traccia da a una linea parallela a bc di lunghezza indefinita e sia essa ad; traccia da b verso ad una linea doppia rispetto ad ab e sia essa db. Poi traccia la linea da d a c. Dico che tutte le linee che si possono condurre da b verso cd descrivono, attraverso la rotazione, sezioni coniche uguali o alla piramide71 bc o alla conica bd, poiché da bc e bd si originano superfici uguali che sono il doppio della superficie piana del cerchio di cui ab è il semidiametro. Precedentemente è stato mostrato che le intermedie si rapportano allo stesso modo, per esempio, bi e bg o altre del genere. È evidente, infatti, che le superfici non possono essere maggiori di quella che risulta da bc, né minori di quella che risulta da bd. Poiché queste sono uguali, così lo saranno tutte le intermedie. Descrivi il quadrante di un cerchio, di cui ab è il semidiametro, e sia esso be. È chiaro, da quanto detto, che la superficie che si origina dalla curva be è uguale a quelle suddette72.
58. Considera linee curve, ma non circolari, generate da una linea che si muove sui suoi due punti estremi con moto non uguale, come se la retta ab si muovesse su b più [velocemente] di come si muove su a; poni che a si muove sulla linea ac e b sulla curva bd: se ciò avviene regolarmente, allora quando a sarà giunta al centro di ac, anche b giungerà al centro di bd (cfr. figura 25). Può anche essere che un punto si muova regolarmente con un moto continuo uguale, e un altro con un moto non uguale: per esempio, [un punto può muoversi] all’inizio più velocemente, poi in modo più lento e continuo, con una irregolarità per cosi dire regolare73. Da questi diversi movimenti si generano diverse curvature: alcune saranno uguali a sezioni coniche, altre a sezioni trasversali cilindriche o a sezioni oblique sferiche74.
59. Da ciò si ha che le superfici curve delle sezioni che si definiscono parabole e quelle delle trasversali cilindriche non derivano direttamente dal movimento di una linea. Se vuoi cercare i rapporti di queste sezioni, procedi in questo modo: considera l’eccesso della corda sulla freccia; questo eccesso sarà pari al movimento della linea uguale alla freccia su uno dei suoi punti75, mentre il movimento dell’altro punto sarà pari alla curva. Perciò, la superficie sarà la metà di quella prodotta dalla freccia sulla curva se la linea non fosse mossa su una delle sue estremità, e sarà maggiore della metà a seconda del rapporto tra il quadrato dell’eccesso76 del suo arco sulla freccia e il quadrato della curva77.
60. Prendi, per esempio, la porzione di cerchio compresa tra [un arco pari a] un sesto della circonferenza, la semicorda e la freccia, e sia essa segnata con ABC; sia ab la semicorda del doppio dell’arco, ac la freccia, d il centro del cerchio. Traccia db, dc e la linea bc (cfr. figura 26). È chiaro che ac e ad sono uguali così come i triangoli DBA e BAC. La porzione [di superficie curvilinea] al di sopra della linea bc, di cui la porzione di cerchio [ABC] eccede il triangolo, deriva quindi dal movimento della freccia ac su entrambe le sue estremità. Se le due estremità si muovessero con lo stesso moto, la porzione al di sopra della linea bc sarebbe uguale alla porzione BAC; ma, poiché le estremità non si muovono con lo stesso moto, allora essa è minore. E, affinché tu veda come esse non si muovono con lo stesso moto, traccia da b verso a la linea uguale ad ac e sia be uguale ad ac. Si muova dunque b sull’arco bc e, mentre b si muove sull’arco bc, sarà necessario che e si muova verso a. Dunque, nello stesso tempo in cui e si muove sulla linea ea, b si muove sull’arco bc. Dunque, la superficie della porzione [di cerchio ABC] supera la metà della porzione di cerchio DBC di una quantità pari al rapporto del quadrato della linea ea e il quadrato della linea uguale alla curva bc. Infatti, il prodotto di ac per l’arco bc dovrebbe essere metà di quello di db per lo stesso arco, essendo ac la metà di db. Ma, poiché l’estremità che resta fissa in d si muove su ac, allora supera la metà. La curva bc è quindi il triplo di ea, e così [la porzione di cerchio ABC] supera di un nono la metà [della porzione di cerchio DBC], e la porzione sopra la linea bc sarà due noni della metà [della porzione di cerchio DBC]. Così si opera nelle sezioni delimitate da linee curve.
61. Ora, vorrei parlare di come trasformare una linea curva in una [linea] retta, ma non come ho fatto nel primo libro, cioè trasformando la retta in curva, ma immediatamente, ossia mediante una sottile coincidenza, di cui questa è la proposizione78.
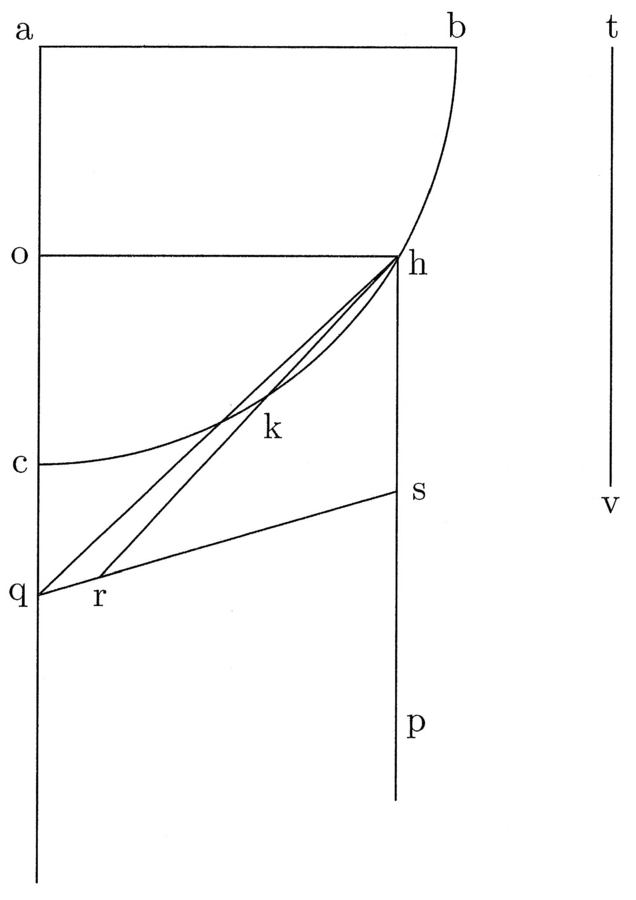
62. Descrivi un quarto di cerchio79, traccia la prima linea dal centro verso il punto d’inizio dell’arco, una seconda linea, della stessa lunghezza della prima, perpendicolare al punto di tangenza della prima con l’arco, una terza, dal centro all’estremità, uguale al lato del triangolo inscritto al cerchio, una quarta dall’estremità della seconda all’estremità della terza. Se ora porti una quinta linea dall’inizio del quadrante alla quarta in modo che la corda che va dal punto di tangenza di questa quinta linea e la curva all’estremità di tutto il quadrante, ossia la sesta linea, sia uguale alla quinta linea, la quinta sarà minore del quadrante e precisamente della metà della parte della linea compresa tra la curva e la quarta (cfr. figura 27).
Sia be il quadrante descritto intorno al centro a, ab la prima linea, bc la seconda uguale e perpendicolare ad ab, abc l’angolo retto, aed la terza linea uguale al lato del triangolo inscritto, e cd la quarta linea. Traccia poi da b una linea verso cd, e sia questa bg; nel punto in cui essa taglia il quadrante be, poni f, e sia questa la quinta linea. Da f traccia la sesta che è la corda fe. Dico che se fe è uguale a bg, allora bg è minore del quadrante be della metà di fg. Aggiungi, quindi, la metà di fg ad bg e sia gh la metà di fg. Dico che bh è uguale alla curva be80.
63. Dimostrazione. Per prima cosa suppongo che la differenza tra la somma tra la quinta e la sesta e la parte compresa tra la curva e la quarta linea, che chiamo sempre parte, è uguale a quella che c’è tra la parte della quinta linea che è la corda, e la sesta linea, che è la corda della parte residua dell’arco del quadrante; e che questa differenza tra la quinta linea, che è la minore del quadrante, e la sesta che, sommata alla parte, è maggiore, è il doppio della differenza tra la quinta linea, che è minore della curva del quadrante, e la sesta linea che, sommata alla parte, è maggiore del quadrante; e che dunque, quanto maggiore è la loro differenza, tanto più lunga è la linea che si trova al centro tra la quinta e la sesta sommata alla parte, linea che chiamo linea di mezzo; e che quanto meno esse differiscono, tanto minore è la linea di mezzo81. Suppongo, in secondo luogo, che la sesta, sommata alla parte, possa superare il quadrante della metà della parte. Infatti, essa può superarli di una parte minore e di una maggiore, e così, anche di una parte che non è né maggiore, né minore della metà.
64. Da ciò inferisco che questa sesta [linea], sommata alla parte, eccede il quadrante, così come il quadrante eccede la quinta [linea]; che la parte è uguale alla differenza delle corde e la sesta è uguale alla quinta. Le altre, infatti, si rapportano tra di loro di conseguenza. Se lo neghi, perché dici che la differenza delle corde è minore della parte, allora la linea di mezzo anche è minore; e [se lo neghi], perché il minore è sottratto alla sesta [linea] sommata alla parte come prima, dato che la parte è per sé maggiore e la metà della parte è maggiore della metà della differenza delle corde, questo è impossibile: è impossibile, cioè, che la linea, da cui si sottrae di meno, sia minore di quanto sarebbe se si sottraesse di più. Allo stesso modo, se dici che la differenza delle corde è maggiore della parte, allora la linea di mezzo sarà maggiore e tuttavia si sottrarrà più di prima, quando era sottratta la metà della parte, che dici minore, il che è di nuovo impossibile. Di conseguenza, è evidente che, se la sesta [linea], sommata alla parte, eccede [l’arco de] il quadrante della metà della parte, sarà necessario che la parte sia uguale alla differenza delle corde e, di conseguenza, che la sesta [linea] sia uguale alla quinta, che è quanto si voleva trovare.
65. Da quanto detto segue facilmente la quadratura del cerchio. Infatti, il medio proporzionale tra bh e il diametro del cerchio è il lato del quadrato che quadra il cerchio (cfr. figura 28).
Infatti, segue che se bx è uguale a bh, allora nella rotazione descrive una sezione conica la cui superficie è uguale alla metà di quella della sfera e il cui bordo ha una lunghezza uguale a un quarto della circonferenza del cerchio maggiore di questa sfera, che è ciò che si cercava in particolare.
66. Ora, diversamente si trova una linea retta uguale al[l’arco di un] quadrante, e cioè in questo modo. Se la sesta linea, sommata a una parte della quinta linea, è uguale al[l’arco di un] quadrante, è necessario che siano uguali tra di loro. Si utilizzi la figura precedente e sia bpq la quinta [linea] e ep la sesta (cfr. figura 29).
Dico che, se ep e pq sono uguali al[l’arco del] quadrante be, allora ep sarà uguale a eq. Per dimostrarlo, suppongo, in primo luogo, che, se porti la quinta [linea] da b al centro della quarta [linea] cd, che è v, la parte tv sarà la più corta tra tutte le altre e aumenterà di continuo al di sopra e al di sotto. In secondo luogo, suppongo che la sesta [linea], sommata a questa parte minima, sia maggiore del[l’arco del] quadrante, e così occorre che la sesta [linea], sommata alla parte che deve essere uguale al[l’arco del] quadrante, sia minore. In terzo luogo, suppongo che si possa dare una sesta [linea] che, sommata alla parte, sia uguale al[l’arco del] quadrante. In quarto luogo, suppongo che la somma delle seste [linee] e delle parti aumenti contemporaneamente e di continuo da e verso b, mentre le parti diminuiscono82. Da queste supposizioni, che sono evidenti e facili a chiunque, si dimostra la proposizione.
67. Infatti, se dirai che la sesta [linea] ep è maggiore della parte pq, allora essa sarà maggiore della metà del[l’arco del] quadrante. E dunque si avrà che la sesta [linea] er è uguale alla metà del quadrante e la parte rs sarà maggiore di pq, per la prima ipotesi. La somma di er e rs sarà maggiore del[l’arco del] quadrante e contemporaneamente minore della somma di ep e pq, che, per la quarta ipotesi, è uguale al[l’arco del] quadrante. E così, la minore sarà maggiore della maggiore, il che è impossibile. E se dirai che ep è minore di pq, segue la stessa cosa; infatti, sarà minore della metà del[l’arco del] quadrante. Si avrà che et è uguale alla metà del[l’arco del] quadrante, la cui parte tv sarà minore della parte pq, e di conseguenza la somma di et e tv sarà minore della somma di ep e pq. Così, la maggiore sarà minore della minore, il che è, come nel primo caso, impossibile. Il motivo per cui la somma della sesta [linea] e della parte può essere uguale al[l’arco del] quadrante è chiaro: è evidente che ciò accade quando la sesta è uguale alla parte della quinta, il che è ciò che si cercava.
68. Dalla suddetta scoperta, se vuoi, [potrai] ricavare come ridurre ogni porzione di superficie sferica in una superficie conica o in una cilindrica, anche se non conosci il rapporto tra una porzione di superficie sferica e la superficie di tutta la sfera, e ciò nel modo seguente: sia, per esempio, il quadrante ABC come quello di prima; traccia il suo arco hc che conosci e che è pari a due terzi del quadrante (cfr. figura 30).
Traccia la perpendicolare da h ad ac, e sia questa ho. ho sarà, dunque, la semicorda del doppio arco83. Prendi una linea retta uguale alla curva hc, e sia questa tv, la cui metà è la corda ck. Da h traccia una linea retta passante per k che sia uguale a tv e sia essa hkr. Quindi, fa’ passare da un punto qualsiasi della linea hp, per esempio s, una linea da r verso aq, e sia essa sq, in modo che la linea condotta da h al punto dove aq taglia la linea, vale a dire q, sia il doppio di hs. La superficie cilindrica generata da hs sarà uguale alla superficie sferica generata dall’arco hc, alla superficie conica generata da hq e alle intermedie che sono tracciate da h verso sq, come quanto fatto in precedenza, il che è assolutamente evidente dalle premesse. E così, se sai che una superficie cilindrica è uguale a [quella della] sfera, sarai capace di trovare grazie a ciò una [superficie] conica uguale, il cui bordo ha una lunghezza pari a [quella della] linea curva del cerchio maggiore.
69. E poiché, grazie ad Archimede
70. A proposito di questo, già Archimede
71. Adesso voglio capire come si giunge alla quadratura del cerchio attraverso le lunule, strada che gli antichi hanno percorso invano87. L’obiettivo è trovare, tra il lato del poligono circoscritto al cerchio e il lato del poligono inscritto, una linea che tagli la lunula in modo che il triangolo88 sia uguale alla porzione del cerchio di cui quello sarà stato l’arco (cfr. figura 31). Per esempio, sia bc l’arco del cerchio di centro a, e sia bc uguale a un terzo della circonferenza, alla quale è circoscritto il triangolo di lato ef; una volta tracciate le linee af e ae, sia la linea cb la corda o il lato del triangolo inscritto. Voglio determinare una linea ik, compresa tra ef e bc, che tagli la lunula LMN, in modo che essa sia uguale alle porzioni BIL e CKN e il triangolo AIK sia uguale alla porzione di cerchio ABMC89.
72. Per questa ricerca, suppongo che il lato [del poligono] inscritto sia minore dell’arco e che quello [del poligono] circoscritto sia maggiore [dell’arco], e che sia tanto maggiore quanto minore è il lato [del poligono] inscritto. In secondo luogo, suppongo che possano cadere due linee tra il lato [del poligono] inscritto e il lato [del poligono] circoscritto, di cui una è uguale all’arco e l’altra è posta in modo tale che il triangolo rettangolo risulti uguale alla porzione di cerchio. Si indichi come prima [linea] quella che coincide con il lato [del poligono] inscritto, come seconda quella uguale all’arco, come terza quella che è posta in modo tale che il triangolo rettangolo risulti uguale alla porzione di cerchio, come quarta quella che coincide con il lato del poligono circoscritto. In terzo luogo, suppongo che queste quattro linee si rapportino tra di loro in modo tale che, quando cresce una, crescono tutte e, quando diminuisce una, diminuiscono tutte; perciò, all’aumentare una, segue che aumenta anche l’altra. In quarto luogo, suppongo che quanto più aumentano, tanto più differiscono, e quanto più diminuiscono, tanto meno differiscono. In quinto luogo, quanto più le linee differiscono, tanto più differiscono i loro quadrati.
73. Da ciò affermo che: quanto maggiore è la quarta linea, tanto maggiori sono la terza, la differenza delle linee e [quella] dei loro quadrati. Allo stesso modo, quanto maggiore è la seconda linea, tanto maggiori sono la prima, la differenza delle linee e [quella] dei loro quadrati. Similmente, quanto maggiore è la differenza tra il quadrato della quarta linea e il quadrato della terza, tanto maggiore è la differenza tra il quadrato della seconda e il quadrato della prima, e così anche la differenza delle differenze. Di conseguenza, tanto maggiore è la quarta linea, tanto maggiori sono la prima, le differenze dei loro quadrati, e la differenza delle differenze tra la quarta e la terza, da un lato, e tra la seconda e la prima, dall’altro. A seconda di come si rapportano il quadrato della quarta linea e il quadrato della prima, si rapporteranno le differenze tra la quarta linea e la terza, da un lato, e tra la seconda linea e la prima, dall’altro. Questo significa che, se il quadrato della seconda linea è maggiore del quadrato della prima di una certa quantità, e se il quadrato della quarta linea è il doppio del quadrato della prima, allora il quadrato della quarta linea sarà maggiore del quadrato della terza [e precisamente]90 del doppio; e se il rapporto tra il quadrato della quarta e il quadrato della prima è diverso, anche il rapporto tra le quantità di tali differenze è diverso.
74. Se lo negassi, e dicessi che il rapporto tra il quadrato della quarta linea e il quadrato della prima è di tre a uno, ma che il rapporto tra l’eccesso del quadrato della quarta sulla terza e l’eccesso del quadrato della seconda sulla prima non è lo stesso, e che anzi l’eccesso del quadrato della quarta sul quadrato della terza è pari a tre e l’eccesso del quadrato della seconda sul quadrato della prima è pari a uno, dico che ciò implicherebbe una contraddizione. [In questo caso], infatti, risulta che la prima e la seconda linea sono minori e più simili alla prima e alla seconda [del caso precedente], le quali si rapportano in modo tale che la differenza sia la metà [della differenza tra la terza e la quarta]. Infatti, quanto minore è la differenza degli eccessi, tanto più simili e minori sono le linee, e da ciò segue che la prima e la seconda sono maggiori della prima e della seconda, che differiscono della metà dalla differenza tra la quarta e la terza. Infatti, quanto più la differenza tra la quarta e la terza linea supera la differenza tra la seconda e la prima, tanto maggiori e differenti risultano la seconda e la prima. Saranno, quindi, maggiori della prima e della seconda dove la differenza è la metà, allorché si pone la differenza uguale a un terzo della differenza della quarta e della terza. Esse saranno così maggiori e minori, più simili e più dissimili, e ciò è contraddittorio. La stessa contraddizione seguirebbe se si ponesse che la differenza tra la seconda e la prima linea è maggiore della metà della differenza tra la quarta e la terza. E questa contraddizione si verificherebbe in tutti i casi in cui il rapporto tra l’eccesso del quadrato della quarta sulla terza e l’eccesso del quadrato della seconda sulla prima fosse diverso da quello tra il quadrato della quarta e il quadrato della prima.
75. Se dunque, con questo sussidio, volessi tagliare una lunula, o quadrare un cerchio, fa’ in questo modo, per esempio in un quadrato (cfr. figura 32).
Sia dunque bc il quadrante descritto intorno al centro a. Traccia da a verso b e c [due] linee di lunghezza indefinita, e traccia la corda bc. Il lato [del quadrato] circoscritto eof che tange l’arco in o; traccia il semidiametro ao, poi segna la seconda linea gh uguale all’arco e laddove essa taglia ao si ponga i. Poi, si tracci la terza linea kl , e dove essa taglia ao, si ponga m. Se, quindi, la terza, cioè, kl, è tale che il suo quadrato è minore del quadrato di ef del doppio della differenza tra il quadrato di bc e il quadrato di gh, e se risulta che il prodotto di ao per ih è uguale al prodotto di am per ml, allora otterrai quel che cercavi. Altrimenti, apporta le opportune modifiche finché risulti ciò.
76. Un esempio numerico. Si ponga il semidiametro ao uguale a 7, il cui quadrato è 49; bc sarà la radice di 98 ed ef la radice di 196. Si ponga gh uguale a 11, il suo quadrato sarà 121 da cui sottrai 98: resta 23. Da 196 sottrai il suo doppio, cioè, 46: resta 150. Se il prodotto di 7 per 5 più la metà [di uno] fosse eguale al prodotto della metà della radice di 150 per se stesso, cioè ad am per ml, che è lo stesso, dato che am è uguale a ml, allora otterresti quello che cercavi, e il doppio di ml sarebbe il lato del quadrato uguale al cerchio e un quarto della circonferenza sarebbe 11. Ma, se fai bene i calcoli, troverai che supera di poco 1191.
77. A livello pratico è piuttosto difficile trovare le linee intermedie, la seconda e la terza. Per risparmiarti la fatica, fa’ così (cfr. figura 33): traccia una linea ac pari a 7, come il semidiametro, la cui metà è b; traccia le perpendicolari cd e be; sia dc uguale a ac e eb uguale ad ab e traccia la linea aed. Segna su cd il semidiametro e sia cf uguale al semidiametro; segna la metà della corda del quadrante, ossia bc nella figura precedente, su be, e sia bg uguale alla metà della corda dell’arco del quadrante. Traccia la linea fg e, poiché cd è il quadrato la cui radice è cf, e bg la radice di be, allora cerca, tra be e cd, i quadrati delle metà delle linee intermedie, cioè, della seconda e della terza. Per esempio, sia ik il quadrato della metà della seconda linea, e dove essa taglia fg poni l. Vedi di quanto ik supera be e fa’ che cd superi del doppio la terza mn in modo che be superi mn di una quantità doppia di quella di cui ik supera be; laddove mn taglia fg poni o. Se, dunque, dal prodotto di mo per se stesso si avrà lo stesso risultato del prodotto del semidiametro per li, otterrai ciò che cercavi, e, raddoppiando mo, si avrà il lato del quadrato del cerchio; altrimenti, apporta le opportune modifiche finché risulti così. Come hai operato nel quadrante, così potrai procedere, in maniera proporzionale, negli altri archi di cui ci siamo occupati in precedenza, [potrai] tagliare le lunule e rettificare il cerchio92.
78. Adesso, tuttavia, voglio trattare brevemente anche di altri modi possibili per risolvere immediatamente il cerchio in qualsiasi poligono tu voglia, senza necessariamente risolvere prima la circonferenza del cerchio in una linea retta. Lascio questo compito come esercizio a coloro che hanno più tempo libero di me.
79. Se descrivi i lati dei quadrati circoscritti e inscritti al quadrante di un cerchio e se tracci una linea dal centro del cerchio fino al punto in cui il lato del circoscritto tocca la circonferenza, un’altra dal centro all’estremità del lato fino a chiudere il triangolo, e poi una linea dal centro al lato del circoscritto, [passando] per un punto qualsiasi dell’arco, in modo tale che un’altra linea parallela ai lati dei poligoni vada da un lato all’altro del triangolo [passando] per lo stesso punto dell’arco, allora questa linea sarà uguale alla [somma delle due] porzioni che la linea tracciata dal centro e passante per lo stesso punto dei lati dei suddetti poligoni ritaglierà tra la stessa linea e l’altra, che è il lato del triangolo, condotta fino al punto di tangenza: questa linea parallela sarà la metà del lato del poligono corrispondente all’arco uguale al cerchio.
80. Sia descritto un cerchio attorno al centro a. Voglio trovare un quadrato uguale ad esso (cfr. figura 34).
Segno il quadrante, che indico con bc, e traccio i lati del quadrato: sia de il lato del quadrato circoscritto, che tocca il cerchio nel punto f; traccio af, ad e bc come lato del quadrato inscritto. Dove bc taglia af, pongo k. Traccio, quindi, da a verso df una linea che passi per un qualsiasi punto dell’arco bf, e sia g il punto di tangenza di questa linea con l’arco. Dove essa taglia il lato bk, si ponga l, e dove taglia il lato df, si ponga m. [Passando] per g, tiro la linea parallela a df, da af ad ad, e sia essa hgi. Dico che se hi è uguale [alla somma di] lk e mf, hi è la metà del lato del quadrato uguale al cerchio.
81. Per comprendere ciò, bisogna in primo luogo considerare quanto segue: descrivi un cerchio attorno al centro a, traccia nel punto f la tangente ad esso di lunghezza indefinita e la linea af; poi tira da a alla tangente la linea ac che taglia il cerchio nel punto g e traccia dal punto o della linea af una linea all’infinito [passante] per g e parallela alla tangente. Su questa linea, attraverso un’altra linea da a alla tangente, si ricaverà un’equatrice93, e traccia hrd in modo che or sia l’equatrice. La chiamo così perché pone sotto alla lunula OGF, che essa ricava dall’area del cerchio, la lunula HRG avente la stessa grandezza, chiudendo così il triangolo rettangolo ARO in modo tale che risulti uguale alla porzione di cerchio AHF (cfr. figura 35).
82. In secondo luogo, osservando la figura con la tangente e la linea su cui è ricavata l’equatrice, bisogna considerare che da qualsiasi punto del cerchio si può tracciare una corda in modo che una sua parte tra af e ac, aggiunta a cf, sia uguale alla suddetta equatrice. Sia h il punto sul cerchio e ik la parte [di corda] tra ac e af (cfr. figura 36).
83. In terzo luogo, utilizzando la figura precedente con la tangente e la linea su cui è ricavata l’equatrice, bisogna considerare che, se si prende un’altra linea su ac, per esempio al, e questa viene ruotata dal lato destro tenendo fisso a, allora arriva a un certo punto del cerchio dal quale, se si traccia una corda parallela alla tangente fino alla linea af, la parte tra ac e af aggiunta a cf sarà uguale all’equatrice, tagliata da al (cfr. figura 37). Sia h quel punto sul cerchio, hk la semicorda, ik la parte e or la parte dell’equatrice. Non può esserci un altro punto diverso da h in cui si verifica quanto detto; infatti, al di qua di h le parti superano l’equatrice, al di là di h l’equatrice supera le parti. Ciò è vero se hf è un semiquadrante, altrimenti sposta il punto g finché risulti ciò.
84. Dunque, nel caso in cui si verifichi l’uguaglianza, dico che le parti sono uguali alla vera equatrice e che questa è or. Se lo negassi e dicessi che le parti sono minori della vera equatrice, cioè di or, allora, se le parti dovessero essere uguali, la linea da a, che le dovrebbe tagliare, cadrebbe necessariamente tra c e d, e così anche l’arco gf sarebbe minore di quanto dovrebbe essere e la lunula GOF sarebbe minore di HRG. Ma, poiché dici che or è minore dell’equatrice, allora questa cade al di sopra di or verso la tangente e or al di sotto di essa, verso hk; di conseguenza, or taglia un arco maggiore rispetto all’equatrice, la lunula GOF sarà maggiore di HRG e quindi [l’arco] sarà contemporaneamente maggiore e minore. Quindi, se dicessi che le porzioni sono maggiori e or maggiore dell’equatrice, seguirebbe la stessa contraddizione. La proposizione è dunque evidente.
85. Ora, per ultimo, illustrerò come trovare nello stesso tempo tutti i lati che vuoi dei poligoni uguali al cerchio. Questa è la proposizione: siano dati il semidiametro del cerchio, i semilati dei poligoni circoscritti e le linee inscritte di complemento94. Se si conduce una linea dal centro al lato del [poligono] circoscritto, essa taglia una parte più piccola sulla linea di complemento del poligono inscritto e una parte maggiore sul semilato del poligono circoscritto che, sommate, sono uguali al semilato del poligono uguale al cerchio: allora, se altre linee fossero tracciate attraverso le parti di tali linee in modo che dette parti si rapportino alle precedenti parti dei semilati come i semilati di un poligono presi insieme si rapportano ai semilati dell’altro, esse taglierebbero in modo simile le parti, la minore dalla linea inscritta di complemento e la maggiore dal semilato del poligono circoscritto, le quali sono uguali al semilato del poligono uguale al cerchio (cfr. figura 38).
86. Sia descritto un cerchio di centro a, il cui semidiametro sia ab; siano tracciati il semilato del triangolo circoscritto bc, la linea di complemento de, il semilato del quadrato circoscritto bf e la linea di complemento gh. Allo stesso modo, se vorrai, potrai tracciare i semilati dei vari poligoni. Traccia ora una linea da a a bc e, dove taglia de, poni i, e, dove taglia bc, poni k. Traccia, poi, un’altra linea da a a bc e, dove taglia gh, poni l e, dove taglia bc, poni m. Dico che se la parte più piccola di gh, che è gl, aggiunta alla più grande di bf, che è fm, è uguale al semilato del quadrato uguale al cerchio, allora, se la parte più piccola di de, che è di, si rapporta a gl come bc più de si rapporta a bf più gh e allo stesso modo ck95 si rapporta a fm, allora di più ck sarà il semilato del quadrato uguale al cerchio, e, viceversa, il semilato del quadrato uguale al cerchio si rapporterà al semilato del triangolo uguale al cerchio come le parti suddette [si rapportano tra di loro]. Come hai proceduto in questi poligoni, procedi in tutti gli altri96.
87. Da ciò segue questa proposizione. Infatti, dal diverso numero di lati dei diversi poligoni uguali a uno stesso cerchio, segue un diverso numero dei lati di poligoni circoscritti e delle linee di complemento dei [poligoni] inscritti. Di conseguenza, i lati, presi insieme, si rapportano nello stesso modo in cui si rapportano i lati presi singolarmente. Da ciò, affinché il rapporto dei lati sia lo stesso, anche il rapporto tra le parti che si formano [sui lati] dal centro attraverso le linee per costruire il semilato del poligono uguale al cerchio deve essere lo stesso.
88. Non c’è alcun dubbio tuttavia che si possa dividere la linea tracciata dal centro sui semilati in parti che siano uguali alle linee cercate. Ma potrebbe essere difficile [sapere] come si possano trovare linee di complemento che, sommate ai semilati del poligono circoscritto, danno i lati di poligoni della stessa superficie. Per esempio, se si somma de a bc, si ha il lato del triangolo, e così, se si somma gh a bf si ottiene il lato del quadrato uguale. Ma il rapporto dei lati si conosce facilmente da quanto detto sopra. Si ponga invece la linea di complemento nel triangolo uguale al semilato del poligono inscritto, per esempio de, e si dispongano le altre linee di complemento allo stesso modo. Si definiscono «complementi» perché, sommati ai semilati dei poligoni circoscritti, danno i semilati dei poligoni della stessa area.
89. Ci potrebbe essere anche un dubbio che le parti abbiano davvero il rapporto che devono avere. In tal caso potrai procedere così. Traccia ab di una certa lunghezza e, allo stesso modo, una linea da a [che passi] per f e una linea no, uguale a bc più de; dividi quest’ultima in due parti che stanno tra di loro come gh e bf, e siano esse op e pn. Riportale parallelamente a bc tra le suddette linee che partono da a [e passano] per b e per f. La linea tracciata da a attraverso gh taglia una parte di op, che si rapporta alla parte tagliata da gh come si rapportano i lati tra loro. Sia, dunque, oq la parte sulla linea op, che si rapporta a gl come deve essere. Se, dunque, di è uguale a op, allora hai quella parte. Fa’ lo stesso con l’altra parte della linea no, che è rs, e sia rs uguale a pn. Riportala, come hai fatto prima con l’altra parte, tra le linee che partono da a [e passano] per b e per f, e se la parte tagliata dalla linea aq su rs, ossia st, sarà uguale a ck, avrai ciò che cercavi. Altrimenti, apporta le opportune modifiche finché otterrai questo risultato. Questo è un procedimento universale, valido in tutti i poligoni.
90. Da ciò capisci che possiedi un’arte che ti consente di ridurre in una superficie rettilinea qualsiasi porzione di cerchio ricavabile attraverso i raggi97 dal centro, anche se [la porzione] non ha alcuna proporzionalità98 con l’intero [cerchio], e di trasformare, grazie all’equatrice, qualsiasi arco di circonferenza in una linea retta, anche se l’arco non ha alcuna proporzionalità con l’intera circonferenza, secondo quanto abbiamo detto in precedenza.
91. [E’ ora chiaro che la quadratura del cerchio finora sempre cercata, e, come si sa, non ancora trovata, è stata sufficientemente spiegata. Infatti, essa può essere conosciuta o attraverso la riduzione di una linea retta in una curva di circonferenza99 — e così è trattata nel primo libro — o, al contrario, attraverso la riduzione di una curva di circonferenza in una linea retta — e così la trovi esposta in due modi in questo secondo libro —, oppure insieme, nel caso in cui, con la riduzione della curva in retta, si trova il lato del quadrato uguale al cerchio, o ancora senza alcuna riduzione della retta in curva e viceversa, ma trovando semplicemente il lato del quadrato. Anche questi procedimenti li puoi trovare descritti nelle pagine precedenti. È dunque chiaro che questa parte finora sconosciuta è stata abbondantemente e dettagliatamente spiegata, e da questa ne seguono altre che, senza di essa, non potevano essere conosciute, ossia i complementi matematici. Così sia]100.
FACILISSIMA RETTIFICAZIONE DI UN CERCHIO
92.101 Sia descritto un cerchio attorno al centro a, e siano tracciati il diametro bac e la corda massima prolungata all’infinito che taglia ad angolo retto bac, e sia essa dae (cfr. figura 39).
Se attorno a un punto di ac, per esempio f, che dista da b una lunghezza pari alla corda dell’arco di un terzo del cerchio, descriverai un cerchio il cui semidiametro è fb, questo cerchio taglierà sulla corda maggiore la [linea] retta gh, uguale, o quasi, alla metà del cerchio. Infatti, se da b e c traccerai le [linee] rette verso g e h, la superficie BGCH sarà uguale o quasi alla superficie del cerchio BCDE.
93. Per intendere ciò, descrivi il cerchio BCDE attorno ad a, come prima (cfr. figura 40); traccia la corda dell’arco pari a un sesto del cerchio, e sia questo lm, poi [la corda dell’arco pari a] un quarto [del cerchio], e sia questo ik, e [la corda dell’arco pari a] un terzo [del cerchio], e sia no. Tieni conto che, poiché ogni corda è minore del suo arco e nell’arco maggiore la differenza tra questo e la corda è maggiore, allora il cerchio, che deve passare per b, deve avere il centro sul diametro bc e deve tagliare sulla corda estesa [una parte] uguale all’arco. Questo cerchio avrà il centro necessariamente oltre a, verso c, a una distanza [da b] che è tanto maggiore quanto maggiore è l’arco, a cui la corda è sottesa. Il cerchio minimo, di cui non si può dare uno minore, avrà il centro in a e il semidiametro ab. Invece, il cerchio massimo avrà il centro oltre a verso c, alla massima distanza da a, e il semidiametro massimo. Questo cerchio deve tagliare sulla corda massima una [linea] retta uguale al semicerchio, e questo semidiametro massimo è ciò che si cerca.
94. In secondo luogo, bisogna assicurarsi che è possibile determinare una corda che sia la media [proporzionale] tra le corde poste in proporzione ad essa102. Definisco corde «in proporzione» quelle corde – di cui una è tracciata come minore, l’altra come maggiore –, poste in modo che distino dalla [corda di mezzo] una lunghezza pari all’arco [compreso tra le corde], come ik da lm e da no. Infatti, come l’arco il è uguale a in, così lm e no sono dette [corde] in proporzione a ik. Dico che è possibile determinare una corda dove entrambe le [corde] in proporzione hanno quadrati, che, presi insieme, sono maggiori del doppio del quadrato della corda di mezzo. Così, se rispetto alla corda lm si tracciano altre corde in proporzione [ad essa], i quadrati di queste saranno sempre maggiori del doppio del quadrato di lm. Infatti, si può determinare la media proporzionale dove i quadrati delle due [corde] in proporzione saranno minori del doppio del quadrato della corda di mezzo, come nel caso delle [corde] in proporzione a no. Così, si può determinare la corda dove i quadrati delle due [corde] in proporzione saranno uguali al doppio del quadrato della corda di mezzo, perché, quanto minore è il quadrato della corda minore in proporzione rispetto al quadrato della corda di mezzo, tanto maggiore è il quadrato della [corda] maggiore, e poiché i quadrati delle due [corde] in proporzione saranno uguali al doppio del quadrato della corda di mezzo, è evidente che questa corda sarà ik. Infatti, la somma del quadrato di lm e il quadrato di no sarà eguale al doppio del quadrato di ik. Così, anche la somma tra il quadrato della corda maggiore, cioè de, e il quadrato della [corda] in proporzione ad essa, cioè il quadrato della corda minima, sarà eguale al doppio del quadrato di ik. E poiché il quadrato della corda minima non può avere alcun valore, è chiaro che il quadrato del diametro è uguale al doppio del quadrato di ik, cioè del lato del quadrato inscritto. Questo è vero e vale per tutte e due le corde in proporzione a ik103.
95. In terzo luogo, suppongo che ik superi del doppio i due semidiametri, ossia quello del cerchio massimo, che si cerca, e quello del cerchio minimo, il cui semidiametro è ab, e questo lo do come noto. Da lì, determino due corde in proporzione a ik che, prese insieme, saranno uguali ai due semidiametri. Infatti, si possono dare corde in proporzione maggiori, cioè, vicine a ik, corde minori, massimamente distanti da ik e, quindi, anche uguali.
96. In quarto luogo, da ciò deduco che no è il semidiametro, o quasi, del cerchio che si vuole trovare. Infatti, poiché i quadrati delle corde in proporzione uguali ai due semidiametri sono uguali al doppio del quadrato di ik e lm è il semidiametro del cerchio minimo, se si sottrae il quadrato [del semidiametro del cerchio minimo] al doppio del quadrato di ik, resta il quadrato di no. Di conseguenza no sarà il semidiametro del cerchio massimo che si vuole trovare104.
97. In quinto luogo, deduco che, se no è il semidiametro, allora, se su af si trova un punto p tale che ap si rapporti ad af come la freccia dell’arco ibk si rapporta alla freccia del semicerchio DBE, p sarà il centro del cerchio e pb il suo semidiametro che taglia, sulla corda prolungata da ik, qr, la quale, raddoppiata, è uguale a gh. E se procederai così per tutte e due le corde in proporzione, e troverai il centro facendo il rapporto delle frecce, le parti che si formeranno sulle corde prolungate, prese insieme, saranno sempre uguali a gh, anche se non ogni parte di una delle corde è uguale al suo arco, e così sarà per tutte le infinite corde in proporzione ad essa. Con la stessa regola potrai trovare [linee] rette uguali al semicerchio. Se tuttavia no è il semidiametro, allora queste parti non concorderanno. E dunque occorrerà modificare [il semidiametro] fino a quando concorderanno. Tuttavia, che la superficie BGCH è uguale alla superficie del cerchio risulta sufficientemente chiaro da quanto detto sopra.
98. In sesto luogo, deduco che le porzioni di cerchio comprese tra corde in proporzione si rapportano al cerchio nello stesso modo in cui l’arco compreso tra tali corde si rapporta alla circonferenza del cerchio. Prendi, per esempio, che la porzione di cerchio compresa tra lm e no sia un sesto del[la superficie del] cerchio, essendo l’arco ln e l’arco mo un sesto della circonferenza. Infatti, quanto più la parte compresa tra ik e lm è minore di un dodicesimo, tanto più la parte tra ik e no è maggiore di un dodicesimo del cerchio. E da questa considerazione potrai ottenere diverse parti di porzioni di cerchio e rendere uguali triangoli diversi. Quanto detto sia sufficiente.
Note a piè pagina
Niccolò V (ca. 1397–1455), il cui vero nome era Tommaso Parentucelli, nacque nel 1397 a Sarzana. Egli studiò a Bologna e giunse nel 1426 a Roma. Sotto Cosimo dei Medici prese la direzione della Biblioteca Fiorentina, nel 1444 fu nominato cardinale e vescovo di Bologna, e nel 1447 divenne papa. Umanista e amante delle scienze, il pontefice stipendiò traduttori per realizzare la versione latina di opere greche, fece lavorare filologi alla migliore definizione di testi classici, fece trascrivere e comprare manoscritti. Raccolse oltre milleduecento manoscritti greci e latini, alcuni di eccezionale importanza, che spaziano in molti campi della cultura umanistica, arricchendo così la Biblioteca Vaticana di molti manoscritti. Cfr. Vasoli 1968, 69–121; Meuthen 1989, 421–499; Manfredi 1994.
Il De mathematicis complementis è l’opera scientifica principale di Cusano sia per lunghezza sia per contenuto. Di essa si conoscono due versioni: la prima comprende un solo libro, scritto nei primi giorni del settembre 1453; la seconda comprende un secondo libro scritto il 24 novembre 1454. Il primo libro fu redatto in parte a Roma, da cui Cusano si era allontanato alla fine del maggio 1453, in parte a Bressanone, dove il cardinale si recò a fine giugno con la missione di riformare la vita spirituale nella sua diocesi. Il primo libro suscitò le perplessità del suo amico Toscanelli, perplessità che si trovano nella lettera De quadratura circuli e si focalizzano sull’ipotesi di una proporzionalità regolare nei poligoni intermedi tra il triangolo inscritto e il cerchio isoperimetrico: «Da ciò, quindi, è chiaro che se il triangolo ha l’ampiezza minima, la prima linea si differenzia al massimo dalla seconda, e se il cerchio ha l’ampiezza massima, la prima e la seconda linea coincidono, e così sarà, con le debite proporzioni, nei poligoni intermedi» (Cusanus 2010i, 7, 1–4). Pare che Toscanelli avesse scosso la certezza di Cusano, tanto che questi decise di inviare la lettera a Peurbach per avere il suo parere. Nel frattempo, egli trovò nuove dimostrazioni, che espose in un secondo libro, in aggiunta al primo. Tuttavia, neanche questi nuovi tentativi soddisfarono gli “specialisti” del tempo, perciò Cusano fece un ennesimo tentativo di rettificazione nella Declaratio rectilineationis curvae. Regiomontano, che all’epoca studiava la quadratura del cerchio e conosceva bene quella del cardinale, fu molto critico riguardo a I complementi matematici. Il titolo I complementi matematici non deve lasciar pensare che si tratti di un’opera integrativa, di rifinura o di completamento. L’intento di Cusano è quello di dare compiutezza e di perfezionare tutta la geometria, risolvendo definitivamente la questione in cui anche il grande Archimede si era imbattutto e aveva fallito, ossia la quadratura del cerchio: «a colui che vorrà applicare ancor di più la propria mente, ciò che non era conoscibile né conosciuto in geometria si paleserà chiaramente. È per questa ragione che tale scoperta merita di portare il nome di complemento» (Cusanus 2010i, 40, 8–10).
La traduzione delle opere di Archimede fu ordinata da Niccolò V a Iacopo Cassiano, detto Iacopo da Cremona (ca. 1395–ca. 1454): questi era un ecclesiastico e per 14 anni fu allievo di Vittorino da Feltre (ca. 1378–1446) e suo successore come educatore dei figli di Ludovico Gonzaga di Mantova (1412–1478). Dal 1449, a Roma, Iacopo tradusse manoscritti greci su commissione di Niccolò V e nel 1451 fu convocato come esperto per valutare la traduzione dell’Almagesto di Tolomeo procurata da Giorgio di Trebisonda (1395–ca. 1473) e dichiarata inadeguata soprattutto da Bessarione (1403–1472). Anche Iacopo espresse parere negativo e per questo si inimicò Giorgio. Morì tra il 1451 e il 1454. La traduzione di Archimede fu conclusa sicuramente verso la fine dell’estate del 1450, fu condotta sul codice A, che andò nelle mani di Lorenzo Valla (ca. 1407–1457) e sparì nel corso del sec. XVI. I contemporanei, che ignoravano la traduzione duecentesca, senz’altro peggiore, del domenicano Guglielmo di Moerbeke (1215–ca. 1286), accolsero con interesse la versione del Cassiano. Oltre a Cusano, se ne servì Regiomontano, il quale la trascrisse in vista di una propria più accurata traduzione. Servendosi appunto di questa copia (oggi codice Cent. V 15 della Stadtbibliothek di Norimberga), portata da Regiomontano in Germania intorno al 1468, Thomas Gechauff, detto Venatorius (ca.1488–1551) pubblicò la traduzione nell’editio princeps del corpus di Archimede (Archimedes 1544). L’opera denuncia comunque – specie nella resa dei passi più complessi – limiti evidenti, dovuti probabilmente più all’approssimativa preparazione tecnica del traduttore che a un’imperfetta conoscenza del greco. È anche possibile che alla morte di Cassiano la traduzione non avesse ancora raggiunto la versione definitiva. Come evidenzia Nicolle 1998, nota 1, 82, stando alla ricostruzione di Marshall Clagett (1964–1984a, III, 321–342), Cusano ebbe accesso a questa traduzione e alle sue fonti solo a partire dall’anno 1453; cfr. anche D’Alessandro e Napolitani 2012.
Per «recta» si intende qua, come in tutti gli scritti matematici, la linea dritta.
Cfr. Cusanus 2010j, 1, 2.
Cusano usa il termine «proportio». Si è preferito qui tradurre con «proporzionalità», nella scia di Luca Pacioli, che molto probabilmente aveva letto i lavori di Cusano, così come le opere di Archimede tradotte in latino, tra il 1449 e il 1453, da Iacopo da San Cassiano (Iacobus Cremonensis). Nel 1489, Pacioli si trovava a Roma, e Pierleone da Spoleto lo introdusse nelle corti cardinalizie (cfr. Pacioli 1494; Giusti e Maccagni 1994; Giusti e Martelli 2010 (in part. Ulivi, 19–58); Esteve e Martelli 2011). Cfr. Cusanus 2010j, nota12. Sul procedimento archimedeo tramite la spirale, cfr. Cusanus 2010c, 2, 11–18; Cusanus 2010d, 16, 6–12.
Si è tradotto «figura multiangula» con il termine poligono. Cusano intende qui non soltanto poligoni di più lati, bensì poligoni regolari e precisamente poligoni isoperimetrici, aventi cioè lo stesso perimetro. Cfr. Cusanus 2010b. Anche nel caso di «figura (o superficies) poligoniae», «multiangulae», o «figura quadrata» o «figura circolare» si tradurrà semplicemente con poligono, quadrato, cerchio ecc. a meno che il contesto non richieda diversamente.
Dal momento che è chiaro che Cusano intende per «potentia» la seconda potenza, si tradurrà semplicemente con «quadrato».
Si suppone implicitamente che i poligoni siano tutti dello stesso perimetro (isoperimetrici). Il riferimento è a Euclide, che riguarda in realtà soltanto il pentagono: «Intorno a un cerchio dato circoscrivere un pentagono sia equiangolo che equilatero» (Euclide 2007, IV, 12, 963) e non tutti i poligoni regolari.
Per «figura rectilinea» si intende una figura delimitata da lati dritti. Il termine «figura» è reso a volte alla lettera, a volte con «poligono», a seconda del contesto.
Cfr. Cusanus 2010b, 5, 5–8; Bradwardine 1495b, II, 5, concl. 5 («circulus autem totus est angulus»). Il ragionamento di Cusano s’incentra sull’idea che il cerchio ha ovunque angoli, per cui è come un poligono regolare con un numero infinito di angoli.
Come si è tradotto «trigonus», «triangulus» con
«triangolo», così si è tradotto «tetragonus» con «quadrato».
Qui si afferma per la prima volta che si tratta di poligoni
regolari di ugual perimetro. Il fatto che  cresce con n crescente mentre r
decresce, viene utilizzato infra, I. 4 e in I. 10 ciò viene
espresso con delle modifiche.
cresce con n crescente mentre r
decresce, viene utilizzato infra, I. 4 e in I. 10 ciò viene
espresso con delle modifiche.
Per «peripheria» s’intende la linea di contorno. A seconda della figura, si tradurrà con perimetro o circonferenza.
Cfr. Cusanus 2010i, 21 e 10.
Per rispettare al meglio lo spirito del linguaggio cusaniano, a differenza sia di Hoffmann che traduce «capacitas» con «Fläche» (Hofmann e Hofmann 1980, 71), sia di Nicolle che traduce il termine latino con «Surface» (Nicolle 1998, 54), si è preferito in questo caso differenziare i due termini (capacitas e superficies), utilizzati entrambi da Cusano, rendendo il latino capacitas con ampiezza. In altri passi si è tradotto con estensione o superficie.
Si trova qui l’idea del cerchio come poligono regolare di un numero infinito di lati.
«erit sic proportionabiliter in mediis polygoniis»: è questa la proposizione più discutibile, oggetto di critica da parte di Toscanelli. In una nota a margine scritta di proprio pugno nel manoscritto Cu (Gestrich 1992, 219, 52r), si fa riferimento all’obiezione sollevata da Toscanelli, che mette in dubbio l’esattezza di tale proporzionalità. Si tratta di uno scritto indirizzato al cardinale e più tardi inoltrato a Peurbach (Cusanus 2010a). Da ciò l’esigenza da parte di Cusano di aggiungere il secondo libro dei Complementi matematici (cfr. Cusanus 2010i, nota1; Cusanus 2010j, 3, 9–15; Cusanus 2010i, 22).
Cusano scrive «superficies quadrangularis». A differenza del termine «tetragononus», l’espressione «figura quadrangularis» – come anche «quadrangulus» – è equivoca: Cusano la riferisce tanto al quadrato quanto al rettangolo e al parallelogramma. Di volta in volta, a seconda del contesto, si renderà «quadrangularis» con la figura corrispondente. Sull’utilizzo, da parte di Cusano, del termine «quadrangulus» invece di «quadratus» e sull’influenza dalla terminologia matematica medioevale, cfr. Hofmann 1966, 98–136, spec. 105.
Cfr. Cusanus 2010b, 38 e Cusanus 2010j, 2, 1–3; una versione più precisa si trova in Cusanus 2010i, 17. Cusano poteva leggere la prop. 1 de La misura del cerchio di Archimede in Bradwardine 1495b, III, 6, concl. 5e in Da Novara 2005, VI, 13.
Cfr. Cusanus 2010j, 2, 8–11; una versione più precisa si trova in: Cusanus 2010i, 33. È il riferimento più frequente di Cusano agli Elementi di Euclide: «Sottrarre dalla retta data la parte prescritta» (Euclide 2007, VI, prop. 9, 1041).
L’allusione è a Bradwardine 1495b, II, 5, concl. 1 (hysoperimetrum); II,4,concl.2 (poligonium); II,1 (isopleurus); Gerbertus 1899, V, 3 (hysopleuros); cfr. anche Cusanus 2010b, 4, 1–3; Cusanus 2010j, 2, 5–8. Nel manoscritto di Bruxelles si fa inoltre riferimento alle argomentazioni di Roger Bacon sulle figure isoperimetriche (specie nella formulazione della Prop. 13), soprattutto alla proprietà isoperimetrica della sfera, di cui si parla anche in Bradwardine 1495b, II, 5, concl. 5, e si legge la spiegazione dal greco del termine isoperimeter fornita nella concl. 1 di Bradwardine 1495b, II, 5. Sul tema degli isoperimetrici, cfr. Cusanus 2010b.
Come in tutti gli scritti matematici, Cusano utilizza il
termine «diameter» per indicare la diagonale in base a una
etimologia inesatta da «
Cusano scrive «embadum», termine che si ritrova in Bradwardine 1495b, 75r–81v: «In trigono ortogonio cuius podismus est pedum xxv embadum»; in Oresme 1966, f. 240r: «In trigono ortogonio cuius podismus est pedum xxv embadum». Cfr. anche la Practica geometriae di Leonardo Pisano: «ad quam mensuram colligere embada, hoc est areas camporum, monstrabo» (Pisanus 1862, II, 3).
Il termine «aequalis» è reso con «uguale» lasciando al contesto di chiarire se si tratta di uguaglianza di lunghezze, di superfici o di volumi. In questo caso è chiaro che si tratta di una equivalenza.
Per una dimostrazione, cfr. Hofmann e Hofmann 1980, nota 21, 217. Qui il riferimento è al libro I del De sphera et de cilindro di Archimede (Archimedes 1910a; Archimede 1974, 69–180).
Il termine «similis» è reso con «simile», lasciando al contesto di chiarire se si tratta di uguaglianza, di somiglianza, di corrispondenza. Cfr. Cusanus 1994, 5, 6ss..
Come nota Hofmann e Hofmann 1980, nota 23, 218, con la divisibilità illimitata del continuum si tocca un argomento discusso con fervore da molto tempo nella scuola nominalistica di Parigi.
Cfr. Cusanus 2010i, 6, 6–II. Questa è la tesi principale dei trattati più antichi sulle figure di ugual perimetro; cfr. Busard 1980, prop. 6, 80; Bradwardine 1495b, II, 4, concl. 5; De Muris 1998, 315ss. Sul tema, cfr. Gericke 1982, 160–187; Di Meglio 2010, 15–21; Heath 1921, II, 211; Porter 1933.
Cfr. Bradwardine 1495b, II, 4, concl. 1; II, 4, concl.2; II, 4, concl.5, dove si dà la seguente dimostrazione: «Se abc è un triangolo equilatero e adce un rettangolo con superficie e altezza uguali ad esso, il perimetro del triangolo è maggiore del perimetro del rettangolo. Se dunque il rettangolo ADGF viene trasformato in triangolo di ugual perimetro, la sua superficie è maggiore di quella del triangolo ecc.». Bradwardine sostiene che questo procedimento si può generalizzare, ma tralascia la singola esposizione. Cfr. anche Busard 1980, prop. 1, 69.
Cfr. Cusanus 2010j, 3, 9–15; Cusanus 2010i, 7, 1–3. Se si indica con f la
superficie del cerchio, con n il numero
dei lati del poligono, con  la sua superficie, con
la sua superficie, con 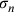 il
semidiametro del cerchio iscritto (la linea “prima”) e con
il
semidiametro del cerchio iscritto (la linea “prima”) e con
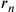 il
semidiametro del cerchio circoscritto (la linea “seconda”),
allora:
il
semidiametro del cerchio circoscritto (la linea “seconda”),
allora: 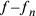 diminuisce al diminuire di
diminuisce al diminuire di 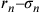 . Dunque, s’intende la
decrescita “regolare” di
. Dunque, s’intende la
decrescita “regolare” di 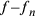 con
con 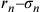 decrescente. Il carattere
puramente ipotetico dell’impostazione viene ulteriormente
sottolineato dalla formulazione iniziale “se si pone”.
decrescente. Il carattere
puramente ipotetico dell’impostazione viene ulteriormente
sottolineato dalla formulazione iniziale “se si pone”.
Questa prima ipotesi significherebbe, come risulta dal
calcolo successivo, che 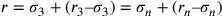 .
Cusano ipotizza dapprima
.
Cusano ipotizza dapprima 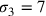 quindi
quindi 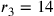 , come era già
accaduto in Cusanus 2010g, 10; ne risulta
, come era già
accaduto in Cusanus 2010g, 10; ne risulta 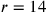 . Cusano parte dunque da
. Cusano parte dunque da 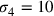 , quindi
, quindi
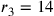 che è
approssimativamente esatto perché
che è
approssimativamente esatto perché 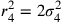 . Anche in questo
caso ottiene
. Anche in questo
caso ottiene 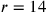 . Nel suo calcolo la questione
viene gestita all’esatto contrario. Se qui
. Nel suo calcolo la questione
viene gestita all’esatto contrario. Se qui 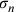 non avesse il
valore esatto, bensì maggiore,
non avesse il
valore esatto, bensì maggiore,  ad esso
appartenente, sarebbe troppo grande come pure il secondo che
risulta da
ad esso
appartenente, sarebbe troppo grande come pure il secondo che
risulta da  ; ne
consegue che
; ne
consegue che  appartenente alla seconda sarebbe
troppo piccolo ecc.
appartenente alla seconda sarebbe
troppo piccolo ecc.
In questo caso si è reso il termine «portio» con «parte»; si è preferito utilizzare il termine «parte» in riferimento alle porzioni di linea retta, ossia ai segmenti, o di linea curva, mentre si è utilizzato il termine «porzione» per esprimere la parte di una superficie, in genere riferita a un segmento circolare o a un settore circolare.
Questa seconda ipotesi significherebbe: 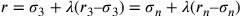 ;
dove per
;
dove per 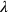 s’intende una frazione. Questo
paragrafo e il successivo mancano in 7 dei manoscritti più
antichi a noi noti de I Complementi
matematici.
s’intende una frazione. Questo
paragrafo e il successivo mancano in 7 dei manoscritti più
antichi a noi noti de I Complementi
matematici.
Ciò che qui è interessante, al di là dei casi particolari
usati da Cusano, è l’intuizione di una funzione di 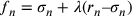 per
per
 che
cresce in modo monotono o decresce in modo monotono. Se qui
che
cresce in modo monotono o decresce in modo monotono. Se qui
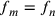 ,
allora la funzione è costante. Il valore della funzione ad
esso appartenente può essere determinato mediante
,
allora la funzione è costante. Il valore della funzione ad
esso appartenente può essere determinato mediante  come r.
come r.
Per «aliquota» s’intende: contenuta un numero intero di volte, ossia un sottomultiplo intero. Cfr. Bradwardine 1495b, 68: «pars autem aliquota est illa quae, aliquotiens sumpta, reddit aequaliter summum suum. Pars vero non-aliquota est illa quae nullatenus, aliquotiens sumpta, reddit aequaliter summum suum» («Una parte aliquota è invero quella che, presa un determinato numero di volte, dà come risultato il suo tutto. Una parte non aliquota è quella che, presa un qualsiasi numero di volte, non dà come risultato il suo tutto» (in Clagett 1964–1984a, 493. trad. nostra).
Si veda la formulazione, leggermente diversa, in Cusanus 2010j, 3, 9–15.
Per «aequalem» si intende qui «della stessa lunghezza».
Ciò si richiama al procedimento desunto in Cusanus 2010j, 4–5, ma vi è un’ abbreviazione del testo e una lieve modifica della figura.
Cfr. Cusanus 2010j, 4–5.
Cfr. Cusanus 2010j, fig.~3; Da Novara 2005, IV, 9. Questa figura ha portato John Wallis (1616–1703) a credere, a torto, che Cusano avesse avuto l’intuizione della costruzione e delle proprietà della cicloice. Cfr. lo scambio epistolare tra Wallis e Leibniz, in: Leibniz 1849–1863, IV, 5–82, spec: Wallis–Leibniz, 4/5/1697 e 11/12/1697 (9–10); Leibniz–Wallis, 29/3/1697 (13); Leibniz–Wallis, 7/6/1697 (27).
Riecheggiano in questo passo le ultime frasi del Cusanus 2010j, 11, 4–5; 12, 1–5: «è la suprema perfezione dell’arte geometrica, alla quale fino ad oggi non risulta che gli Antichi siano pervenuti. L’arte delle trasformazioni geometriche, […] è ora sufficientemente compiuta poiché essa ha portato alla quadratura del cerchio. E noi pensiamo che niente più di quanto c’è da sapere in geometria resterà nascosto a colui che vorrà ricercare con diligenza in questo campo». Poco più avanti Cusano, per indicare il seno utilizza l’espressione «semicorda dell’arco doppio» secondo un’invenzione indiana tramandata dagli arabi all’occidente medievale (cfr. Taton 1957–1958, I, 161). Cfr. Cusanus 2010m, 1, 11ss.; 8, 1–4.
Letteralmente: «multiangula similium laterum».
L’espressione latina è «medietas duplae», già utilizzata ne
Le trasformazioni geometriche (Cusanus 2010b, 40) e ne La quadratura del
cerchio (Cusanus 2010j, 9, 8), è un’espressione idiomatica intraducibile in sè,
ed è legata al problema della duplicazione del cubo.
Algebricamente si tratta della radice di 2. Vescovini (1972, nota 10) sottolinea che l’espressione si rifà alla
tradizione matematica medievale con cui Cusano allude alla
dimostrazione dell’irrazionalità della  , spesso citata in
Aristotele e menzionata anche in Oresme 1966, 160 e in Bradwardine 1495b, III–1. Oresme chiama il rapporto
, spesso citata in
Aristotele e menzionata anche in Oresme 1966, 160 e in Bradwardine 1495b, III–1. Oresme chiama il rapporto 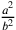 la metà di
la metà di 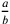 (cfr. Oresme 1966, 454). La proportio proportionum,
cioè la proporzione tra due rapporti
(cfr. Oresme 1966, 454). La proportio proportionum,
cioè la proporzione tra due rapporti 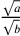 e
e 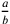 è espressa
dal rapporto
è espressa
dal rapporto 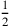 . Se la proportio dupla è il quadrato, la metà,
ossia la medietas duplae, è la radice.
Cfr. Oresme 1966, 454; Pedersen 1953, 1–134ss. Cusano si riferisce a questa terminologia
matematica di Bradwardine, di Oresme e di altri studiosi interessati agli
incommensurabili e ai rapporti irrazionali. Sul tema, cfr.
Rommevaux 2003, 401–418.
. Se la proportio dupla è il quadrato, la metà,
ossia la medietas duplae, è la radice.
Cfr. Oresme 1966, 454; Pedersen 1953, 1–134ss. Cusano si riferisce a questa terminologia
matematica di Bradwardine, di Oresme e di altri studiosi interessati agli
incommensurabili e ai rapporti irrazionali. Sul tema, cfr.
Rommevaux 2003, 401–418.
Cfr. Cusanus 2010j, 9.
Si ritrova, parola per parola, la fine di Cusano 2010j, 10–11, con gli stessi valori numerici.
Il riferimento è al primo scritto matematico, il De geometricis transmutationibus.
Cusano parla di «sectores».
La scoperta di Cusano è che in ogni poligono la differenza fra l’apotema (prima linea) e il raggio del cerchio isoperimetrico al poligono è un segmento minore della freccia che ha con quest’ultima un rapporto costante.
Qui termina la prima versione dei Complemeti matematici. In Cu è stata aggiunta una nota a margine del testo tramandata nelle copie posteriori e ripresa anche nelle diverse edizioni a stampa nonostante non appartenga al testo. Aggiunto in Bl, essa recita: «Se questa scoperta è vera, accade che la linea tracciata dalla prima linea del triangolo alla prima del cerchio isoperimetrico passa attraverso le prime rette di tutti i poligono intermedi. Ma se non è vero che la linea passa in questo modo, e se fosse invece vero che una curva di una qualche curvatura passi dalla prima del triangolo attraverso le prime di tutti i poligoni fino alla prima del cerchio, allora questa scoperta non sarebbe sufficiente. E poiché il dubbio c’è, ho apportato in un secondo libro altre mie invenzioni che fugano il dubbio in questione».
In questo caso il termine «aequalis» sta a significare che il movimento di b descrive una linea che ha la stessa lunghezza del lato bc.
Cusano considera «aequaliter» il movimento che concerne o la rotazione di un segmento (intorno ad un asse attraverso una delle sue estremità) o lo spostamento di un segmento perpendicolare alla sua direzione o infine lo spostamento di un segmento nella sua direzione. Sebbene intuisca il “fluido” andamento del movimento, ciò che a Cusano interessa è soprattutto la relazione geometrica del movimento ipotizzato (cfr. Hofmann e Hofmann 1980, 221, nota 41).
Si trovano qui tre figure assolutamente identiche a tre configurazioni descritte da Oresme. La prima è la rappresentazione del movimento di una linea ab che ruota intorno ad a; la seconda la rappresentazione del movimento uniforme di una linea ab; infine vi è la rappresentazione della generazione dei cerchi mediante il movimento di una linea ab che ruota completamente intorno ad a. Questa coincidenza suggerisce che Cusano abbia letto il trattato di Oresme.
La figura 18 è invertita da sinistra a destra in Cu. Cusano non dispone della rappresentazione in prospettiva, che rende possibile oggi la comprensione delle sue figure.
Si tratta in pratica del tronco di cilindro.
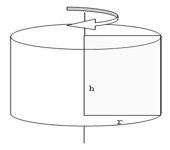
Il termine tecnico «ductio» significa a volte il movimento di costruzione geometrica, a volte l’operazione aritmetica di moltiplicare. Come Hofmann suggerisce (Hofmann e Hofmann 1980, nota 55, 223), è probabile che il primo modo in cui Cusano utilizza tale termine abbia influenzato l’utilizzo di esso come metodo geometrico d’integrazione e ipotizza un’influenza diretta di Cusano (i cui scritti erano assai conosciuti all’epoca) su Gregorio di San Vincenzo (1584–1667), il quale nell’Opus geometricum ad mesolabum per rationum, proportionalitatumque novas proprietates parla appunto di «ductus plani in planum» (Di San Vincenzio 1668, VII, 241ss.).
Con «avanzamento» e «arretramento» si traducono i termini «progressio» e «descensio».
Le figure 18 e 19 sono invertite da sinistra a destra nel Codex Cusanus 219 (Gestrich 1992).
Per «quadrangulus rectilineus» Cusano intende qui un parallelogramma.
Si può comprendere così la figura (mantello di tronco di cono):
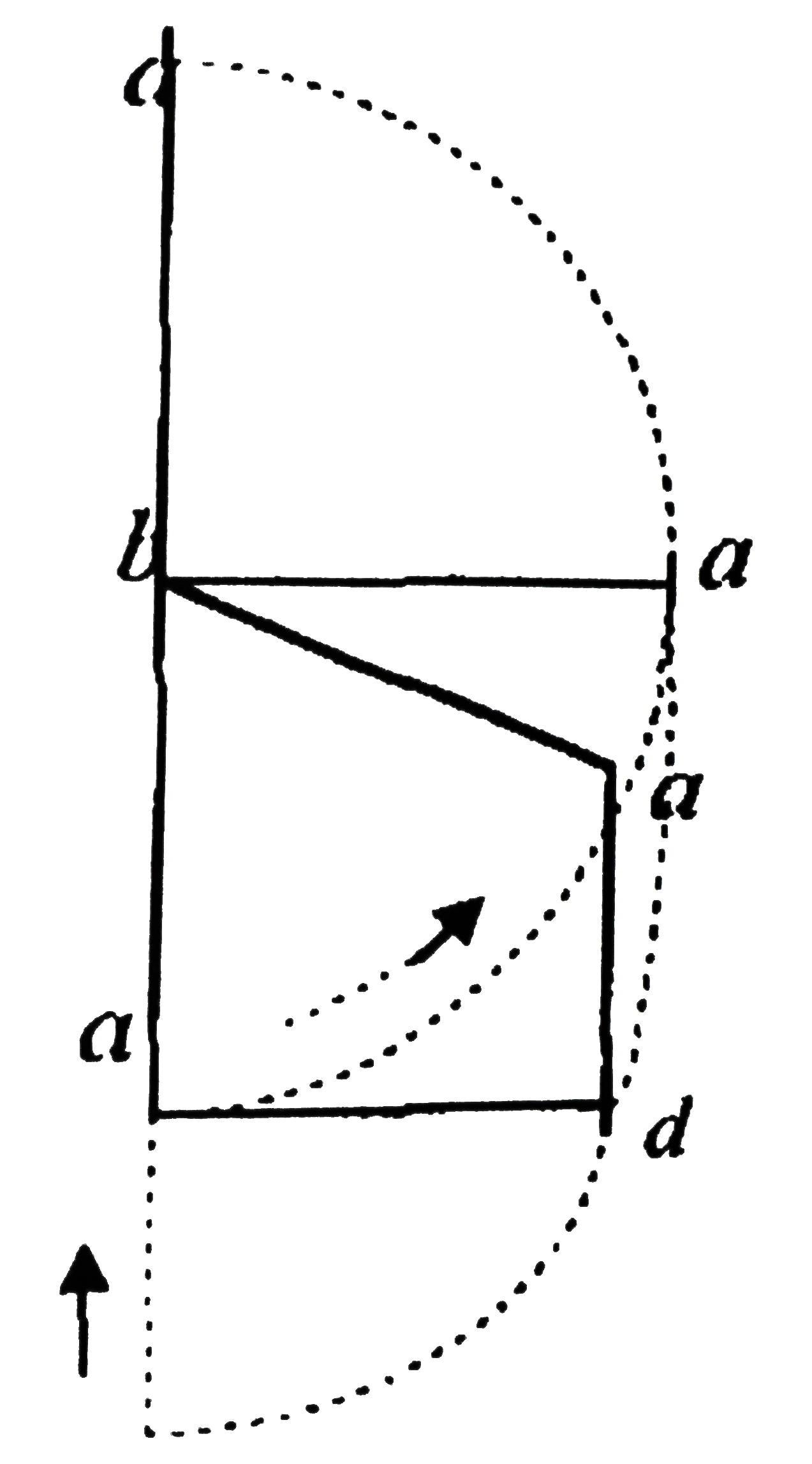
mediante la rotazione di ab risulta
la superficie del cerchio 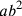 . Nello stesso tempo ab si eleva sull’altezza ad generando un anello circolare.
. Nello stesso tempo ab si eleva sull’altezza ad generando un anello circolare.
«rombhus» è il termine utilizzato da Cusano per intendere un solido formato da due coni uguali.
Riportiamo qui la figura tratta da J. M. Nicolle (Nicolle 1998, 85, nota 34) che ben rappresenta il movimento di generazione delle coniche pensato da Cusano.
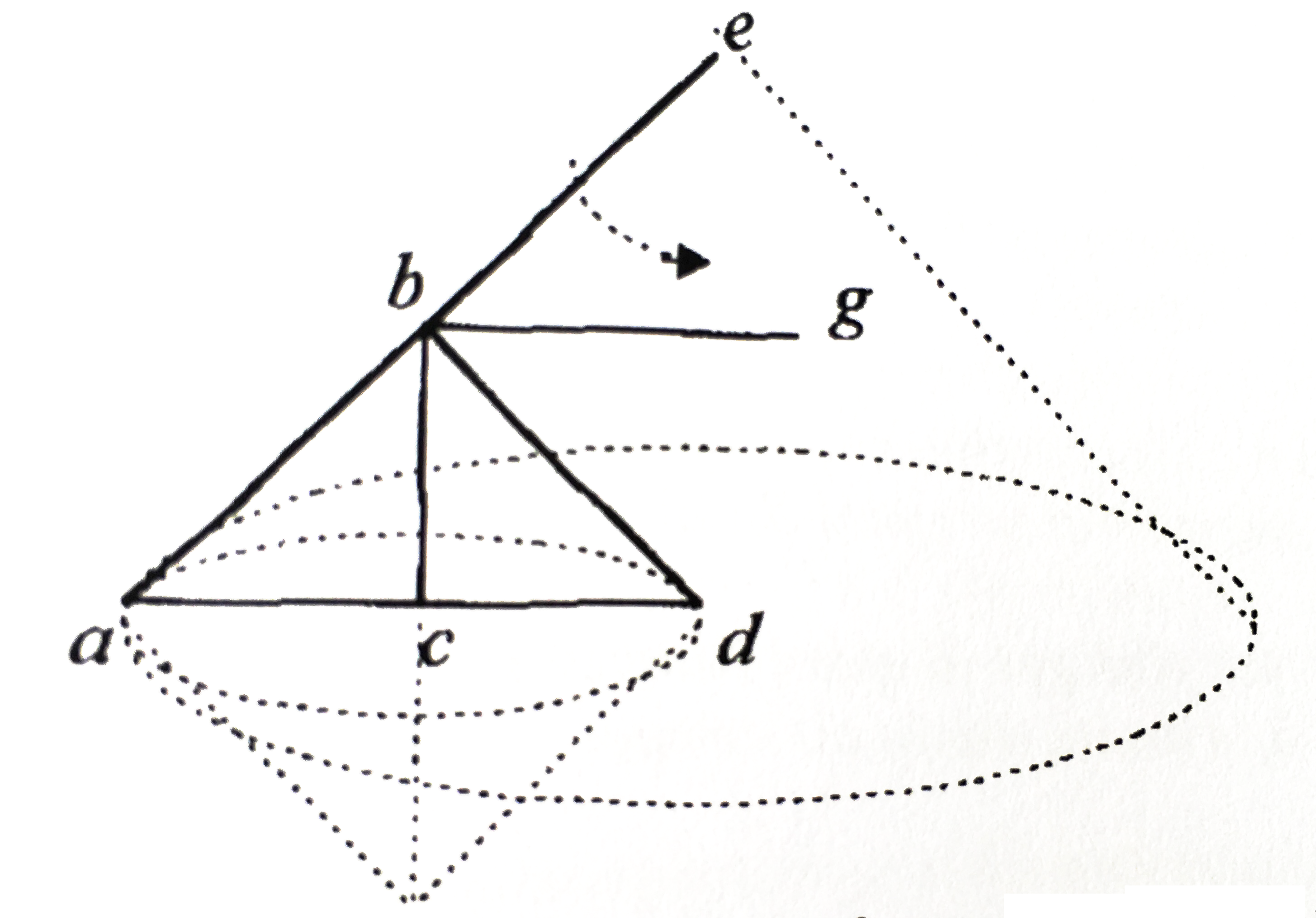
Il «rombhus» di cui parla Cusano è il solido generato dalla rotazione del triangolo attorno alla base, ossia un solido risultante dall’unione di due coni, congruenti con la base comune e con i vertici opposti rispetto al piano della base. L’altezza del triangolo è il raggio dei due coni, mentre l’altezza di ciascuno dei due coni ha misura pari a metà della misura della base. La conclusione di questo paragrafo («Sai, dunque, che, quando il cono e il cilindro hanno la stessa base e il lato del cono è uguale all’altezza del cilindro, la superficie del cilindro è sempre doppia rispetto a quella del cono, e se è maggiore dell’altezza del cilindro, la superficie sarà maggiore, e se è minore dell’altezza del cilindro, la superficie sarà minore, in maniera proporzionale»), riprende Johannes de Tinemue. Cfr. De Tinemue 1964, I, prop. 2 cor. 462, 23–26.
La figura è preceduta da una figura intermedia nel Codex Cusanus 219 (Gestrich 1992), che porta alle sfere (cfr. Nicolle 1998, 85, nota 34).
«Alia curvitate curvae»: il termine «curvitas» è equivoco, significando a volte la quantità d’inflessione della curva, a volte l’essenza dell’essere curvo (cfr. Hofmann e Hofmann 1980, nota 49, 222). L’espressione «curva aliqua curvitate» potrebbe avere un senso ontologico: sarebbe una curva che parteciperebbe dell’essere curvo. Qui Cusano vede la soluzione – la funzione asintotica – ma la scarta subito. Cfr. anche Cusanus 2010e, 10. Facendo seguito alla dottrina di Oresme sulle latitudines formarum (cfr. Oresme 1968), con «curvitas uniformiter difformis» bisogna intendere una curva avente una variazione di curvatura costante. Tuttavia, vista la non chiarezza da parte di Cusano, non ci è dato sapere che tipo di curvatura egli abbia in mente. Sul tema, cfr. Hofmann e Hofmann 1980, nota 6, 234.
Cfr. Archimedes 1910a, I, 33: «la superficie di ogni sfera è quadrupla del suo cerchio massimo» (tr. cit., p. 152); Johannis de Tinemue (1964, I, prop. 6, 480, 42ss.); Busard 1980, prop. 7.
Nel testo dei manoscritti e delle prime stampe si trova per errore «pyramidalis», anziché «columnalis». Omnisanctus notò l’errore e lo corresse nell’edizione p.
Si tratta delle sezioni coniche che risultano dalla rotazione della figura intorno all’asse ad. La figura considerata si ritrova nel primo tentativo di rettificazione nella prima parte del secondo libro, dove Cusano determina un tronco di cono il cui mantello è uguale alla superficie della semisfera. L’approssimazione viene generalizzata poco più tardi a tutti quegli archi più piccoli del settore circolare.
L’espressione latina è «per aequalem scilicet inaequalitatem».
Per «sectio trasversalis cylindri» bisogna intendere una sezione obliqua di cilindro, vale a dire un’ellisse; quanto alla «sectio obliqua sferica» Cusano sembra dimenticare che si tratta molto semplicemente di un cerchio.
Il testo parla dell’eccesso della corda rispetto alla
freccia mentre ab è una semicorda; si
ha 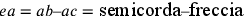 .
.
In tutti i manoscritti si trova l’espressione «excessus arcus super sagittam», tuttavia con esso sicuramente s’intende «excessus semichordae super sagittam». La correzione fu effettuata anche da Omnisanctus nell’edizione p.
Come osserva Hofmann (Hofmann e Hofmann 1980, nota 57, 223), la regola esposta è inesatta; essa può essere risultata da generalizzazioni di particolari osservazioni su un sesto di cerchio.
Cfr. Cusanus 2010g, 31–33. Secondo Hofmann la dimostrazione che segue non vale che per un angolo di 60 gradi e a condizione di accettare un’ampia approssimazione. Tutto il procedimento è esposto in Hofmann e Hofmann 1980, nota 59, 223.
In Cu le figure dal 52 al 54 sono ruotate di 90 gradi, con ad a formare la base (cfr. Gestrich 1992).
Dalla prop. 32 del libro II degli Elementi di Euclide si ha che 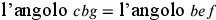 . Poniamo sulla linea prolungata bc il segmento
. Poniamo sulla linea prolungata bc il segmento 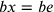 , cosicché il triangolo BGX
, cosicché il triangolo BGX  il triangolo EFB. Da ciò segue (Euclide 2007, III, 20) che il punto g si trova sull’arco xgb congruente all’arco bfe. Se si pone il raggio di entrambi i
cerchi in questione con la lettera r,
si ha che:
il triangolo EFB. Da ciò segue (Euclide 2007, III, 20) che il punto g si trova sull’arco xgb congruente all’arco bfe. Se si pone il raggio di entrambi i
cerchi in questione con la lettera r,
si ha che: 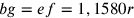 ;
;  e
e 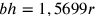 . Questo risultato è
piuttosto preciso (poiché l’arco misura 1,5708r), ma resta al di sotto del limite di
Archimede (1,5704 r).
. Questo risultato è
piuttosto preciso (poiché l’arco misura 1,5708r), ma resta al di sotto del limite di
Archimede (1,5704 r).
Il ragionamento di Cusano è il seguente: ![\frac{(bg+ef+fg)}{2}=bg+[\frac{(ef–bf)}{2}]](../../../media/sources/13/23/EOAineq_23_46.png) .
Poco più avanti (64, 1–5) dalla dimostrazione che segue si
capisce che il medium deve essere posto
in relazione alla differenza tra le corde. Cusano non era
ancora del tutto convinto di tale dimostrazione e pertanto
cercò di dare una delucidazione più chiara, ma ancora
insufficiente, nella Declaratio
rectilineationis curvae, indirizzata a Peurbach.
.
Poco più avanti (64, 1–5) dalla dimostrazione che segue si
capisce che il medium deve essere posto
in relazione alla differenza tra le corde. Cusano non era
ancora del tutto convinto di tale dimostrazione e pertanto
cercò di dare una delucidazione più chiara, ma ancora
insufficiente, nella Declaratio
rectilineationis curvae, indirizzata a Peurbach.
Anche con quest’altro tentativo risulta un’approssimazione
al di sotto del limite di Archimede. Infatti, l’angolo 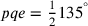 ; q si trova dunque sull’arco di
circonferenza attraverso b ed e, il cui centro taglia a metà l’arco be. Da ciò risulta che
; q si trova dunque sull’arco di
circonferenza attraverso b ed e, il cui centro taglia a metà l’arco be. Da ciò risulta che  , mentre
l’arco
, mentre
l’arco 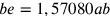 . Questa approssimazione resta dunque al di sotto
del limite archimedeo di 1,57042 ab. Se
il punto di divisione q si trova su c, allora
. Questa approssimazione resta dunque al di sotto
del limite archimedeo di 1,57042 ab. Se
il punto di divisione q si trova su c, allora  ; se esso si
trova su d, allora
; se esso si
trova su d, allora 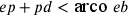 . Cusano deduce
che esiste un punto intermedio tale che
. Cusano deduce
che esiste un punto intermedio tale che 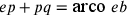 . È
chiaro che la somma
. È
chiaro che la somma 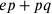 aumenta continuamente quando p si muove sull’arco eb verso b, ma il
punto di partenza del moto non è c: è
il punto di intersezione di bd con
l’arco eb. Il punto r non può essere dunque a destra, ma a
sinistra di p.
aumenta continuamente quando p si muove sull’arco eb verso b, ma il
punto di partenza del moto non è c: è
il punto di intersezione di bd con
l’arco eb. Il punto r non può essere dunque a destra, ma a
sinistra di p.
Il testo che segue contiene una generalizzazione delle prime proposizioni sui tronchi di cono aventi la stessa superficie laterale. Per «semicorda del doppio arco», si intende il seno. Cfr. infra, nota 46.
Cfr. Archimedes 1910a, I, 42: «la superficie di qualunque segmento sferico minori di un emisfero è uguale ad un cerchio il cui raggio è uguale al [segmento di retta] condotto dal vertice della sezione sulla circonferenza del cerchio base del segmento sferico». Cfr. anche Archimedes 1910a, prop. 43 e De Tinemue 1964, prop. 3 (532, 1–6).
Archimede, nel De Quadratura parabuli, scrive: «…qualunque segmento compreso da una retta e da una sezione di cono rettangolo è quattro terzi del triangolo avente la stessa base della sezione e altezza uguale» (Archimede 1974, prop. 505). Hofmann e Hofmann 1980, nota 72, 227 evidenzia che, nel definire la parabola, egli si rifà all’antica scuola di geometria di Menecmo (ca. 380 a.C.– ca. 320 a.C.), allievo di Eudosso, noto per la sua basilare scoperta delle sezioni coniche e per aver dato una soluzione all’annoso problema della duplicazione del cubo servendosi appunto di sezioni coniche: parabola e iperbole.
Anche qui Cusano parla della possibilità di rettificare la curva per approssimazione continua; non di quella esatta che egli, da fedele aristotelico, considerava razionalmente impossibile. Egli immaginava di poter ottenere l’estensione della parabola e dell’ellissi dalla superficie usando il procedimento contrario a quello sopra indicato. Quando parla di una linea avente una «curvitatem regularem», Cusano intende evidentemente un arco senza punti di flessione con una curvatura che si modifica continuamente, come si riscontra nell’esempio indicato dell’ellissi.
Questa strada d’accesso alla quadratura del cerchio, inaugurata da Ippocrate di Chio, non risulterà utile a Cusano, tanto più che egli confonde lunula e segmento circolare. Cfr. Cusanus 2010c, 6, 3–5.
L’espressione latina è «triangulus rectilinealis», ossia delimitato da lati dritti.
In questo caso si tratta di eguagliare il settore circolare.
Il ragionamento di Cusano è il seguente. Se si pone
 = prima
linea;
= prima
linea;  =
seconda linea,
=
seconda linea,  = terza linea e
= terza linea e  = quarta linea,
allora si ha che: Se si pone:
= quarta linea,
allora si ha che: Se si pone: 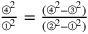 .
Da ciò segue che, se
.
Da ciò segue che, se 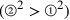 e se
e se  , allora
, allora
 . Cfr. Hofmann e Hofmann 1980, nota 75, 228 e Nicolle 1998, nota 51, 86.
. Cfr. Hofmann e Hofmann 1980, nota 75, 228 e Nicolle 1998, nota 51, 86.
Si cerca la terza linea kl. Se
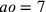 ;
; 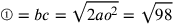 ;
; 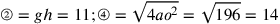 .
Applicando la relazione:
.
Applicando la relazione: 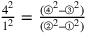 ,
si ha
,
si ha  ,
ossia
,
ossia 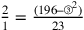 . Si
ha dunque che
. Si
ha dunque che  ;
; 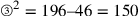 e
e  .
.
Cusano pone il semidiametro 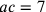 ;
; 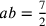 ;
; 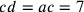 ;
; 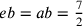 ;
;
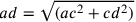 ;
;  . Subito dopo la
descrizione il discorso diventa molto generale e non c’è una
vera dimostrazione. Cusano conclude dicendo semplicemente:
«apporta le opportune modifiche finché risulti così».
. Subito dopo la
descrizione il discorso diventa molto generale e non c’è una
vera dimostrazione. Cusano conclude dicendo semplicemente:
«apporta le opportune modifiche finché risulti così».
Cusano intende per «aequatrix» una linea parallela alla tangente e perpendicolare al raggio, tale che essa tagli due sezioni uguali, l’una nel cerchio sotto il punto di tangenza; l’altra fuori del cerchio sotto l’equatrice.
Cusano intende per «linee di complemento» le semicorde del poligono inscritto corrispondenti ai semilati dei poligoni tangenti al quadrante, ossia del poligono circoscritto. Egli giustifica questa dimostrazione poco più avanti.
Tutti i manoscritti e le prime stampe presentano qui erroneamente bk al posto di ck. In p Omnisanctus corresse l’errore.
Se 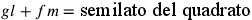 ,
allora, se
,
allora, se 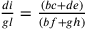 ,
e se
,
e se 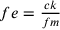 , allora
, allora  . Per una puntuale analisi di questa
costruzione, cfr. Hofmann e Hofmann 1980, nota 85, 230, in cui si mostra che il ragionamento cusaniano dà
buone approssimazioni nel caso di differenze relativamente
insignificanti.
. Per una puntuale analisi di questa
costruzione, cfr. Hofmann e Hofmann 1980, nota 85, 230, in cui si mostra che il ragionamento cusaniano dà
buone approssimazioni nel caso di differenze relativamente
insignificanti.
Il termine latino è «sectores». Cfr. Cusanus 2010d, 28.
Con «proporzionalità» qui si intende un rapporto esprimibile con un numero intero.
Il termine latino è «curvam peripheriam», che, sebbene abbia un’estensione semantica maggiore di arco di circonferenza, è inteso da Cusano nel suddetto significato, visto che fa riferimento al libro primo, in cui si affronta precisamente tale problema.
Quest’ultimo paragrafo, menzionato come Vacat, è cancellato nel folio 65v di Cu (Gestrich 1992).
Il titolo è scritto in rosso in Cu (Gestrich 1992).
Per meglio rendere il concetto, si è tradotto qui il termine «comparates» con la perifrasi «corde in proporzione». Le «corde comparate» sono una nozione nuova introdotta da Cusano, non riscontrabile in altri autori.
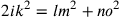 e
e  ; dunque:
; dunque:  e
e 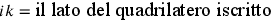 .
.
Hofmann e Hofmann 1980, nota 94, 233 rimanda al secondo capitolo del De geometricis transmutationibus dove Cusano enuncia, e tenta di dimostrare, la tesi generale che vale per tutte le sezioni del cerchio comprese tra corde in proporzione al lato ik del quadrato.