1. PAOLO: Sommo Padre, tu sai che, fin dalla mia infanzia, ho cercato la verità che sembra risplendere in maniera più chiara nelle matematiche1 e sai anche quanto io desideri trovare la quadratura del cerchio, che non è stata ancora trovata. Perciò ti prego, fammi sapere se, dopo avermi inviato i libri – per me alquanto oscuri e discutibili – sui Complementi matematici, ti è venuto in mente un altro procedimento più attendibile2.
IL CARDINALE NICOLA: Certo, [penso di averne uno] facile e, come credo, indiscutibile.
PAOLO: Dimmi, ti prego.
2. NICOLA: So che è ti è ben noto tutto ciò che riguarda la questione, eccetto soltanto quest’unica cosa, ossia come, dato il cerchio di una circonferenza, tu possa determinare una linea retta della stessa lunghezza.
PAOLO: Sì, è così; infatti, so da Archimede
3. NICOLA: Per darti quindi un’idea di ciò che resta, considera questa proposizione: se si aggiunge la corda del quadrante di un cerchio dato al suo semidiametro, si ottiene il diametro del cerchio circoscritto al triangolo isoperimetrico alla circonferenza del cerchio dato.
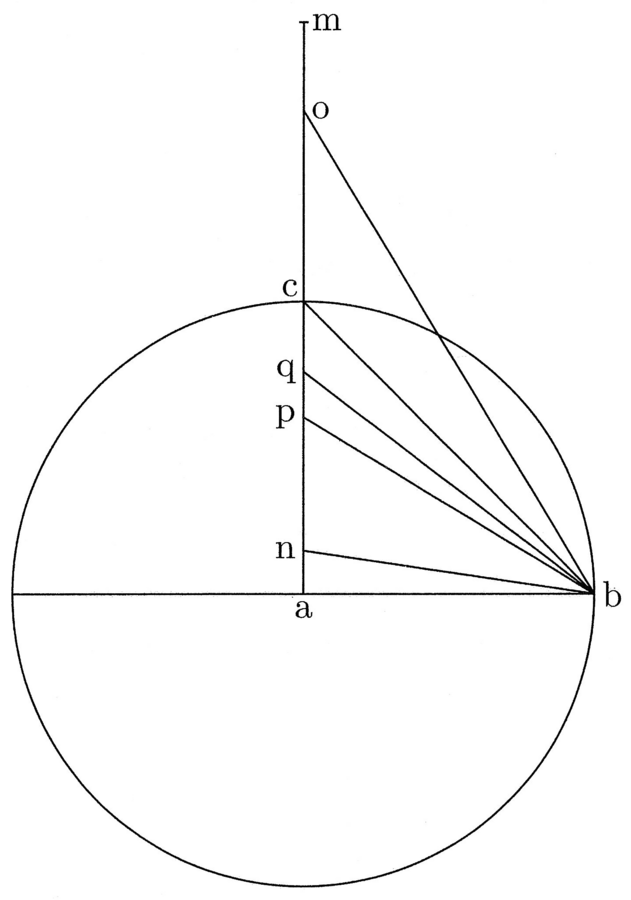
Sia, per esempio, BCDE il cerchio dato, descritto intorno ad a, e sia bc il quadrante (cfr. figura 1); si traccino la corda bc e le linee ab e ac5 e si descriva un altro cerchio intorno allo stesso centro a il cui diametro fg sia uguale alla somma di ab e bc, e precisamente gh sia uguale a ba e hf uguale a bc. Sia inscritto il triangolo IKL. Dico che [il perimetro di] questo triangolo rettilineo6 è uguale alla circonferenza BCDE7.
PAOLO: Questo procedimento è facile e assai prezioso, se dimostrerai che è vero.
4. NICOLA: Ci proverò. Riprendendo la figura sopra descritta del cerchio dato, prolungherò la linea ac all’infinito, e sia essa ma; dico, senza dubbio, che è possibile tracciare una qualsiasi linea da b ad am tale che, se a questa si aggiunge un’altra che sta ad essa come il lato del quadrato alla diagonale8, si ottiene una linea uguale al diametro del cerchio circoscritto al triangolo isoperimetrico al cerchio dato (cfr. figura 2).
PAOLO: Lo ammetto. Infatti, è possibile tracciare una linea da b ad am in modo tale che, se a questa si aggiunge un’altra che sta ad essa come il lato [del quadrato] alla diagonale, risulti una linea minore del diametro del cerchio circoscritto al triangolo isoperimetrico al cerchio dato. È quel che accade nel caso in cui si traccia [la linea] verso un punto n, vicino ad a; allo stesso modo è possibile tracciare un’altra linea verso un punto o, vicino al punto m, che, aggiunta al lato [del quadrato], sia maggiore [del diametro]. Quindi, tra n e o ci sarà un punto tale che la linea tracciata da b a questo punto, aggiunta al lato [del quadrato], sarà uguale, cioè, né maggiore né minore, al diametro del cerchio circoscritto al triangolo isoperimetrico al cerchio dato9.
5. NICOLA: Dico pertanto a ragione che se prendi bn e [aggiungi a questa] tutti i lati10 che vuoi, la linea che ne deriva sarà minore del semidiametro11 del cerchio circoscritto al triangolo e [precisamente sarà minore] di tanto quanto sono i lati che avrai aggiunto, tranne uno. E se prendi bo e [aggiungi a questa] tutti i lati che vuoi, la linea che ne deriva sarà maggiore del semidiametro del cerchio circoscritto al triangolo e di tanto quanto sono i lati che avrai aggiunto, tranne uno. Così, ci sarà un punto tra n e o, tale che la linea condotta da b a questo punto sarà uguale al semidiametro del cerchio circoscritto al triangolo e di tanto quanto sono i lati che avrai aggiunto, tranne uno. Questo non può che trovarsi nel punto c in cui il lato è uguale al semidiametro del cerchio dato, cioè, uguale a ba; altrimenti, se il lato fosse maggiore o minore di ba, questo non sarebbe possibile12.
6. PAOLO: Concordo con te sul primo punto, cioè che bn, aggiunto a tutti i lati che vuoi, resta minore del diametro del cerchio circoscritto al triangolo isoperimetrico di tanto quanto sono i lati, tranne uno. Intendo “tranne uno” perché aggiungi un solo lato alla linea bn per ottenere il diametro del cerchio circoscritto; infatti, poiché bn più il lato è minore di questo diametro e il lato è minore di ab, tutto questo è evidente13. In modo contrario si comporta la linea bo e anche questo è evidente. Quindi, è certo che, se si deve giungere all’uguaglianza in qualche punto intermedio, questo punto è c, per la ragione che ho detto. Se infatti il lato fosse minore o maggiore della linea ab, ciò non seguirebbe in alcun modo. Ma cosa accadrebbe se qualcuno negasse che si dà tale punto tra n e o14?
NICOLA: Chi nega che tra il minore e il maggiore cada nel mezzo l’uguale, nega che si possa dare un triangolo isoperimetrico al cerchio. Io, tuttavia, presuppongo la quadratura del cerchio come possibile e di conseguenza tutto ciò senza cui essa non è possibile15.
7. PAOLO: Potrei dire che ciò nonostante è possibile, ma che non lo è per tutti i lati aggiunti alla linea così che risulti quel diametro del cerchio circoscritto al triangolo e di tanto quanto sono i lati, tranne uno, poiché potrei dire che tra n e c cade un punto p, e che la linea bp più il suo lato è uguale al diametro del suddetto cerchio circoscritto.
8. NICOLA: Allora non neghi che se si sommasse bp a due lati, questa somma sarebbe uguale al diametro in questione, ma a quello che è minore del semidiametro del cerchio dato, poiché il lato è minore di ab16.
PAOLO: Come potrei negarlo?
NICOLA: Prendi un punto sopra p e sia questo q; dove bq più il lato è tanto maggiore del diametro in questione quanto il lato è minore della linea ab, allora ciò è possibile. Non è forse vero che questo bq sommato ai due lati fa il diametro e, con esso, il semidiametro del cerchio dato?
PAOLO: Chi potrebbe dubitarne?
NICOLA: E che avverrebbe se cercassi una linea, che, sommata al lato, superi il detto diametro, di tanto quanto i due lati sono minori dei due semidiametri del cerchio dato?
PAOLO: Occorre che il punto si trovi ancora più vicino al punto c.
NICOLA: E che accadrebbe se volessi che la linea, oltre ai diversi lati aggiunti, fosse uguale a più semidiametri?
PAOLO: Sarebbe necessario prolungare il punto fino a raggiungere c.
NICOLA: Giusto! Se dunque procedessi così all’infinito, alla fine arriveresti necessariamente17 al punto c, mentre al di qua del punto c il lato sarebbe sempre minore di ab.
PAOLO: Hai perfettamente ragione.
9. NICOLA: E’ evidente che ciò non è possibile, ossia che tra n e o cada un punto tale che la linea ad esso condotta si rapporta così che, se a questa si aggiunge un numero qualsiasi di lati, essa sarà uguale al diametro del cerchio circoscritto al triangolo isoperimetrico e di tanti quanti sono i lati aggiunti, tranne uno; ma questo sarà il punto c. E se dicessi che il punto si trova oltre c dal lato di o, seguirebbe la stessa contraddizione mediante la dimostrazione inversa, poiché si tornerebbe necessariamente al punto c.
10. PAOLO: Non posso negare che sia come hai chiaramente dimostrato; sembra evidente che chi afferma che il punto si trovi al di qua o al di là di c, sarebbe in errore e l’errore proviene da quella stessa posizione, poiché ogni linea maggiore di bc, sommata al suo lato, è maggiore del diametro del cerchio circoscritto al triangolo isoperimetrico e ogni linea minore, sommata al suo lato, è minore del diametro18.
NICOLA: Questo potrebbe essere dimostrato anche con un altro procedimento, e ci sono vari modi per trovare facilmente dal sapere scientifico i diametri dei cerchi inscritti e circoscritti ai poligoni isoperimetrici ai cerchi dati, poiché il poligono più esteso avente infiniti lati coincide con il cerchio; ma questo procedimento è sufficiente, il resto lo lascio a te.
11. PAOLO: E’ sufficiente conoscere il modo di
trasformare una circonferenza in una retta e viceversa una retta in
una curva; a partire da ciò, tutto quello che finora era sconosciuto
nelle matematiche può essere scoperto, come tu hai tentato nei tuoi
Complementi matematici19. Pertanto, se qualcuno vorrà ridurre la curva in retta,
moltiplicherà il semidiametro del cerchio dato per la semiretta
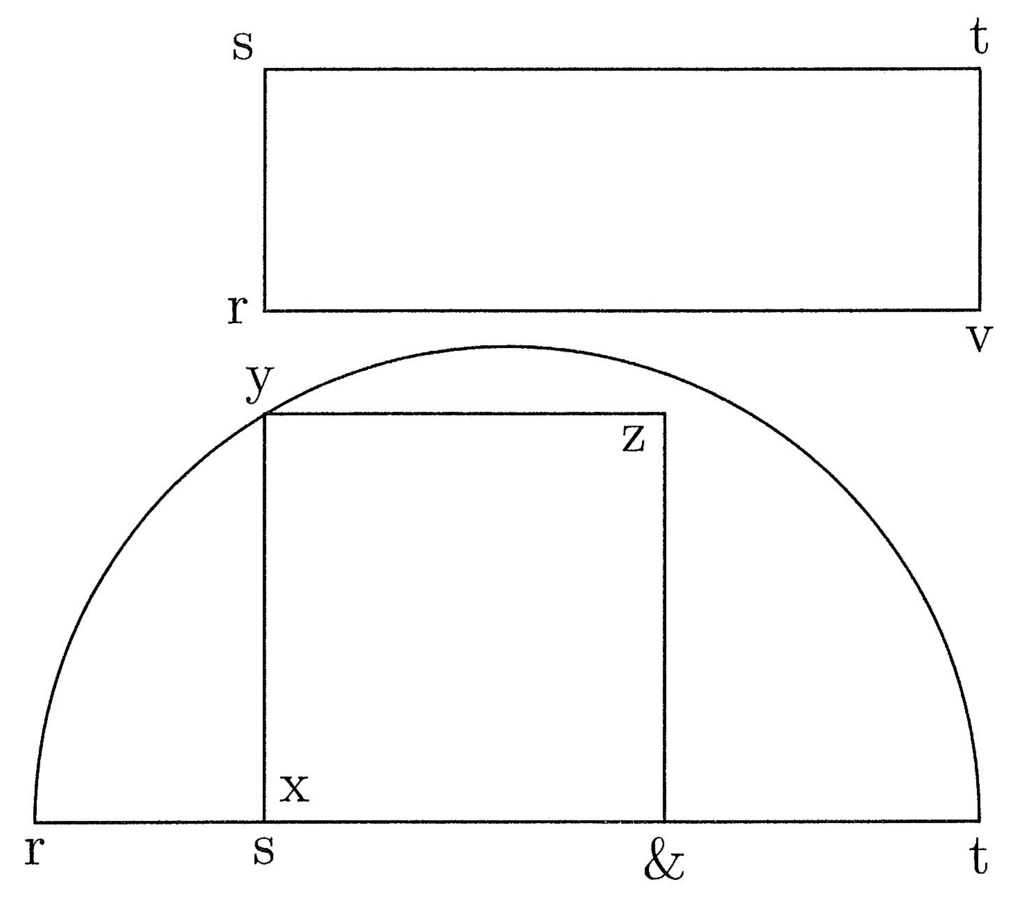
uguale alla circonferenza. Sia, per esempio, rs uguale ad ab e st uguale della somma dei tre lati ikl; se si chiude il rettangolo RSTV uguale alla
superficie del cerchio BCDE, si trova il medio proporzionale tra rs e st secondo
Euclide
Fine. Bressanone. 1457
‹Appendice›
12. Il punto è questo: il processo all’infinito20. Infatti, se esiste quel punto, la somma della linea tracciata da b ad esso e il lato è tale che, se aggiungessi lati all’infinito, non faresti altro che aggiungere infiniti ba al diametro del cerchio circoscritto al triangolo isoperimetrico. È chiaro allora che la somma della linea e il lato è uguale al diametro del cerchio circoscritto e che il lato è uguale a ba, e il punto sarà c.
13. Se davvero si nega il processo [all’infinito] allora è chiaro che qualsiasi punto si segni al di qua di c, anche se si pone che la somma di ba e il lato supera il diametro del cerchio circoscritto, allora un certo numero di lati più la somma della linea e il lato farà sempre il diametro del cerchio circoscritto e tutte le linee ba, e puoi sempre aumentare quel numero, se il punto supera di molto c, e mai cessa quest’accrescimento, perché non c’è un punto al di qua di c, dove la somma della linea con il lato supera numericamente il diametro del cerchio circoscritto, per quanto infiniti siano i lati superati dalle linee infinite, essendo qualsiasi lato di una qualche lunghezza minore della linea ba. Quella lunghezza moltiplicata all’infinito sarà sempre maggiore della lunghezza di cui la somma della linea con il lato eccede il diametro del cerchio circoscritto eccedente.
14. Dico inoltre: non c’è dubbio che la somma di ba e il lato superi il diametro del cerchio circoscritto al poligono della massima estensione, avente cioè infiniti angoli, che si trasforma nel diametro del cerchio isoperimetrico. Così, se aggiungi tutti i lati che vuoi, essi superano sempre tutte linee ba e precisamente della lunghezza con la quale bc supera ba, come si sa. Poiché, se prendi un altro poligono al di qua di quello più esteso, allora quell’eccesso è minore, e così all’infinito e, poiché tra il più esteso e il meno esteso cadono infiniti poligoni, nel triangolo quell’eccesso sarà minore, se sarà così piccolo che non possa essercene uno minore. Se infatti potesse esserci uno minore, non sarebbe il poligono più piccolo. Invece la lunghezza, di cui non si può dare una minore, non è una lunghezza, ma un punto21. Così la linea bc non è maggiore in lunghezza di quella che si cerca.
15. Al contrario: sia bn la linea, che, sommata al suo lato, sia uguale al diametro del circoscritto al poligono più esteso. È evidente che bn supera ba, il semidiametro del cerchio isoperimetrico, più di quanto il diametro del circoscritto superi il diametro del cerchio, ossia di tanto quanto bn supera ba, come si sa; e meno negli altri poligoni man mano che l’estensione diminuisce. Dunque nel poligono con la minima estensione questa linea non deve superare il suo lato ba più dell’eccesso di quanto il diametro del circoscritto supera il diametro del cerchio isoperimetrico. Se dunque nel poligono più esteso quest’eccesso è massimo, cioè non c’è uno maggiore, e in quelli meno estesi esso diminuisce progressivamente, nel poligono meno esteso esso sarà il minimo, di cui non c’è uno minore. Di conseguenza il suo lato sarà uguale a ba. Se infatti fosse minore di ba, è chiaro che supererebbe ba più di quanto deve eccedere nel poligono meno esteso; se fosse maggiore di ba, allora eccederebbe di meno; sarà dunque bc, il cui lato è ba.
Note a piè pagina
Questo testo non sembra trattarsi di una finzione narrativa, ma piuttosto del resoconto di una discussione reale avvenuta tra Cusano e Toscanelli, che potremmo datare nella prima metà del 1457, e collocare prima del De caesaera circuli quadratura del 6.8.1457, in cui è presentata un’idea nuova per attuare la quadratura del cerchio. Da quanto si afferma in questo passo si può dedurre che Toscanelli aveva contestato anche la versione ampliata de i Complementi matematici in cui Cusano ammette i difetti di quel procedimento, tanto più che spera di dare da quel momento in poi una nuova e migliore approssimazione.
Come negli altri scritti matematici, anche in questo testo Cusano utilizza il termine «quadrangulus» per indicare il rettangolo. Cfr. Archimedes 1910b, prop. 1: «Ogni cerchio è equivalente a un triangolo rettangolo nel quale uno dei lati perpendicolari è uguale al raggio del cerchio e la base (cioè, l’altro lato perpendicolare) è uguale alla circonferenza del cerchio».
Qui l’uguaglianza sta a indicare l’equivalenza.
Si tratta, come si nota dal disegno, dei raggi del cerchio BCE.
Il termine «rectilineus» sta per «delimitato da lati dritti».
Cusano approssima il diametro 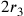 del cerchio circoscritto al cerchio
avente la stessa circonferenza del triangolo equilatero
mediante:
del cerchio circoscritto al cerchio
avente la stessa circonferenza del triangolo equilatero
mediante: 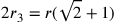 . Dunque il cerchio
isoperimetrico sarebbe uguale a
. Dunque il cerchio
isoperimetrico sarebbe uguale a r](../../../media/sources/13/26/EOAineq_26_3.png) e così
e così 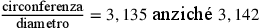 . L’approssimazione è quindi
insufficiente.
. L’approssimazione è quindi
insufficiente.
Come negli altri scritti matematici, Cusano utilizza il termine «diameter» per indicare la diagonale. Cfr. Cusanus 2010i, 9, 3 e Cusanus 2010d, 26.
Si ha, dunque, un segmento 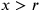 , cosicché
, cosicché 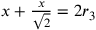 .
.
Bisogna intendere «cum» nel significato di «più», ossia nel senso di un’addizione.
Come nota Nicolle 1998, nota 5, 103, si tratta di semidiametro e non di diametro.
Ora si afferma che 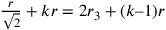 .
.
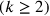 .
.
Il punto di partenza è la diseguaglianza 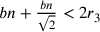 , nel caso
che
, nel caso
che 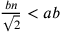 . Da ciò si
conclude che
. Da ciò si
conclude che 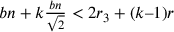 .
.
Se all’inizio aveva accettato l’ipotesi di Cusano, ora
Toscanelli incalza Cusano insistendo sul problema dell’esistenza
di un punto esatto che permetta di realizzare la quadratura del
cerchio. La sua obiezione costituisce il nocciolo della
questione: se deve essere 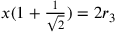 , allora
, allora
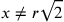 ,
ma
,
ma 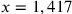 , non
, non
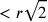 ,
come Toscanelli pensava, presupponendo p tra
n e c, bensì più
grande. Questo era accessibile anche ai matematici del tempo con
l’utilizzo dei limiti di Archimede per
,
come Toscanelli pensava, presupponendo p tra
n e c, bensì più
grande. Questo era accessibile anche ai matematici del tempo con
l’utilizzo dei limiti di Archimede per 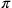 .
.
Cfr. Cusanus 2010c, 3–11.
Ora ha inizio la parte più interessante del dialogo. Cusano
vuole mostrare che l’uguaglianza ![x+\frac{x}{\sqrt{2}}=2r_3[=2,418r]](../../../media/sources/13/26/EOAineq_26_17.png) non
può avere altra soluzione che
non
può avere altra soluzione che 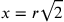 , e a questo fine si serve di
una dimostrazione indiretta: se fosse
, e a questo fine si serve di
una dimostrazione indiretta: se fosse 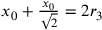 e
e 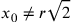 , allora
si potrebbe appurare che le soluzioni
, allora
si potrebbe appurare che le soluzioni 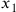 ,
, 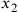 ,….
,…. 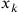 …. dell’equazioni
…. dell’equazioni 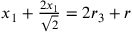 ;
;
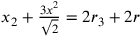 , ….
, ….
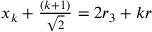 ,….
andrebbero in modo monotono da
,….
andrebbero in modo monotono da 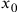 verso
verso 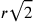 , e che
, e che 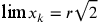 (con
(con 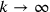 ). Poiché
Cusano vuole che tutti le
). Poiché
Cusano vuole che tutti le 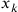 siano uguali, egli deve rendere
ognuno di loro uguale a
siano uguali, egli deve rendere
ognuno di loro uguale a 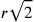 . In realtà
. In realtà 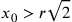 , per cui
il tutto non è che un tentativo ingegnoso, ma privo di
significato nel caso in questione.
, per cui
il tutto non è che un tentativo ingegnoso, ma privo di
significato nel caso in questione.
Nel termine «necessario» è racchiusa tutta la questione. Come è possibile che una procedura portata all’infinito possa condurre alla fine a un punto?
Come scrive Hofmann e Hofmann (1980, nota 12, 241–242), in Bb si dà un lunga
spiegazione di questo passo il cui contenuto è: se si accetta il
processus in infinitum, allora il
discorso fila. Se invece lo si ritiene inammissibile, allora ci
si avvicina sì al punto c attraverso un
aumento costantemente del valore k del
raggio da aggiungere all’infinito, senza tuttavia mai
raggiungerlo. Del resto 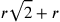 è maggiore del raggio del
cerchio circoscritto 2r, quello avente la
massima superficie tra i poligoni regolari isoperimetrici e
maggiore del raggio del cerchio circoscritto
è maggiore del raggio del
cerchio circoscritto 2r, quello avente la
massima superficie tra i poligoni regolari isoperimetrici e
maggiore del raggio del cerchio circoscritto 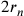 , di uno degli altri
poligoni isoperimetrici
, di uno degli altri
poligoni isoperimetrici 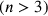 . La differenza tra le due
espressioni diminuisce col diminuire di n
e raggiunge il suo minimo 0 quando il poligono contiene la più
piccola superficie possibile
. La differenza tra le due
espressioni diminuisce col diminuire di n
e raggiunge il suo minimo 0 quando il poligono contiene la più
piccola superficie possibile 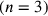 . Ora si determini
. Ora si determini 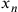 da
da 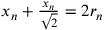 . Così
. Così
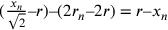 ha il suo massimo valore per
ha il suo massimo valore per  , ossia il poligono isoperimetro
avente la massima superficie; diminuendo n diminuisce continuamente la differenza e
raggiunge il suo minimo (0) per
, ossia il poligono isoperimetro
avente la massima superficie; diminuendo n diminuisce continuamente la differenza e
raggiunge il suo minimo (0) per 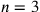 , ossia il poligono isoperimetrico
avente la superficie minima. Dunque
, ossia il poligono isoperimetrico
avente la superficie minima. Dunque 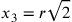 .
.
Cfr. Cusanus 2010i, 31–35.
[Il contenuto dell’appendice è scritto a margine in Ob, mentre si trova all’interno del testo in To ed è assente in n e b].
Cusano si rifà qui alla definizione euclidea del punto
«