La stessa unità di misura di ciò che è rettilineo e ciò che è curvilineo

Federica De Felice

La stessa unità di misura di ciò che è rettilineo e ciò che è curvilineo

Chapter structure

Download Chapter

TY - CHAP
T1 - La stessa unità di misura di ciò che è rettilineo e ciò che è curvilineo
T2 - Niccolò Cusano. Scritti matematici: Introduzione, traduzione e note
A1 - Federica De Felice
AB - Cusano è un personaggio chiave della cultura occidentale: molti e importanti sono i contributi che egli dà in ambito filosofico, giuridico, religioso e politico. Gli studi critici hanno evidenziato e continuano a evidenziare i diversi aspetti della sua vastissima e poliedrica attività speculativa. Meno noti, ma altrettanto significativi, sono l’impegno e la perspicacia con i quali il cardinale cerca di risolvere questioni strettamente matematiche, alle quali si dedica costantemente e intensamente per oltre quindici anni, dal 1445 al 1459, in mezzo a bufere politiche, conflitti territoriali, progetti di riforma e delusioni personali. Si tratta delle seguenti opere, qui tradotte e commentati, per la prima volta, in italiano: De geometricis transmutationibus, De arithmeticis complementis, De circuli quadratura, Quadratura circuli, De mathematicis complementis, Declaratio rectilineationis curvae, De una recti curvique mensura, Dialogus de circuli quadratura, De caesarea circuli quadratura, De mathematica perfectione, Aurea propositio in mathematicis.

In questi scritti Cusano cerca di risolvere il problema della quadratura del cerchio e della rettificazione del cerchio, che, pur non essendo nuovo tra i matematici del tempo, viene affrontato da Cusano con tentativi e procedure logico–geometriche aventi una notevole portata storica, non tanto per i risultati raggiunti, che sono fallimentari, quanto per la forma mentis che l’approccio di Cusano sottende. Negli scritti matematici, infatti, emerge una nuova filosofia della mente che riconosce nella dimensione dello spazio (inteso come il luogo della mens–mensura) la condizione metodologica della possibilità del darsi della coincidentia oppositorum. Proprio l’intuizione dinamica dello spazio, per quanto deformata dalla possente immaginazione del filosofo e irretita entro una forma eminentemente teologica, costituirà uno stimolo fondamentale per i nuovi «Archimede» del Rinascimento, suggerendo ai posteri molto più di quanto non sia in grado di dimostrare.
PB - Max-Planck-Gesellschaft zur Förderung der Wissenschaften
PY - 2020
SN - 978-3-945561-50-8
L1 - https://edition-open-sources.org/media/sources/13/25/sources13_chap25.pdf
LK - https://edition-open-sources.org/sources/13/25/index.html
C1 - by-sa
DO - 10.34663/9783945561515-25
LA - it
ER -

1. Poiché mi sono reso conto che nelle scienze geometriche mancava una regola pratica per commisurare¹ ciò che è curvilineo e ciò che è rettilineo, e, per questo motivo, tali scienze risultano imperfette, e che molte altre cose che sembrano possibili non hanno potuto trovare compimento, allora ho fatto non poca fatica per riuscire a comprendere quest’arte. Se ho raggiunto il mio scopo, lo giudicherai, tu, lettore².

2. Dico, inoltre, che ciò che è curvilineo e ciò che è rettilineo hanno la stessa misura se sono misurati con la stessa unità di misura, se, per esempio una linea retta ha tanti piedi dritti quanto un arco [ne ha] curvi.

Prima proposizione

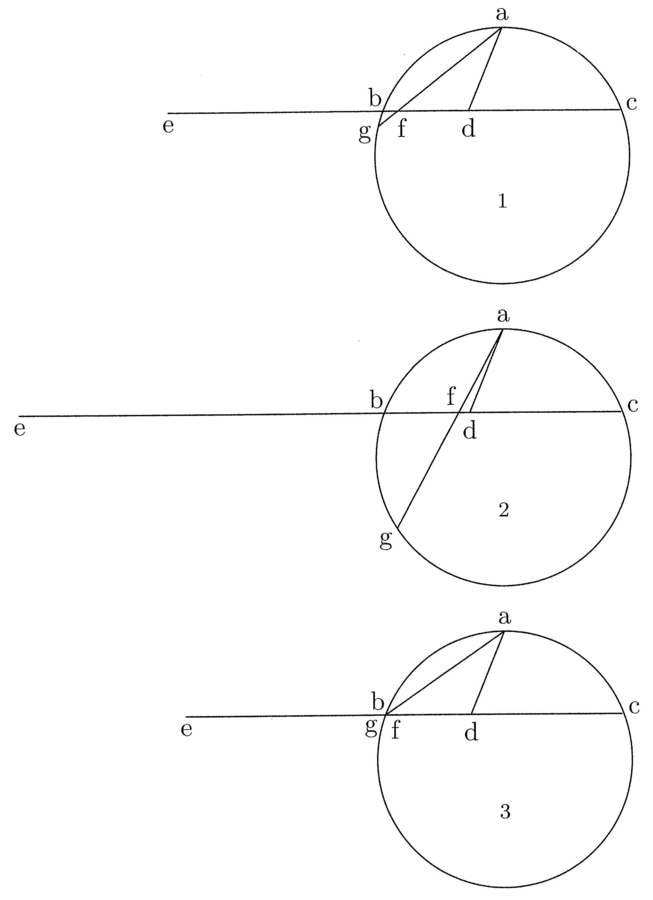
3. Dato un arco, trovare una retta della stessa misura (cfr. figura 1).

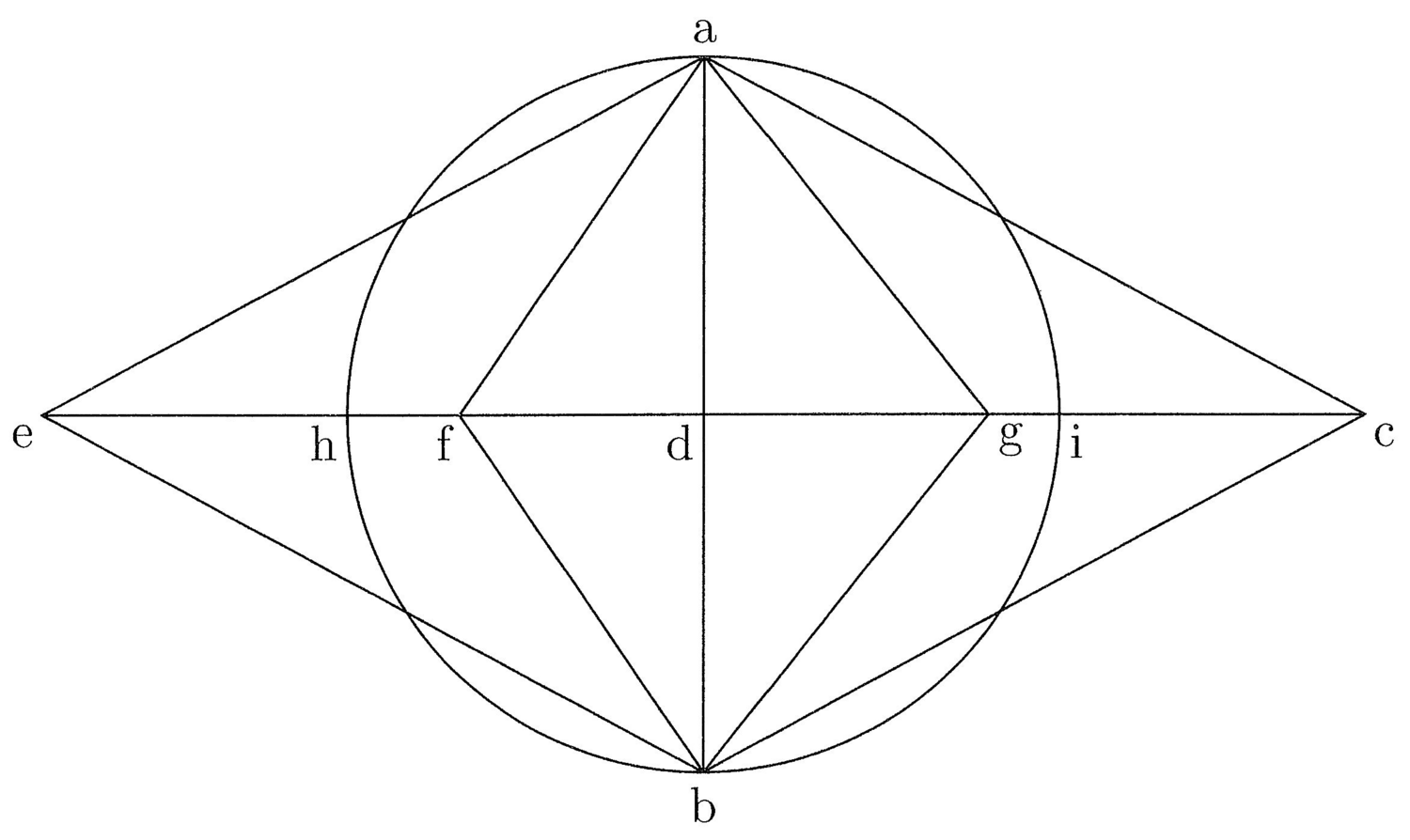
Sia bc l’arco dato il cui centro è a; si tracci la corda bc e su di essa si fissi il punto d, equidistante da a e da b: questo è il punto di tale regola. Da questo punto, fai passare attraverso b una retta fino ad e in modo tale che, se tracci da a attraverso de una corda ag uguale alla metà di de, questa corda passa attraverso un punto f della linea de. Sia ora df la quarta parte di de. La linea retta de ha appunto la stessa misura dell’arco bc.

4. Per dimostrare ciò, faccio due ipotesi³. In primo luogo che de può essere tracciato in modo che tra il punto f, attraverso cui passa la corda, com’è stato detto, e l’estremità e della linea de, il segmento [fe] sia uguale a tre quarti della retta commensurabile. E questo è evidente da sé. Infatti è certo che può essere tracciato in modo che fe sia maggiore, come nella seconda figura, e in modo che sia minore, come nella terza figura; e ancora, in modo che essa non sia né maggiore né minore⁴. In secondo luogo, suppongo che quanto più de è minore [dell’arco], tanto più fe è minore in rapporto a de, e df maggiore, e accade il contrario quando de è maggiore [dell’arco]. Anche questo è evidente alla vista nella seconda e terza figura⁵.

fig. 1

5. Dico, dunque, che la prima ipotesi è verificata, o quando de è la retta cercata, cioè della stessa misura dell’arco, oppure quando essa è minore o maggiore. Se si verifica il primo caso, ottengo ciò che cercavo; dunque df sarà necessariamente la quarta parte di de. Se dici che questo si verifica quando de è minore della retta avente la stessa misura [dell’arco], ciò è impossibile. Infatti, poiché dalla seconda ipotesi fe è minore in rapporto a de e df è maggiore di un quarto della retta avente la stessa misura [dell’arco], e secondo te, [fe] sarà uguale ai tre quarti della retta commensurabile, de non sarà minore della retta avente la stessa misura [dell’arco], bensì maggiore. Analogamente, se dici che si verifica quando de è maggiore della retta avente la stessa misura [dell’arco], ciò implica la stessa contraddizione.

Seconda proposizione

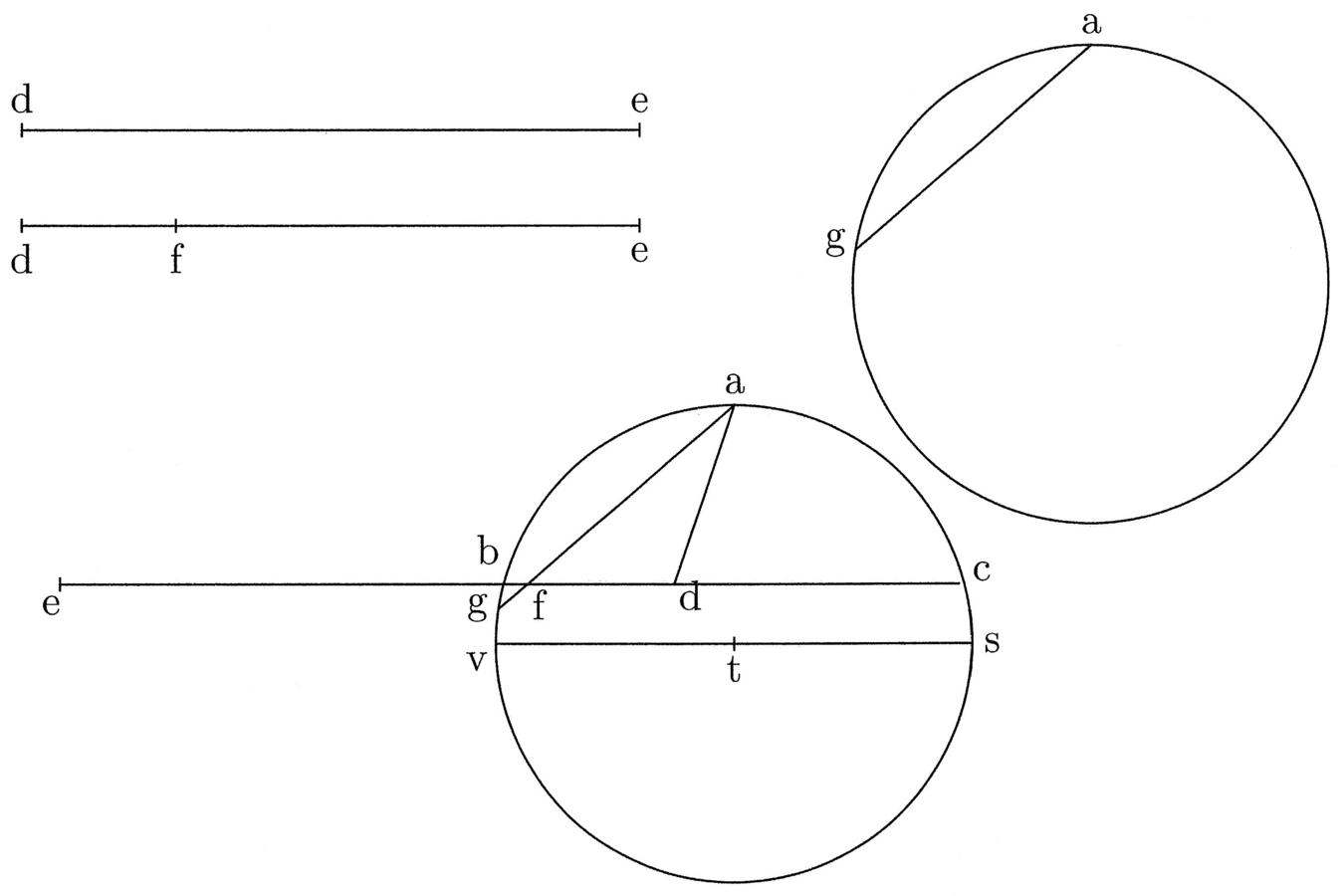
6. Dato un cerchio, trovare un arco della stessa misura di una retta data (cfr. figura 2).

fig. 2

Sia data la retta de; sia dato un cerchio il cui centro è t e il diametro stv; e sia a il centro di tutti gli archi. Da a traccia la corda ag, uguale alla metà di de, e su de segna la sua quarta parte con df, e avvicina de parallelamente a tv, in modo che f cada sulla corda ag e indica con b il punto d’intersezione con la circonferenza del cerchio. Allora, se d è equidistante da b e da a, ba sarà la metà dell’arco cercato. Prolunga quindi bd fino a toccare la circonferenza in c e otterrai l’arco bc della stessa misura della retta de. Il tutto è evidente da quanto detto sopra.

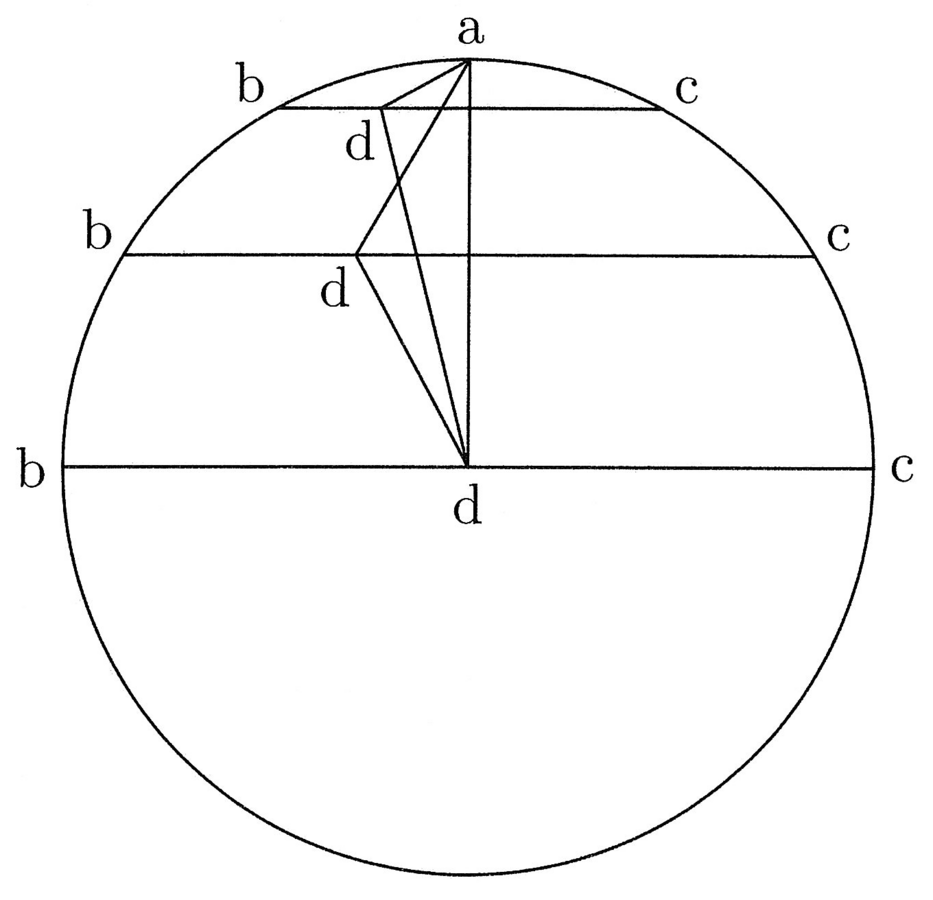
7. Per vedere che d è il punto di questa regola, il quale, se la corda ag ha la stessa misura dell’arco ba, dista la metà di ag dal punto di intersezione f, dove ag interseca bcd⁶, considera che quanto maggiore è la corda bc, tanto più [il punto] d si allontana da b e da a e si avvicina al centro del cerchio; quanto minore [è la corda bc], avviene il contrario, e ciò è evidente (cfr. figura 3).

fig. 3

Dunque, sulla massima corda, d si allontana minimamente dal centro del cerchio e massimamente da b e da a. Sulla corda minima, d si allontana massimamente dal centro e minimamente da b e da a. Perciò, d si trova, sulla corda massima, al centro del cerchio e, su quella minima, sulla sua circonferenza⁷. Ma è certo che, sia sulla massima corda sia su quella minima, d è equidistante da b e da a e lo stesso è su tutte le corde intermedie. Da ciò, si deduce che se bc è la corda dell’arco pari alla terza parte della circonferenza del cerchio, allora il punto d sarà equidistante dal centro e da b ed a.

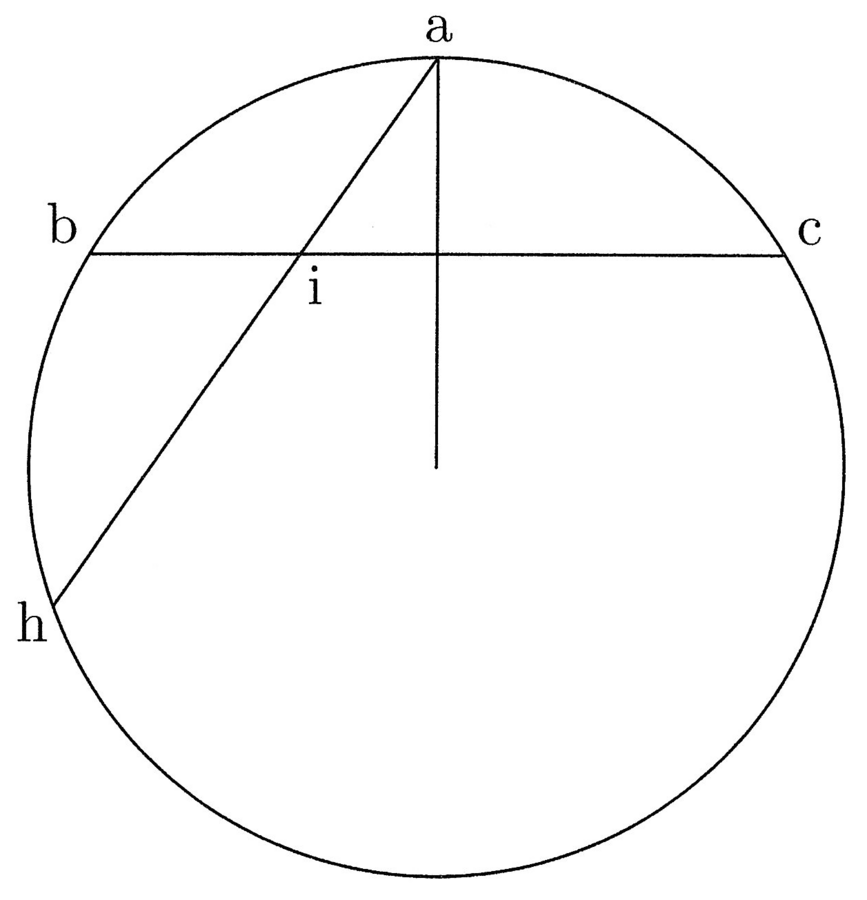
8. Inoltre, si può tracciare da a attraverso bc la corda ah che taglia [bc] nel punto i (cfr. figura 4). Dico che aih può essere tracciata così che ai sarà la distanza del punto d da a su questa corda ah. Questo è certo. Così sarà anche quando ah è uguale a bc e il punto di intersezione i sarà equidistante da b e da a, come d lo sarà da entrambe. E se ah è minore, questo non è possibile, perché allora ai sarebbe maggiore di prima, quando essa era uguale. E se ah è maggiore, è altrettanto impossibile, perché ai sarebbe minore di prima, quando essa era uguale.

fig. 4

Terza proposizione

9. Determinare una retta avente la stessa misura dell’arco di una semicirconferenza e una figura rettilinea avente la stessa misura⁸ della superficie curva corrispondente.

fig. 5

Sia dato un cerchio e sia bc l’arco della semicirconferenza, con centro a, e d il punto della regola equidistante da a e b, che in questo caso si trova al centro del cerchio (cfr. figura 5). Traccia la linea ad, prolunga, quindi, db fino a de in modo che, se ottieni come metà di de la corda ag, tracciata da a attraverso de, essa passa su de per il punto f che dista da d la quarta parte di de, come sopradetto. Poi chiudi il triangolo rettangolo per mezzo del lato ae. Dico che l’area del triangolo rettangolo ADE ha la stessa misura dell’area del semicerchio e che de ha la stessa misura dell’arco bc. Il secondo punto è evidente da quanto sopradetto. Il primo punto è evidente allo stesso modo, come prima, attraverso due ipotesi⁹, di cui la prima è: si può determinare de e chiudere il triangolo rettangolo attraverso ea in modo che se si traccia la corda afg che è la metà di de da a per de, l’area [del triangolo] AFE sarà uguale a tre quarti dell’area del semicerchio. È evidente, poiché si ottiene là dove essa è maggiore e là dove è minore, e quindi anche dove non è né maggiore né minore. In secondo luogo, suppongo che quanto minore sarà de, tanto minore sarà quest’area AFE in rapporto all’area intera del triangolo rettangolo ADE, e quanto maggiore esso sarà, tanto maggiore sarà l’area. La prima ipotesi è quindi verificata quando l’area del triangolo rettangolo ADE ha la stessa misura dell’area del semicerchio, e si ottiene ciò che si cercava; invece, se essa è minore o maggiore, entrambi i casi implicano contraddizione esattamente come detto sopra.

10. È pertanto chiaro che, se il triangolo rettangolo, di cui un lato è il semidiametro e l’altro è perpendicolare a questo, ha la stessa misura dell’intera circonferenza del cerchio, l’area di quel triangolo rettangolo ha la stessa misura dell’area del cerchio. E, poiché qualsiasi poligono può essere trasformato in un altro, potrai assegnare all’area del cerchio l’area di ugual misura di un triangolo, di un quadrato, di un pentagono, di qualsiasi altro poligono e di qualsiasi parte di cerchio anche se non ha la stessa misura del cerchio. Potrai anche stabilire angoli in rapporto a rette date e a tutte le figure in modo che abbiamo la stessa misura l’una nell’altra. Dico che si possono realizzare notevoli trasformazioni, conservando la superficie di ciascuna figura e la sua natura propria e invariabile, e, attraverso quest’arte, scoprirai altre cose nascoste che difficilmente si possono spiegare, anche nelle sezioni e nelle curve che mutano uniformemente¹⁰. Potrai anche disporre di angoli e strumenti con i quali molto facilmente e velocemente potrai fare le costruzioni suddette, che lasciamo alla tua operosità¹¹.

fig. 6

11. L’area AGBF ha la stessa misura della metà del[l’area del] cerchio e l’area ABE ha la stessa misura dell’area del cerchio; il medio proporzionale tra il semidiametro ad e la retta ed avente la stessa misura della metà della circonferenza del cerchio, come insegna Euclide, VI, 9¹², è il lato del quadrato la cui area ha la stessa misura di quella del cerchio (cfr. figura 6). La retta df misura un ottavo della circonferenza del cerchio, e così l’area del triangolo rettangolo ADF misura un ottavo dell’area del cerchio¹³. Dunque, quando hai una retta della stessa misura di un arco, hai anche l’area di una figura rettilinea della stessa misura dell’area di una porzione di cerchio.

Fine.

Note a piè pagina

1

La parola «commensurare», come in seguito «commensurabilis» è equivoca: essa significa «avere uguale misura», ma Cusano la utilizza per indicare una uguaglianza sia tra lunghezze sia tra superfici. Qui si tratta di una uguaglianza di misura. Cfr. Nicolle 1998, nota 2, 97.

2

Il testo è dello stesso periodo de I complementi matematici, ma non se ne può dare la data esatta. Tuttavia, poiché si fa riferimento al contenuto de I complementi matematici nelle tre tesi, possiamo ipotizzare che esso sia stato composto verosimilmente subito dopo il testo più lungo. Cfr. Hofmann e Hofmann 1980, nota 8, 239.

3

Hofmann e Hofmann 1980, (nota 2, 237–238) mostra, attraverso precisi calcoli, come l’approssimazione proposta da Cusano nel calcolo del rapporto tra corda e arco, per un angolo minimo, resti meramente teorica, perché, stando alle premesse, risulterebbe un’equazione di 4 °grado (per 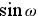$\sin\omega$ ), che può accadere solo in rari casi particolari.

4

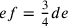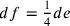La prima tesi sostiene che esiste un punto f su de tale che $ef=\frac{3}{4} de$ e quindi $df=\frac{1}{4} de$ .

5

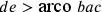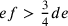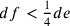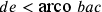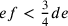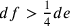La seconda tesi sostiene che il punto e si trova su de. Se $de>\text{arco }bac$ , allora $ef>\frac{3}{4} de$ e $df<\frac{1}{4} de$ , ma se $de<\text{arco }bac$ , allora $ef<\frac{3}{4} de$ e $df>\frac{1}{4} de$ .

6

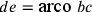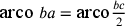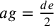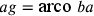$de=\text{arco }bc$ ; $\text{arco }ba=\text{arco}\frac{bc}{2}$ ; $ag=\frac{de}{2}$ ; quindi $ag=\text{arco }ba$ .

7

Cusano non identifica la curva tracciata per tutte le posizioni di de.

8

In questo caso il termine «commensurabilis» sta a significare una equivalenza, ossia un’uguaglianza tra aree.

9

Il secondo punto concerne il rapporto di una retta a una curva ed è dimostrata nella tesi precedente. Il primo punto concerne il rapporto di una superficie rettilinea ad una superficie curva ed è l’oggetto di questa terza proposizione.

10

È qui il presupposto sbagliato di Cusano: egli pensa che, grazie a rapporti proporzionali, si possano stabilire variazioni uniformi e che le variazioni si possano rappresentare sempre attraverso linee rette. Cusano tocca qui tutti i punti espressi ne I complementi matematici, in particolare le costruzioni mediante angoli fissi, la trattazione delle sezioni coniche e delle curvature (cfr. Cusanus 2010i, 55, 70). Facendo seguito alla dottrina di Oresme 1968 sulle latitudines formarum, con «curvitas uniformiter difformis» bisogna intendere una curva avente una variazione di curvatura costante. Sul tema, cfr. Hofmann e Hofmann 1980, nota 6, 234.

11

Cfr. Cusanus 2010b, 32, 33 e 39.

12

Cfr. Da Novara 2005, VI, 13.

13

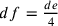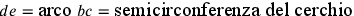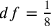Se $df=\frac{de}{4}$ ; $de=\text{arco }bc=\text{semicirconferenza del cerchio}$ ; allora $df=\frac{1}{8}$ della circonferenza.