1. Sebbene già da molto tempo dallo studio della geometria abbiamo tratto una speculazione più elevata e un’utilità generale, tuttavia, fra le innumerevoli e serie preoccupazioni che ha la legazione apostolica, si è piacevolmente insinuata, tra le conversazioni degli studiosi, l’affermazione secondo la quale è possibile conoscere la quadratura del cerchio, che [tuttavia] non è stata [ancora] trovata. Recentemente, andando a cavallo, abbiamo risolto la questione, e abbiamo messo per iscritto ciò a cui siamo pervenuti1.
2. Leggiamo che nessuno più di Archimede
3. Consideriamo il triangolo11 e il cerchio aventi la massima ampiezza12. Nel triangolo, i semidiametri dei cerchi, inscritto e circoscritto, si rapportano in modo contrario al semidiametro del cerchio, nel quale l’inscritto e il circoscritto coincidono. Essi infatti differiscono massimamente nel triangolo, dove il semidiametro del circoscritto è il massimo e quello dell’inscritto è il minimo, e la loro somma è la minima. Accade esattamente il contrario nel cerchio, dove la loro somma, uguale al diametro del cerchio, è la massima13. Per questo sappiamo che tutti i poligoni intermedi, isoperimetrici ed equiangoli, a seconda della loro superficie, si avvicinano in quelle linee per eguagliare il semidiametro del cerchio. Se dunque si segnassero la lunghezza dell’eccesso del semidiametro del cerchio rispetto al semidiametro del cerchio inscritto al triangolo e la lunghezza della quale il semidiametro del cerchio è minore del semidiametro del cerchio circoscritto al triangolo, allora ogni poligono intermedio, a seconda della sua superficie, si comporterà in maniera proporzionale con l’aumento del semidiametro del cerchio inscritto a sé rispetto al semidiametro dell’inscritto al triangolo, e con la diminuzione del semidiametro del cerchio circoscritto a sé dal semidiametro del cerchio circoscritto al triangolo14. Infatti, poiché queste lunghezze variano a seconda della diversa superficie, il rapporto di quelle non può essere diverso dal rapporto delle loro superfici. Inoltre è sempre necessario che, come l’eccesso si rapporta all’eccesso, così la differenza si rapporta alla differenza, dal momento che la superficie segue una variazione così come un’altra, e segue questa né più né meno di quella. In tutti i poligoni, dunque, l’eccesso e la differenza si rapporteranno tra di loro in maniera inversa nella stessa proporzione. Di conseguenza, se è dato un unico rapporto e si conoscono queste lunghezze in un determinato poligono noto, si può fare lo stesso anche nel cerchio. E poiché nel cerchio l’eccesso e la differenza, insieme, sono uguali al semidiametro [del cerchio] inscritto al triangolo, come si capisce da sé, allora, se, conformemente al rapporto trovato, si dividesse il semidiametro del cerchio inscritto nel triangolo e si aggiungesse il segmento maggiore allo stesso semidiametro del cerchio inscritto al triangolo, si avrebbe il semidiametro del cerchio isoperimetrico e tutto ciò che si cerca.
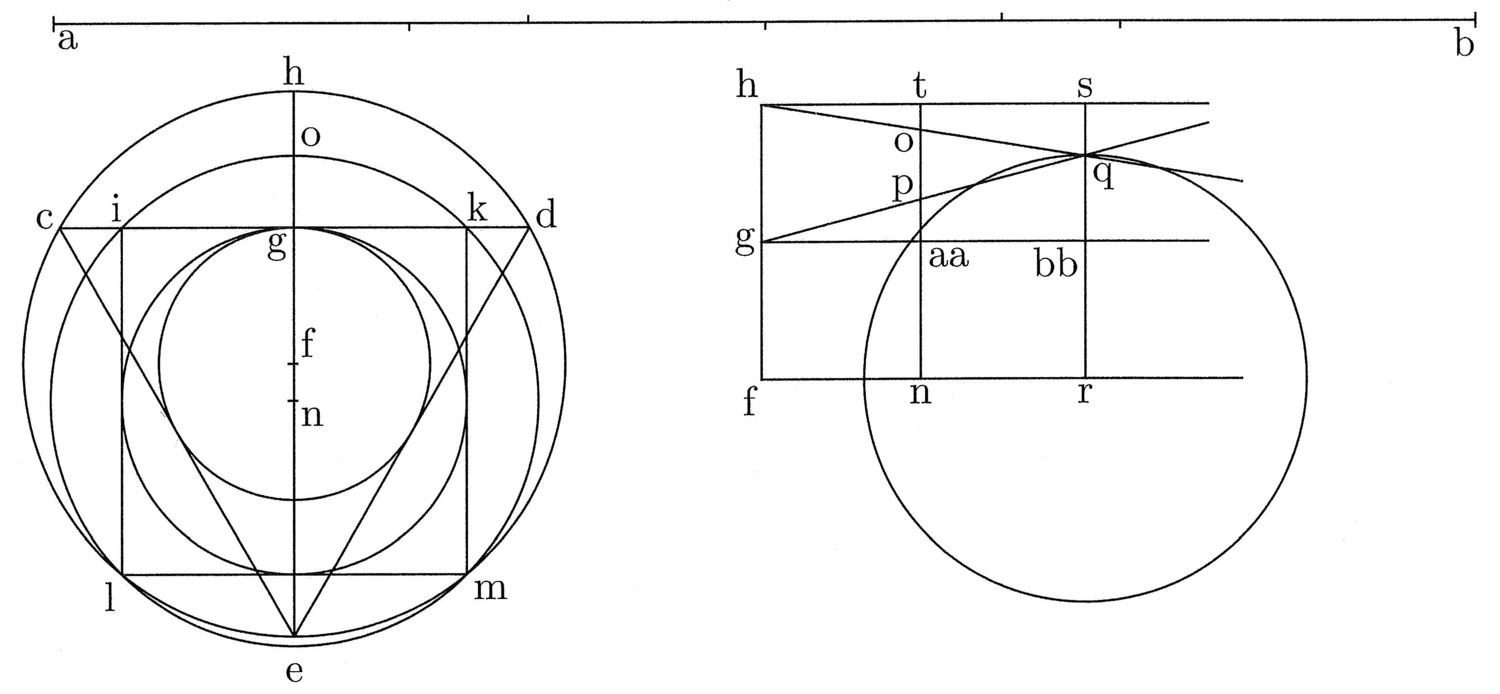
4. Ti renderemo questa parte più chiara nel modo seguente (cfr. figura 1). Partendo dalla linea ab divisa in tre parti, si disegni il triangolo CDE. Sul suo lato cd si riporti un quarto di ab, ossia ik, e da questo si costruisca il quadrato IKLM. Si disegnino il cerchio inscritto e circoscritto; sia fg il semidiametro del cerchio inscritto nel triangolo, fh quello del circoscritto; sia ng quello dell’inscritto al quadrato, no quello del circoscritto; si tracci poi la linea fh e si segni il suo punto medio con g. Si traccino, a partire da f, g, h, linee di lunghezza a piacere, e, parallelamente a fh, la linea tn, il cui punto medio è aa; in seguito, si segni con np il semidiametro del cerchio inscritto in un poligono isoperimetrico qualunque, per esempio un quadrato, e con no il semidiametro del circoscritto. Traccia una linea all’infinito da g attraverso p, un’altra allo stesso modo da h attraverso o, e segna con q il loro punto d’intersezione. Traccia la linea sr, che passi per q, parallelamente a fh, e segna con bb il suo punto medio. Diciamo che rq è il semidiametro del cerchio cercato, la cui circonferenza è uguale alla linea retta ab15.
5. Ciò si prova facilmente e in vari modi. Dunque, prendendo la figura precedente, si ponga la linea g bb come la differenza tra la superficie del triangolo e quella del cerchio isoperimetrico; e che da rs si muova una linea parallelamente al lato fh; è evidente che le linee hq e gq tagliano tutte le [linee corrispondenti alle] differenze fra i semidiametri dei cerchi inscritti e circoscritti di tutti i poligoni, dal triangolo fino al cerchio, dove [inscritto e circoscritto] coincidono. È evidente anche che quella linea in movimento taglia sulla linea bb g contemporaneamente tutte le [linee corrispondenti alle] differenze di superficie fra il triangolo e il cerchio. Infatti, quanto minore è la differenza fra i detti semidiametri, tanto più estesa è la figura; perciò, il cerchio è, fra tutte le figure, quella con la massima superficie, poiché qui [i semidiametri] coincidono, e il triangolo è la figura con la minima superficie, poiché qui [i semidiametri] differiscono al massimo. Sia dunque tn la linea in movimento, che taglia la linea g bb nel punto aa, e sia po la differenza dei semidiametri nel quadrato; di conseguenza, se g bb è uguale alla differenza della superficie del triangolo e quella del cerchio isoperimetrico, allora g aa è uguale alla differenza della superficie del triangolo e quella del quadrato. E poiché np è, per quanto premesso, il semidiametro del cerchio inscritto al quadrato, e aa p è il suo eccesso rispetto al semidiametro fg del cerchio inscritto al triangolo, da ciò, bb q sarà l’eccesso del semidiametro del cerchio isoperimetrico rispetto al semidiametro del cerchio inscritto al triangolo. Infatti, come si sa, bb g sta a aa g come bb q sta a aa p. Inoltre, le differenze fra i semidiametri dei cerchi inscritti nei poligoni isoperimetrici corrispondono alle differenze delle superfici. Infatti, la differenza delle superfici nei poligoni equiangoli e isoperimetrici non può derivare che dalla differenza dei semidiametri dei cerchi inscritti, poiché, si sa che la superficie risulta dal prodotto del semidiametro in questione – che varia in queste diverse figure – per la semicirconferenza, che resta sempre la stessa. Così, se ponessi la linea bb s, cioè [la somma dei] due eccessi dei semidiametri, corrispondente all’eccesso della superficie del cerchio sul triangolo, allora nel quadrato un tale eccesso di superficie corrisponderà alla linea uguale alle due linee to e p aa, poiché il rapporto fra questa linea e s bb è lo stesso di quello fra p aa e bb q, come sopra. Oppure, se dicessi che la superficie del triangolo è minore di quella del cerchio, come la linea hg, allora quella del quadrato sarà minore, come po16.
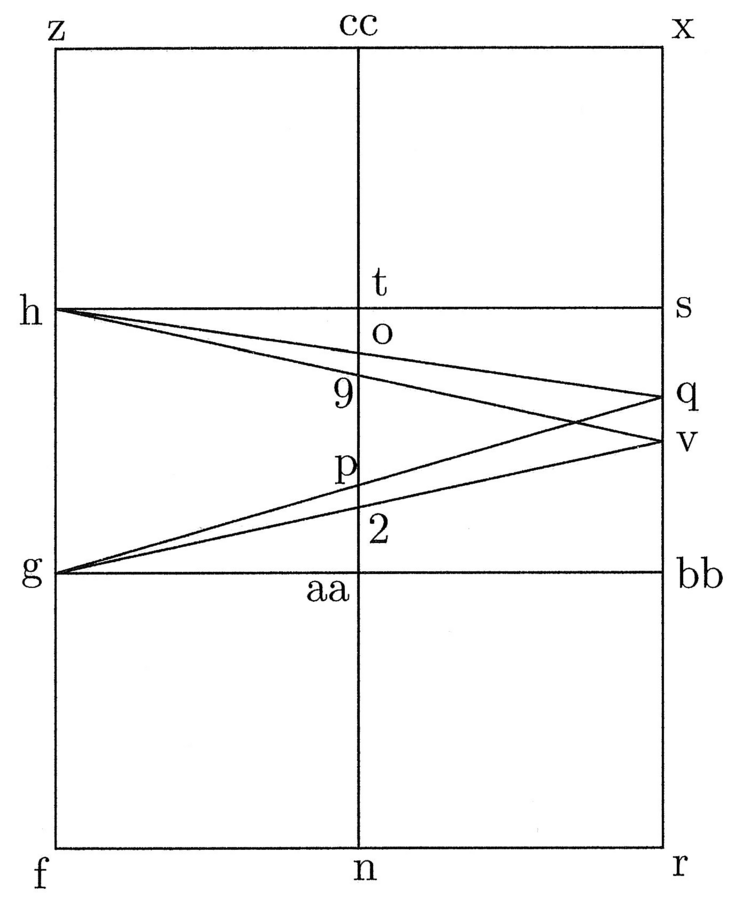
6. Ma, se ora tu negassi e sostenessi che il semidiametro del cerchio è minore, per esempio che la sua estremità fosse a metà fra s e v, che è il punto in cui termina la linea g, così che rv sia il semidiametro del cerchio isoperimetrico, allora, se si prolunga vs fino a diventare uguale a rv – che è rx – e, similmente, si prolunga fh fino a diventare uguale a rx, cosicché fz risulti uguale a rx, traccia la linea zx, e da u le linee su g e su h, e, laddove intersecano la linea tn, segna 2 e 9 (cfr. figura 2). Prolunga tn fino a zx, e sia cc n uguale rx. Dico che se il diametro dell’inscritto nel cerchio isoperimetrico aggiunge al semidiametro del cerchio inscritto nel triangolo una linea pari a bb v, allora il semidiametro del cerchio inscritto nel quadrato aggiunge aa 2. Dunque, se il semidiametro del cerchio inscritto nel quadrato aggiunge una linea pari a aa p, allora il semidiametro del cerchio isoperimetrico aggiunge una linea pari a bb q. Questo è evidente da sé, se il rapporto fra le linee aggiunte è uguale a quello fra bb v e aa 2 e si conosce la linea aggiunta nel quadrato, che è uguale a a ap. Dunque, essa sarà nel cerchio uguale a bb q, essendo il rapporto fra aa p e bb q, uguale a quello fra aa 2 e bb v17.
7. Che proprio questo è il rapporto è ciò che si
dimostrerà. Infatti, se si pone che rv è il
semidiametro del cerchio inscritto nel cerchio, allora vx sarà il semidiametro del circoscritto. Queste
due linee coincidono nel cerchio isoperimetrico. È evidente che rx è la linea formata da quei due semidiametri,
allo stesso modo fz è uguale ad essa ed è
formata dai due semidiametri dell’inscritto e del circoscritto al
triangolo. Dunque, in tutti i poligoni compresi fra il triangolo e
il cerchio, questi due semidiametri sono tali che non saranno né
minori di fz, né maggiori di rx, e quindi saranno sempre uguali. Nel quadrato,
n cc sarà dunque uguale a questi due
semidiametri. E poiché 2 9 è necessariamente
uguale a po, essendo il triangolo GHQ uguale
al triangolo GHV – qv infatti è parallelo a
gh – e allo stesso modo o
2 e gh paralleli, allora 9 2 sarà uguale a po, come
tu sai da Euclide
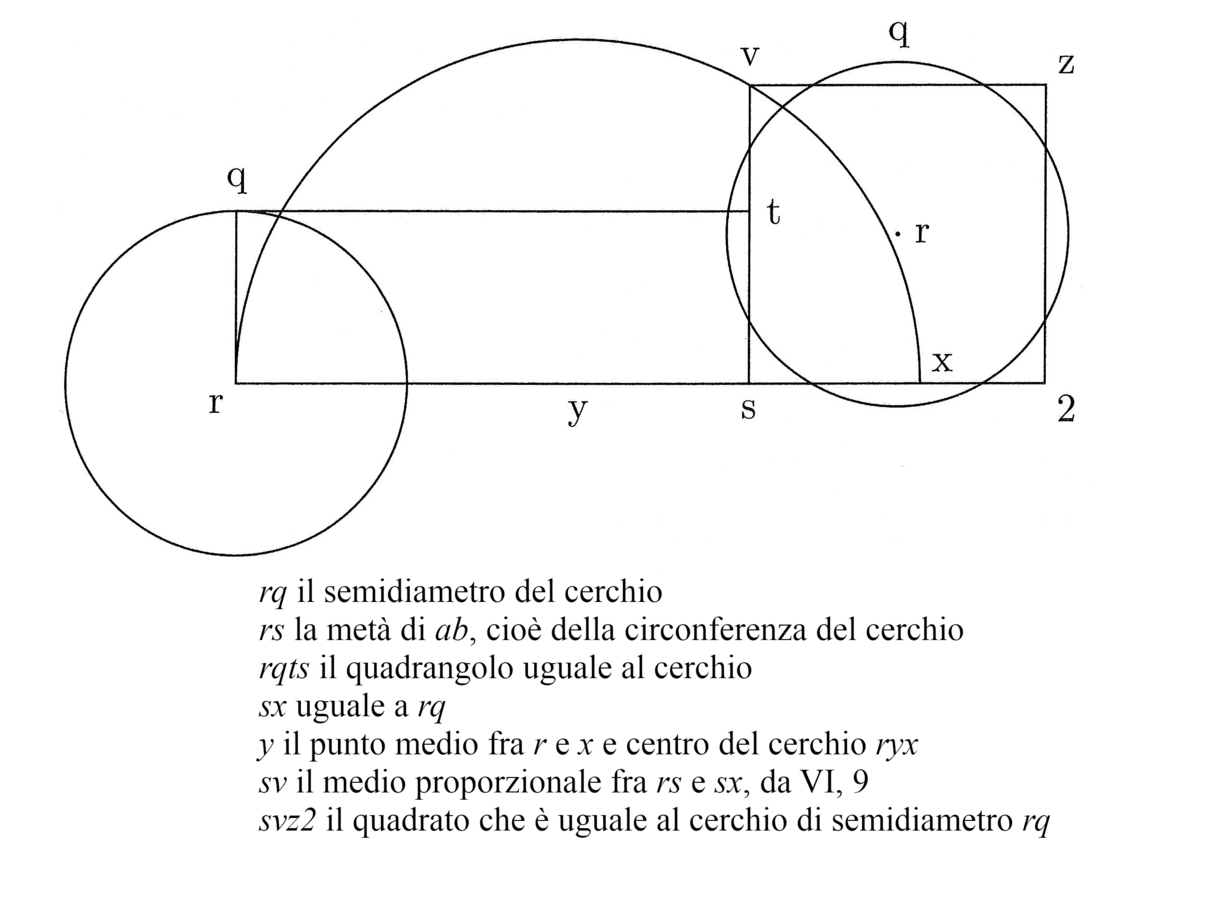
8. Altrimenti detto: la superficie del cerchio è massima rispetto alla superficie del triangolo e la differenza fra i semidiametri del cerchio inscritto e di quello circoscritto è nulla, ossia la minima in assoluto, poiché non può esserci una minore. Ma la differenza fra i semidiametri del cerchio inscritto e di quello circoscritto al triangolo è massima e l’eccesso della superficie del triangolo rispetto a se stesso è nullo o il minimo in assoluto. Sia dunque ab una qualsiasi linea uguale alla differenza fra i semidiametri nel triangolo nonché all’eccesso della superficie del cerchio rispetto alla superficie del triangolo (cfr. figura 4); si faccia di questa linea il lato del quadrato ABCD, e sia ab uguale alla differenza fra i semidiametri più quella differenza minima della superficie del triangolo con la sua propria superficie, sia cd l’eccesso della superficie del cerchio rispetto alla superficie del triangolo più la differenza minima in assoluto dei semidiametri. Si tracci la diagonale19 bc. Dico che in tutti i poligoni intermedi fra il triangolo e il cerchio, le linee corrispondenti agli eccessi della superficie rispetto alla superficie del triangolo, aggiunti alla differenza fra i semidiametri, non possono essere né maggiori né minori di ab o cd, come è evidente.
Si tracci dunque la linea ef, uguale e parallela ad ab e a cd, sia essa tagliata da bc nel punto g; sia ge uguale alla differenza fra tali semidiametri nel quadrato; è chiaro che gf sarà uguale all’eccesso della superficie del quadrato rispetto alla superficie del triangolo. Il rapporto fra la superficie del quadrato rispetto alla superficie del triangolo sarà dunque uguale all’eccesso della superficie del cerchio rispetto alla superficie del triangolo, cioè come quello fra gf e cd. Si segni su fg l’eccesso20 del semidiametro dell’inscritto nel quadrato rispetto al semidiametro dell’inscritto nel triangolo, e sia esso fh; si tracci una linea da b attraverso h fino alla linea cd, e sia i il punto di intersezione. Dico che di è l’eccesso del semidiametro del cerchio isoperimetrico rispetto al semidiametro del cerchio inscritto nel triangolo; infatti, il rapporto fra fg e dc è uguale a quello fra fh e di. Tuttavia la differenza di superficie fra i poligoni equiangoli e isoperimetrici rispetto alla superficie del triangolo non risulta se non dalla differenza dei semidiametri dei cerchi inscritti [al poligono] rispetto al semidiametro del cerchio inscritto nel triangolo. Il rapporto fra gli eccessi di superficie rispetto alla superficie del triangolo è dunque uguale al rapporto fra la differenza tra i semidiametri dei cerchi inscritti [al poligono] e il semidiametro del cerchio inscritto nel triangolo. Da ciò risulta quanto si cercava21.
Seni e corde
9. Da ciò si potrà ora ricavare la conoscenza perfetta delle corde e degli archi22. Se infatti il rapporto tra l’eccesso del semidiametro del cerchio inscritto a un poligono equiangolo e isoperimetrico dopo il triangolo, rispetto al semidiametro del cerchio inscritto al triangolo, e l’eccesso del semidiametro del cerchio circoscritto al triangolo rispetto al semidiametro del circoscritto a questo poligono, è sempre lo stesso, e se questi eccessi, uniti contemporaneamente alla loro differenza, cioè alla freccia23, sono uguali alla freccia del lato del triangolo, come risulta da quanto detto sopra, allora, una volta conosciuto il rapporto fra questi eccessi, che tuttavia non può essere colto numericamente come non si può determinare la metà della doppia proporzionale24, l’arte di ogni sapere sulle corde e sugli archi è trovata.
10. Si può trovare tuttavia il rapporto fra gli
eccessi per approssimazione numerica in questo modo: sia il
semidiametro del cerchio circoscritto al triangolo uguale 14. Il
semidiametro del cerchio inscritto sarà 7, il cui quadrato è 49;
il quadrato del semilato del triangolo sarà tre volte tanto, ossia
147 e il quadrato del semidiametro del cerchio circoscritto sarà
quattro volte tanto, ossia 196. Il semilato del quadrato sarà
dunque la radice25 di 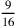 [e] del quadrato del semilato
del triangolo, ossia la radice di 82 più
[e] del quadrato del semilato
del triangolo, ossia la radice di 82 più 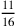 ; il semidiametro del cerchio
inscritto sarà altrettanto; il semidiametro del cerchio
circoscritto sarà la radice del doppio, ossia 165 più
; il semidiametro del cerchio
inscritto sarà altrettanto; il semidiametro del cerchio
circoscritto sarà la radice del doppio, ossia 165 più 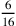 . Sottrai
dunque la radice di 49 dalla radice di 82 più
. Sottrai
dunque la radice di 49 dalla radice di 82 più 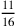 . La
differenza ottenuta è l’eccesso del semidiametro del cerchio
inscritto al quadrato rispetto al semidiametro del cerchio
inscritto nel triangolo, che farà poco più di 2. Sottraendo la
radice di 165 più
. La
differenza ottenuta è l’eccesso del semidiametro del cerchio
inscritto al quadrato rispetto al semidiametro del cerchio
inscritto nel triangolo, che farà poco più di 2. Sottraendo la
radice di 165 più 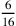 dalla radice di 196, si
otterrà poco più di 1. In questo modo otterrai gli eccessi e il
loro rapporto è ciò attraverso cui si può ricercare qualsiasi
cosa. Se infatti sottraessi questi eccessi dalla freccia del lato
del triangolo, cioè 7, allora resterebbe la freccia [del lato] del
quadrato. Se dunque dividessi 7 secondo il suddetto rapporto di
eccessi, e aggiungessi la parte più grande al semidiametro del
cerchio inscritto al triangolo, avrai il semidiametro del cerchio
isoperimetrico26.
dalla radice di 196, si
otterrà poco più di 1. In questo modo otterrai gli eccessi e il
loro rapporto è ciò attraverso cui si può ricercare qualsiasi
cosa. Se infatti sottraessi questi eccessi dalla freccia del lato
del triangolo, cioè 7, allora resterebbe la freccia [del lato] del
quadrato. Se dunque dividessi 7 secondo il suddetto rapporto di
eccessi, e aggiungessi la parte più grande al semidiametro del
cerchio inscritto al triangolo, avrai il semidiametro del cerchio
isoperimetrico26.
11. In questo modo, dal quadrato del lato del triangolo o del quadrato, potrai trovare anche il quadrato del lato di qualsiasi poligono; e, da questa conoscenza e dal rapporto fra gli eccessi si giunge alla freccia e al semidiametro del cerchio inscritto, e da ciò, alla corda. È la massima perfezione dell’arte geometrica, alla quale finora non ci risulta che gli antichi siano pervenuti. L’arte delle trasformazioni geometriche è ora compiuta, un’arte che poco fa, se pure non in maniera esaustiva, abbiamo descritto sufficientemente, dato che ha portato alla quadratura del cerchio27.
12. E pensiamo che nulla più di ciò che c’è da sapere nelle geometrie resterà nascosto a colui che vuole ricercare con diligenza in questo campo. Ho scritto soprattutto queste cose per mostrare la potenza dell’arte delle coincidenze, attraverso la quale si svela tutto ciò che è nascosto in ogni questione. Infatti, solo e soltanto dalla coincidenza dei semidiametri del cerchio inscritto e di quello circoscritto, diversi in ogni poligono, e coincidenti soltanto nel cerchio, questa ricerca ci ha condotto alla meta.
Gloria a Dio.
Note a piè pagina
Cusano scrive questo trattato nel 1453 per risolvere il problema della quadratura del cerchio mediante la coincidenza degli opposti. Non disponendo né del simbolismo algebrico, né dell’analisi geometrica, né del calcolo funzionale, la sua dimostrazione poggia unicamente su rapporti proporzionali stabiliti attraverso il metodo degli isoperimetri. Dopo aver esposto rapidamente la questione, Cusano anticipa il principio della sua dimostrazione (ripresa anche nel §5): nei poligoni regolari e isoperimetrici, dal triangolo al quadrato, ecc. … fino al cerchio, la differenza di superficie fra il cerchio inscritto e il cerchio circoscritto è massima nel triangolo, diminuisce nel quadrato, ecc. fino al cerchio, dove essa è minima sempliciter. Nel cerchio, infatti, l’inscritto e il circoscritto coincidono. Secondo Cusano basta determinare il rapporto fra questi cerchi, tramite i loro semidiametri, per trovare il rapporto fra la superficie di un cerchio e quella di un quadrato. Egli procede in tre tempi: all’inizio, mostra che le variazioni delle linee esprimono le variazioni delle superfici (fig. 1); poi mostra la regolarità delle variazioni (fig. 2); infine, dopo aver ricapitolato i rapporti fra cerchio, rettangolo e quadrato (fig. 3), riprende la dimostrazione della regolarità delle variazioni (fig. 4). La fine del testo enuncia una generalizzazione trigonometrica del suo principio, e procede a un calcolo approssimativo di π, prima di concludere con un elogio della coincidenza degli opposti.
Con rettangolo si traduce «quadrangulus». In questo, come negli altri scritti matematici, il termine «figura quadrangularis» è equivoco: Cusano lo riferisce tanto al quadrato quanto al rettangolo e al parallelogramma. Di volta in volta, a seconda del contesto, si renderà il termine «quadrangularis» con la figura corrispondente. Sull’utilizzo, da parte di Cusano, del termine «quadrangulus» invece di «quadratus» e sull’influenza dalla terminologia matematica medioevale, cfr. Hofmann 1966, 98–136, spec. 105.Cfr. Cusanus 2010c, 3, 5.
Si è tradotto qui «isopleura» con «equiangoli» ossia, nel linguaggio attuale, «regolare»; Cusano riprende il metodo degli isoperimetrici attraverso la Geometria speculativa di Bradwardine o il De Ysoperimetris di Zénodoros tradotta dal greco (cfr. Busard 1980, 1, 6). L’utilizzo di tale metodo è stato oggetto di un’aspra critica da parte di Jean Borrel (Cfr. Buteus 1559). Cfr. Cusanus 2010b, 4, nota 6 e 8. Sul tema, cfr. Gericke 1982, 160–187; Di Meglio 2010, 15–21; Heath 1921, II, 2019–211; Porter 1933.
Cfr. Cusanus 2010i, 10.
È verosimile che Cusano non conoscesse il De spiralibus di Archimede, ma soltanto l’ottavo capitolo del libro De arte mensurandi di de Muris. Cfr. Clagett 1964–1984a, III, 45–88, 309ss.; Clagett 1964–1984a, IV, 308–310.
Cusano accusa l’Archimede delle Spirali di petitio principii, perchè, a suo parere, la determinazione meccanica delle proprietà del movimento generatore della curva spirale esigeva la conoscenza del rapporto fra le diverse unità di misura spaziale del moto rettilineo e del moto circolare, cioè esigeva quella commensurabilità aritmetica fra raggio e circonferenza che doveva essere il risultato e non il presupposto della costruzione stessa. Sul tema, cfr. De Bernart 2002a, 339–382, spec. 370–374.
Cusano non utilizza «triangulum», ma «trigonum». Infatti, la figura che egli costruisce è composta da tre lati; in nessun momento egli considera il valore degli angoli.
Il termine «capacitas» è qui tradotto con ampiezza; tuttavia, per rispettare al meglio lo spirito del linguaggio cusaniano, a differenza sia di Hofmann che traduce «capacitas» con «Fläche» (cfr. Hofmann e Hofmann 1980, 59) sia di Nicolle che traduce il termine latino con «Surface» (cfr. Nicolle 1998, 38), si è preferito differenziare, laddove è possibile, i due termini (capacitas e superficies), utilizzati entrambi da Cusano, rendendo il latino capacitas a volte con ampiezza, altre volte, a seconda del contesto, con estensione o superficie.
Cfr. Cusanus 2010i, 4–8. Per meglio comprendere il testo, utilizziamo il
simbolismo al quale siamo oggi abituati. Se si chiama n il numero dei lati di un poligono, r il semidiametro del cerchio circoscritto,
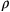 il
semidiametro del cerchio inscritto, si trova che se n cresce, allora
il
semidiametro del cerchio inscritto, si trova che se n cresce, allora 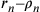 decresce. Da cui si può
ricavare il rapporto seguente fra il triangolo e un qualsiasi
altro poligono isoperimetrico e regolare:
decresce. Da cui si può
ricavare il rapporto seguente fra il triangolo e un qualsiasi
altro poligono isoperimetrico e regolare: 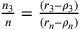 .
.
Nella prima figura, con la linea ab
divisa in tre parti, si disegna il triangolo CDE. Sul suo lato
cd si riporta tracciando ik, un quarto di ab;
da là, si costruisce il quadrato IKLM. Si disegnano i cerchi
inscritti e circoscritti; siano essi fg,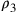 ,fh,
,fh,
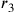 per il
triangolo e ng,
per il
triangolo e ng, 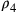 no,
no,
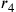 per il
quadrato; si traccia in seguito la linea fh e si segni il punto medio con g. La seconda figura, accanto alla fig. 1 e
da essa tratta, è destinata, con una nuova «tavola delle
proporzioni», a mostrare sulla linea tn
(= fh) la regolarità delle variazioni di
lunghezza dei semidiametri, seguendo la proporzione sopra
definita. Si tracci a partire da f,g,h
delle linee di lunghezza qualunque, poi, parallelamente a fh, si tracci tn il
cui punto medio è aa; in seguito, si
tracci
per il
quadrato; si traccia in seguito la linea fh e si segni il punto medio con g. La seconda figura, accanto alla fig. 1 e
da essa tratta, è destinata, con una nuova «tavola delle
proporzioni», a mostrare sulla linea tn
(= fh) la regolarità delle variazioni di
lunghezza dei semidiametri, seguendo la proporzione sopra
definita. Si tracci a partire da f,g,h
delle linee di lunghezza qualunque, poi, parallelamente a fh, si tracci tn il
cui punto medio è aa; in seguito, si
tracci 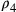 il
raggio del cerchio inscritto in un poligono isoperimetrico
qualunque, per esempio un quadrato, np, e
il
raggio del cerchio inscritto in un poligono isoperimetrico
qualunque, per esempio un quadrato, np, e
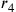 , no. Si tracci da g
attraverso p una retta all’infinito, e,
nello stesso modo, da h attraverso o una retta all’infinito. Si indichi con q il punto d’intersenzione. Poi si tracci
attraverso q, parallelamemnte a fh, la linea sr, il
cui punto medio bb. Si afferma che rq è r, il raggio del cerchio cercato la cui
circonferenza è uguale ad ab.
, no. Si tracci da g
attraverso p una retta all’infinito, e,
nello stesso modo, da h attraverso o una retta all’infinito. Si indichi con q il punto d’intersenzione. Poi si tracci
attraverso q, parallelamemnte a fh, la linea sr, il
cui punto medio bb. Si afferma che rq è r, il raggio del cerchio cercato la cui
circonferenza è uguale ad ab.
Secondo la posizione di q, i rapporti
fra i lati dei triangoli rettangoli simili esprimono sempre la
medesima proporzione: 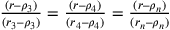 .
.
Rispondendo a un’obiezione, Cusano riprende la dimostrazione
della medesima proporzione sulla figura 2 che non è che una
variante della precedente: si tratta in pratica di mostrare che
la lunghezza r si rapporta alla lunghezza
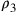 e
e
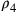 secondo
un rapporto costante. Se si nega e si sostiene che r è più piccolo, la sua estremità è al centro
fra s e v, e
coincide con il punto finale della linea g, in modo tale che rv
è r. Allora, se vs
si estende in modo tale che esso diventa uguale a rv e a rx, e se,
ugualmente a rx, esso si estende tanto
quanto fh, reso fh
uguale rx, fz
uguale a rx, si traccia la linea zx e dopo v le linee
su g e h. Laddove
esse intersecano la linea tn, si segnano
2 e 9. Si prolunga
tn fino a zx,
cosicchè cc n risulti uguale a rx. Dico che se 2r si aggiunge a
secondo
un rapporto costante. Se si nega e si sostiene che r è più piccolo, la sua estremità è al centro
fra s e v, e
coincide con il punto finale della linea g, in modo tale che rv
è r. Allora, se vs
si estende in modo tale che esso diventa uguale a rv e a rx, e se,
ugualmente a rx, esso si estende tanto
quanto fh, reso fh
uguale rx, fz
uguale a rx, si traccia la linea zx e dopo v le linee
su g e h. Laddove
esse intersecano la linea tn, si segnano
2 e 9. Si prolunga
tn fino a zx,
cosicchè cc n risulti uguale a rx. Dico che se 2r si aggiunge a 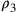 , l’eccesso è pari
a bbv (
, l’eccesso è pari
a bbv (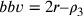 ) e allora
) e allora 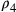 eccede
eccede 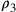 della lunghezza
aa 2. Dunque, se a
della lunghezza
aa 2. Dunque, se a 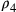 si aggiunge aa p, allora a r si
aggiunge a bb q. Da ciò, appare che il
rapporto della somma è come quella fra bb
u e aa 2. Si conosce la somma nel
quadrato, si sa che essa è uguale ad aa
p. Dunque, essa sarà nel cerchio uguale a bb q, e il rapporto fra aa
p e bbq è lo stesso di quello fra
aa 2 e bb v.
si aggiunge aa p, allora a r si
aggiunge a bb q. Da ciò, appare che il
rapporto della somma è come quella fra bb
u e aa 2. Si conosce la somma nel
quadrato, si sa che essa è uguale ad aa
p. Dunque, essa sarà nel cerchio uguale a bb q, e il rapporto fra aa
p e bbq è lo stesso di quello fra
aa 2 e bb v.
Da Euclides 1883–1888, I, 37 (I triangoli costruiti sulla stessa base e fra le medesime parallele sono uguali), l’uguaglianza delle superfici dei triangoli dipende dalla medesima base fra le medesime parallele. Da Euclides 1883–1888, VI, 4 (Fra i triangoli equiangoli, i lati attorno agli angoli uguali sono proporzionali; e i lati che sottendono gli angoli uguali sono omologhi), la proporzione delle rette corrisponde ai triangoli dai medesimi angoli.
Letteralmente «linea diametrale». In tutti gli scritti Cusano
utilizza diamentro per indicare la diagonale. Cusano utilizza il
termine «diameter» per indicare la diagonale, in base a una
etimologia inesatta da «
A partire da questo passaggio, Cusano utilizza l’espressione ambigua «additio super» che designa non l’operazione di aggiungere, ma il risultato di questa operazione, in qualche modo il «surplus»; si ritrova l’idea di eccesso, con cui si preferisce tradurre.
La proporzione fra la superficie del quadrato rispetto alla
superficie del triangolo sarà come l’eccesso della superficie
del cerchio rispetto alla superficie del triangolo, cioè come
gf rispetto a cd:
 .
Si ha dunque:
.
Si ha dunque: 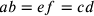 ;
; 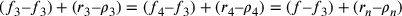 .
Si segni su fg l’eccesso
.
Si segni su fg l’eccesso 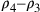 ossia fh; e si segni una linea da b attraverso h fino
alla linea cd, e il punto di contatto sia
i. di è l’eccesso di
ossia fh; e si segni una linea da b attraverso h fino
alla linea cd, e il punto di contatto sia
i. di è l’eccesso di 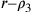 . Il rapporto tra
fg e dc è uguale a
quello tra fh e di:
. Il rapporto tra
fg e dc è uguale a
quello tra fh e di: 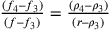 .
La differenza di superficie fra i poligoni regolari e
isoperimetrici e la superficie del triangolo
.
La differenza di superficie fra i poligoni regolari e
isoperimetrici e la superficie del triangolo 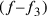 non risulta che
la differenza
non risulta che
la differenza 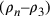 .
.
Il titolo latino De sinibus et chordis somiglia al titolo dell’opera di Peurbach, Tractatus super propositiones Ptolemaei de sinubus et chordis (prima del 1461) che, secondo Taton 1957–1958, II, 15 è uno dei primi trattati di trigonometria scritti in Europa.
È necessario prendere il concetto di freccia nel senso più ordinario di retta perpendicolare al centro della corda dell’arco. Luca Pacioli la definisce così: «Si chiama freccia questa linea retta che parte dal punto mediano dell’arco di qualche porzione di cerchio per cadere in squadra nel mezzo della sua corda. Essa è detta freccia in relazione con la parte della circonferenza che si chiama arco, per somiglianza con l’arco materiale per il quale sono anch’esso usuali questi tre termini: corda, arco e freccia» (Pacioli 1509, 134).
«medietas duplae». Si tratta di un’espressione idiomatica
intraducibile in sè, utilizzata anche ne Le
trasformazioni geometriche e ne I
complementi matematici (cfr. Cusanus 2010j, 9–8; Cusanus 2010i, 36). Vescovini 1972, nota10 sottolinea che si tratta di un termine della
tradizione matematica medievale con cui Cusano allude alla
dimostrazione dell’irrazionalità della 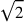 , spesso citata in
Aristotele e menzionata anche in Oresme 1966, 160 e in Bradwardine 1495b, III, 1. Oresme chiama il rapporto
, spesso citata in
Aristotele e menzionata anche in Oresme 1966, 160 e in Bradwardine 1495b, III, 1. Oresme chiama il rapporto 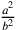 la metà di
la metà di 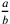 (cfr. Oresme 1966, 454). La proportio proportionum,
cioè la proporzione tra due rapporti
(cfr. Oresme 1966, 454). La proportio proportionum,
cioè la proporzione tra due rapporti 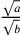 e
e 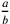 è espressa
dal rapporto
è espressa
dal rapporto 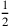 . Se la proportio dupla è il quadrato, la metà,
ossia la medietas duplae, è la radice.
Cusano si riferisce a questa terminologia matematica di
Bradwardine, di Oresme e di altri studiosi interessati agli
incommensurabili e ai rapporti irrazionali. Cfr. Rommevaux 2003, 401–418; Pedersen 1953, 134ss..
. Se la proportio dupla è il quadrato, la metà,
ossia la medietas duplae, è la radice.
Cusano si riferisce a questa terminologia matematica di
Bradwardine, di Oresme e di altri studiosi interessati agli
incommensurabili e ai rapporti irrazionali. Cfr. Rommevaux 2003, 401–418; Pedersen 1953, 134ss..
Essendo il simbolo della radice quadrata un’invenzione posteriore a Cusano (Stifel 1544, f–225v), si è preferito non utilizzare tale simbolo nella traduzione.
Il calcolo finale sul valore di 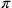 può comprendersi così: siano
può comprendersi così: siano
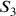 , il lato
del triangolo e
, il lato
del triangolo e  , il lato del quadrato;
, il lato del quadrato; 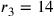 ;
; 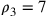 ; il quadrato
del semilato del triangolo è
; il quadrato
del semilato del triangolo è 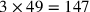 ; e
; e 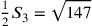 ;
; 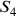 , essendo il lato
del quadrato,
, essendo il lato
del quadrato, 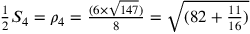 ;
;
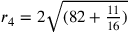 . Si
sottrae
. Si
sottrae ![\rho_4–\rho_3=[\sqrt{(82+\frac{11}{16})}]–\sqrt{49}=9,093–7=2,093](../../../media/sources/13/22/EOAineq_22_47.png) (il semidiametro dell’inscritto nel quadrato meno il
semidiametro dell’inscritto nel triangolo). Si sottrae
(il semidiametro dell’inscritto nel quadrato meno il
semidiametro dell’inscritto nel triangolo). Si sottrae
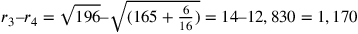 (il semidiametro del cerchio circoscritto al triangolo meno il
semidiametro del cerchio circoscritto al quadrato).
(il semidiametro del cerchio circoscritto al triangolo meno il
semidiametro del cerchio circoscritto al quadrato). ![\frac{(\rho_4–\rho_3)}{[(\rho_4–\rho_3)+(r_3–r_4)]}=\frac{2,093}{(2,093+1,170)}\approx\frac{2}{3}](../../../media/sources/13/22/EOAineq_22_49.png) ;
;
![r=[{\frac{5}{3}}]\rho_3={1+\frac{(\rho_4–\rho_3)}{[(\rho_4–\rho_3)+(r_3–r_4)]}}\rho_3=[{1+\frac{2,093}{(2,093+1,170)}}]\rho_3=(\frac{5,356}{3,263})\rho_3=1,647\rho_3](../../../media/sources/13/22/EOAineq_22_50.png) ;
;
 ;
;
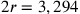 ;
;
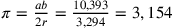 .
.
Cfr. Cusanus 2010i, 36–38.