De mathematicis complementis Beatissimo Papae Nicolao Quinto. Nicolaus cardinalis Sancti Petri ad Vincula

1. Tanta est potestas summi tui pontificatus, Nicolae quinte, pater beatissime, ut per eos, qui vim eius attente consideraverunt, assimiletur potentiae quadrandi rotundum et quadrum circulandi, quasi maior illi dari non possit. Verum, cum in te non tantum primatus sit clavis et potestas scientiae supremaeque hierarchiae ecclesiae, sed velut perfectus magister omnium scibilium ex tuo felicissimo ingenio incomparabilis notitiae esse iudiceris ab omnibus. Id magnificentissime effecisti, ut omnium tam Graecorum quam Latinorum scripta, quae reperiri queunt, tua mirifica diligentia in omnium nostrum notitiam accuratissime pervenerint, ita, ut etiam geometrica non neglexeris, quae sane omni honore digna a maioribus nostris habita fuerunt.

2. Tradidisti etenim mihi proximis diebus magni Archimedis geometrica Graece tibi praesentata et tuo studio in Latinum conversa, quae mihi tam admiranda visa sunt, ut circa ipsa non nisi magna cum diligentia versari potuissem. Ex quo id effectum est, ut meo studio et labore complementum aliquod illis addiderim, quod tuae sanctitati offerre decrevi. Solum enim te dignum scio, ut quae a saeculo incognita remanserunt, per te cunctis patescant. Et non tantum scibilia, quae semper circa quaesitam circuli quadraturam versari consueverunt, sed et quae in omni mathematica perfectione praestant complementum, ex his ipsis meo iudicio perfecte consequi possint.

[LIBER PRIMUS]

3. Testimonio omnium, qui se ad geometrica contulerunt, nemo propinquius Archimede ad circuli pervenit quadraturam. Qui videns illam attingi non posse, nisi curva circularis linea in rectam resolvatur, nisus est hanc artem mediante helica ostendere. Sed quia proportio motus signi a centro per semidiametrum ad motum, in quo in eodem tempore aliud signum per circumferentiam movetur, sine qua helica describi nequit, se habet ut semidiameter ad circumferentiam, quae non est scita, sed quaeritur. Hinc videtur ipsum defecisse. Facilius enim erit circulum quadrare quam helicam describere et contingentem eidem in fine circulationis applicare. Remanet igitur ex his, quae Archimedes reliquit, haec ars adhuc penitus abscondita. Ego autem quamvis multos in vanum laborasse in hac legerim indagatione, temptare coepi, si forte haec difficultas possit medio coincidentiarum finem capere, uti in aliis scientiis vim illam maximam esse comperi. Et visum est mihi quod data possibilitate, quam passim omnes admittunt, faciliter possit huius scientia pariter et praxis modo, quo sequitur, adipisci.

4. Primo advertendum quod in figura multiangula seu polygonia, quae habet aequalia latera, punctus unus aequedistans a medio et fine laterum centrum dicitur et linea ab illo centro ducta ad medium lateris est semidiameter circuli inscripti eidem et vocetur prima linea. Et alia linea ducta ab eodem centro ad finem lateris seu angulum aliquem est semidiameter circuli circumscripti eidem et vocetur secunda linea. Hae duae lineae in omni multiangula diversae sunt quantitatis et tanto plus, quanto latus eius maius. Nam potentia secundae lineae continet potentiam primae et cum hoc potentiam medietatis lateris, quia latus trianguli orthogonii, quod opponitur angulo recto, ut ostendit Euclides.

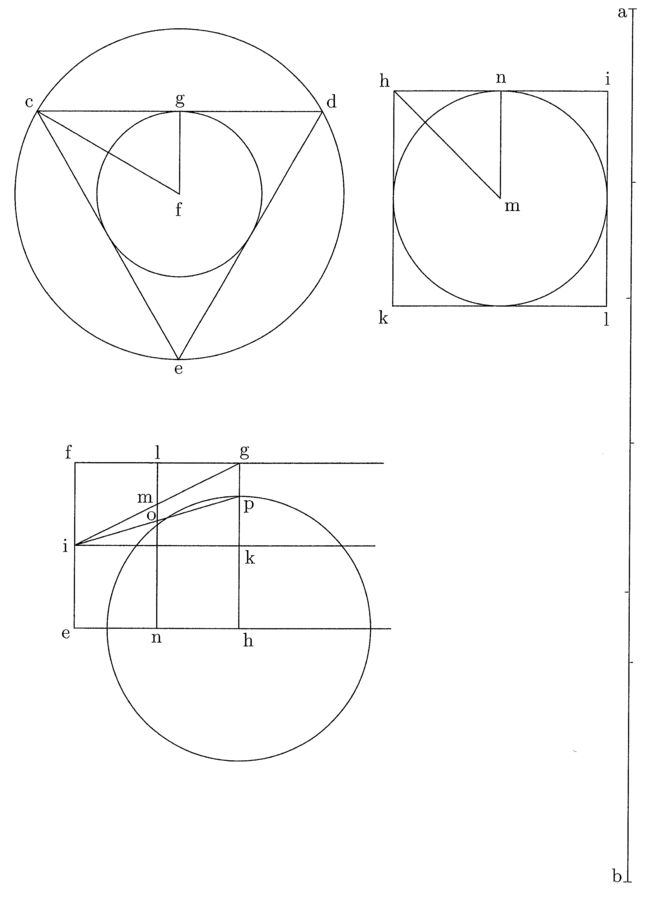
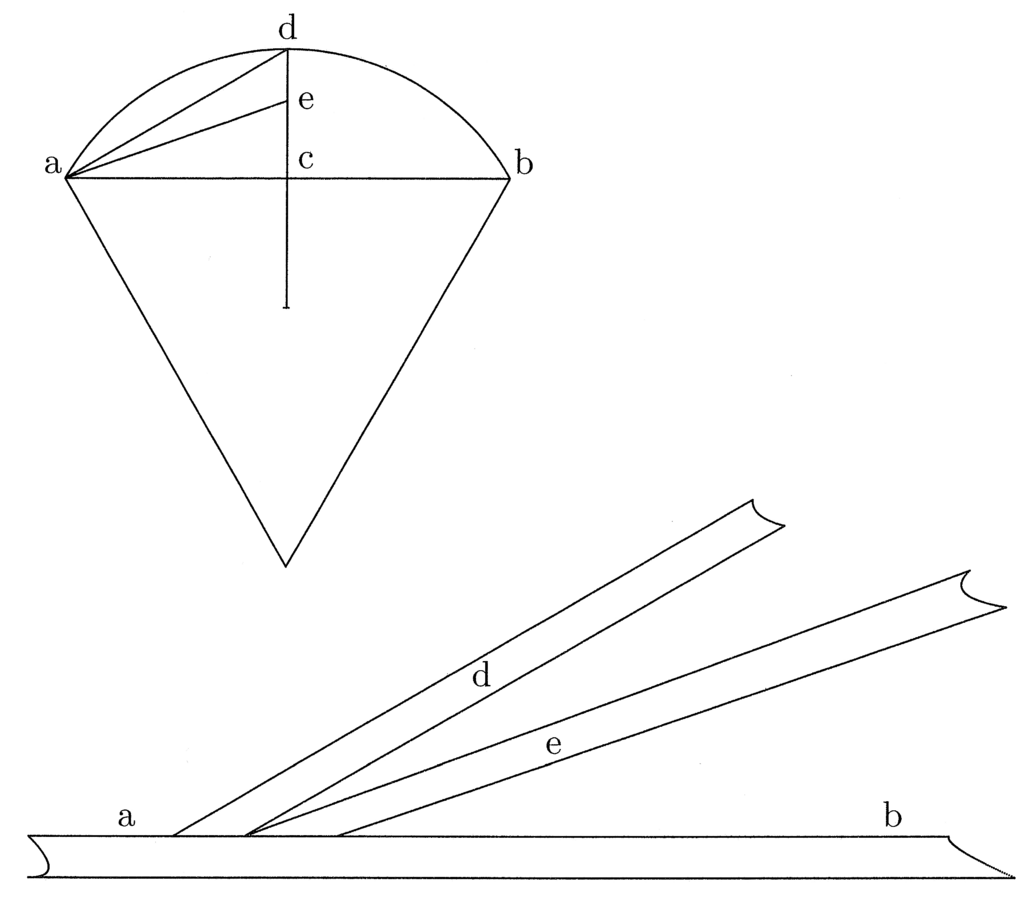
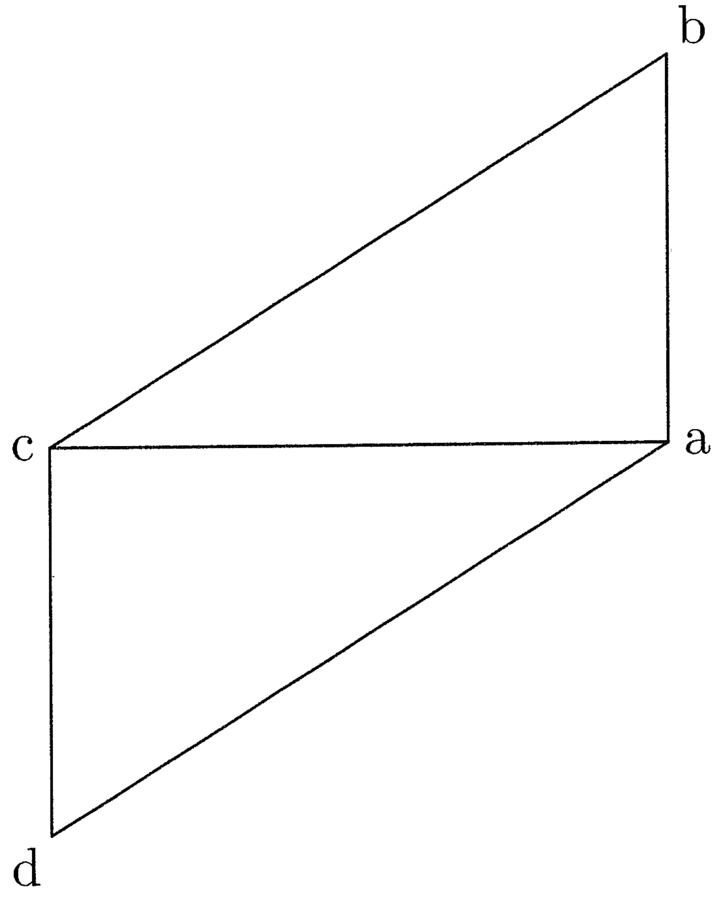
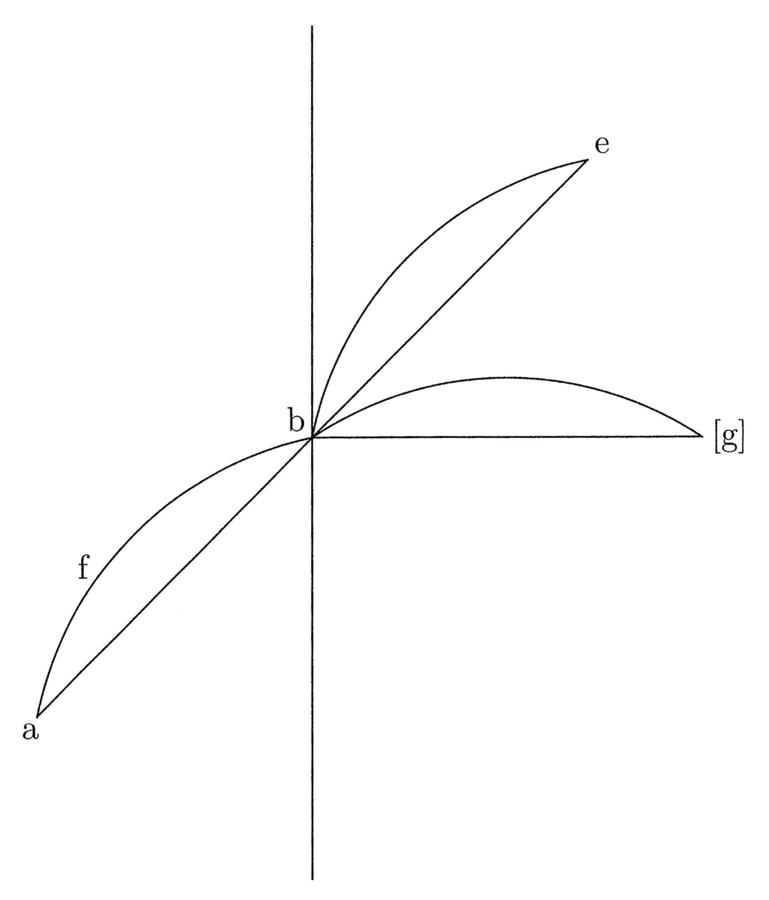
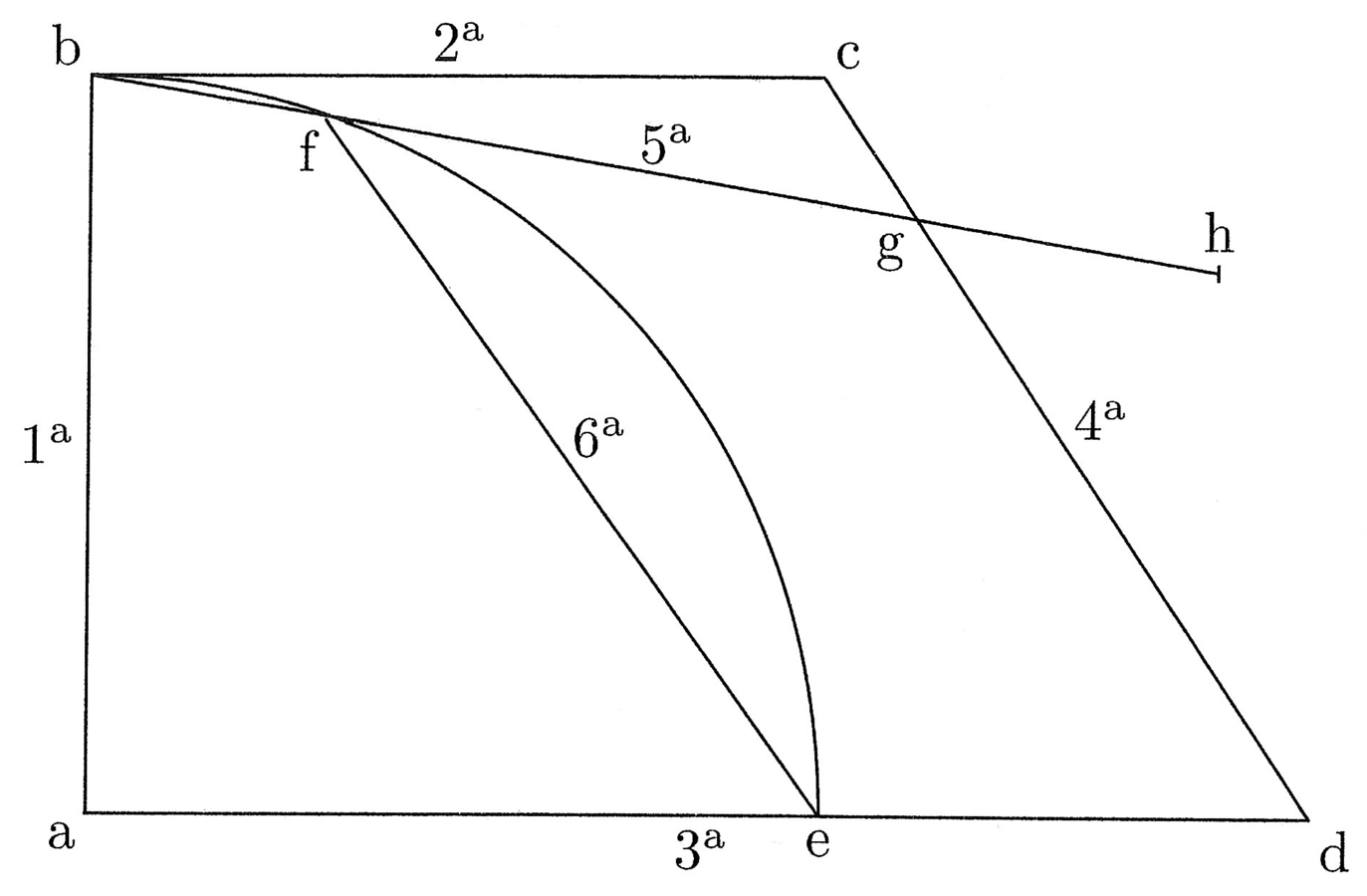
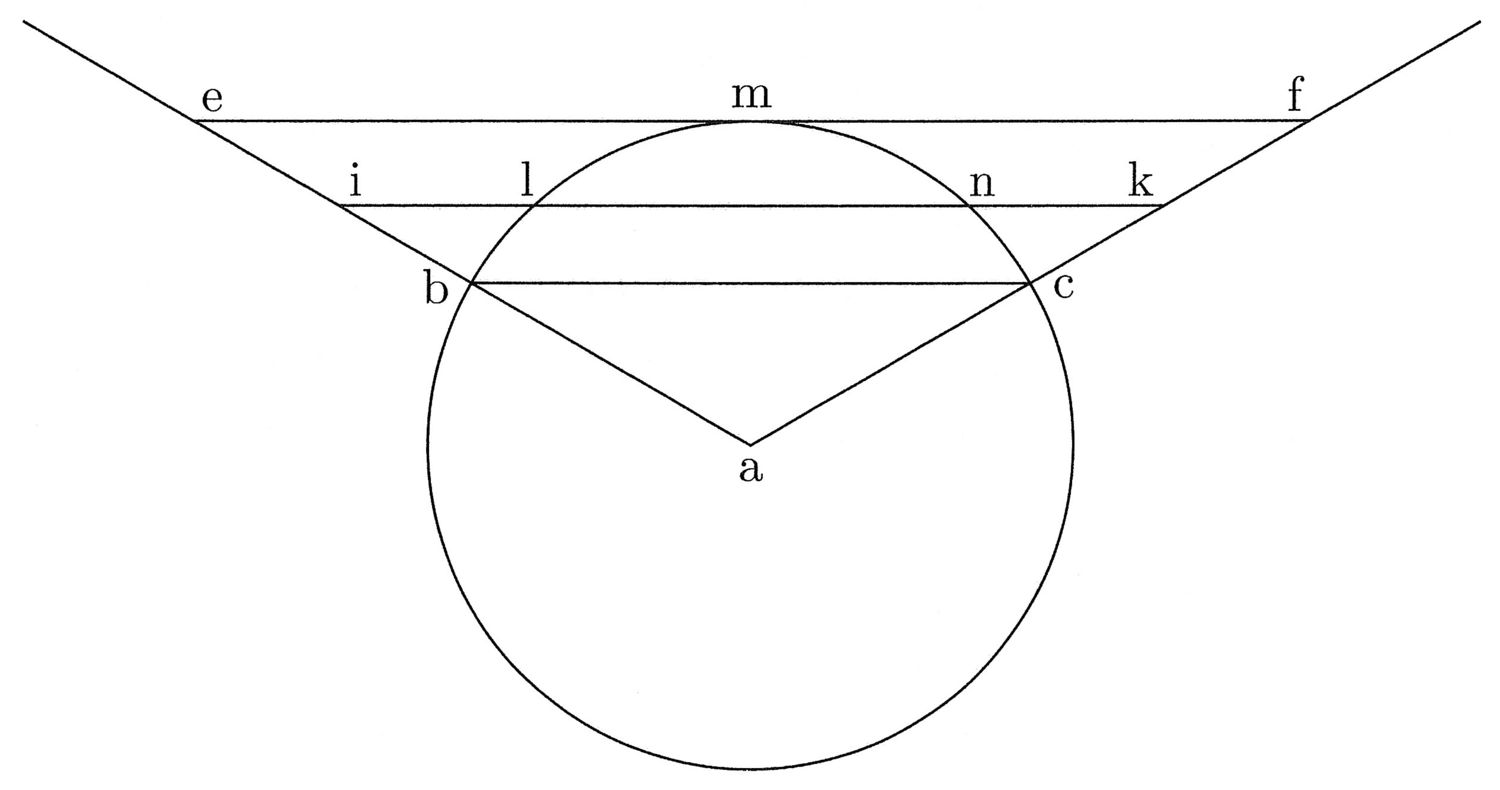
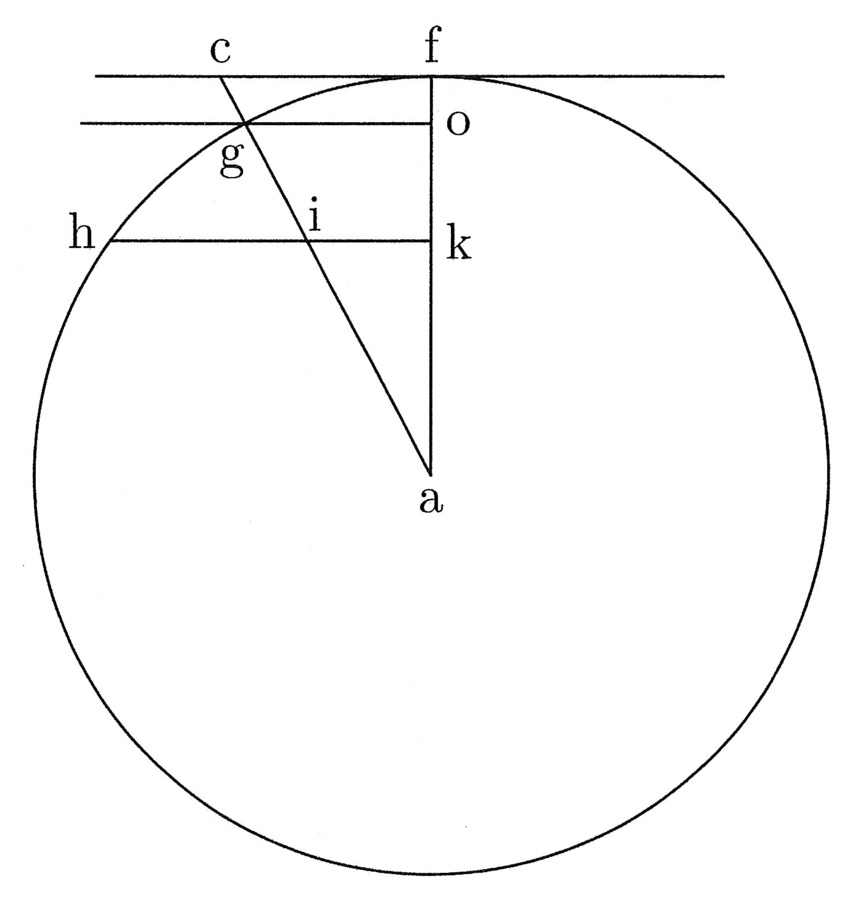
5. Et quia prima figurarum rectilinearum est triangulus, hinc in eo differunt in quantitate prima et secunda lineae maxime. In circulo vero coincidunt, quia ibi centrum aequaliter distat a circumferentia; medium enim et finis lateris coincidunt et est undique angulus. Est autem prima linea in trigono brevissima et secunda longissima. In eiusdem peripheriae tetragono prima post primam trigoni brevissima et sic secunda post secundam trigoni longissima et ita consequenter. Et quoniam prima in tetragono tali longior est prima in trigono, si ducitur prima in tetragono in medietatem peripheriae et similiter prima in trigono in eandem medietatem, diversas superficies, quae aequantur polygoniis, oriri constat (cfr. figura 1).

6. Unde excessus superficiei illius, quae ex prima tetragoni ducta in medietatem peripheriae, super superficiem, quae oritur ex ductu primae trigoni in eandem medietatem peripheriae, est excessus capacitatis tetragoni super capacitatem trigoni, et sic quidem in cunctis polygoniis ex excessu primae lineae cuiuslibet super primam trigoni isoperimetri deprehenditur excessus capacitatis ipsius polygoniae super capacitatem trigoni. Quanto autem differentia primae et secundae linearum est minor, tanto excessus primae lineae polygoniae super primam trigoni maior. Et quia in circulo coincidunt prima et secunda, excessus semidiametri circuli isoperimetri super primam trigoni est maximus et hinc circuli capacitas super capacitatem trigoni maxima. Unde linea una recta, quae in trigono ad tria latera est extensa, ut sit illius superficiei perimeter, in tetragono ad quattuor latera extenditur, ut sit tetragoni perimeter, et adhuc plus in pentagono. Si autem maxime extenditur, ita quod plus extendi non possit, erit perimeter circuli.

7. Ex his patet, quod si trigonus est minimae capacitatis, ubi prima et secunda lineae maxime differunt, et circulus maximae capacitatis, ubi prima et secunda lineae coincidunt, erit sic proportionabiliter in mediis polygoniis. Quare, si ponitur excessus capacitatis circuli super trigonum, ut est differentia primae et secundae lineae in trigono, erit excessus capacitatis circuli super tetragonum ut differentia primae et secundae lineae in tetragono et ita consequenter, cum ad maiorem excessum primae lineae unius super primam lineam alterius sequatur minor differentia primae et secundae in excedente quam sit primae et secundae in excessa. Ex quo faciliter dato excessu primae in una aliqua super primam trigoni et differentia differentiarum primae et secundae illius capacioris et primae et secundae trigoni potest haberi semidiameter circuli isoperimetri, cuius scilicet circumferentia aequatur tribus lateribus trigoni aut quattuor tetragoni.

8. Quo scito patet circuli quadratura. Nam si ducitur semidiameter illius circuli isoperimetri in medietatem peripheriae, oritur superficies quadrangularis, quae nec maior nec minor esse potest superficie circulari, ut Archimedes faciliter ostendit. Haec superficies quadrangularis in quadratam ducitur, quoniam costa eius erit medium proportionale inter semidiametrum circuli et semiperipheriam eius, quae ex nona sexti Euclidis invenitur. Omnia haec quamvis manifesta sint, volo tamen illa etiam illis, qui mathematicis operam non impenderunt, clarissima facere. Figurae autem multiangulae similium laterum et aequalium peripheriarum, de quibus loquar, polygoniae isopleures et isoperimetrae ex conformitate Graecae linguae apud aliquos reperiuntur nominari.

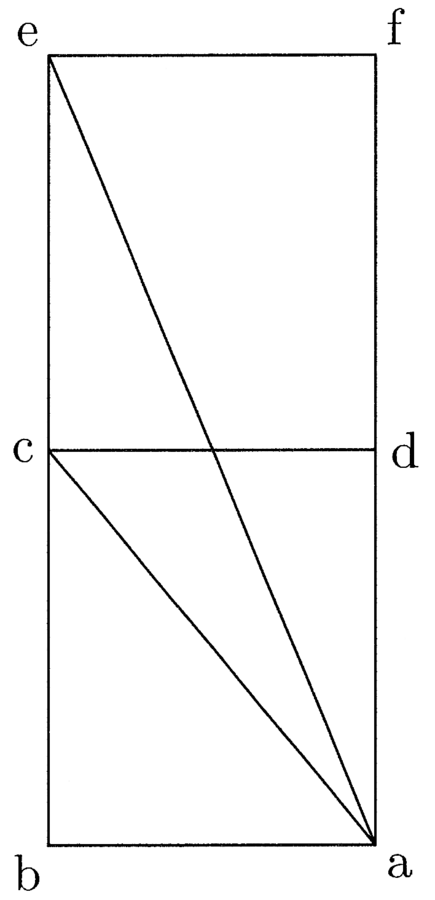
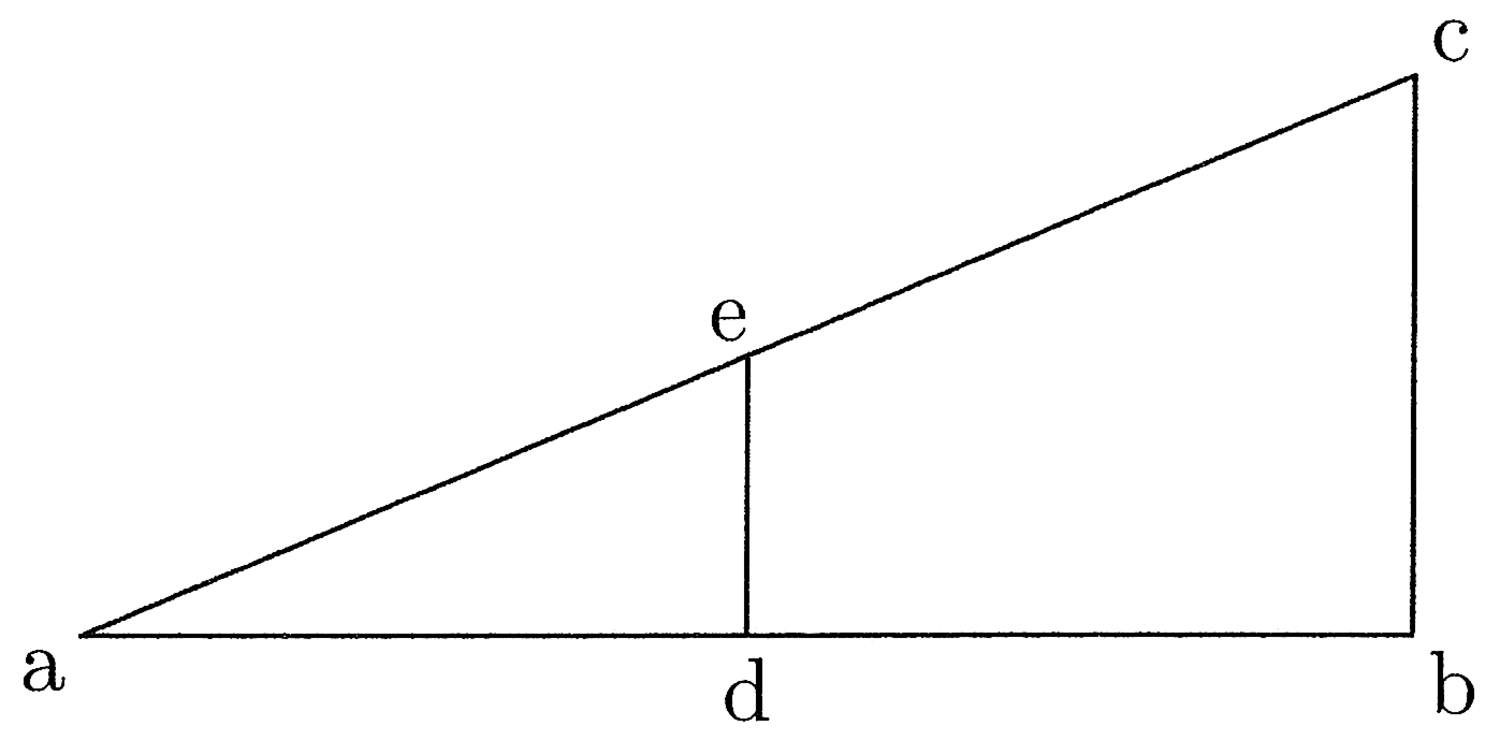
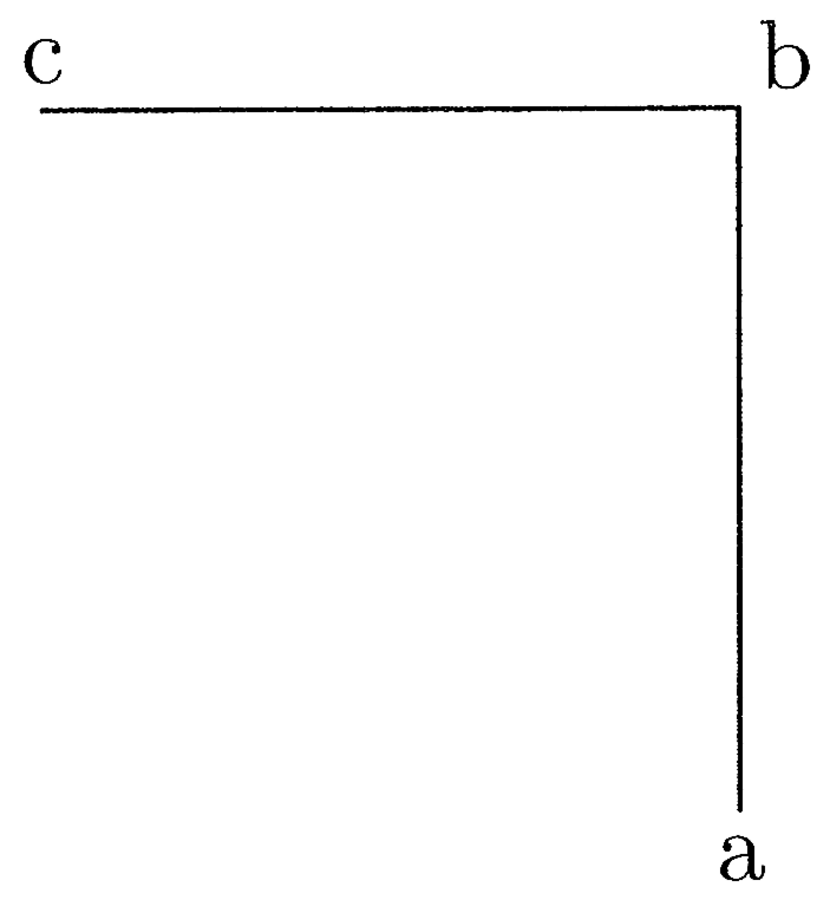
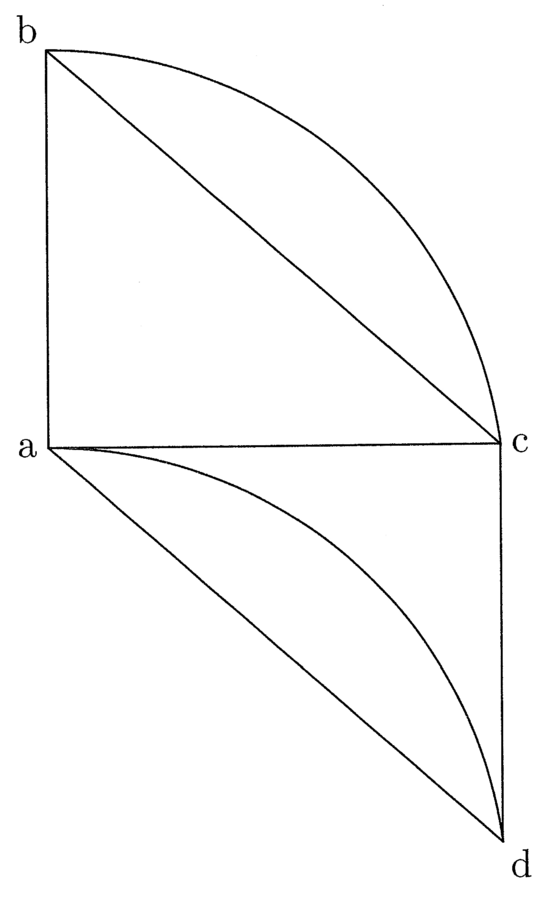
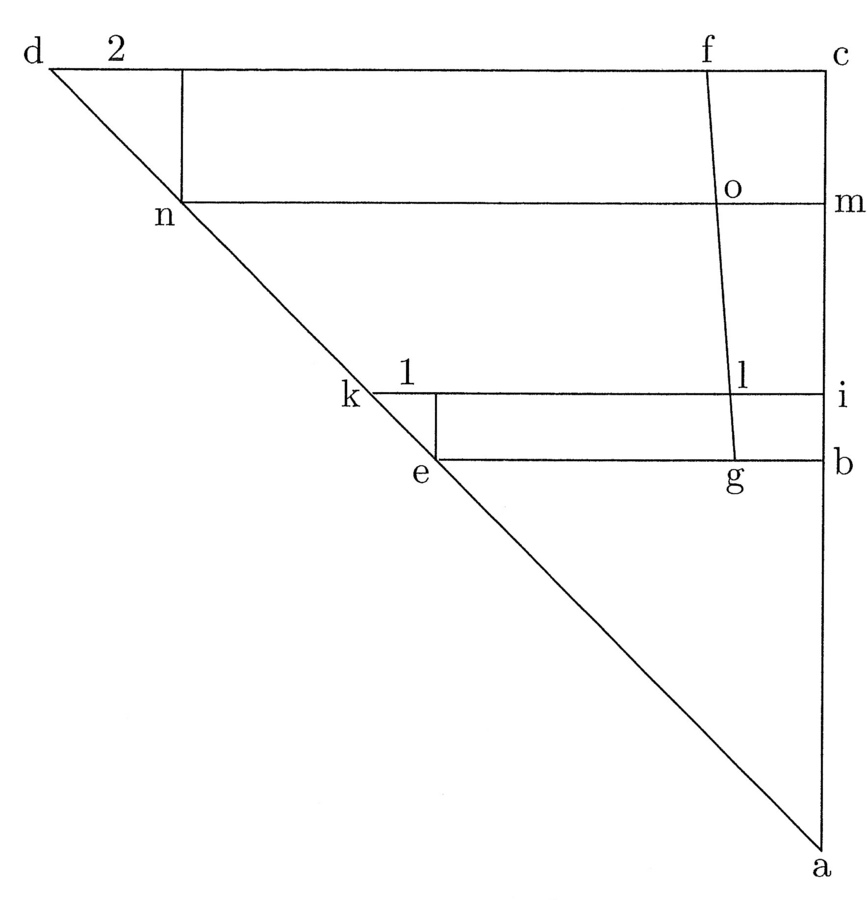
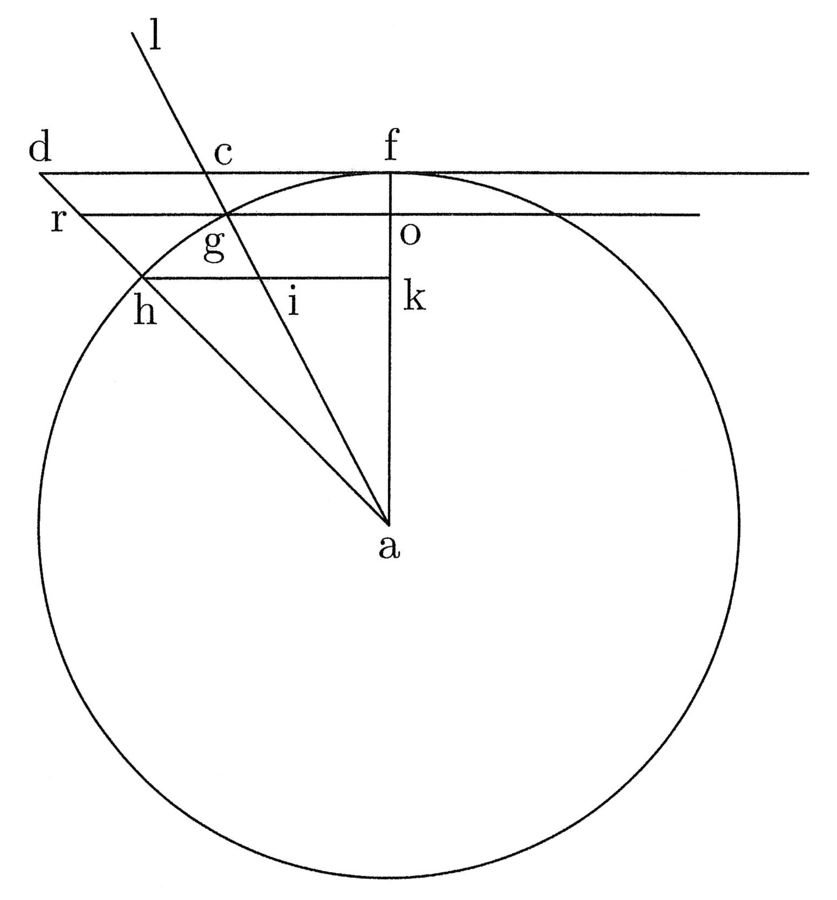
9. Si ducitur linea recta in lineam rectam, oritur figura quattuor rectorum angulorum, et si eadem ducitur in duplam, oritur dupla, et ita deinceps. Et si recta ducitur de angulo in angulum, diameter est, quia in duo dividit (cfr. figura 2).

Ut si ab linea ducitur in bc, oritur figura quadrangularis abcd habens quattuor angulos rectos. Et si ab ducitur in be, quae sit dupla ad bc, oritur quadrangulus abef, qui est duplus ad abcd. Linea vero ac diameter est, similiter et ae.

Prima propositio

10. Multiplicatio primae lineae in medietatem peripheriae aequatur embado polygoniae.

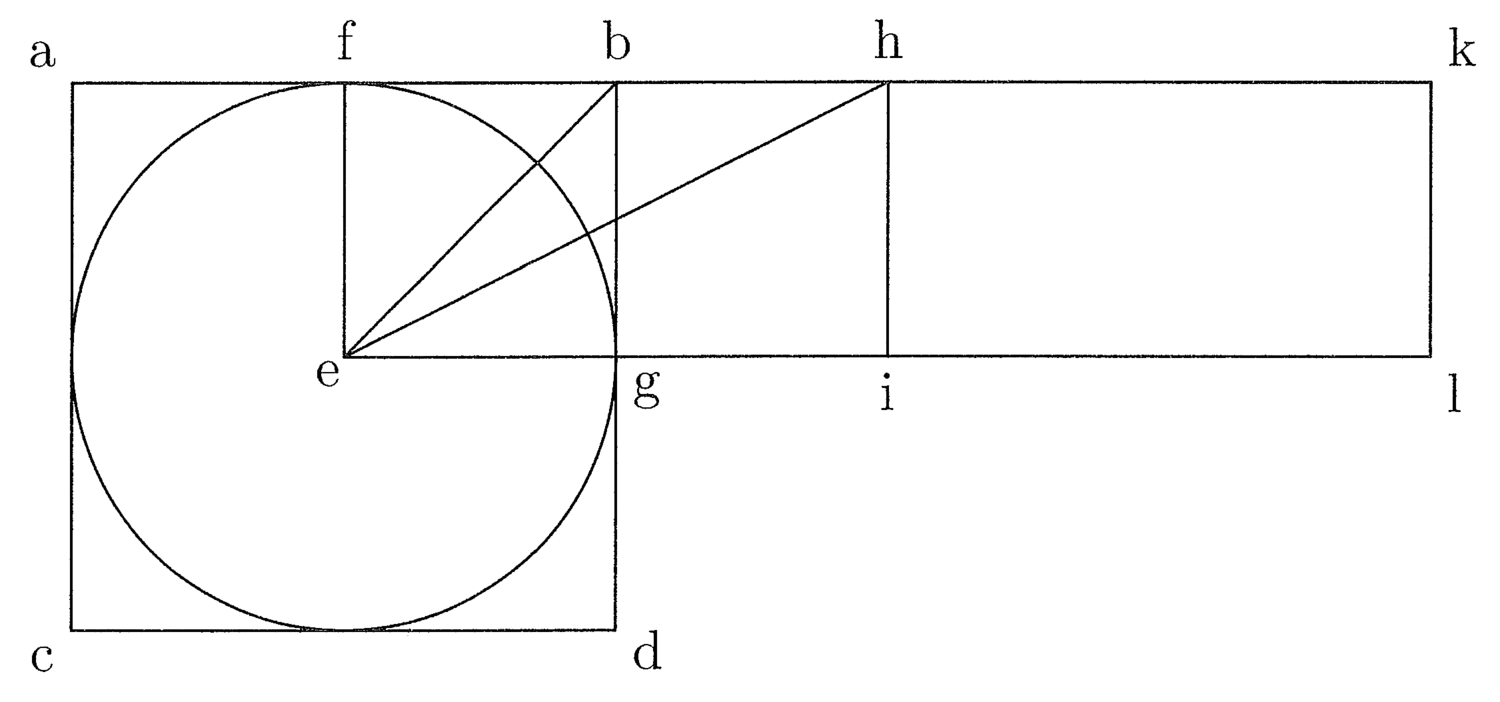
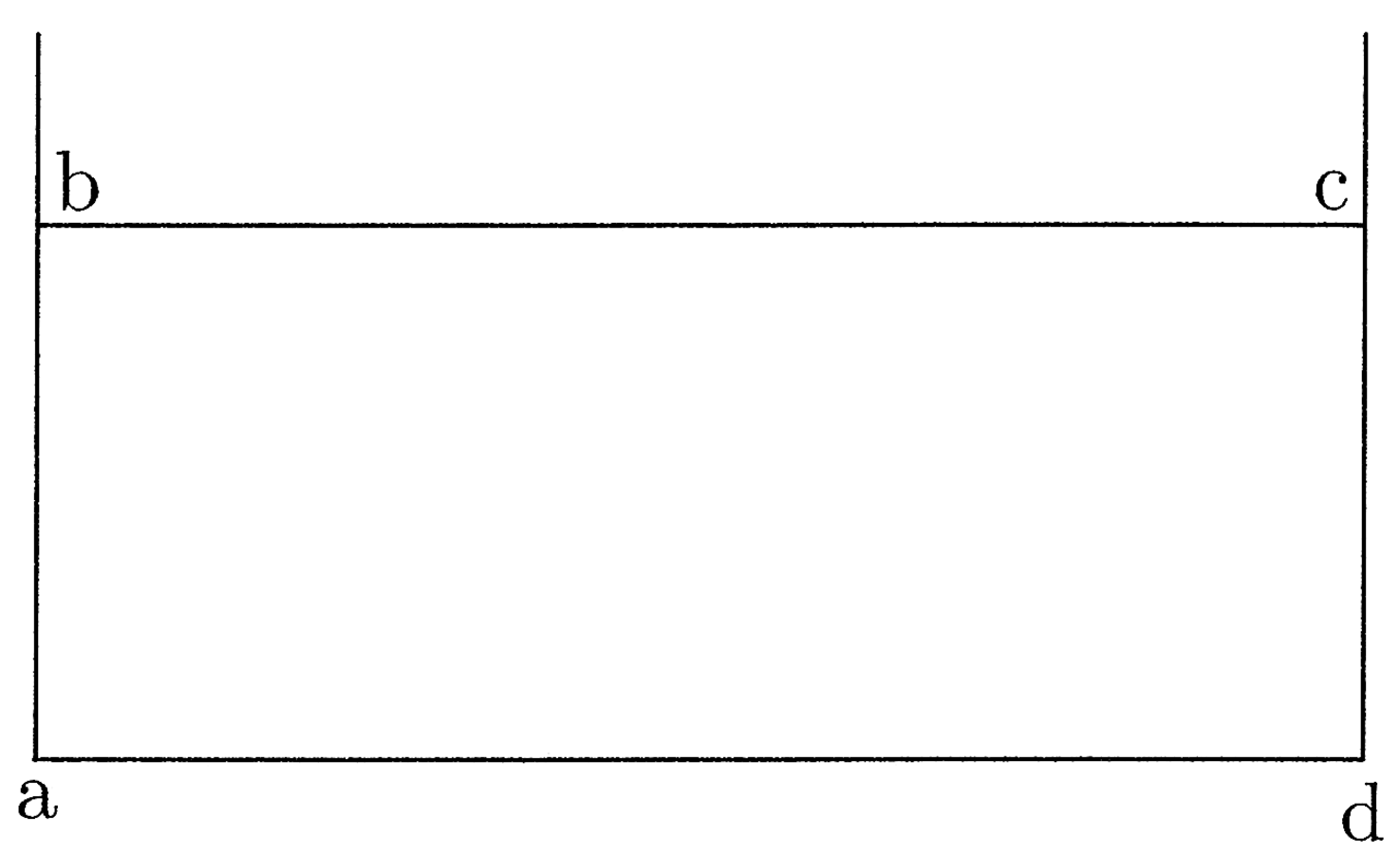
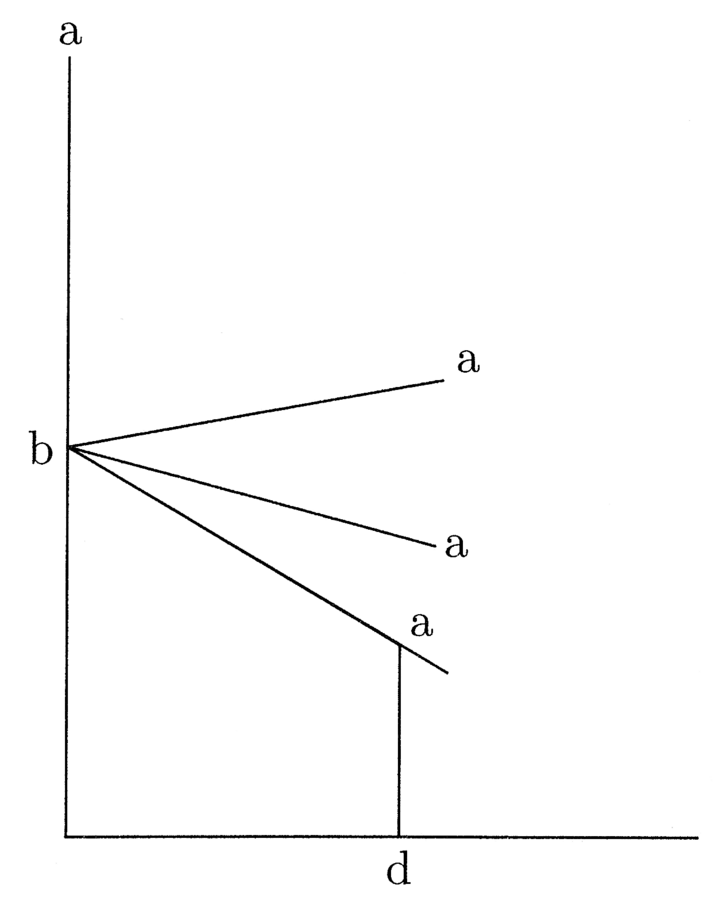
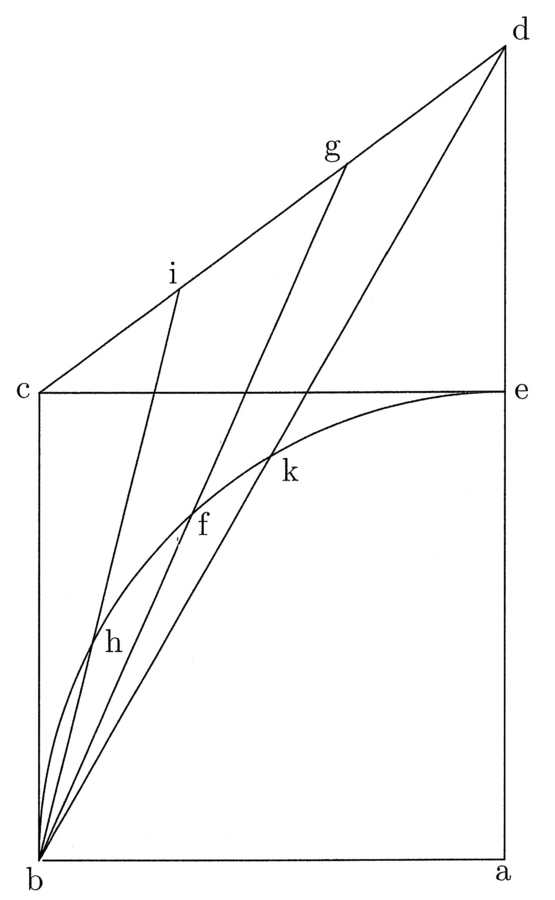
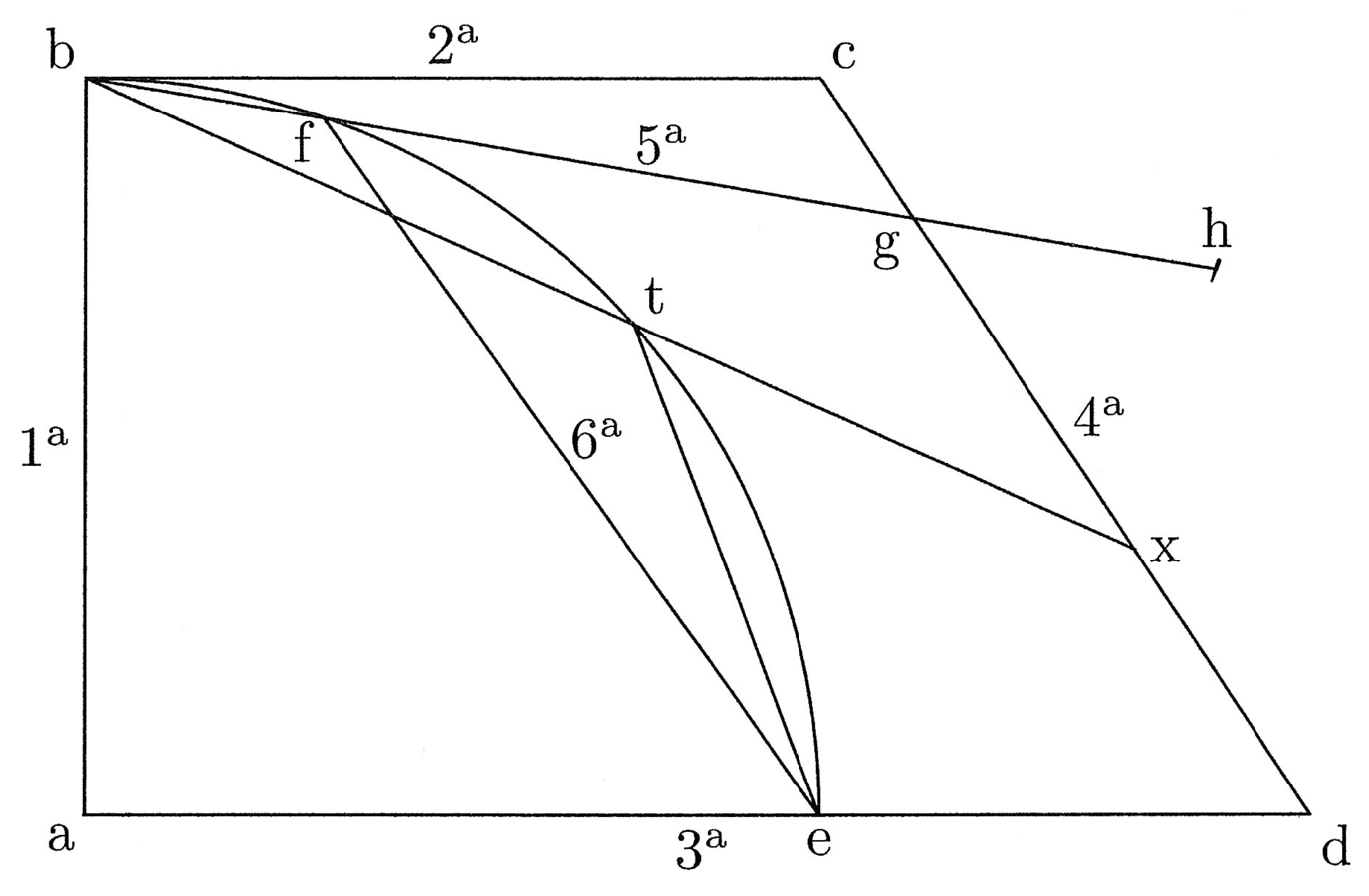
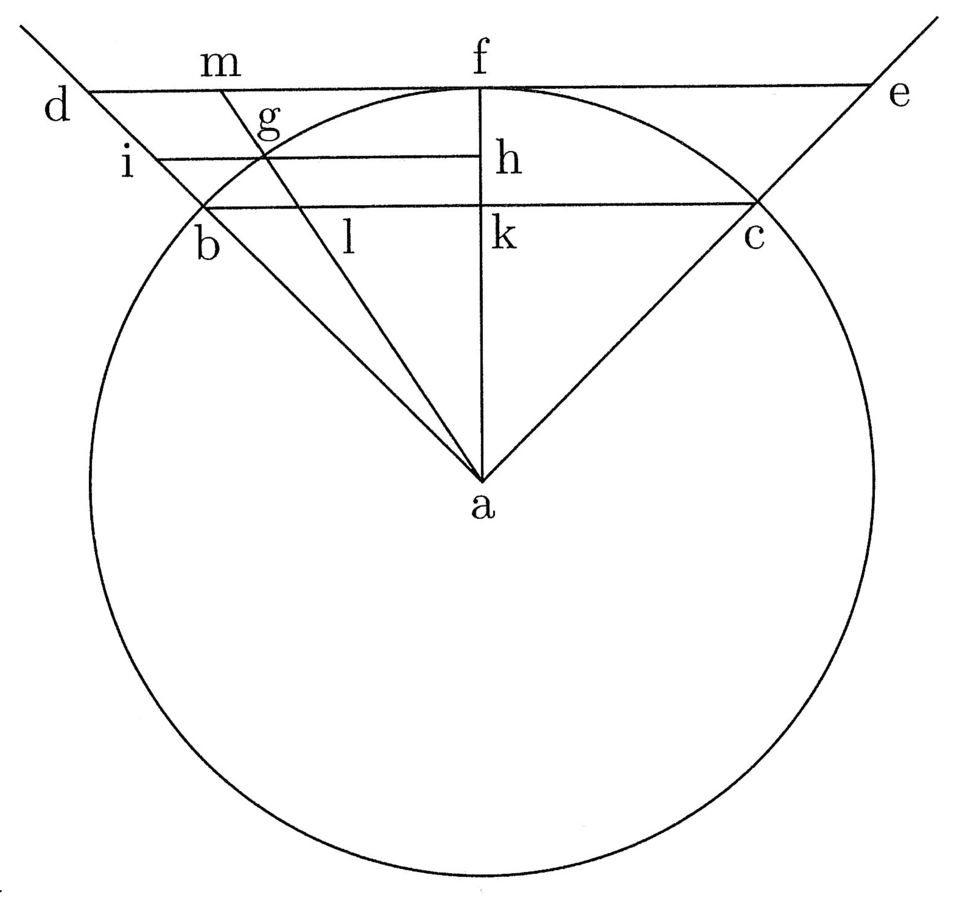
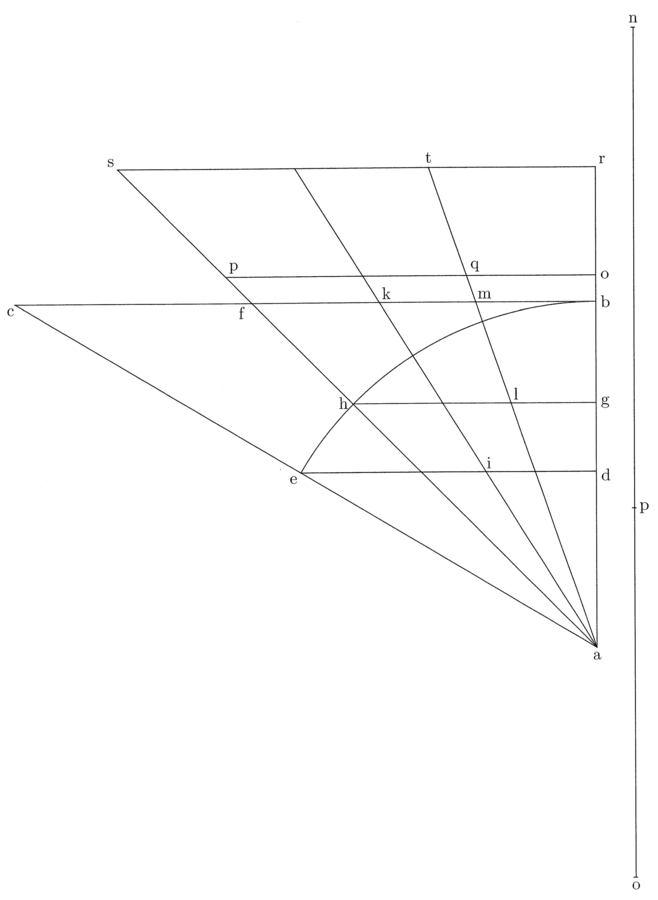
Sit abcd figura quadrata quattuor rectorum angulorum et aequalium laterum. Cui inscribatur circulus super e centro, ita quod tangat quattuor latera quadrati in medio, et trahatur de e ad contactum, ubi circulus tangit ab, linea ef, quae est prima, quia semidiameter inscripti, et trahatur eb linea et similiter de e ad contactum, ubi circulus bd latus tangit, et sit eg, et dupletur linea fb, et sit fh, et similiter dupletur eg, et sit ei dupla, et claudatur quadrangulus per lineam ih, et ducatur eh diameter. Manifestum est ex praemissa efb et ebh triangulos esse aequales. Primus enim est medietas primi quadranguli, quia eb diameter, et efh triangulus est medietas secundi quadranguli, qui est duplus ad primum, quia eh diameter (cfr. figura 3).

11. Erit igitur ebh triangulus ut efb. Duplicentur lineae fh et ei, et sit fk dupla ad fh et el dupla ad ei, et claudatur quadrangulus per lineam lk. Et quia efb triangulus est octava pars quadrati abcd, aequabitur efkl quadrangulus abcd quadrato. Sed fk est medietas peripheriae abcd. Aequatur enim duobus lateribus quadrati, et ef prima linea ducta est in medietatem peripheriae, quare patet propositum. Et sicut in quadrato, ita in omnibus polygoniis eodem modo constat, omnes enim in duplo plures triangulos orthogonios resolvuntur quam latera habeant, et proceditur pari modo, ut praemittitur.

Propositio secunda

12. Peripheria polygoniae, quae est circumscripta circulo, est maior peripheria circuli et tanto plus, quanto habuerit pauciora latera. Contrarium, si circulo fuerit inscripta.

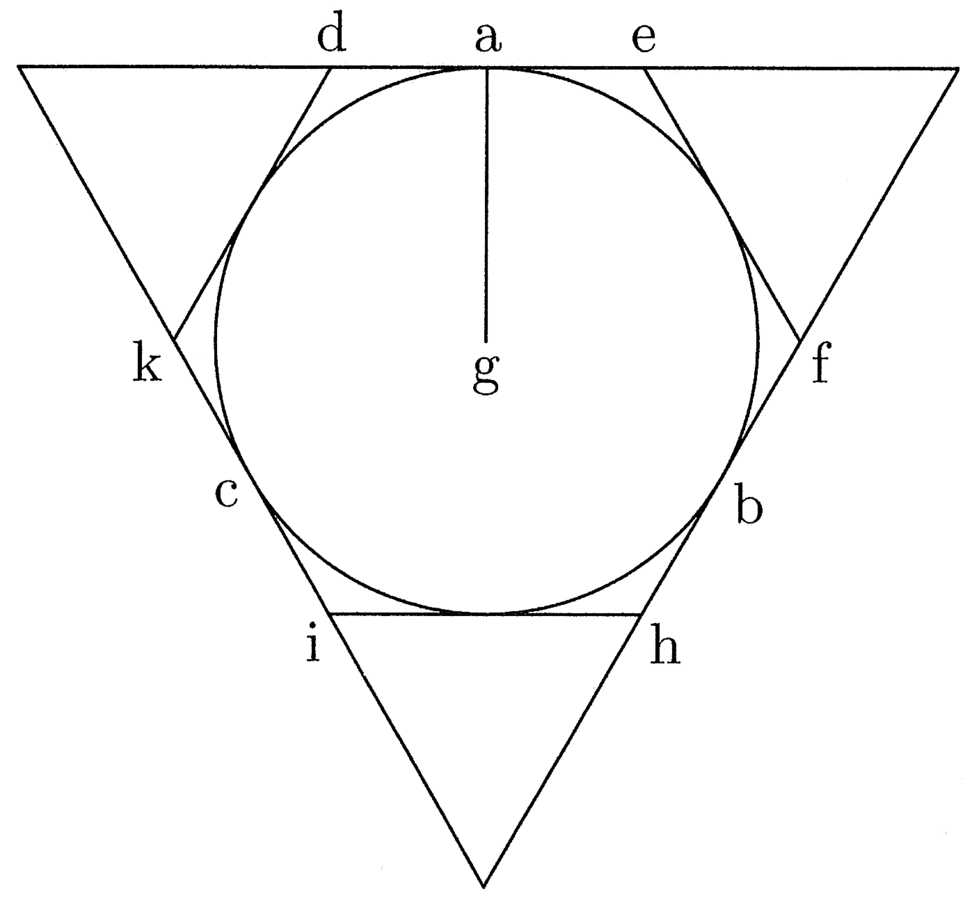
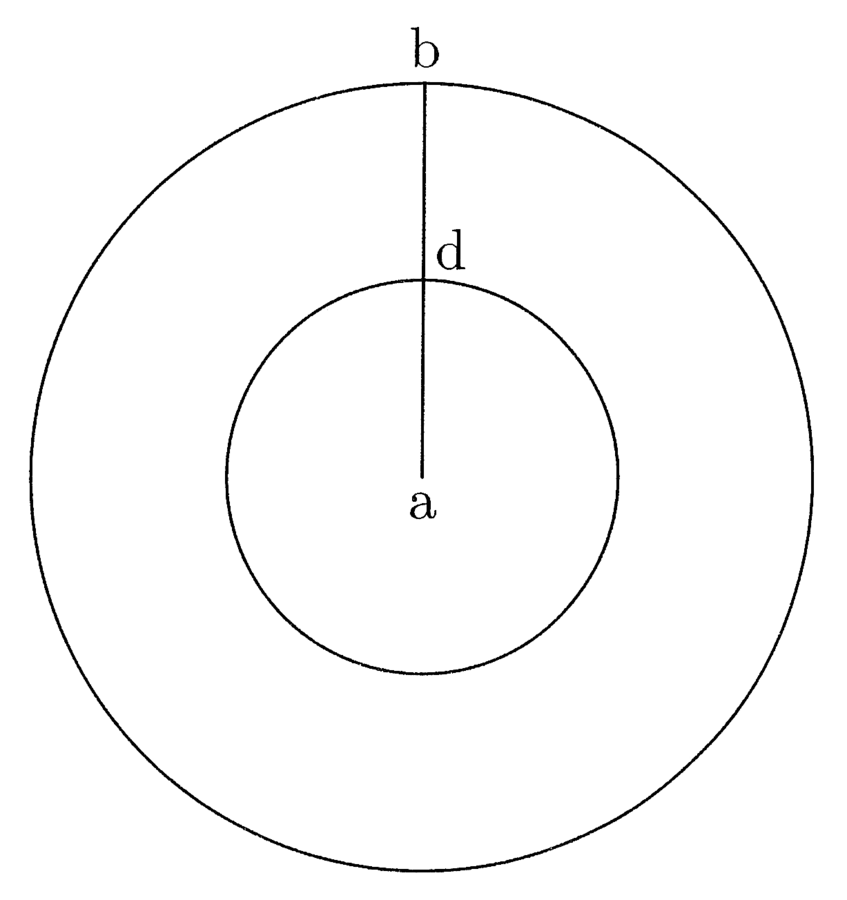
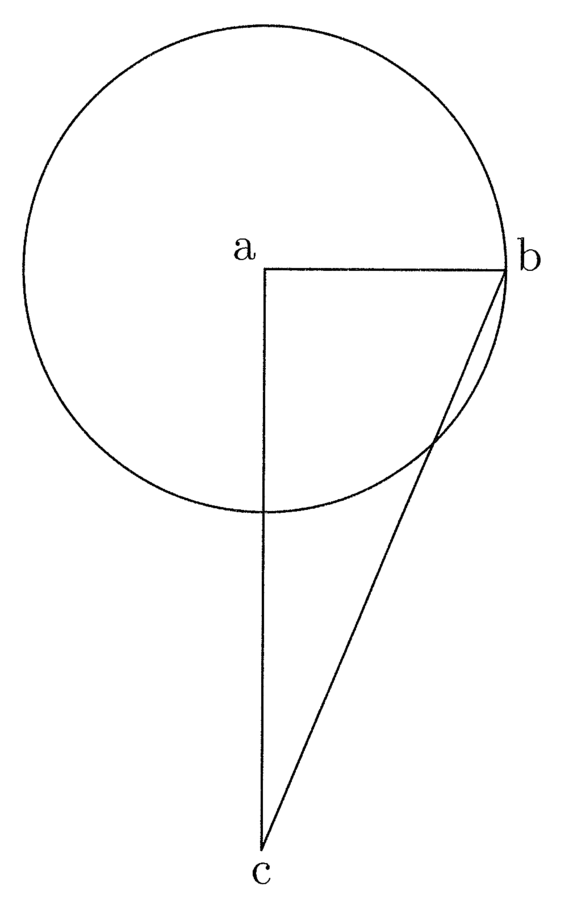
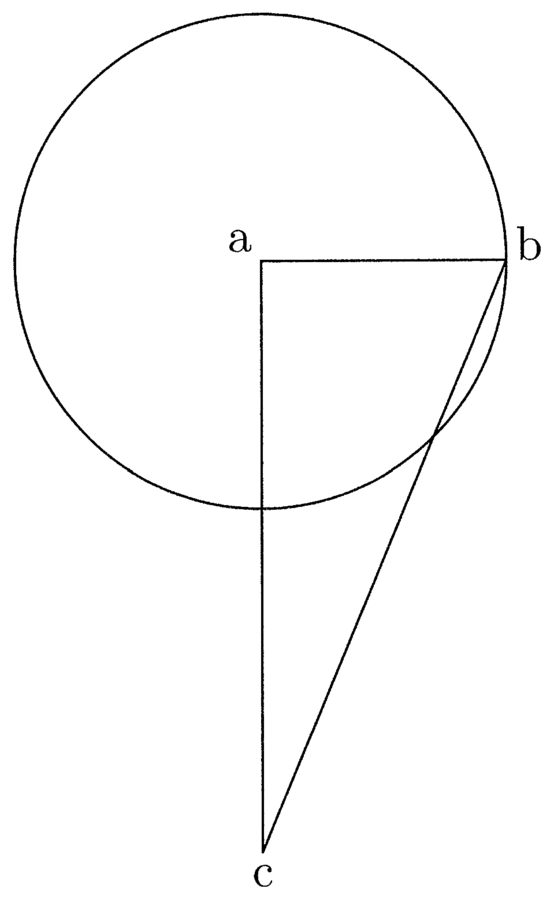
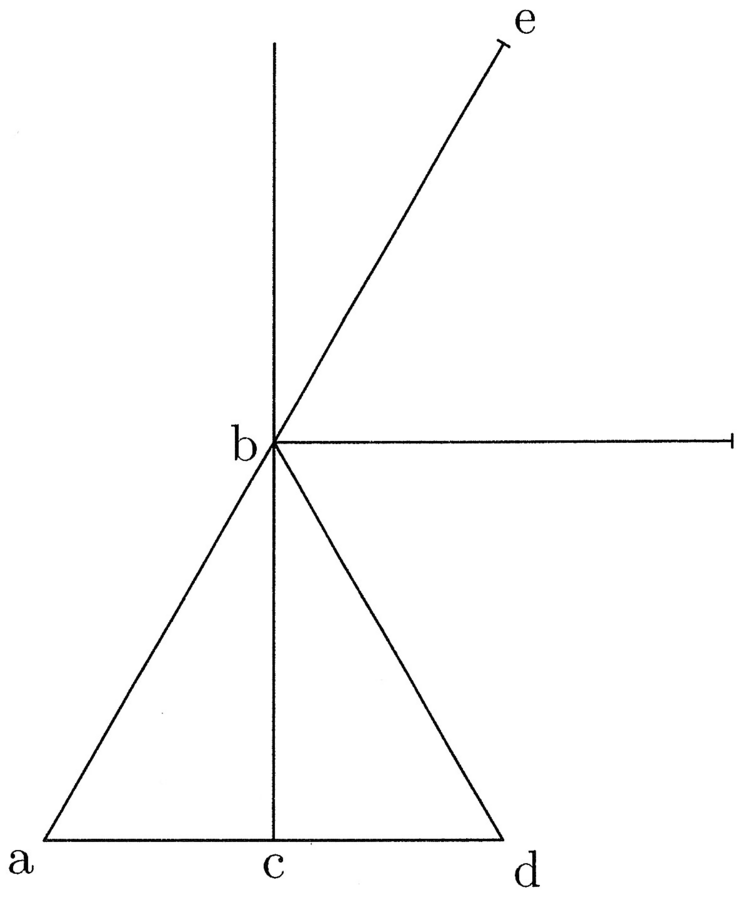
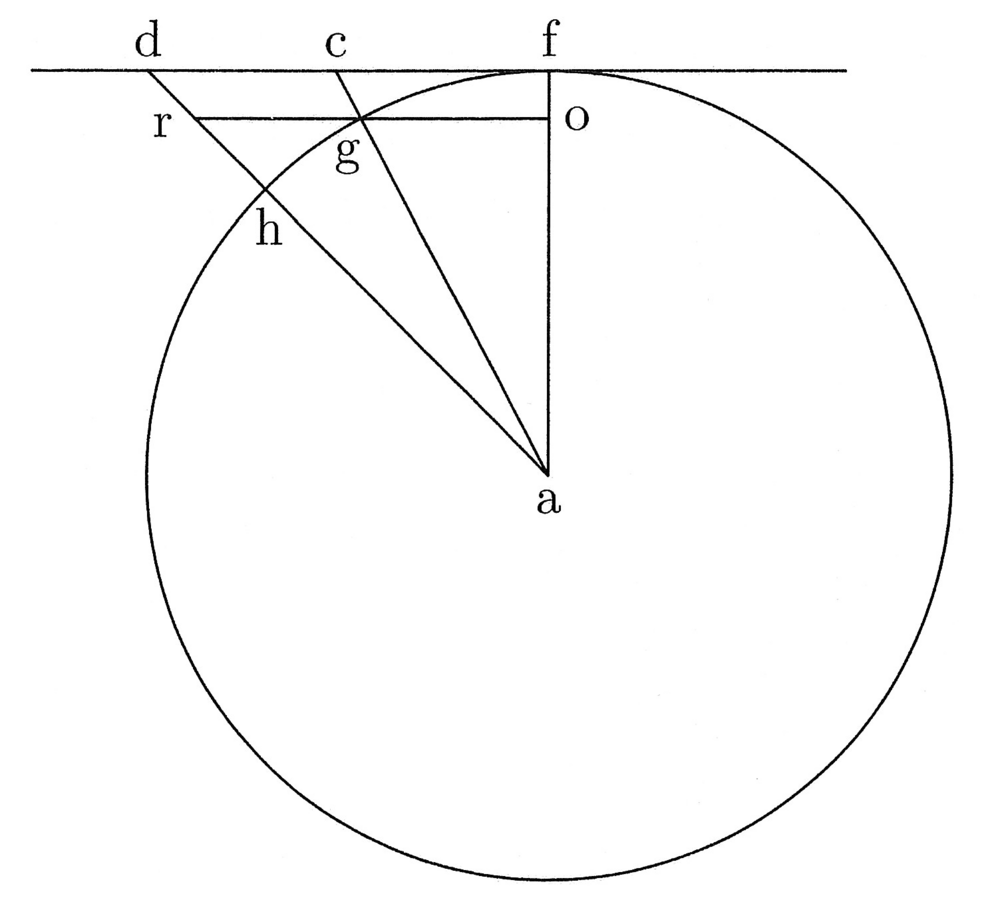
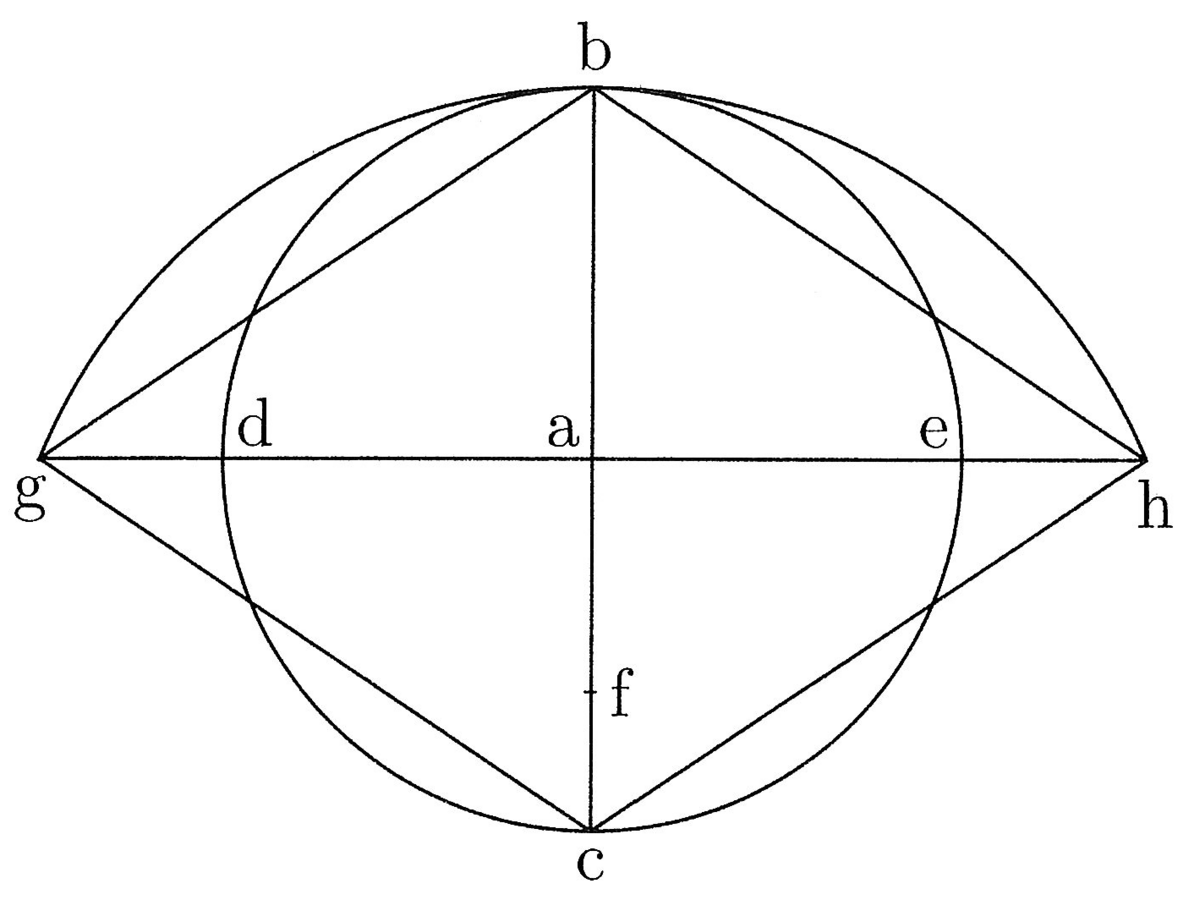
Circumscribatur circulo abc triangulus et hexagonus defhik, et de g centro trahatur ga semidiameter circuli, quae erit prima trianguli et hexagoni. Si igitur ag ducitur in medietatem peripheriae trigoni, oritur quadrangulum aequale trigono. Embadum seu area trigoni in se continet aream circuli inscripti (cfr. figura 4).

13. Erit igitur area circuli minor, quare peripheria circuli minor peripheria trigoni, et sic peripheria hexagoni minor peripheria trigoni et peripheria circuli minor peripheria hexagoni, quare patet propositum. In polygoniis inscriptis contrarium, nam area circuli maior. Quare quadrangulum ei aequale constituitur ex multiplicatione semidiametri in lineam, quae erit maior quam medietas peripheriae cuiuscumque polygoniae inscriptibilis. Continet igitur area circuli aream hexagoni inscripti et illa hexagoni continet aream trigoni. Erit igitur peripheria circuli maior, deinde hexagoni post trigoni et sic pariformiter in omnibus.

Tertia propositio

14. Inter rectas et circulares lineas minor illa, quae alteri subtenditur, et inter diversas illa subtensa, quae minor, minus exceditur ab illa, cui subtenditur.

Tertia circumferentiae circuli, quae subtenditur lateri trigoni, est minor lateri, et sexta pars eiusdem circumferentiae, quae subtenditur lateri hexagoni, similiter est minor. Et quia talis peripheria hexagoni minor est illi peripheriae trigoni, hinc minus exceditur proportionaliter sexta circumferentiae circuli a latere hexagoni quam tertia a latere trigoni. Sic tertia circumferentiae circuli proportionaliter plus excedit latus trigoni inscripti quam sexta latus hexagoni inscripti.

Propositio quarta

15. Circulus aequalis peripheriae polygoniae est maior circulo inscripto eidem et minor circumscripto, et quanto polygonia fuerit plurium laterum, tanto illis similior.

Patet. Nam latus polygoniae est minus quam arcus cui subtenditur, qui est arcus circuli circumscripti, et maius quam arcus ei subtensus, qui est circuli inscripti. Et quia inscriptus et circumscriptus sunt similiores, quando polygonia est plurium laterum, erunt igitur tunc etiam similiores circulo isoperimetro.

Quinta propositio

16. Inter quamcumque inscriptam polygoniam et circulum possunt cadere polygoniae maiores illi et minores circulo infinitae. Sic inter circumscriptam et circulum minores polygoniae et maiores circulo.

Patet ex divisione continui per partes proportionales in infinitum. Data enim chorda cuiuscumque arcus erit chorda medii arcus minor. Ita in infinitum. Et chordae sunt latera polygoniarum. Sic de lateribus polygoniarum circumscriptarum, quia si datur latus circumscriptae polygoniae, cui subtenditur arcus, dabitur latus minus, cui subtenditur medietas arcus, ita in infinitum.

Propositio sexta

17. Quadrangulus surgens ex multiplicatione semidiametri in semiperipheriam circuli nec maior nec minor est area circuli.

Patet ex praemissis. Nam peripheria polygoniae circumscriptibilis est maior peripheria circuli, sicut et area eius maior areae circuli. Et peripheria polygoniae inscriptibilis est minor peripheria circuli, sicut et area. Igitur multiplicatio semidiametri circuli in medietatem peripheriae suae est maior omni area polygoniae inscriptibilis et minor omni area polygoniae circumscriptibilis. Et cum data area maiori polygoniae inscriptae et minori circulo semper dari possit polygonia inscriptibilis maior, sic data area maiori circulo semper potest dari circumscriptibilis polygonia minor. Igitur patet propositum.

Septima propositio

18. Capacitas circuli excedit capacitatem omnium polygoniarum isoperimetrarum.

Patet. Nam prima linea in omnibus polygoniis est minor prima linea circuli, et peripheria est una in omnibus. Plus igitur resultabit de multiplicatione primae circuli in medietatem peripheriae quam in aliqua.

Propositio octava

19. Capacitas trigoni isoperimetri est minima.

Patet, quia habet latus maximum. Plus igitur excedit peripheriam inscripti quam aliqua polygonia. Quare circulus inscriptus ei est minor omnibus inscriptis aliis. Igitur prima eius minima, hinc et capacitas minima.

Nona propositio

20. Quanto polygonia talis plurium fuerit laterum, tanto capacior.

Patet, quia cum habeat latera breviora, et potentia secundae lineae sit potentia primae et medietatis lateris. Igitur tunc prima et secunda lineae minus inter se differunt et plus assimilantur primae circuli isoperimetri. Latus enim breve minus exceditur ab arcu.

Propositio decima

21. In capaciori polygonia necesse est primam lineam esse longiorem et secundam breviorem.

Colligitur ex praemissis. Nam cum circulus eidem inscriptus sit similior circulo isoperimetro, quia capacior et circulus isoperimeter capacissimus, igitur prima linea illius polygoniae longior et latus eius minus. Minus enim latus minus exceditur ab arcu, quare propinquius accedit ad circulum isoperimetrum. Et quia latus est minus, igitur secunda linea minus differt a prima et ideo etiam similior primae circuli isoperimetri, erit igitur brevior in capaciori. Et haec est principalis propositio ad inveniendum id quod inquirimus.

Undecima propositio

22. Si ponitur excessus capacitatis circuli super capacitatem trigoni ut differentia primae et secundae lineae trigoni, erit excessus capacitatis circuli super capacitatem polygoniae mediae inter trigonum et circulum ut differentia primae et secundae lineae eiusdem, et si ponitur excessus ut medietas aut alia pars differentiae primae et secundae in trigono, ita erit in mediis.

Puta ponatur, quod excessus capacitatis circuli super capacitatem trigoni sit ut differentia primae et secundae, et sit in numeris prima trigoni 7 et secunda 14. Erit differentia 7. Et prima circuli isoperimetri erit 14, quia maior prima trigoni per differentiam, quae est 7. Dico, quod prima circuli erit maior prima cuiuslibet mediae polygoniae per quantitatem differentiae primae et secundae eiusdem. Ut in tetragono, ubi differentia sit 4, excedit prima circuli primam tetragoni in 4. Erit igitur tunc prima tetragoni 10. Si dixeris tetragonum capaciorem in habitudine ad circulum, erit igitur prima eius longior. Sit igitur ut 11, cui adde differentiam, et habebis 15. Et quia 15 excedit 14, erit incapacior per praemissam, sic capacior et incapacior. Similiter, si dixeris tetragonum minus capacem. Puta ut 9, erit secunda 13, sic minor 14, quare capacior per praemissam. Ita capacior et incapacior, quod est inconveniens. Et haec ostensio procedit in omnibus.

23. Considera igitur, quod quamcumque portionem sagittae addit una polygonia, ut oriatur prima circuli, similem omnes addunt. Et ut hoc clare videas, sic procede. Patet ex praemissis, si prima capacioris polygoniae est maior quam incapacioris, quod illa semper erit minor aliqua prima alicuius polygoniae, cum inter quamcumque dabilem, quae minor est circulo, possint dari maiores in infinitum. Et ita talis semper est minor prima circuli. Sic si fuerit minor illa, erit maior secunda linea alicuius polygoniae et sic maior prima circuli. Ideo, si posueris ex additione alicuius portionis sagittae ad primam polygoniae resultare primam circuli isoperimetri, sic necesse erit ex portione similis habitudinis ad sagittam additae primae in quibuscumque intermediis polygoniis accidere.

24. Puta si duae tertiae sagittae trigoni ad primam eius additae efficiunt primam circuli, sic erit in pentagono, hexagono et omnibus. Nam si dixeris in aliqua resultans plus aut minus esse, hoc erit necessario propter maiorem capacitatem. Si igitur dixeris eam maiorem, hoc non est possibile; nam oporteret eam esse minorem prima circuli, et quia prima circuli est idem cum prima trigoni addita portione dicta sagittae, ita foret maior et minor. Similiter, si dixeris propter capacitatem minorem, oporteret simul dicere eandem et maiorem.

25. Palam ex hoc etiam, quod si duae polygoniae sic se habuerint, quod similis portio sagittae addita ad primas efficit hinc inde aequale, ita erit necessario in omnibus. Nam aut illae duae polygoniae habent alias in medio inter eas, ut trigonus et pentagonus habent tetragonum. Tunc necesse est sic esse in tetragono sicut in trigono et pentagono. Nam si dixeris lineam resultantem maiorem ob maiorem capacitatem tetragoni quam trigoni, ita erit etiam minor, quia minor capacitas tetragoni quam pentagoni. Ita si dixeris ob capacitatem lineam resultantem minorem, quia etiam erit simul et maior, quod est impossibile. Sic si dixeris duas illas sine medio sequi, ut trigonus et tetragonus, et negaveris idem in pentagono. Tunc, quia aut dixeris maiorem ob maiorem capacitatem pentagoni et hoc non potest dici, nam tetragonus est capacior, ubi non est maior: a fortiori non erit maior in pentagono, sed potius minor. Sic si dixeris minorem, non valet, quando in tetragono non est minor. Sic patet sequi inconveniens, si in aliis non eveniret idem.

26. Ad hoc sequitur, quod si ex simili portione in duabus polygoniis modo dicto eadem linea exoritur, quod illa erit semidiameter circuli isoperimetri. Nam cum in circulo isoperimetro prima et secunda linea sint una, hinc, si additur ad primas polygoniarum quaecumque portio sagittarum, sive lineae ascendant sive descendant sive maneant eaedem, semper ultima erit prima circuli isoperimetri. Puta si addo ad primas unam quartam sagittae, tunc erunt continue maiores, et maxima erit ultima et prima circuli. Et si addo tres quartas, erunt continue minores, et ultima erit minima et prima circuli. Et si addo talem portionem, quod in duabus resultat eadem linea, tunc sic erit in omnibus. Unde cum ultima tunc sit ut prima, erit quaelibet prima circuli. Ex quo etiam manifestum est capacitatem circuli excedere capacitatem cuiuslibet polygoniae secundum lineam eandem in qualibet habitudinem tenentem ad sagittam suam. Et ita etiam quaelibet capacior polygonia omnes minus capaces exsuperat secundum lineam eandem in qualibet habitudinem ad suam sagittam retinentem.

27. Poterit et hoc aliter ostendi (cfr. figura 5). Et sit ab linea secunda trigoni, quam dividat c, trahas orthogonales de a b c aequales bc et claude figuram per lineam def. Et quia prima linea trigoni est ac, erit prima circuli isoperimetri plus quam fe: sit igitur ut fh, et sit eh duae tertiae ed. De h trahe aequedistantem ad bd et sit hi, trahe similiter lineam ch. Manifestum est quod, si fh est prima circuli isoperimetri, quod tunc primae lineae polygoniarum mediarum erunt maiores ac et minores fh et quae capacior huius prima similior fh. Est etiam manifestum, quod sicut ai et ih simul sunt prima trigoni et differentia primae et secundae eiusdem, quae est sagitta lateris eius, et cum hoc duae tertiae sagittae, quod sic in polygoniis mediis lineae trahi possunt aequedistantes ad ai, quae terminantur in ih et af. Quae iunctae residuae lineae ih aequantur primae lineae polygoniae mediae, sagittae et duabus tertiis sagittae eiusdem, ut in trigono dictum est. Et notum est, quod quanto polygonia illa fuerit incapacior, tanto hae duae lineae simul erunt longiores, quia incapacior habet maius latus et hinc maiorem sagittam. Sic erunt illae duae lineae longissimae in trigono, in circulo isoperimetro brevissimae, quia circulus caret latere et per consequens sagitta, et duae lineae in polygoniis erunt una in circulo.

28. Dico igitur quod, si de h versus i signaveris sagittam alicuius polygoniae mediae et lineam de termino sagittae aequedistantem ad ai traxeris, tunc ch linea secabit illam in duas lineas, quarum minor erit pars sagittae et maior prima polygoniae illius. Puta sit hk sagitta tetragoni et trahatur de k aequedistans ad hf, quae sit kl, et ubi illam secat ch, pone m. Dico km fore duas tertias hk, quod de se notum est. Habet enim se mk ad kh sicut ci ad ih. Et dico ml fore primam lineam tetragoni. Si negaveris aut igitur dixeris tetragonum capaciorem aut incapaciorem: si capaciorem, tunc prima eius debet esse maior lm et tunc lk et kh simul sunt minores prima linea tetragoni, eius sagitta et duabus tertiis sagittae, quod implicat contradictionem. Nam si debet tetragonus esse capacior, ut dicis, oportet quod lk et kh excedant primam tetragoni, sagittam et eius duas tertias. Eodem modo implicat contradictionem, si dixeris tetragonum incapaciorem. Nam tunc oportebit lm esse minorem et lk et kh simul esse maiores prima linea tetragoni, sagitta et duabus tertiis eiusdem. Ita de aliis polygoniis. Quare patet, si prima circuli isoperimetri excedit primam trigoni per partem aliquotam sagittae trigoni, etiam excedit primam lineam cuiuslibet polygoniae mediae per similem partem aliquotam sagittae polygoniae illius, et dicere aliud implicat contradictionem.

Propositio duodecima

29. Habitudo excessus capacitatis circuli super capacitatem trigoni isoperimetri ad excessum capacitatis polygoniae mediae super capacitatem eiusdem trigoni est sicut sagitta trigoni ad lineam, quantum est sagitta polygoniae mediae eidem minorem.

Ut si ponitur excessum capacitatis circuli super capacitatem trigoni esse ut 7, erit capacitas tetragoni super trigoni secundum lineam, a qua sagitta tetragoni est subtracta. Puta si sagitta fuerit 4, erit capacitas tetragoni ut tria. Hoc corollarium patet ex praemissis.

Tredecima propositio

30. Per scientiam excessus capacitatis alicuius polygoniae mediae super capacitatem trigoni isoperimetri scitur capacitas circuli isoperimetri.

Manifestum est, cum habitudo sit nota, quod tunc uno excessu noto notus erit et alius. Sed quia excessus in tetragono, pentagono, hexagono vel alia media polygonia sciri potest per scientiam primae lineae trigoni et polygoniae mediae, tunc et circuli isoperimetri.

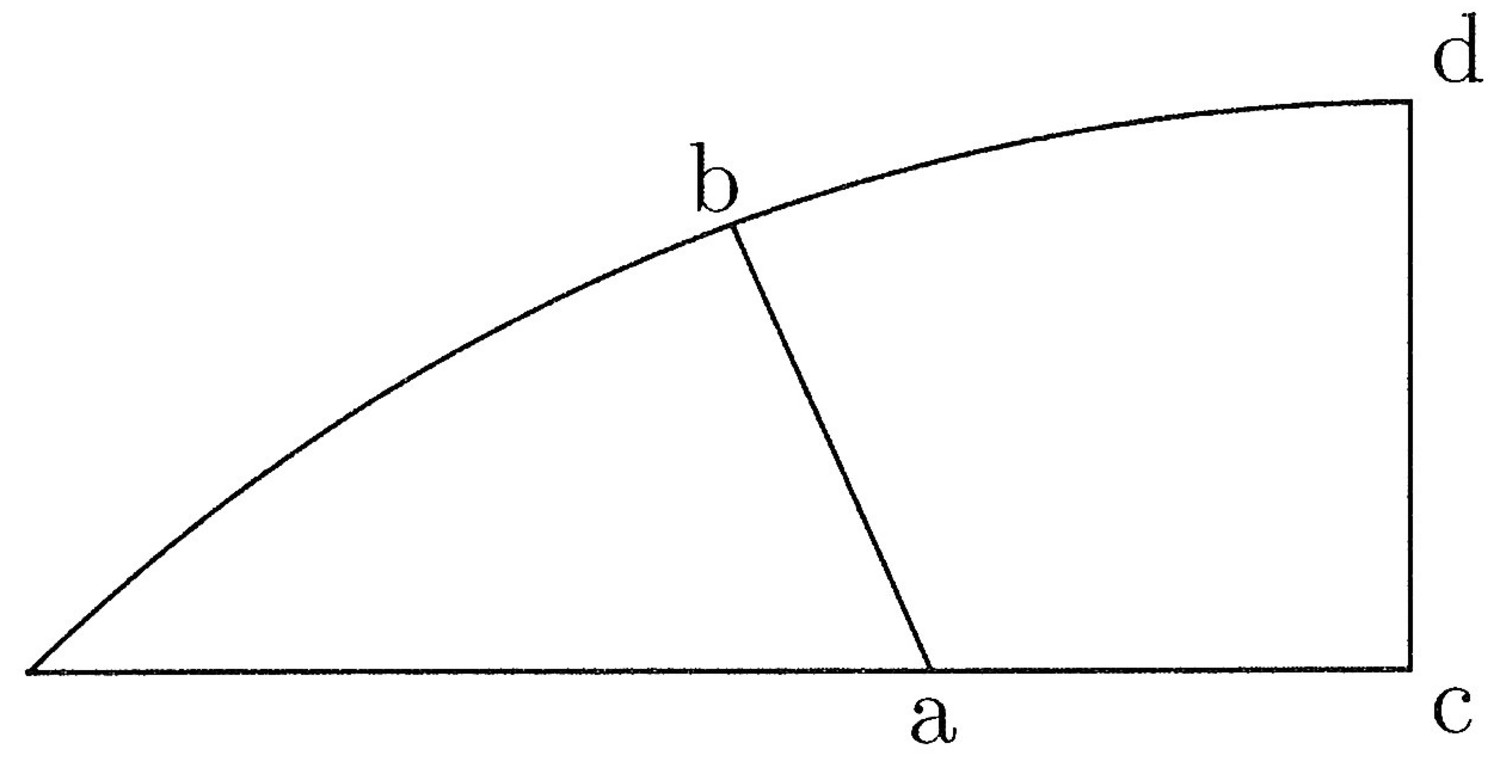
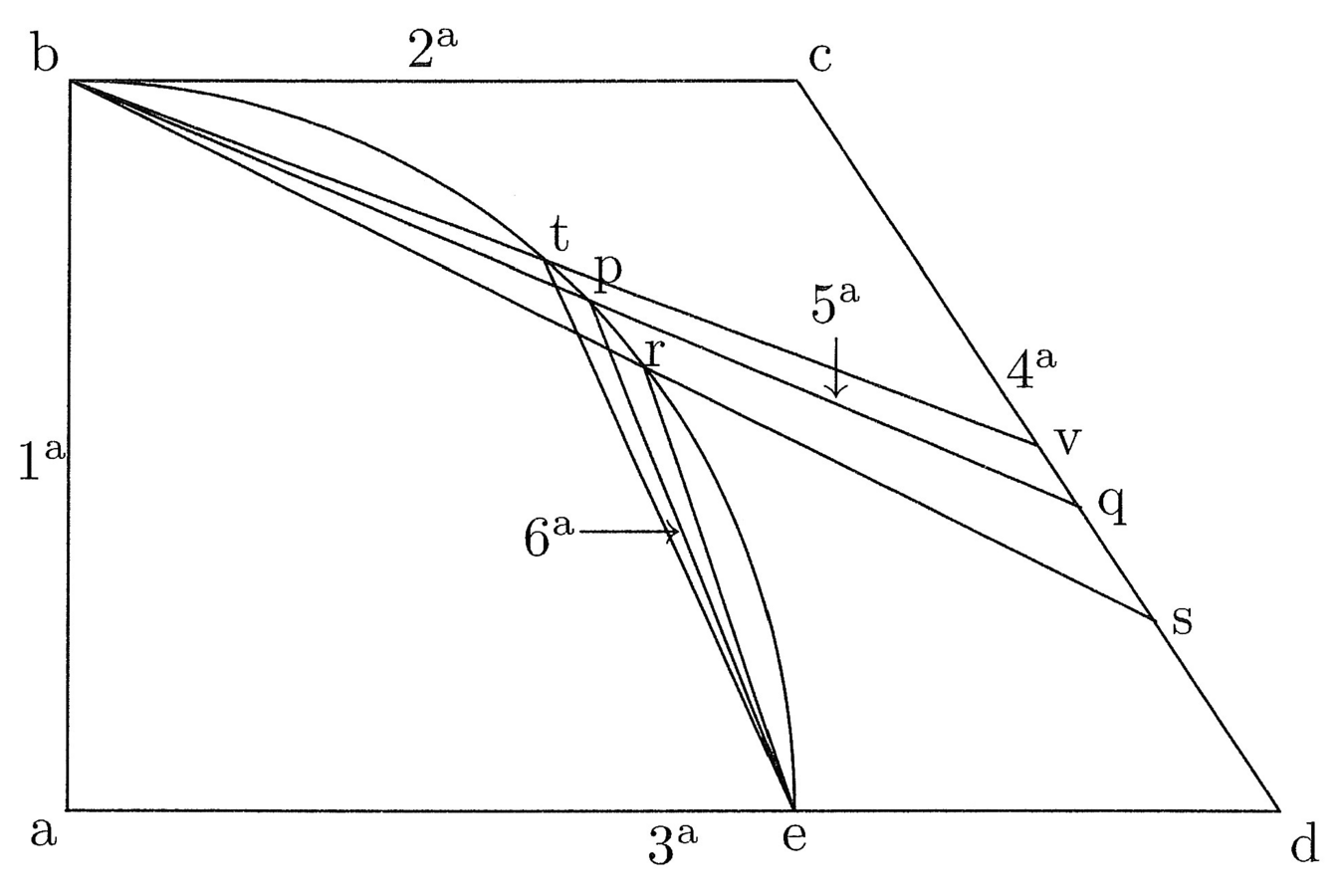
31. Datae rectae curvam circularem aequalem assignare (cfr. figura 6).

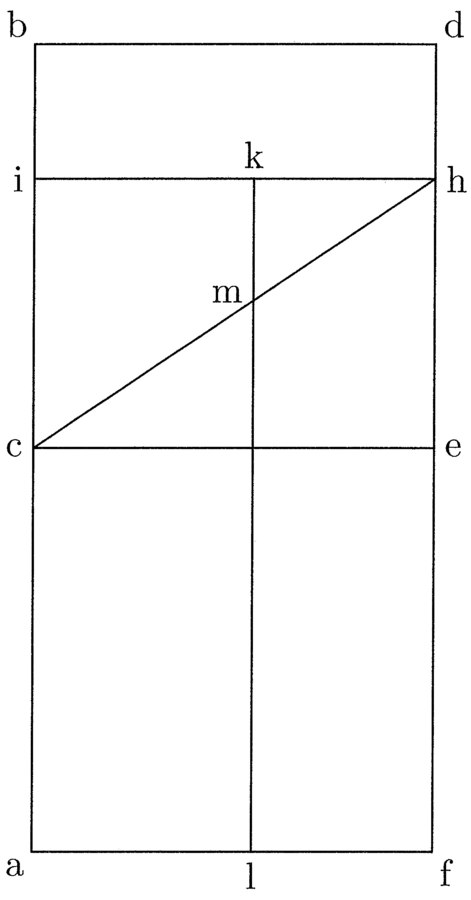
Sit recta ab et factis ex ea trigono et tetragono ut praemittitur, sit ef linea secunda trigoni, quam quadra, et sit efgh. Divide per medium per lineam ik, trahe lineam ig, quaere, ubi ig et fg distant per differentiam primae et secundae tetragoni, et trahe lineam aequedistantem ef et sit ln et differentia lm. Signa in nl primam tetragoni, quae sit no, trahe de i per o lineam ad gh, et ubi eam scindit, pone p. Manifestum est ex praemissis hp semidiametrum circuli, cuius peripheria aequatur peripheriis trigoni et tetragoni seu lineae rectae ab, quod est intentum.

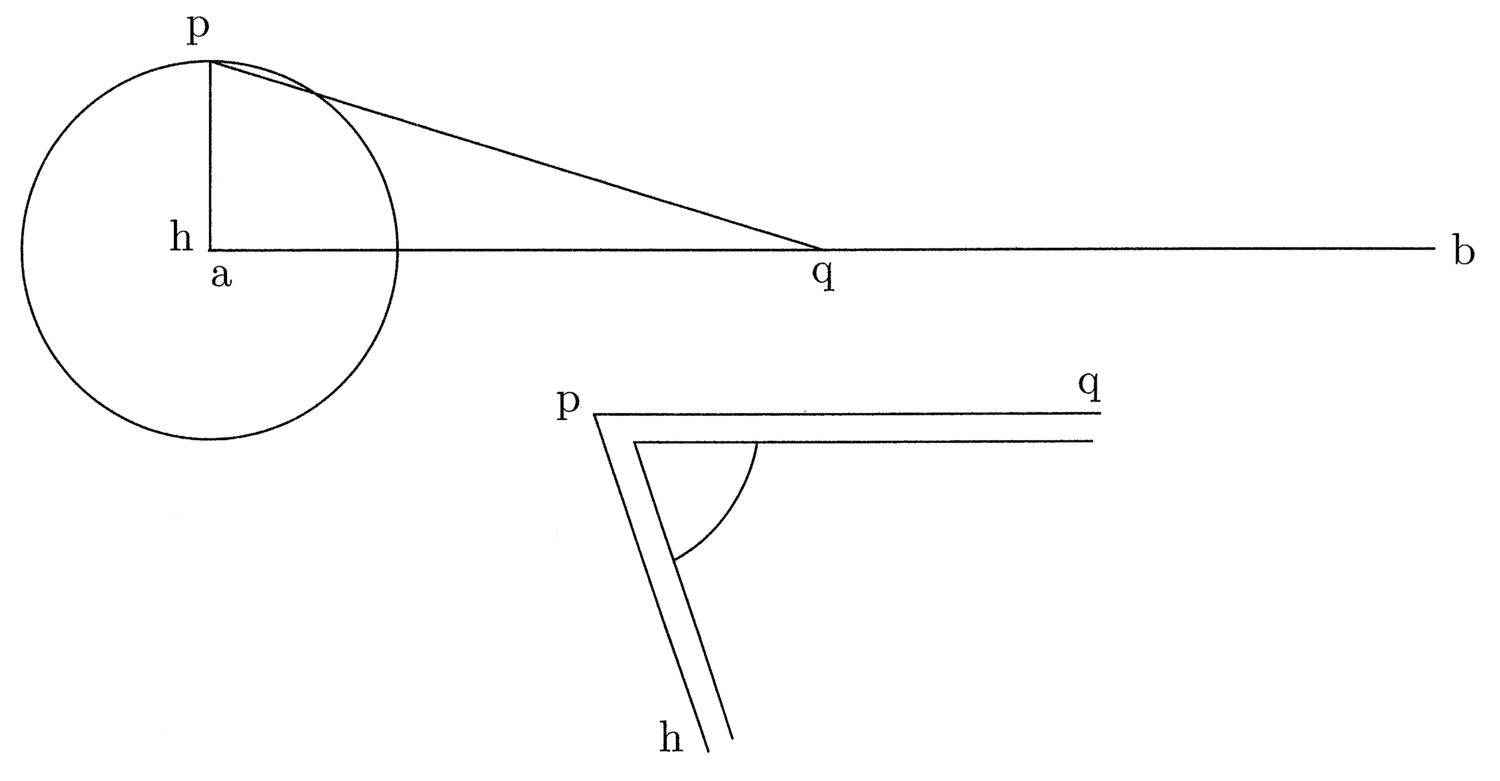
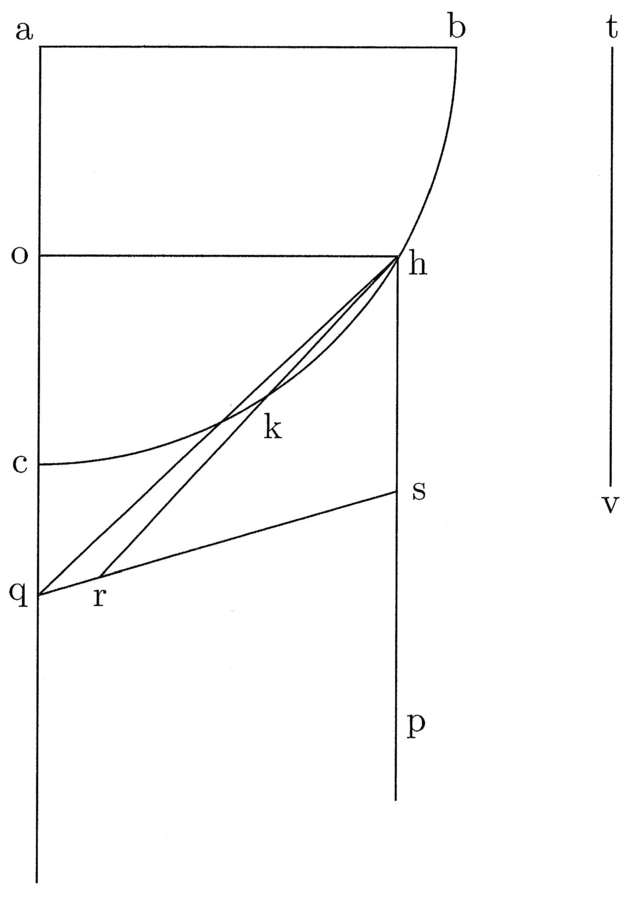
32. Datae curvae circulari aequalem rectam assignare (cfr. figura 7).

Istud si breviter facere volueris, facito angulum, per quem reperias hoc modo: Ad hp semidiametrum circuli praemissi iunge in centro lineam ab orthogonaliter et ad eius medietatem, quae sit q, trahe pq, et habes angulum hpq. Quem facito in aere aut ligno, et quando circularem lineam in rectam resolvere cupis, facito lineam indefinitae quantitatis, quae ad angulum rectum concurrat cum semidiametro in centro, et pone angulum in contactu semidiametri et circumferentiae minus latus super semidiametrum. Et maius latus anguli abscindet in linea indefinitae quantitatis portionem aequalem semiperipheriae.

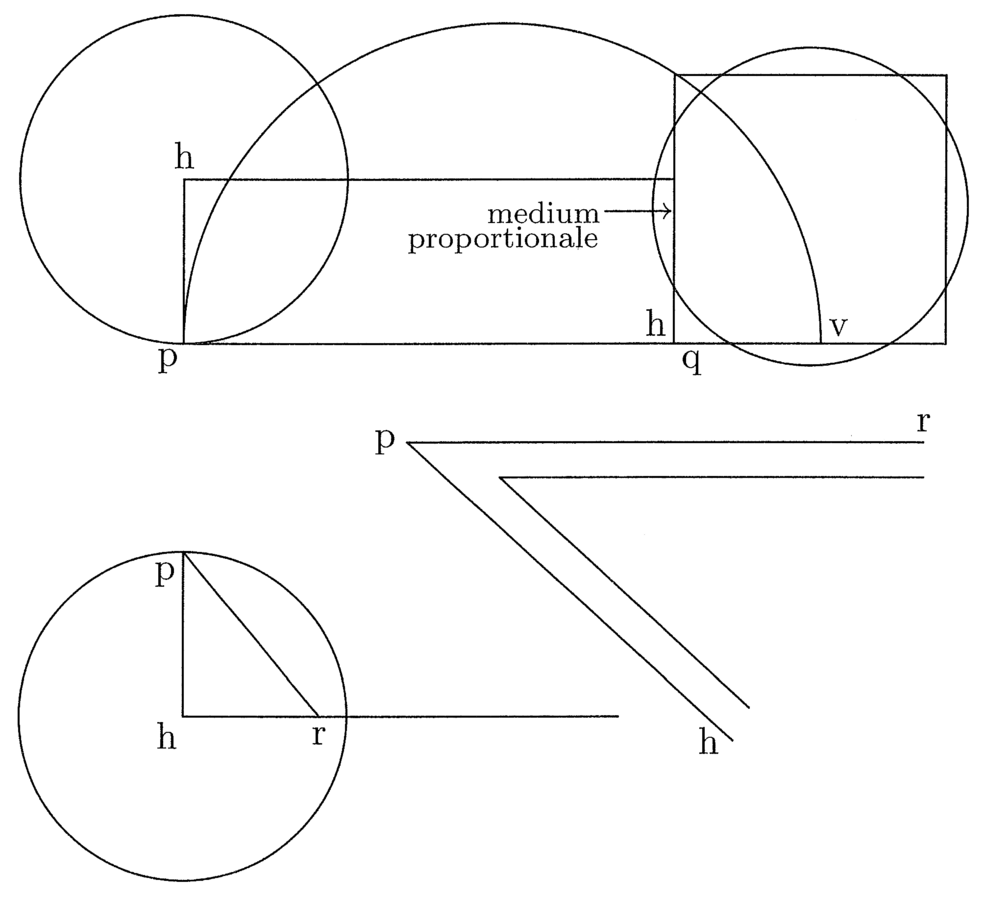
33. Dato circulo quadratum aequale assignare (cfr. figura 8).

Hoc sic facito: Inter hp et medietatem ab recipias medium proportionale per nonam sexti Euclidis, quoniam est costa quadrati aequalis, et medietatem huius costae signa in linea, quae ad angulum rectum coniungitur hp in centro, et sit hr: trahendo pr et habes angulum hpr. Quem facito ex aere vel ligno, et modo, quo supra, cum illo omnes circulos quantocius quadrare poteris.

34. Dato quadrato circulum ei aequalem assignare.

Erige de medietate lateris rectam orthogonaliter et pone super illam angulum statim praemissum elevando, quousque longius latus anguli cadat super finem lateris quadrati, et linea erecta usque ad punctum anguli erit semidiameter circuli aequalis quadrato. Omnia ista patent de se propter identitatem proportionis semidiametrorum ad circumferentiam et costas quadratorum in omnibus circulis.

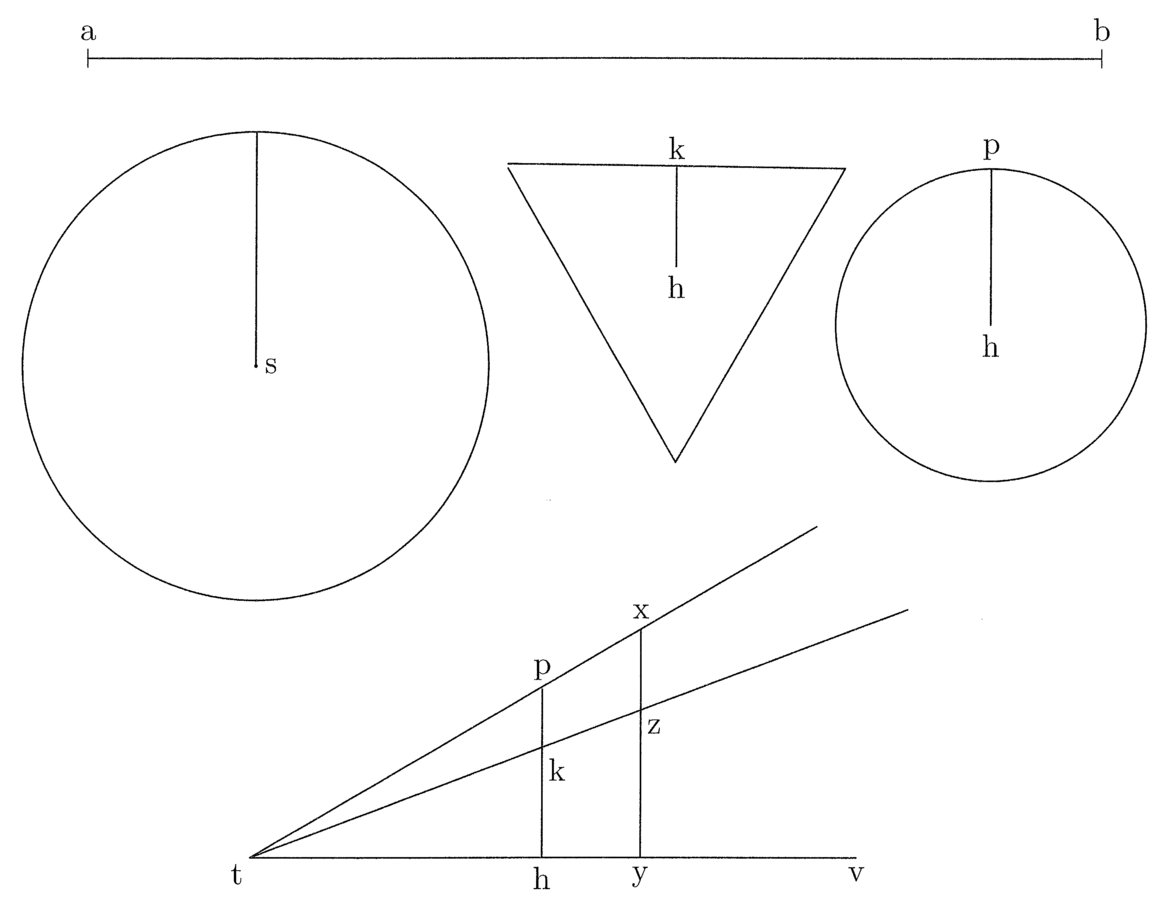
35. Sine istis duobus angulis facere poteris ex praemissis per identitatem proportionis eius, quod addit semidiameter circuli super semidiametrum trigoni (cfr. figura 9). Puta si vis dati circuli circumferentiam, quae sit s, transferre in rectam, sume qualemcumque lineam, ut ab, et reperias circumferentiam sibi aequalem per praemissa. Deinde erige lineam unam, quae sit hp, orthogonaliter super aliam, quae sit tv, et sit hp semidiameter circuli, et signa in illa hk semidiametrum trigoni isoperimetri circulo trahendo de t per h k lineas. Deinde semidiametrum dati circuli s aequedistanter trahe ad hp inter lineam tv et eam, quae de t transit per p, et sit xy, et ubi xy scinditur per lineam de t per k, signa z. Clarum est yz esse semidiametrum circuli inscripti trigono isoperimetro circulo s. Ita reperies rectam quaesitam.

36. Ex antehabitis quicquid hactenus in geometricis ignotum fuit, inquiri poterit. Fuit autem incognita perfectio artis de sinibus et chordis. Nemo umquam scire potuit chordam arcus gradus unius et duorum et quattuor et ita consequenter, quae nunc sic habetur. Manifestum est omnem multiangulam similium laterum ex differentia primae et secundae linearum ad habendum semidiametrum circuli isoperimetri aequalis proportionis partem addere super primam, et similiter omnem excessum, quo prima linea cuiuscumque primam trigoni excedit, et excessum, quo secunda trigoni secundam alterius excedit, eandem semper in omnibus tenere proportionem. Ex quibus ars generalis de sinibus et chordis elicitur, sine qua geometria hactenus mansit incompleta. Quomodo autem ad praxim huius accedere queas in propinquis numeris, sic investigabis. In veris enim est impossibile, quia medietas duplae est innumerabilis, cum nec par nec impar, quae cadet in hac ratione.

37. Esto igitur quod semidiameter circuli trigono circumscripti sit 14. Erit semidiameter inscripti 7, cuius quadratum 49, et quadratum semilateris trigoni ter tantum, scilicet 147, et quadratum semidiametri circumscripti quater tantum, scilicet 196. Erit igitur semilatus tetragoni radix 9/16, id est novem sextae decimae, quadrati semilateris trigoni, scilicet radix 82 cum 11/16, et talis erit semidiameter inscripti. Erit autem semidiameter circumscripti radix dupli numeri, scilicet 165 cum 6/16. Subtracta igitur radice de 49 a ra- dice de 82 cum 11/16 differentia est additio semidiametri inscripti tetragono super semidiametrum inscripti trigono, quae erit aliquid plus quam duo. Et subtracta radice de 165 cum 6/16 a radice de 196, quae erit parum plus quam unum, habes additiones, et earum habitudo est illa, per quam omnia investigantur. Nam si has additiones subtraxeris a sagitta lateris trigoni, scilicet 7, remanet sagitta tetragoni. Si igitur diviseris 7 secundum praefatam habitudinem additionum et maiorem addideris super semidiametrum inscripti trigono, habes semidiametrum circuli isoperimetri.

38. Poteris etiam ex quadrato lateris trigoni aut quadrati scire sic quadratum lateris cuiuslibet polygoniae dabilis, et ex eius scientia et habitudine additionum devenitur ad sagittam et semidiametrum inscripti, et sic scitur arcus chordae. Et haec est perfectio ultima geometricae artis, ad quam hactenus veteres non legi pervenisse. Est etiam nunc ars completa geometricarum transmutationum, quam ante minus, tamen sufficienter quoad quadraturam circuli descripsi.

39. Adhuc ut latus cuiuscumque multiangulae quantocius vertas in curvam, facere poteris instrumentum duplicis anguli. Ut si latus sit ab trigoni, cuius sagitta seu primae et secundae linearum differentia, quod idem est, sit cd, et additio semidiametri circuli super primam trigoni sit ce. Tunc si de a per e lineam traxeris et similiter de a per d aliam, duo anguli circa a constituentur. Redige igitur bae et bad in unum aereum instrumentum, quod applica in omnibus ita, ut iam in trigono, sic quod latus ab eiusdem iaceat super latus multiangulae et latus ad contingat finem sagittae. Tunc latus ae ostendit additionem super primam illius multiangulae, ut sit semidiameter circuli isoperimetri. Descripto igitur arcu secundum hoc et tractis sectoribus de centro ad fines lateris arcus, qui cadet inter sectores, aequabitur lateri dato. Procedit veritas huius ex aequali habitudine portionis addendae super primam multiangulae, ut fiat semidiameter circuli isoperimetri, ad totam differentiae primae et secundae linearum multiangulae, quae differentia sagitta nominatur (cfr. figura 10).

40. Adhuc ex praemissis constat, quod sicut quaecumque recta potest esse latus trigoni, tetragoni, pentagoni et ita consequenter, sic data recta dari poterunt innumerae curvae ei aequales, et quod propterea poterunt reperiri anguli, qui se habent ut datae lineae, scilicet ut costa et diameter quadrati vel diameter circuli et circumferentia eius et ita de omnibus, et superficies, quae se habeant ut lineae datae. Ex quo illa, quae non solum in geometricis fuerunt hucusque occulta, sed et in musicis et in musicalibus instrumentis ignorata, venari poterunt, ita quod si quod scibile umquam fuit in geometricis et non scitum, amplius volenti ingenium applicare clare patefiat. Et ob hoc haec adinventio merito nomine complementi sortitur et digna est, ut per admirandam potentiam tuam, beatissime pater, quam omnes catholici adeo stupent, ut te ab admiranti dictione papae papam appellent, in omnium notitiam deducatur.

[LIBER SECUNDUS]

42. Adicio nunc alias quasdam meas adinventiones circa superficierum ad invicem transmutationes, quas ut priores sanctitati tuae dedico, qui in omnibus principatum tenes et solus dignus es, ut cuncta tibi patescant.

43. Lineam figuram motus puncti concipio. Quae si recta fuerit, tunc si uno eius termino fixo manente movetur, hic motus recte per triangulum orthogonium figuratur (cfr. figura 11). Ut si ab linea movetur a stante, motus figuratur per triangulum abc. Si enim motus b est ut latus bc, tunc sic proportionabiliter omnia puncta dabilia. Puta si d est punctus medius, tunc de est ut motus d, et de latus est medium ad bc (cfr. figura 12). Si vero ab recta movetur aequaliter in a sicut in b, motus configuratur per duplicem orthogonium sive quadrangulum abcd; omnia enim puncta dabilia aequaliter moventur. Si vero a movetur similiter et b, sed inaequaliter, hoc fieri potest infinitis modis et unica figura non poterit configurari.

44. Ex prima configuratione motus lineae rectae, cuius unus terminus manet fixus, sequuntur ista: Scilicet quod superficies, quae est mensura motus lineae, quae ex revolutione lineae exoritur, habet lineam curvam peripherialem, quae ex puncto b exoritur, et superficiem circularem, quae ex linea ab provenit. Quod si in ab aliqualem punctum signaveris, puta in medio, qui sit d, peripheria ex d erit se habens ad peripheriam ex b sicut in configuratione de latus ad bc latus; sunt enim peripheriae mensurae motus punctorum. Unde necesse erit omnem semidiametrum ad circumferentiam eandem tenere mensuram (cfr. figura 13).

45. Deinde quia superficies ex motu semidiametri super peripheriam constituitur et una est omnium semidiametrorum ad peripherias habitudo, illa erit habitudo superficierum quae potentiarum semidiametrorum. Quare superficies circuli habens semidiametrum ut quattuor ad superficiem illius, quae habet semidiametrum ut duo, quadrupla est. Quae conicarum superficierum ad invicem et ad suas bases habitudo ex hoc habetur. Nam cum semidiameter basis et latus trianguli, quod conicam describit, moveantur uno terminali earum puncto fixo et super eadem basis circumferentia, illa erit superficierum habitudo, quae linearum, ex quarum motu ipsae superficies constituuntur. Uti est semidiameter basis et latus illud trianguli, ex quo conica, ut ab et bc (cfr. figura 14).

46. Ex secunda configuratione motus lineae aequaliter in omnibus punctis motae sequitur quod superficies, quae ex tali motu constituitur, dupla est ad illam, quae ex primo motu. Quare si semidiameter movetur secundo motu super eadem peripheria, super qua primo motu mota est, oritur superficies dupla ad primam. Unde necesse erit quod multiplicatio semidiametri in semiperipheriam aequetur superficiei circulari. Dico autem, quando ambo terminalia puncta aequaliter moventur (cfr. figura 15).

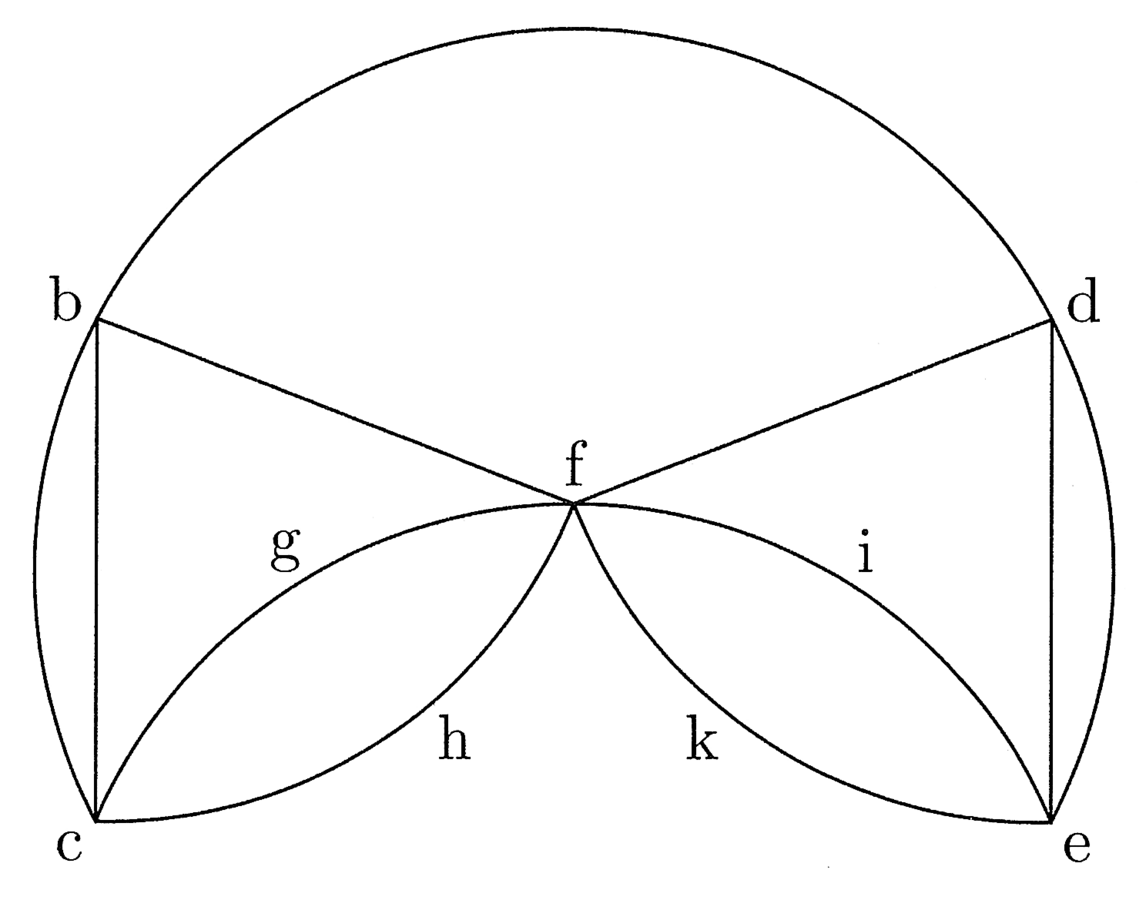
Nam si unus moveretur super concavitate alicuius arcus et alius super convexitate eiusdem, superficies non foret dupla ad illam, quae fuit exorta ex motu eiusdem lineae uno termino eius fixo stante et alio in concavitate arcus moto, licet arcus sint aequales. Ut si arcus bd est ut arcus ce, si bc linea movetur superficiem describendo, quae clauditur inter rectas bc et de et curvas bd et ce, licet super aequalibus arcubus moveatur, non tamen describit duplam superficiem ad motum ab aequalis bc fixo a stante et b moto usque in d per aequalem arcum, quia b movetur in concavitate bd arcus, sed c de linea bc in convexitate. Minuit autem convexitas, quantum sunt illae portiones fgch et fiek.

47. Ex hoc quae circa habitudines cylindrorum seu rotundarum columnalium superficierum et suarum basium et cylindralium, conicarum curvarum atque planarum circularium omnis scientia elicitur. Nam constat columnam rotundam, cuius altitudo est ut semidiameter basis, habere duplam superficiem basis. Nam linea, quae basim efficit, movetur uno puncto eius terminali stante, alio circumferentiam describente et illamet columnarem superficiem constituit per motum aequalem utriusque terminalis puncti super eadem circumferentia basis, ut ex abc angulo recto super a circumvoluto describitur basis per ab et per bc duplex superficies cylindrica, quia bc aequalis ab aequaliter in b et c punctis terminalibus movetur (cfr. figura 16).

48. Sic pariformiter in conicis. Si abc triangulus, cuius angulus bac rectus super ac revolvitur, et bc latus fuerit duplum ad ab, aequabitur illa conica superficies priori columnari, et si feceris circulum, cuius semidiameter dupla foret ad ab, eius superficies plana aequabitur ambabus, columnari et conicae simul (cfr. figura 17).

49. Palam ex his, si circumferentialis linea circuli in rectam redigeretur et duceretur in ipsam semidiameter, superficies quadrangula, quae surgeret, dupla foret ad circularem, cuius erat circumferentia. Nam haec ductio motus esset, ubi ambo terminales puncti aequaliter moverentur, sed constitutio circuli ex motu eiusdem lineae altero puncto stante oritur. Recte igitur dictum est a multis, quod ductio seu multiplicatio semidiametri in semicircumferentialem lineam efficit superficiem aequalem circulo.

50. Adhuc est alius motus compositus, scilicet progressionis et descensionis, ut in figura. Nam, ut concipis, ab movetur duplici motu, super ac scilicet continue progrediendo et simul descendendo aequaliter (cfr. figura 18). Erit mensura progressionis ac, descensionis ab et descensionis et progressionis simul bc. In quanto enim tempore progreditur de a in c, in tanto descendit b per bc, ut veniat in c, et exoritur figura abcd. bc in se complicat duplicem motum descensionis ab et progressionis ac, quare potentia bc est ut ab et ac. Ex hoc nota, quomodo ex motu lineae simul oriuntur duo trianguli et quadrangulus.

51. Si autem ab movetur progrediendo in ac et descendendo inaequaliter, ita tamen, quod illa inaequalitas est aequalis arcui, tunc oritur figura abcd, et quoniam bc arcus in se complicat motum progressionis et descensionis inaequalis, igitur cb arcus est maior linea cb (cfr. figura 19). Et dico motum descensionis inaequalem, quia postquam b pervenit ad medium arcus, non descendit per medium sui infra ca, sicut quando descendit per medium lineae bc. Et considera quomodo a describit arcum ad. Movetur igitur a in convexitate et b in concavitate, et quantum addit concavitas super lineam cb, tantum convexitas minuit. Quare curva superficies inter arcum bc concavum et arcum aequalem ad convexum aequatur quadrangulo rectilineo abcd, et ita habes quomodo eadem quantitas inter maiores curvas cadit et minores rectas. Possunt ex his varii alii compositi motus concipi modi, quos nunc transeo, quia quisquam per se illos concipere poterit.

52. Si ad tertium motum, quando ambo termini lineae moventur, sed inaequali motu, advertis, clare comperies secundum proportionem motuum superficies attingi (cfr. figura 20). Et ut facilius inducaris, concipito ab lineam duplicem et divisibilem usque ad b punctum, qui indivisibilis utriusque divisae terminus maneat. Esto igitur quod a stante b moveatur. Si tunc a divisum elevaveris, ut circa b fiat angulus, tunc secundum circumferentiam, quam a mobile describit, ad circumferentiam, quam b describit, scire poteris proportionem superficierum. Puta esto quod a mobile elevetur, ut constituat talem angulum, quod linea, quae de a cadit usque ad punctum, qui ita distet ab horizonte, sicut a fixum, et sic ad sit medietas ab, tunc ba mobile describet superficiem conicam, quae erit maior plana circulari, quam ab describit, pro medietate, et ita proportionaliter in omnibus. Quare patet, quod quando a mobile elevatur, ut eius motus sit duplex ad motum ab, scilicet quando erit ex ipsis linea una, tunc ba mobile describet superficiem triplam et planam ad superficiem, quam ab describit. Et illa est ultima et maxima; quae in medio cadunt, proportionabiliter apprehendes. Ex quo habes, quomodo portiones conicas, quae habeant proportionem quam volueris ad basim, constituere poteris, et similiter, quomodo superficies rhombicas, quae ex duabus conicis unam basem habentibus reducere poteris in alias. Et quaeque circa hoc scire optas, ex hoc faciliter elicies.

53. Est autem advertendum ex praemissis, quomodo in conicis possis procedere. Ut si abc triangulus sit et ab latus describens conicam et cb semidiameter basis, trahe lineam ac in continuum et de b duc lineam, ut facias aequalem triangu lum, qui sit bdc (cfr. figura 21). Manifestum est, si ad fixa manente circumvolvitur triangulus abd, rhombum oriri ex duobus aequalibus conis. Trahe igitur ab in continuum, et sit be ut ab. Clarum est, si circumvolvitur ut prius, lineam be efficere superficiem triplam ad superficiem ab et conicam superficiem ae quadruplam ad eam, quae ex ab. Unde si bd elevaveris in medium inter bd et be, efficiet superficiem duplam sicut bd aequalem et bc triplam, et semper pervenietur ad medium, quando faciet angulum rectum cum semidiametro basis, et si minus vel plus elevatur, minus et plus efficiet, ut haec ex praemissis nota sunt. Habes igitur, quod quando conus et columna rotunda habent eandem basem et latus coni est ut altitudo columnae, superficies columnae semper est dupla ad superficiem coni, et si plus, plus, si minus, minus proportionabiliter.

54. Si feceris latus coni chordam arcus describendo arcum super ipsum, ut super ab latus afb arcum et super be eundem arcum, erit superficies ex curva afb tertia superficiei, quae ex curva be. Et ita, si volueris duplam, facito, ut in conicis dictum est. Unde si afb est quadrans, palam ex circumvolutione semisphaericam oriri superficiem et ex bg curva duplam eius, scilicet superficiem curvam aequalem superficiei ‹sphaerae›, cuius cb maioris circuli semidiameter, et ex bc curva triplam (cfr. figura 22).

Ex quo elicias, quomodo in talibus curvis superficiebus poteris qualem volueris multiplicationem efficere.

55. Si feceris arcum lineam curvam curvitate alicuius sectionis parabolae aut transversae cylindri, quae sectiones non sunt circulares, sed alia curvitate curvae, eodem modo procedendo aequalis erit proportio superficierum.

56. Si ab stante a circumducto circularem planam superficiem descripseris et quadrantem descripti circuli uno eius terminali puncto ad b iuncto, alio, qui sit c, ut a fixo stante super ac circumduxeris, superficies ex quadrante dupla erit ei, qui ex linea ab exoritur (cfr. figura 23). Patet, nam ex bc oritur superficies semisphaerica et ab circulus maximus, cuius quattuor superficies aequantur superficiei sphaerae, ut probat Archimedes.

57. Si volueris cylindricam, sphaericam ac conicam superficies et infinitas portiones conicas describere eiusdem superficiei, sic facito (cfr. figura 24):

Sit ab semidiameter alicuius circuli, cui iunge ad angulum rectum bc aequalem ab, trahe de a aequedistantem ad bc in infinitum et sit ad, trahe de b ad ad lineam duplam ad ab, et sit bd dupla ad ab. Deinde trahe lineam de d ad c. Dico quod omnes lineae, quae duci possunt de b ad cd in circumvolutione describunt portiones conicas aequales vel pyramidali bc vel conicae bd, quod ex bc et ex bd oriantur aequales, quae sunt duplae ad planam circuli, cuius ab semidiameter. Superius est manifestatum, quod vero mediae sic se habeant, puta bi et bg et quaeque tales. Patet, nam non possunt superficies esse maiores illi, quae ex bc, nec minores illi, quae ex bd. Quae cum sint aequales, erunt et similiter omnes mediae aequales. Describe quadrantem circuli, cuius ab semidiameter, et sit be. Manifestum ex praemissis superficiem, quae ex curva be oritur, illis aequalem.

58. Curvas lineas, non tamen circulares, ex inaequali motu lineae in ambobus suis terminalibus punctis causatas concipito, ac si ab recta moveretur et b plus quam a (cfr. figura 25).

Puta a movetur per lineam ac et b per curvam bd et si regulariter, tunc quando a pervenit ad medium ac, etiam b pervenit ad medium bd. Potest etiam unus punctus moveri regulariter continuo aequali motu et alius inaequali motu. Puta in principio velociori et continue tardiori successive et regulariter per aequalem scilicet inaequalitatem. Ex his diversitatibus varias contingit oriri curvitates; aliquae erunt ut sectiones conicae, aliae ut transversales cylindricae aut obliquae sphaericae sectiones.

59. Ex quo curvae superficies sectionum, quae parabolae dicuntur, et transversalium cylindrorum non causantur directe ex motu lineae. Si volueris inquirere portionum illarum habitudines, ita facito: Considerabis excessum chordae super sagittam, et ille excessus erit ut motus lineae aequalis sagittae in uno eius puncto, alius motus alterius puncti erit ut curva. Unde superficies erit medium eius, quod fit ex ductu sagittae in curvam ac si non foret linea mota in uno eius termino, et erit ultra medium secundum habitudinem potentiae excessus arcus super sagittam ad potentiam curvae.

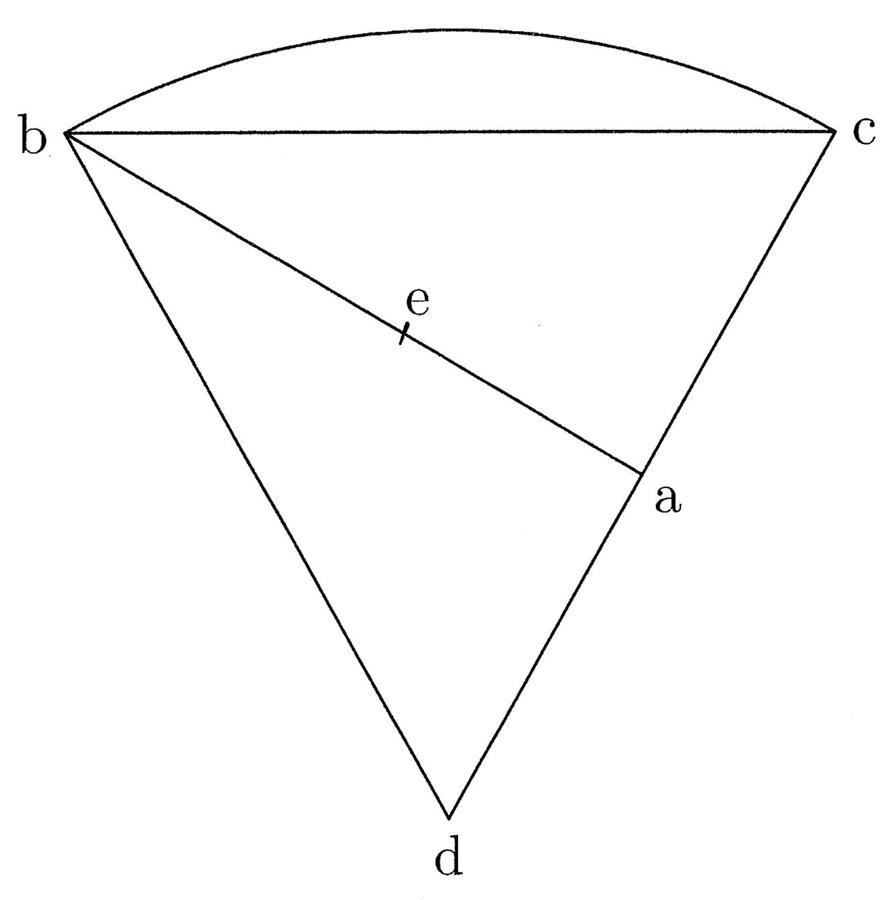
60. Puta esto quod abscisio sit in circulo et quod per semichordam et sagittam sextae circumferentiae, quae signetur per abc, et sit ab semichorda duplicis arcus et ac sagitta et centrum circuli d (cfr. figura 26). Trahe db et dc et lineam bc. Manifestum est ac et ad aequari et triangulos dba et bac. Portio igitur super lineam bc, in qua excedit abscisio triangulum, venit ex motu ac sagittae in ambobus terminis. Et si ambo termini fuissent aequaliter moti, portio super lineam bc esset aequalis toti abscisioni bac, sed quia inaequaliter moti sunt termini, ideo est minor. Et ut videas, quomodo inaequaliter moti, signa de b versus a aequalem ac, et sit be ut ac. Moveatur igitur b super arcu bc, et dum sic b movetur super bc arcu, necesse erit e moveri versus a. Movetur igitur in eodem tempore, quo b per arcum, e per lineam ea. Quae igitur est habitudo potentiae ea lineae ad potentiam rectae, quae aequatur bc curvae, tanto excedit superficies abscisionis medietatem portionis circuli dbc. Deberet enim esse medietas ductio ac in arcum bc illius, quod fit ex ductu db in eundem arcum, cum ac sit medietas db. Sed quia movetur terminus in ac, qui manet fixus in db, ideo excedit medietatem. Esto igitur quod bc curva sit tripla ad ea. Tunc excedit medietatem in una nona medietatis, et erit portio super lineam bc duae nonae medietatis. Ita in sectionibus curvis operare.

61. Propono nunc modum tradere, quomodo curva linea in rectam vertitur, non ut in primo libello per medium versionis rectae in curvam, sed immediate et hoc per subtilem coincidentiam, cuius haec est propositio.

62. Descripta quarta circuli et linea prima a centro ad principium arcus tracta, et secunda linea de contactu primae cum arcu orthogonaliter eiusdem quantitatis cum prima, et tertia a centro per finem, quae sit ut latus trigoni inscripti circulo, et quarta de fine secundae ad finem tertiae. Si tunc de principio quadrantis lineam quintam duxeris ad quartam taliter, quod chorda, quae a contactu illius quintae, ubi curvam secaverit, ad finem totius quadrantis ducta, quae sit sexta linea, quintae fuerit aequalis, erit quinta minor quadrante quanta est medietas portionis eius cadentis inter curvam et quartam (cfr. figura 27). Sit super a centro quadrans be descriptus et linea prima ab, et secunda bc angulum rectum cum ab faciens aequalis eidem, et tertia linea aed ut latus trianguli inscripti, et quarta linea cd. Trahe deinde de b lineam ad cd, quae sit bg, et ubi secaverit quadrantem be, pone f, et sit quinta linea. De f trahe sextam, quae sit chorda fe. Dico si fe est ut bg, tunc bg est minor quadrante be medietate fg. Adde igitur medietatem fg super bg, et sit gh medietas fg. Dico bh aequari curvae be.

63. Ostensio. Praesuppono primo quod quinta et sexta cum portione, quae cadit inter curvam et quartam, quam semper portionem voco, non differant nisi ut pars quintae, quae est chorda, et sexta, quae est chorda residui arcus quadrantis, differunt; et quod illa differentia, qua quinta minor quadrante et sexta cum portione maior differunt, est duplex quantitas, scilicet quantum quinta est minor curva, quae est quadrans, et sexta cum portione maior quadrante; et quod ideo quanto plus differunt, tanto linea maior, quae mediat inter quintam et sextam cum portione, quam lineam voco medium, et quanto minus differunt, tanto medium minus. Secundo praesuppono quod sexta cum portione potest excedere quadrantem in medietate portionis. Nam in minore parte et in maiori potest excedere; ideo etiam in nec minori nec maiori quam medietate.

64. Ex his infero talem sextam cum portione ita excedere quadrantem, sicut quadrans quintam, et quod portio est ut differentia chordarum, et sexta est ut quinta. Illa enim se habent consequenter. Si negas, quia dicis differentiam chordarum minorem portione, tunc medium etiam minus, et quia minus subtrahitur a sexta cum portione quam prius, cum portio per se sit maior et medietas portionis maior medietate differentiae chordarum, hinc hoc est impossibile, scilicet quod linea fiat minor, si ab ea minus subtrahitur, quam si ab ea plus subtraheretur. Sic, si dixeris differentiam chordarum maiorem portione, tunc medium erit maius et tamen plus subtrahitur quam prius, quando medietas portionis, quam minorem dicis, subtrahebatur, quod iterum est impossibile. Quare patet, si sexta cum portione excedit quadrantem in medietate portionis, necesse erit portionem aequari differentiae chordarum et per consequens sextam aequari quintae, quod fuit intentum.

65. Ex his sequitur circuli facilis quadratura. Nam medium proportionale inter bh et diametrum circuli est latus tetragoni cum circulum quadrantis (cfr. figura 28). Sequitur etiam quod si bx aequatur bh, quod in circumvolutione describit portionem conicam, cuius superficies aequatur medietati sphaerae, et longitudo quartae circumferentiae maioris circuli eiusdem sphaerae, quod singulariter fuit quaesitum.

66. Adhuc aliter recta quadranti aequalis hoc modo reperitur. Si linea sexta cum portione quintae lineae aequantur quadranti, eas inter se aequari necesse est. Ut si servata figura praemissa quinta fuerit bpq et sexta ep, dico si ep et pq aequantur quadranti be, tunc ep erit aequalis pq (cfr. figura 29).

Pro cuius ostensione primo suppono quod si de b quintam duxeris ad medium cd quartae, ut est v, portio illius ut tv erit inter portiones brevissima et continue supra et infra augetur. Secundo suppono quod sexta cum portione illa minima est maior quadrante, et ita oportet sextam cum portione, quae debent aequari quadranti, esse minores. Tertio suppono quod possit sexta dari cum portione aequalis quadranti. Quarto suppono quod de e versus b sextae cum portionibus simul continue augentur, licet portiones etiam minuantur. Istae suppositiones cuilibet de facili patere possunt, ex quibus ostenditur propositio.

67. Nam si dixeris sextam ep maiorem portione pq, erit igitur maior medietate quadrantis. Esto igitur quod er sexta aequetur medietati quadrantis, et sit portio rs, quae erit maior pq per primam suppositionem. Erit igitur er et rs maior quadrante et tamen simul sunt minores ep et pq per quartam suppositionem, quae ponuntur aequari quadranti. Et ita minor erit maior maiore, quod est impossibile. Sic si dixeris ep minorem pq, sequitur idem; nam tunc erit minor medietate quadrantis. Esto igitur quod et aequetur medietati quadrantis, cuius portio tv erit minor quam portio pq, quare et et tv erunt minores ep et pq. Sic maior erit minor minore, quod similiter est impossibile, et quia sextam cum portione posse quadranti aequari est manifestum. Patet hoc esse, quando sexta aequatur portioni quintae, quod est intentum.

68. Ex hac iam dicta inventione, si vis, elicias, quomodo omnem portionem superficiei sphaerae poteris reducere in superficiem conicam aut cylindricam, etiam si tibi proportio ipsius superficiei sphaerae ad totius sphaerae superficiem ignota foret, hoc modo. Et sit exempli gratia quadrans ut prius abc, et huius arcum notum signa, qui sit hc, et sit hc duae tertiae quadrantis (cfr. figura 30).

Trahe lineam rectam de h super ac orthogonaliter, quae sit ho. Erit igitur ho semichorda duplicis arcus. Accipe rectam aequalem curvae hc et sit tv, huius medietas sit chorda ck. Duc de h per k aequalem tv et sit hkr. Fac igitur de puncto aliquo lineae hp, qui sit s, lineam transire per r ad aq, quae sit sq, ita quod linea de h ad punctum, ubi aq lineam tangit, scilicet q, perducta sit dupla ad hs. Et erit superficies cylindrica ex hs aequalis superficiei sphaerali ex arcu hc et superficies conica ex hq et mediae, quae de h ad sq ducentur, uti in praemissa, et hoc patet totum ex praemissis. Et ita habes artem, quomodo, si sciveris cylindricam superficiem aequalem sphaerali, poteris ex hoc reperire conicam aequalem, cuius longitudo sit ut longitudo lineae curvae circuli maioris.

69. Et quoniam ex Archimede artem habes omnem portionem superficiei sphaerae in circularem planam reducendi et ex praemissis patet, quomodo illa in cylindricam reducitur et consequenter in conicam, ex quibus et isto nunc praemisso patet, quomodo omnem curvam, etiam si ignoras eius habitudinem ad totum maiorem circulum, poteris in rectam reducere, et haec ars subtilis est excedens circuli quadraturam. Et e converso, si habueris lineam rectam aequalem curvae, poteris superficiem cylindricam et alias conicas consequenter reperire illi sphaerali aequales.

70. Ex quo iam patefecit Archimedes in quadratura parabolae, quomodo superficies illa potest in quadratam reduci ostendens superficiem illam ex recta et sectione coni rectanguli esse sesquitertiam ad triangulum habentem basim ipsam rectam parabolae et altitudinem ipsius parabolae. Et nunc constat, quomodo quadratum potest in circularem duci superficiem ac quod illi possit cylindrica et conica aequalis assignari. Ideo ex praemissis habes modum lineam curvam sectionis illius parabolae in rectam reducendi, et si ingenium applicaveris, omnem curvitatem regularem etiam sectionis transversalis cylindri poteris sic rectificare.

71. Volo nunc investigare, quomodo per lunulas quadratura circuli investigetur, quam viam veteres frustra attemptarunt. Et est intentio inter latus polygoniae circumscriptum circulo et latus polygoniae inscriptum reperire lineam, quae secet lunulam ita, quod triangulus rectilinealis aequetur portioni circuli, cuius ille fuerit arcus (cfr. figura 31).

Puta esto quod super a centro circuli bc arcus sit tertia circumferentiae, cui ef latus trigoni circumscribatur lineis af et ae tractis, et cb linea sit chorda sive latus trigoni inscripti. Volo signare lineam inter ef et bc, quae sit ik, quae secet lunulam lmn ita, quod sit aequalis portionibus bil et ckn, ut aik triangulus aequetur abmc portioni circuli.

72. Pro cuius investigatione suppono latus inscripti esse minus arcu et circumscripti maius et plus maius quam inscripti minus. Secundo, quod duae lineae cadere possunt inter latus inscriptum et circumscriptum, quarum una aequetur arcui et alia aequet triangulum rectangulum portioni circuli; et vocetur prima, quae est latus inscriptum; secunda, quae aequatur arcui; tertia, quae aequat triangulum rectangulum portioni circulari; et quarta, quae est latus polygoniae circumscriptae. Tertio suppono quod illae quattuor lineae sic se habent, quod quando una crescit, omnes crescunt et quando una decrescit, omnes decrescunt; nam ad augmentum unius sequitur quod et alia augeatur. Quarto, quod quanto magis crescunt, tanto magis differunt et quanto magis decrescunt, tanto minus differunt. Quinto, quod quanto magis differunt lineae, tanto plus differunt potentiae earum.

73. Ex his sic arguo: Quanto quarta maior, tanto tertia maior et differentia linearum et potentiarum earum maior. Sic quanto secunda maior, tanto prima maior et differentia linearum et potentiarum earum maior. Sic quanto differentia potentiarum quartae et tertiae maior, tanto secundae et primae maior et differentia illarum differentiarum maior. Quare quanto quarta maior, tanto prima maior et differentiae potentiarum ipsarum maiores et differentia differentiarum quartae et tertiae ex una et secundae et primae ex alia maiores. Secundum igitur habitudinem differentiae potentiarum quartae et primae se habebunt differentiae quartae et tertiae ex una et secundae et primae ex alia, ita scilicet, quod si potentia secundae est maior potentia primae in aliqua quantitate et potentia quartae est dupla ad potentiam primae, erit potentia quartae maior potentia tertiae in dupla quantitate, et si est alia habitudo potentiarum quartae et primae, alia est habitudo quantitatum talium differentiarum.

74. Si negaveris et dixeris habitudinem potentiae quartae ad potentiam primae esse duplam et non excessum potentiae quartae super tertiam ad excessum potentiae secundae super primam, sed quod excessus potentiae quartae super potentiam tertiae sit ut tria et excessus potentiae secundae super potentiam primae sit ut unum: hoc dico implicare contradictionem. Nam sequitur quod prima et secunda lineae sunt minores et aequaliores quam prima et secunda, quae sic se habent, quod differentia est medietas. Quanto enim differentia excessuum minor, tanto lineae similiores et minores, et cum hoc sequitur, quod prima et secunda sint maiores quam prima et secunda, quae differunt in medietate differentiae quartae et tertiae. Nam quanto differentia quartae et tertiae magis excedit differentiam secundae et primae, tanto secunda et prima sunt maiores et inaequaliores. Erunt igitur maiores primis et secundis, ubi differentia est medietas, cum differentia ponatur una tertia differentiae quartae et tertiae. Sic erunt maiores et minores, similiores et dissimiliores, quod implicat. Simile inconveniens sequitur, si poneretur, quod differentia secundae et primae foret maior medietate quartae et tertiae. Et hoc inconveniens sequitur in omnibus, si habitudo excessuum potentiae quartae super tertiam et secundae super primam dicitur alia quam potentiae quartae super potentiam primae.

75. Si igitur hoc medio volueris lunulam abscindere seu circulum quadrare, sic facito, et sit in tetragono (cfr. figura 32).

Esto igitur quod super a centro bc quadrans sit descriptus. Trahe lineas sectores de a per b et c in infinitum, trahe chordam bc et latus circumscriptum eof et in o tangat arcum; trahe semidiametrum ao, signa deinde secundam lineam aequalem arcui, quae ponatur esse gh, et ubi secat ao, ponatur i. Deinde signetur tertia linea, quae sit kl, et ubi secat ao, ponatur m. Si igitur tertia, scilicet kl, talis est, quod eius potentia est in dupla quantitate minor potentia ef quam potentia bc potentiae gh, et cum hoc id, quod fit ex ductu ao in ih, est aequale ei, quod fit ex ductu am in ml, habes intentum; si non, varia, quousque eveniet.

76. Exemplum in numeris. Esto quod ao semidiameter sit 7, cuius quadratum 49; erit bc radix de 98 et ef radix de 196. Esto igitur quod gh ponatur 11, erit eius quadratum 121, a quo subtrahe 98, manent 23. Duplum huius, scilicet 46, subtrahe de 196, manent 150. Si ductio 7 in 5 cum dimidio aequaretur ductioni medietatis radicis de 150 in se sive am in ml, quod idem est, cum am sit ut ml, tunc haberes intentum, et lm esset costa quadrati aequalis circulo, et quarta circumferentiae esset 11. Sed si bene calculas, reperies 11 parum excedere.

77. Est aliquantulum difficile in praxi reperire has lineas medias secundam et tertiam. Unde pro alleviatione laboris sic facito (cfr. figura 33): Fac lineam ac, quae aequetur 7 semidiametris, cuius medium sit b. Trahe orthogonales ad c et b, et sit dc ut ac et eb ut ab, et trahe lineam aed. Signa in cd semidiametrum et sit f ut semidiameter, et medietatem chordae quadrantis, scilicet bc in praemissa figura, signa in be et sit bg ut medietas chordae arcus quadrantis. Trahe lineam fg, et quia cd est potentia f radicis eius et bg radix be, tunc inter be et cd quaere potentias medietatum mediarum linearum, secundae scilicet et tertiae. Puta sit potentia medietatis secundae ut ik, et ubi secat fg, signa l et vide quantum ik excedit be, et fac cd in duplo excedere tertiam, quae sit mn, ita quod be excedat mn in dupla quantitate, qua ik excedit be, et ubi mn secat fg, pone o. Si tunc ex ductu mo in se idem eveniet, quod ex ductu semidiametri in li, habes intentum et mo duplicata erit costa quadrati circuli; si non, varia, quousque eveniet.

Et sicut in quadrante operatus es, proportionabiliter poteris in aliis arcubus prioribus attentis operari et lunulas abscindere et circulum rectilineare.

78. Volo autem adhuc alios quosdam possibiles modos tangere, quomodo scilicet omnis circulus immediate in quam volueris resolvitur polygoniam absque eo, quod peripheriam circuli curvam prius in rectam lineam resolvi oporteat, quos pro exercitio ad magis otiosos remitto.

79. Si quadranti circuli latera circumscriptae et inscriptae tetragonorum descripseris atque a centro circuli ad punctum, ubi circumscriptae latus circumferentiam contigerit, lineam duxeris et aliam a centro ad finem lateris triangulum claudendo traxerisque deinde a centro per aliquem punctum arcus ad latus circumscriptae lineam tali modo, quod alia linea aequedistans lateribus polygoniarum transiens de latere ad latus trianguli per eundem punctum arcus fuerit aequalis duabus portionibus, quas prior linea a centro ducta per eundem punctum de lateribus polygoniarum dictarum secaverit inter ipsam lineam et aliam, quae est latus trianguli, ad punctum contingentiae ductam: erit linea illa aequedistans medietas lateris polygoniae arcui correspondentis circulo aequalis.

80. Ut si super a centro describatur circulus, cui volo tetragonorum aequalem invenire (cfr. figura 34).

Quadrantem signo, qui sit bc, et traho latera tetragonorum, et sit latus tetragoni circumscripti de, et tangat circulum in f puncto. Traho af et ad et bc latus tetragoni inscripti, et ubi bc secat af, pono k. Traho deinde de a per aliquem punctum arcus bf lineam ad df et sit punctus in arcu g, et ubi secat latus bk, ponatur l, et ubi latus df, ponatur m; et per g traho aequedistantem ad df de af ad ad, et sit hgi. Dico si hi est aequalis lk et mf simul, hi est medietas lateris tetragoni circulo aequalis.

81. Pro intellectu huius primo considerandum quod si super a centro circulum descripseris et contingentem indefinitae quantitatis eidem in puncto f adiunxeris tracta linea af et deinde de a ad contingentem lineam ac duxeris, quae secet circulum in g puncto, duxerisque aequedistantem ad contingentem de puncto lineae af, qui sit o, per g in infinitum, illa erit, de qua per aliam lineam de a ad contingentem aequatrix abscinditur, et sit hrd ita quod or sit aequatrix. Quam sic voco, quia lunulae ogf, quam de area circuli abscindit, substituit hrg aequalem quantitate claudendo triangulum rectilineum aro aequalem portioni circuli ahf (cfr. figura 35).

82. Secundo considerandum figura cum contingente et linea, de qua aequatrix abscinditur, servatis, quod de aliquo puncto circuli potest chorda sic trahi, quod portio eiusdem inter af et ac addita ad cf aequetur illi dictae aequatrici, et sit punctus in circulo h et portio inter ac et af ik (cfr. figura 36).

83. Tertio considerandum, quod figura priori cum contingente et linea de qua aequatrix abscinditur servatis, si alia mobilis linea iaceat super ac, quae sit al et illa versus sinistrum a fixo manente revolvatur, perveniet usque ad aliquem punctum circuli, a quo si ducitur chorda aequedistans contingenti usque ad lineam af portio illius inter ac et af addita ad cf aequabitur aequatrici, quae per al abscinditur. Et sit punctus ille in circulo h et semichorda hk et portio ik et abscisio aequatricis or. Nec potest esse alius punctus quam unus ille h, in quo sic eveniet; nam ante illum portiones excedunt aequatricem et post illum aequatrix vincit portiones. Hoc verum, si hf fuerit semiquadrans, et si non, varia g punctum, quousque eveniet (cfr. figura 37).

84. Dico igitur hoc casu aequalitatis portiones esse aequales verae aequatrici et illam esse or. Si negaveris et dixeris portiones fore minores verae aequatrici et similiter or, tunc, si portiones deberent esse aequales, oporteret lineam de a, quae illas abscindere deberet, cadere inter c et d, et ita arcus gf foret minor quam esse deberet et lunula gof minor quam hrg. Sed quia dicis or minorem aequatrice, igitur aequatrix cadit supra or versus contingentem et or infra eam versus hk; quare ipsa or abscindit maiorem arcum quam aequatrix, et lunula gof erit maior quam hrg, et ita erit minor et maior. Sic si dixeris portiones maiores et or maiorem aequatrice, idem sequitur inconveniens. Patet igitur propositum.

85. Pandam nunc ultimo, quomodo simul reperiuntur quae volueris latera polygoniarum aequalium circulo, cuius haec est propositio.

Si semidiametro circuli et semilateribus polygoniarum circumscriptarum et lineis complementi inscriptis linea de centro ad semilatus circumscriptae ducta abscindit minorem portionem de linea complementi unius inscriptae et maiorem de semilatere eiusdem circumscriptae, quae simul aequantur semilateri polygoniae aequalis circulo: tunc, si aliae lineae sic ductae fuerint per portiones talium linearum, quod ipsae portiones se habeant ad priores portiones semilaterum, sicut semilatera simul iuncta unius polygoniae ad semilatera simul iuncta alterius, tales similiter abscindunt portiones, minorem de linea complementi inscripta et maiorem de semilatere circumscriptae, quae aequantur semilateri talis polygoniae aequalis circulo (cfr. figura 38).

86. Esto quod super a centro circulus sit descriptus, cuius semidiameter sit ab, tractis semilatere trigoni circumscripti bc et linea complementi de et tractis etiam semilatere tetragoni circumscripti bf et linea complementi gh. Et si volueris, poteris plurium polygoniarum trahere similiter semilatera. Trahe deinde lineam de a ad bc, et ubi abscindit de, pone i, et ubi bc, pone k. Deinde trahe aliam de a ad bc, et ubi abscindit gh, pone l, et ubi abscindit bc, pone m. Dico si abscisio minor gh, quae est gl, una cum maiore bf, quae est fm, aequantur semilateri quadrati aequalis circulo, tunc si abscisio minor de de, quae est di, se habet ad gl sicut bc cum de ad bf cum gh, et sic se similiter habuerit ck ad fm: erit di cum ck semilatus trigoni aequalis circulo, et habebit se ad semilatus quadrati, sicut se habent portiones dictae ad invicem. Et uti facis in illis, facito in omnibus polygoniis.

87. Procedit haec propositio ex eo. Nam ex varietate laterum diversarum polygoniarum aequalium uni circulo sequitur varietas laterum polygoniarum circumscriptarum et linearum complementi inscriptarum. Quare sicut se habent illa latera, ita et ista simul sumpta. Hinc et abscisiones, quae fiunt per lineas a centro ex lateribus ad constituendum semilatus polygoniae aequalis circulo, tenere debent eandem habitudinem ad invicem, ut eiusdem habitudinis latera efficiant.

88. Non est autem dubium lineam de centro portiones abscindere posse de semilateribus, quae aequentur quaesitae. Sed posset difficultas esse, quomodo sciri possint lineae complementi, quae additae ad semilatera polygoniarum circumscriptarum efficiunt latera polygoniarum eiusdem areae. Puta si de additum ad bc ponitur latus trigoni, quod tunc gh additum bf efficit latus aequalis tetragoni. Sed habitudo laterum de facili scitur ex superioribus. Ponitur autem linea complementi in trigono semilatus polygoniae inscriptae, ut est de, et alia complementa secundum hoc adaptantur. Dicuntur complementa, quia additae ad semilatus polygoniarum circumscriptarum constituunt semilatera polygoniarum aequalium arearum.

89. Posset etiam dubium esse, an portiones teneant habitudinem, quam debent. Unde poteris sic facere. Trahe ab in longum et similiter lineam de a per f in longum et lineam unam, quae sit no, aequalis bc et de, divide in duas portiones, quae se habeant ut gh ad bf, et sint op et pn. Hanc aequedistanter ad bc inter dictas lineas de a per b et per f colloca, et linea, quae de a per gh ducitur, abscindit portionem de op, quae se habet ad portionem abscisam de gh sicut est proportio laterum. Sit igitur portio in op linea oq, quae se habet ad gl sicut debet. Si igitur di est ut oq, tunc habes illam portionem. Sic facito de alia portione lineae no, quae sit rs, et sit rs ut pn. Applica inter lineas de a per b et f ut prius cum alia portione, et si portio, quae per lineam aq in rs abscinditur, quae sit st, fuerit ut ck, habes intentum; si non, varia, ut fiat. Et haec est via universalis in omnibus polygoniis.

90. Elicias ex hoc te artem habere omnem portionem circuli, quae per sectores a centro abscindi potest, etiam ad totum improportionalem in rectilinealem superficiem reducere posse et omnem portionem circumferentiae etiam improportionalem ad totum medio aequatricis secundum praemissa in lineam rectam convertendi.

91. [Patet nunc circuli quadraturam semper quaesitam hactenus, ut creditur, non inventam sufficienter explicatam. Nam aut ipsa sciri potest per reductionem rectilineae in curvam peripheriam, et eo modo tradita est in primo libello, aut e converso per reductionem curvae peripheriae in rectam lineam, et ita duplici modo eam reperies in hoc secundo libello traditam, aut simul cum reductione curvae in rectam reperiendo costam quadrati aequalis circulo, aut sine omni reductione rectae in curvam vel e converso, sed simpliciter reperiendo costam quadrati, et hi modi similiter reperiuntur supra annotati. Sic constat hanc partem hactenus ignoratam abunde sufficienterque explicatam, ex qua alia sequuntur, quae sine ista sciri non poterant, quae sunt mathematicae complementa. Amen.]

FACILLIMA CIRCULI RECTILINEATIO

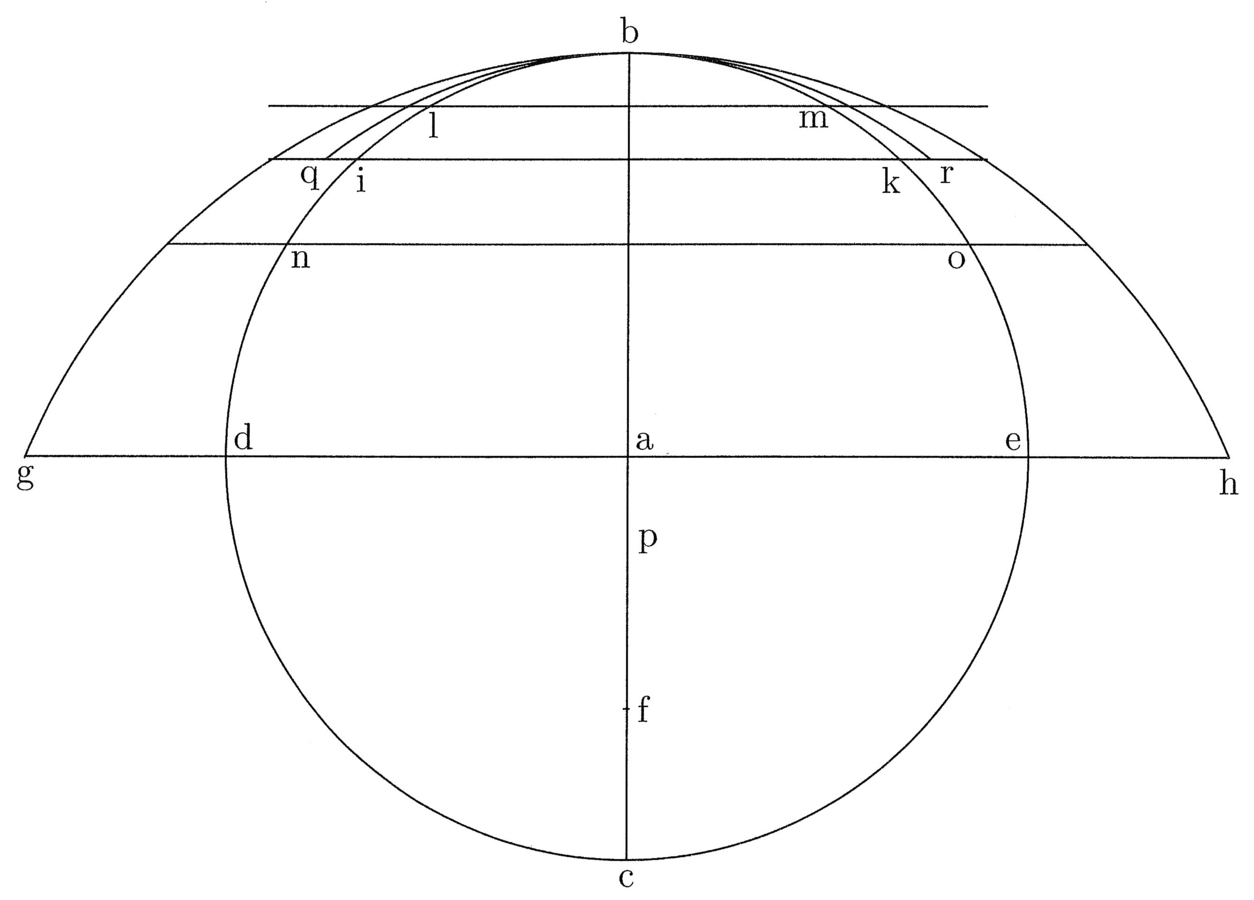
92. Descripto super a centro circulo et tracta diametro bac atque maxima chorda in infinitum extensa, quae orthogonaliter secet bac, quae sit dae, si tunc super aliquo puncto ac, qui de b distet secundum longitudinem chordae arcus tertiae partis circuli, qui sit f circulum, cuius semidiameter sit fb, descripseris, ille de maxima chorda abscindet rectam gh medietati circuli aequalem vel propinquam. Quod si de b et c rectas ad g h traxeris, erit superficies bgch aequalis vel propinqua superficiei circuli bcde (cfr. figura 39).

93. Ad cuius intellectum describe circulum super a, qui sit bcde ut prius, et trahe chordam arcus sextae partis circuli, et sit lm, et quartae partis, quae sit ik, et tertiae partis, quae sit no, et considera, ex quo omnis chorda est minor arcu et plus chorda maioris arcus, quod tunc circulus, qui debet per b transire et habere centrum in bc diametro et secare de chorda extensa aequale arcui, ille habebit necessario centrum ultra a versus c tanto distantius quanto arcus maior, cui chorda subtenditur. Et minimus omnium, quo non potest dari minor, habebit centrum in a, cuius semidiameter ab. Maximus autem circulus habebit centrum ultra a versus c maxime distans ab a, cuius semidiameter maxima. Qui circulus abscindere debet de maxima chorda rectam aequalem semicirculo, et illa maxima semidiameter quaeritur (cfr. figura 40).

94. Secundo est attendendum quod chorda aliqua potest signari, quae sit media inter chordas ei compares. Et voco compares chordas, quarum una minor signata et alia maior sic, quod per arcum aequalem distent a signata, uti ik ab lm et no. Nam cum il arcus sit ut in, tunc lm et no dicuntur compares ik. Dico quod potest chorda signari, ubi omnes duae compares habent potentias, quae simul iunctae sunt maiores duabus potentiis chordae mediae, ut si ad lm chordam compares aliquae traherentur, earum potentiae semper erunt maiores duabus potentiis lm. Potest etiam chorda media signari, ubi potentiae omnium duarum comparium erunt minores duabus potentiis chordae mediae, ut comparium ad no. Ita potest signari chorda, ubi omnium duarum comparium potentiae erunt aequales duabus potentiis chordae, quia quanto potentia minoris comparis est minor potentia chordae mediae, tanto maioris comparis est maior, et quia tunc omnium duarum comparium potentiae erunt aequales duabus potentiis chordae mediae, patet illam esse chordam ik. Nam potentia lm cum potentia no aequantur duabus potentiis ik. Sic et potentia maximae chordae, scilicet de, cum compari, scilicet cum potentia minimae chordae, aequabitur duabus potentiis ik. Et quia potentia minimae chordae non est aliqua, patet potentiam diametri aequari duabus potentiis ik sive lateris tetragoni inscripti. Ita de omnibus duabus comparibus ik. Hoc verum.

95. Tertio suppono quod ik bis excedit duas semidiametros, scilicet maximi circuli, qui quaeritur, et minimi, cuius semidiameter est ab , et hoc notum relinquo. Ex quo elicio duas compares chordas ad ik dabiles, quae simul iunctae aequabuntur illis duabus semidiametris. Nam dabiles sunt compares maiores, scilicet prope ik, et dabiles sunt minores distantissime ab ik, igitur et aequales.

96. Quarto elicio ex his no esse semidiametrum vel prope quaesiti circuli. Nam cum potentiae comparium aequivalentium duas semidiametros aequentur duabus potentiis ik, et lm sit semidiametro minimi circuli, cuius potentia si de duabus potentiis ik subtrahitur, remanet potentia no. Quare no erit semidiameter maximi circuli quaesiti.

97. Quinto elicio, quod si no est semidiameter, tunc si in af reperitur punctus, qui sit p ita, quod ap se habeat ad af sicut sagitta arcus ibk ad sagittam dbe semicirculi, erit p centrum circuli et pb eius semidiameter, qui de ik chorda extensa abscindit qr, quae duplicata aequabitur gh. Et si de omnibus duabus comparibus sic feceris ex proportione sagittarum centro inveniendo, abscisiones, quae de extensis comparibus fient, simul iunctae semper aequabuntur gh, licet non omnis abscisio unius comparis aequetur suo arcui, et ita de infinitis comparibus. Per eandem regulam abscindere poteris rectas aequales semicirculo. Si vero no est semidiameter circuli, non concordabunt istae abscisiones. Ideo varietur, quousque concordabunt. Quod autem superficies bgch aequetur superficiei circuli, satis patet ex praemissis.

98. Sexto elicias, quomodo portiones circuli inter compares cadentes se habent ad circulum, sicut se habet arcus inter compares ad circumferentiam circuli. Puta inter lm et no portio circuli est sexta circuli, quia arcus ln et arcus mo sunt sexta circumferentiae. Quanto enim portio inter ik et lm est minor duodecima, tanto portio inter ik et no est maior duodecima parte circuli. Et per hanc considerationem poteris varias abscisiones portionum circuli facere et varios triangulos aequare. Et haec sufficiant.