PAULUS. Pater optime, quia me nosti a puero veritatem quaesivisse, quae in mathematicis clarius videtur relucere, atque quantum cupiam hactenus ignotam circuli quadraturam: si igitur post mihi missos tuos de mathematicis complementis, utique mihi obscuros atque incertos libellos, alius certior modus incidit, rogo communices.
NICOLAUS CARD. Immo facilis et ut puto certus.
PAULUS. Dicito, quaeso.
2. NICOLAUS. Omnia tibi nota scio, quae ad rem pertinent, solum hoc unico dempto, scilicet ut datae circumferentiae circuli scias rectam lineam ei aequalem assignare.
PAULUS. Ita est. Nam mihi ex Archimede
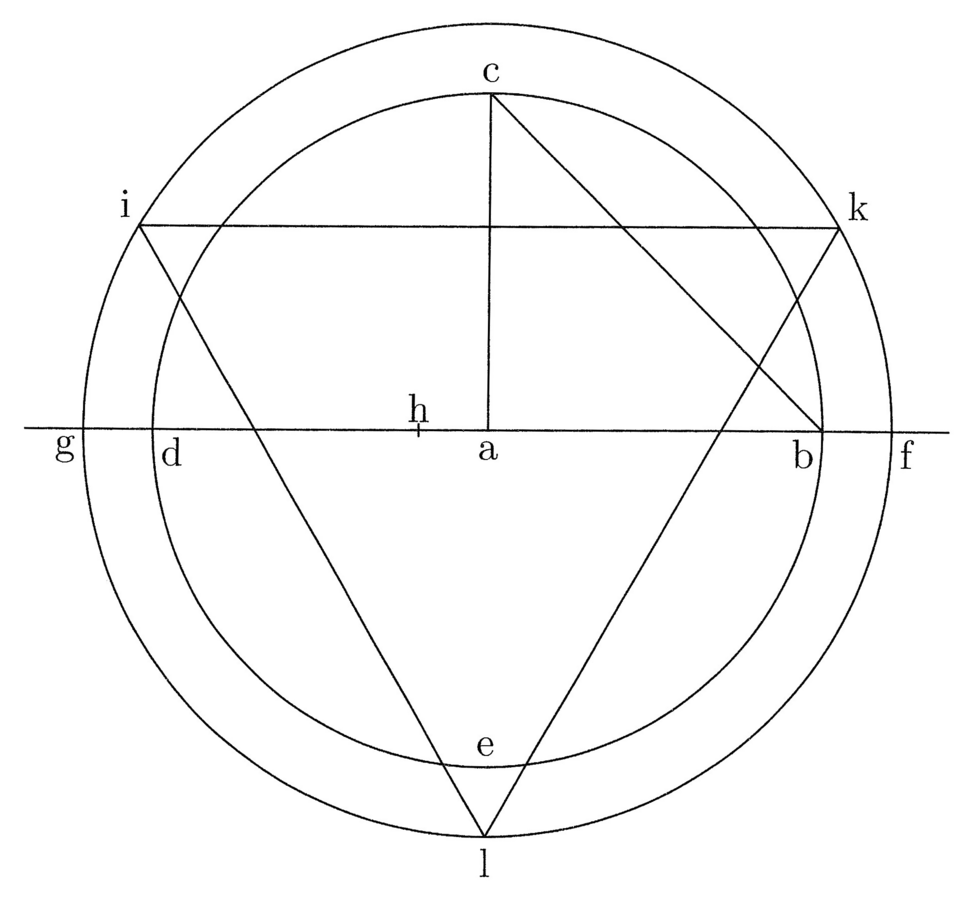
3. NICOLAUS. Ut igitur tibi pandam conceptum circa id, quod restat, accipe propositionem: Si chorda quadrantis dati circuli fuerit addita semidiametro eiusdem, oritur diameter circuli circumscripti trigono isoperimetro circumferentiae dati circuli (cfr. figura 1).
Puta sit datus circulus super a descriptus bcde et bc quadrans, tracta chorda bc et lineis ab et ac, et sit alius circulus super eodem a centro descriptus, cuius diameter fg sit ut ab et bc, scilicet gh ut ba et hf ut bc, et inscribatur trigonus ikl. Dico illum trigonum rectilineum aequari circumferentiae curvae bcde.
PAULUS. Facilis est haec praxis atque carissima, si hoc verum ostenderis.
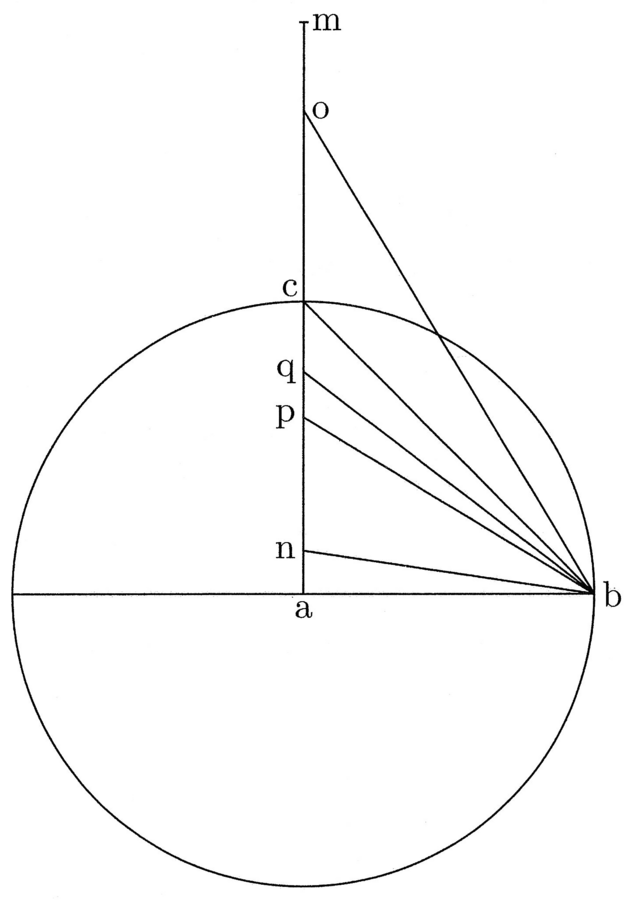
4. NICOLAUS. Conabor. Servata descriptione dati circuli lineam ac continuabo in infinitum, quae sit ma. Dico non dubium de b ad am lineam aliquam posse lineam duci, quae sic se habet, quod si ei additur alia linea, quae se habeat ad ipsam sicut costa ad diametrum quadrati, exsurget linea aequalis diametro circuli circumscripti trigono isoperimetro dati circuli (cfr. figura 2).
PAULUS. Admitto. Nam potest dari linea sic de b ad am tracta, cui si additur alia habens se ad ipsam ut costa ad diametrum, oritur linea minor diametro circuli circumscripti trigono isoperimetro dati circuli. Ut si trahitur ad punctum prope a, quae ponatur esse n, et sic potest dari alia, quae ad punctum prope m, puta o, trahatur, quae cum costa sit maior. Igitur inter n et o erit punctus, ad quem si trahitur linea de b, illa cum costa erit aequalis, nec maior scilicet nec minor diametro circuli circumscripti trigono isoperimetro dati circuli.
5. NICOLAUS. Bene dico igitur, quod sicut si acceperis bn cum quotquot volueris costis suis, linea quae oritur erit minor diametro circuli circumscripti trigono et tot semidiametris dati circuli, quot costas addideris, una costa dempta. Et si acceperis bo cum tot costis suis sicut volueris, exsurget linea maior semidiametro circuli circumscripti trigono et tot semidiametris dati circuli, quot costas addideris, una dempta. Igitur etiam erit punctus inter n et o, ad quem si de b lineam traxeris, sic se habebit, quod ipsa erit aequalis diametro circuli circumscripti trigono et tot semidiametris dati circuli, quot costas addideris, una dempta. Hoc autem non est possibile nisi in puncto c, cuius costa est ut semidiameter dati circuli, scilicet ut ba; alias, si costa foret maior aut minor quam ba, non erit hoc possibile.
6. PAULUS. Fateor primum, scilicet quod bn cum tot costis sicut placuerit sumptis maneat minor diametro circuli circumscripti trigono isoperimetro et tot semidiametris dati circuli, una dempta. Intelligo una dempta, quia unam costam iungis lineae bn pro diametro circuli circumscripti; nam cum bn cum costa sit minor quam illa diameter et costa sit minor quam ab, patet totum. Sic contrario modo se habet linea bo, et etiam patet. Est etiam certum, si sic debet fieri quoad aequalitatem in aliquo medio puncto, quod ille sit c ob rationem quam dixisti. Si enim costa foret minor aut maior ab linea, nullo modo sequeretur. Sed quid, si quis negaret punctum talem dari inter n et o?
NICOLAUS. Qui negat inter minus et maius cadere medium aequale, negat dari posse trigonum isoperimetrum circulo. Ego autem praesuppono quadraturam circuli possibilem et per consequens omnia, sine quibus non est possibilis.
7. PAULUS. Possem dicere nihilominus possibilem, sed non esse hoc possibile de quotquot costis ad lineam addendis, ut diameter illa circuli circumscripti trigono et tot semidiametris dati circuli una dempta oriantur, quia possem dicere, quod punctus cadat inter n et c, qui ponatur esse p, et quod linea bp cum costa aequetur diametro dicti circuli circumscripti.
8. NICOLAUS. Tunc non negas, quin si bp caperetur cum duabus costis, quod tunc foret aequalis diametro dicto, sed cum hoc minor semidiametro dati circuli, quia costa minor quam ab.
PAULUS. Quomodo negarem hoc?
NICOLAUS. Esto igitur, quod recipiam punctum supra p, qui sit q, ubi bq cum costa sit tantum maior diametro dicto, quantum una costa minor linea ab; hoc quidem tunc est possibile. Nonne hoc dato bq cum duabus costis valeret dictum diametrum et cum hoc semidiametrum dati?
PAULUS. Quis dubitat?
NICOLAUS. Quid, si quaererem lineam, quae cum costa excederet diametrum dictam, quantum duae costae sunt duabus semidiametris dati circuli minores?
PAULUS. Oporteret punctum esse adhuc propinquiorem puncto c.
NICOLAUS. Quid, si adhuc pluribus costis additis velles lineam pluribus semidiametris aequari?
PAULUS. Necesse foret continue punctum accedere ad c.
NICOLAUS. Recte dicis. Si igitur in infinitum sic processeris, necessario ultimo ad c punctum devenires, cum ante c punctum costa semper sit minor ab.
PAULUS. Optime dicis.
9. NICOLAUS. Constat igitur, quod hoc non est impossibile, scilicet quod inter n et o cadat punctus, ad quem linea ducta sic se habeat, quod quotquot costas ei addideris, ipsa erit aequalis diametro circuli circumscripti trigono isoperimetro et tot semidiametris dati circuli, quot addideris costas una dempta; sed ille erit c punctus. Et si dixeris punctum ultra c versus o esse, idem inconveniens sequitur contrario modo arguendo, quia devenietur necessario iterum ad c punctum.
10. PAULUS. Non possum negare quin ita sit, ut clare ostendisti. Manifeste enim constat, quod qui punctum citra vel ultra c dixerit esse, ille errat, et error convincitur ex ipsius positione, quoniam omnis linea maior bc cum costa sua est maior diametro circuli circumscripti trigono isoperimetro, et minor cum costa est minor diametro.
NICOLAUS. Posset adhuc alia via id ipsum ostendi, et plures modi sunt diametros circulorum inscriptorum et circumscriptorum polygoniis isoperimetris datis circulis faciliter reperiendi ex scientia, quod capacissima polygonia infinitorum laterum coincidit cum circulo. Sed sufficit iste modus; reliquum ad te remitto.
11. PAULUS. Satis est scire modum curvam
circumferentiam in rectam lineam transmutandi et converso rectam in
curvam, ex quo omnia, quae hactenus in mathematicis ignorabantur,
possunt elici, prout in mathematicis tuis tetigisti complementis.
Qui igitur reduxerit curvam in rectam, ducat semidiametrum dati
circuli in semirectam aequalem circumferentiae. Puta sit rs ut ab et st ut medietas trium linearum ikl, concludendo quadrangulum rstv, qui erit ut area circuli bcde, reperiat medium proportionale inter rs et st per nonam sexti
Euclidis
Finis. Brixinae. 1457.
‹Appendix›
12. Punctus stat in hoc, scilicet in processu in infinitum. Nam si est punctus ille, ad quem linea de b ducta cum costa sic se habet, quod si costas infinitas addideris, non secus feceris, quam si ba infinities ad diametrum circumscripti trigono isoperimetro addideris. Clarum est tunc lineam cum costa aequari diametro circumscripti et costam aequari ba, et erit c punctus.
13. Si vero negatur processus, tunc clarum est, quod qualiscumque punctus signetur citra c, etiam si bc ponitur cum costa excedere diametrum circumscripti, tunc semper certus numerus costarum additus ad lineam cum costa efficit diametrum circumscripti et tot lineas ba, et potest semper ille numerus augeri, si punctus magis accedit ad c, et numquam cessat illa adauctio, quia non est punctus citra c, ubi linea cum costa in numeris excedat diametrum circumscripti, quantum infinitae costae ab infinitis lineis ba exceduntur, cum quaelibet costa in aliqua quantitate sit minor ba linea. Quae quantitas infinities multiplicata maior semper erit quam quantitas excessus lineae cum costa diametrum circumscripti excedentis.
14. Adhuc dico: non dubium bc cum costa excedere diametrum circumscripti capacissimae polygoniae, scilicet infinitorum angulorum, quae convertitur cum diametro circuli isoperimetri. Ideo si addideris quotquot volueris costas, semper excedunt tot lineas ba, et hoc in quantitate, qua bc excedit ba, ut est notum. Quod si receperis aliam polygoniam citra capacissimam, tunc excessus ille est minor, et ita in infinitum, et cum inter capacissimam et incapacissimam cadere possint infinitae polygoniae, erit in trigono ille excessus, si erit saltem ita parvus, quod non potest esse minor. Si enim posset esse minor, non esset polygonia incapacissima. Quantitas autem, quae non potest esse minor, non est quantitas, sed punctus. Sic linea bc non est aliqua quantitate maior quam illa, quae quaeritur.
15. Aliter: Esto quod bn sit linea, quae cum costa sua aequetur diametro circumscripti capacissimae polygoniae. Manifestum est, quod bn excedit ba, semidiametrum circuli isoperimetri, plus quam diameter circumscripti diametrum circuli scilicet in tantum, quantum bn excedit ba, ut est notum; et in aliis polygoniis minus capacibus continue minus. In minime igitur capaci minime debet linea illa costam suam excedere ba ultra excessum, quam diameter circumscripti excedit diametrum circuli isoperimetri. Sicut igitur in maxime capaci excessus ille est maximus, qui non potest esse maior, et continue minor in minus capacibus, erit in minime capaci minimus, qua non potest esse minor. Quare erit costa illius ut ba. Si enim foret minor quam ba, manifestum est, quod plus excederet ba quam in incapacissima fieri debet; si maior ba, tunc minus; erit igitur bc, cuius costa ba.