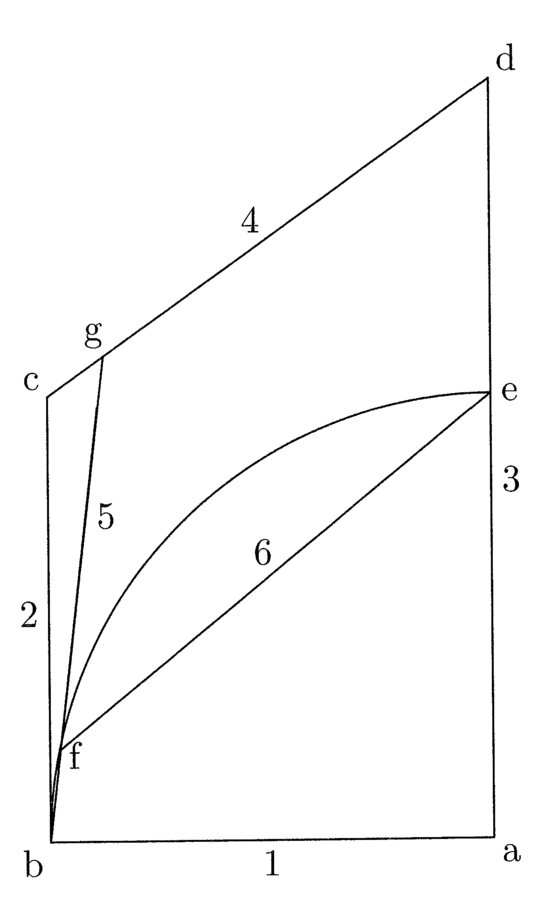
Prima ipotesi
1. La sesta [linea], sommata alla metà della parte1 della quinta, che cade tra la curva e la quarta, può essere uguale alla curva be2. Questa ipotesi è esatta, come è dimostrato nello scritto3(cfr. figura 1).
Seconda ipotesi
2. La sesta, sommata alla metà del segmento [della quinta], e la quinta sommata alla metà della differenza tra la corda, che è la sesta, e parte della quinta, che pure è una corda, possono essere uguali al doppio della curva be. Questa ipotesi è dimostrata, come quella precedente, nel testo4. Ci può essere infatti un caso dove questa somma è maggiore del doppio della curva be, un caso dove essa è minore, come pure uno dove essa è uguale5.
3. Dico che questa seconda ipotesi non ha luogo se non laddove la differenza è uguale al segmento [della quinta], e ciò dimostra la prima ipotesi. Infatti, se dicessi che nella seconda ipotesi la differenza è maggiore del segmento [della quinta], allora la quinta sarebbe minore della sesta. La quinta è uguale alla sesta, quando la differenza delle corde è uguale al segmento della quinta, è minore se la differenza è maggiore, ed è maggiore se la differenza è minore, come è evidente da sé6.
4. Sia dunque aggiunta alla sesta l’intero segmento e alla quinta l’intera differenza. Così [la sesta e la quinta] saranno uguali e ciascuna [sarà] maggiore della curva be. Se dunque si sottrae una [lunghezza] uguale cosicché ciascuna sia uguale alla curva be, allora è necessario sottrarre dalla somma tra la sesta e il segmento [della quinta] più della metà del segmento, quando si pone il segmento minore della differenza, mentre bisogna sottrarre dalla differenza meno della metà– e tanto meno della sua metà, quanto più della metà del segmento di prima – così che restino contemporaneamente la metà del segmento e la metà della differenza, che, aggiunte alla sesta e alla quinta, risultano il doppio della curva be, come è evidente da sé. Dunque la sesta, aggiunta alla metà del segmento [della quinta], sarà maggiore della curva be; e non uguale alla curva be, poiché la differenza supera la parte7.
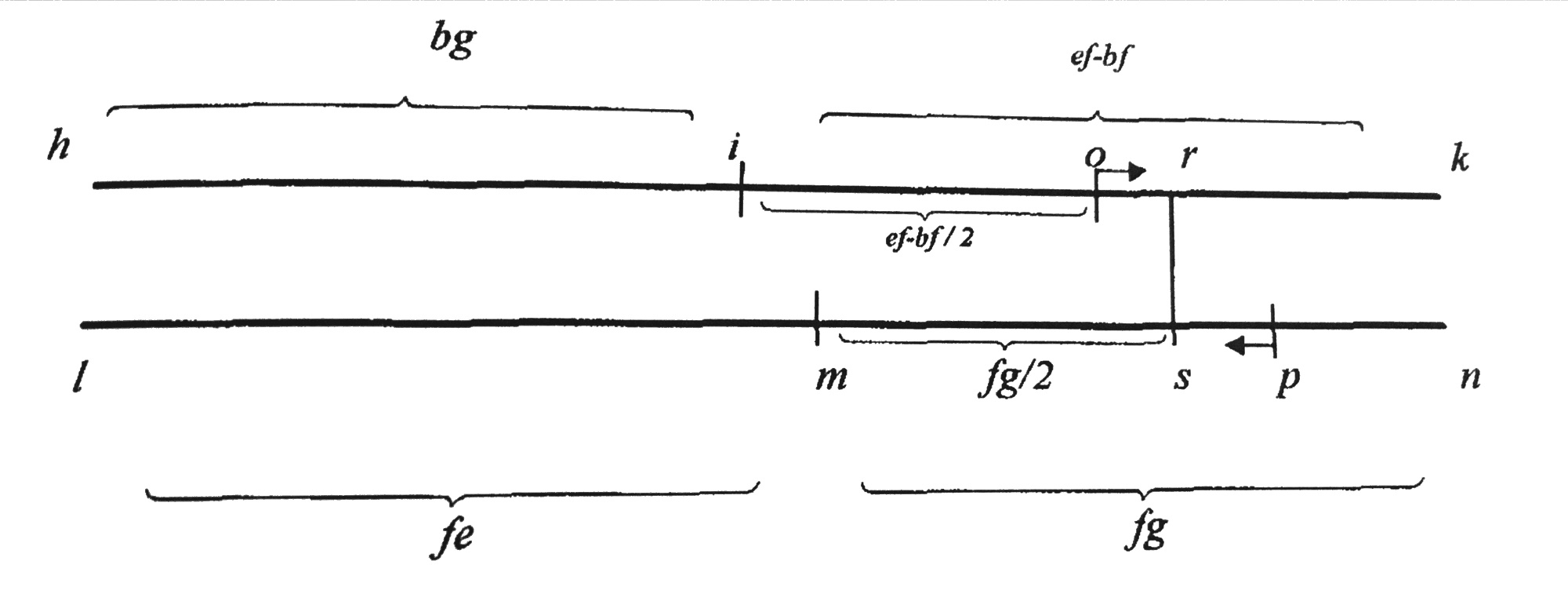
5. Supponi che la quinta bg aggiunta alla metà della differenza tra la sesta fe e la corda della quinta bg, e la sesta ef aggiunta alla metà del segmento fg siano contemporaneamente uguali al doppio della curva be, e che la differenza tra ef e fb sia maggiore di fg. Sia dunque la linea hi uguale alla quinta bg, a cui si somma la differenza, che sarà uguale a ik. Sotto la linea data sia tracciata un’altra linea lm uguale alla sesta fe, alla quale si aggiunge il segmento fg, e sia mn uguale a fg; la linea hk è uguale alla linea ln. Si segni la metà della differenza, che è io, e la metà del segmento, che è mp. Si tracci la perpendicolare tra p e o, che è rs. Dunque, quanto minore è ms rispetto alla metà del segmento, che è mp, tanto maggiore è ir rispetto alla differenza, che è io. Perciò ls sarà uguale alla curva be. E così la sesta lm aggiunta alla metà del segmento è maggiore della curva be. Quindi laddove la sesta, aggiunta alla metà del segmento deve essere uguale alla curva be, la metà della differenza non sarà maggiore della metà del segmento (cfr. figura 2).
6. Così, se dici che la differenza è minore del segmento, segue che la sesta sommata alla metà del segmento è minore della curva be. Dunque, se la sesta sommata alla metà del segmento deve essere uguale alla curva be, allora la differenza tra la sesta e la corda della quinta non deve essere né maggiore né minore del segmento. In questo caso, la prima [ipotesi] dimostra la seconda, ossia che la somma della quinta, aggiunta alla metà della differenza, e la sesta, aggiunta alla metà del segmento, è uguale al doppio della curva be, quando la differenza è uguale al segmento, e cioè, quando la quinta è uguale alla sesta, e questo è stato spiegato.
7. Ecco un eccellente procedimento dimostrativo, poiché sia che tu dica che la differenza è uguale al segmento nella seconda ipotesi, sia [che tu dica] che non è uguale, segue che la differenza è uguale al segmento nella prima ipotesi8 e di conseguenza anche nella seconda. E questa è in un certo senso una coincidenza di opposti, poiché, affermando che la differenza non è uguale al segmento, segue che è uguale, e il falso si annulla da sé.
Note a piè pagina
Per rendere la lettura più scorrevole, il termine «portio», reso ora con «parte», verrà tradotto con «segmento».
Questo opuscolo è destinato a Peurbach. Essa vuole dare una spiegazione del procedimento di rettificazione della curva presentato ne I complementi matematici (Cusanus 2010i, 62–63). Conosciamo il testo da n e dalla ristampa in b. Non sappiamo nulla del periodo in cui fu composto.
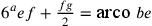 .
.
![6^{a}
ef+\frac{fg}{2}+[5^{a} bg+\frac{(ef–bf)}{2}]=2\text{arco
}be](../../../media/sources/13/24/EOAineq_24_2.png) . Cfr. La figura 27 in Cusanus 2010i, 62–63, che concorda nelle linee essenziali con la figura 1
in esame.
. Cfr. La figura 27 in Cusanus 2010i, 62–63, che concorda nelle linee essenziali con la figura 1
in esame.
Scegliendo opportunamente il punto f, la somma ![(ef+\frac{fg}{2})+[bg+\frac{(\text{corda
}ef–\text{corda }bf)}{2}]](../../../media/sources/13/24/EOAineq_24_3.png) può essere uguale al
doppio dell’arco be. Se f cade dopo b,
allora
può essere uguale al
doppio dell’arco be. Se f cade dopo b,
allora ![6^{a}ef+\frac{fg}{2}+[5^{a}bg+\frac{(ef–bf)}{2}]>2\text{arco
}be](../../../media/sources/13/24/EOAineq_24_4.png) ; se f cade al centro
dell’arco be, allora
; se f cade al centro
dell’arco be, allora ![6^{a}ef+\frac{fg}{2}+[5^{a}bg+\frac{(ef–bf
)}{2}]<2\text{arco }be](../../../media/sources/13/24/EOAineq_24_5.png) . Dunque, a seconda di dove
cade il punto f, si ha una diversa
uguaglianza. Bisogna trovare una posizione intermedia tale
che:
. Dunque, a seconda di dove
cade il punto f, si ha una diversa
uguaglianza. Bisogna trovare una posizione intermedia tale
che: ![(6^{a}ef+\frac{fg}{2})+[5^{a}
bg+\frac{(ef–bf)}{2}]=2\text{arco }be](../../../media/sources/13/24/EOAineq_24_6.png) e per Cusano
questo accade quando
e per Cusano
questo accade quando 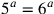 e dunque quando
e dunque quando 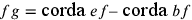 .
.
Dalle due relazioni: 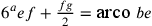 e
e ![{(6^{a}ef+\frac{fg}{2})+[5^{a}bg+\frac{(ef–bf)}{2}]=2\text{arco
}be}](../../../media/sources/13/24/EOAineq_24_10.png) risulta che
risulta che 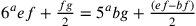 ,
e, se
,
e, se 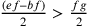 ,
allora
,
allora 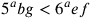 .
.
Ora Cusano vuole dimostrare che il segmento 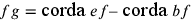 e di conseguenza che
e di conseguenza che 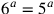 . Del segmento in questione
egli dà una descrizione solo generale del procedimento da lui
intrapreso; nei trattati successivi lo esporrà nei
particolari.
. Del segmento in questione
egli dà una descrizione solo generale del procedimento da lui
intrapreso; nei trattati successivi lo esporrà nei
particolari.
Il punto finale è che 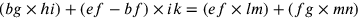 . Questa è una identità che si può
facilmente dimostrare. Cusano afferma inoltre che la somma dei
segmenti è maggiore della curva be.
Come mostra Hofmann e Hofmann 1980, nota 6, 237, questo non vale in tutti i casi, ma solo per quella
posizione di f, per la quale l’angolo
. Questa è una identità che si può
facilmente dimostrare. Cusano afferma inoltre che la somma dei
segmenti è maggiore della curva be.
Come mostra Hofmann e Hofmann 1980, nota 6, 237, questo non vale in tutti i casi, ma solo per quella
posizione di f, per la quale l’angolo
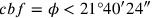 .
L’approssimazione affermata da Cusano risulta da quella
posizione
.
L’approssimazione affermata da Cusano risulta da quella
posizione 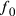 di f, in cui
di f, in cui 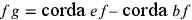 .
Questo vale per
.
Questo vale per 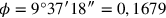 e da ciò, in
prima approssimazione, si ha che
e da ciò, in
prima approssimazione, si ha che 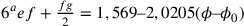 ;
;
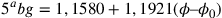 ;
;
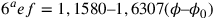 ;
;
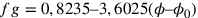 . Se
consideriamo 1,5697 (invece di 1,5708) un soddisfacente valore
approssimativo per
. Se
consideriamo 1,5697 (invece di 1,5708) un soddisfacente valore
approssimativo per 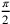 , allora il ragionamento
di Cusano (di rinforzare l’esattezza del risultato attraverso
il procedimento dimostrativo indiretto mediante il maggiore e
il minore), è vero, posto che ci si limiti a un’ampiezza
piuttosto ridotta dell’angolo
, allora il ragionamento
di Cusano (di rinforzare l’esattezza del risultato attraverso
il procedimento dimostrativo indiretto mediante il maggiore e
il minore), è vero, posto che ci si limiti a un’ampiezza
piuttosto ridotta dell’angolo 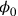 . Tuttavia il testo è espresso
in modo difficile e poco chiaro, e soprattutto è inesatta
l’osservazione che rs cade
perfettamente a metà tra o e p. Cusano confonde «tra» con «a metà
di».
. Tuttavia il testo è espresso
in modo difficile e poco chiaro, e soprattutto è inesatta
l’osservazione che rs cade
perfettamente a metà tra o e p. Cusano confonde «tra» con «a metà
di».
Nel procedimento sopra illustrato l’uguaglianza tra il segmento e la differenza delle corde con riferimento alla prima ipotesi può essere constatata così: «dove la sesta aggiunta alla metà del segmento deve essere uguale alla curva be, la metà della differenza non sarà maggiore della metà del segmento» e «se la sesta, aggiunta alla metà del segmento deve essere uguale alla curva be, allora la differenza tra la sesta e la corda sulla quinta non deve essere né maggiore né minore del segmento».