3.1 Uno sguardo sinottico
Dal breve profilo bio–bibliografico delineato emerge che Cusano, nell’arco di un quindicennio, tra il 1445 e il 1459, in mezzo a bufere politiche, conflitti territoriali, progetti di riforma e delusioni personali, pur se impegnato nell’attività legale e di negoziazione, riesce non solo a non interrompere la costante applicazione allo studio, ma anche a scrivere testi incentrati su tentativi geometrico-costruttivi atti a trovare la soluzione a un problema di carattere strettamente matematico: la quadratura del cerchio.
Si tratta delle seguenti opere: De geometricis transmutationibus (1445), De arithmeticis complementis (due versioni; 1450), De circuli quadratura (luglio 1450), Quadratura circuli (estate 1453), De mathematicis complementis (la prima versione, in un libro, viene compiuta a Bressanone nel settembre del 1453, la seconda edizione, che include due libri, fu ultimata nel novembre 1454), Declaratio rectilineationis curvae (1454), De una recti curvique mensura (1454), Dialogus de circuli quadratura (1457), De caesarea circuli quadratura (1457), De mathematica perfectione (due versioni; 1458), Aurea propositio in mathematicis (1459).
Questi scritti possono essere suddivise in tre parti. La prima comprende il De geometricis transmutationibus, il De arithmeticis complementis e il De circuli quadratura. Queste opere, scritte tra il 1445 e il 1450, sono strettamente collegate tra loro per contenuto e procedimento. In essi Cusano si sforza di portare a compimento la quadratura del cerchio attraverso il metodo dell’isoperimetria, che in queste opere è tuttavia soltanto abbozzato e non chiaramente spiegato.
La seconda comprende il Quadratura
circuli, la Declaratio rectilineationis
curvae, il De una recti curvique
mensura e l’opera maggiore, il De
mathematicis complementis, elaborati tra il 1453 e il 1457.
Cusano si propone di utilizzare poligoni dello stesso perimetro
per formare un cerchio isoperimetrico, e realizzare così la
quadratura del cerchio. Il procedimento e l’approssimazione cui dà
luogo tale tentativo vengono sottoposti al giudizio di
Toscanelli
La terza parte consta di cinque opere, scritte tra il 1457 e il
1459: l’opera che lo stesso Cusano considera come la più
importante, il De mathematica perfectione
(di cui è stata tramandata anche una forma
prior), il Dialogus de circuli
quadratura, il De caesarea circuli
quadratura, l’Aurea propositio in
mathematicis. In queste opere Cusano si sforza di correggere
gli errori rilevati da Toscanelli
Tutti gli scritti matematici gravitano intorno alla vexata quaestio della quadratura del cerchio, a
cui nessuno – sostiene Cusano nel De
mathematicis complementis e, ancor prima, nel De quadratura circuli – ha saputo approssimarsi
più di quanto abbia fatto Archimede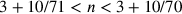 ). Cusano
era inoltre a conoscenza dell’altro e più complesso procedimento
di determinazione della misura della circonferenza realizzato dal
matematico greco nelle Spirali, come emerge
nella Quadratura circuli, nel De mathematicis complementis e nel De mathematica perfectione7.
). Cusano
era inoltre a conoscenza dell’altro e più complesso procedimento
di determinazione della misura della circonferenza realizzato dal
matematico greco nelle Spirali, come emerge
nella Quadratura circuli, nel De mathematicis complementis e nel De mathematica perfectione7.
Sulla scia di Archimede
3.2 Metodo di archificazione e coincidentia oppositorum
In più passi il cardinale afferma che il motivo per cui gli
antichi non sono riusciti nell’impresa è dovuto al fatto che essi
si sono impegnati (invano) a cercare la quadratura del cerchio
partendo dal cerchio, anziché dal quadrato. Dato un cerchio,
Archimede
Tuttavia, incalza Cusano, per pervenire alla conoscenza di ciò che è ignoto occorre muovere da ciò che è noto. Il cerchio, al pari dell’infinito, non è misurabile, ma è essa stessa la misura8, sicché non è possibile partire dal cerchio per giungere all’aequalitas con il quadrato. Per questo Cusano cerca di mettere in atto un altro metodo, che non sia quello di esaustione/compressione. Oltre a questo errore di prospettiva, Cusano individua un’altra motivazione, di natura ancora più profonda, del fallimento di coloro che lo hanno preceduto:
Gli antichi hanno cercato l’arte di rendere il cerchio uguale al quadrato[...]; nell’uguaglianza hanno presupposto la coincidenza del cerchio e del quadrato [...], ma hanno fallito poiché la ragione non ammette la coincidenza degli opposti. La coincidenza infatti doveva essere cercata intellettualmente9.
Per far sì che il quadrato sia uguale al cerchio è necessario che il quadrato si identifichi con il cerchio («in identitatem cum circulo se resolvat»10). Tale identità, tuttavia, non può essere raggiunta tramite la ragione (per rationem)11, la quale giudica impossibile la coincidenza dei contraddittori12, ma intellectualiter, ossia mediante una superiore visione mentale che scorge tale coincidenza all’infinito, attraverso la serie illimitata di determinazioni finite13. L’intuizione intellettuale è così in grado di cogliere ciò che non esiste come limite concreto14.
Nello specifico, la circostanza razionalmente inimmaginabile della coincidenza del curvo col retto può avvenire in due casi solo apparentemente distinti: nell’infinitamente grande e nell’infinitamente piccolo. Nel primo caso si può immaginare un poligono che al crescere indefinito dei suoi lati tende a coincidere con la circonferenza ad essa tangente. Nel secondo caso si può pensare di restringere, per così dire, all’infinito la corda (ossia il lato del poligono inscritto o circoscritto) fino a che essa non si distingua dall’arco di circonferenza sotteso. La perfezione matematica consiste nella reciproca commensurabilità (adaequatio) tra ciò che è retto e ciò che è curvo.
La mia intenzione è quella di arrivare alla perfezione matematica attraverso la coincidenza degli opposti. E poiché questa perfezione consiste per tutti nel rendere una grandezza rettilinea uguale a una [grandezza] curvilinea, mi propongo di cercare il rapporto di due linee rette che stanno tra loro come la corda e il suo arco15.
Negli scritti matematici il principio teo–epistemologico della coincidentia oppositorum costituisce il filo conduttore che lega i molteplici – e con variazioni in certi casi significative – tentativi di Cusano di quadrare il cerchio e viene ad assumere una forte e crescente tensione costruttiva. Ripercorrendo analiticamente il contenuto di tali scritti nel loro ordine di composizione, Joseph Ehrefried Hofmann ha rintracciato in essi uno sviluppo considerevole sul piano metodologico–scientifico, che dai primi incerti approcci alla questione dell’incommensurabilità retto/curvo, svolti nel primo scritto (De geometricis transmutationibus del 1445), attraverso un sistematico ricorso al principio sovrarazionale della coincidentia oppositorum, approderebbe nell’ultimo scritto (Aurea propositio del 1459) a un tentativo di fondazione esclusivamente razionale delle proprie argomentazioni16.
Ora, il procedimento più adatto a «figurare» geometricamente la
coincidenza è quello dell’«archificazione»17, che Cusano preferisce all’impostazione classica greca,
a cui Archimede
Con «archificazione» s’intende un procedimento di determinazione degli angoli, tipica della matematica indiana, e, da questa, attraverso gli arabi, filtrato in Occidente, secondo cui l’angolo viene immaginato come il risultato di una curvatura (da ciò l’idea di archificazione) della retta e direttamente misurato, in quanto tale, sulla circonferenza di un cerchio. Questo procedimento differisce molto dalla matematica greca, che procedeva alla determinazione degli angoli attraverso i rapporti fra linee rette.
Muovendo dal poligono regolare con il numero minore di lati (il triangolo equilatero) cui è inscritto e circoscritto un cerchio, Cusano osserva che al crescere dei lati dei poligoni isoperimetrici, attraverso quelle che egli chiama transmutationes geometrices, il cerchio inscritto e quello circoscritto finiscono per coincidere con la circonferenza, considerata come un poligono di un numero infinito di lati (e angoli). Di questa il cardinale cerca di calcolare il raggio come quella grandezza in cui la serie delle grandezze corrispondenti agli apotemi dei poligoni isoperimetrici di un numero sempre maggiore di lati e la serie, opposta alla prima, delle grandezze decrescenti corrispondenti ai raggi degli stessi poligoni, pervengono al loro punto di coincidenza19. In questo modo, percorrendo illimitatamente il finito, le figure, trapassando l’una nell’altra, entrano in una circolazione infinita, in cui il triangolo (la figura geometrica con il minor numero di lati e angoli) viene a coincidere con il cerchio (la figura geometrica con il numero infinito di lati e angoli), che complica in sé tutte le figure20. Dunque, attraverso un processo di infinita approssimazione asintotica, si giunge alla quadratura del cerchio o, per meglio dire, a una sorta di circolazione del quadrato21.
Non possiamo sapere se e quanto Cusano potesse, se pur
indirettamente, essere a conoscenza dei precedenti indiani del suo
metodo (anche se è certo che il suo corrispondente Georg von
Peurbach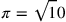 )22; certamente a quel tempo la matematica dell’Occidente
latino derivava dalla mediazione operata dalla cultura araba sui
testi di scienza e di filosofia greche e, soprattutto nel campo
della trigonometria, il sapere arabo era largamente debitore di
quello indiano. Detto ciò, è probabile che il particolare metodo
di archificazione attraverso poligoni isoperimetrici seguito da
Cusano sia stato influenzato dai riferimenti presenti nella Geometria speculativa di Bradwardine
)22; certamente a quel tempo la matematica dell’Occidente
latino derivava dalla mediazione operata dalla cultura araba sui
testi di scienza e di filosofia greche e, soprattutto nel campo
della trigonometria, il sapere arabo era largamente debitore di
quello indiano. Detto ciò, è probabile che il particolare metodo
di archificazione attraverso poligoni isoperimetrici seguito da
Cusano sia stato influenzato dai riferimenti presenti nella Geometria speculativa di Bradwardine
Non va neanche trascurata in proposito l’influenza che può avere esercitato su Cusano l’Ars magna di Lullo: oltre che ad aver potuto indirizzare Cusano verso il metodo degli isoperimetri, la matematica “empirica” di Lullo (presente nell’Ars magna e sviluppata nel De quadratura et triangulatura circuili e nel Liber de nova geometria)24, pur costituendo un episodio del tutto insignificante sul piano propriamente scientifico, poteva avergli suggerito un approccio al problema della quadratura del cerchio che faceva leva sul presupposto che all’interno della realtà vi fosse il principio divino della sua strumentalizzazione e quindi della “manipolabilità” mentale delle strutture concettuali in funzione del conseguimento di una verità teologica25.
Questo approccio, sostanzialmente diverso rispetto alla rigida impalcatura assiomatico–deduttiva della scienza greca, pur essendo meno rigoroso, doveva apparire più duttile e funzionale allo scopo che Cusano intendeva perseguire, ossia l’«adaequatio recti et curvae», perché permetteva di muovere, di «transmutare» le figure l’una nell’altra fino a farle coincidere all’interno di uno spazio mobile, concepito come luogo di grandezze tanto rettilinee quanto curvilinee, di rapporti sia razionali sia irrazionali.
In questo modo, attraverso la riproposizione del punto di vista banausico e non rigoroso dell’archificazione, il principio della coincidentia conferiva alla dimensione pratica della geometria una nuova rilevanza teorica.
3.3 Dimensione pratica e dimensione teorica della geometria
Dalla lettura degli Scripta mathematica emerge un dato di importanza capitale ai fini di un’analisi attenta della portata storica degli scritti matematici di Cusano. Le costruzioni cusaniane condotte secondo il procedimento dell’archificazione si configurano come tentativi di considerare nuovi punti di vista sul problema della quadratura del cerchio; emerge una nuova dimensione, quella della geometria pratica, in cui, nonostante la mancanza delle appropriate tecniche algebriche e geometriche che consentiranno nei secoli a venire lo sviluppo rigoroso di quei punti di vista, si esprimono una forza di immaginazione e una precisione di pensiero destinati a incidere non poco sulla problematica filosofico-scientifica dei tempi successivi.
Va anche sottolineato che, nei medesimi anni in cui si dedica agli scritti matematici, Cusano scrive il De staticis experimentis (1450), in cui propone un metodo empirico di quadratura del cerchio. Nel quarto dei dialoghi dell’Idiota, il rapporto approssimativo tra il cerchio e il quadrato viene calcolato sperimentalmente con l’uso della bilancia26.
Per evidenziare la nuova prospettiva filosofica di Cusano,
bisogna tenere presente, come ben sottolinea Luciana De
Bernart27, che, nella concezione della matematica del Medioevo –
già presente in Boezio
Tuttavia, mentre nell’ambiente padovano queste teorie erano
state sviluppate in senso strettamente matematico o nella philosophia naturalis, Cusano le elabora in
direzione teologica, secondo una tradizione già inaugurata dalle
scuole ispirate alle ultime dottrine di Duns Scoto
Cusano opera dunque una sorta di inversione di rotta, anzi un vero e proprio rovesciamento, del tradizionale rapporto instaurato nel Medioevo tra geometria pratica e geometria speculativa: quest’ultima diventa ora non il mezzo, bensì il fine (e l’origine) della prima e la geometria, nella sua dimensione pratico–costruttiva, trova ora la sua legittimità in sede teorica, facendo uscire quest’ultima dai margini del modello assiomatico–costruttivo della geometria classica.
3.4 Lo spazio come luogo della mente
Un aspetto originale della dimensione concettuale entro cui si muove Cusano è l’idea di uno spazio “malleabile”, di una spazialità dotata di una fluidità intrinseca, che consente all’immaginazione di far tendere le determinazioni oppositive della ratio verso il punto metafisico (teologico) della loro coincidenza31.
Tale “fluidità” deriva dal fatto che, per Cusano, lo spazio geometrico è un prodotto della mente umana e, in quanto prodotto, può essere non solo misurato, ma anche, in qualche modo, manipolato. Se, infatti, è vero che lo spazio geometrico (mentale) e lo spazio fisico (reale) non corrispondono perché non derivano dallo stesso autore, è altrettanto vero che tanto l’autore (umano) dello spazio geometrico, quanto l’autore (divino) dello spazio fisico hanno la medesima potenza creatrice: questo di un infinito Uno assoluto, quello dei rapporti seriali, ossia di proporzioni continue attraverso cui le opposizioni dello spazio mentale tendono verso l’unità metrica32. Certamente, e Cusano lo dice espressamente nel De theologicis complementis, l’unità, nella quale gli opposti coincidono, è il fondamento originario ed è proprio perché pre–supposto che esso può fungere da punto di tendenza della serialità33.
La natura costruttiva – quindi dinamica e seriale – delle
relazioni geometriche stabilite dal cardinale riflette a sua volta
la concezione cusaniana dello spazio come il luogo della mens nel quale si esplica l’attività di mensura.34 L’intelletto solo, in quanto uno e indivisibile –
concezione che egli eredita molto probabilmente da Biagio
Pelacani
Come «il numero non dipende dalle cose numerate»38, così le rappresentazioni/costruzioni non dipendono dalle figure rappresentate, bensì dall’attività dell’intelletto.
Il concetto chiave espresso nel De docta ignorantia per cui la transumptio ad infinitum è possibile grazie al processo “aggiuntivo” di infinitizzazione dello spazio geometrico attuato dalla mente umana, è ripreso nell’Idiota de mente, del 1450, opera scritta nello stesso periodo di composizione del De circuli quadratura, in cui Cusano scrive che «…mentem esse ex qua omnium rerum terminus et mensura»39.
La mente umana, simile alla mente divina40, è una forza essenzialmente creativa, progettuale, che produce “da sé” i contenuti – in se sempre congetturali – del suo sapere41. Tali contenuti, ossia le nozioni, i concetti e le operazioni con i quali la mente cerca di quadrare il cerchio, la mente li trae, li dispiega e li sviluppa a partire da se stessa perché ad essa pre–disposti, e, in quanto tali, assimilabili42.
Più che l’attitudine, comune a molti esponenti della tradizione
neoplatonica da Proclo
Il problema matematico della quadratura del cerchio ha una natura paradossale perché illumina la mente della sua costitutiva opacità. La mente umana, confrontandosi con il problema della quadratura del cerchio, diventa consapevole che: 1. il suo ragionare è sempre oppositivo45; 2. è essa stessa il principio d’unità di quelle opposizioni.
La ragione contraddice in un certo senso il proprio modus operandi: più tenta di elevarsi alla semplice unità in cui gli opposti non sono opposti, più diventa consapevole della sua impotenza e del suo legame necessario e imprescindibile con il mondo dell’alterità, trasportando così la divisione e l’opposizione dentro se stessa46. Tuttavia, proprio perché ha il potere («posse») di far coincidere gli opposti, ossia di tendere all’aequalitas, la mente assomiglia a dio. Una somiglianza che certamente non concerne i suoi prodotti, inevitabilmente destinati alla propinquitas e alla impraecisio, ma la sua capacità di costruire strumenti e determinare procedimenti (proportiones continuae) adeguati a far coincidere ciò che alla ragione appare come incommensurabile (quadrato/cerchio; retto/curvo) attraverso la logica eminentemente ‘seriale’ di mediazione degli «opposti» geometrici.
La matematica, mostrando (alla ragione che la utilizza) l’impossibilità di pervenire all’absoluta praecisio, costituisce, per così dire, la condizione della possibilità di questa impossibilità; le ingegnose trasmutationes geometrices attraverso le quali Cusano cerca instancabilmente di giungere alla perfezione matematica, cioè alla quadratura del cerchio, dimostrano l’impossibilità di dimostrare la quadratura del cerchio perché l’aequalitas, nella quale gli opposti coincidono, è visibile solo trascendendo qualsiasi comparativa proportio: «cum inter illas quantitates adeo contraria forte non cadat numerabilis habitudo. Necesse erit igitur me recurrere ad visum intellectualem»47.
3.5 Le fonti
Come abbiamo già evidenziato, le questioni relative alla quadratura del cerchio e alla rettificazione del cerchio non sono argomenti nuovi tra gli intellettuali del tempo: la maggior parte dei matematici del tempo s’interessa al metodo delle figure isoperimetriche48, uno su tutti, Raimondo Lullo, il quale, nella Geometria Nova e, in particolare, nel De quadratura et triangulatura circuli49, tenta di risolvere la questione della quadratura del cerchio.
Il discorso sulle fonti è molto ampio e qui ci limiteremo a
fare brevi accenni su alcuni autori a cui Cusano si ispira per le
sue riflessioni sulla matematica50: da Anselmo d’Aosta
Sebbene non vi siano riferimenti espliciti negli Scritti matematici, sono molte le fonti che
influenzano la filosofia matematica di Cusano, tra questi
Plotino
Se gli autori appena citati, insieme a molti altri che qui non
possiamo analizzare (tra questi, Dionigi, Alberto Magno
L’impressionante inventario della biblioteca di Cusano
conservata a Kues realizzato agli inizi del Novecento da Joseph
Marx60 è inevitabilmente incompleto e a volte impreciso: una
delle difficoltà è che ciascun volume rilegato contiene più opere
i cui titoli non sono facilmente reperibili. D’altra parte questa
biblioteca è stata largamente ampliata dopo la morte del suo
fondatore, ma manca ancora un indice dei testi e il fatto che lo
stesso Marx non abbia rilevato alcun titolo di Archimede
Certamente Biagio Pelacani
Un’altra fonte è Nicola d’Oresme
3.6 Cusanus… geometra ridiculus? La recezione degli scritti matematici
Visti i numerosi e importanti legami di Cusano con i vari
esponenti della cultura del tempo, è certo che i manoscritti
matematici, composti tra il 1445 e il 1459, circolano da subito
tra le persone con cui il cardinale può e sa di potersi
confrontare riguardo a specifici argomenti, tra cui
Toscanelli
Nel 1533 viene pubblicato a Norimberga, ad opera di Johannes
Schöner
Schöner
Questi scritti erano stati inviati da Cusano al suo amico Georg
von Peurbach
Schöner
Quest’edizione norimberghese è molto importante perché, pur
comprendendo solo un’esigua parte dell’opera matematica cusaniana,
dà conto del metodo di Cusano e documenta le obiezioni ad esso
mosse da matematici specialisti come Toscanelli
Nel dialogo De quadratura circuli secundum
Nicolaum Cusensem (composto nel 1464)71 Regiomontano
Il giudizio severo di Regiomontano
E ha ragione Regiomontano
Tuttavia, il livello delle argomentazioni cusaniane è notevole, e di queste si può comprendere la portata solo a patto di rispettarne, per quanto possibile, il decorso logico, che, per la sua peculiare natura filosofica – e non soltanto per l’inadeguatezza delle tecniche di calcolo storicamente disponibili (all’epoca non esistono il simbolismo algebrico, il metodo analitico, il concetto di funzione, definizioni precise per la trigonometria) – si presenta irriducibile ai presupposti eminentemente formali su cui si fonda la possibilità di applicare l’algebra alla geometria77.
Non bisogna dimenticare che l’intento che anima le indagini
matematiche di Cusano è quello di mostrare la sorprendente potenza
del principio della coincidenza e, da questo punto di vista, la
quadratura del cerchio rappresenta ai suoi occhi un caso, il più
“visibile”, di coincidentia oppositorum in
atto78. Ed è soprattutto per questo aspetto che Giordano
Bruno
Negli scritti matematici di Cusano emerge la chiara
consapevolezza che la condizione metodologica di possibilità del
darsi della coincidentia non può che
risiedere in una diversa impostazione geometrica, in una
dimensione dello spazio come il luogo della mens–mensura. Certamente la nuova filosofia
della mente resta irretita entro una forma eminentemente teologica
di intuizione teorica che, di fatto, non permetteva di
padroneggiare «la potenza insita nella serialità che tale
intuizione conteneva e a sintetizzare la rigidità delle
determinazioni geometriche e la mobilità operativa della mens»81. E tuttavia, proprio quell’intuizione dinamica, per
quanto deformata dalla poderosa immaginazione teorica del
filosofo, sarà uno stimolo di notevole portata innovativa ai nuovi
«Archimede
Ora, se da un lato lo scritto di Regiomontano
Da questo punto di vista, Cusano può essere considerato un pensatore–limite che, con le sue innovazioni teoriche, anche in campo matematico, seppe, come sintetizza felicemente John Hopkins, «spalancare la porta della modernità senza però riuscire a oltrepassarne la soglia»86.
Ancora, suggestionato dal principio lulliano di strumentalità del sapere, Cusano concepisce la mente umana in termini di «partecipazione» alla natura creativa della mente divina, il che si riflette sull’idea che la matematica non è solo theoria, bensì un modo per costruire i concetti necessari per comprendere il mondo, uno strumento operativo prodotto dalla mente dell’uomo per cogliere la struttura del mondo.
La stessa idea che gli oggetti matematici non esistono indipendentemente dall’intelletto umano, ma ne sono una creazione, è una concezione della matematica che sarà accettata pienamente nel mondo scientifico soltanto nel XIX sec, fermo restando che in Cusano tale creazione non è assoluta, bensì partecipativa o assimilativa dell’assoluto.
Nel De mathematicis complementis Cusano,
dopo aver discusso l’opera con Toscanelli
L’idea che il cerchio è un poligono con un numero infinito di
lati sarà ripresa nella metà del Cinquecento dal monaco matematico
Michael Stifel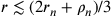 , dove
, dove 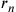 e
e 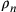 sono i raggi di una
successione di poligoni regolari inscritti e circoscritti al
cerchio, isoperimetrici a un cerchio di raggio r90.
sono i raggi di una
successione di poligoni regolari inscritti e circoscritti al
cerchio, isoperimetrici a un cerchio di raggio r90.
È inoltre evidente l’influenza che le sue riflessione
eserciteranno su alcuni pensatori del Cinquecento, ad esempio sul
cusaniano Charles De Bouelles
Anche la problematica sul concetto di minimo e di massimo,
ampiamente utilizzato negli scritti matematici, influenzerà
profondamente i pensatori successivi, tra cui Johannes
Kepler
In questa scia, nel 1747, Abraham Kästner
Moritz Cantor
Ancora, dalla metà del secolo scorso sono stati prodotti studi specifici sulle opere matematiche di Cusano, che, nonostante – e forse grazie a – gli inevitabili limiti dell’impostazione metodologica –, sottolineano l’importanza degli scritti matematici di Cusano nell’ambito dello sviluppo di quella forma mentis matematica tipicamente moderna che si è andata progressivamente affermando tra il XV e ei XVI secolo attraverso cunicoli spesso oscuri e inconsapevoli99.
Note a piè pagina
Per un’attenta analisi dei concetti di infinito, numero e tempo presso i greci, cfr. Mondolfo 1967.
Cfr. Pacioli 1494 e Pacioli 1509.
Cfr. De Bernart 2002a, 352. Per quanto riguarda modi e forme della recezione di Archimede da parte di Cusano, si veda l’esaustiva trattazione di Clagett 1964–1984b, III, 3, 297–315.
Cfr. Da Cremona 1984. D’Alessandro e Napolitani hanno rinvenuto l’autografo della traduzione di Iacopo nel codice Nouv. Acq. Lat. 1538 della Bibliothèque Nationale de France e hanno dimostrato che l’umanista cremonese utilizzò per la sua traduzione un modello greco non riconducibile a nessuno dei manoscritti greci di Archimede a noi noti. Cfr. D’Alessandro e Napolitani 2012.
Cfr. Manfredi 1994; Vasoli 1968.
«circulum non mensurari, sed mensurare» (Cusanus 1994, XI, 10). Cfr. Counet 2005, 273–290.
«Quaesiverunt veteres artem aequandi circulum quadrato [...] coincidentiam circuli et quadrati in aequalitate praesupposuerunt […] sed quia ratio non admittit coincidentias oppositorum, defecerunt. Coincidentia autem quaeri debuit intellectualiter» (Cusanus 1994, IV, 4–26).
«Ma la forza infinita è incommensurabile rispetto a tutto ciò che non è infinito, come l’ampiezza del cerchio resta incommensurabile rispetto a tutto ciò che non è circolare» (Cusanus 2010c, 28, 9–10). Cfr. anche Cusanus 1972a, I, 3, 9. Sul tema, cfr. Hofmann 1964, 398–403.
Cfr. Cusanus 1972b, II, 2, 81.
Cfr. Cusanus 2010d, 2–3. La tesi della congetturalità della conoscenza, ossia dell’irraggiungibilità della precisione, non sfocia in un esito scettico, dato che, per Cusano, essa è «positiva assertio veritatem partecipans» (Cusanus 1972b, I, 13) e rappresenta cioè la ratio essendi di ogni nostra ricerca. Cfr. Vaiati 1970, 163–172; Koch 1953, 7–48; Miller 1991, 119–140; Pasqua 2013, 345–357; Schulze 1978.
Lo stesso discorso vale per diagonale e il lato del quadrato o per la circonferenza e il suo diametro: «sappiamo che tra la diagonale e il lato di un quadrato non è possibile trovare alcun rapporto che sia esprimibile in termini matematici, perché non possono esserci due numeri il cui rapporto sia precisamente come quello [che vi è tra la diagonale e il lato][…] E sebbene quel rapporto appia possibile, questa possibilità non è mai data in atto. L’atto sarebbe invece quella precisione per la quale i numeri starebbero tra di loro in un rapporto preciso[…] La precisone è presente in quel concetto che esprime ciò che per noi è impossibile concepire» (Cusanus 1973, 42).
Cfr. Hofmann e Hofmann 1980, Einführung.
È il termine usato da Cantor 1894–1908, II, 187.
Cfr. Cantor 1894–1908, II, 208. Cfr. Sfez 2005.
Per un’analisi dettagliata dei procedimenti matematici impiegati da Cusano nella quadratura del cerchio, cfr. De Bernart 1999; Nagel 1984.
Il cerchio infinito è utilizzato da Cusano come simbolo dell’unità infinita del massimo, in quanto «il cerchio è la figura perfetta dell’unità e della semplicità» (Cusanus 1972a, I, 21, 63, 5). Cfr. anche Cusanus 1972a, 64. Per questa ida Hofmann rinvia a Boethius 1867, II, 30, 121, 20ss.. Cfr. anche Volkmann-Schluck 1984, 42. Nella stessa scia, l’immagine della sfera, in quanto «ultima perfectio figurarum, qua maior non est» (Cusanus 1972a, XXIII, 71, 3–5), viene ad essere la rappresentazione più perfetta di Dio inteso come massimo assoluto e può essere ricondotta alla seconda sentenza del Liber XXIV philosophorum («Deus e st sphaera infinita cuius centrum est ubique, circumferentia nusquam»), che Eckhart riporta nei suoi scritti, scritti posseduti e fittamente annotati dal Cusano (Cod. Cus. 21). Cfr. Eckhart 1964, 95; Wackerzapp 1962, 140; Murawski 2016, 97–110. Sul simbolo della sfera infinita, cfr. Mahnke 1937, spec. 48ss.; Blumenberg 1960, 159ss.
Cfr. Cürsgen 2007.
Cfr. Hofmann 1942.
Questo interesse può spiegare perché Cusano si fosse applicato, a un certo punto della sua formazione, a trascrivere, di proprio pugno, il manoscritto lulliano De quadratura et triangulatura circuli. Cfr. l’introduzione di questo testo.
«se si costruirà un vaso cilindrico di diametro ed altezza note ed un altro cubico del medesimo diametro e della stessa altezza, e si peserà l’acqua di cui sono stati riempiti, mediante la diversità dei pesi si troverà la proporzione tra il quadrato inscritto ed il cerchio in cui è inscritto e quindi, con una congettura approssimata (propinqua coniectura), si troverà la quadratura del cerchio» (Cusanus 1983c, 138). Cfr. Estrada 2008, 135–146.
Cfr. Folkerts 1970.
Sul nesso teologia e matematica, cfr. Cfr. Cusanus 1994, spec. II, III; Cusanus 2010d, 1; Böhlandt 2009; Cassirer 1927, 70; Counet 2005, 273–290.
«dal momento che la mente umana, alta similitudine di Dio, partecipa, per quanto le è possibile, della facoltà della natura creatrice, essa tare da se stessa, quale immagine della forma onnipotente, gli enti di ragione a somiglianza degli enti reali» (Cusanus 1972b, I, 1, 5). Cfr. anche Cusanus 1983a, 6, 88, 19–20; Hopkins 2002, 13–29.
Cfr. Flasch 1973; Nicolle 2002, 85–88. Unità e punto non coincidono esattamente, ma vi è una corrispondenza tra serie numeriche e figure geometriche. A differenza del punto, che, in quanto complicazione della linea (cfr. Cusanus 1988a, I, 10, 10), è la più piccola non–grandezza iniziale da cui si generano tutte le grandezze: linee, superfici e figure solide («Quantitas, quae non potest esse minor, non est quantitas, sed punctus» (Cusanus 2010g, 14, 10–11), l’unità non ha posizione perché è immateriale: «omnis autem numerus ab uno est, in quo complicatur. Sicut igitur ex puncto fluit linea, ita ab uno numerus» (cfr. Cusanus 1994, IX, 44–45). E ancora: «unitas igitur, sine qua numerus non numerus esset, est in pluraliatem et hoc quidem est unitatem explicare, omnia scilicet in pluralitate esse» (Cusanus 1972a, II, 3). È evidente l’influenza del Commento al primo libro degli Elementi di Euclide di Proclo, secondo il quale l’unità, per la sua semplicità e indivisibilità, è più perfetta del punto e precede il punto. Dall’uno derivano tutti i numeri, fungendo da unità di misura di tutte le grandezze intermedie: cfr. Proclus 1873. Il testo greco verrà stampato nel 1533 a Basel, da Simon Grynaeus, e la traduzione latina si avrà per opera di Francesco Barozzi (1537–1604) solo nel 1560, dopo quasi un secolo dalla morte di Cusano, che chiaramente attinse anche ad altri manoscritti. É tuttavia indubbio che copie manoscritte di Proclo circolassero nel XV secolo e sappiamo anche che Bessarione, a cui Cusano era legato, possedeva molte copie. Di conseguenza, nulla vietata a Cusano l’accesso al Commentarius nella versione greca, o che qualcuno abbia potuto tradurlo per lui. Come scrive Eisenkopf 2005, 225: «Proklos wird von Cusanus in Verbindung mit der Zahl nicht explizit erwähnt, da er diesen aber aufmerksam rezipierte und Proklos an die pythagoreische Zahlenspekulation genauso anknüpfte wie er die Überlegungen Euklids kommentierte und systematisierte, ist auch er als wichtige Quelle des cusanischen Denkens anzusehen. Dies zeigt aber auch, dass die Quellen, auf die sich Cusanus bezieht, aus zweiter und dritter Hand stammen und exakte Zuordnungen im einzelnen schwierig sein dürften». Cfr. anche Carratelli 1998, 201–225.
Cfr. Cusanus 1983a, I, 63; Cusanus 1988b, 6, 1ss.; Cusanus 2007, CLXX, 3, 13–17: «Illa ‹anima› mensurat, dividit et componit et numerat. Illa facit ex se mensuras, et vocatur mens a mensurando». L’etimologia che connette mens con mensurare deriva molto probabilmente da Alberto Magno (ca. 1206–1280). Cfr. Magnus 1972, I, 31, XXXVII, pars I, 16b, 63ss., che Cusano cita in un sermone (Cusanus 2007, CLXXIV, 12, 1–6). Cfr. anche Aquinas 1975–1976, q. 10, art. 1, 210ss..
Per primo Thomas Bradwardine, nel Tractatus de proportionibus del 1328, nota che nel concetto di proporzione di uguaglianza (proportio o ratio aequalitatis) «nessun rapporto è maggiore o minore di un rapporto di uguaglianza». Da ciò deriva la nozione di verità come praecisio, concetto che viene sviluppato da Biagio Pelacani, in particolare nel suo Commento al Trattato sulle proporzioni, «per dimostrare, in termini matematici, la natura indivisibile dell’intelletto»: la proportio aequalitatis, espressa dalla proporzione 1 : 1, è per Biagio un’unità che è in proporzione di uguaglianza solo con se stessa, il rapporto dell’uno con se stesso; tale concetto indica un’unità intellettuale identica solo a se stessa, un punto matematico indivisibile: l’indivisibile, infatti, non è né uguale né disuguale rispetto a nessuna cosa, essendo identico a sé stesso.
«sebbene l’unità debba essere considerata come il padre dell’uguaglianza , in quanto l’uguaglianza è l’unità presa una sola volta […], tuttavia l’uguaglianza assoluta complica in sé l’unità[…] Nell’unità, in effetti, non si vede che l’uguaglianza» (Cusanus 2001, 28, 20–25).
Cfr. Cusanus 2001, 25, 20.
Cusanus 1983a, I, 57. Ancora, nel De venatione sapientiae, Cusano scrive: «La mente umana, che è un’immagine della mente assoluta e che è libera secondo il modo che è proprio dell’uomo, pone nei suoi concetti limiti a tutte le cose […] E qualunque cosa si propone di fare, la mente la determina prima dentro di sé, ed è pertanto il limite di tutte le sue opere. Inoltre, tutte le cose che essa fa non la delimitano al punto che essa non possa farne di più, per cui essa è, a modo suo, un limite senza limite. Su questo argomento ho scritto nel mio libro De mente» (Cusanus 1982, XXVII, 82, 13–20).
L’analogia tra l’attività creatrice della mens divina e quella della mens humana e il tema dell’assimilazione sono un tema di fondo del pensiero di Cusano e ricorre costantemente in tutti i suoi scritti. Cfr. Cusanus 1983a, I, 72, 6–9; Cusanus 1988b, 6, 2–5; Cusanus 1972b, I, 1, 5, 3–10; Cusanus 1988a, II, 93, 17. Molte chiare sono le parole espresse nel De venatione sapientiae: «dato che la conoscenza è assimilazione, l’intelletto trova tutte le cose in se stesso come in uno specchio vivo dotato di vita intellettuale; e quando guarda dentro se stesso, vede in se stesso tutte le cose assimilate. E questa assimilazione è un’immagine viva del creatore e di tutte le cose» (Cusanus 1982, XVII, 50, 1–5). Cfr. Kremer 2004, 1–49; Schwaetzer 2005, 113–132.
Cfr. Cusanus 1972a, I, 5, 14, 18–20; Cusanus 1972b, I, 1, 5, 4–7; II, 17, 178, 3–7; Cusanus 1988b, 7, 2–5; 56, 57; Cusanus 1988a, II, 93, 1–18; Cusanus 1973, 43, 7–13; Cusanus 1983a, I, 70, 2; 97, 2; 98, 10; 104, 2; 157, 13. In tutti i passi citati Cusano sottolinea il carattere spontaneo e attivo della mente umana, che trae da sé («a se exserit») gli enti matematici, i numeri e le forme delle cose.
Da questo punto di vista è significativo, come sottolinea Van Velthoven 1977, 97–98, che Cusano attribuisca all’uomo la creatività, un termine che nella teologia medioevale, è riservato esclusivamente a Dio. Cfr. Aquinas 1918, 1926, 1930, II, 21, 98–99: Quod solius Dei est creare: «creatio est propria Dei actio […] Nulla igitur substantia praeter Deum potes aliquid creare». Un’analisi dettagliata della mens in Cusano è svolta da Leinkauf 2006. Va qui sottolineato, come ha messo ben in rilievo Joseph Stallmach, che: «Wenn also der Geist als Geist durch schöpferische Spontaneität gekennzeichnet ist, so der endliche Geist als endlicher gerade durch den assimilativen und konformativen Charakter eben dieser schöpferischen Tätigkeit. Sein Begreifen ist entium assimilatio so wie das göttliche entium creatio ist. Der menschliche Geist hat seine eigene Welt, sein eigenes Universum, aber dieses ist eine universitas assimilationis rerum» (Stallmach 1967, 50–54, cit. 52).
Le parole pronunciate da Proclo nella Teologia platonica circa «l’attitudine ad elevare propria del numero» (Proclus 2005, IV, 34, 16–23, trad. 599) sembrano quasi riecheggiare nell’incipit del De circuli quadratura, in cui Cusano esordisce dicendo: «All’inizio ti ho invitato a passare da queste matematiche alla teologia attraverso la via dell’assimilazione; questo, infatti, è il modo più adatto di elevarsi» (Cusanus 2010c, 28ss.).
Cfr. Oberrauch 1993a.
«In Metaphysica autem dicit curvum et rectum in natura contrariari, quare unum non posse converti in aliud» (Cusanus 1988c, XXVIII, 45). Nella stessa scia, Vengeon 2006, 222: «...selon lui, l’impossibilité de la quadrature du cercle équivaut à l’expression géométrique du principe de non contradiction».
Cfr. Cuozzo 2002, 47ss.; Cusanus 2010h, 25–30. In questo senso si può dire che la ragione ha una natura paradossale in quanto è essa stessa la condizione di possibilità dell’impossibilità di cogliere l’infinito. Sul tema cfr. De Felice 2019, 61–76.
Cfr. Cusanus 2010d, 2–3. Cfr. Cusanus 1994, II–III.
Cfr. Hofmann 1942, 21–37.
Cfr. Flasch 2008; Nicolle 1998, 128–150.
Cfr. Haubst 1952b, 420–447.
Cfr. Haubst 1952a, 255ss.; Rusconi 2008, 59–70. Per quel che concerne l’influenza lulliana e il ruolo di mediazione svolto da Eimerico, cfr. Hofmann 1942, 21–37; Colomer 1964, 198–213; Colomer 1961; Vescovini 2005b, 139–154; Calma e Imbach 2009, 15–51; Imbach 2011.
Oltre a quelli citati, di particolare interesse sono gli studi di Vansteenberghe 1928, 275–284 e di Vescovini 1997, 393–413 e 1983, 661–684, che mettono in luce l’origine ermetica della matematica di Cusano, impostando le basi per un confronto tra l’opera del cardinale e quella di Bonaventura di Bagnoregio (ca. 1217–1274).
La versione latina degli Elementi di Euclide, realizzata da Campano dall’arabo, probabilmente elaborata sulla base della traduzione in latino di Adelardo di Bath (XII sec.), viene pubblicata da Ehrard Ratdolt a Venezia nel 1482 e costituisce la prima edizione stampata di Euclide. In seguito Simon Grynaeus curerà l’editio princeps in greco nel 1533, alla quale aggiungerà il testo greco del Commento al I libro di Proclo. Nel frattempo appariranno due edizioni latine ad opera di Bartolomeo Zamberti (ca. 1473–ca.1543) nel 1505 e di Luca Pacioli nel 1509 che si richiamano rispettivamente alla tradizione greca di Teone di Alessandria (commentatore di Euclide vissuto nel IV secolo) e alla tradizione latina di Campano. Un’edizione comparata delle due traduzioni latine verrà pubblicata da Jacques Lefèvre d’Etaples a Parigi nel 1516. Cfr. Crapulli 1969, 14–15. Cfr. Kästner 1796–1800, 289–299; Weissenborn 1882, 1–7; Heath 1926, I–92ss.
Di questo testo, così come dell’Arithmetica speculativa, non abbiamo notizie certe sulla data di pubblicazione. Cfr. Bradwardine 1495b, 115–120.
Cfr. Bradwardine 1328, 64–140.
Cfr. De Muris 1998.
Cfr. Clagett 1968.
Solo nel 1565 si procedette a scorporare gli scritti cusaniani dell’edizione norimberghese dalla critica di Regiomontano e a comprenderli nell’edizione di Basilea. Per le informazioni sulle edizioni degli Scritti matematici di Cusano, cfr. Hofmann e Hofmann 1980, LI–LII.
Da questo punto di vista, concordiamo con l’analisi di Luciana De Bernart, secondo cui «la risonanza dell’edizione norimberghese degli scritti di Cusano va considerata sono un episodio, anche se di estrema importanza, nel quadro dell’influenza dell’opera matematica cusaniana sul pensiero matematico successivo» (De Bernart 2002b, 38).
Cfr. Cardano 1663, IV.
Cfr. Counet 2005, 286–290.
Da questo punto di vista, Müller parla di una doppia matematica in Cusano: una geometria aritmetica (matematica deduttiva) e una geometria speculativa (matematica induttiva), mostrando, nella scia delle analisi di Bocken 2005, 201–220, che vi è un gap, all’interno della riflessione cusaniana, circa il rapporto tra algebra e geometria (cfr. Müller 2010, 45–46; 76–77).
Cfr. Counet 2000.
Folkerts non esita a definire la matematica cusaniana come un prezioso contributo espresso, tuttavia, in una forma inadeguata: «Allerdings hat die unzureichende mathematische Form dazu geführt, daß der wertvolle Gehalt seiner mathematischen Schriften in Vergessenheit geriet. Erst im 20. Jahrhundert haben sich die Mathematikhistoriker, vor allem J. E. Hofmann, ernsthaft mit den Schriften des Cusanus beschäftigt und festgestellt, daß sich hinter seinen Formulierungen zukunft-sweisende Ideen verbergen, u. a. infinitesimale Ansätze und Vorstellungen über funktionale Abhängigkeiten. Daher kann man Cusanus als einen Wegbereiter der neuzeitliche Mathematik sehen» (Folkerts 2003, 332).
La lettura dello spazio geometrico si riflette sulla concezione cusaniana del movimento, che risulta eminentemente estensiva, senza tuttavia riuscire a contemplare il fattore temporale. Come mostra De Bernart, questa mancata intuizione – presente tra l’altra già in Archimede – non permette a Cusano di tradurre in termini di uniformità la differenza dei percorsi cinematici generatori delle grandezze, il che rende praticamente impossibile portare a termine le trasmutationes geometrices messe in atto al fine di giungere alla quadratura del cerchio (cfr. De Bernart 2002b, 61–62).
Cfr. Müller 2014, 86–102. Conclude sinteticamente Simon: «Hätte Cusan die theoretische Durchbildung Regiomontans besessen und wäre seine Zeit nicht durch den Dienst der Kirche und den beklagenswerten Kampf um sein Bistum Brixen so völlig in Anspruch genommen worden, Cusan stände als reiner Mathematiker eben so groß da, wie als Theosoph und mathematischer Philosoph» (Simon 1912, 128–337).
Hopkins 1996, 83. Cfr. anche Gadamer 1970, 39–48; Cassirer 1920. A sottolineare la natura ambigua, persino contraddittoria, dell’opera politica, metafisica e scientifica di Cusano è Maurizi 2008, il quale, analizzando i concetti di concordantia, coincidentia e praecisio, vede nella filosofia di Cusano l’espressione di una ricerca provocante, capace di interrogare la modernità stessa.
Cfr. Uzielli 1894; De Bernart 1999.
Cfr. Cusanus 2010f, 6. Sul ruolo di mediazione svolto da Toscanelli tra Cusano e gli intellettuali del Quattrocento italiano, cfr. Flasch 2002, 175–193, spec. 182ss..
Cfr. AA.VV. 1964; Orbetello 1965.
Cfr. Nagel 2007; Watanabe 2011.
Cfr. Johannes 1938, II, 23. Sull’influenza di Cusano su Kepler, cfr. Omodeo 2014, 215–226; Bialas 2003, 45–53; Koyré 1973, 336.
Cfr. Vescovini 1998a, 107: «Tuttavia anche sul piano strettamente matematico Cusano ha avuto il merito di introdurre una problematica sul concetto di minimo e di massimo, di indivisibile, tutta una tematica del limite e dell’illimitato, delle grandezze infinite, che è stata certamente feconda nella direzione della riflessione successiva sul concetto di infinitesimo».
Cfr. Gauss 1984, 435–455.
Si tratta di un lungo articolo scritto da Kästner nel 1747 e pubblicato nell’Hamburgische Magazine. L’articolo è stato riprodotto in Kirsch 2007.
Kirsch 2007, 4–22. Cfr. anche Nagel 2007.
Cfr. Cantor 1965, 51–203.
