2. Un’inattesa persecuzione mi ha recentemente trattenuto nella fortezza di Andratz che in tedesco prende il nome di Buchenstein1. Lassù, in mezzo alle Alpi, privato dei miei libri e approfittando di questo ristoro, ho iniziato a indagare se fosse possibile ottenere, in modo chiaro e facile, la sempre cercata, e, come si dice, non ancora trovata, quadratura del cerchio2. Dopo i tanti e vari procedimenti, che ho riportato nei miei libri scritti su questo argomento, me ne è venuto in mente uno più chiaro e a me più caro, che offro qui di seguito alla Tua maestà come degno regalo per la Tua Altezza. Infatti, per il fatto che si sa che ciò che finora si è cercato come qualcosa di estremamente singolare può essere trovato solo con profondissimo acume e una passione fortissima, chi sarebbe più degno di riceverlo se non il sommo imperatore che si diletta come il più nobile dei principi anche in questi segreti ragionamenti?
3. Benché questo piccolo regalo sia minuscolo di fronte alla tua innata clemenza, so che lo apprezzerai molto e verso di me, tuo umile servitore, sarai senz’altro più benevolo. Prendendo esempio dalla riduzione delle figure l’una nell’altra, capirai come all’imperatore spetti il potere di trasformare ciò che è rotondo in ciò che è poligonale e viceversa, e di tradurre talvolta la severità della legge in clemenza e talvolta la clemenza in rigore. Questo spetta solo a Te, che sei indipendente dalle leggi, essendo tu la fonte unica delle leggi civili alle quali tutti gli altri devono sottomettersi per legge3.
Proposizione
4. Se dal centro a di un cerchio dato tracci [due] linee verso due punti della circonferenza, g e f, distanti l’una dall’altra un dodicesimo della circonferenza e se da un punto d della linea ag conduci all’infinito la perpendicolare che taglia af in modo che la linea compresa tra il punto d’intersezione c e la circonferenza sia la metà di ad e se indichi con x il punto sulla perpendicolare tale che la linea tracciata dal centro a verso questo stesso punto sia il doppio della linea ad, allora dx sarà un sesto della circonferenza del cerchio dato (cfr. figura 1).
Questo perchè ad sarà il semidiametro del cerchio inscritto nel triangolo isoperimetrico al cerchio dato, ax il semidiametro del cerchio circoscritto al triangolo in questione e dx la metà del lato del suddetto triangolo4.
Dimostrazione
5. Si dimostra così: poiché è certo che ga è maggiore dei 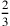 del semilato del triangolo e
minore del semilato5, mantenendo la stessa figura, si segnino, usando
l’immaginazione, su ga e su fa rispettivamente le linee go e fp uguali ai
del semilato del triangolo e
minore del semilato5, mantenendo la stessa figura, si segnino, usando
l’immaginazione, su ga e su fa rispettivamente le linee go e fp uguali ai
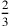 [del
semilato]. Si tracci, quindi, da un punto di ag fino a toccare af la
perpendicolare, la quale si rapporta alle due linee che stanno
sopra di essa su ga e fa come queste si rapportano a go e fp6. Questo è possibile perché si dà un punto vicino a g dove il rapporto è maggiore e un punto vicino
a o dove il rapporto è minore; pertanto,
c’è un punto intermedio dove esso non è né maggiore né minore.
Così, ancora, si può dare una perpendicolare che si rapporta alle
linee che stanno sotto di essa fino ad o e
p allo stesso modo in cui queste si
rapportano a og e pf, seguendo lo stesso procedimento di
prima7.
[del
semilato]. Si tracci, quindi, da un punto di ag fino a toccare af la
perpendicolare, la quale si rapporta alle due linee che stanno
sopra di essa su ga e fa come queste si rapportano a go e fp6. Questo è possibile perché si dà un punto vicino a g dove il rapporto è maggiore e un punto vicino
a o dove il rapporto è minore; pertanto,
c’è un punto intermedio dove esso non è né maggiore né minore.
Così, ancora, si può dare una perpendicolare che si rapporta alle
linee che stanno sotto di essa fino ad o e
p allo stesso modo in cui queste si
rapportano a og e pf, seguendo lo stesso procedimento di
prima7.
6. Dico che queste due perpendicolari coincidono
in una sola che taglia parti uguali da og
verso l’alto e da fp verso il basso e di
conseguenza anche da go verso il basso e da
pf verso l’alto. Diversamente, come si
dimostrerà più avanti, ciò è impossibile. Questa perpendicolare
sarà dunque 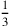 del semilato, per esempio dc; e poiché ca è il
doppio di dc, ca sarà uguale a fp, pa uguale a fc e fc
uguale a do. Inoltre, poiché fc è anche uguale a oa,
fc sarà la metà di da; e poiché dc è
del semilato, per esempio dc; e poiché ca è il
doppio di dc, ca sarà uguale a fp, pa uguale a fc e fc
uguale a do. Inoltre, poiché fc è anche uguale a oa,
fc sarà la metà di da; e poiché dc è 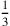 del semilato del triangolo
isoperimetrico, triplicato il semilato che tocca il cerchio
inscritto in d, ad
sarà il semidiametro di questo cerchio inscritto. E questo era ciò
che si cercava.
del semilato del triangolo
isoperimetrico, triplicato il semilato che tocca il cerchio
inscritto in d, ad
sarà il semidiametro di questo cerchio inscritto. E questo era ciò
che si cercava.
7. Che la perpendicolare che si abbassa da g e l’altra che si innalza da o coincidono nel punto d, come detto prima, è così evidente: infatti, la perpendicolare che si abbassa fino al suddetto rapporto non può stare al di sopra di d; è evidente, poiché le linee al di sopra della perpendicolare qui sono minori della metà di go e di fp e la perpendicolare è certamente maggiore della metà di go. Essa non può nemmeno scendere al di sotto di d perché qui le due linee al di sopra della perpendicolare sono maggiori della metà di go e di fp e la perpendicolare è minore della metà di go. Se, dunque, la perpendicolare che si abbassa non può che cadere in d, allora anche quella che si innalza non può che cadere in d, poiché in d le linee che stanno sopra e quelle che stanno sotto sono uguali e dunque le perpendicolari coincidono. Questo era ciò che si doveva dimostrare8.
8. Può essere dimostrato anche in un altro modo. In primo luogo, suppongo di poter segnare il semidiametro del cerchio inscritto nel triangolo isoperimetrico del cerchio dato su ag, e immaginiamo che sia ad. Se pure esso è maggiore della metà di ag, sarà tuttavia di molto minore dei due terzi [di ag], come risulta dalla dimostrazione appena effettuata, da cui segue che il diametro del cerchio, triplicato di un settimo va oltre la circonferenza. Si può anche condurre dal punto d una perpendicolare dx di lunghezza indefinita e far ruotare af da ag attorno al centro a del cerchio dato finché la linea compresa tra dx e la circonferenza sia la metà di ad. È evidente. Infatti, se af si trova vicino a g, questa linea è maggiore della metà di da, ma se si avvicina al punto in cui dx taglia la circonferenza, allora è minore; dunque essa si trova in un punto [intermedio] né maggiore né minore. Se tuttavia questa linea è uguale alla metà di ad, allora la parte restante di af compresa tra dx e a sarà uguale a gd più la metà di da. E tralascio tutto il resto in quanto noto.
9. In secondo luogo suppongo che se la perpendicolare da d, per esempio dx, è un sesto della circonferenza del cerchio dato, allora la linea ax sarà il doppio di ad e le tre linee saranno note una a una: la prima è dg, l’altra è la linea di af al di sopra di dx e la terza è quella compresa tra d e af. E questo è certo.
10. In terzo luogo suppongo che se af taglia la circonferenza in un punto che dista dal punto g un dodicesimo della circonferenza, allora la linea dc della perpendicolare dx, compreso tra d e la linea fa, sarà un terzo di dx che è uguale a un sesto della circonferenza del cerchio. Infatti, un terzo [di dx] sarà la metà del semidiametro del cerchio; il quadrato del suo semidiametro è un terzo del quadrato del semidiametro ax, dunque i due terzi del semilato del triangolo inscritto nello stesso cerchio. Questo è evidente, infatti il quadrato del semilato del triangolo si rapporta al quadrato del semidiametro come 3 a 4. Dunque il quadrato dei due terzi del semilato si rapporta al quadrato del semilato intero come 4 a 9 e il quadrato del semidiametro sarà uguale a 12, di cui un terzo è pari a 4 e questo è certo.
11. In quarto luogo, suppongo che ora ruoti af fino al punto in cui le tre linee, di cui si parla nella seconda ipotesi, saranno uguali a dx. Infatti, se af si situa vicino a g, esse saranno minori; se dista dal punto g più di un dodicesimo della circonferenza, saranno maggiori. In un determinato punto, quindi, esse non saranno né maggiori né minori di dx, e questo si trova a un sesto della circonferenza del cerchio.
12. In quinto luogo suppongo che ora ax ruoti fino a quando il secondo è maggiore della metà di ad; allora la prima e la seconda, prese insieme, sono maggiori della linea restante. Chiamo “linea restante” quella parte di af dalla quale è stata sottratta la seconda. Se la seconda è minore della metà di ad, allora la prima e la seconda, prese insieme, sono minori della linea restante. Tuttavia quanto più af si allontana dal punto g, maggiore sarà la somma delle tre; e quanto più la seconda è maggiore, minore sarà la somma delle tre linee, e quanto più essa è minore, maggiore sarà la somma9.
13. Dico dunque che quando af è posto sul punto della circonferenza che dista da g un dodicesimo della circonferenza, allora le tre linee prese insieme sono uguali a dx, cioè a un sesto della circonferenza, dato che la seconda è la metà di ad e la prima e la seconda prese insieme sono uguali alla linea restante che, unita alla terza, è uguale a dx.
14. Se qualcuno negasse questo, allora dovrebbe negare che la seconda è la metà di ad. Perciò, se lo nega e afferma che le tre linee sono minori di dx, è necessario che sostenga che la seconda è tale che le tre linee siano minori, come se la seconda fosse la metà di ad. Così, dalla quinta ipotesi, egli deve affermare che la seconda è maggiore della metà di ad e se è così allora, stando alla suddetta ipotesi, la prima e la seconda insieme superano la linea restante ca, che, unita alla terza cd, è uguale a dx; è evidente che le tre linee non sono minori, ma maggiori di dx. Così, se egli afferma che le tre linee sono maggiori, deve necessariamente sostenere che la seconda è minore della metà di ad; e se è così, allora la prima e la seconda sono minori della linea restante che, unita alla terza, è uguale a dx. Le tre linee saranno dunque minori; e qualunque cosa dica chi nega quanto abbiamo affermato, risulta il contrario dalla quinta ipotesi. Ne consegue necessariamente che la proposizione è vera, che ad è il semidiametro del cerchio inscritto al triangolo isoperimetrico, cf è la sua metà e dx è uguale a un sesto della circonferenza del cerchio dato di cui ag è il semidiametro. E questo è ciò che si cercava.
15. Diversamente: dico che le tre linee sono uguali alla metà del lato del triangolo isoperimetrico e di conseguenza che la prima e la seconda prese insieme sono uguali ai due terzi di questo e che la seconda è la metà del semidiametro del cerchio inscritto nel triangolo.
16. Se una di queste affermazioni è vera, tutte
le altre sono vere e questo è certo. Se lo neghi, cadi in
contraddizione. Infatti, se, considerando la figura di sopra, dici
che le tre linee sono minori del semilato del triangolo in
questione, allora dici che la seconda è maggiore e minore della
metà del semidiametro del cerchio inscritto al triangolo in
questione. Se dici che essa è maggiore, affermi che le tre linee
prese insieme sono minori, come se la seconda fosse la metà del
semidiametro del cerchio inscritto nel triangolo. Infatti, quanto
maggiore è la seconda, tanto minori sono le tre linee dalla quinta
ipotesi. Dici, infatti, che la seconda è minore della metà del
semidiametro in questione perché affermi che la prima e la
seconda, prese insieme, sono minori della linea restante di af da cui è stata tolta la seconda10. Altrimenti, infatti, le tre linee non sarebbero minori
della metà del lato del triangolo. Dici anche che la terza è
maggiore e minore di 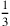 del semilato del triangolo. Se
infatti le tre linee prese insieme sono minori della metà del lato
del triangolo e se la somma della prima e la seconda è maggiore
della linea restante di af, allora la terza
è minore di
del semilato del triangolo. Se
infatti le tre linee prese insieme sono minori della metà del lato
del triangolo e se la somma della prima e la seconda è maggiore
della linea restante di af, allora la terza
è minore di 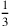 del semilato; e poiché la
prima e la seconda sono ancora minori della linea restante di af, allora la terza è maggiore di
del semilato; e poiché la
prima e la seconda sono ancora minori della linea restante di af, allora la terza è maggiore di  del semilato;
la stessa cosa accade quando dici che le tre linee sono maggiori
del semilato. È dunque chiaro che chi nega afferma due
contraddizioni.
del semilato;
la stessa cosa accade quando dici che le tre linee sono maggiori
del semilato. È dunque chiaro che chi nega afferma due
contraddizioni.
17. È evidente che il diametro di un cerchio dato
è uguale alla somma del semidiametro del cerchio inscritto al
triangolo isoperimetrico e dei 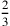 del lato del triangolo11. Pertanto, se la linea fosse uguale al diametro
triplicato per
del lato del triangolo11. Pertanto, se la linea fosse uguale al diametro
triplicato per 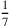 di esso e se a quella
togliessi il semidiametro del cerchio inscritto corrispondente e i
di esso e se a quella
togliessi il semidiametro del cerchio inscritto corrispondente e i
 del
lato del triangolo, allora questa somma sarebbe maggiore del
diametro, perché la linea uguale al diametro triplicato per
del
lato del triangolo, allora questa somma sarebbe maggiore del
diametro, perché la linea uguale al diametro triplicato per
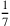 di
esso è maggiore della circonferenza; e se la linea fosse uguale al
diametro triplicato e ai
di
esso è maggiore della circonferenza; e se la linea fosse uguale al
diametro triplicato e ai 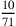 di esso e se ad essa
togliessi il semidiametro del cerchio inscritto nel triangolo in
questione e
di esso e se ad essa
togliessi il semidiametro del cerchio inscritto nel triangolo in
questione e 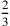 del lato del triangolo allora
questa somma sarebbe insieme minore del diametro, perché il
diametro, triplicato per i suoi
del lato del triangolo allora
questa somma sarebbe insieme minore del diametro, perché il
diametro, triplicato per i suoi 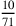 , è minore della
circonferenza, come Archimede
, è minore della
circonferenza, come Archimede
18. Bisogna anche considerare che chi nega la quadratura del cerchio, al fine di non affermare che ciò che è curvo e ciò che è rettilineo coincidono, afferma, attraverso la sua negazione, che due contraddizioni coincidono. Se si applicherà accuratamente, mostrerà che le proposizioni matematiche sono vere perché in caso contrario seguirebbe la quadratura del cerchio, e parimenti perché in caso contrario seguirebbe che il cerchio non si può quadrare. Perciò, dall’affermazione e dalla negazione della quadratura del cerchio possono essere provate come vere tutte le proposizioni matematiche, di cui ho già detto abbastanza altrove13, così, la dotta ignoranza è venuta a capo di tutto ciò che bisogna sapere per rispondere alla domanda se ci sia una coincidenza delle contraddizioni oppure no. Su ciò ho scritto qualcosa, anche se in maniera del tutto insufficiente, in tre libri14.
19. Tuttavia è certo che se si moltiplica il
semidiametro ga del cerchio dato per ab e si triplica per dx,
si ottiene un rettangolo uguale al cerchio (cfr. figura 2); e se si cerca
per la nona proposizione del sesto libri di Euclide
Terminato il 6 Agosto 1457 presso Andratz.
Note a piè pagina
Questo opuscolo, indirizzato all’imperatore Federico IV, è stato completato il 6 Agosto 1457 quando Cusano era trattenuto dal 10 Luglio nella fortezza di Andratz, isolato e privato dei suoi libri. Alla fine del testo (§18) il cardinale manifesta una velata avversione verso i suoi oppositori sulla questione della quadratura del cerchio.
Se indichiamo con n il numero di
lati del poligono, 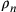 il diametro del suo cerchio
inscritto (la “prima”),
il diametro del suo cerchio
inscritto (la “prima”),  il semidiametro del suo cerchio
circoscritto (la “seconda”),
il semidiametro del suo cerchio
circoscritto (la “seconda”), 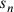 il suo lato, allora si può
riassumere la proposizione in questo modo: se
il suo lato, allora si può
riassumere la proposizione in questo modo: se 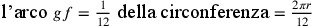 , se
, se
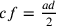 e se
e se 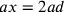 , allora
, allora 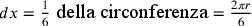 . La ragione sta nel
fatto che
. La ragione sta nel
fatto che 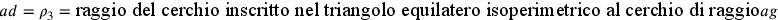 ;
; 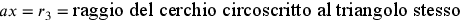 ;
; 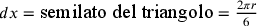 . Secondo Hofmann e Hofmann (1980, nota 3, 243),
. Secondo Hofmann e Hofmann (1980, nota 3, 243), 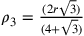 e se il perimetro del triangolo è U avremo
e se il perimetro del triangolo è U avremo ![U=6\rho_3\sqrt{3}=2r[\frac{18}{(4+\sqrt{3})}]](../../../media/sources/13/27/EOAineq_27_12.png) ;
;
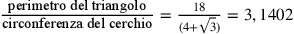 . Questo
valore approssimativo di
. Questo
valore approssimativo di 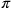 è di poco più piccolo del limite
inferiore di (3,1408).
è di poco più piccolo del limite
inferiore di (3,1408).
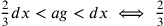 ;
;
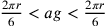 . Questa
diseguaglianza si ottiene così: nel cerchio di raggio r la circonferenza
. Questa
diseguaglianza si ottiene così: nel cerchio di raggio r la circonferenza 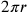 è uguale a
è uguale a 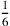 del
semilato
del
semilato  del triangolo equilatero isoperimetrico al
cerchio, e da un lato è maggiore di 6r
(dall’esagono regolare inscritto); dall’altro è minore di 8r (dal quadrato inscritto), così da un lato
del triangolo equilatero isoperimetrico al
cerchio, e da un lato è maggiore di 6r
(dall’esagono regolare inscritto); dall’altro è minore di 8r (dal quadrato inscritto), così da un lato
 ; dall’altro
; dall’altro 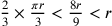 .
.
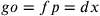 ;
;
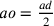 ;
; 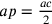 . La
perpendicolare taglia ag in d e af in c, così, per determinare ad, si tstabilisce il punto d su ag grazie alla
proporzione continua:
. La
perpendicolare taglia ag in d e af in c, così, per determinare ad, si tstabilisce il punto d su ag grazie alla
proporzione continua: 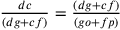 .
Poniamo
.
Poniamo 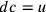 ,
così
,
così 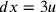 ,
,
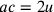 ,
,
 ;
;
 ,
, 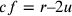 ;
; 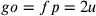 . Per la
proposizione
. Per la
proposizione ![\frac{u}{[2r–u(2+\sqrt{3})]}=\frac{[2r–u(2+\sqrt{3})]}{4u}=\sqrt{(\frac{u}{4u})}=\frac{1}{2}](../../../media/sources/13/27/EOAineq_27_35.png) ,
si ha
,
si ha 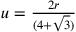 ,
,  .
.
Si può anche determinare d con la
proporzione: 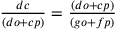 . Ponendo
. Ponendo 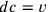 , risulta che
, risulta che 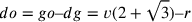 ,
, 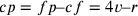 ; così la
proposizione si trasforma in
; così la
proposizione si trasforma in ![\frac{v}{[v(6+\sqrt{3})–2r]}=\frac{[v(6+\sqrt{3})–2r]}{4v}=\frac{1}{2}](../../../media/sources/13/27/EOAineq_27_42.png) e
e 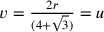 .
.
Si tratta di dimostrare che queste due determinazioni di d coincidono in una sola.
 ;
; 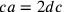 ;
; 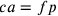 ;
; 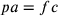 ;
; 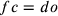 ;
; 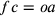 ;
; 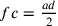 ;
;
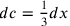 ; quindi
; quindi 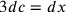 ;
; 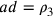 . Se la
perpendicolare fosse sopra d allora
. Se la
perpendicolare fosse sopra d allora
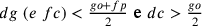 . Se la perpendicolare fosse
sotto d allora
. Se la perpendicolare fosse
sotto d allora 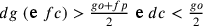 . Accade
solo in d che
. Accade
solo in d che 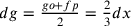 .
Dunque:
.
Dunque: 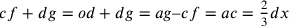 .
.
Si possono ricapitolare le cinque ipotesi e le loro concatenazioni:
in primo luogo: 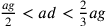 ;
da cui
;
da cui 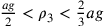 ;
;
in secondo luogo: se 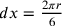 , allora
, allora 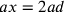 e dunque si
conosceranno dg, cf e dc.
e dunque si
conosceranno dg, cf e dc.
in terzo luogo: se  allora
allora 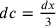 ;
;
in quarto luogo: 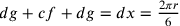 ;
;
in quinto luogo: 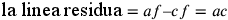 . Se
af si allontana da g allora
. Se
af si allontana da g allora  ; se
; se 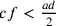 ,
allora
,
allora 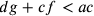 . Più af si allontana da g
più (
. Più af si allontana da g
più (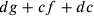 )
cresce; più cf cresce più (
)
cresce; più cf cresce più (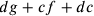 ) decresce; più
cf decresce più (
) decresce; più
cf decresce più (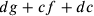 ) cresce.
) cresce.
Se 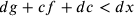 , allora
, allora  e
e
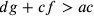 .
Ma
.
Ma 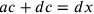 ;
dunque
;
dunque 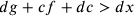 . Se
. Se 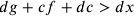 , allora
, allora
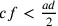 e
e 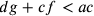 . Ma
. Ma
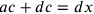 ;
quindi
;
quindi 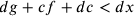 . Pertanto l’ipotesi di
partenza è esatta:
. Pertanto l’ipotesi di
partenza è esatta: 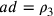 ;
; 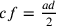 ;
; 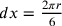 .
.
Sappiamo che  ;
;
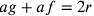 ;
;
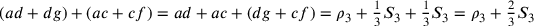 .
.
Cfr. Cusanus 2010c, 25.


