1. Capacitates omnium polygoniarum isoperimetrarum ad invicem et ad circulum isoperimetrum eandem proportionem habent quam primae lineae unius ad primas lineas alterius et ad semidiametrum isoperimetrum. Similiter excessus capacitatis aliarum a triangulo supra triangulum in eadem proportione se habent ad capacitatem trianguli, quam habent excessus primarum linearum aliarum figurarum a triangulo ad primam trianguli lineam.
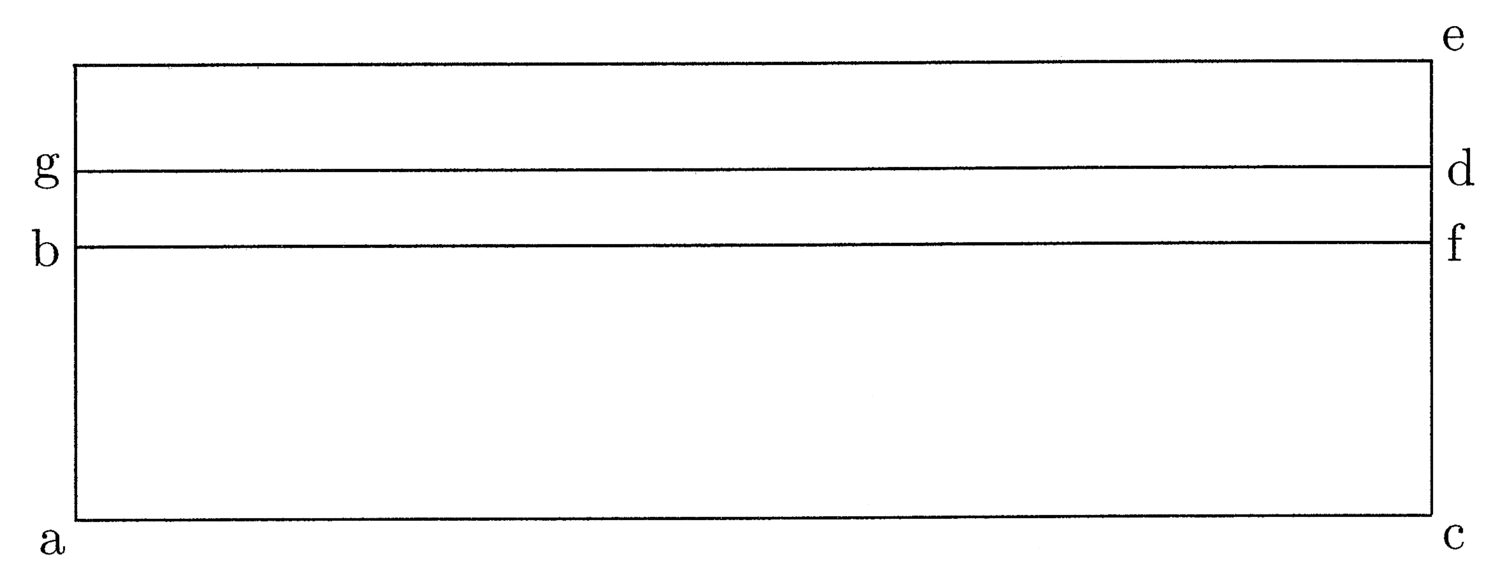
2. Verbi gratia: Sit prima trianguli ab, prima alterius figurae mediae ut quadrati cd, prima circuli sive semidiameter ce, sit ac semicircumferentia omnium istarum superficierum, quoniam sunt isoperimetrae (cfr. figura 1).
Erit superficies ae capacitas circuli,
superficies ad capacitas figurae mediae ut
quadrati, superficies af capacitas trianguli.
Dico primo, quod qualis est proportio superficiei ae ad ad superficiem,
talis est ce lineae ad cd lineam, et qualis proportio est ad superficiei ad af
superficiem, talis est cd lineae ad cf lineam, per primam enim sexti Euclidis
3. Si a secunda extremitate primae circuli ad secundam trianguli linea recta ducatur aequedistanter basi, in ea proportione, qua dividet excessum secundae supra primam ipsius trianguli, in eadem proportione dividet excessus secundarum a primis omnium aliarum figurarum mediarum.
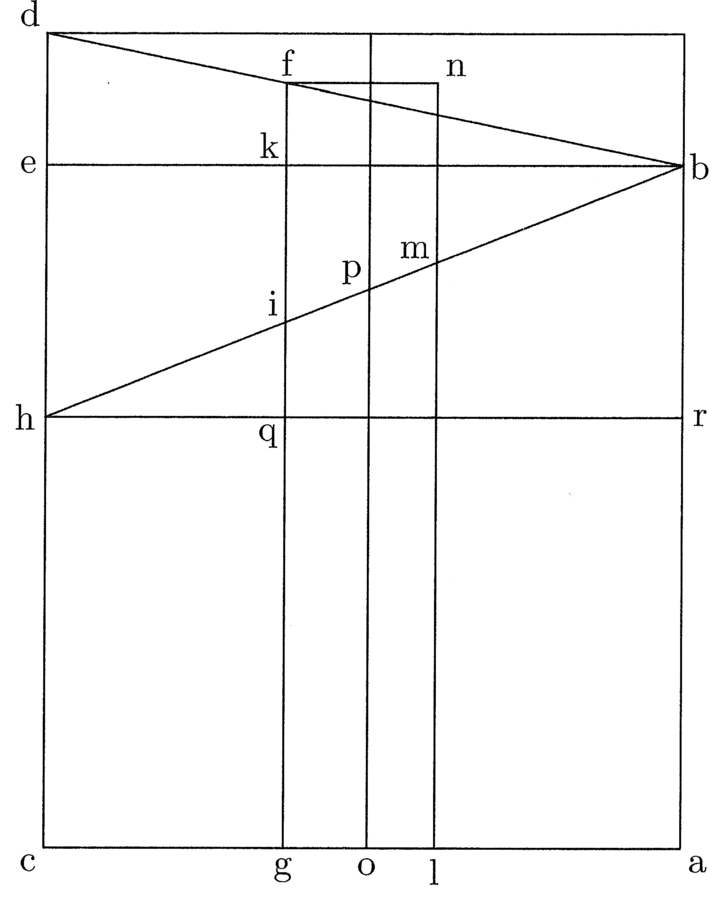
4. Sit supra extremitatem lineae ac erecta linea ab, quae sit prima circuli, et super alia extremitate dictae lineae ac sit erecta linea cd, quae sit secunda trianguli. Quia linea ab est minor linea cd, si a puncto b trahatur linea be aequedistans basi ac, perveniet ad lineam cd et dividet excessum secundae a prima, qui est hd, in quadam proportione de ad eh. Dico quod si prima et secunda alicuius figurae mediae describatur, ut gi prima et gf secunda, quod excessus secundae a prima, qui est fi, dividetur ab ipsa be linea in puncto k in eadem proportione, quae erit fk ad ki ductis lineis db hb ita, quod erit eadem proportio fk ad ki, quae de ad eh. Totus enim triangulus dhb divisus est per aequedistantem basi fi. Erit ergo proportio eb ad kb sicut dh ad fi, et eadem proportio erit de ad kf et eh ad ki propter similitudinem triangulorum sicut eb ad kb. Sicut ergo de ad fk, ita eh ad ki; permutatim ergo sicut de ad eh, ita fk ad ki. Ergo illi excessus proportionabiliter sunt divisi, quod fuit probandum (cfr. figura 2).
5. Forte dicitur, quod si gf est secunda unius figurae mediae, quod gi non erit prima. Erit ergo prima eiusdem figurae aut maior gi aut minor. Sit primo maior, et sit lm. Quam extendo sursum usque ad n, ita quod ln sit aequalis gf, et traho lineam fn aequedistanter basi propter eandem longitudinem duarum linearum gf et ln. Inter duo ergo puncta g, l sunt signandae plures primae et secundae lineae figurarum mediarum. Signetur una, et sit op prima, qua extendatur usque ad secundam eiusdem figurae. Aut proveniet infra lineam fn aut in ipsa linea aut supra. Non infra ipsam nec in ipsa, quia est secunda figurae minoris capacitatis; ergo deberet esse longior. Non tamen potest poni longior, quia gf est posita inter figuras minoris capacitatis et esset brevior, quod est impossibile, quia non diminuendo procederem secundae lineae versus capaciores figuras incedendo, quod est impossibile. Eodem modo dicetur impossibile sequi, si dicatur, quod prima eius erit minor gi. Cum ergo nec maior nec minor dici potest, ipsa gi erit prima, quia omnes excessus secundarum a primis in eadem proportione dividentur, quod fuit probandum.
6. Haec videtur declaratio undecimae conclusionis vestrae, in qua pendet tota demonstratio quadraturae. Nam qualis est proportio hq ad qi, talis est hr ad rb. Istarum autem quattuor linearum proportionalium tres primae sunt notae: hq prima, quia subtractio sagittae quadrati vel alterius mediae a sagitta trigoni; qi secunda est etiam nota, quia excessus primae tetragoni a prima trigoni; tertia etiam est nota hr, quia sagitta trigoni. Si ergo multiplices hr in qi et dividas per hq, habetur rb nota, quae adiuncta primae trigoni ra erit ab nota prima circuli sive semidiameter, quod intenditur. Sed non video, cur duae lineae hb et bd, concludentes omnes illos excessus primarum et secundarum, non possent esse curvae omni genere curvitatis, et tunc non procederet demonstratio. Erit enim illud, quod in decima tua conclusione dixisti, quod primae capaciorum erunt semper maiores et secundae minores.
7. Haec volo mihi in praesenti sufficiant. Multa habeo, quae me movent, quod istae coincidentiae sive intensiones et remissiones formarum non per lineas rectas signari debeant, ut moderni ponunt, sed in aliud tempus reservo. Vale.
8. Detur venerabili nostro fideli dilecto magistro
Georgio Peurbachio