1. Le ampiezze1 di tutti i poligoni isoperimetrici hanno tra loro e con il cerchio isoperimetrico lo stesso rapporto che esiste fra le prime linee2 dell’uno e le prime linee dell’altro, e con il semidiametro isoperimetrico3. Ugualmente, gli eccessi delle ampiezze delle figure diverse dal triangolo rispetto all’ampiezza del triangolo hanno lo stesso rapporto di quello che gli eccessi delle prime linee di queste altre figure hanno rispetto alla prima linea del triangolo4.
2. Per esempio: Sia ab la
prima linea di un triangolo, sia cd la prima
linea di un’altra figura intermedia, per esempio del quadrato, ce la prima linea del cerchio ossia il suo
semidiametro, ac la semicirconferenza di
tutte queste superfici, essendo esse isoperimetriche
(cfr. figura 1). La superficie di ae5 sarà l’ampiezza del cerchio, la superficie di ad sarà l’ampiezza di una figura intermedia come
il quadrato, la superficie di af sarà
l’ampiezza del triangolo. Dico per prima cosa che il rapporto tra la
superficie di ae e la superficie di ad è uguale a quello tra la linea ce e la linea cd e che il
rapporto fra la superficie di ad e la
superficie di af è uguale a quello tra la
linea cd e la linea cf, per la prima proposizione del libro VI di
Euclide
3. Se dalla seconda estremità della prima [linea] del cerchio alla seconda [linea] del triangolo si conduce una linea retta parallela alla base, il rapporto tra questa e l’eccesso della seconda sulla prima dello stesso triangolo che essa taglia è lo stesso di quello tra essa e l’eccesso delle seconde dalle prime di tutte le altre figure intermedie8.
4. Sia tracciata su un’estremità della linea ac la perpendicolare ab, e sia questa la prima linea del cerchio, e sull’altra estremità di detta linea ac la perpendicolare cd, e sia questa la seconda linea del triangolo. Poiché la linea ab è minore della linea cd, se dal punto b si traccia la linea be parallela alla base ac, questa linea arriva alla linea cd, e divide l’eccesso della seconda sulla prima, che è hd, nello stesso rapporto che esiste tra de e eh. Dico che se si segnano la prima e la seconda di un’altra figura intermedia, per esempio con gi la prima e con gf la seconda, allora l’eccesso della seconda sulla prima, che è fi, è diviso nel punto k dalla linea be, nello stesso rapporto che esiste tra fk e ki, condotte dalle linee db e hb, così che il rapporto tra fk e ki sarà lo stesso di quella tra de e eh. Infatti, l’intero triangolo DHB è diviso dalla retta parallela alla base fi. Il rapporto tra eb e kh sarà dunque uguale a quello tra dh e fi, e il rapporto tra de e kf ed eh e ki, per la similitudine dei triangoli, sarà uguale al rapporto tra eb e kb. Dunque, de sta a fk come eh sta a ki, e permutando, de sta a eh come fk sta a ki9; dunque, questi eccessi sono divisi in maniera proporzionale, il che era ciò che bisognava dimostrare (cfr. figura 2).
5. Si può anche dire che, se gf è la seconda di una sola delle figure
intermedie, allora gi non sarà la prima10. La prima di queste figure sarà o maggiore o minore di gi. Sia presa inizialmente maggiore e sia essa
lm. La prolungo verso l’alto fino a n, in modo che ln sia
uguale a gf, e traccio la linea fn parallelamente alla base, per il fatto che le
due linee gf e ln
hanno la stessa lunghezza. Fra i due punti, g
e l, si possono tracciare molteplici linee
prime e seconde di figure intermedie. Se ne tracci una, e sia op la prima, e la si prolunghi fino alla seconda
della stessa figura: essa cadrà o sulla linea fn, o al di sotto o al di sopra di essa. Ma non
potrà cadere né sotto né sulla linea, poiché essa è la seconda di
una figura di superficie minore; e dunque dovrebbe essere più lunga;
e tuttavia, non può essere posta più lunga [di ln], poiché ![gf[=ln]](../../../media/sources/13/30/EOAineq_30_19.png) , è posta fra figure di superficie
minore, e sarebbe più corta, il che è impossibile, dato che le linee
seconde non vanno diminuendo nella direzione delle figure di
superficie crescente, e ciò è impossibile. Sarebbe parimenti
impossibile se si dicesse che la prima di queste figure è minore di
gi. Non potendo essere né maggiore né minore,
gi sarà essa stessa la prima, poiché tutti
gli eccessi delle seconde sulle prime sono divisi nello stessa
rapporto, il che è ciò che bisognava dimostrare.
, è posta fra figure di superficie
minore, e sarebbe più corta, il che è impossibile, dato che le linee
seconde non vanno diminuendo nella direzione delle figure di
superficie crescente, e ciò è impossibile. Sarebbe parimenti
impossibile se si dicesse che la prima di queste figure è minore di
gi. Non potendo essere né maggiore né minore,
gi sarà essa stessa la prima, poiché tutti
gli eccessi delle seconde sulle prime sono divisi nello stessa
rapporto, il che è ciò che bisognava dimostrare.
6. Questa sembra la spiegazione della vostra undicesima conclusione, da cui dipende tutta la dimostrazione della quadratura11. Infatti, hq si rapporta a qi come hr si rapporta a rb. Inoltre, di queste quattro linee in proporzione12, le prime tre sono conosciute, la prima hq è nota, poiché è la differenza tra la freccia del quadrato – o di un’altra figura intermedia – e la freccia del triangolo; qi, la seconda, è anch’essa nota, poiché è l’eccesso della prima del quadrilatero13 sulla prima del triangolo. La terza hr è anch’essa conosciuta, poiché è la freccia del triangolo. Se dunque moltiplichi hr per qi, e dividi per hq, ottieni rb, che, aggiunto alla prima linea del triangolo, ra, darà ab, la prima del cerchio, cioè il suo semidiametro cercato. Ma non vedo perché le due linee hb e bd, entro cui sono compresi tutti gli eccessi delle prime e delle seconde, non possano essere curve di ogni genere di curvatura, nel qual caso la dimostrazione non porterebbe ad alcuna conclusione14. Accadrà infatti ciò che hai detto nella decima conclusione, cioè che le prime linee delle superfici più estese saranno sempre maggiori e le seconde sempre minori15.
7. Penso che quanto detto sia sufficiente. Molti altri punti mi danno da pensare, per esempio che quelle coincidenze, o accrescimento e diminuzione delle forme, non debbano essere rappresentate mediante linee rette, come dicono i moderni; ma è una questione che riservo a un altro momento16. Ti saluto.
8. Sia data al nostro venerabile e fedele caro
maestro, l'astronomo George Peurbach
Note a piè pagina
Il termine «capacitas» è qui tradotto con ampiezza. Come negli altri scritti matematici, per rispettare al meglio lo spirito del linguaggio cusaniano, a differenza sia di J. E. Hofmann che traduce «capacitas» con «Fläche» (cfr. Hofmann e Hofmann 1980, 128) sia di J.-M. Nicolle che traduce il termine latino con «Surface» (cfr. Nicolle 1998, 49), si è preferito qui differenziare i due termini (capacitas e superficies), utilizzati entrambi da Cusano, rendendo il latino capacitas a volte con ampiezza, altre volte, a seconda del contesto, con estensione o superficie.
La prima linea designa il semidiametro del cerchio inscritto al poligono in questione; la seconda linea designa il semidiametro del cerchio circoscritto al poligono.
Sebbene sulla data di composizione di questa lettera non si abbiano notizione certe e documentate, è molto probabile che essa sia stata scritta nell’inverno, tra il 1453 e il 1454. I primi editori hanno creduto che si trattasse di un testo di Cusano, ma in realtà si tratta di una critica di Toscanelli alla proposizione fondamentale de I complementi matematici, ossia la proposizione 12, come emerge da due note a margine di Cu scritte dallo stesso Cusano. Essa deve essere letta fra il libro I e il libro II de I complementi matematici. Dall’ultima frase del testo si evince che il testo doveva essere dato a Peurbach, e da questi a Regiomontano. Nel 1533 fu pubblicato in n da Johannes Schöner.
Dalla relazione 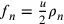 (cfr. Cusanus 2010i, 1) si deduce la proporzionalità tra
(cfr. Cusanus 2010i, 1) si deduce la proporzionalità tra 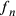 e
e 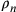 , e in particolare
tra
, e in particolare
tra 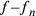 e
e
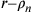 . Se si
chiama n il numero dei lati del poligono,
f la sua superficie,
. Se si
chiama n il numero dei lati del poligono,
f la sua superficie, 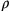 il semidiametro del
suo cerchio inscritto (la linea «prima»), r il semidiametro del suo cerchio
circoscritto (la linea «seconda»), allora:
il semidiametro del
suo cerchio inscritto (la linea «prima»), r il semidiametro del suo cerchio
circoscritto (la linea «seconda»), allora:
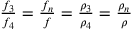 .
Da ciò si evince:
.
Da ciò si evince:  .
.
Per tradizione si designano le superfici rettangolari attraverso la loro diagonale. Così, nella figura, ad designa la superficie del rettangolo AGDC.
Cfr. Euclide 2007, VI, 1: «I triangoli e i parallelogrammi che sono sotto la stessa altezza sono l’uno proporzionale all’altro come le loro basi».
Toscanelli pone 4 proporzioni:
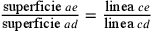 ;
;
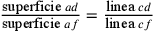 ;
;
 ;
; 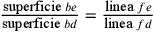 .
.
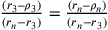 .
.
Si tratta di dimostrare che: 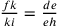 . Posto
. Posto
 e
e 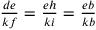 ,
si ha:
,
si ha: 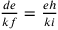 ; permutando,
si ottiene
; permutando,
si ottiene 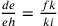 .
.
Toscanelli inizia qui una dimostrazione indiretta per mostrare che gi è necessariamente la linea «prima», sempre continuando a presupporre la proporzionalità sostenuta da Cusano e rifacendosi a I complementi matematici. Cfr. Cusanus 2010i, 11.
Cfr. Cusanus 2010i, 22.
Considerando i due triangoli rettangoli BHR e IHQ, si ha:
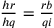 , da cui si
deduce
, da cui si
deduce 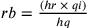 .
.
Del quadrilatero, se si prende come esempio di figura intermedia un quadrato.
Toscanelli avanza qui la sua obiezione: le linee db e hb sono
effettivamente linee rette? o meglio, saranno esse curve
incurvate l’una verso l’altra? La proposizione sostenuta da
Cusano è la stessa qualunque sia n, il
numero dei lati del poligono isoperimetrico? Come mostra Hofmann e Hofmann 1980, nota 5, 234, se ad esempio poniamo il raggio isoperimetrico uguale
a r, si ha 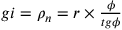 ;
;
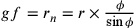 ;
;
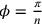 . Attribuendo al punto
g un’ascissa proporzionale a
. Attribuendo al punto
g un’ascissa proporzionale a  ;
è chiaro che hb è rappresentata da una
retta, cosa che non accade con db.
Ponendo ad esempio
;
è chiaro che hb è rappresentata da una
retta, cosa che non accade con db.
Ponendo ad esempio 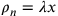 ;
; 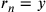 (dove per
(dove per 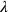 si intende un
fattore di proporzionalità positivo costante) si ha
si intende un
fattore di proporzionalità positivo costante) si ha  .
Qui
.
Qui 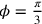 corrisponde al valore
iniziale
corrisponde al valore
iniziale 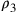 ,
e
,
e 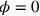 corrisponde al valore finale r. Il
rapporto
corrisponde al valore finale r. Il
rapporto  oscilla nel campo
oscilla nel campo 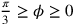 tra i valori
0, 558 e 0,500. Se ora determiniamo
tra i valori
0, 558 e 0,500. Se ora determiniamo 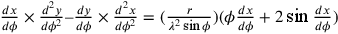 ci
accorgiamo che la curva tra b e d è senza punti di flessione e devia dalla
corda db soltanto un po’ verso il basso.
Il riferimento all’obiezione riportato nella nota a margine dei
Complementi matematici scosse Cusano al
punto che rinunciò alla proposizione e decise di scrivere il
secondo libro.
ci
accorgiamo che la curva tra b e d è senza punti di flessione e devia dalla
corda db soltanto un po’ verso il basso.
Il riferimento all’obiezione riportato nella nota a margine dei
Complementi matematici scosse Cusano al
punto che rinunciò alla proposizione e decise di scrivere il
secondo libro.
Cfr. Cusanus 2010i, 21.
La teoria delle intensiones et remissiones formarum è ripresa da Oresme 1968. Cfr. Hofmann e Hofmann 1980, nota 6, 234.
Da quest’ultima frase sembra che Toscanelli abbia fatto appello all’autorità di Peurbach per esaminare la questione.


