Reverendissimo in Christo Patri, domino
Antonio
1. Sollicita est nobilis mens vestra, P. reverendissime, ut videat etiam hebetiorum speculationes, et a me alias novi aliquid deposcebat. Et quoniam me a palatio pes morbidus excusavit, biduo domi sedens mathematicam perfectionem, quam mitto, conscripsi, quatenus virtutem coincidentiarum experimento ignotorum hactenus in theologicis inquisitionibus commendarem. Omne enim scibile mathematicum ex ipsa, uti exempla quaedam subiungo, attingitur in his obscuris semper quam avide quaesitis, quae nulli hactenus patuerunt. Quomodo autem mathematica nos ducant ad penitus absoluta divina et aeterna, melius me novit doctissima paternitas vestra, qui estis theologorum vertex. Quandam etiam meae considerationis circa speculum et aenigma parvam alligavi scripturam: ubi si R. P. V. modicum versari dignabitur, subito videbit, si visum mentis recte in rerum conieci principium, haec talia, quae etiam a doctissimis scribi timebantur. Quoniam minus apte panduntur quam contemplentur, non erubui P. V. mittere, cuius iudicio dirigi opto, sciens me non alieno, sed patri, qui me amat, communicare secreta, quae mihi pretiosiora fortassis videntur quam existant: correcturus aestimationem secundum vestram sententiam, quam istis libellis supplex ascribi deposco.
2. Intentio est ex oppositorum coincidentia mathematicam venari perfectionem. Et quia perfectio illa plerumque consistit in rectae curvaeque quantitatis adaequatione, propono habitudinem duarum rectarum linearum se ut chorda ad suum arcum habentium investigare, sciens illa habita me medium habere curvam quantitatem cum recta adaequandi; et quoniam ad has inveniendas necesse est me alicuius chordae ad arcum habitudinem scire, ut ex illa cognita pergere queam ad artem. Sed quomodo est possibile me cuiusquam datae chordae ad arcum habitudinem scire, cum inter illas quantitates adeo contrarias forte non cadat numerabilis habitudo?
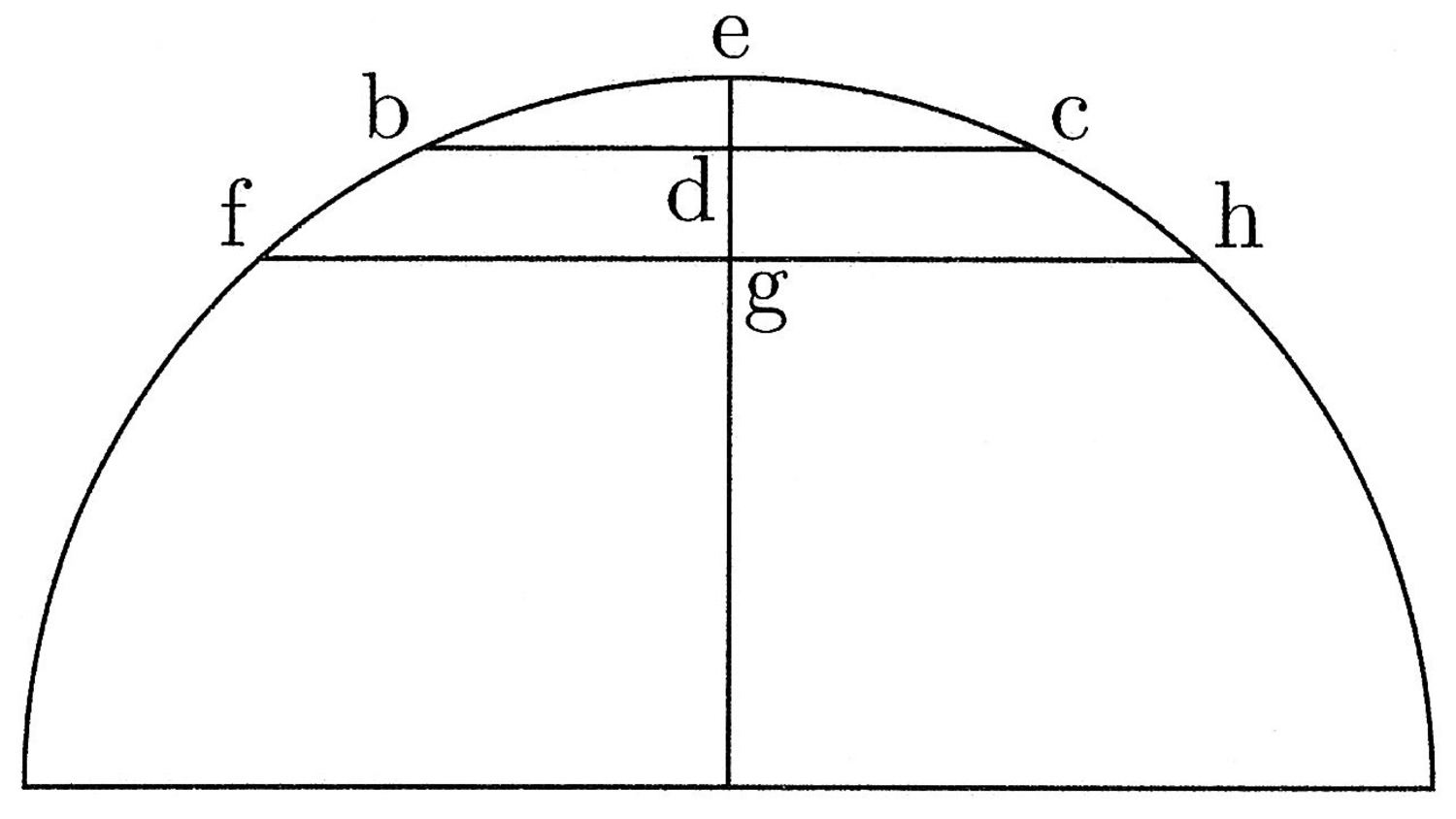
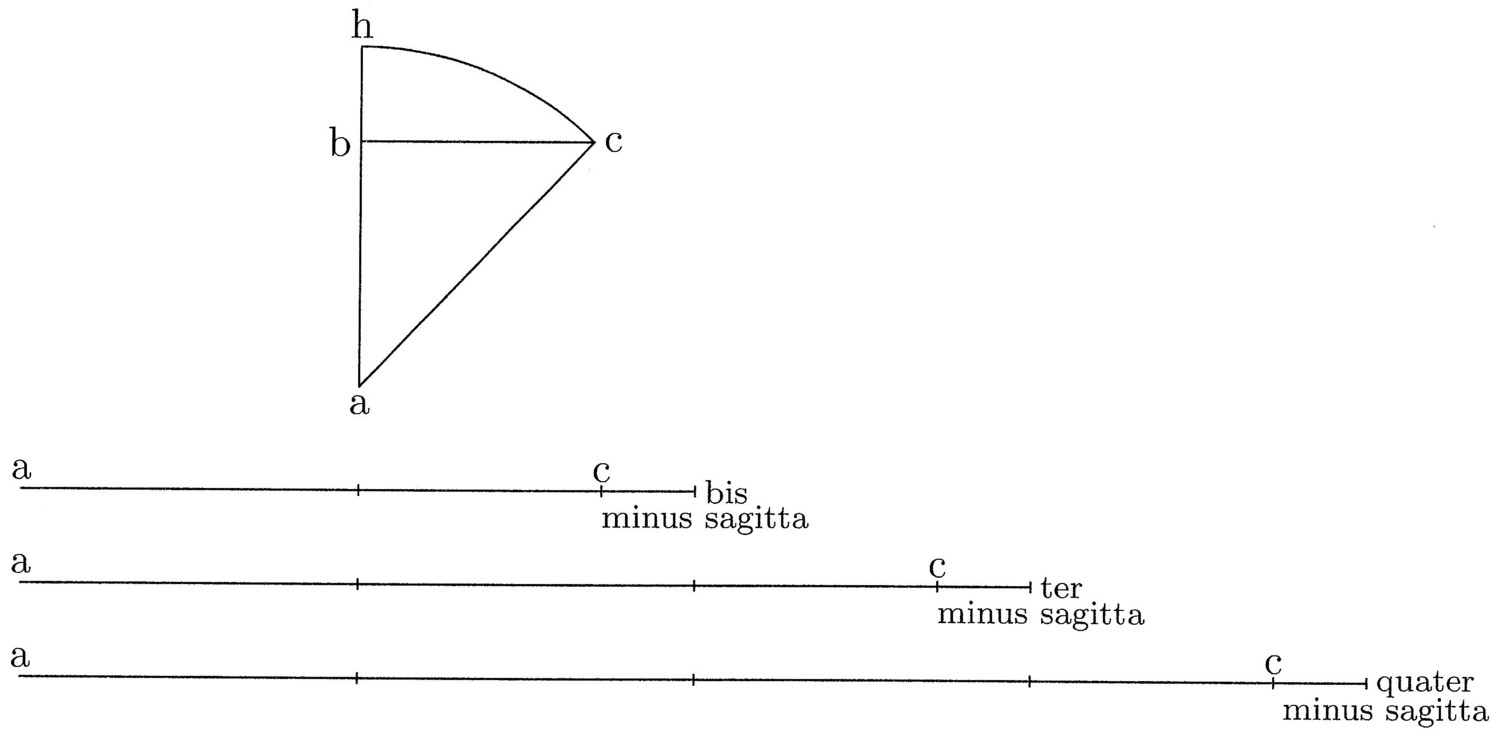
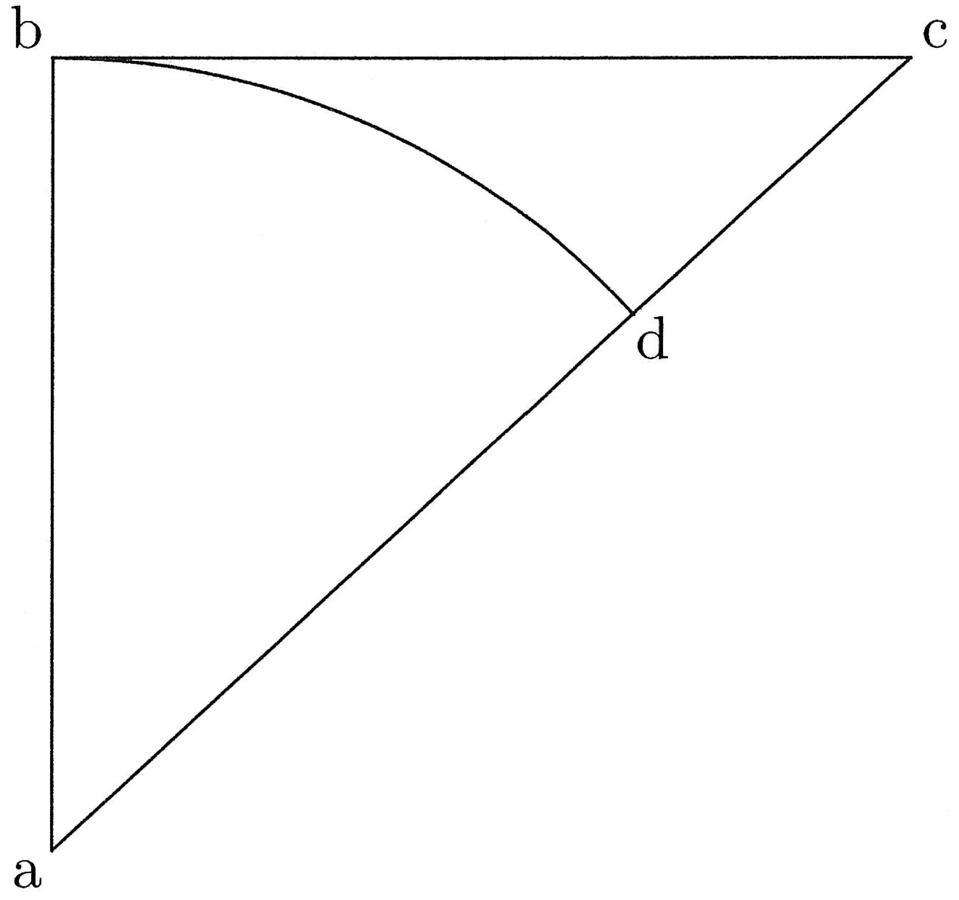
3. Necesse erit igitur me recurrere ad visum intellectualem, qui videt minimam, sed non assignabilem chordam cum minimo arcu coincidere. Nam quanto chorda minor, tanto sagitta adhuc minor, ut de sagitta chordae bc est minor quam ge sagitta chordae fh, quia bc minor fh, et ita consequenter (cfr. figura 1).
4. Minima igitur chorda, qua minor dari non posset, si signabilis foret, non haberet sagittam, et ita etiam non foret minor arcu suo. Coincideret igitur ibi chorda et arcus, si ad minimam quantitatem in talibus deveniretur. Hoc videt bene intellectus necessarium, licet sciat nec arcum nec chordam, cum sint quantitates, esse simpliciter minimas in actu et posse, cum continuum sit semper divisibile. Ad hauriendum autem scientiam habitudinis respicio ad intellectualem visionem et dico me videre, ubi est chordae et arcus aequalitas, scilicet in simpliciter minimo utriusque. Ex hac visa aequalitate pergo ad inquirendum intentum medio trianguli orthogonii, et hoc per propositionem, quae sequitur.
Propositio
5. Si orthogonii latus, quo non est maius, ponitur linea prima et semidiameter circuli, et latus, quo non est minus, secunda linea et semichorda, et reliquum latus tertia linea: quae erit semiarcus ad semichordam habitudo, illa erit lineae aequalis tribus primis lineis ad lineam aequalem duabus primis cum tertia.
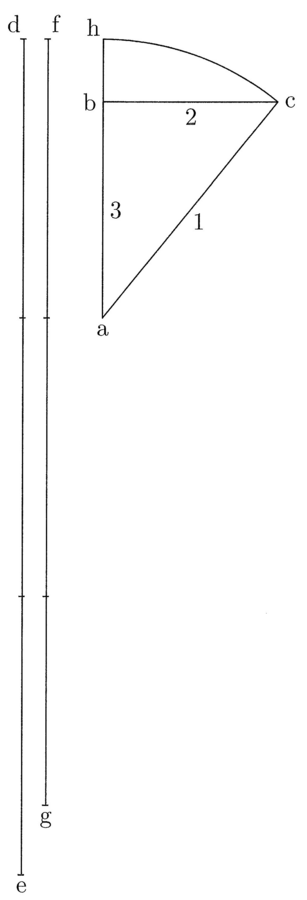
Ut si orthogonius est abc et ac latus, quo non est maius, prima linea et semidiameter circuli, et bc latus, quo non est minus, secunda linea et semichorda, et ab latus tertia linea, et hc semiarcus, et de aequalis tribus lineis ac, et fg aequalis duabus ac cum una ab. Dico, quod quae est habitudo hc ad bc illa est de ad fg (cfr. figura 2).
Explanatio propositionis
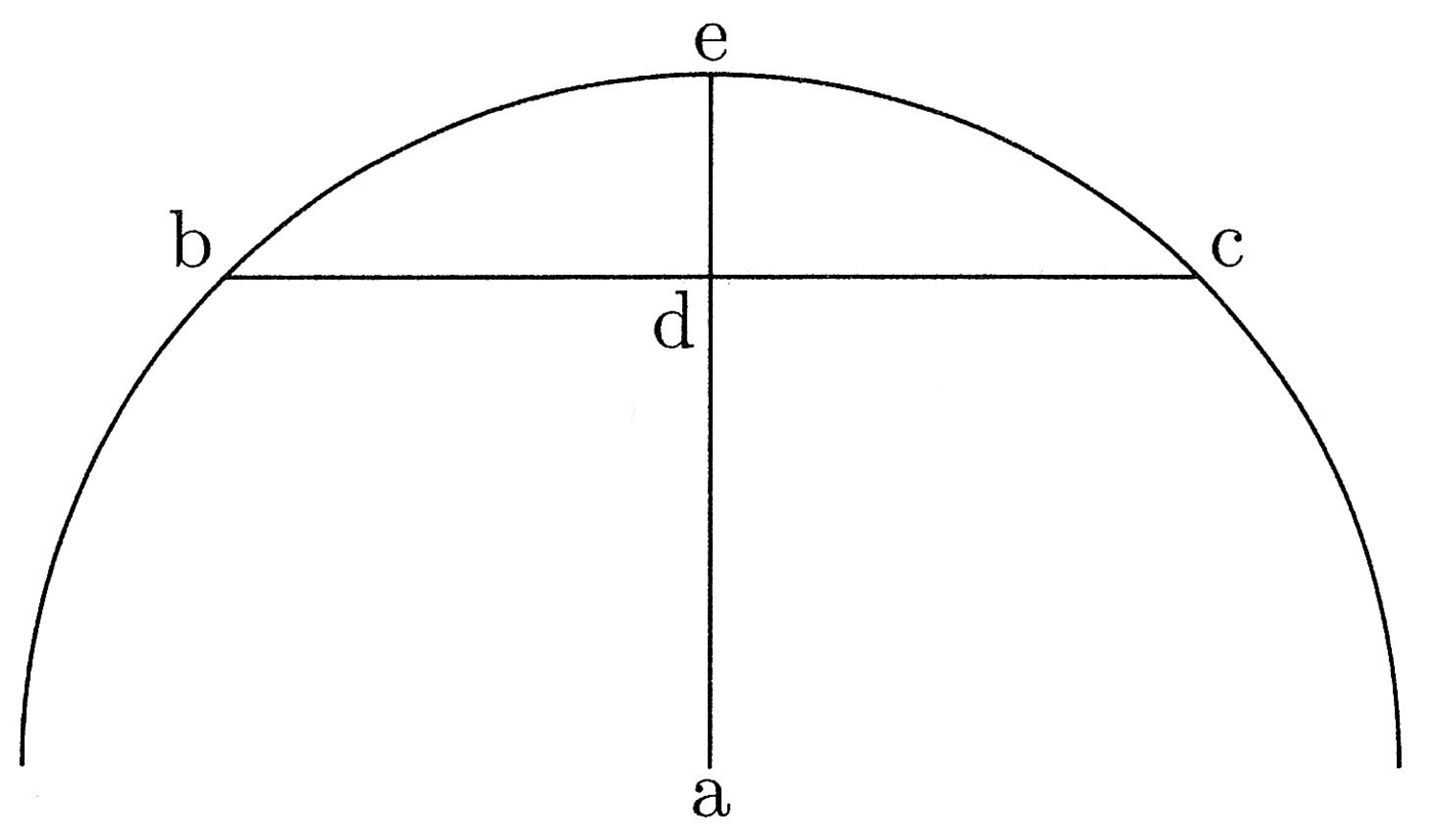
6. Orthogonius est tanto minor, quanto prima linea tertiam minus excedit. Si igitur posset dari minimus orthogonius, prima tertiam non excederet, et quia secunda linea foret minima, tunc cum ponatur semichorda, ipsa non foret minor semiarcu secundum praemissa.
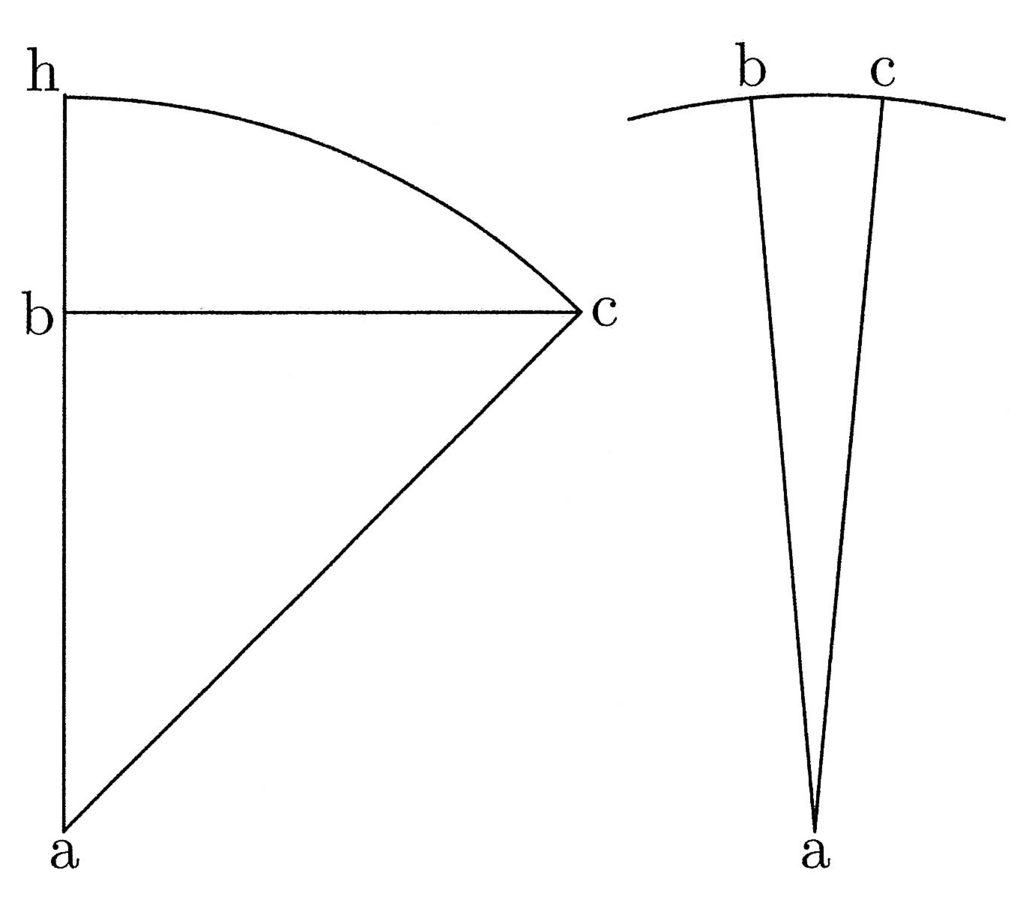
Maximus autem orthogonius est, quando prima tertiam excedit maxime. Et hoc erit, quando tertia erit ut secunda, qua non est minor, et tunc secunda est semichorda quadrantis. Et sit ille orthogonius abc (cfr. figura 3).
Dico possibile esse, quod aliqua linea addatur ac et eadem addatur ab, et maior se habeat ad minorem ut hc semiarcus ad bc semichordam. Hanc lineam posse dari, quae addatur ac et ab, ut praefertur, certum relinquo, cum possit linea aliqua dari, quae addita ad ac et ab efficiat lineas maioris habitudinis quam est habitudo hc semiarcus ad bc, et possit dari linea, quae addita efficiat lineas minoris habitudinis quam hc ad bc, et hoc certum. Igitur et dari posse eam, quae addita efficiat lineas nec maioris nec minoris habitudinis quam hc ad bc, manifestum, cum non repugnet lineas rectas se habere ut chorda ad arcum, sive chorda sit arcui commensurabilis sive incommensurabilis.
7. Constat autem, quod qualiscumque illa linea fuerit, si in minimo orthogonio etiam ad ac et ab additur, propositio verificatur, cum ibi prima et tertia sic sint eadem sicut semiarcus et semichorda. Quare qualiscumque illa linea fuerit, quae additur, propositio vera manet. Et quia sic est, quod linea, quae additur in maximo orthogonio, est etiam illa, quae additur in minimo, igitur et in omnibus orthogoniis intermediis eadem manebit.
Et haec est radix huius scientiae, ex qua sequitur, quod si reperio lineam, quam addo in orthogonio, cuius bc est semichorda quadrantis, et quam etiam addo, ubi bc est semichorda hexagoni, et quae hinc inde reperio, tenent habitudinem ad invicem sicut arcus scilicet ut tria ad duo. Patet me lineam addendam in omnibus invenisse, et hoc est indubitatum.
8. Hoc faciliter sic patet. Possibile est lineam aequalem tertiae adiunctis duabus primis orthogonii ad lineam ex prima adiunctis quattuor se|cundis in aliquo loco se habere ut semichorda ad semiarcum. Hoc certum. Nam datur, ubi in minus, ut in maioribus orthogoniis, et ubi in plus, ut in minoribus, ut de se patet: datur igitur in aliquo loco, ubi nec in plus nec in minus. Ubicumque hoc fuerit, oportet per praemissa, quod sit eadem linea, quae additur ad tertiam et quae additur ad primam. Sed quae additur ad tertiam, est prima bis. Igitur quae additur ad primam, erit similiter ut prima bis, et ita erit, ubi secunda erit medietas primae, scilicet semichorda arcus hexagoni. Quare addenda est diameter.
9. Sic poteris et aliter idipsum videre. Puta datur, ubi prima bis cum secunda bis se habet ad primam ter sicut semichorda ad semiarcum, arguendo ut ante: Sed cum una debet esse linea addita ad tertiam et primam, et ad primam additur prima bis, et prima bis additur ad secundam bis, erit secunda bis ut tertia, et quae additur, erit diameter. Et consimilia facere poteris argumenta, quot placuerint.
Sed propositio dicit lineam addendam ad ac et ab esse diametrum sive duplam ad ac, quod idem est. Poteris hoc experiri ex iam dicto, scilicet an in omnibus proportionabiliter idem eveniat.
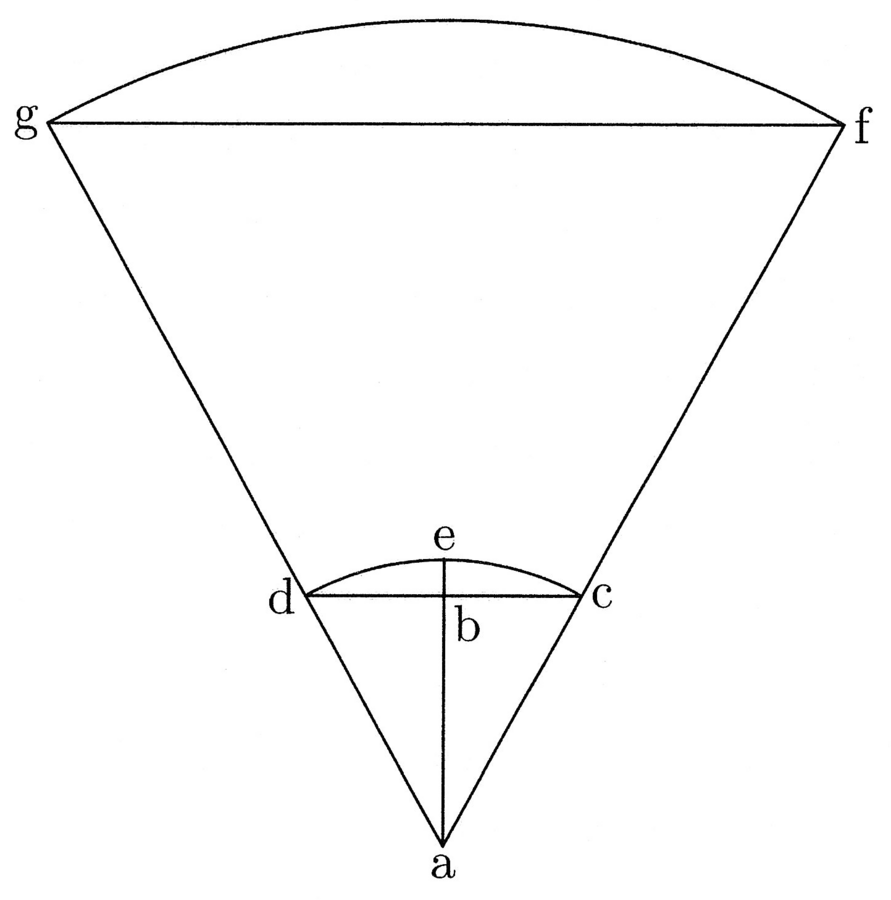
10. Sed ut tu videas utique sic esse, ut habet propositio, sumas duplicem orthogonium, ut est abc et abd, et describe arcum dc continuando etiam ab ad arcum, et sit be sagitta (cfr. figura 4). Dico possibile esse aliquem triangulum ex orthogoniis compositum sic se habere, quod si ac et ad continuantur in infinitum, et chorda aliqua, quae sit aequedistans ad dc, fiat aequalis ad, ac et ab, ut gf: quod tunc arcus, cuius gf chorda, excedat chordam in be sagitta, scilicet in tantum, quantum ae excedit ab.
11. Hoc quidem in aliquo loco possibile esse negari nequit, puta ubi tres semidiametri minus sagitta sunt triplae ad chordam. Tamen sive ibi sive alibi sit, non variat; sufficit, quod in aliquo loco est possibile.
Et hoc si volueris ut ante probare, poteris: quia datur, ubi excessus est in minus quam sagitta, et datur, ubi in plus; et haec certa relinquo. Datur igitur, ubi nec in plus nec in minus modo praemisso. Ubicumque autem hoc fuerit, patet ac, ad cum ab se habere ad ac ter sicut chorda ad arcum. Patet, quia ac ter cum ac ter minus sagitta in aliquo loco aequentur chordae et arcui simul, et hoc certum, aut igitur ibi, ubi arcus excedit chordam in dicta sagitta. Et habetur propositum aut citra vel ultra. Si citra: tunc, cum arcus chordam minus excedat quam in dicta sagitta, ideo chorda erit maior quam ubi arcus excedit chordam in dicta sagitta, quod est impossibile, scilicet minorem arcum habere maiorem chordam. Sic, si diceretur quod ultra: oporteret maiorem arcum habere minorem chordam. Quare linea ad ac et ab addenda est ac bis seu diameter circuli, et haec est veritas.
12. Cur autem sit diameter eiusdem circuli, forte dici poterit, quod cum linea addenda sit alicuius circuli diameter. Non dicetur, quod sit maioris circuli diameter, quia tunc non haberet veritatem in maximo circulo, quo actu non est maior. Nec potest dici, quod sit minoris, quia in minimo circulo actu non haberet veritatem; et ita in nullo, cum id, quod de circulo ut de circulo dicitur, omnibus convenire necesse sit. Et si omnibus non convenit, tunc nulli: sive tamen illa sive alia sit ratio, non refert. Sic patet propositionis intellectus.
13. Adiciam aliam eiusdem lineae addendae ostensionem (cfr. figura 5). Dabilis est linea, cuius ac est pars aliquota, quae ad lineam, quam excedit in quantitate, qua ac excedit ab, se habet in maiori habitudine quam hc ad bc: uti est linea ad ac dupla. Et dabilis est linea, cuius ac est pars aliquota, quae ad lineam, quam excedit in quantitate, qua ac excedit ab, habet minorem habitudinem quam hc ad bc: uti est quadrupla ad ac. Et haec verissima. Quare dabilis est linea, cuius ac est pars aliquota, quae ad lineam, quam excedit in quantitate, qua ac excedit ab, se habet in habitudine qua hc ad bc. Et haec, cum sit necessario maior dupla et minor quadrupla, erit tripla ad ac. Quare addenda ad ac erit dupla ad ipsam seu diameter.
14. Ut autem in numeris tu videas illa vera, quae
de dupla et quadrupla ad ac dixi, ponas
secundum propinquitatem Archimedis
15. Causa autem, cur procedit argumentatio, quod linea, quae quaeritur, debet esse pars aliquota ac, est ista: Quia cum debeat esse una in omnibus orthogoniis, tunc necesse est, quod respiciat ac, quae etiam est una in omnibus, et non ab vel bc, quae semper variantur. Possent alii innumerabiles modi ostensionis propositionis adduci, sed isti sunt fundamentales et sufficientes.
16. Multa hic propalantur abscondita, quoniam
vides, quomodo id, quod verificatur de maximo et minimo,
verificatur de mediis, et quod ille, qui videt maximum coincidere
cum minimo, quoniam maximum pariter et minimum, ille in ipso videt
omnia. Et praxim habes venandi scientiam commensurationis
contrariorum, quae incommensurabilia videntur. Haec mihi magna et
prius intacta videntur. Archimedes
Corollarium
17. Illa est habitudo trium semidiametrorum ad tres semidiametros minus sagitta chordae quadrantis et minoris, quae est cuiuslibet arcus ad suam chordam (cfr. figura 6).
Ut si bc sit chorda quadrantis vel minoris arcus, et de a centro per d medium bc ad e circumferentiam sector ducatur. Illa est habitudo ae ter sumpta ad ae bis sumpta cum ad, quae arcus ad bc chordam. Cum autem dicitur de chorda quadrantis et minoris, patet ideo, quod in maiori chorda latus orthogonii, quo non est minus, non possit esse semichorda, quod tamen requiritur. Et clare patet corollarium ex praemissis.
Corollarium
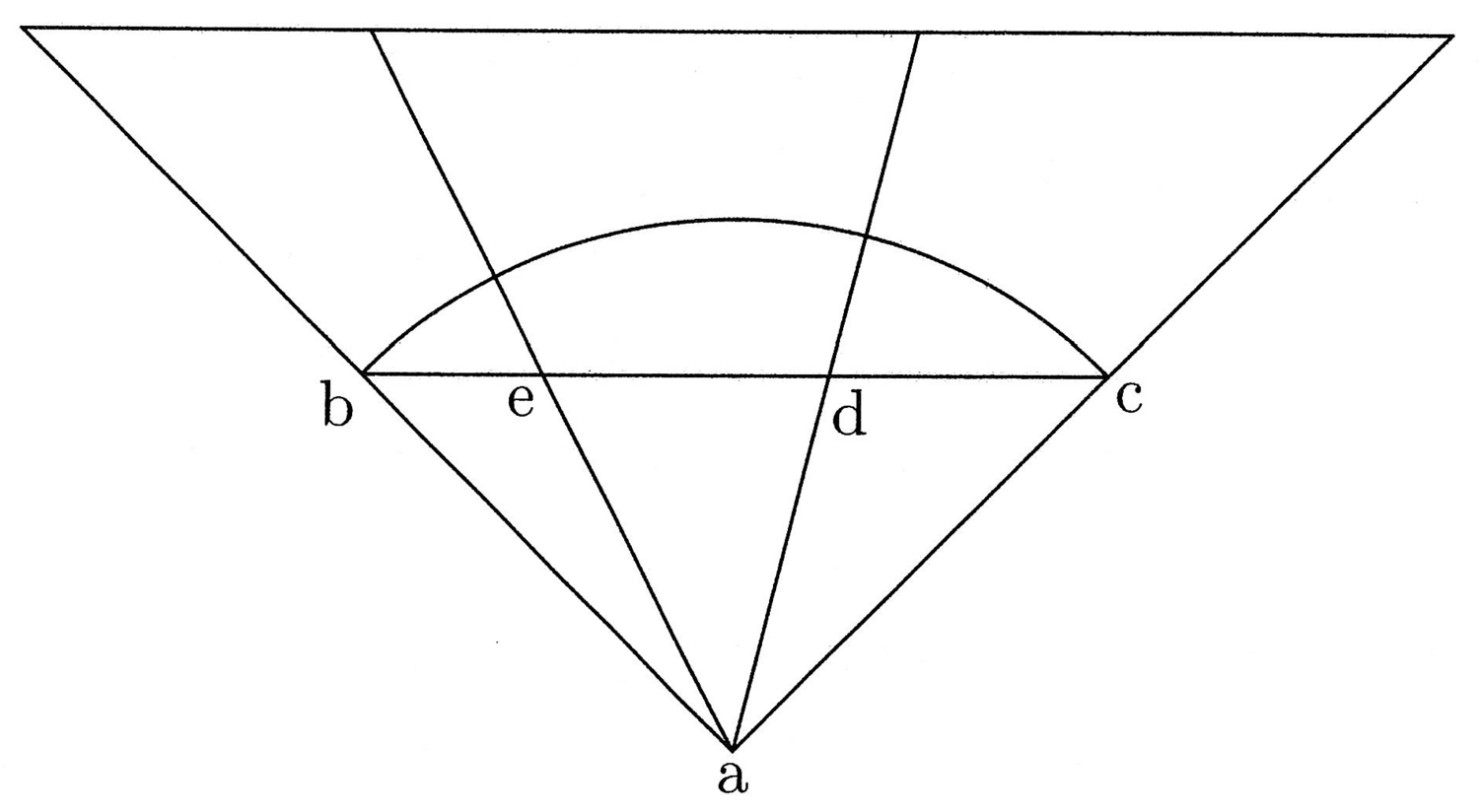
18. Datum arcum in rectam resolvere.
Arcus enim, si est quadrans et minor, ipsum sic recipito; si maior, partem eius recipito aliquotam, quae sit quadrans aut minor. Et sit bc arcus quadrantis in rectam resolvendus (cfr. figura 7). Trahe de a centro lineas per b et c in infinitum et aliam ad medium chordae, scilicet ad, et inter infinitas lineas unam aequedistantem ad bc chordam describe, quae sit aequalis ab, ad et ac, et sit ef aequalis illis. In ef signa ab, et sit fg ut ab, et trahe ag lineam notando, ubi chordam bc secat, ponendo h litteram. Dico hc esse tertiam arcus. Tripla igitur hc, et redegisti arcum in rectam. Vel trahe aequedistantem ad bc versus centrum, quae sit ikl, ita quod ai, ak et al simul aequentur bc chordae, et ai erit tertia arcus. Haec omnia de se patent.
Corollarium
19. Datam rectam in arcum resolvere.
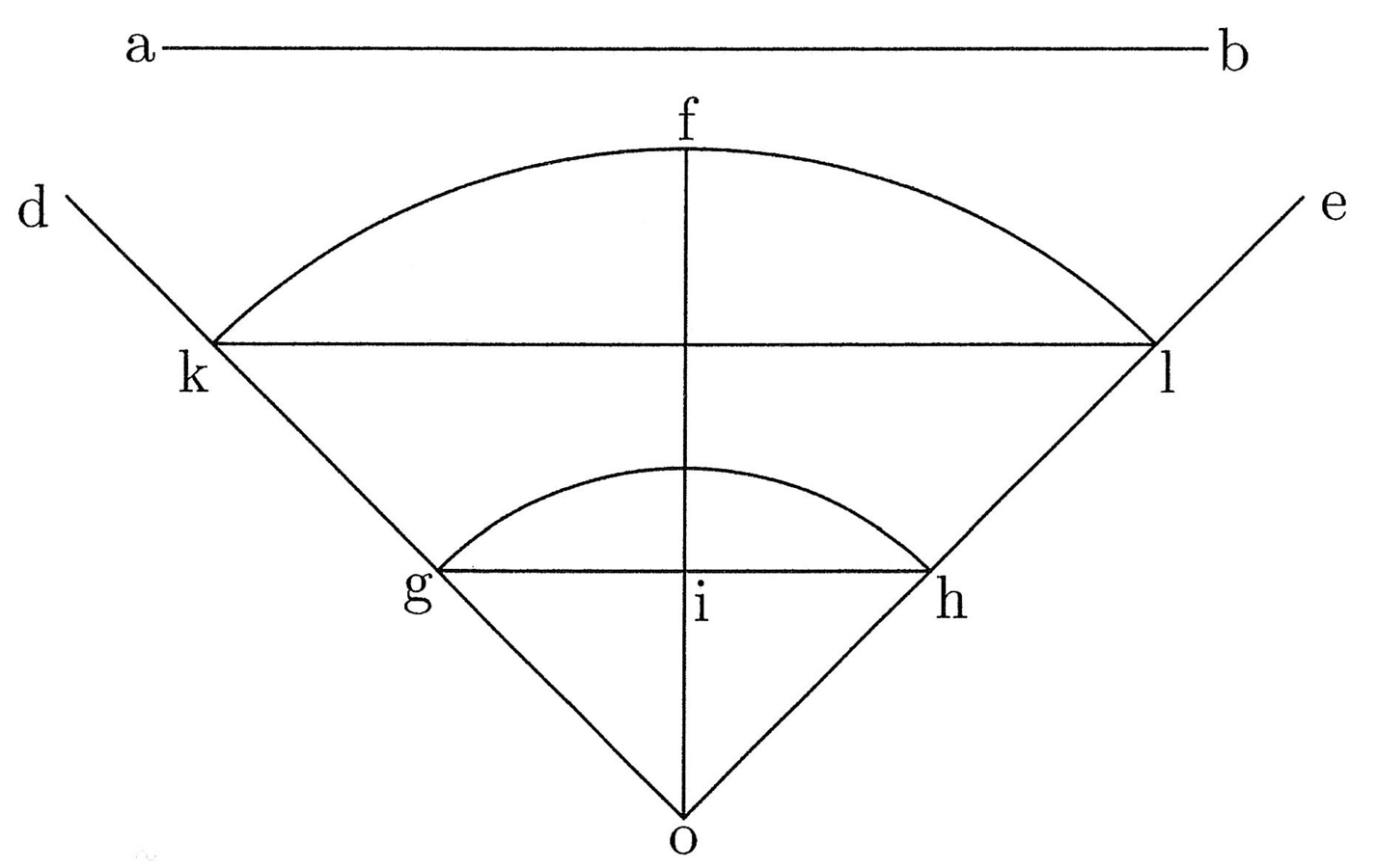
Sit ab recta, quam si vis in quadrantem alicuius circuli resolvere, fac de o centro lineas, quae rectum angulum constituunt, exire indefinitae quantitatis, quae sint od et oe, et aliam fac transire e medio anguli, scilicet of, et tertiam partem ab lineae resolvendae signa in od et oe, et sit og ut tertia ab, similiter et oh, trahendo gih (cfr. figura 8). Et consequenter trahe aequedistantem ad gih aequalem og, oi et oh, et sit kl illis aequalis, et describe quadrantem, cuius kl chorda, quia ille est, cui ab aequatur. Et si in alium arcum resolvere volueris, qui fuerit minor quadrante, eodem modo facito; si maior, recipito partem aliquotam. Puta vis in circulum reducere, recipito quartam partem rectae et resolve in quadrantem, et totum in circulum reduxisti.
20. Si vero datam rectam in arcum dati circuli resolvere volueris, vel cum tota vel parte aliquota eius, procede modo quo supra, angulum od et oe variando, quousque attingas chordam, quae og, oi et oh aequetur.
Corollarium
21. Datum arcum unius circuli in arcum alterius circuli resolvere.
Hoc fit resolvendo ipsum primo in rectam, deinde rectam in arcum alterius modo praemisso.
Corollarium
22. Angulos, qui se habent ut datae lineae, assignare.
Hoc fit in resolvendo lineas in arcus eiusdem circuli et a centro sectores ad fines talium arcuum trahendo.
Corollarium
23. Quae est habitudo semidiametri ad semidiametrum minus sagitta, illa est tertiae arcus ad excessum, quo chorda duas tertias arcus sui excedit (cfr. figura 9). Puta sit bc chorda quadrantis, et in illa per praemissa signasti duas tertias arcus, scilicet cd et de. Dico quod habitudo de tertiae arcus ad eb excessum, quo chorda duas tertias excedit, est sicut semidiameter ad semidiametrum minus sagitta. Patet corollarium ex praemissis. Et habet veritatem in maximo et minimo orthogonio et in omnibus mediis.
Corollarium
24. Chordam dati arcus partis aliquotae semicirculi assignare.
Puta tu vis ex scientia chordae quadrantis scire chordam arcus, qui est medietatis quadrantis. Tu nosti partem chordae quadrantis, quae aequatur tertiae arcus, et recipis medietatem illius et addis ei similem, et quaeris excessum, qui se habeat ad unam tertiam sicut semidiameter minus sagitta ad semidiametrum.
25. Subiciam adhuc curiosa corollaria.
Si tres semidiametri minus sagitta erunt triplae ad chordam, erit arcus ut semidiameter.
Si erunt duplae ad chordam, arcus se habebit in proportione sesquialtera ad semidiametrum.
Tres semidiametri sunt medium proportionale inter tres semidiametros minus sagitta et semicirculum.
Si tres semidiametri minus sagitta fuerint multiplices ad chordam, sic erunt et tres semidiametri minus sagitta ad chordam medietatis arcus et cuiuslibet partis aliquotae proportionabiliter.
Tria latera trigoni aequilateri erunt ut circumferentia circuli illius, cuius diameter est tertia pars duorum laterum et lineae rectae de uno latere ad medium lateris sibi oppositi.
26. Si a centro tres lineae ducantur, una per principium chordae quadrantis aut minoris arcus, alia per medium, tertia per finem, quae in linea aequedistanti chordae terminentur, ita quod illarum trium linearum habitudo ad chordam sit ut circumferentiae ad arcum, tunc linea ducta per principium chordae triplicata est aequalis circumferentiae.
Arcus aequalis tribus quartis diametri excedit chordam suam in medietate sagittae.
Diameter circuli est aequalis duabus tertiis laterum trigoni isoperimetri et semidiametro circuli eidem trigono inscripti.
Excessus semicirculi super duas chordas quadrantis est ut excessus diametri quadrati aequalis tertiae parti eius super suam costam.
Habitudo trium diametrorum circuli ad suam circumferentiam est ut 14 cum radice de 36 et 3/4 ad 21.
Scientia chordarum nunc exstat perfecte adinventa.
Scientia quadraturae circuli suum finem sortita existit. Secundum datarum linearum habitudinem sive commensurabilium sive incommensurabilium lineas et superficies rectas et curvas atque corpora dari docet haec ars perfectissima.
Adhuc ex coincidentia minimae contingentiae et minimi arcus propositionem recipio, quae est talis:
Propositio
27. Si ponitur secundum latus orthogonii semidiameter circuli et tertium linea contingens circulum vel e converso, et descriptus fuerit circulus, quae erit habitudo contingentis ad arcum, qui cadit intra orthogonium, illa et rectae atque curvae superficierum (cfr. figura 10).
Ut si orthogonius fuerit abc et bc contingens et ab semidiameter circulo descripto, cuius bd portio cadit intra orthogonium, quae est bc ad bd, illa abc rectae superficiei ad abd curvam superficiem.
Probatio huius est: Quia cum sic sit in minimo, si dari posset, igitur et in omnibus, cum non referat, utrum orthogonius sit maximus vel non.
28. Datam superficiem ex arcu et sectoribus constitutam in orthogonium resolvere.
Ut sit abc, resolvatur bd arcus in rectam, quae sit bc, et claudatur orthogonius per ac. Et ita habes, sive bc sit ad circumferentiam proportionabilis sive non, quomodo in rectam superficiem redigatur. Et habes, quomodo circulum in orthogonium resolvis et demum in quadratum seu aliam figuram.
29. Datam superficiem rectam in portionem circularem resolvere.
Ex praemissis patet, quod si est orthogonius, quomodo hoc fiat; si non est, redigatur in orthogonium.
Abscisiones ex chorda et arcu in rectas aut circulares resolvere, de se patet.
30. Abscisionum sphaerae habitudo curvae superficiei ad rectam basis est ut linea de cenit ad centrum basis cum semidiametro basis ad ipsam semidiametrum.
Patet, quia in minima abscisione, ubi recta superficies coincidit cum curva et cenit cum centro, ita est; ideo in omnibus.
Curva superficies medietatis sphaerae est dupla ad rectam circuli basis.
Datam curvam sphaerae superficiem in rectam resolvere, circularem et rectilinealem.
Sphaeram in cubum et cubum in sphaeram resolvere.
Simili modo in aliis curvis superficiebus ad minima respiciendo habitudines elice. Et quidquid scibile est humanitus in mathematicis, mea sententia hac via reperietur.
Deo laus.