1. Affermi di essere circondato da diversi studiosi che scrivono sulla quadratura del cerchio, e mi solleciti, ora che godo della necessaria calma, a fornirti un’esposizione soddisfacente di ciò che si può sapere su questo argomento. Apprendi ciò che penso mediante la proposizione che segue. Tuttavia sappi che, per te, ho trattato l’argomento in modo che tu, mediante la via dell’assimilazione1, una volta messi da parte gli studi matematici, possa dedicarti più facilmente alla teologia2.
Proposizione
2. Se si può dare una circonferenza di cerchio uguale3 al perimetro di un dato triangolo, allora il semidiametro di questo cerchio supera della sua quinta parte la linea tracciata dal centro del triangolo al punto del lato che dista dall’angolo un quarto del lato4.
3. Ci sono coloro che ammettono la quadratura del cerchio. Essi devono necessariamente sostenere che le circonferenze dei cerchi possono essere uguali ai perimetri dei poligoni5, poiché il cerchio è uguale al rettangolo6, il cui lato minore è il semidiametro del cerchio e il lato maggiore è la semicirconferenza7. Allorché dunque si rendesse il quadrato uguale al cerchio in tale rettangolo, allora si avrebbe la linea retta uguale alla linea curva. Da ciò si arriverebbe all’uguaglianza tra la circonferenza del cerchio e il perimetro del poligono, come è evidente da sé.
4. Queste persone ammettono anche l’argomento seguente, senza il quale essi non arriverebbero a nulla, e cioè che: dove si può dare un maggiore e un minore, si può altresì dare un uguale. Poiché si può dare un quadrato maggiore di un cerchio – come è quello circoscritto – e uno minore – come è quello inscritto –, allora se ne può dare anche uno uguale, che non sarà né circoscritto, né inscritto, ma inscritto e circoscritto allo stesso tempo. Lo stesso argomento essi ammettono per le circonferenze: poiché si può dare una circonferenza di cerchio maggiore del perimetro di un triangolo – come è la circonferenza del cerchio circoscritto al triangolo –, e una minore del perimetro del triangolo – come è la circonferenza del cerchio inscritto –, si può dare anche una circonferenza uguale al perimetro di un triangolo, e questo cerchio non è né circoscritto né inscritto, ma circoscritto e inscritto allo stesso tempo.
5. Ci sono anche coloro che negano la quadratura del cerchio, e questi negano tutto ciò che è stato ora detto. Essi affermano infatti che questo argomento – dove si può dare un maggiore e un minore si può dare un uguale – non vale in matematica: infatti, si può dare un angolo di incidenza maggiore dell’angolo retto e uno minore dell’angolo retto8 e tuttavia mai un angolo uguale9. Dunque, questo argomento non vale nelle grandezze incommensurabili. Se infatti si desse un angolo di incidenza maggiore di una parte aliquota10 dell’angolo retto e minore di un parte aliquota dell’angolo retto, allora si darebbe anche un [angolo] uguale. Ma, siccome l’angolo di incidenza non ha proporzionalità11 con l’angolo retto, esso non può essere maggiore o minore di una parte aliquota dell’angolo retto, e dunque mai uguale12. E poiché nessuna proporzionalità può esistere fra una superficie circolare e una superficie rettilinea13, così come non può esistere fra l’angolo di incidenza e l’angolo retto, allora anche qui l’argomento non è valido14.
6. Ciò è chiaro da quanto segue: ogni grandezza riducibile in un’altra si comporta necessariamente in modo tale che una qualunque parte dell’una possa essere parte dell’altra15, essendo il tutto nient’altro che la somma delle sue parti. Ma una lunula16, che è ricavata dal cerchio tramite una linea retta, non può essere ridotta, rispetto ai suoi angoli d’incidenza, che sono parti della sua grandezza, in una figura rettilinea: dunque, neanche rispetto alla sua totalità17. È altrettanto evidente che se un cerchio è riducibile in un quadrato, allora necessariamente le sue lunule saranno riducibili in figure rettilinee; ma poiché la prima è impossibile, allora la seconda, da cui essa deriva, deve essere altrettanto impossibile. È dunque chiaro che il semicerchio non può essere ridotto a una figura rettilinea, e di conseguenza non possono esserlo né il cerchio né alcuna sua parte18.
7. Ciascun angolo d’incidenza supera un altro o è superato da un altro di una quantità pari a un angolo rettilineo, con il quale non può avere alcuna proporzionalità. Da ciò deriva che tutte le porzioni di cerchio delimitate da linee rette non sono in alcun modo proporzionali al cerchio. E poiché la porzione maggiore è quella delimitata dal [semi]diametro, allora tutte le altre non sono ad esso proporzionali. Dunque, non può essere ricavata alcuna parte aliquota dal cerchio attraverso tali linee, perché questa parte non avrebbe alcuna proporzionalità con la porzione maggiore, cioè con il semicerchio. Ebbene, questo argomento non vale: si ricavino una lunula maggiore di un terzo del cerchio e un’altra minore di un terzo del cerchio, e dunque una uguale a un terzo del cerchio. Ne consegue che le porzioni che sono delimitate da una linea retta minore del diametro non sono in alcun modo riducibili a figure rettilinee, perché esse sono parti aliquote del cerchio, e perché ne deriverebbe la quadratura del cerchio, se esse potessero essere ridotte a figure rettilinee19.
8. Da ciò deduci che tutto ciò da cui segue la quadratura del cerchio è impossibile. Il cerchio ha dunque, per la sua singolarità, la seguente proprietà: come non è possibile ridurre un angolo di incidenza in un angolo rettilineo, allo stesso modo non è possibile ridurre un cerchio in una figura rettilinea. Come si dà un angolo rettilineo maggiore dell’angolo di incidenza di una quantità pari all’angolo di contingenza, che è una quantità divisibile solamente nel suo genere, dato che per ogni angolo di contingenza si possono dare un angolo di contingenza maggiore e uno minore, così, tuttavia, dal momento che l’angolo di contingenza è minore di ogni angolo rettilineo, si può allora dare un angolo rettilineo maggiore di un angolo di contingenza dato, che tuttavia non è maggiore di una parte aliquota dell’angolo rettilineo. Ugualmente, si può dare un angolo di incidenza minore di un angolo rettilineo dato, ossia minore di una quantità pari all’angolo di contingenza, che, tuttavia, non è una parte aliquota dell’angolo di incidenza, ma è minore di ogni parte aliquota di questo.
9. In questo modo si può dire che, dato un cerchio, si può dare un quadrato che, anche se fosse maggiore del cerchio, non lo sarebbe tuttavia di una parte aliquota di questi, cioè del quadrato. E, dato un quadrato, si può dare un cerchio minore del quadrato, che non sarà tuttavia minore di una parte aliquota del cerchio. Di conseguenza, da ciò si avrebbe che si potrebbe dare un quadrato maggiore, ma non di una parte aliquota di esso; e che, dato un qualsiasi quadrato, se ne potrebbe [sempre] dare un altro che si avvicini al cerchio in modo sempre più preciso, sebbene nessuno si avvicinerà ad esso in modo assolutamente preciso e nessuno sarà minore di esso di una parte aliquota del cerchio, e viceversa.
10. Ritengo questa posizione come la più vera. Ora, poiché i poligoni non sono grandezze dello stesso genere del cerchio, anche se si trova un solo poligono più simile, in termini di grandezza, a un cerchio dato rispetto a un altro, varrà tuttavia la regola: nelle cose che ammettono il più e il meno, non si arriva al massimo assoluto nell’essere e nella potenza. Infatti l’ampiezza20 del cerchio è ciò che è il massimo assoluto in rapporto alle ampiezze dei poligoni, che ammettono il più e il meno, e che, per questo, non raggiungono l’ampiezza del cerchio, come i numeri non raggiungono l’ampiezza dell’unità, e le molteplicità non raggiungono la potenza di ciò che è semplice.
11. I sostenitori della prima opinione credono che sia sufficiente che, dato un cerchio, si possa dare un quadrato che non sia né maggiore, né minore del cerchio. Ogni grandezza è infatti maggiore di una parte aliquota di essa o di un’altra, alla quale è rapportata. Stessa cosa, se essa fosse minore. Ma, se un dato quadrato non è maggiore o minore del cerchio della più piccola parte assegnabile del quadrato o del cerchio, allora lo definiscono come uguale. È così, infatti, che essi hanno concepito l’uguale, ossia come ciò che è uguale a un altro, che non supera un altro, né è superato da un altro, di nessuna parte aliquota, per piccola che sia. Se si concepisce in questo modo l’uguale, penso che sia vero che si possa dare una circonferenza di cerchio uguale al perimetro di un poligono dato, e viceversa. Ma se si concepisce l’uguaglianza in maniera assoluta, per quel che spetta a una grandezza, senza tenere conto delle parti aliquote, allora i secondi avranno ragione nel dire che non si può assegnare una grandezza non circolare perfettamente uguale a una grandezza circolare; e questo per la spiegazione del principio [che è alla base] della proposizione, ossia: se al perimetro dato di un triangolo, etc.21 Sia sufficiente quanto detto. Grazie a ciò puoi comprendere quanto ho scritto su questo argomento in modo diverso in alcuni altri miei libri22.
Spiegazione della proposizione
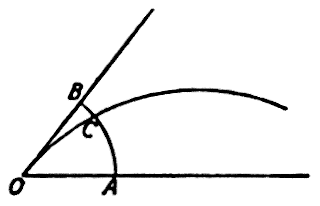
12. Per spiegare la proposizione si consideri il triangolo ABC nel quale è inscritto il cerchio EFG attorno al centro d e al quale è circoscritto il cerchio HI (cfr. figura 1). Si tracci la linea de in modo che e sia il centro fra a e b; poi si tracci la linea db. Si tracci una linea da d al centro fra e e b, e sia essa dk. Dico che dk è minore del semidiametro del cerchio isoperimetrico al triangolo di un quarto dello stesso dk.
13. Si aggiunga quindi un quarto a dk; e sia dl maggiore di dk di un quarto di dk. Dico che dl è il semidiametro del cerchio isoperimetrico al triangolo. Si descriva quindi il cerchio LMN. Dico che la circonferenza LMN è uguale al perimetro [del triangolo] ABC, cioè che [la circonferenza] LMN non è né maggiore, né minore della più piccola parte aliquota, qualunque essa sia, del perimetro [del triangolo] ABC.
14. Per dimostrarlo procedo così e dico che, se si deve tracciare una linea da d verso eb, che è il semidiametro del cerchio isoperimetrico al triangolo, è necessario che essa si rapporti alla somma dei lati del triangolo come il semidiametro del cerchio [si rapporta] alla circonferenza. Ma, poiché il semidiametro non ha alcuna proporzionalità con la circonferenza, né in lunghezza né in potenza, cioè, poiché l’area del quadrato del diametro, che è la [seconda] potenza23 del semidiametro, non ha alcuna proporzionalità con l’area del cerchio, allora essa non dovrebbe avere neanche alcuna proporzionalità con l’area del quadrato uguale al quadrato della linea della circonferenza, se potesse essere dato. È chiaro che né la linea cercata, né il suo quadrato possono essere proporzionali alla linea de o db, i cui quadrati sono proporzionali al quadrato di eb. Pertanto, non si può tracciare questa linea da d a una parte aliquota di eb o di db, così come la sua estremità [k], posta tra e e b, non potrà distare da e di una linea che sia proporzionale a eb o db; poiché, se così fosse, allora il quadrato sarebbe sempre proporzionale a eb, come è evidente24. Di conseguenza, non si può assegnare alcun punto su eb verso cui si possa tracciare una linea che sia esattamente quella che si sta cercando. Ma sicuramente su eb esiste un punto verso cui si può tracciare una linea che non sarà né maggiore né minore di alcuna parte aliquota, per quanto piccola sia, di quella cercata. Di conseguenza dico che, come non è possibile tracciare alcuna linea – che può essere quella che si sta cercando – da d a eb, verso una parte aliquota di eb, allo stesso modo non può esistere una linea tale che sia proporzionale alla linea cercata, come è evidente, visto che i quadrati di tutte queste linee sono proporzionali al quadrato della linea eb25.
15. Dico inoltre che, se è vero che nessuna linea è perfettamente proporzionale alla linea cercata, una tuttavia sarà più proporzionale delle altre. E questo è evidente; infatti, anche se tutte non fossero proporzionali a de e eb, tuttavia, malgrado tutto, una sarà più proporzionale a eb e db rispetto alle altre, e dunque meno proporzionale alla linea cercata. Perciò, questa, fra tutte, è la più non–proporzionale a eb, de e db, e la meno non–proporzionale alla linea cercata. Esiste quindi una linea, fra tutte quelle che si possono tracciare da d verso le parti di eb, che sarà quella meno non–proporzionale alla linea cercata
La ricerca della proporzionale
16. Tuttavia, per cercare la proporzionale, si deve considerare che, fra le linee non– proporzionali, alcune si rapportano come il lato e la diagonale [del quadrato]26, e [in questo caso] non si può mai trovare una proporzionalità così esatta che l’eccesso non sia maggiore di una parte aliquota: per esempio, un decimo della diagonale è minore di un settimo del lato, e l’eccesso è maggiore di una parte aliquota della diagonale e del lato; allo stesso modo in qualsiasi parte minore27.
17. Un’altra non–proporzionalità è quella fra l’angolo di incidenza e l’angolo rettilineo. Infatti, la linea che corrisponde all’angolo di incidenza non è proporzionale alla linea che corrisponde all’angolo rettilineo, e la metà dell’angolo rettilineo è maggiore della metà dell’angolo di incidenza, e precisamente della metà dell’angolo di contingenza. Questa metà è pertanto minore di ogni parte aliquota, sia dell’angolo rettilineo, sia dell’angolo di incidenza28.
18. Che tuttavia sia possibile trovare un tale rapporto fra le linee risulta chiaramente da quanto segue: infatti, essendo l’angolo una superficie e la linea il limite della superficie29, è chiaro che, come l’angolo di contingenza è una superficie divisibile, anche il suo limite, ossia la linea che delimita questo angolo in quanto superficie, è divisibile allo stesso modo. Ugualmente, la linea che delimita la superficie dell’angolo rettilineo è divisibile a seconda della divisibilità della superficie. Si può dunque sottrarre dalla linea che delimita la superficie dell’angolo rettilineo la linea che delimita l’angolo di contingenza, e così la linea che delimita l’angolo di incidenza non è proporzionale alla linea che delimita l’angolo rettilineo secondo la linea che delimita l’angolo di contingenza. Pertanto, poiché questa linea che delimita l’angolo di contingenza è minore di qualsiasi parte aliquota della linea che delimita un angolo rettilineo o un angolo di incidenza, la proposizione risulta evidente30.
19. E in ciò potrai osservare come, prima di qualsiasi divisibilità di una linea retta, la linea non è sottoponibile ad alcuna divisibilità, grazie alla quale una linea retta può tagliare un’altra. Tuttavia, anche se questa linea non è divisibile mediante quel tipo di divisione, con cui una retta è divisa da una retta — e, da questo punto di vista, essa è come un punto estremo irraggiungibile —, essa, tuttavia, è, a suo modo, divisibile mediante una curva. Perciò, quella linea, poiché delimita una superficie, è detta linea divisibile, sebbene possa apparire indivisibile in rapporto a una linea delimitata da un punto. Come, infatti, la divisibilità di una superficie termina nella linea che, rispetto alla superficie, è indivisibile, poiché essa non è divisibile nel modo in cui lo è una superficie, tuttavia la linea che delimita una superficie, considerata in sé stessa, è una grandezza divisibile; allo stesso modo, la divisibilità della linea retta attraverso un’altra retta termina nel punto limite della divisione e della linea, e, in quanto estremità della linea, è indivisibile nel modo in cui lo è una retta; tuttavia, considerato in sé stesso, è una grandezza divisibile31. È dunque possibile che una linea sia minore o maggiore di un’altra, non tuttavia di una qualsiasi parte aliquota o di una parte aliquota maggiore, ma di una parte aliquota minore. Da ciò, puoi ricavare che cosa si debba intendere per linee e punti indivisibili.
20. Dico, dunque, che, anche se si può tracciare da d verso eb una linea proporzionale a quella cercata, in modo che l’eccesso non sia maggiore di una parte aliquota, tuttavia nessuna linea può essere tracciata in modo che l’eccesso sia minore di una parte aliquota. Dico, inoltre, che, anche se si potessero tracciare innumerevoli linee siffatte, una sarà più precisa dell’altra, ma nessuna sarà in assoluto la più precisa.
21. Vediamo, dunque, quale fra tutte queste linee siffatte l’intelletto umano riesce a cogliere. È chiaro che se la linea, che deve essere proporzionale a quella cercata, è prolungata di una qualsiasi parte aliquota di essa, per esempio di un terzo, un quarto o altro, allora resta sempre proporzionale. Se dunque questa linea è prolungata di una lunghezza pari al rapporto della linea compresa tra la sua estremità su eb ed e e la linea ab, o pari al rapporto della linea compresa tra la sua estremità su eb e b e la linea ab, allora essa resta sempre proporzionale. Dunque, i rapporti o sono tali che per mezzo di uno di essi si giunge alla linea cercata, oppure non lo sono. Se non lo sono, allora, attraverso quella linea che noi presupponiamo come proporzionale alla linea cercata non nota, non potremo sapere nulla di quella cercata. Infatti, poiché la linea cercata non è nota e il prolungamento non ci conduce a essa, ma a una linea maggiore o minore, che non conosciamo, non potremo conoscere l’eccesso della linea cercata completamente ignota.
22. Se dicessi di essere arrivato alla linea cercata attraverso un altro prolungamento e non attraverso entrambi, sarebbe la stessa cosa, poiché noi non conosciamo attraverso quale prolungamento ciò accade e dove questa linea cade, visto che possono cadere infinite [linee] fra e e b. Se dicessi che i prolungamenti sono uguali e tuttavia minori o maggiori della linea cercata non nota, di nuovo non si potrebbe mai arrivare alla linea cercata.
23. La [linea] proporzionale, di cui l’intelletto umano può servirsi in questo genere di procedimenti per arrivare alla linea cercata, deve essere dunque necessariamente quella che, attraverso entrambi i prolungamenti uguali, che sia l’una o che sia l’altra, si presenta come la linea cercata, e questa è la linea tracciata da d al punto medio tra e e b, cioè a f. Ed essa è la sola per la quale il rapporto della distanza da e alla linea ab è lo stesso del rapporto della distanza da b alla linea ab32; prolungata di questo rapporto, cioè di un quarto della sua lunghezza, essa ci conduce alla linea cercata, e, procedendo in questo modo, è possibile per noi trovare ciò che si cerca, anche se si potrebbe trovare un’altra più precisa attraverso altri procedimenti33.
24. Ma non pensare affatto che questa sia una pura congettura, così che per nessun’altra ragione l’intelletto umano sarebbe condotto ad asserire ciò; potrai fare tu un sillogismo che, in questo caso, tranne l’estrema precisione e nei limiti della differenza, è ammesso per la più piccola parte aliquota (cfr. figura 2).
Infatti, se si traccia una linea da d a un punto vicino a e, per esempio g, e la si prolunga secondo il rapporto tra eg e ab, essa è minore di quella cercata; e se la si prolunga secondo il rapporto tra gb e ab, essa è altresì minore di quella cercata; e se si traccia un’altra linea da d a un punto vicino a b, per esempio h, e la si prolunga secondo il rapporto tra eh e ab, essa è maggiore di quella cercata, e, allo stesso modo, secondo il rapporto tra hb e ab, essa è maggiore di quella cercata, come si mostra qui [dai due lati]. Dunque, si può tracciare un’altra [linea] da d ad eb, che, prolungata secondo il rapporto tra la linea compresa fra la sua estremità ed e e ab, non è né più grande né più piccola di quella cercata. Allo stesso modo, se ne può tracciare un’altra da d ad eb, che, prolungata secondo il rapporto della linea compresa fra l’estremità e b e ab, non è né più grande né più piccola di quella cercata. Ma poiché queste due linee, dai cui prolungamenti deve risultare la linea cercata, non possono essere diverse, visto che le linee diverse che si estendono da d ad eb non possono essere proporzionali con la stessa precisione a quella cercata, ma l’una sarà sempre più precisa dell’altra, allora, essendo prolungate secondo diversi rapporti tra le loro parti ed esse stesse, non possono pervenire ugualmente alla medesima linea cercata. Sarà quindi necessario che una sola sia la linea e uno solo il suo prolungamento, il che è possibile solo nel punto f. Di conseguenza, una spiegazione sufficiente di tutto ciò che si può sapere su questo modo di procedere è quella data nella proposizione così spiegata.
25. Tuttavia, poiché ti ho dimostrato tutto ciò che si può sapere sull’uguaglianza dei perimetri delle figure curvilinee e di quelle rettilinee — e cioè in che modo la cosa più vera che si sa è che l’uguaglianza non può essere conosciuta, e che ciò che al massimo si può sapere in questo ambito è rivelato in una breve proposizione —, ho così soddisfatto, per quanto ho potuto, il tuo desiderio. Ebbene sappi questo: tu possiedi il mezzo per cercare tutto ciò che si può sapere in ambito matematico. Nelle matematiche ogni proposizione attraverso cui si consegue l’uguaglianza precisa tra cerchio e quadrato è impossibile, e ogni proposizione, dal cui contrario si inferisce tale precisione, è necessaria. Affermo anzi che chi, nelle matematiche, sa ricondurre ogni ricerca a ciò, ha raggiunto la perfezione di quest’arte. Infatti, non c’è niente di vero in quelle proposizioni dal cui opposto non consegue l’uguaglianza tra il cerchio e il quadrato, e questa è la soluzione più soddisfacente di ogni ricerca matematica.
26. Da quanto ora esposto, ho tuttavia già spiegato ciò che, nella trasformazione delle figure [geometriche] e nei rapporti irriducibili a numeri [interi], si può sapere senza la massima precisione, e tuttavia al di qua di ogni errore, percepibile o ipotizzabile, anche della più piccola parte aliquota. In base a quanto detto sai che il diametro del cerchio sta alla sua circonferenza come due volte e mezzo la radice del numero 1575 sta a sei volte la radice del numero 2700. E, per quanto non sia precisissimo, [tale rapporto] non è tuttavia né maggiore né minore di un minuto o di una qualsiasi parte che si può dare di un minuto. Pertanto, non si può sapere quanto esso manchi della massima precisione, non potendo essere determinato mediante un numero comune34. Perciò, questo difetto non è emendabile, poiché può essere colto solamente da un intelletto superiore e in nessun caso attraverso l’esperienza dei sensi. Ora, già solo da ciò puoi capire che il valore più preciso si coglie in un ambito inaccessibile al nostro sapere, la cui conoscenza non ho letto sia stata finora trasmessa.
27. Oltre a ciò, sembra tuttavia utile osservare che, come vedi in questo caso, una figura, come il cerchio, non può essere colta attraverso un’altra, per esempio il quadrato, o viceversa, in modo così preciso da non poter essere colta in maniera ancora più precisa, anche se il difetto non è affatto percettibile. Allo stesso modo, in ogni ricerca del vero dove cerchiamo di conoscere qualcosa attraverso un’altra cosa, ossia ciò che è ignoto attraverso ciò che è noto, bisogna tener conto della stessa cosa, e cioè che si raggiunge il vero in modi vari e diversi, [restando, tuttavia] al di qua della massima precisione; infatti, si può raggiungere una maggiore precisione con un procedimento piuttosto che con un altro, ma non c’è nessun procedimento con cui si possa raggiungere la massima precisione, anche se l’errore non è manifesto; questo perché la misura con la quale l’uomo si mette alla ricerca del vero non è in alcun modo proporzionale [al vero], per cui chi si acquieta, accontentandosi di restare al di qua della precisione, non coglie l’errore. E in ciò sta la differenza tra gli uomini, poiché alcuni si vantano di essere pervenuti alla precisione, che i più sapienti riconoscono come irraggiungibile, così che risultano più dotti quelli che hanno conoscenza della loro ignoranza35.
28. All’inizio ti ho invitato a passare da queste matematiche alla teologia attraverso la via dell’assimilazione; questo, infatti, è il modo più adatto di elevarsi. Le dottrine matematiche, infatti, trattano di ciò che viene colto con le vere forze della mente, in quanto considerano le figure nella loro verità, prive della materia mutevole36. Per questo motivo, una volta che si sia lasciata la molteplicità delle figure dietro di sé, ci si eleva più facilmente, attraverso una sorta di assimilazione, alla prima forma, cioè alla forma delle forme del tutto assoluta. Tutti i teologi, infatti, cercano una qualche precisione, in modo da poter raggiungere con essa l’eternità del cerchio, che è semplicissima e assolutamente una. Ma la forza infinita è incommensurabile rispetto a tutto ciò che non è infinito, come l’ampiezza del cerchio resta incommensurabile rispetto a tutto ciò che non è circolare37.
29. Dunque, come il cerchio è la figura geometrica perfetta38, che complica in sé tutte le perfezioni delle figure, e la sua ampiezza [complica] l’ampiezza di tutte le figure39 e non ha nulla in comune con ogni altra figura, dal momento che è assolutamente una e semplice in sé, così l’eternità assoluta è la forma di tutte le forme, che complica in sé ogni perfezione, e la sua forza onnipotente abbraccia tutte le forze delle forme, tutte le specie, senza tuttavia avere niente in comune con tutte le altre forme. E come il cerchio, per il fatto di non avere né inizio né fine, ha una certa somiglianza con l’eternità40, e nella sua ampiezza, che racchiude le ampiezze di tutte le figure, rappresenta una qualche immagine dell’onnipotenza, e nella sua connessione, mediante la quale la circonferenza è unita all’ampiezza, rappresenta una qualche immagine del nesso infinito e pieno d’amore41, così noi intuiamo nell’essenza divina l’eternità che ha in sé l’onnipotenza, e in queste il nesso infinito. Nell’eternità intuiamo il principio senza principio42 e diciamo che esso è il principio paterno. Nell’onnipotenza, che è dal principio senza principio43, intuiamo il principio illimitato che procede dal principio. Nel nesso infinito intuiamo il nesso pieno d’amore del principio senza principio e del principio che procede dal principio. Per il fatto che nell’essenza divina intuiamo l’eternità, intuiamo il Padre44. Per il fatto che intuiamo in questa stessa essenza la potenza dell’eternità, che non può che essere infinita, essendo la potenza dell’eternità, ossia del principio senza principio, intuiamo l’uguaglianza dell’unità eterna, cioè il Figlio del Padre. Per il fatto che intuiamo il nesso pieno d’amore dell’unità eterna e della sua uguaglianza, intuiamo lo Spirito. Dunque, nell’unità semplicissima dell’eternità intuiamo l’uguaglianza, fortissima e potentissima, e viceversa, nell’uguaglianza l’unità, e, allo stesso modo, intuiamo nel nesso l’unità e l’uguaglianza. Senza l’unità dell’essere eterno niente può essere. Senza l’uguaglianza di questa unità, niente può essere così com’è. Senza il nesso dell’essere e dell’essere così, niente può essere così com’è. Dunque, senza il principio unitrino, niente può essere45.
30. Tutto ciò è rappresentato [sotto forma di immagine] nel cerchio: attraverso la sua ampiezza e il nesso strettissimo attraverso cui il cerchio si congiunge massimamente con se stesso, vediamo che esso è coerente e unito per natura. Dopo di che notiamo che tutti i poligoni sono costituiti da un perimetro, da un’ampiezza, e da un nesso [dell’uno e dell’altro] con l’immagine del cerchio, e che tutti i perimetri dei poligoni derivano dalla circonferenza del cerchio, e tutte le ampiezze dei poligoni si allontanano in maniera non–proporzionale dall’ampiezza del cerchio, e la stessa cosa accade per tutti i nessi [degli uni e degli altri]; in questo modo, notiamo che analogo è anche il rapporto tra le [diverse] specie delle cose sensibili e la forma delle forme, così che le specie di queste cose sensibili sono in rapporto a Dio pressappoco come il triangolo, il quadrato, il pentagono, ecc. sono rapportati al cerchio.
31. Tuttavia, ciascuno di questi poligoni ha una perfezione circoscritta, al di fuori della quale non è, né può essere. L’essere del triangolo non può in alcun modo esistere al di fuori della triangolarità. E la stessa cosa vale per il quadrato, ecc. Dunque, ogni specie riposa all’interno del suo ambito, che è racchiuso nel suo perimetro, al di fuori del quale né può, né desidera essere. Infatti, come è ben noto, il triangolo cesserebbe tutto [il suo] essere, se passasse a quadrato. Dunque, dalla propria natura, attraverso la quale ha l’essere e l’essere così, nessuna specie può essere condotta alla distruzione, poiché essa riposa all’interno dei limiti della sua natura specifica. E questa quiete è proprio sua, poiché, entro il perimetro della sua perfezione, ha a suo modo la forza divina, nella quale gode del nesso pieno d’amore46.
32. Dunque, ogni specie sensibile ha, nel modo che le è proprio, una certa misura in comune con l’eternità, con la potenza e con il nesso d’amore infinito, sebbene in questa misura non vi sia nulla di proporzionale; la stessa cosa vale per ogni poligono che ha una potenza e un’ampiezza limitate, ha un nesso e un’unione deboli, e non può avere alcuna proporzionalità con l’unità circolare dell’eternità47, con la sua ampiezza inesauribile e la sua unione infinita, anche se tutto ciò che un poligono ha, lo ha in modo tale che, nella natura del triangolo e del quadrato, può partecipare della potenza del cerchio. Il rapporto fra le specie sensibili e la forma delle forme è dunque lo stesso che intercorre fra i poligoni e il cerchio. Inoltre, poiché esistono molti modi d’essere del triangolo, visto che una cosa è il triangolo rettangolo, un’altra è il triangolo acutangolo, e un’altra è il triangolo ottusangolo, e all’interno di ciascuno di questi tipi di triangolo rientrano diversi modi d’essere a seconda della varietà della materia, tutti questi modi sono delle contrazioni individuali48. Infatti le specie, considerate veramente in se stesse, rientrano in vari modi a seconda della varietà della materia. Infatti il triangolo è rappresentato meglio e più perfettamente in oro che in acqua o in qualsiasi altra materia labile49, e inoltre è colto più adeguatamente con l’intelletto di come è raffigurato in una qualsiasi materia.
33. Da ciò osserviamo come tutti i poligoni possono essere inscritti a un cerchio, e come, nel cerchio, tutti sono contenuti meglio di come sono nella materia, poiché là essi sono il cerchio. E in ciò vediamo che, se tutti i poligoni possono essere inscritti a un cerchio percepito attraverso i sensi e se il cerchio dell’eternità è l’atto di tutte le possibilità, allora, come tutti i poligoni possono essere inscritti in modo sensibile al cerchio, così, nella specie o forma dell’eternità tutte le specie sono in atto la stessa forma eterna. E come la forma del triangolo ha l’essere più vero nella nostra mente che nella materia variabile, così nella mente eterna o Verbo, dove sono la verità stessa, tutte le specie delle cose hanno l’essere più vero rispetto a quello che possiedono nella diversità individuale50.
34. Andando ancora oltre, osserviamo che i cerchi sono vari, e che non può che esservi un solo cerchio massimo, verissimo, sussistente in sé, eterno e infinito51, al quale non ci si eleva attraverso gli altri cerchi, per quanto grandi, poiché, nelle cose che ammettono un più e un meno, non si perviene al limite massimo assoluto52. E di questo cerchio infinito consideriamo cose meravigliose e inesprimibili, che altrove ho trattato più diffusamente.53
35. Diciamo, dunque, che esistono nature circolari che non possono essere principio di se stesse, poiché esse non sono come il cerchio massimo assoluto, l’unico che è l’eternità stessa54. Gli altri cerchi, sebbene non sembrino avere un inizio e una fine, in quanto sono considerati per astrazione dal cerchio percepito attraverso i sensi, sono tuttavia cerchi il cui essere proviene dal primo cerchio infinito eterno, non essendo essi l’eternità infinita stessa, e questi cerchi, in paragone con ii poligoni ad essi inscritti, sono per così dire una specie d’eternità e di perfetta semplicità. Essi hanno, infatti, un’ampiezza che eccede l’ampiezza di tutti i poligoni in modo non proporzionale55, e sono la prima immagine del primo cerchio infinito, anche se, a causa dell’infinità del primo, non sono ad esso paragonabili. E ci sono nature che hanno un certo movimento circolare e senza fine intorno all’essenza del cerchio infinito, che complicano in loro la forza di tutte le altre specie, che, dalla loro forza complicativa, esplicano, mediante assimilazione, tutte le altre specie, che intuiscono tutto in loro, che si contemplano come immagine del cerchio infinito e che, attraverso questa stessa immagine, cioè attraverso se stesse, si elevano alla verità dell’eternità o all’esemplare stesso: queste sono le nature intellettuali che abbracciano tutto tramite la loro forza intellettuale56.
36. Ora, tutte le figure cercano, per quanto possono, di misurare l’ampiezza della verità eterna. Ma come tra il finito e l’infinito non esiste alcuna proporzionalità, così Dio resta una precisione sconosciuta57, al di sopra di ogni ricerca, e così è non soltanto sconosciuto, ma è anche quella stessa precisione sconosciuta che non può essere conosciuta in nessuna cosa conoscibile. Ogni creatura, infatti, si sforza di definire il proprio Dio nei limiti della propria natura. Come un triangolo vorrebbe [per così dire] «triangolare» un cerchio, un quadrato «quadrarlo», e così via per tutti gli altri poligoni, così anche l’intelletto vorrebbe intendere [Dio]58. Ma, sebbene Dio – che non ha parti, dal momento che è la semplicità infinita – non ecceda di alcuna parte aliquota nessuno dei vari modi di misurare in maniera specifica, egli eccede tuttavia ogni misura propria della grandezza, dal momento che egli è superiore a qualsiasi modo in cui si possa ricercare. E così eccede tutte le misure più accurate, le frazioni più piccole, poiché è la più sottile di tutte queste frazioni, cosicché non si può raggiungere la sua precisione, né crescendo né decrescendo59.
37. Tuttavia, a ogni natura è sufficiente raggiungere Dio nella sua specie e nel modo in cui può. Così, infatti, essa [ogni natura] è in quiete, perché, al di fuori della sua specie, non lo ricerca, né ne coglie l’esistenza. Dunque, questa sufficiente comprensione, con la quale essa lo raggiunge nella sua specie e nel modo in cui può, è la sua quiete60, perché è ciò che sazia il movimento della sua natura.
38. Questo è quanto ci illustra, mediante l’assimilazione, l’indagine che abbiamo condotto sul triangolo nel tentativo di elevarlo fino a eguagliare [il suo perimetro] alla circonferenza del cerchio. E abbiamo raggiunto la quiete mediante l’unico procedimento che, sebbene abbia dei difetti, abbiamo riconosciuto come il più preciso, ossia elevando il triangolo fino a renderlo uguale al cerchio. Questo procedimento non converrebbe alla specie dei quadrati. Se, tuttavia, un quadrato si elevasse, nel modo che gli è proprio, fino a eguagliare il cerchio, potrebbe rallegrarsi di aver raggiunto la quiete, anche se non ci fosse precisione, purché un altro quadrato non fosse più perfetto nella sua specie. Lo stesso vale per le altre figure.
39. Allo stesso modo, ogni intelletto giungerà alla quiete se, nel modo in cui è dato alla sua specie, avrà sentito di essersi elevato fino a uguagliare l’infinito, pur restando la precisione divina sempre inaccessibile61. Queste e infinite altre cose potrai ricavare da te. È sufficiente averle trattate in questo modo. Così sia.
Note a piè pagina
Il termine «adsimilatio» designa un processo per analogia o somiglianza. Sul tema, cfr. Kremer 2004.
Il destinatario di questo scritto non è noto: potrebbe trattarsi del cardinale Bessarione, ma si tratta di un dato incerto, non supportato da alcuna fonte diretta o indiretta (cfr. Carratelli 1998, 201–225). Nel periodo in cui sembra sia stato concluso il De circuli quadratura, ossia il 12 Luglio 1450 (cfr. Liebmann 1929, 261), Cusano si trova a Rieti. Dal punto di vista della produzione letteraria, il 1450 è uno degli anni più fecondi del Cardinale: il 15 Luglio scrive il libro I del De sapientia, l’8 Agosto il libro II, il 23 Agosto il De mente, e il 13 Settembre, sempre dello stesso anno, pubblica il De staticis experimentis. Dall’attenta ricostruzione di Hofmann e Hofmann 1980, nota 1, 201, si può affermare che, da un punto di vista cronologico, questo testo è preceduto soltanto da due scritti: il De geometricis transmutationibus e il De complementis arithmeticis. Esso presenta un’attenta discussione sulla quadratura del cerchio e, benché non proponga alcun avanzamento di rilievo sulla questione, risulta tuttavia molto interessante per il suo contenuto filosofico: Cusano mette in opera il suo progetto di condurre il lettore alla teologia attraverso la matematica: quadrare il cerchio significa comprendere Dio, sicché l’ars matematica si configura un modo, anzi “il” modo più efficace per comprendere l’incomprensibile. Tale nexus è tuttavia realizzabile solo mediante una riflessione di natura epistemologica sull’omogeneità delle grandezze e sui limiti della nostra conoscenza, che si conclude, nella seconda parte del testo, con la ripresa delle idee già esposte nel De docta ignorantia, il che conferisce al trattato un tono mistico-simbolico, molto diverso dal discorso iniziale.
Il termine «aequalis» è reso con «uguale», lasciando al contesto di chiarire se si tratta di un’uguaglianza di lunghezze, di superfici o di volumi. In questo caso è chiaro che si tratta di un’uguaglianza di lunghezze, ma subito più avanti Cusano utilizza lo stesso termine per intendere un’uguaglianza di superfici, ossia un’equivalenza. La proposizione che Cusano sta enunciando è la prima proposizione del De geometricis transmutationibus, che rappresenta l’oggetto del dibattito fra Cusano e i matematici del tempo. Subito dopo egli si serve della prima proposizione de La misura del cerchio di Archimede, che Cusano poteva leggere in Bradwardine 1495b, III, 6, concl. 5.
Cfr. Cusanus 2010b, 9.
Con poligono si traduce «figura poligonya», ossia figura costituita da più lati.
Con rettangolo si traduce «quadrangulus». Va sottolineato che in questo, come negli altri scritti matematici, il termine «figura quadrangularis» è equivoco: Cusano lo riferisce tanto al quadrato quanto al rettangolo e al parallelogramma. Di volta in volta, a seconda del contesto, si renderà il termine «quadrangularis» con la figura corrispondente. Sull’utilizzo, da parte di Cusano, del termine «quadrangulus» invece di «quadratus» e sull’influenza dalla terminologia matematica medioevale, cfr. Hofmann 1966, 98–136, spec. 105.
Cfr. Cusanus 2010b, 36, 7–16.
Bisogna intendere qui «rectus» nel senso di rettilineo, più che di ortogonale: si tratta cioè dell’angolo formato dall’intersezione di due rette.
Come sottolinea Nicolle 1998, nota 4, 34, Cusano si riferisce qui a una discussione sul principio di omogeneità delle grandezze, di cui tuttavia non indica i protagonisti. Tale principio è stato stabilito nell’antichità da Eudosso e da Archimede (cfr. Gardies 1988). Il rifiuto della proposizione secondo cui «se si può dare un maggiore e un minore allora si può altresì dare un uguale» si trova in Da Novara 2005, III, 15 e in Bradwardine 1495b, II, 3, concl. 7.
Per «aliquota» s’intende: contenuta un numero intero di volte, ossia un sottomultiplo intero. Cfr. Bradwardine 1328, 68: «pars autem aliquota est illa quae, aliquotiens sumpta, reddit aequaliter summum suum. Pars vero non-aliquota est illa quae nullatenus, aliquotiens sumpta, reddit aequaliter summum suum» («Una parte aliquota è invero quella che, presa un determinato numero di volte, dà come risultato il suo tutto. Una parte non aliquota è quella che, presa un qualsiasi numero di volte, non dà come risultato il suo tutto»). La citazione si trova in Clagett 1964–1984b, 493.
Cusano usa il termine «proportio». Si è preferito qui tradurre il termine latino con «proporzionalità», nella scia di Pacioli 1494, il quale molto probabilmente aveva letto i lavori di Cusano, così come le opere di Archimede tradotte in latino, tra il 1449 e il 1453, da Iacopo da San Cassiano (Iacobus Cremonensis). Nel 1489 Pacioli si trova a Roma, e Pierleone da Spoleto lo introduce nelle corti cardinalizie. Cfr. Giusti e Maccagni 1994; Giusti e Martelli 2010 (in part. Ulivi 2010; Esteve e Martelli 2011). La scelta della traduzione adottata è dovuta al fatto che, stando alla definizione attuale di proporzione, tra due grandezze c’è rapporto («habitudo»), e non proporzione, la quale ha luogo invece tra più rapporti: date le grandezze A, B, C, D, con A, B omogenee e C, D omogenee, si dice che sono in proporzione se il rapporto tra A e B è uguale al rapporto tra C e D. Cusano utilizza i termini «habitudo» e «proportio» con una certa leggerezza. Quando in seguito si leggerà «linee proporzionali», ciò è stato fatto solo per rendere la lettura del testo più scorrevole.
Nel Medioevo per angolo di incidenza si intende l’angolo formato dall’intersezione di un arco e una retta, all’interno dell’arco, mentre per angolo di contingenza quello formato dall’intersezione di un arco e una retta, all’esterno dell’arco, ossia fra l’arco e la tangente. Un angolo retto (nel senso di ortogonale) può dunque essere definito come la somma di un angolo di incidenza e di un angolo di contingenza. L’angolo di contingenza, per quanto piccolo, è considerato all’epoca come una grandezza, e, come tale, è «divisibilis in infinitum», ossia suscettibile di aumento e diminuzione continui, a seconda che il raggio dell’arco aumenti o diminuisca (cfr. Bradwardine 1495b, II, 4, concl. 6).
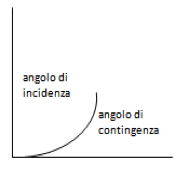
Ciò dà luogo a una difficoltà insormontabile: essendo l’angolo di contingenza un angolo “infinitesimale”, l’angolo di contingenza è fondamentalmente incommensurabile all’angolo di incidenza e all’angolo rettilineo, e incommensurabili sono pure l’angolo di incidenza e l’angolo rettilineo (cfr. Bradwardine 1495b, II, 4, concl. 7). La questione di cui discute Cusano non è come calcolare la progressione continua verso l’infinitamente piccolo di un angolo di contingenza, bensì com’è possibile porre nella medesima proporzione grandezze curve e grandezze rettilinee. Cfr. Wertz 2001.
Per «superficie rectilinea», Cusano intende una superficie delimitata da lati dritti. Cusano parla anche di «figura rectilinea» sempre per intendere una figura delimitata da linee diritte.
Cfr. Da Novara 2005, III, 15.
Cfr. la definizione 1 di Eudosso posto all’inizio del libro
V degli Elementi di Euclide: «
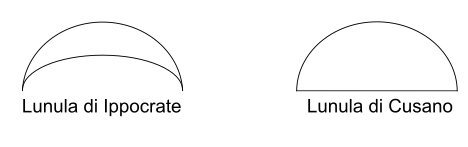
Per lunula Cusano non intende una porzione di cerchio delimitata da due archi di cerchio di raggio diverso (come per Ippocrate di Chio), ma una porzione di cerchio delimitata da una retta, ossia un segmento circolare. Questa concezione deriva da Bradwardine 1495b, III, 6, concl. 5: «Aliam probationem minoris tangit Aristoteles per portiones lunares, quam tamen reputat in aliis locis philosophiae insufficientem, et ideo de ea non curo ad presens». Cfr. anche De Muris 1998, VI, 25–32, 259–266. È tuttavia parimenti possibile che Cusano intenda per lunula non una superficie, bensì la lunghezza della circonferenza compresa tra la circonferenza e la linea retta. Qui, visto il contesto, sembra più plausibile la prima ipotesi, ossia che Cusano consideri la lunula come una superficie, sebbene le oscillazioni terminologiche e i presupposti cusaniani rendano problematica un’interpretazione univoca. Stessa cosa si ritrova in Cusanus 2010i, 81.
Cfr. Cusanus 2010i, 71–77.
Qui si tratta dell’impossibilità della quadratura del cerchio per approssimazione attraverso le lunule, metodo ripreso più tardi nel Cusanus 2010i, 71–77. Sul procedimento cusaniano della quadratura «per lunulas», cfr. Böhlandt 2002, 72ss, Müller 2005.
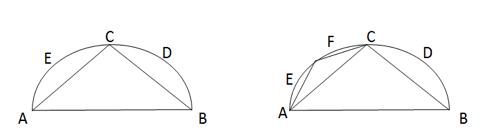
Sia ACB un arco di cerchio; 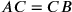 ;
; 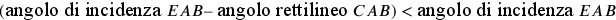 ;
; 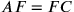 ;
; 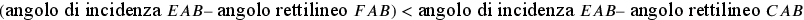 . Se si continua il
procedimento, si diminuisce sempre più il resto dell’angolo di
incidenza, e tuttavia non si esaurisce mai, poiché un angolo
di incidenza non può essere trasformato in un angolo
rettilineo. Infatti:
. Se si continua il
procedimento, si diminuisce sempre più il resto dell’angolo di
incidenza, e tuttavia non si esaurisce mai, poiché un angolo
di incidenza non può essere trasformato in un angolo
rettilineo. Infatti:  e
e 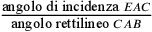 è «per
definitionem» irrazionale. Ma poiché
è «per
definitionem» irrazionale. Ma poiché 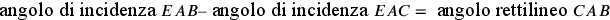 , allora
, allora
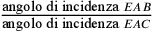 deve
essere irrazionale, e così il rapporto delle superfici dei
segmenti circolari è inesprimibile. Su questo punto, cfr.
Hofmann e Hofmann 1980, nota 9, 203.
deve
essere irrazionale, e così il rapporto delle superfici dei
segmenti circolari è inesprimibile. Su questo punto, cfr.
Hofmann e Hofmann 1980, nota 9, 203.
È interessante notare questa inversione – errata – del
ragionamento di Cusano: se finora Cusano aveva sostenuto che
la quadratura del cerchio è impossibile per l’impossibilità di
trasformare porzioni di cerchio in figure rettilinee, ora
invece afferma che è impossibile trasformare le porzioni di
cerchio in figure rettilinee perché ne conseguirebbe la
quadratura del cerchio, il che è impossibile. Tradotto:
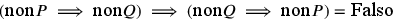 .
.
Per rispettare al meglio lo spirito del linguaggio cusaniano, a differenza sia di J. E. Hofmann che traduce «capacitas» con «Fläche» (Hofmann e Hofmann 1980, 40), sia di J.M. Nicolle che traduce il termine latino con «Surface» (Nicolle 1998, 26), si è preferito differenziare i due termini (capacitas e superficies), utilizzati entrambi da Cusano, rendendo il latino capacitas a volte con ampiezza, altre volte, a seconda del contesto, con estensione o superficie.
Cfr. Cusanus 2010j, 2.
Cusano si riferisce qui agli unici due testi che precedeno questo scritto: il De geometricis transmutationibus e il De complementis arithmeticis.
Poiché Cusano riferisce il termine «potentia» sempre alla seconda potenza, da questo momento si tradurrà «potentia» con «quadrato».
Il ragionamento di Cusano è il seguente:
dl non è proporzionale a de o db, poiché il
diametro non è proporzionale alla circonferenza, benché
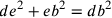 .
.
dl è proporzionale a dk, secondo la costruzione 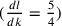 . Cerchiamo
quindi una proporzione per dk.
. Cerchiamo
quindi una proporzione per dk.
dk non è proporzionale a eb o db; ek non è proporzionale a eb o db.
fra le possibili linee proporzionali a eb o db, dk non è il segmento cercato o proporzionale al segmento cercato.
Cusano utilizza il termine «diameter» per indicare la
diagonale, in base a una etimologia inesatta da «
Riguardo all’incommensurabilità tra il lato e la diagonale
del quadrato Cusano si ispira a Da Novara 2005, X, 7, add e a Bradwardine 1495b, III, 5, concl. 3: «Se esistono tre linee proporzionali, la seconda è
più potente della prima». Da ciò si evince che la linea media
proporzionale fra il lato e il diametro è incommensurabile a
ciascuno in lunghezza così come in potenza. Se indichiamo la
diagonale D con 10d e il lato S con
7s, allora 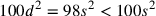 , e così
, e così
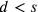 , o
, o
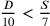 , come
affermato.
, come
affermato.
Che la metà dell’angolo rettilineo sia più grande dell’angolo di incidenza della metà dell’angolo di contingenza corrispondente è un’affermazione che non risulta presente in alcun tetso del tempo. Si può quindi ricostruire questo ragionamento che confronta angoli rettilinei e angoli curvilinei:
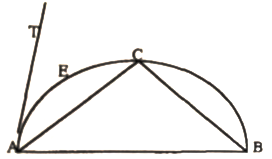
TAB  angolo rettilineo
angolo rettilineo
EAB  angolo di incidenza
angolo di incidenza
TAE  angolo di contingenza
angolo di contingenza
TAC 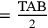
EAC 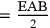
TAC  EAC, poiché TAC
EAC, poiché TAC  EAC
EAC 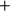 TAE.
TAE.
Cusano trae questa definizione dell’angolo come superficie da una fonte che non è né Da Novara 2005, I, né Bradwardine 1495b, I, 1. Una simile concezione si ritrova nell’XI sec., in un testo De Geometra che va sotto il nome di Gerbert di Aurillac, il futuro papa Silvestro II (ca. 945–1003): «Angulus est spatium, quod sub duabus lineis se invicem tangentibus continetur» («l’angolo è uno spazio contenuto tra due linee tangenti l’uno all’altra» (Gerbertus 1899, 66). Cusano, qui e altrove, non sembra avere una concezione chiara della superficie, attraverso cui egli vorrebbe rappresentare l’angolo. Riprendiamo la figura posta da Hofmann e Hofmann (1980, nota 18, 205):
Verosimilmente Cusano pensa l’angolo rettilineo AOB intorno al punto O delimitato dall’arco AB e pone OC come tangente a OB. AC sarebbe, per così dire, l’unità di misura per l’angolo di incidenza, CB per il corrispondente angolo di contingenza, a condizione che il raggio dell’arco ACB sia considerato come una grandezza infinitesimale. Cfr. Gerbertus 1899, 4, 3; 2, 2.
Inizia qui una discussione sulla divisibilità di una grandezza di un genere per un’altra di un genere diverso (una linea per una superficie, un punto per una linea, una linea retta per una linea curva, ecc.), in cui Cusano espone un procedimento piuttosto farraginoso.
Si vede qui una difficoltà del ragionamento di Cusano,
conseguente dal suo procedimento di annullamento progressivo
dell’angolo concepito come superficie: se una superficie si
divide in linee, la linea si divide in punti, e il punto
stesso sarà divisibile, sebbene sia indivisibile
«rectilinealiter». Quest’idea di punto contraddice la
definizione euclidea del punto «
La soluzione arriva come una visio:
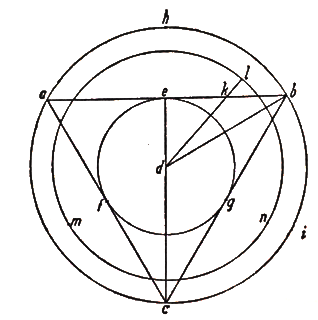
il segmento cercato passerà per f, la
metà di eb, perché 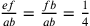 . Questa rivelazione fa da
corollario all’ambiguità generale del discorso di Cusano: egli
afferma che l’esatta quadratura del cerchio è impossibile da
conoscere, ma, allo stesso tempo, tenta una soluzione che fa
leva sulla nozione di mediana. Cfr. Cusanus 2010b, 7–16.
. Questa rivelazione fa da
corollario all’ambiguità generale del discorso di Cusano: egli
afferma che l’esatta quadratura del cerchio è impossibile da
conoscere, ma, allo stesso tempo, tenta una soluzione che fa
leva sulla nozione di mediana. Cfr. Cusanus 2010b, 7–16.
Cusano si rende conto che non esiste un numero intero che esprima il rapporto tra la metà del lato eb o il raggio della circonferenza circoscritta db (o di quella inscritta de) al triangolo equilatero iniziale e il raggio dl del cerchiò isoperimetrico, così come non esiste un numero intero che esprima il rapporto tra dl e eb o tra dk e eb.
Cusano tuttavia sa che si possono approssimare attraverso numeri razionali questi rapporti tra linee. E pensa che ciò si possa realizzare con la stessa «praecisio» con la quale l’angolo rettilineo si rapporta all’angolo di contingenza, ossia fino alla conformità tra le grandezze infinitesimali. Cusano sa di muoversi su un terreno pericoloso, perciò si serve di una visio capace di andare in soccorso alla ragione.
Per «comune» Cusano qui intende un numero intero. Cusano dà
come valore approssimativo 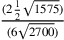 .
Secondo J. E. Hofmann (Hofmann e Hofmann 1980, nota 23, 207) ci sarebbe qui un’ottima approssimazione di
.
Secondo J. E. Hofmann (Hofmann e Hofmann 1980, nota 23, 207) ci sarebbe qui un’ottima approssimazione di
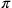 . Nel
sistema di numerazione sessagesimale,
. Nel
sistema di numerazione sessagesimale,  .
I due limiti di Archimede sono:
.
I due limiti di Archimede sono: 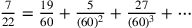 e
e 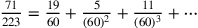 .
Il valore proposto da Cusano è:
.
Il valore proposto da Cusano è: 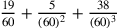 .
.
Cfr. Cusanus 1972b, I, 10, 51, 1–6. Dopo questo punto inizia una seconda parte di carattere metafisico, cui la trattazione matematica fin qui condotta è in qualche modo propedeutica.
Cfr. Cusanus 1972a, I, 3, 9.
Cfr. Cusanus 1994, 5, 23–30.
Cfr. Cusanus 1972a, I, 21, 64.
Cfr. Cusanus 1988c, 13, 1–10.
Cfr. Cusanus 1972a, I, 5, 120.
Cfr. Cusanus 1972a, I, 21, 64.
Cfr. Cusanus 1988b, 55, 8–10. Visto il contesto, si è preferito tradurre il termine «labilis» con «fragile», a differenza sia di J. E. Hofmann che traduce con «veränderlich» (Hofmann e Hofmann 1980, 54), sia di J.M. Nicolle che rende il termine latino con «variable» (Nicolle 1998, 32).
Cfr. Cusanus 1994, 9, 1–4.
Cfr. Cusanus 1972b, 2, 55, 18.


