Al reverendissimo D. Antonio, Padre in Cristo, cardinale della Santa Romana Chiesa, sacerdote di San Crisogono, La perfezione matematica di Niccolò, cardinale di San Pietro in Vincoli1.
1. La vostra nobile mente, Padre reverendissimo, è attenta a considerare le speculazioni anche delle menti ottuse e altre volte mi ha richiesto qualcosa di nuovo. E, dato che un piede malato mi ha tenuto fuori dalla corte papale, costringendomi a stare due giorni a casa, ho redatto La perfezione matematica, che vi invio, al fine di raccomandarvela, in quanto sperimento in essa la forza [della dottrina] delle coincidenze finora sconosciuta nelle questioni teologiche. Infatti, da essa, come mostrano gli esempi che aggiungo, si attinge tutto ciò che c’è da sapere in matematica, in quelle oscure questioni da sempre studiate con estremo zelo, ma che finora non hanno portato a niente. D’altra parte, in che modo la matematica ci conduce quasi all’assoluto divino ed eterno, la vostra dotta paternità lo sa meglio di me, voi che siete l’apice dei teologi. Ho inoltre inviato un piccolo scritto su come considero lo specchio e le immagini enigmatiche2, nel quale, se il reverendo padre vorrà interessarsene un po’, vedrà ad un tratto, se ho ben diretto la visione della mente al principio delle cose, ciò che anche i più dotti hanno temuto di scrivere. Essendo tutto ciò più facile da contemplare che da spiegare, non mi sono vergognato a inviarvelo, e spero di essere guidato dal vostro giudizio, sapendo che a nessun altro, se non al padre che mi ama, comunico questi segreti che mi sembrano forse più preziosi di quanto siano in realtà: correggerò la mia valutazione secondo il vostro giudizio, che supplico di inserire in questi scritti.
2. La mia intenzione è quella di arrivare alla perfezione matematica attraverso la coincidenza degli opposti. E poiché questa perfezione consiste per tutti nel rendere una grandezza rettilinea uguale a una [grandezza] curvilinea3, mi propongo di cercare il rapporto di due linee rette4 che stanno tra loro come la corda e il suo arco; una volta conosciuto questo rapporto, so come rendere una grandezza curvilinea uguale a una rettilinea; ma, per scoprire tali linee, è necessario che io conosca il rapporto fra una corda e il suo arco, affinché, una volta conosciuto tale rapporto, sia in grado di progredire in quest’arte. Ma come posso conoscere il rapporto fra una qualunque corda data e il [suo] arco, visto che forse fra queste grandezze così diverse non c’è alcun rapporto numericamente determinabile?
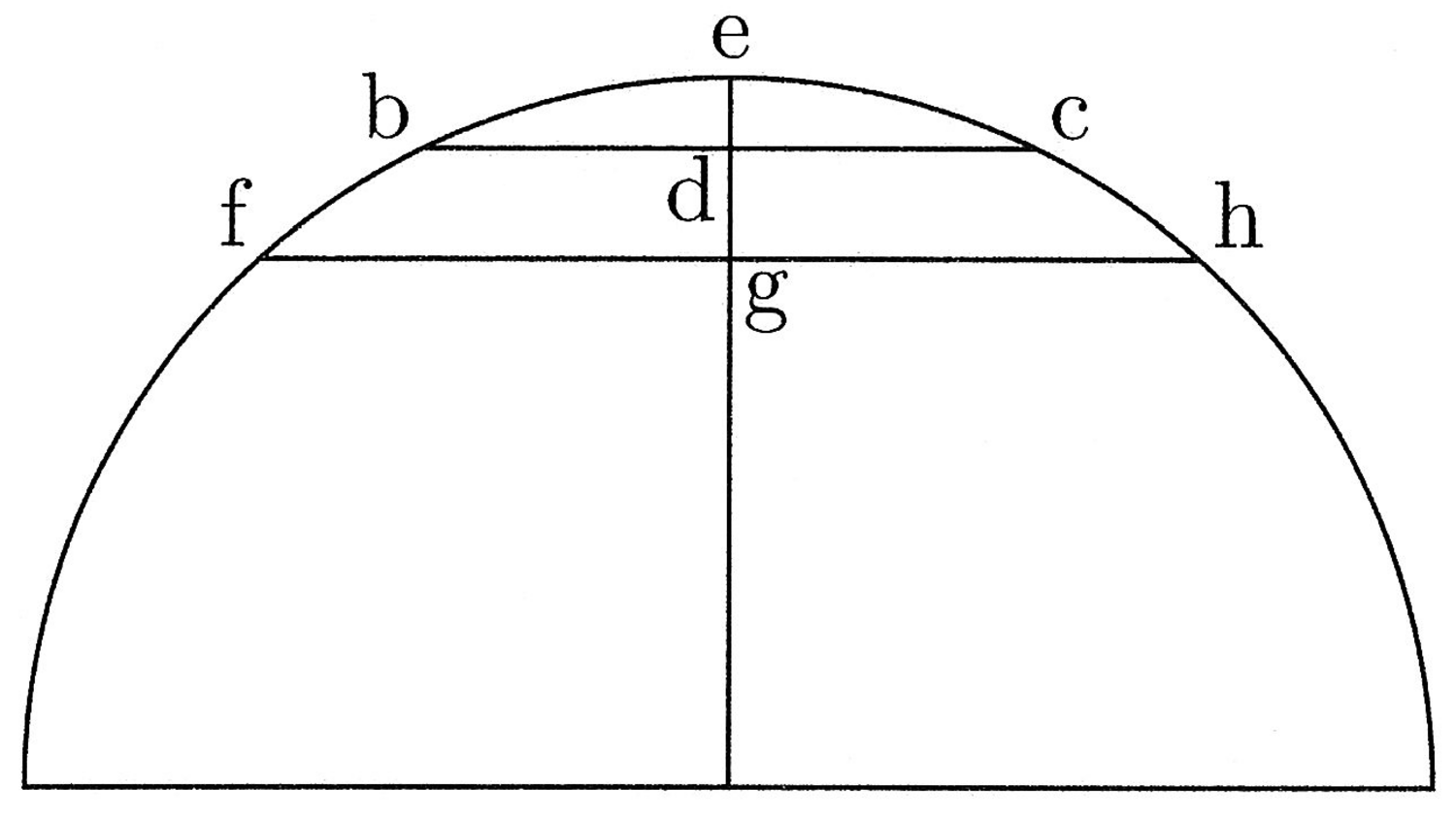
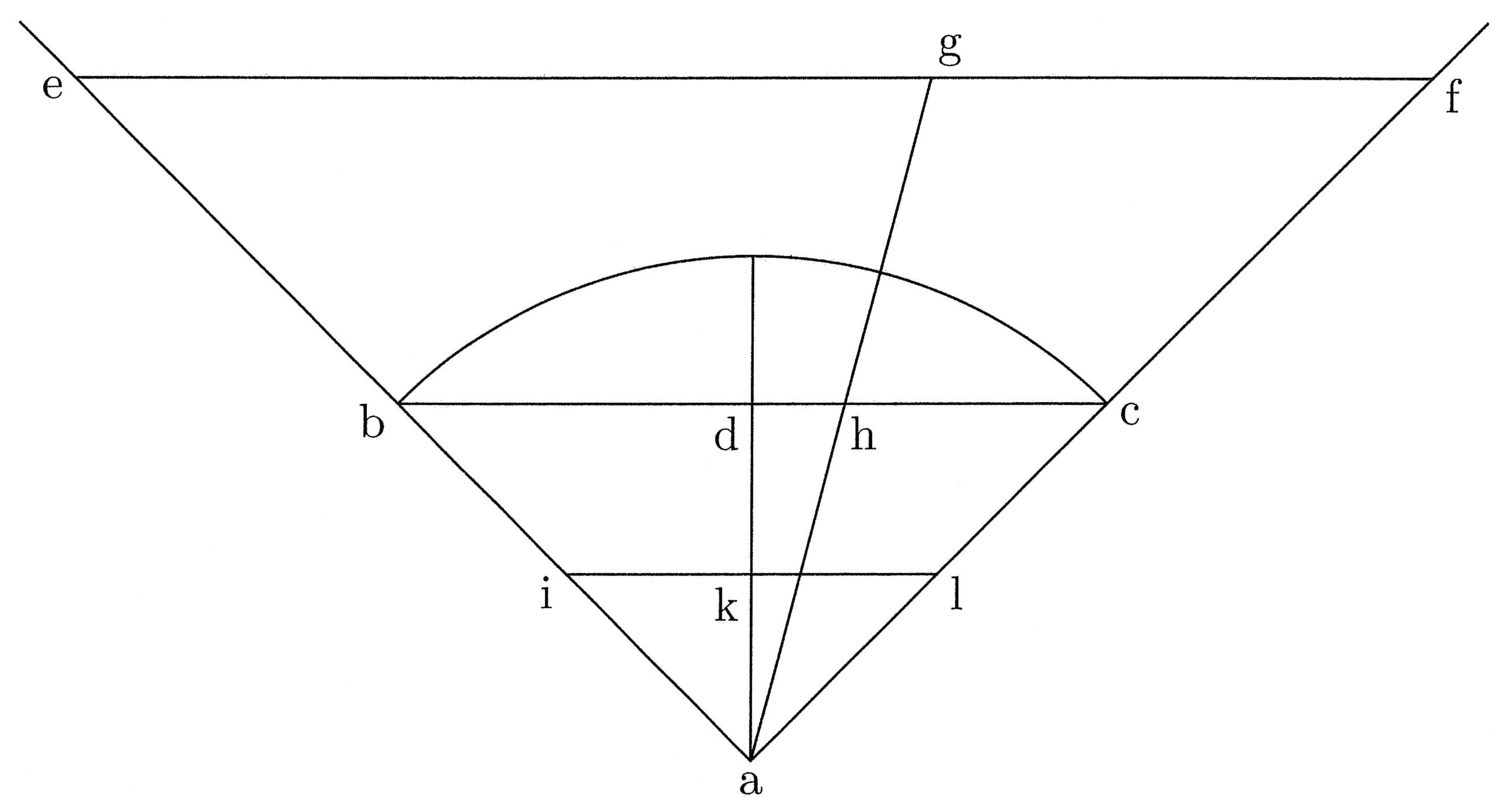
3. Sarà dunque necessario che ricorra alla visione intellettuale, che vede coincidere la corda minima, ma non determinabile, con l’arco minimo. Infatti, quanto più la corda è minore, tanto più la freccia diminuisce, come la freccia de della corda bc è minore della freccia ge della corda fh, poiché bc è minore di fh, e così via5(cfr. figura 1).
4. Dunque, la minima corda, di cui non si può dare una ancora minore, se fosse determinabile, non avrebbe una freccia [corrispondente], e non sarebbe neanche minore del suo arco. Qui, dunque, corda e arco coinciderebbero, se in essi si pervenisse alla grandezza minima. L’intelletto vede ciò perfettamente come necessario, sebbene sappia che né l’arco né la corda – essendo grandezze – sono le minime in assoluto, né in atto, né in potenza, dal momento che il continuo è sempre divisibile6. Per pervenire tuttavia alla conoscenza del loro rapporto, mi affido alla visione intellettuale, e dico di vedere dove si trova l’uguaglianza fra la corda e l’arco, ossia nel minimo assoluto7 di ciascuno dei due. Vista questa uguaglianza, proseguo la ricerca per mezzo di un triangolo rettangolo, e ciò mediante la proposizione seguente.
Proposizione
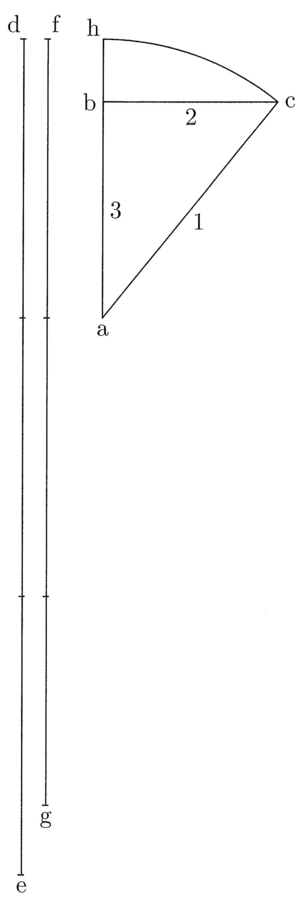
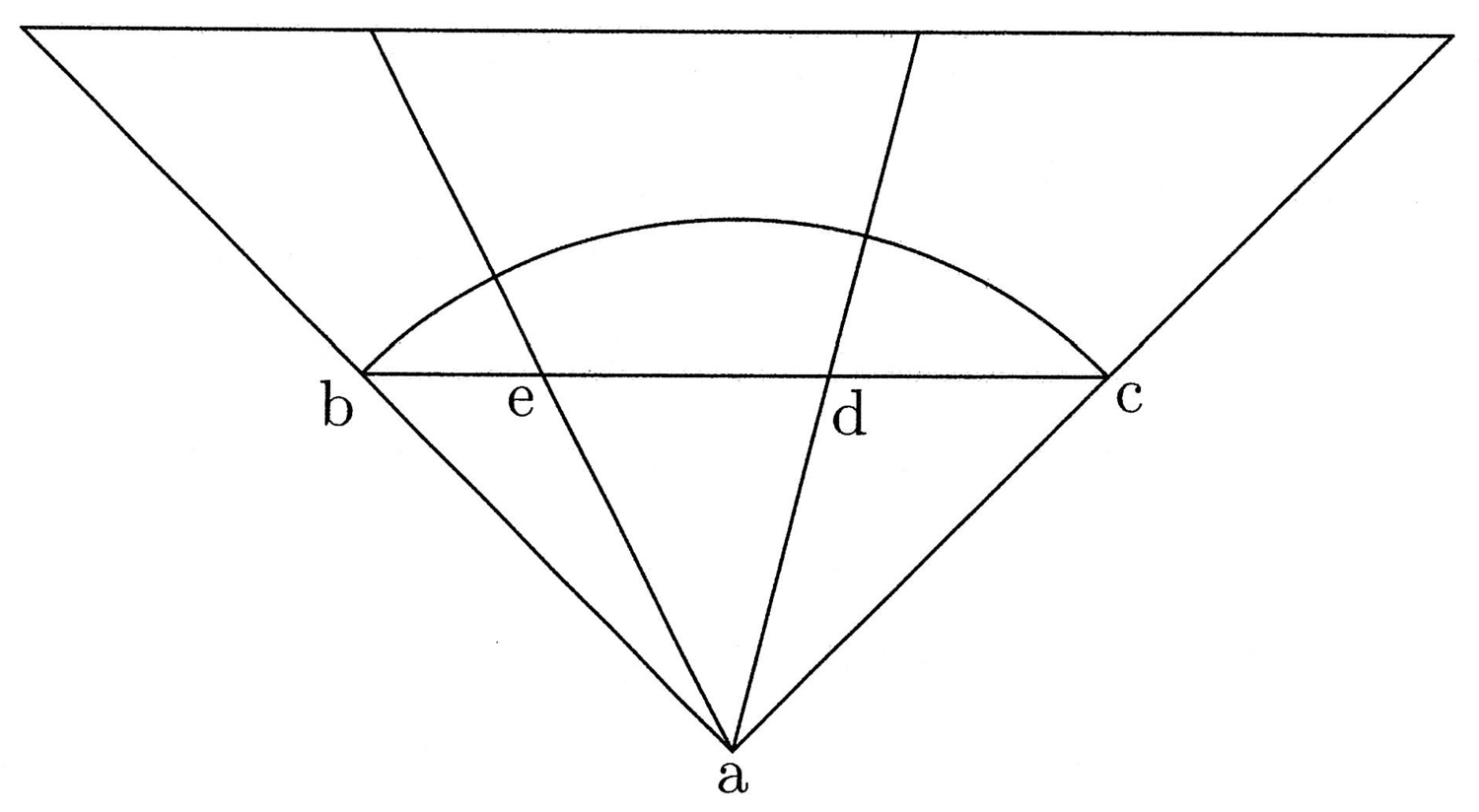
5. Se si pone il lato maggiore di un triangolo rettangolo come prima linea e come semidiametro del cerchio, il lato minore come seconda linea e come semicorda, e il lato restante come terza linea, il rapporto fra il semiarco e la semicorda sarà uguale a quello tra la linea uguale a tre volte la prima linea e la linea uguale a due volte la prima più la terza8(cfr. figura 2). Così, se il triangolo rettangolo è ABC, il lato maggiore ac è la prima linea e il semidiametro del cerchio, il lato minore bc è la seconda linea e la semicorda, il lato ab è la terza linea e hc è il semiarco, de è uguale a tre ac, e fg è uguale a due ac più ab. Dico che il rapporto fra hc e bc è uguale a quello fra de e fg.
Spiegazione della proposizione
6. Un triangolo rettangolo è tanto minore, quanto minore è la differenza tra la prima linea e la terza. Se dunque si potesse dare il minimo triangolo rettangolo, non ci sarebbe alcuna differenza tra prima linea e la terza; e poiché la seconda linea sarebbe la minima, allora, posta la semicorda, questa non sarebbe minore del semiarco, stando alle premesse.
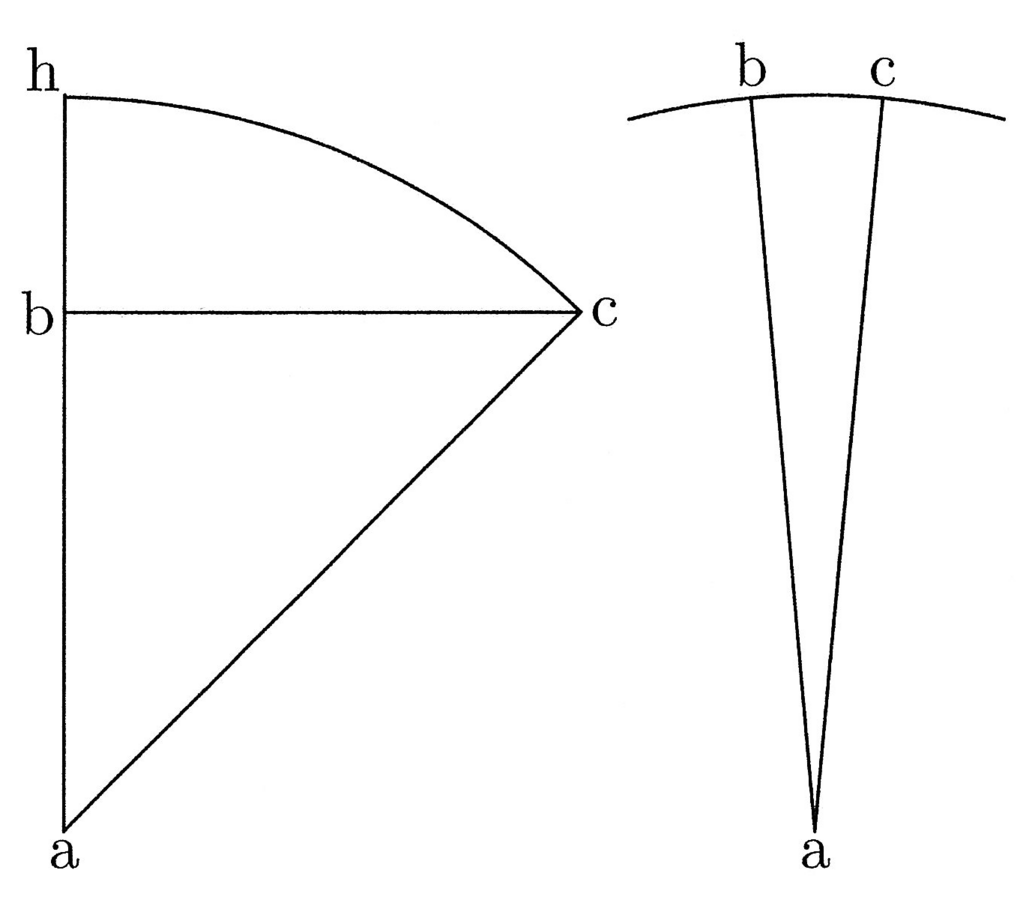
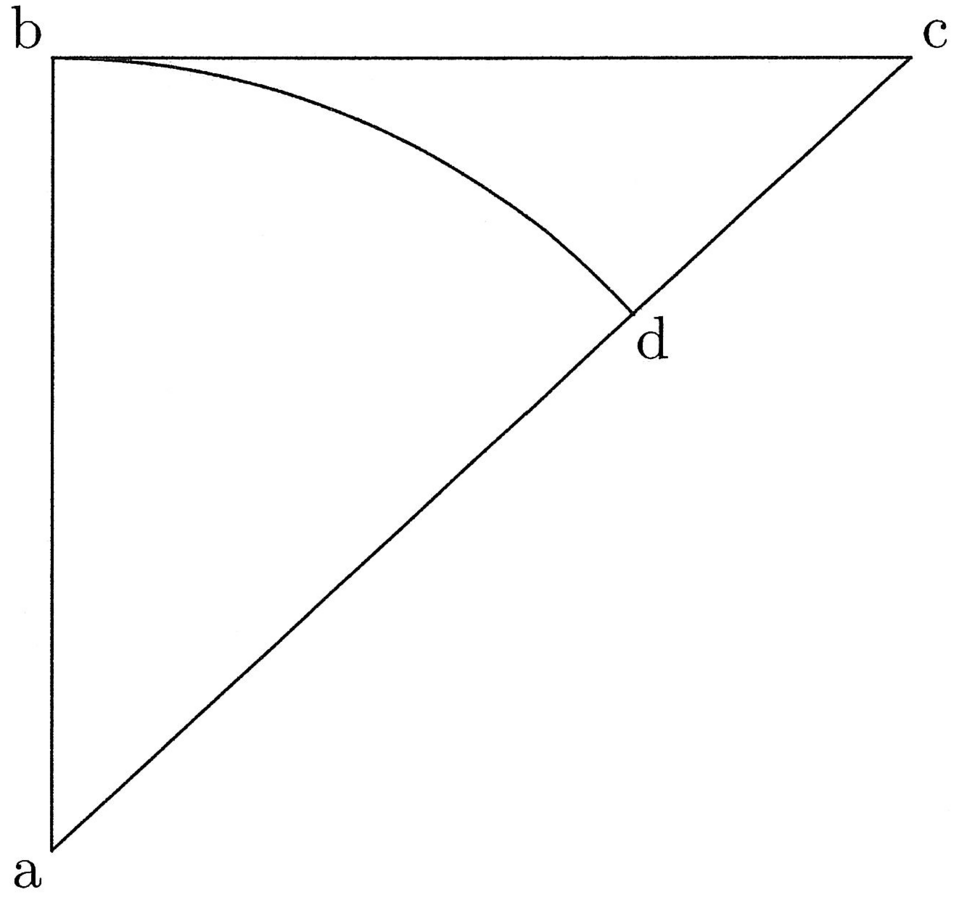
Il triangolo rettangolo massimo si ha invece quando la differenza tra la prima e la terza linea è massima. Ciò accade quando la terza linea è uguale alla seconda, della quale non c’è una linea minore, e così la seconda è la semicorda del quadrante. Sia ABC il triangolo rettangolo (cfr. figura 3).
Dico che è possibile che, se si aggiunge una linea ad ac, e si aggiunge la stessa linea ad ab, la maggiore si rapporti alla minore come il semiarco hc si rapporta alla semicorda bc. Do come certo che possa esservi una tale linea che si aggiunge ad ac e ad ab, come posto sopra, dal momento che si può dare una linea che, aggiunta ad ac e ad ab, formi linee il cui rapporto è maggiore di quello fra il semiarco hc e bc, ed è certo che si può dare una linea che, aggiunta, formi linee il cui rapporto è minore di quello fra hc e bc. Dunque, [è certo che] se ne può dare anche una che, aggiunta, formi linee il cui rapporto non né maggiore, né minore di quello fra hc e bc, dal momento che non è contraddittorio che le linee rette si rapportino tra loro come la corda e l’arco, ossia che la corda sia commensurabile o incommensurabile rispetto all’arco9.
7. È chiaro anche che, qualunque sia questa linea, se nel triangolo rettangolo minimo essa è aggiunta anche ad ac e ad ab, la proposizione è verificata, essendo qui la prima e la terza uguali, così come lo sono il semiarco e la semicorda. Di conseguenza, qualunque sia la linea aggiunta, la proposizione resta vera. E poiché la linea che si aggiunge nel triangolo rettangolo massimo è la stessa che si aggiunge in quello minimo, essa resterà la medesima in tutti i triangoli rettangoli intermedi.
E questa è la base di tale dottrina, da cui consegue che, se trovo la linea che bisogna aggiungere nel triangolo rettangolo di cui bc è la semicorda del quadrante, e la aggiungo anche laddove bc è la semicorda dell’esagono, allora scopro che il rapporto tra tali linee è uguale a quello tra gli archi, ossia di 3 a 2. È chiaro che ho trovato la linea che bisogna aggiungere in tutti i casi, e su questo non c’è dubbio.
8. Ciò risulta così chiaro facilmente. È possibile che il rapporto tra la linea uguale alla somma fra la terza [linea] e due volte la prima linea del triangolo rettangolo e la linea risultante dalla somma fra la prima [linea] e quattro volte la seconda [linea] sia in qualche caso uguale a quello tra la semicorda e il semiarco. Questo è certo. Infatti, si dà un caso in cui il rapporto è minore, come nei triangoli rettangoli maggiori, e uno in cui esso è maggiore, come in quelli minori, il che di per sé è evidente. Si dà dunque un caso in cui esso non è né maggiore né minore. In qualsiasi caso ciò accada, bisogna, per quanto premesso, che la linea aggiunta alla terza sia la stessa di quella aggiunta alla prima. Ma quella aggiunta alla terza è due volte la prima. Di conseguenza, quella aggiunta alla prima sarà due volte la prima, e ciò accadrà dove la seconda è la metà della prima, vale a dire la semicorda dell’arco dell’esagono. Di conseguenza, bisogna aggiungere il diametro10.
9. Potrai vedere questo così e anche in un altro modo. Se, per esempio, si desse un caso in cui il rapporto tra la somma di due volte la prima e due volte la seconda e tre volte la prima è uguale a quello tra la semicorda e il semiarco, si argomenterebbe come prima; ma, poiché la linea aggiunta alla terza e alla prima dev’essere la stessa, e poiché alla prima si aggiungono due volte la prima, e queste si aggiungono a due volte la seconda, allora due volte la seconda sarà uguale alla terza, e la linea aggiunta sarà il diametro. E potrai apportare tutti gli argomenti simili che vorrai.
Tuttavia, la proposizione dice che la linea aggiunta ad ac e ab è il diametro, ossia il doppio di ac, il che è lo stesso11. Da quanto detto potrai provare che lo stesso accade in tutti i casi in modo proporzionale.
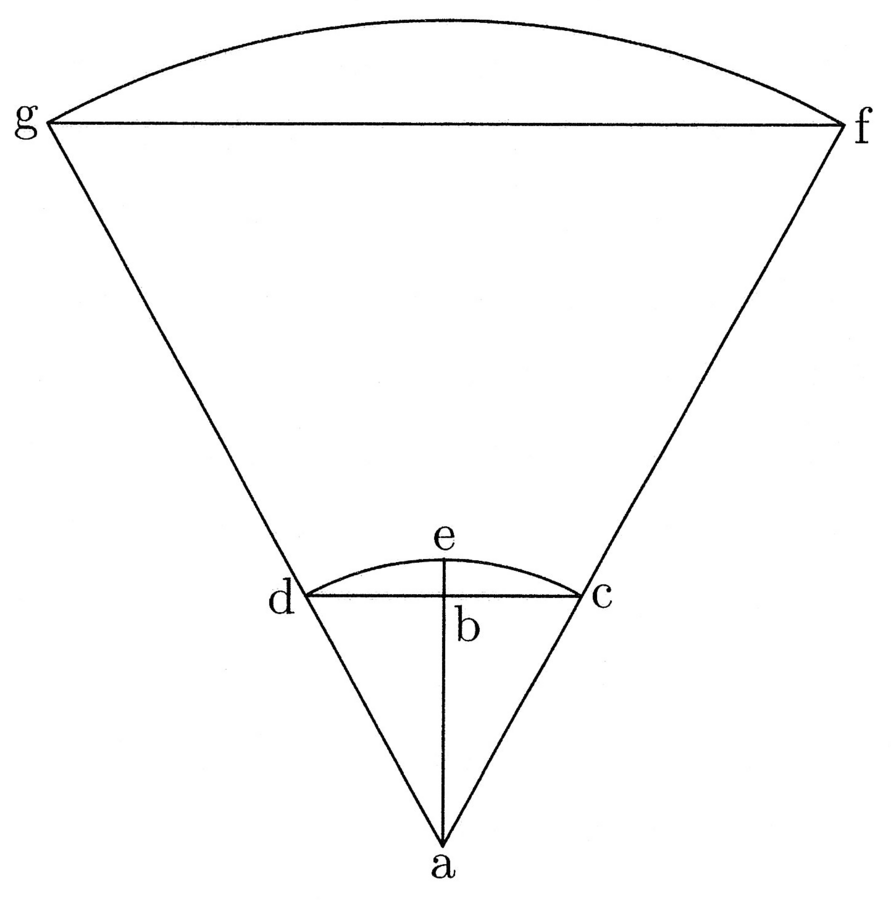
10. Ma, affinché tu veda che è così come afferma la proposizione, prendi un doppio triangolo rettangolo, come sono ABC e ABD, descrivi l’arco dc, prolunga anche ab fino a toccare l’arco, e sia be la freccia (cfr. figura 4). Dico che è possibile che un triangolo composto da questi triangoli rettangoli sia tale che, se ac e ad sono prolungate all’infinito, e una corda, come gf, è parallela a dc ed è uguale a [la somma di] ad, ac e ab, allora l’arco, di cui gf è la corda, supererà la corda della freccia be, ossia di tanto quanto ae supera ab.
11. Non si può negare che ciò in qualche caso sia possibile, per esempio [nel caso in cui] tre semidiametri meno la freccia sono il triplo della corda; tuttavia, se ciò accada in questo o in un altro caso, non cambia: è sufficiente che sia possibile [almeno] in un caso12.
E se volessi, potresti provarlo come prima, poiché ciò si dà nel caso in cui l’eccesso è minore della freccia, e dove l’eccesso è maggiore, e questo lo do per certo. Esso inoltre si dà nel caso in cui [l’eccesso] non è né maggiore, né minore, secondo quanto ho detto in precedenza. In qualsiasi caso ciò accada, è evidente che [la somma di] ac, ad e ab si rapporta a tre ac come la corda all’arco. Ciò è evidente poiché [la somma di] 3ac e 3ac meno la freccia, in qualche caso, è uguale a [la somma de] la corda e l’arco — e questo è certo —, o anche [nel caso in cui] l’arco supera la corda di suddetta freccia. E si ottiene quel che si cerca [ossia l’uguaglianza], o all’interno o all’esterno. Se [tale uguaglianza] si realizza all’interno, allora, poiché l’arco supera la corda di una lunghezza minore della suddetta freccia, la corda sarà maggiore del caso in cui l’arco supera la corda della suddetta freccia, ma è impossibile che un arco minore sottenda una corda maggiore. Lo stesso accadrebbe se si affermasse che [l’uguaglianza], avviene all’esterno: un arco più grande sottenderebbe una corda minore. Perciò la linea da aggiungere ad ac e ab è 2ac, ossia il diametro del cerchio, e questa è la verità.
12. Tuttavia, poiché è il diametro dello stesso cerchio, si potrà forse dire che, in qualsiasi cerchio, la linea da aggiungere è il diametro: non si dirà che è il diametro di un cerchio maggiore, poiché allora non si avrebbe la verità nel cerchio massimo di cui non ce n’è uno che sia in atto maggiore. E neanche si potrà dire che è di un cerchio minore, poiché nel cerchio minimo in atto non si avrebbe la verità, e quindi in nessun cerchio, dal momento che ciò che si dice di un cerchio in quanto cerchio deve necessariamente valere per tutti [i cerchi]. E se non vale per tutti, allora non vale per nessuno; tuttavia, non importa che la ragione sia questa o un’altra. Il senso della proposizione è così evidente.
13. Aggiungerò un’altra dimostrazione di questa linea che deve essere aggiunta13(cfr. figura 5). Si supponga una linea, di cui ac è una parte aliquota14, che si rapporta alla linea che essa supera della stessa lunghezza di cui ac supera ab, in un rapporto maggiore di quello fra hc e bc: sia tale linea il quadruplo di ac. Queste cose sono assolutamente vere. Di conseguenza, si può dare una linea, di cui ac è una parte aliquota, che si rapporta alla linea che essa supera della lunghezza di cui ac supera ab come hc si rapporta a bc. Questa linea, essendo necessariamente maggiore del doppio e minore del quadruplo, sarà tripla rispetto ad ac. Per questo, bisogna aggiungere ad ac il doppio di se stessa, vale a dire il diametro.
14. Perché tu veda anche numericamente quelle
verità che ho detto sul doppio e sul quadruplo di ac, poni, secondo l’approssimazione di
Archimede
15. Invece il motivo per cui l’argomentazione afferma che, della linea che si sta cercando, ac deve essere una parte aliquota è questo: poiché deve essere la stessa linea in tutti i triangoli rettangoli, è necessario che si prenda ac, che è anche la sola e unica in tutti, e non ab o bc che variano sempre. Si potrebbero aggiungere altri innumerevoli modi per dimostrare la proposizione, ma questi sono [quelli] fondamentali e sufficienti.
16. Molte cose nascoste si sono qui svelate,
poiché vedi come ciò che si verifica per il massimo e il minimo si
verifica per gli intermedi, e colui che vede il massimo coincidere
con il minimo, cogliendo insieme il massimo e il minimo, in ciò
vede tutto16. E, mediante questo procedimento, saprai come misurare
grandezze diverse, che sembrano incommensurabili. Tutto ciò mi
sembra importante e finora intentato. Archimede
Corollario
17. Il rapporto fra tre semidiametri e tre semidiametri meno la freccia della corda di un quadrante o18 di un [arco] minore è uguale a quello fra un arco qualsiasi e la sua corda (cfr. figura 6).
Sia bc la corda di un quadrante o di un arco minore e si conduca una linea dal centro a fino a toccare la circonferenza nel punto e, passando per il punto medio di bc, ossia d. Il rapporto fra tre ae e la somma di due ae e ad è uguale al rapporto fra l’arco e la corda bc. Parlando della corda del quadrante o di un [arco] minore, è evidente che sulla [corda] maggiore il lato minore del triangolo rettangolo non può essere la semicorda, che tuttavia è ciò che si richiede. Il corollario risulta chiaramente evidente dalle premesse.
Corollario
18. Risolvere un dato arco in una retta.
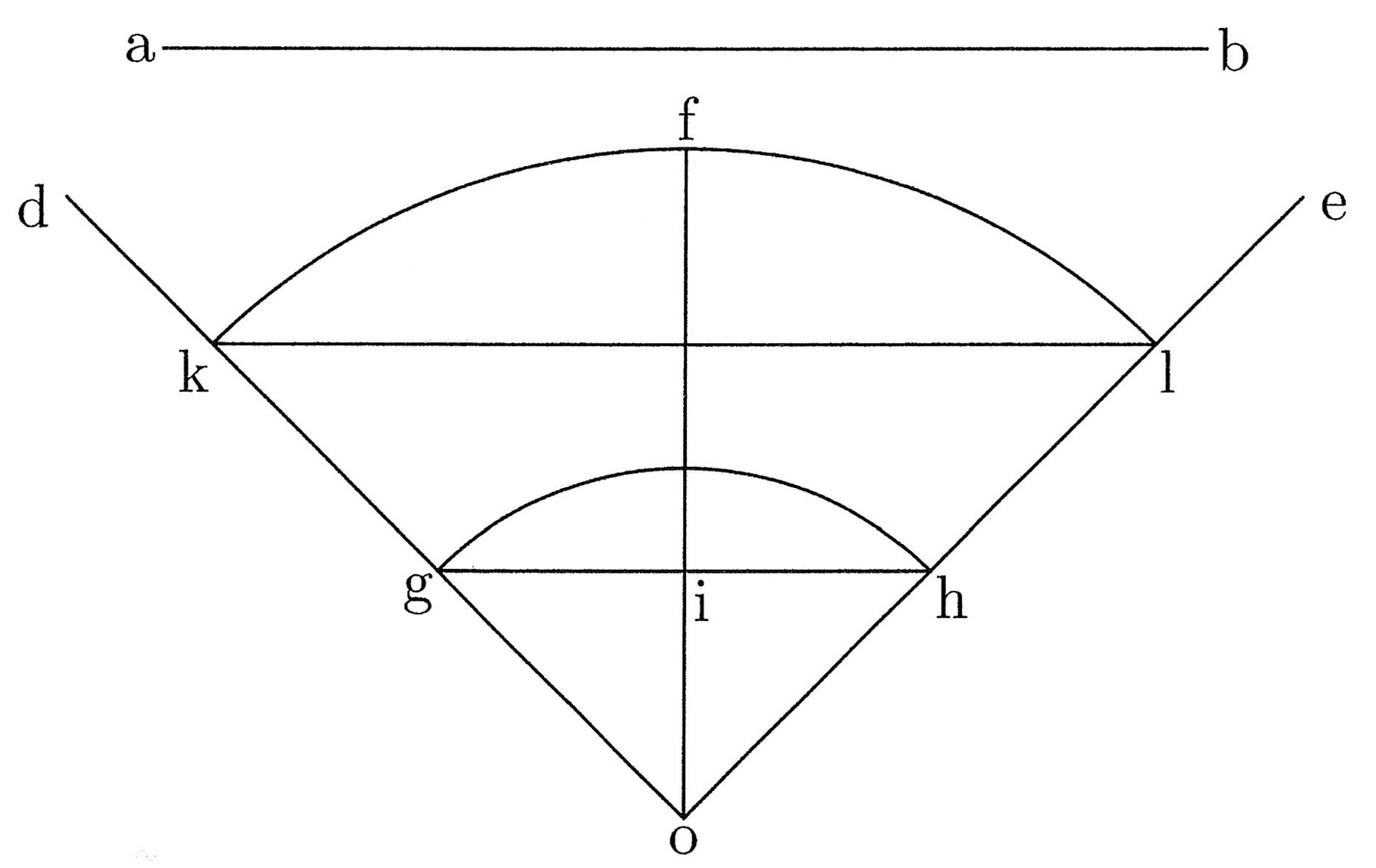
Se l’arco è un quadrante o un [arco] minore, prendilo così com’è; se è maggiore, prendi la parte aliquota di esso in modo che sia un quadrante o un [arco] minore. Sia bc l’arco del quadrante da risolvere in una retta (cfr. figura 7). Traccia dal centro a linee di lunghezza infinita che passano per b e c, e un’altra, ad, che taglia la metà della corda, e, fra le infinite linee, descrivi una linea ef parallela alla corda bc che sia uguale a [la somma di] ab, ad e ac.
Su ef riporta ab, e sia fg uguale ad ab. Traccia la linea ag, e indica con la lettera h il punto in cui essa taglia la corda bc. Dico che hc è un terzo dell’arco. Dunque, triplica hc, e hai trasformato l’arco in una retta. Oppure traccia la linea parallela a bc verso il centro, ossia ikl, in modo che [la somma di] ai, ak e al siano uguali alla corda bc, e ai sarà un terzo dell’arco. Tutto ciò è evidente da sé19.
Corollario
19. Risolvere una data retta in un arco.
Sia ab la linea retta che vuoi risolvere nel quadrante di un qualsiasi cerchio: traccia dal centro o linee perpendicolari di lunghezza indefinita, ossia od e oe, e fai passare dalla metà dell’angolo un’altra linea, of, e segna la terza parte della linea ab, che vuoi risolvere [in arco], su od e oe, e sia og un terzo di ab, e allo stesso modo oh; traccia gih (cfr. figura 8).
Di conseguenza, traccia kl parallela a gih, uguale a [la somma di] oh, oi e oh, e descrivi il quadrante avente come corda kl, poiché è la linea a cui ab è uguale. E se volessi risolverla in un altro arco, minore di un quadrante, fa in questo modo. Se esso è più grande, prendi una parte aliquota. Per esempio, se vuoi ridurla a un cerchio, prendi la quarta parte della linea retta, risolvila in un quadrante e hai ridotto il tutto in un cerchio.
20. Se tu volessi veramente risolvere una data retta nell’arco di un dato cerchio, nella sua totalità o in una sua parte aliquota, procedi come sopra descritto, variando l’angolo [compreso tra] od e oe fino a raggiungere la corda uguale a [la somma di] og, oi e oh20.
Corollario
21. Risolvere un dato arco di cerchio nell’arco di un altro cerchio.
Ciò si ottiene risolvendolo dapprima in una retta, e poi la retta in un arco di un altro cerchio, come descritto sopra.
Corollario
22. Trovare angoli che si rapportano tra loro come linee date.
Ciò si ottiene risolvendo le linee in archi di uno stesso cerchio, e tracciando dal centro i raggi21 fino agli estremi di tali archi22.
Corollario
23. Il rapporto fra il semidiametro e il semidiametro meno la freccia è pari al rapporto fra un terzo dell’arco e l’eccesso di cui la corda supera due terzi del suo arco (cfr. figura 9).
Sia bc la corda di un quadrante; su di essa hai segnato, stando a quanto premesso, due terzi dell’arco, cioè cd e de. Dico che il rapporto fra un terzo dell’arco de e l’eccesso eb, di cui la corda supera i due terzi, è pari al rapporto fra il semidiametro e il semidiametro meno la freccia23. Questo corollario è evidente da quanto premesso. Ed è vero nel triangolo rettangolo massimo, in quello minimo, e in tutti quelli intermedi.
Corollario
24. Trovare la corda di un dato arco di una parte aliquota di un semicerchio.
Poni il caso che, una volta conosciuta la corda di un quadrante, tu voglia conoscere la corda di un arco pari alla metà del quadrante. Conoscendo la parte della corda del quadrante che è uguale a un terzo dell’arco, prendi la sua metà, aggiungi a questo uno simile24, e cerca l’eccesso che si rapporta a un terzo come il semidiametro meno la freccia si rapporta al semidiametro25.
25. Aggiungerò qui precisi corollari.
Se tre semidiametri meno la freccia sono il triplo della corda, l’arco sarà uguale al semidiametro.
Se essi sono il doppio della corda, l’arco si rapporterà al semidiametro come tre a due26.
Tre semidiametri sono il medio proporzionale fra tre semidiametri meno la freccia e il semicerchio27.
Se tre semidiametri meno la freccia sono multipli della corda, tre semidiametri meno la freccia saranno multipli della corda della metà dell’arco e in modo proporzionale di una qualsiasi parte aliquota.
I tre lati di un triangolo equilatero saranno uguali alla circonferenza di un cerchio, il cui diametro è la terza parte dei due lati e della linea retta condotta da un lato alla metà del lato opposto28.
26. Se dal centro si conducono tre linee – una che passi per il punto iniziale della corda del quadrante o di un arco minore, l’altra per la metà, la terza per il punto finale – che terminano su una linea parallela alla corda, di modo che il rapporto fra queste tre linee e la corda sia pari a quello fra la circonferenza e l’arco, allora la linea condotta per il punto iniziale della corda, triplicata, è uguale alla circonferenza.
L’arco uguale a tre quarti del diametro supera la sua corda della metà della freccia.
Il diametro di un cerchio è uguale a due terzi dei lati di un triangolo isoperimetrico e al semidiametro del cerchio inscritto nello stesso triangolo.
L’eccesso del semicerchio sulle due corde di un quadrante è pari all’eccesso della diagonale29 del quadrato sul suo lato, se la diagonale è uguale alla terza parte del semicerchio30.
Il rapporto di tre diametri di un cerchio e la sua
circonferenza è uguale al rapporto tra 14 più la radice di 36 per
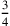 e
2131.
e
2131.
La dottrina sulle corde è ora esaurientemente trattata.
La dottrina della quadratura del cerchio è giunta ormai al suo fine. Quest’arte assolutamente perfetta insegna che, a seconda del rapporto fra date linee, siano esse commensurabili o incommensurabili, si danno linee, superfici delimitate da linee dritte32, da linee curve, e solidi.
Dalla coincidenza fra la tangente minima e l’arco minimo traggo, inoltre, la seguente proposizione:
Proposizione
27. Se si pone il secondo lato di un triangolo rettangolo come semidiametro di un cerchio, e il terzo come linea tangente al cerchio, o viceversa, e sarà descritto il cerchio, il rapporto fra la tangente e l’arco che cade dentro il triangolo rettangolo, sarà pari al rapporto fra la superficie delimitata da linee dritte e quella delimitata dalla linea curva (cfr. figura 10).
Se ABC è il triangolo rettangolo, bc la tangente, e ab il semidiametro del cerchio descritto, il cui arco bd cade nel triangolo rettangolo, il rapporto fra bc e bd sarà pari al rapporto fra la superficie delimitata da linee diritte ABC e la superficie delimitata dalla linea curva ABD.
La dimostrazione è la seguente: ciò si verifica nel minimo, se si potesse dare, e quindi in tutti i casi, poiché non è necessario stabilire che il triangolo rettangolo sia o no il massimo.
28. Risolvere una superficie data, delimitata da un arco e da raggi33, in un triangolo rettangolo.
Dato ABC, si risolva l’arco bd nella linea retta bc, e si chiuda il triangolo rettangolo con ad. Così, che bd sia o meno proporzionale alla circonferenza, sai come si riconduce una [qualunque] superficie a una superficie delimitata da linee diritte. E sai come risolvere un cerchio in un triangolo rettangolo, e così in un quadrato o in un’altra figura.
29. Risolvere una data superficie delimitata da lati diritti in una porzione di cerchio34.
Da quanto premesso la soluzione è evidente se essa è un triangolo rettangolo. Se così non è, [la] si riduce in triangolo rettangolo.
Risolvere le porzioni di cerchio comprese fra corda e arco35 in [superfici] delimitate da linee dritte e in quelle delimitate da linee circolari, è evidente da sé.
30. Il rapporto tra la superficie curva di una sezione di sfera36 e la [superficie della] base piana [di tale sezione], è come [quello tra] la linea dallo zenith al centro della base [della sezione], più il semidiametro della base [della sezione], e il suo semidiametro.
Ciò è evidente, dal momento che è così nella sezione minima dove la superficie della base piana coincide con quella curva, e dove lo zenith coincide con il centro. Lo stesso accade in tutti gli altri casi.
La superficie curva della metà di una sfera è il doppio della superficie piana del cerchio della base.
Risolvere una superficie curva data di una sfera in una superficie piana circolare e con lati diritti.
Risolvere una sfera in un cubo, e un cubo in una sfera37.
Allo stesso modo ricava i rapporti in tutte le altre superfici curve, facendo riferimento a quelli minimi. E tutto ciò che si può umanamente conoscere nelle matematiche38 si trova, a mio avviso, con tale procedimento.
Gloria a Dio39.
Note a piè pagina
Il 30 settembre 1458, dopo aver definitivamente perduto la sua diocesi, Cusano incontra a Roma il cardinale spagnolo di S. Crisogono, Don Antonio Cerdá y Lloscos (cfr. Hofmann e Hofmann 1980, nota 2, 246), il quale gli sollecita di scrivere qualcosa di nuovo. Cusano scrive per lui La perfezione matematica, in cui, dopo i diversi tentativi precedentemente provati, rinuncia a trovare il rapporto esatto tra una grandezza rettilinea e una grandezza curvilinea e ricorre all’intuizione. Cusano considera quest’opera come il suo migliore trattato matematico e lo annota espressamente sotto il titolo del De mathematicis complementis, al margine di Cu, dove si legge che il De mathematica perfectione: «prevalet omnibus». In questo testo Cusano si serve della visio intellectualis, già ampiamente utilizzata nel De beryllo, come una vera e propria via demonstrandi: portando al limite minimo l’arco e la corda, la freccia risulta nulla e la curva coincide perfettamente con la retta, e ciò che è vero per il massimo e per il minimo è vero per tutti i valori intermedi (cfr. Cusanus 2010i, 7, 1–4). Tale uguaglianza (aequalitas), attuandosi nel minimo assoluto, non è esprimibile attraverso un numero razionale e, alla fine dello scritto, Cusano escogita una serie di operazioni realizzabili attraverso la coincidenza degli opposti e lascia credere al trionfo di tale metodo, rinunciando a determinare l’esatta quadratura del cerchio. Come annota Nicolle (1998, nota 21, 121), le ultime sei pagine di C sono state cancellate, senza dubbio con una pietra pomice. Nel Marzo 1968 il presidente della Cusanus–Gesellschaft di Trêves ha portato il documento al dipartimento del Ministero Tedesco della Criminalità. Attraverso metodi chimici è stato possibile ritrovare le tracce di inchiostro e ricostruire il testo. Si tratta di una prima versione cancellata del De mathematica perfectione. Ipotesi probabili sul perché siano state cancellate sono avanzate da Marco Böhlandt (2002, 104–109; cfr. anche Böhlandt 2005, 3–40). È molto probabile che Il De mathematica perfectione e il De beryllo siano state prodotti nel medesimo periodo e, poiché nel De beryllo si trovano argomenti generali sulla filosofia e sulla teologia simili a quelli esposti nella prima versione del De mathematica perfectione, è verosimile che Cusano non abbia voluto riportarli nella versione definitiva. Una squadra diretta da Rudolf Haubst ha proceduto alla decifrazione e Joseph Ehrefred Hofmann ha pubblicato il risultato di questo lavoro in Hofmann e Haubst 1973, 13–57. Nel 1983 Klaus Reinhardt ha ritrovato e ha trascritto un manoscritto integro nel codice To (Biblioteca Capitular, f. 188r–191r) molto simile a quello di Reinhardt 1986, 96–141. Sulla base di C e le integrazioni da parte di Reinhardt è stato ricostruito integralmente la forma prior del De mathematica perfectione ed è oggi disponibile in Cusanus 2010h, 183–199. Di questa forma prior abbiamo tradotto tre parti, riportati nell’ultima nota della presente traduzione: il primo estratto comprende i paragrafi 4–7; il secondo estratto i paragrafi 20–21; il terzo i paragrafi 25–30.
Il termine latino è «aenigma». Cfr. Cusanus 1988b, 1, 2–10.
Qui Cusano parla di «quantitas curva et rectilinea», ossia una figura delimitata da linee dritte e una figura delimitate da linee curve.
Per «linee rectae» si intendono linee dritte, ossia non curve.
Cfr. Cusanus 1988b, 1, 2–5.
In questo passaggio, come in Cusanus 2010c, 17, dove si legge: «punctum, qui est terminus divisionis et lineae, et est rectilinealiter indivisibilis in quantum terminus lineae, in se tamen est quantitas divisibilis» e in Cusanus 2010g, 14: «Quantitas autem, quae non potest esse minor, non est quantitas, sed punctus», vi è una confusione di Cusano sul concetto di punto e di continuo. Cusano assimilare e non assimila la più piccola grandezza restante fra la corda e l’arco a un punto. Secondo Hofmann e Hofmann 1980, nota 4, 246, il valore di questa grandezza non è né indefinito, né un minimo, ma l’intervallo che noi chiamiamo infinitesimo e, su questa scia, Nicolle si chiede se Cusano possa essere considerato un precursore di Cavalieri (Nicolle 1998, nota 2, 120). Ora, sebbene la storia della matematica, da Euclide in poi, sia piena di considerazioni sugli infinitesimi, nessuno, matematicamente parlando, fino al Seicento, è andato oltre il metodo di esaustione. Così scrive Counet: «Finally both quantities [decreasing arc and chord] vanish according to rational mathematics, but intellectual intuition grasps something that is not zero (we would speak today of the rapport, which is not equal to zero even if the terms are)» (Counet 2005, 273–290, cit. 288).
Per «minimus simpliciter» s’intende il limite minimo infinito.
ac è la prima, ab
è la seconda, bc è la terza.
L’approssimazione è: 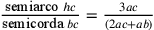 ; bc
corrisponde al «sinus», che altrove (Cusanus 2010i, 68, 6), e poco più avanti in questo scritto Cusano chiama
«semicorda del doppio arco», secondo un’invenzione indiana
trasmessa attraverso gli arabi all’Occidente medioevale (cfr.
Taton 1957–1958, I, 161).
; bc
corrisponde al «sinus», che altrove (Cusanus 2010i, 68, 6), e poco più avanti in questo scritto Cusano chiama
«semicorda del doppio arco», secondo un’invenzione indiana
trasmessa attraverso gli arabi all’Occidente medioevale (cfr.
Taton 1957–1958, I, 161).
Poiché Cusano aveva affermato che la seconda bc dovesse essere il lato minore del
triangolo, il triangolo rettangolo isoscele risulta il più
grande possibile tra quelli ammessi. Cusano suppone
l’esistenza di una grandezza t tale che
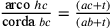 .
.
Hofmann riporta una nota presente in Cu non presente nelle versioni stampate. Si
ha: 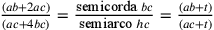 ;
anche
;
anche 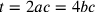 (cfr. Hofmann e Hofmann 1980, nota 10, 247).
(cfr. Hofmann e Hofmann 1980, nota 10, 247).
Si ha: 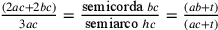 ; si
suppone che
; si
suppone che 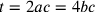 ; così,
; così, 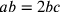 e
e 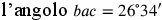 .
.
La regola generale è la seguente: 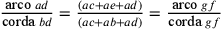 . Se la corda
. Se la corda 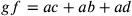 , allora
, allora
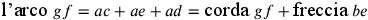 .
.
In Cu 219, la figura è orizzontale.
Si ha: ![[\frac{(4ac)}{(4ac–bh)}=\frac{(ac+3ac)}{(ab+3ac)}]<\frac{\text{semiarco
}hc}{\text{semicorda
}bc}<[\frac{(ac+ac)}{(ab+ac)}=\frac{2ac}{(2ac–bh)}]](../../../media/sources/13/28/EOAineq_28_12.png) .
Da cui:
.
Da cui: 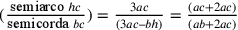 .
.
Per «aliquota» s’intende: contenuta un numero intero di volte, ossia un sottomultiplo intero. Scrive Bradwardine 1328, 68: «pars autem aliquota est illa quae, aliquotiens sumpta, reddit aequaliter summum suum. Pars vero non-aliquota est illa quae nullatenus, aliquotiens sumpta, reddit aequaliter summum suum» («Una parte aliquota è invero quella che, presa un determinato numero di volte, dà come risultato il suo tutto. Una parte non aliquota è quella che, presa un qualsiasi numero di volte, non dà come risultato il suo tutto» (in Clagett 1964–1984a, 493,trad. nostra).
Da ![[\frac{28}{26}<\frac{11}{10}<\frac{14}{12}]](../../../media/sources/13/28/EOAineq_28_14.png) Cusano conclude che
Cusano conclude che 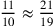 .
Hofmann fa notare che il valore numerico approssimativo di
.
Hofmann fa notare che il valore numerico approssimativo di
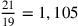 per
per 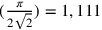 è esatto
nonostante l’approssimazione utilizzata insufficiente di
è esatto
nonostante l’approssimazione utilizzata insufficiente di
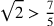 ; il valore
numerico esatto in base alla regola di Cusano sarebbe
; il valore
numerico esatto in base alla regola di Cusano sarebbe 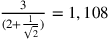 (Hofmann e Hofmann 1980, nota 14, 248).
(Hofmann e Hofmann 1980, nota 14, 248).
Cfr. Cusanus 1972a, I, 4, 11.
In latino si legge «et», che è qui da intendersi nel senso di «o» alternativo.
La regola è la seguente: 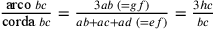 . Il secondo metodo non è
sostanzialmente diverso dal primo.
. Il secondo metodo non è
sostanzialmente diverso dal primo.
Oggi siamo soliti costruire secondo lo svolgimento di Huygens 1656, prop. 13: se ABC è il triangolo dato e 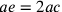 , ec interseca nel punto x la tangente del punto h. Il semiarco
, ec interseca nel punto x la tangente del punto h. Il semiarco 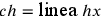 ; quindi il
; quindi il 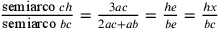 .
Questo procedimento si utilizza tanto per rendere lineare un
arco quanto per rendere curva una linea.
.
Questo procedimento si utilizza tanto per rendere lineare un
arco quanto per rendere curva una linea.
Cusano utilizza il termine generico di «sectores».
Cfr. Cusanus 2010k, 6, 1–3.
Se si definisce R il semidiametro, C la corda, F la freccia
e A l’arco, si ottiene: 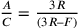 . Se ne
ricava che
. Se ne
ricava che 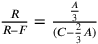 .
.
«similis» è inteso qui come uguale.
Il ragionamento sembra essere il seguente: conosci la parte
della corda del quadrante che è uguale al terzo dell’arco
(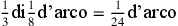 ),
prendi la sua metà (
),
prendi la sua metà (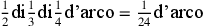 ),
aggiungi ad esso lo stesso (
),
aggiungi ad esso lo stesso (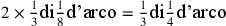 )
e trovi l’eccesso che si rapporta al terzo (
)
e trovi l’eccesso che si rapporta al terzo (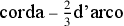 ); questo è definibile come
il quarto proporzionale.
); questo è definibile come
il quarto proporzionale.
Cfr. nota 23. Il punto di partenza è la regola: 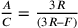 . Si
ricava che
. Si
ricava che 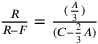 .
Da ciò consegue che
.
Da ciò consegue che 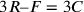 e dunque
e dunque 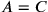 . Ma, essendo
. Ma, essendo
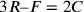 ,
allora
,
allora 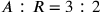 .
.
La regola 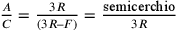 non vale sempre, ma soltanto per
non vale sempre, ma soltanto per 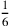 . Si tratta apparentemente
di una conseguenza errata, derivante dal fatto che Cusano non
distingue tra le frecce che appartengono ad archi diversi.
. Si tratta apparentemente
di una conseguenza errata, derivante dal fatto che Cusano non
distingue tra le frecce che appartengono ad archi diversi.
Il triangolo equilatero di lato c e
altezza h è tale che: 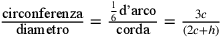 .
Questa proposizione si comprende facilmente se si riporta la
regola alla formula inversa
.
Questa proposizione si comprende facilmente se si riporta la
regola alla formula inversa 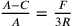 .
.
Cusano utilizza il termine «diameter» per indicare la
diagonale in base a una etimologia inesatta da «δύο» e
«
L’affermazione segue dalla seguente formula:  .
.
Generalmente et indica l’operazione
di addizione. Questo rapporto deriva dalla regola sopra
enunciata per un sesto di cerchio, con 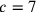 , per cui
, per cui 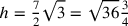 .
.
Si è qui tradotto «superficies recta» con «superficie delimitata da linee dritte» e non con «superficie piana». Quest’ultimo significato avrebbe senso se si volesse distinguere la «superficies recta» dalla «superficies curva», come quella di una sfera; ma qui sembra che Cusano tenga conto di due e non di tre dimensioni, cioè ragioni nel piano, anziché nello spazio.
Come nei Cusanus 2010i, n. 90, 3, qui Cusano utilizza il termine «sectores» per indicare i raggi. Si tratta in pratica di un settore circolare.
Qui per «portio circularis» Cusano intende il settore circolare.
Qui per «abscissio» Cusano intende il segmento circolare. Quanto segue nel testo deriva da Archimedes 1910a, I, 30, 42–43 (Archimede 1974, 146–147).
Qui Cusano intende la calotta sferica.
Cfr. Cusanus 2010b, 44.
Rispetto alla versione ultima, la forma prior del De mathematica perfectione (Cusanus 2010h) presenta tre passaggi in cui emergono differenze interessanti rispetto alla versione definitiva. Riportiamo qui la traduzione dei tre estratti:
Primo estratto (4–7): «Si deve considerare quindi in che modo, se applico la visione intellettuale a qualsiasi grandezza, per esempio a una linea, vedendola nella necessità d’essere, che non può essere né maggiore né minore, vedo quella grandezza come assoluta, […], ossia come misura adeguata di ogni grandezza, e, come in una grandezza, lo stesso vale per il triangolo, il cerchio e per tutte le altre figure; e come vedo che tutte le cose del genere della grandezza che sono nella necessità dell’essere della grandezza sono la grandezza assoluta stessa, così tutte le cose che sono assolutamente nella necessità dell’essere sono la necessità stessa. E da ciò considero di vedere la verità e la conoscenza delle cose là dove tutte le cose sono le stesse, cioè la necessità dell’essere. Dunque, se voglio trovare come si possa conoscere l’uguaglianza tra una grandezza rettilinea e una grandezza curvilinea è necessario che io sia guidato dalla visione intellettuale, la quale intuisce la loro uguaglianza nel cerchio massimo e nello stesso tempo nel cerchio minimo. Infatti, finché l’intelletto intuisce il cerchio nella necessità dell’essere, cioè così che non può essere né maggiore né minore, essendo il massimo e nello stesso tempo il minimo, esso vede il cerchio assoluto complicare ogni cerchio, e che la proporzione è vera in esso, dato che la corda e l’arco si identificano, e le linee, che sono limitate sulla corda, sono le stesse che sono limitate sull’arco, come sono note a chi le osserva. Dunque, da ciò che si vede qui, si ha che, nei cerchi sensibili, la vera conoscenza sta nella proporzione che sono le esplicazioni della complicazione del cerchio assoluto, come io ne ho trattato nei precedenti libri sulla dotta ignoranza. Come, infatti, nei [cerchi] sensibili, la corda e l’arco differiscono e variano, mentre sono lo stesso assoluto nel cerchio massimo assoluto, così in essi le linee limitate differiscono proporzionalmente. Da ciò, nello stesso modo, deriva la diversità della corda e dell’arco nei cerchi sensibili, poiché la semplicità del primo cerchio assoluto non può, come è comprensibile, essere sensibile, dato che la rettitudine della sua circonferenza, man mano che discende dalla sua perfezione, declina in curvatura; così la corda, che è sottesa all’arco, non può essere come l’arco. E poiché forse non sei molto abituato alle visioni intellettuali, e non sai cogliere la coincidenza del cerchio massimo con il cerchio minimo, [né cogliere] che la circonferenza è uguale alla linea retta, poiché né la ragione né l’immaginazione colgono ciò – infatti, essendo precedente alla grandezza divisibile, trascende tutte le capacità ‹conoscitive›, tranne quella intellettuale – ti guiderò affinché tu possa comprendere».
Questa esposizione è interessante perché precisa la nozione di visio intellectualis, annunciata in modo molto laconico nella versione definitiva: «Sarà dunque necessario che io ricorra alla visione intellettuale, che vede coincidere la corda minima, ma non determinabile, con l’arco minimo» (3, 1–3). Nella prima versione Cusano puntualizza che la visione intellettuale deriva da una certezza logica: essa è una «necessità dell’essere» (necessitas essendi). Ancora, oltre che annullare la nozione di quantitas al fine di realizzare l’uguaglianza delle grandezze, la visione intellettuale porta a grandezze assolute, minimo e massimo, ossia a figure perfette non percepite attraverso i sensi; la visione intellettuale, inoltre, annulla la differenza fra più e meno nell’assoluto, dove il minimo e il massimo coincidono, essendo l'atto di tutte le possibilità.
Secondo estratto (20–21): «Ora voglio trasformare una porzione di cerchio o un cerchio in un triangolo rettangolo. Considero in che modo nel cerchio massimo il triangolo rettangolo e la porzione o il cerchio coincidono, cioè sono uguali, dato che retta e arco sono uguali. Da ciò vedo che, se i due lati del triangolo rettangolo che formano l’angolo retto sono uguali al semidiametro e alla porzione dell’arco, le superfici saranno uguali in tutti i cerchi, proprio come nel ‹cerchio› massimo esse coincidono. E la coincidenza che si vede nel ‹cerchio› massimo si vede anche nel triangolo rettangolo minimo in qualsiasi cerchio. È dunque chiaro che il triangolo rettangolo, di cui un lato è ‹uguale› al semidiametro del cerchio e l’altro con cui il lato forma l’angolo retto è uguale alla circonferenza del cerchio, è uguale alla circonferenza più il cerchio. In questo modo determinerai in maniera proporzionale le porzioni ‹di cerchio›; si risolve ogni triangolo rettangolo in rettangolo o in quadrato o in altri poligoni grazie a ciò che è conosciuto in matematica. E così tu hai l’arte ‹di trasformare› una superficie delimitata da linee curve in una superficie delimitata da linee dritte, quadrangolare, triangolare o in un’altra figura».
La versione definitiva (27, 1–9) appare molto meno empirica, più «teorica», e cancella tutti i riferimenti alla nozione di coincidenza.
Terzo estratto (25–30): «Ho così voluto rivelare queste cose attraverso degli esempi, per dare occasione agli studiosi di meditare sul modo in cui si ottiene la conoscenza delle cose dalla visione intellettuale che si eleva al minimo e al massimo, affinché sappia che che ciò che vede in modo complicato quasi all’origine o al principio, è esplicato nelle figure sensibili e sul modo in cui nella coincidenza degli opposti si vede la complicazione delle cose conoscibili, come in questa matematica, dove si vede coincidere l’arco, la corda e la tangente nel triangolo rettangolo minimo. E così qui si complica il sapere delle cose conoscibili riguardo all’uguaglianza di ciò che è dritto e di ciò che è curvo[…] E, poiché questi esempi sono utilissimi a coloro che ricercano la verità, specie quando quelle questioni che, nonostante il massimo impegno, sono rimaste finora senza risposta, sono ora risolte in modo facile e certo, così, con questo esempio l’intelletto si aiuta e si volge allo scibile teologico, ossia alla coincidenza assoluta del minimo e del massimo o all’opposizione delle opposizioni, così come Dionigi il grande definisce dio come opposizione delle opposizioni, che non è altro che la coincidenza o l’uguaglianza. Infatti quell’uguaglianza innominabile è la forma dell’essere e del conoscere e la si vede attraverso la coincidenza degli opposti prima di ogni posizione e rimozione. A colui che contempla questa considerazione aiuterà moltissimo ricavare che la visione intellettuale è la vita dell’intelletto, che si nutre di verità; infatti, soltanto con tale visione è visibile, ed è spirituale colui che è abituato a quella visione, poiché, tra tutti coloro che si sforzano di parlare della verità, ‹è il solo che può› giudica‹re›, senza essere giudicato da nessuno; infatti soltanto chi apprende, sa riferire cose vere. Quella visione è dunque la luce della ragione, senza la quale ogni discorso è incerto e ogni movimento è ambiguo. La ragione, infatti, senza di essa, non sa fin dove si estende. Infatti soltanto la visione intellettuale è senza errore e senza inganno, e giudica la vera via, che conduce alla visione della verità, e se non è principio, mezzo e fine di ogni movimento della ragione, ogni lavoro è vano, così come colui che ricerca ciò che non conosce si affatica inutilmente. Da ciò, attraverso la fede, è iniziata la vera teologia di Cristo. La fede, infatti, è, per così dire, una sorta di visione, ma enigmatica; si conclude certamente con una visione, che si dice visione faccia a faccia senza enigma, ossia così com’è; e tuttavia non si vede nient’altro rispetto a ciò che si credeva. Dunque, la fede porta ciò che la visione coglie non all’incertezza, ma alla certezza, e ciò che coglie è la felicità, alla quale ogni natura intellettuale aspira attraverso l’attività intellettuale. Tuttavia la visione intellettuale è definita da Dionigi transizione in Dio. E, come colui che vede in questa frase di Euclide, ossia «il punto è ciò che non ha parti», in modo complicato, attraverso la visione intellettuale perfetta, tutto ciò che egli scrisse di geometria, e accede alla conoscenza di questi; così, colui che vede il verbo, attraverso cui egli agì, e il futuro, accede alla sapienza del padre creatore, poiché in quel verbo vede tutto ciò che è stato creato o può essere creato in modo complicato. Questa visione è la transizione alla sapienza, che è Dio. Lo stesso Dottore definisce quella visione anche nutrimento. Infatti l’intelletto si nutre nella visione dell’arte divina, che è il verbo. Ricava, infine, un esempio da come Dio creò il mondo, sebbene il modo divino sia senza modo. Come il matematico forma un concetto nuovo della quadratura del cerchio non a parteire dalla prima materia dell’essere, ma all’interno di se stesso, e poi lo rappresenta all’esterno, e, affinché possa rappresentarlo al meglio adatta gli strumenti e la tavola nella quale descriverà il concetto o il verbo nel modo in cui può cogliere la rappresentazione del suo verbo, e fa ciò per mostrare la gloria o la chiarezza del suo intelletto, la quale è tanto più lodata quanto più è compresa, allo stesso modo Dio ha creato tutto da sé stesso affinché sia manifesta la sua gloria, la quale è tanto più lodata quanto più la sua sapienza è colta o compresa. A Lui lode e gloria nei secoli dei secoli. Fine».
Quest’ultimo passaggio non ha un equivalente nella versione definitiva. Cusano sembra qui formulare qualche idea della sua filosofia della matematica: le dimostrazioni matematiche sarebbero esemplari per la conoscenza di tutte le cose; la visione intellettuale in matematica permetterebbe di spiegare la complicazione e sarebbe dunque una via d’accesso all’essere delle cose.