1. Al fisico Paolo, uomo eccellente e dottissimo, i complementi aritmetici del cardinale Niccolò da Cusa1.
Carissimo Paolo, ho sottoposto a te, che sei instancabile, alcuni complementi sui rapporti aritmetici, affinché tu li corregga, sebbene a te e a tutti possano essere appresi da quanto ho spiegato nel trattato su Le trasformazioni geometriche. Allora, io sostengo che la coincidenza dell’angolo e del lato nei diversi poligoni isoperimetrici ci porta al cerchio isoperimetrico come abbiamo dimostrato nella prima premessa de Le trasformazioni geometriche2. Da ciò si apre a noi una via per calcolare in ogni modo possibile tutto ciò che riguarda un complemento di aritmetica. D’altra parte, ciò che affermo, cioè il rapporto tra corda e arco, è rimasto fondamentalmente sconosciuto fino a questo momento. Nella scoperta [di tale rapporto] consiste quel complemento, e, una volta fatta, non resterà nulla di difficile da calcolare numericamente.
2. Ci sono stati uomini di grande ingegno, primo
fra tutti Archimede
3. Se davvero tale rapporto possa essere conosciuto7 ritengo che l’arte [matematica] possa scoprirlo da quanto ho già detto, e, per essere breve, tralascio l’ultima figura che lì ho posto8(cfr. figura 1).
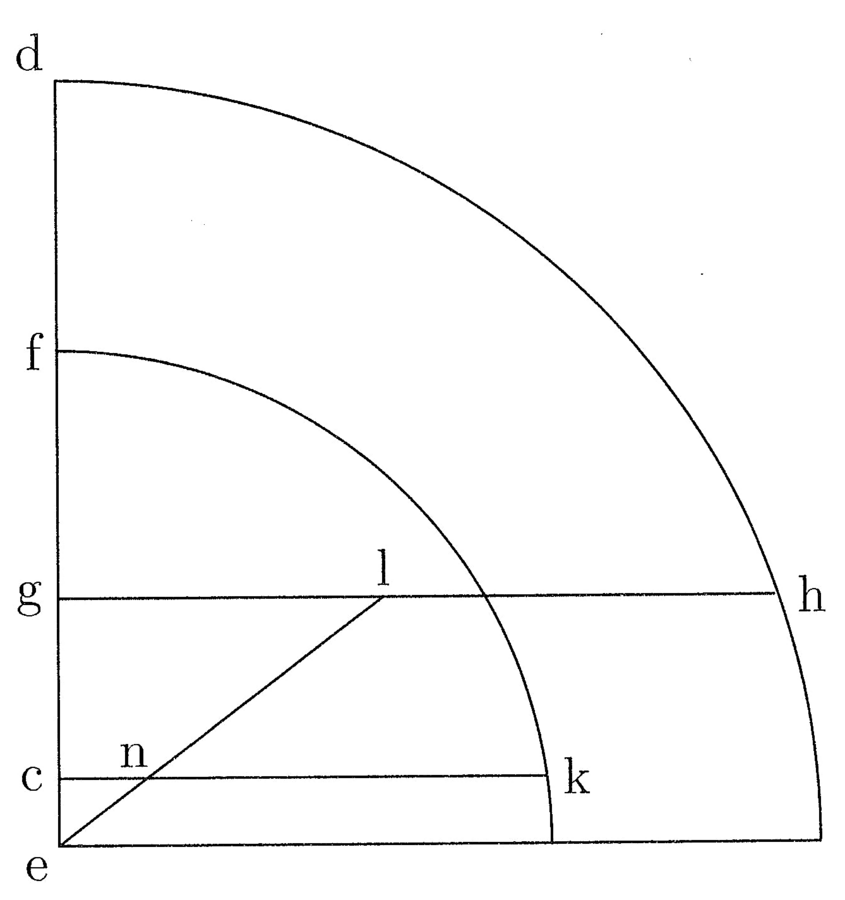
È evidente che il rapporto tra il lato dell’esagono e il semidiametro del cerchio circoscritto al triangolo isoperimetrico è noto mediante i quadrati, poiché, se il quadrato di dg è 4, allora il quadrato del lato dell’esagono isoperimetrico è 3, dato che il lato dell’esagono è uguale alla metà della corda sottesa alla terza parte della circonferenza dello stesso cerchio. È noto, di conseguenza, il quadrato di ed, poiché, se il quadrato di dg è 4, il quadrato di ed è 9, essendo dg il doppio di ge. Così sarà noto anche fe, dal momento che esso è un lato dell’esagono il cui quadrato sta a 3 come il quadrato di dg sta 4; allo stesso modo sarà pertanto noto ec. Le linee ed e ef saranno così note9; e poiché i triangoli EGL e ECN sono equiangoli, i loro lati hanno la stessa proporzionalità10; dunque ge sta a el come ce sta a en11 (cfr. figura 2).
4. Dobbiamo quindi trovare due grandezze di cui la maggiore stia a eg come la minore a ec e, precisamente, in modo tale che, se si sottraggono la maggiore da ed e la minore da ef, le parti restanti siano uguali. Questa parte restante è il semidiametro del cerchio isoperimetrico a un poligono esagonale o a un poligono con tre lati, entrambi isoperimetrici12. Ora, poiché il rapporto tra il perimetro del poligono e de è noto e il rapporto tra il semidiametro del cerchio isoperimetrico e de è noto, allora si potrà conoscere il rapporto tra il diametro e la circonferenza nel modo in cui è possibile conoscere. E cosi saprai che il numero non può cogliere ciò che cerchi, qualsiasi cosa esso sia, sicché l’intelletto comprenda l’ignoranza e il limite della ragione calcolante.
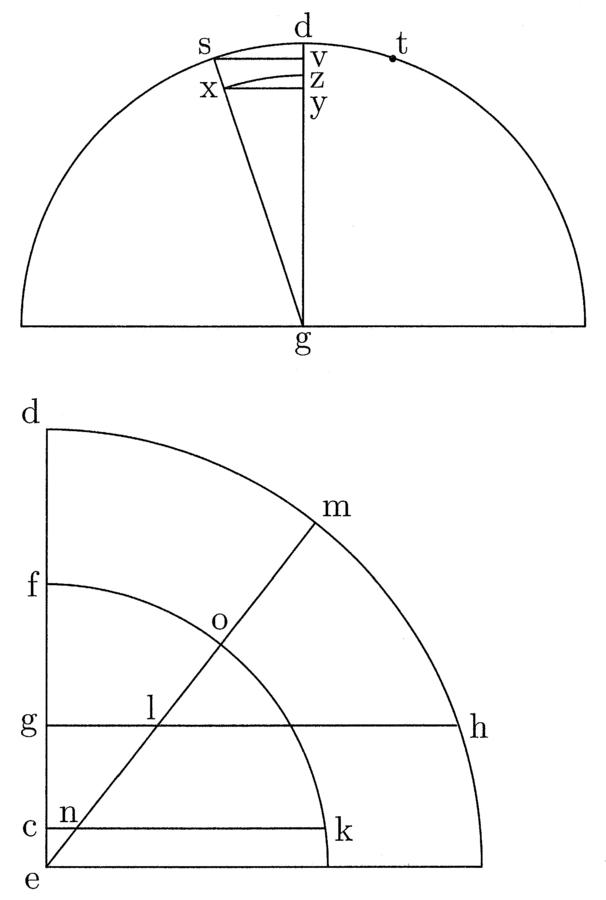
5. Risulta chiaro, da quanto detto, che è possibile cercare il rapporto tra una qualsiasi corda e l’arco e il diametro. Infatti, se al posto di un esagono si mette un qualsiasi poligono, è evidente che è possibile ricavare tutto ciò che si ricava nell’esagono. Per capirlo, descriviamo un semicerchio il cui semidiametro sia uguale al semidiametro del cerchio circoscritto al triangolo; traccia il semidiametro dg dal centro g alla metà dell’arco, e indica sull’arco che si estende da d [verso destra e verso sinistra] l’arco che corrisponde ai lati del poligono che sono le corde che dobbiamo cercare (cfr. figura 3). Posto che tu voglia una corda [che formi con l'arco di circonferenza] un angolo di 45 gradi, segnerai l’arco avente l’angolo di 22 gradi e mezzo. Partendo dal punto d e indicando i punti con s e t, traccia la semicorda da s verso t che s’interseca con il semidiametro dg nel punto v; poiché 45 gradi sono un ottavo della circonferenza, quel poligono avrà altrettanti angoli e lati. Traccia, quindi, la linea che va dal centro g al punto s, dividi la linea corrispondente al perimetro del triangolo in otto parti e fai cadere la metà di una parte parallelamente a sv, tra gs e gd, e sia questa xy. Descrivi, poi, un arco al di sopra di g con semidiametro xg fino a tagliare dg, nel punto z.
6. Successivamente, descrivi due quadranti, come ho appena fatto, disegnando precisamente il semidiametro ed uguale al semidiametro del cerchio circoscritto al triangolo e all’eccesso di questo semidiametro rispetto al semidiametro del cerchio inscritto allo stesso triangolo; segna con ef il semidiametro del secondo quadrante uguale alla linea gx o gz, più zy che è la linea del semidiametro del cerchio circoscritto all’ottagono isoperimetrico che eccede il semidiametro del cerchio inscritto allo stesso ottagono. Traccia la corda gh in modo che la freccia gd sia uguale al semidiametro del cerchio circoscritto al triangolo e un’altra corda ck in modo che fc sia uguale xg, cioè, il semidiametro del cerchio circoscritto all’ottagono13.
7. Traccia, quindi, la linea da e fino a tagliare le circonferenze, i cui segmenti compresi tra l’arco e le sue corde siano uguali, come ho detto, e siano segnate nei punti di intersezione, come in precedenza, con lm e no. Da qui cerca di conoscere ef; ed è noto, come detto prima. Anche lm, che è uguale a no, è noto. Anche el ed eg sono note e perciò è noto anche il rapporto tra el e eg e tra en e ec. Essendo no noto, cerchiamo la linea en, supponendo che sia una lunghezza qualsiasi. Stando a questa ipotesi, secondo il rapporto noto, anche la lunghezza ec sarà necessariamente nota. E se [la misura de]la lunghezza en, che ho ipotizzato, è giusta, allora esamino ef. Da quanto ipotizzato, eo sarà noto e anche cf. Si sottrae dal quadrato di cf o gx il quadrato di xy, che è noto, e la radice della parte restante sarà gy. Così sarà noto zy, e, se esso è uguale a ec, vuol dire che l’ipotesi era corretta, altrimenti si corregge l’errore, e si ricava ciò che si cerca14.
8. In questo modo saranno note tutte le corde che gli antichi, nonostante il massimo impegno, non sono riusciti a trovare15. Come sai, tutti ammettono di non essere riusciti a indicare fino a questo momento il valore preciso delle corde di un grado, due, quattro, otto, ecc. Grazie allo studio del rapporto tra gli archi e le corde si potrà determinare il rapporto dei lati e degli angoli anche di un triangolo sconosciuto e, per mezzo di tali complementi, scoprire tutto quanto è possibile sapere16.
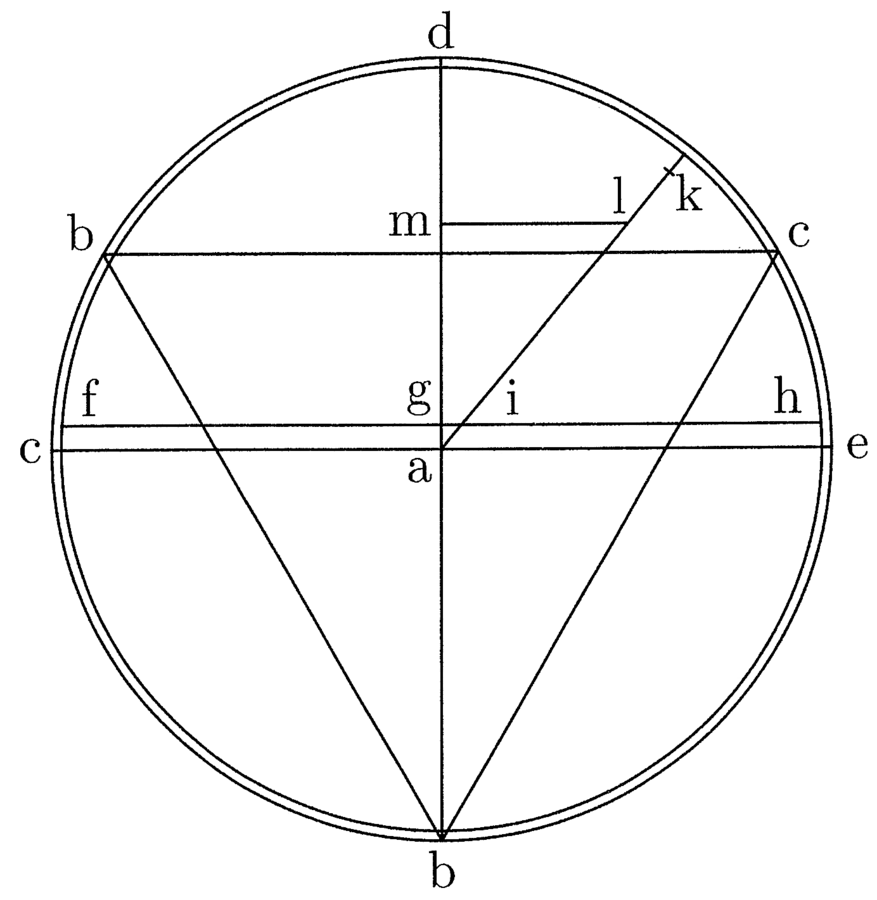
9. Riprendendo la figura del triangolo nella prima ipotesi, descrivo intorno al centro a un altro cerchio, il cui semidiametro sia uguale al semidiametro del cerchio circoscritto all’esagono isoperimetrico più l’eccesso con cui supera il semidiametro del cerchio inscritto allo stesso esagono (cfr. figura 4). Traccia i diametri che si tagliano ad angolo retto al centro e indica i punti d’intersezione [con la circonferenza] con b, c, d, e; traccia la corda, segnata con fgh, la cui freccia è uguale il semidiametro del cerchio circoscritto all’esagono. Traccia, poi, la linea aik che passa per il punto a e per la linea gh in modo da ottenere il semidiametro del cerchio circoscritto all’esagono isoperimetrico.
Segna, quindi, l’eccesso di cb della prima figura su ab della seconda, indicala sulla linea tracciata per a – e sia questa la –, traccia la linea perpendicolare da l ad ad, e indica con m il punto di contatto [con ad] . Essendo cb noto, per la posizione del lato del triangolo inscritto nel cerchio, allo stesso modo è noto ab; e lo saranno anche la e ag. Inoltre, la sta ad am come ai ad ag e, allo stesso modo, la sta ad ai come ma a ag. Si trovi, quindi, un numero che si rapporti in qualche modo a la (noto) in modo che un altro numero stia nello stesso rapporto a ag (noto). In questo modo, aggiungendo la a questo numero trovato e sottraendo questa somma da bc, si otterrà lo stesso resto di quello che si ottiene sottraendo da ab ag aggiunto all’altro numero; con ciò hai calcolato il semidiametro del cerchio. Dunque, una volta considerato il rapporto del triplo del lato del triangolo e del doppio del semidiametro, arriverai così, con una leggera approssimazione, al rapporto tra il diametro e la circonferenza17.
Note a piè pagina
I complementi
aritmetici non sono un testo di aritmetica, come il titolo
suggerirebbe, ma un breve trattato di geometria nel quale Cusano
cerca un’approssimazione di 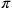 . Il termine aritmetico sta a
indicare la ricerca di un numero (costante) che permetta di
calcolare il rapporto tra il diametro di un cerchio e la
circonferenza. Non c’è nessun riferimento alla coincidentia oppositorum, nessuna allusione
al massimo e al minimo, nessun utilizzo del metodo indiretto
impiegato negli scritti successivi. Si tratta di un testo
semplicemente matematico e, se si mette da parte un cenno
all’ignoranza della ragione osservata dall’intelletto (fine §
4), il testo non presenta alcuna considerazione metafisica.
. Il termine aritmetico sta a
indicare la ricerca di un numero (costante) che permetta di
calcolare il rapporto tra il diametro di un cerchio e la
circonferenza. Non c’è nessun riferimento alla coincidentia oppositorum, nessuna allusione
al massimo e al minimo, nessun utilizzo del metodo indiretto
impiegato negli scritti successivi. Si tratta di un testo
semplicemente matematico e, se si mette da parte un cenno
all’ignoranza della ragione osservata dall’intelletto (fine §
4), il testo non presenta alcuna considerazione metafisica.
Cfr. Cusanus 2010b, 7.
È il primo riferimento esplicito ad Archimede da parte di Cusano.
Tradotto numericamente: 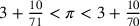 ,
dove
,
dove 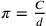 . Cfr. Archimedes 1910b, prop. 3.
. Cfr. Archimedes 1910b, prop. 3.
All’epoca per «numerus» s’intendevano i numeri interi o talvolta quelli razionali. Su questo punto Cusano si ispira a Bradwardine 1495b, III, 4, concl. 1. L’approssimazione di Archimede si trova in Archimedes 1910a, prop. 3, di cui Cusano era a conoscenza grazie al De arte mensurandi di de Muris (1998, prop. 8).
Cusano utilizza il termine «diameter» per indicare la
diagonale, in base a una etimologia inesatta da «δύο» e
«
Per «conosciuto» s’intende espresso numericamente.
La fig. 1 risulta dal trasferimento su un quadrante di due
altre figure. Il seno ef del cerchio
grande di sinistra (che è anche il semilato del triangolo
inscritto) diventa il raggio cf del
cerchio di destra, circoscritto all’esagono. A sinistra,
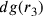 è il
raggio del cerchio circoscritto al triangolo;
è il
raggio del cerchio circoscritto al triangolo; 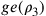 è il raggio
del cerchio inscritto al triangolo;
è il raggio
del cerchio inscritto al triangolo; 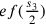 è un semilato del
triangolo. Nella seconda figura
è un semilato del
triangolo. Nella seconda figura 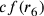 è il raggio del cerchio
circoscritto all’esagono;
è il raggio del cerchio
circoscritto all’esagono; 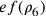 è il raggio del cerchio
inscritto all’esagono; ce è la differenza
dei due raggi
è il raggio del cerchio
inscritto all’esagono; ce è la differenza
dei due raggi 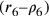 . Nella figura 2 questi
elementi diversi sono riportati sul lato del quadrante. Qui
Cusano inverte c ed e.
. Nella figura 2 questi
elementi diversi sono riportati sul lato del quadrante. Qui
Cusano inverte c ed e.
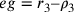 ;
; 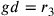 ;
; 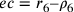 ;
; 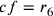 . Da ciò:
. Da ciò: 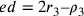 ;
; 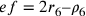 .
.
Cusano usa il termine «proportio». Si è preferito qui tradurre il termine latino con «proporzionalità», nella scia di Pacioli 1494, il quale molto probabilmente aveva letto i lavori di Cusano, così come le opere di Archimede tradotte in latino, tra il 1449 e il 1453, da Iacopo da San Cassiano (Iacobus Cremonensis). Nel 1489 Pacioli si trova a Roma, e Pierleone da Spoleto lo introduce nelle corti cardinalizie. Cfr. Giusti e Maccagni 1994; Giusti e Martelli 2010 (in part. Ulivi 2010); Esteve e Martelli 2011. La scelta della traduzione adottata è dovuta al fatto che, stando alla definizione attuale di proporzione, tra due grandezze c’è rapporto («habitudo»), e non proporzione, la quale ha luogo invece tra più rapporti: date le grandezze A, B, C, D, con A, B omogenee e C, D omogenee, si dice che sono in proporzione se il rapporto tra A e B è uguale al rapporto tra C e D. Cusano utilizza i termini «habitudo» e «proportio» con una certa leggerezza. In seguito si tradurrà tale espressione con «linee proporzionali», per rendere la lettura del testo più scorrevole.
Sul triangolo: 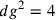 , per cui
, per cui 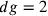 ;
; ![ge=\rho_3[=r_3–\rho_3]=1](../../../media/sources/13/20/EOAineq_20_18.png) ;
; ![ef=\frac{s_3}{2}=\sqrt{3}[=s_6]](../../../media/sources/13/20/EOAineq_20_19.png) .
Sull’esagono,
.
Sull’esagono, 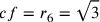 ;
; 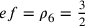
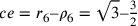 .
.
Si cercano le due grandezze el e en, tali che: el sta a
eg come en sta a
ec. 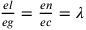 ;
;
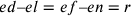 ;
si ha:
;
si ha:  ;
; 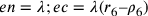 ;
;
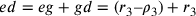 ;
; 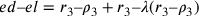 ;
;
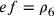 ;
;
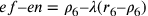 ;
;
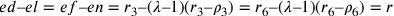 .
Risulta che
.
Risulta che 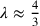 .
.
Secondo Cusano, qualunque sia il numero dei lati del poligono
si ottiene sempre lo stesso rapporto di proporzionalità tra le
corde e gli archi e quindi un valore preciso di r (il raggio del cerchio isoperimetrico ai
poligoni). Si può dire che: 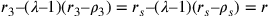 .
.
Dato n, si tratta di determinare
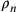 e
e
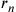 da
da 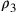 e
e 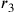 ; si ha cioè
; si ha cioè 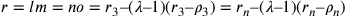 con
con 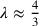 . Inoltre,
essendo
. Inoltre,
essendo 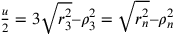 ,
si può determinare
,
si può determinare 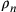 e
e  , e quindi
, e quindi 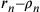 .
.
Cusano crede che sia sufficiente conoscere l’angolo per determinare il seno di un triangolo qualsiasi, e, inversamente, che sia sufficiente conoscere il seno per conoscere l’angolo. Nell’ultimo paragrafo Cusano ritornerà sulla prima premessa del De geometricis transmutationibus.
Il cerchio maggiore è il cerchio circoscritto all’esagono
aumentato del suo stesso eccesso sul cerchio inscritto. 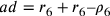 ;
;
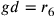 ;
; 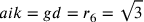 .
Cusano vuole determinare il raggio r del cerchio isoperimetrico
al triangolo equilatero BBC. Egli pone
.
Cusano vuole determinare il raggio r del cerchio isoperimetrico
al triangolo equilatero BBC. Egli pone 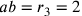 ;
; 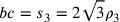 ;
; 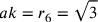 ;
; 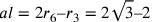 ;
;
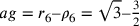 .
Introducendo le costanti
.
Introducendo le costanti 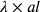 e
e 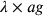 , e
ponendo
, e
ponendo 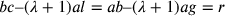 ; e
cioè:
; e
cioè: 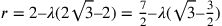 ,
si ha:
,
si ha: 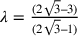 ;
;
![r\approx2[\frac{(7\sqrt{3}–10)}{(2\sqrt{3}–1)}]=1,72](../../../media/sources/13/20/EOAineq_20_57.png) anziché 1,65 e
anziché 1,65 e ![\pi=\frac{(3\sqrt{3})}{2}[\frac{(2\sqrt{3}–1)}{(7\sqrt{3}–10)}]=\frac{[3(39+32\sqrt{3})]}{94}=3,01](../../../media/sources/13/20/EOAineq_20_58.png) ,
che risulta un valore decisamente approssimativo.
,
che risulta un valore decisamente approssimativo.