Quadratura circuli Nicolai de Cusa cardinalis, legati, episcopi brixinensis

1. Quamvis iam dudum a studio geometrico nos altior speculatio ac publica retraxerit utilitas, tamen inter innumeras seriosas curas, quas habet apostolica legatio, se inter colloquia studiosorum delectabiliter immiscuit de quadratura circuli scibili et non scita assertio, quam dum nuper equitando revolveremus, quod attigimus, conscripsimus.

2. Non legimus quemquam propinquius accessisse ad huius notitiam quam Archimedem, qui primo quadrangulum circulo aequari ostendit, in quo semidiameter circuli ducta est in mediam peripheriam. Hoc quidem sic esse necesse est, si hoc censendum est: esse aequale, quod nec maius nec minus esse convincitur. In omnibus enim polygoniis isopleuris et isoperimetris, de quibus solum in hoc scripto loquimur, semidiameter circuli inscripti si ducitur in medietatem peripheriae, oritur quadrangulum aequale. Posse autem inter semidiametrum et medietatem peripheriae medium proportionale facile constitui Euclides ostendit. Quare tale cum sit latus quadrati aequivalentis, conscito quae linea recta aequetur peripheriae circuli, scitur et eius quadratura, et haec est certior ostensio. Sed dum per helicam hanc ultimam partem se reperisse crederet Archimedes, a vero defecit. Helica enim describi nequit nisi signum a centro per semidiametrum in tanto tempore moveatur, in quanto semidiameter pro circuli descriptione circumvolvitur. Descriptio igitur helicae hos motus supponit, quorum habitudo est ut semidiametri ad circumferentiam. Praesupponit igitur id, quod quaerit. Citius enim recta dari potest circulari lineae aequalis quam helica vera figurari.

3. Nos autem considerantes trigonum et circulum in capacitate extrema loca tenere: in trigono semidiametros circulorum, et inscripti et circumscripti, contrario modo se habere cum semidiametro circuli, in quo circuli inscriptus et circumscriptus coincidunt, qui differunt in trigono maxime, esseque ibi semidiametrum circumscripti maximam et inscripti minimam et simul iunctas brevissimas; contrario modo in circulo, ubi simul iunctae sunt diameter circuli maximae. Ob hoc scimus omnes medias polygonias isoperimetras et isopleuras secundum capacitatem in illis ad aequalitatem semidiametri circuli accedere. Si igitur signata fuerit quantitas excessus semidiametri circuli super semidiametrum inscripti trigono et quantitas, qua ipsa semidiameter circuli fuerit minor semidiametro circumscripti trigono, tunc omnis polygonia media secundum suam capacitatem in excessu semidiametri sibi inscripti super semidiametrum inscripti trigono et diminutione semidiametri sibi circumscripti a semidiametro circumscripti trigono proportionaliter se habebit. Nam cum illa ex diversa capacitate varientur, non potest diversa esse habitudo illorum ab habitudine capacitatum. Sic semper necesse est, quod sicut se habet excessus ad excessum, etiam sic se habeat diminutio ad diminutionem, cum capacitas ita sequatur unam diversitatem sicut aliam, et non plus nec minus unam quam aliam. Erunt igitur in omnibus polygoniis excessus et diminutio tales se ad invicem habentes in proportione una. Quare data una habitudine per illorum scientiam in nota aliqua polygonia tunc scitur et in circulo. Et quia excessus et diminutio in circulo simul iuncti aequantur semidiametro inscripti trigono, ut de se patet, igitur si reperta habitudine divideretur secundum eam semidiameter inscripti trigono et maior portio adderetur ad ipsam semidiametrum circuli inscripti trigono, haberetur semidiameter circuli isoperimetri et ita omne quaesitum.

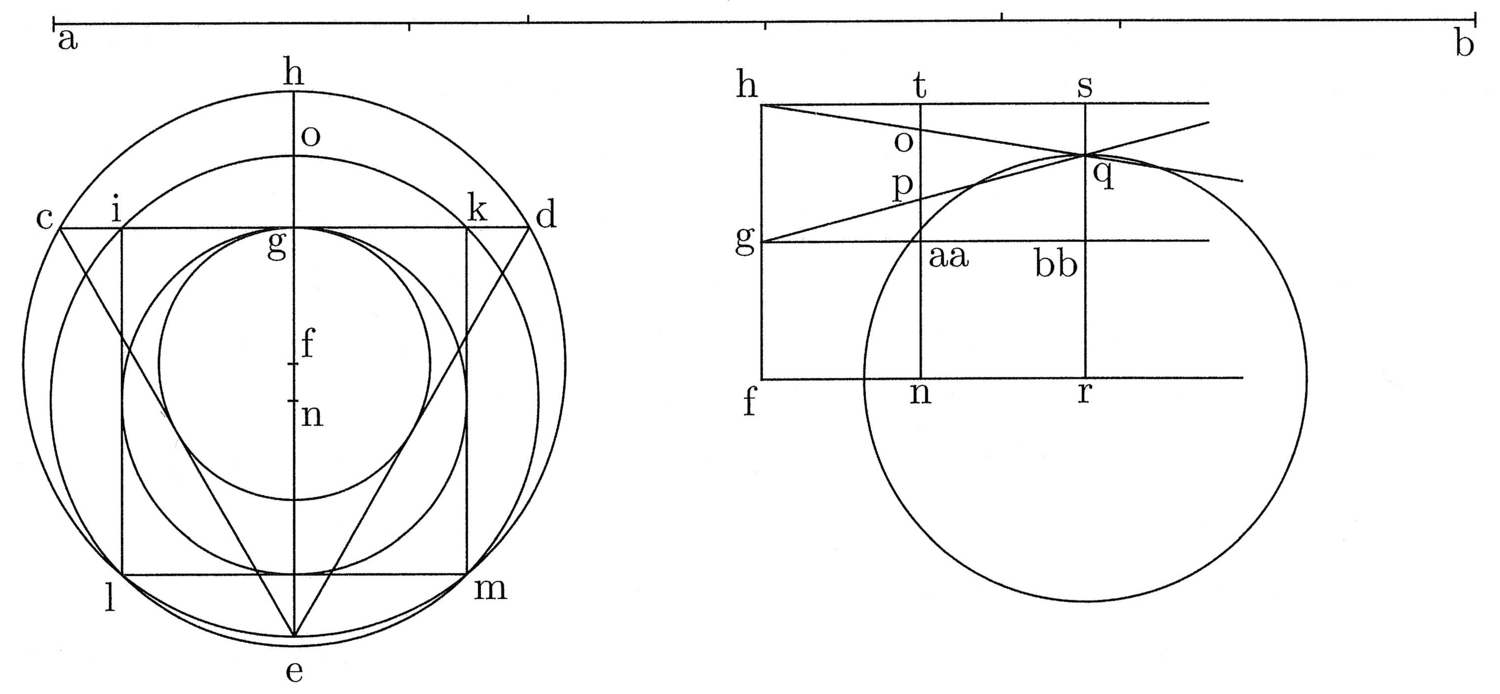
4. Faciemus autem hanc partem tibi hoc modo clariorem (cfr. figura 1). Ex ab linea in tres partes divisa cde triangulus designetur, et in eius latere cd signetur pars quarta ab, quae sit ik, quae quadretur, et sit iklm. Describantur inscripti et circumscripti circuli, et sit inscripti trigono semidiameter fg et circumscripti fh et inscripti tetragono ng, circumscripti no. Signetur deinde linea fh et in eius medio g. Lineis de f, g, h tractis quantumlibet trahatur ad fh aequedistans tn, cuius medium sit aa, et signetur semidiameter inscripti alicuius polygoniae isoperimetrae, puta tetragonae, quae sit np, et semidiameter circumscripti, quae sit no. Et trahe de g per p ‹lineam› in infinitum et similiter de h per o lineam in infinitum, et ubi illae concurrunt, signa q. Trahe per q aequedistantem ad fh, quae sit sr, in cuius medio signa bb. Dicimus rq esse semidiametrum circuli quaesiti et eius circumferentiam aequalem ab lineae rectae.

5. Multipliciter probatur et faciliter. Servata igitur priori figura ponatur g bb lineam esse differentiam capacitatum trigoni et circuli isoperimetri et quod linea de rs moveatur versus fh aequedistanter. Manifestum est lineas hq et gq de illa abscindere omnes differentias semidiametrorum circulorum inscriptorum et circumscriptorum omnium figurarum polygoniarum de trigono usque ad circulum, ubi coincidunt. Est etiam manifestum, quod simul linea illa mota abscindet de linea bb g omnes differentias capacitatum inter trigonum et circulum. Nam quanto differentia semidiametrorum dictarum est minor, tanto figura capacior, ideo circulus capacissima figurarum, quia ibi coincidunt, et trigonus minimae capacitatis, quia ibi maxime differunt. Sit igitur linea mota tn, quae abscindat lineam g bb in aa puncto, et sit po differentia semidiametrorum in tetragono. Quare si g bb est ut differentia capacitatum trigoni et circuli isoperimetri, erit g aa ut differentia capacitatum trigoni et tetragoni. Et quia np est ex praesupposito semidiameter inscripti tetragono et aa p excessus eius super fg semidiametrum inscripti trigono, ideo bb q erit excessus semidiametri circuli isoperimetri super semidiametrum inscripti trigono. Nam quae proportio bb g ad aa g, illa bb q ad aa p, ut notum est. Correspondent autem differentiae semidiametrorum inscriptorum in polygoniis isoperimetris cum differentiis capacitatum. Non enim evenit aliunde capacitatum differentia in isopleuris et isoperimetris nisi ex semidiametrorum circulorum inscriptorum differentia, quoniam capacitas ex multiplicatione illius semidiametri, quae variatur in diversis talibus figuris, in semiperipheriam, quae semper est eadem, exoritur, ut est notum. Sic si posueris bb s, lineam duorum excessuum semidiametrorum, ut excessum capacitatis circuli super trigonum, erit in tetragono excessus talis capacitatis ut linea aequalis duabus to et p aa lineis, et quia una est habitudo illius ad s bb quae p aa ad bb q, igitur ut supra. Vel si dixeris capacitatem trigoni minorem esse quam circuli, ut linea hg, erit tetragoni minor ut po.

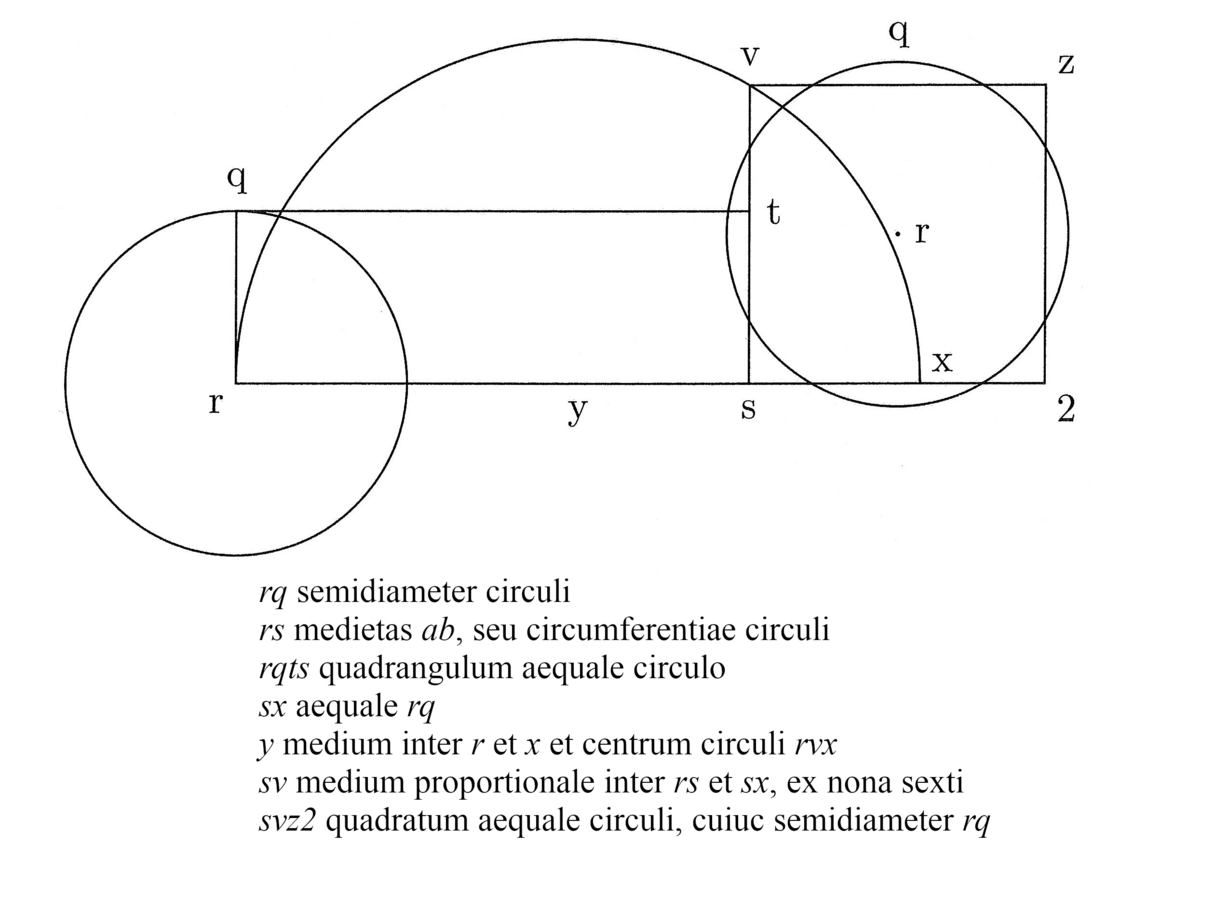
6. Si adhuc negaveris et dixeris semidiametrum circuli minorem esse, puta quod terminetur in puncto medio inter s et terminum lineae g, quae sit v, ita quod rv sit semidiameter circuli isoperimetri, tunc si sic extendatur vs, quousque aequetur rv, et sit rx, et similiter extendatur fh ad aequalitatem rx, et sit fz ut rx; trahe zx lineam, deinde trahe de v lineas ad g et h, et ubi secaverint tn lineam, signa 2 et 9, et tn extendatur usque ad zx, et sit cc n ut rx (cfr. figura 2). Dico, quod si semidiameter inscripti circulo isoperimetro addit super semidiametrum inscripti trigono, quantum est bb v, tunc semidiameter inscripti tetragono addit, quantum est aa 2. Igitur si semidiameter inscripti tetragono addit, quantum est aa p, tunc semidiameter circuli isoperimetri addit, quantum est bb q. Hoc de se patet, si habitudo additionum est ut bb v ad aa 2, et nota est additio in tetragono, quae est ut aa p; igitur erit in circulo ut bb q, cum una sit habitudo aa p ad bb q quae aa 2 ad bb v.

7. Quod autem illa sit habitudo, probatur. Nam si rv ponatur semidiameter inscripti circulo, erit vx semidiameter circumscripti, quae coincidunt in circulo isoperimetro. Et manifestum est, quod rx est linea ex duabus illis semidiametris, et similiter fz est linea illi aequalis et est ex semidiametro inscripti trigono et semidiametro circumscripti eidem. Omnium igitur polygoniarum inter trigonum et circulum duae semidiametri tales non erunt minores fz nec maiores rx et ita semper aequales. Erit igitur n cc aequalis duabus illis semidiametris in tetragono. Et quia 2 9 aequatur necessario po, cum ghq triangulus aequetur ghv ob aequedistantiam qv et gh et similiter o 2 sit aequedistans ad gh, hinc 9 2 erit ut po, ut ex Euclide scilicet 37a primi et 4ta sexti notum tibi existit. Sed po est excessus semidiametri circumscripti tetragono super semidiametrum inscripti eidem, igitur et 2 9. Et cum n 2 aequetur cc 9, igitur n 2 erit ut semidiameter inscripti tetragono et 2 cc ut semidiameter circumscripti eidem. Si igitur ponitur semidiametrum circuli super semidiametrum inscripti trigono addere, quantum est bb v, addet necessario semidiameter inscripti tetragono, quantum est aa 2. Et hae additiones possent capacitates super capacitatem trigoni nominari, cum in isopleuris et isoperimetris capacitatum excessus ex his solum proveniat. Habitudo igitur additionum erit ut aa 2 ad bb v, quod erat probandum. Et ita in omnibus polygoniis pariformiter procedi poterit sicut in tetragono. Ex hoc constat propositum (cfr. figura 3).

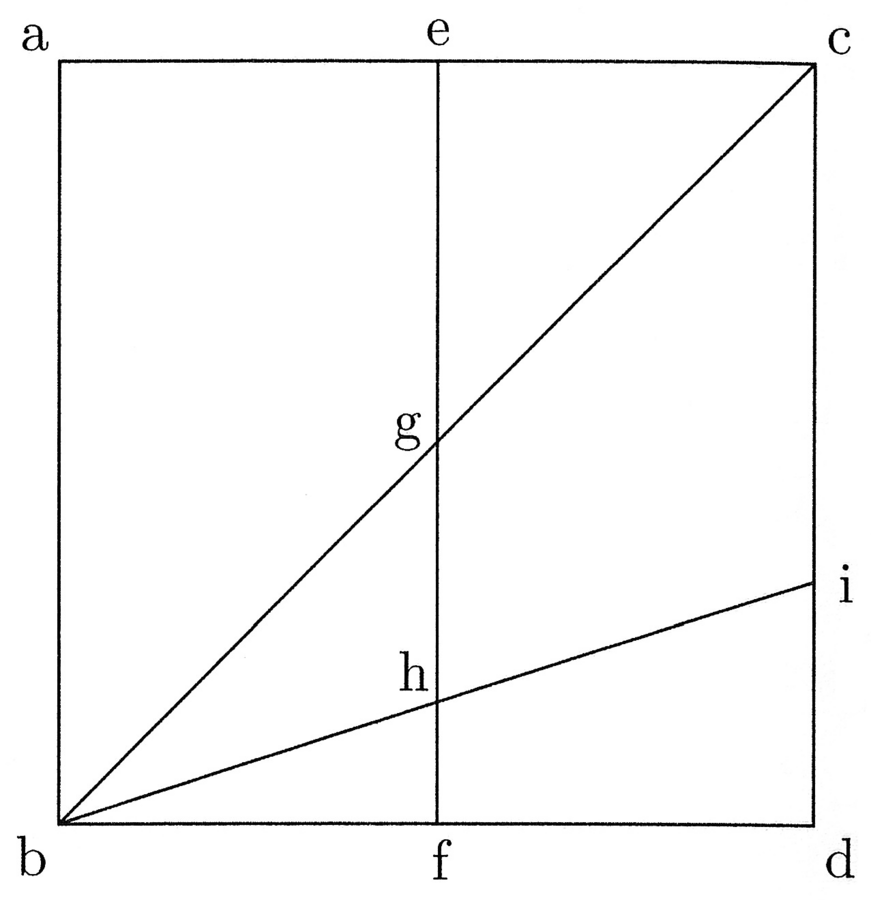
8. Adhuc aliter. Capacitas circuli super capacitatem trigoni est maxima et differentia semidiametrorum circulorum inscripti et circumscripti est nulla seu minima simpliciter, quia minor esse nequit. Sed differentia semidiametrorum circulorum inscripti et circumscripti trigono est maxima, capacitas vero eius super sui ipsius capacitatem est nulla vel minima simpliciter. Esto igitur, quod aliqua linea sit ut differentia semidiametrorum in trigono et etiam sit ut capacitas circuli super trigonum, quae sit ab linea (cfr. figura 4). Quadretur igitur illa et sit quadratum abcd, et sit ab ut differentia semidiametrorum cum illa minima capacitate trigoni super sui ipsius capacitatem, et cd capacitas circuli super trigonum cum illa minima differentia semidiametrorum talium, et trahatur linea diametralis bc. Dico in omnibus polygoniis mediis inter trigonum et circulum lineas capacitatis super capacitatem trigoni cum differentia semidiametrorum non posse esse maiores nec minores ab aut cd, ut de se patet. Esto igitur, quod trahatur ef linea aequalis et aequidistans ad ab et cd, et illa secetur per bc in puncto g, et sit ge ut differentia semidiametrorum talium in tetragono. Manifestum est, quod gf erit ut capacitas tetragoni super trigonum. Erit igitur habitudo capacitatis tetragoni super capacitatem trigoni ad capacitatem circuli super capacitatem trigoni ut gf ad cd. Signatur igitur in fg additio semidiametri inscripti tetragono super semidiametrum inscripti trigono, et sit fh et trahatur de b per h ad cd linea, et contactus sit i. Dico quod di est additio semidiametri circuli isoperimetri super semidiametrum inscripti trigono. Quae enim est habitudo fg ad dc, illa fh ad di. Sed diversitas capacitatis in isopleuris et isoperimetris super capacitatem trigoni non evenit nisi ex diversa additione semidiametrorum circulorum inscriptorum super semidiametrum inscripti trigono. Quae igitur est habitudo capacitatum super trigonum, illa est additionum semidiametrorum inscriptorum super semidiametrum circuli inscripti trigono. Per hoc patet quaesitum.

Eiusdem de sinibus et chordis

9. Ex his nunc circa chordas et arcus scientia perfecta elici poterit. Nam si una est habitudo eius, quod addit semidiameter inscripti polygoniae isopleurae et isoperimetrae post trigonum super semidiametrum inscripti trigono ad id, quod addit semidiameter circumscripti trigono super semidiametrum circumscripti illi polygoniae, et si illae additiones una cum differentia seu sagitta simul iunctae aequivalent sagittae lateris trigoni, ut ex praemissis clare constat: tunc scita habitudine talium additionum, quae tamen numero non attingitur sicut nec medietas duplae, ars est reperta ad omne scibile in chordis et arcubus.

10. Quae autem sit habitudo additionum sic in propinquis numeris investigatur. Esto quod semidiameter circuli trigono circumscripti sit 14. Erit semidiameter inscripti 7, cuius quadratum 49, et quadratum semilateris trigoni ter tantum, scilicet 147, et quadratum semidiametri circumscripti quater tantum, scilicet 196. Erit igitur semilatus tetragoni radix 9/16 [et] quadrati semilateris trigoni, scilicet radix de 82 cum 11/16, et talis erit semidiameter inscripti. Erit autem semidiameter circumscripti radix dupli numeri, scilicet 165 cum 6/16. Subtracta igitur radice de 49 a radice de 82 et 11/16 differentia est additio semidiametri inscripti tetragono super semidiametrum inscripti trigono, quae erit aliquid plus quam duo, et subtracta radice de 165 cum 6/16 a radice de 196, quae erit parum plus quam unum, habes additiones, et earum habitudo est illa, per quam omnia investigantur. Nam si has additiones subtraxeris a sagitta lateris trigoni, scilicet 7, remanet sagitta tetragoni. Si igitur diviseris 7 secundum praefatam additionum habitudinem et maiorem addideris super semidiametrum inscripti trigono, habes semidiametrum circuli isoperimetri.

11. Poteris etiam ex quadrato lateris trigoni aut quadrati scire sic quadratum lateris cuiuslibet polygoniae dabilis, et ex eius scientia et habitudine additionum devenitur ad sagittam et semidiametrum inscripti, et sic scitur chorda. Et haec est perfectio ultima geometricae artis, ad quam hactenus veteres non legimus devenisse. Est etiam nunc ars completa geometricarum transmutationum, quam ante minus, tamen sufficienter quoad quadraturam circuli descripsimus.

12. Et putamus nihil scibilis in geometricis nunc volenti diligenter in hoc medio inquirere remanere occultum. Haec sic maxime scripserim, ut videatur potentia artis coincidentiarum, per quam in omni facultate occulta penetrantur. Ex sola enim coincidentia semidiametrorum inscripti et circumscripti circulorum in omnibus polygoniis differentium et in circulo tantum coincidentium inquisitio nos ad praemissa perduxit.

Laus Deo.