1. A Paolo, [figlio] del maestro Domenico, fisico fiorentino, uomo eccellente e dottissimo, il libro sulle trasformazioni geometriche del cardinale Niccolò da Cusa1.
2. Sebbene gli antichi dotati di grande ingegno abbiano tentato, attraverso una diligente ricerca, di conoscere e trasmettere ai posteri molte cose un tempo oscure, e abbiano fatto utili progressi in molte delle arti più importanti e più nobili, tuttavia, nelle riflessioni più profonde, non hanno raggiunto tutto ciò che desideravano. Il sommo protettore di tutte le cose ha prestabilito questo universo affinché in noi la forza divina di comprendere non si indebolisse, ma fosse rivolta con interesse ancor più vivo a quelle cose che sono nascoste, ma accessibili alla conoscenza. E certamente più forte è la passione con cui siamo spinti ad esplorare ciò che è oscuro, maggiore è la tranquillità con cui ci compiaciamo della potenza della nostra mente. Tuttavia, tra le questioni che sono state d’ostacolo alle faticose speculazioni geometriche, ce n’è una che è rimasta sconosciuta a tutti quelli il cui spessore intellettuale è stato particolarmente apprezzato dai libri a noi tramandati, ossia la possibilità di stabilire un’uguaglianza tra ciò che è retto e ciò che è curvo2 o la loro reciproca trasformazione. A causa dell’impossibilità dell’impresa e per il fatto che la natura ripugna la coincidenza di un’opposizione tanto grande, alla maggior parte di coloro che si sono dedicati a questa ricerca, dopo immensi sforzi, è sembrato che fosse a noi negata la via per giungere a tale conoscenza. Io, invece, pensando che la difficoltà di questa ricerca stesse piuttosto nella debolezza della [mia] conoscenza e nell’incostanza della [mia] attenzione, non avendo un acume particolarmente spiccato tra coloro che vi si dedicano – acume che l’oscurità dell’argomento richiede –, nel tempo libero che avevo a disposizione mi sono dedicato alla nuova arte3, affinché con essa potessi raggiungere ciò che cercavo, e, in vista di fini più elevati, ho faticato molto su di essa, finché ho trovato, tra tutte le mie riflessioni, la seguente facile soluzione. Tuttavia, poiché non potevo confidare nell’oscurità e nella debolezza del mio ingegno per comprendere un’arte così importante e finora sconosciuta, dalla quale non soltanto dipende la perfezione della trasformazione geometrica, ma si delinea anche un’introduzione a studi più elevati, ho deciso di ricorrere direttamente a te, esaminatore espertissimo e difensore zelante della verità, e di rivelare senza indugio il risultato della mia ricerca a un amico coltissimo, affinché esso sia valutato sulla bilancia del giudice più equilibrato. Pertanto, carissimo amico, anche se ti occupi di cose ben più impegnative, non disprezzare questo mio lavoro come rozzo e confuso; essendo corto, si legge velocemente e si comprende molto facilmente. Dunque, in nome dell’amicizia e dell’affetto cordiale che ci lega così tanto e ininterrottamente dagli anni della gioventù e dell’adolescenza, ti prego ora di prestare massima attenzione alla correzione, e di non parlarne ad altri, se non dopo aver apportato le dovute correzioni.
3. Dopo innumerevoli tentativi nei quali mi sono sforzato – tuttavia sempre vanamente – di pervenire all’arte intrapresa4, rivolgendo l’attenzione al principio di cui mi ero servito ne La dotta ignoranza5, mi si è aperta la strada. Inoltre, l’arte che cercavo, oltre a ciò che è stato già tramandato in geometria, permette la trasformazione di ciò che è curvo in ciò che è retto e di ciò che è retto in ciò che è curvo. Poiché il rapporto tra queste grandezze non è esprimibile attraverso un numero razionale, è necessario che il segreto di tale rapporto si celi proprio nella coincidenza degli estremi. Poiché essa ha luogo nel massimo – com’è stato esposto altrove – e il massimo è il cerchio che non si conosce, si dimostra qui che lo stesso deve essere cercato nel minimo, che è il triangolo6.
4. Ora, si chiamano poligoni tutte le figure con molti angoli, equilateri quelle che hanno lati uguali, isoperimetrici quelle che, avendo la stessa lunghezza dei lati, hanno lo stesso perimetro7; è evidente che, tra di essi, il triangolo ha l’ampiezza8 minore. E, poiché un isoperimetrico è tanto più ampio quanto più angoli avrà, il cerchio sarà la figura con la superficie più ampia tra tutte quelle isoperimetriche9. A questa, tuttavia, non si può arrivare moltiplicando gli angoli10, così come non si può determinare il massimo numericamente. Dunque, nessun poligono può avere con la figura circolare isoperimetrica un rapporto esprimibile attraverso un numero razionale.
5. Ma, poiché la differenza di ampiezza tra le figure isoperimetriche corrisponde alle differenze [dei semidiametri] dei cerchi inscritti ad esse11, come è stato già precedentemente osservato, allora né il cerchio inscritto, che è sempre minore, né il cerchio circoscritto, che è sempre maggiore, avrà con il cerchio isoperimetrico un rapporto esprimibile attraverso un numero razionale12. Ma i semidiametri di questi cerchi, di cui abbiamo parlato, sono massimamente disuguali nel triangolo, [dove la differenza è massima], mentre sono progressivamente meno disuguali negli altri [dove la differenza diminuisce]; mentre nel cerchio essi coincidono, poiché, in questo caso, l’inscritto, il circoscritto e la circonferenza coincidono. Bisogna cercare attraverso quale arte vogliamo arrivare a quella coincidenza e a ciò che ci siamo proposti.
6. Ora, per giungere all’arte cercata, sembra che sia necessario: in primo luogo, che a una data retta sia data una curva uguale13; in secondo luogo, che il rapporto tra una curva e l’altra sia lo stesso di quello tra una retta e l’altra; in terzo luogo, che, tra linee date, se ne assegnino due proporzionali; in quarto luogo, che, secondo il rapporto di due rette date, si sappia che a una terza data si dà una quarta14. Il primo punto è stato sin qui sconosciuto, il secondo non è stato ancora esaminato, il terzo è stato trattato da pochi in modo confuso15, il quarto è stato chiaramente spiegato da molti. In questi quattro punti è racchiuso tutto ciò che è utile all’arte della trasformazione, come cercherò di spiegare negli esempi qui sotto riportati, grazie alle seguenti premesse che sono necessarie a tale scopo.
Prima premessa
7. Tutti ammettono che sia possibile che una linea curva non sia né maggiore né minore di una linea retta data, ma non tutti affermano che essa possa essere trovata. Dunque, è possibile che la circonferenza di un qualsiasi cerchio non sia né maggiore né minore del perimetro di un dato poligono, così che queste figure risultino isoperimetriche. Ma come si possa ottenere ciò, è appunto quello che vogliamo indagare16.
8. Poiché il cerchio circoscritto a un poligono equilatero, ossia equiangolo17, è tanto maggiore quanto meno angoli il poligono ha – e quello inscritto tanto minore –, allora nessuno può negare che ogni cerchio inscritto a un poligono equilatero è minore del cerchio isoperimetrico e che ogni cerchio circoscritto è maggiore. Di conseguenza, poiché l’isoperimetrico cade tra l’inscritto e il circoscritto, esso ha un semidiametro maggiore di ogni semidiametro di qualsiasi cerchio inscritto a un qualsiasi poligono isoperimetrico e minore del semidiametro del circoscritto18. Dopo tanti procedimenti ben più difficili, ciò che cerchiamo si paleserà invece come la semplice conseguenza di questa proposizione.
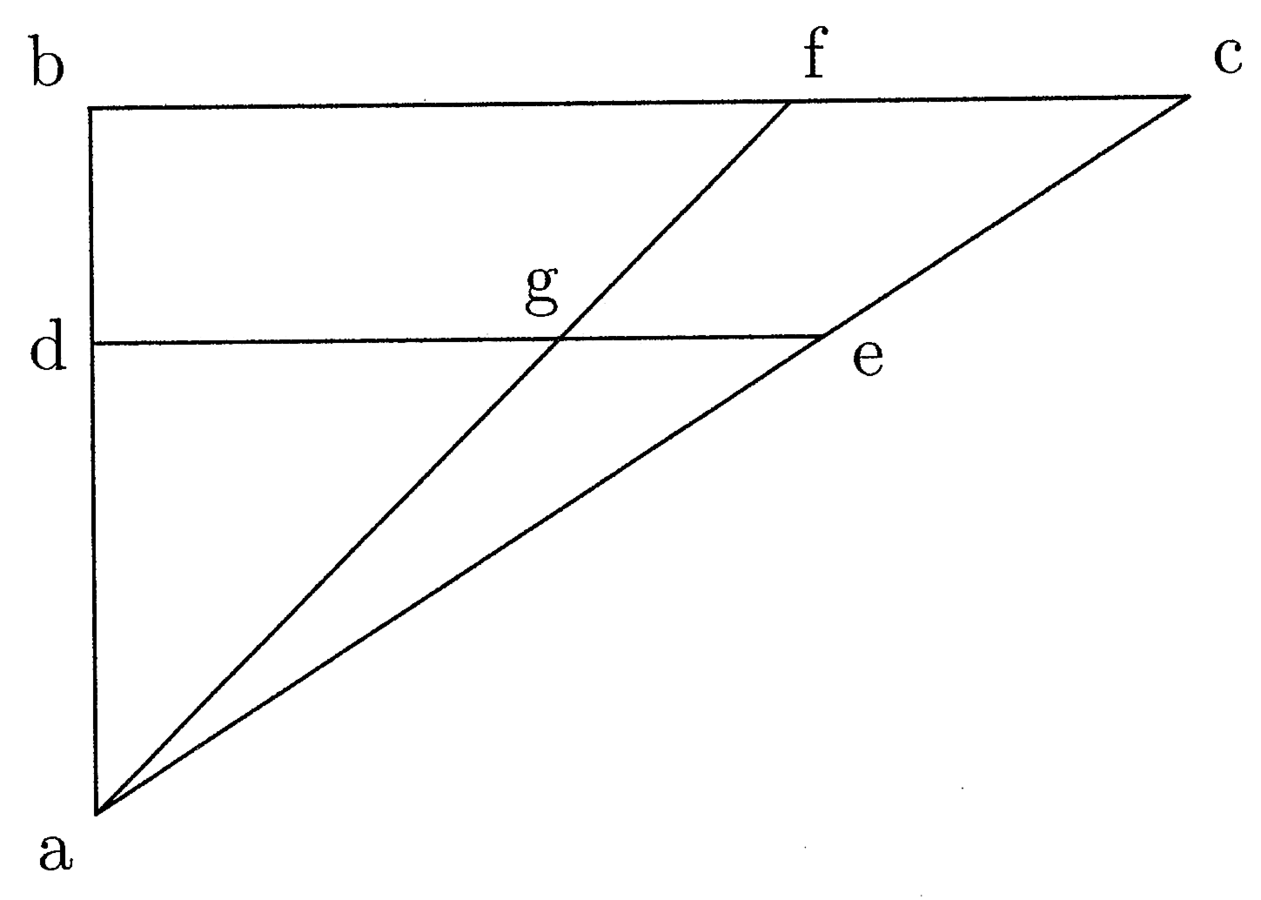
9. Il semidiametro del cerchio isoperimetrico al triangolo inscritto si rapporta alla linea tracciata dal centro del cerchio, al quale il triangolo è inscritto, al punto che segna la quarta parte del lato [del triangolo] secondo un rapporto di 5 a 419.
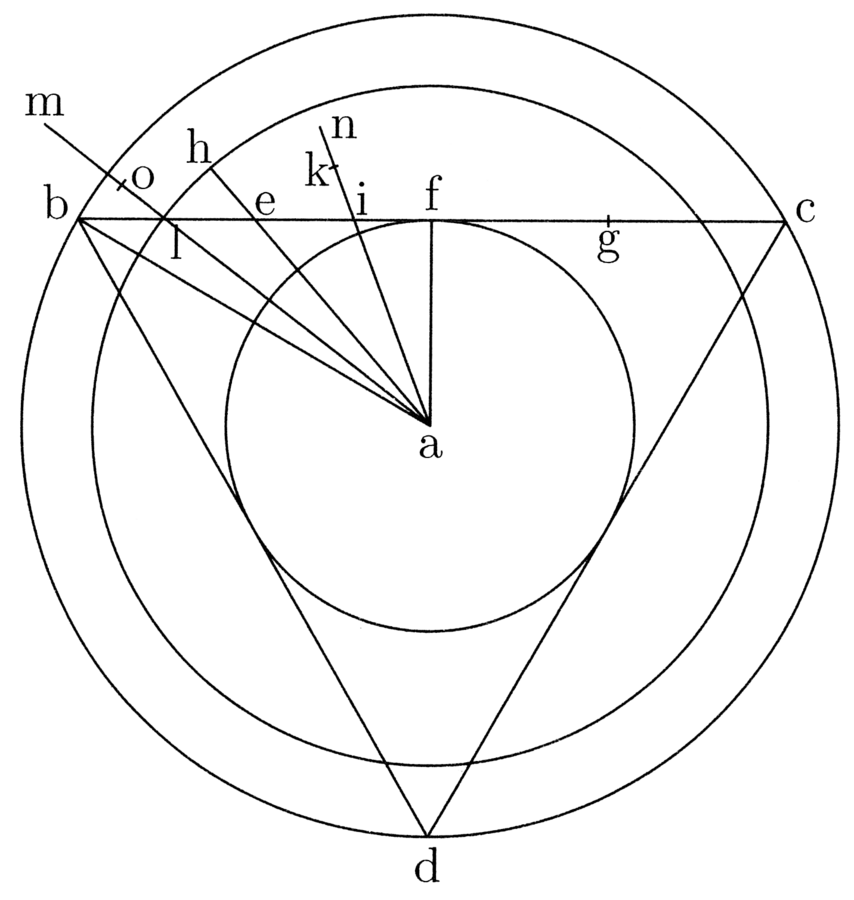
10. Intorno al centro a si descriva un cerchio, nel quale è inscritto il triangolo BCD, con il lato bc diviso in quattro parti uguali attraverso [i punti] e, f, g; dico che, se si prolunga la linea tracciata da a a e di un quarto della sua lunghezza, ottenendo così ah, allora questa sarà il semidiametro del cerchio la cui circonferenza è uguale [alla somma dei] tre lati del triangolo20(cfr. figura 1).
11. Ciò può essere provato molto facilmente in questo modo. Infatti, è chiaro che la linea tracciata da a a f sarà il semidiametro del cerchio inscritto, e precisamente la più piccola di tutti i cerchi inscritti ai poligoni isoperimetrici; e, nello stesso modo, la linea tracciata da a a b sarà il semidiametro del cerchio circoscritto, e precisamente la più grande di tutti i cerchi circoscritti ai poligoni isoperimetrici.
Se tracci una linea da a a i (vicino a f) e la prolunghi secondo il rapporto del segmento21 if sul lato di bc, ottenendo così ak, è chiaro che essa sarà minore del semidiametro del cerchio isoperimetrico, essendo quest’ultimo il più grande di tutti i semidiametri dei cerchi inscritti ai poligoni isoperimetrici. Analogamente, se si prolunga la linea tracciata da a al punto l (vicino a b) secondo il rapporto del segmento di lf su bc, ottenendo così am, è chiaro che essa sarà maggiore di quella cercata, poiché quella che cerchiamo è la più piccola di tutti i ‹semi›diametri dei cerchi circoscritti ai poligoni isoperimetrici. Si può, pertanto, tracciare una linea da a verso qualsiasi punto tra l e i che, prolungata secondo il rapporto del segmento che cade tra questo punto e f sul lato bc, sarà uguale alla linea che cerchiamo22.
12. Allo stesso modo, se si prolunga la linea ai secondo il rapporto di ib su bc, ottenendo così an, è chiaro che questa sarà minore di quella che cerchiamo. E ancora, se si prolunga al secondo il rapporto di lb su bc, ottenendo così ao, è certo che essa sarà maggiore di quella che cerchiamo. C’è, quindi, un punto tra l e i verso cui si traccia la linea da a, tale che, prolungando la linea secondo il rapporto del segmento che si trova tra questo punto e b sul lato bc, essa sarà uguale a quella che cerchiamo. Da qui, trovato il punto, per esempio i, verso cui si traccia una linea da a, se si prolunga quest’ultima secondo il rapporto di entrambi i segmenti (verso b e verso f) sul lato del triangolo, allora essa resta minore; e si trova un altro punto, per esempio l, verso cui è tracciata una linea, che, prolungata secondo il rapporto dell’uno o dell’altro segmento sul lato del triangolo, risulterà sempre maggiore di quella che cerchiamo. Così, ci sarà un terzo punto, verso cui è tracciata una linea da a, che, prolungata secondo il rapporto di qualsiasi segmento sul lato del triangolo, non sarà né maggiore né minore di quella che cerchiamo. È chiaro che questo punto non può che essere e, poiché soltanto in esso il prolungamento secondo i rapporti dell’uno e dell’altro segmento può essere lo stesso23.
13. Potrai anche dire che, se la linea ai si prolunga secondo il rapporto di fi su bc, essa è minore, e, analogamente, se viene prolungata secondo il rapporto del quadrato di if sul quadrato di bf, essa è minore. E se al si prolunga secondo il rapporto di lf su bc, essa è maggiore; analogamente, se viene prolungata secondo il rapporto del quadrato di lf sul quadrato di bf, essa è maggiore. Ci sarà, dunque, un punto tra l e i tale che la linea tracciata dal centro a a questo punto e prolungata secondo i due rapporti già menzionati non sarà né maggiore né minore [di quella cercata] e questo punto è necessariamente e.
14. Potrai ancora aggiungere un terzo rapporto: se ai si prolunga secondo il rapporto del quadrato di if sul quadrato di bf, secondo il rapporto di if su bc e secondo il rapporto di bi su bc, essa sarà sempre minore, e prolungando al secondo quei rapporti, essa sarà maggiore. Ci sarà, dunque, un punto tale che la linea tracciata dal centro a verso tale punto e prolungata secondo quei tre rapporti non sarà né maggiore né minore di quella cercata e questo è il punto e, equidistante da b e da f24.
15. Ciò può essere tuttavia dimostrato anche in questo modo: è chiaro che in tutti i poligoni isoperimetrici la linea tracciata dal centro al punto medio del lato è il semidiametro del cerchio inscritto; e quanto maggiore è l'ampiezza del poligono, tanto più la linea si avvicinerà al semidiametro del cerchio isoperimetrico; allo stesso modo, la linea tracciata dal centro all’estremità del lato è il semidiametro del cerchio circoscritto e sarà progressivamente tanto minore quanto più ampio sarà il poligono. Dunque, tra questi due punti, cioè, tra l’estremità e il punto medio del lato di un poligono, cade un solo punto tale che la linea tracciata dal centro e prolungata secondo il rapporto del quadrato del segmento compreso tra il punto d’intersezione e il punto medio del lato e il quadrato del semilato, o prolungata secondo il rapporto del segmento sul lato, sarà uguale al semidiametro del cerchio isoperimetrico. Su ciò non ci può essere alcun dubbio.
16. Capita tuttavia che nei diversi poligoni questo punto si trovi a una diversa distanza dagli altri due punti, vale a dire, dall’estremità e dal punto medio del lato: quanto più ampio è il poligono, tanto più ci si avvicina al punto medio del lato e ci si allontana dall’estremità. Pertanto nei poligoni più estesi questo punto si avvicina progressivamente alla metà del lato fino a coincidere con tutti e tre i punti nel poligono più ampio; analogamente, è necessario che nei poligoni meno ampi questo punto si allontani dalla metà del lato fino a raggiungere la massima distanza da questi due punti nel poligono minore. Di conseguenza, questo punto medio, che ha la stessa massima distanza dalle estremità, è il punto e, e, nel triangolo, che è la figura meno ampia, questo punto è ciò che si cercava. Perciò ogni semidiametro del cerchio circoscritto cade tra il centro a e qualche punto della linea be prolungata secondo i rapporti premessi del segmento prolungato verso b, e così ae, prolungata in questo modo, è la più piccola di tutte le altre linee; essa è il semidiametro del cerchio isoperimetrico, poiché è il più piccolo semidiametro di tutti i semidiametri dei cerchi che si possono circoscrivere, con cui coincide il semidiametro più grande dei cerchi che si possono inscrivere. Perciò nel punto e si realizza la coincidenza dei semidiametri dei cerchi inscrivibili che crescono da f verso e e i semidiametri dei cerchi circoscrivibili che decrescono da b verso e, una volta che sono stati apportati i prolungamenti secondo i rapporti premessi dei segmenti verso b da un lato e verso f dall’altro25.
Seconda premessa
17. Ho già sostenuto precedentemente26 che si deve premettere come si giunge al rapporto tra una retta e l’altra, e a quello tra una curva e l’altra, poiché, come dimostrerà ciò che segue, la perfezione dell’arte delle trasformazioni che cerchiamo non potrà essere ottenuta senza tener conto di quest’aspetto. E, per questa indagine, ho preso in considerazione un triangolo rettilineo27 nel quale la linea tracciata dal segmento di un lato al corrispondente segmento di un altro lato sia parallela al [terzo] lato che chiude il triangolo, e stia a quest'ultimo nello stesso rapporto con cui il segmento del primo lato, da cui è stata tracciata la linea, sta all’intero lato. Volendo cercare in un arco ciò che ho trovato nel lato dritto, ho notato che se disegnassi il triangolo con un lato curvo e un altro dritto, allora non si potrebbe tracciare dalla parte del lato curvo al corrispondente segmento dell’altro lato alcuna linea che stia al lato dritto secondo il rapporto cercato, se il terzo lato fosse dritto. Infatti, se il lato curvo fosse convesso, è chiaro che una linea dritta tracciata dalla sua metà alla metà del lato dritto sarebbe maggiore della metà del lato dritto che chiude il triangolo. E se invece fosse concavo, la linea dritta tracciata dalla sua metà alla metà del lato dritto sarebbe necessariamente minore della metà del lato dritto che chiude il triangolo.
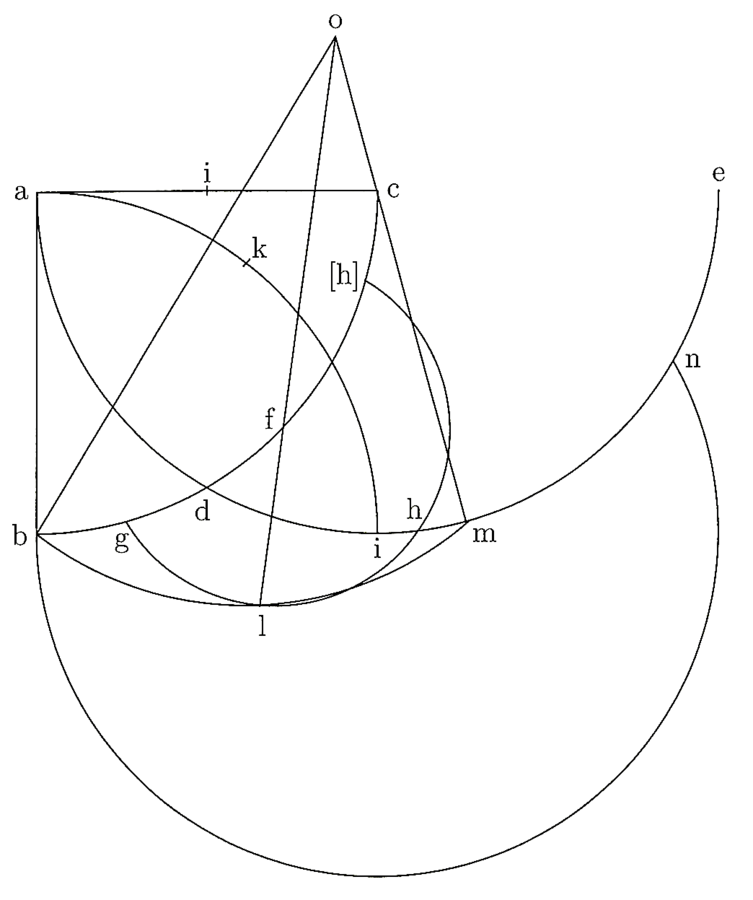
18. Se il [terzo] lato fosse curvo come l’altro, ossia convesso se è convesso o concavo se è concavo, la linea tracciata dal segmento corrispondente sarà maggiore o minore, proprio come nel caso precedente. Ma, se quello stesso lato fosse convesso, mentre l’altro è concavo ed entrambi appartenessero alla stessa circonferenza e fossero uguali, la linea tracciata attraverso i segmenti corrispondenti ai lati curvi serebbe necessariamente maggiore di quella che deve essere cercata secondo il rapporto. Infatti, se le corde fossero sottese agli archi, esse formerebbero lo stesso angolo dell’arco, e, se fossero corde di semiarchi, formerebbero di nuovo lo stesso angolo28. E poiché le corde dei semiarchi sono maggiori delle semicorde dell’arco intero, è evidente che la linea tracciata dalla metà [di uno] alla metà [dell’altro] sarà maggiore, a seconda dell’eccesso della corda del semiarco sul semiarco dell’arco intero.
19. È necessario dunque che l’altro lato sia più corto di quello curvo. Tuttavia quello concavo non può essere più corto. Infatti, se le corde fossero sottese a quegli archi, l’angolo compreso tra le corde sarebbe minore dell’angolo compreso tra gli archi e minore dell’angolo compreso tra le corde dei semiarchi. Da ciò, la linea tracciata da segmento a segmento sarebbe maggiore di quella richiesta. Di consequenza, è necessario che il triangolo che cerchiamo sia tale che, dei suoi tre lati, due siano curvi e di diversa lunghezza, cosicché il lato maggiore sia l’arco più grande della circonferenza e chiuda la superficie [del triangolo] in modo concavo, mentre l’altro [lato] minore sia l’arco più piccolo della stessa circonferenza e chiuda la superficie del triangolo stesso in modo convesso; il terzo lato sia dritto. Inoltre, se sottendi le corde a questi lati curvi, è necessario che l’angolo compreso tra le corde sia maggiore dell’angolo compreso tra gli archi, che l’angolo compreso tra le corde del semiarco sia maggiore dell’angolo compreso tra gli archi e minore dell’angolo compreso tra le corde degli interi archi interi, e precisamente, tanto minore quanto più le corde dei semiarchi eccedono le semicorde degli interi archi. E, ritenendo che con questa via sarebbe stato possibile che, dato il triangolo in questione, le linee tracciate dai segmenti fossero minori, maggiori o uguali a quelle che cerchiamo, ho suggerito di cercare un triangolo il cui lato dritto fosse il semidiametro del cerchio cui appartengono i lati curvi, e il lato curvo maggiore fosse un quadrante.
20. Ho descritto attorno al centro a il quadrante bc e, col piede fisso del compasso in c, ho descritto il semicerchio ade (cfr. figura 2). Ho diviso a metà l’arco bc nel punto f e ho descritto attorno a f il semicerchio gh, il cui semidiametro è uguale alla metà di ac. Attorno a b ho descritto il semicerchio occulto29 ik e ho cercato nella sua circonferenza un punto attorno a cui descrivere un arco (tenendo il piede fisso del compasso su questo punto e l’altro esteso fino a b) che si sviluppa passando attraverso il semicerchio minore gh verso quello maggiore ade, in modo che il punto di intersezione di questo arco con il semicerchio gh, ossia l, sia il centro dell’intero arco, avente la stessa distanza da b e dal punto d’intersezione dell’arco con de, ossia m. In modo analogo, ho tracciato così la linea cm e ho ottenuto il triangolo cercato CBM. Inoltre, cercando il punto m, ho trovato che esso deve distare necessariamente da d una lunghezza pari alla metà dell’arco bc, cioè alla metà del quadrante. Ora, questo punto cade tra il più vicino e il più lontano possibile. Infatti, posto il piede del compasso sulla circonferenza occulta aki, per esempio sul punto a, allora il punto più vicino sarà d, che cade sull’arco bc.
E se porrò il compasso sul punto d’intersezione dell’arco occulto aki e de, cioè su i, e descriverò l’arco bn, allora n sarà il punto più lontano. Infatti non sarà possibile trovare sull’arco de alcun punto più lontano da d. Ma è certo che la distanza tra d e n è pari a un quadrante sull’arco de – e la metà di questa distanza è il punto m – e in esso si trovano gli estremi ridotti all’uguaglianza media. Con questa via ho scoperto il triangolo cercato.
21. Dopo di ciò ho notato che, prolungando cm all’infinito e tracciando allo stesso modo una linea da l attraverso f, queste linee, non essendo parallele, si devono incontrare necessariamente in un punto. Dunque ho segnato il loro punto di intersezione con o. Così, ho osservato che tutte le linee che collegano una parte all’altra nel loro prolungamento devono convergere necessariamente con quelle due linee, nè una deve convergere o prima dell’altra. Di conseguenza tutte convengono nel punto o. Pertanto, se da o si tracciasse una linea passante per una qualsiasi punto del quadrante bc fino all’arco bm, allora il segmento di questa linea retta, che si trova tra i due archi, si rapporterà alla retta cm, come la parte dell’arco compresa tra b e il punto d’intersezione della linea retta e l’arco si rapporta a tutto il quadrante bc. Questo significa che tra l’arco bf e il quadrante bc sussiste lo stesso rapporto di quello esistente tra la linea fl e la linea cm, e questo era ciò che si cercava.
Terza premessa
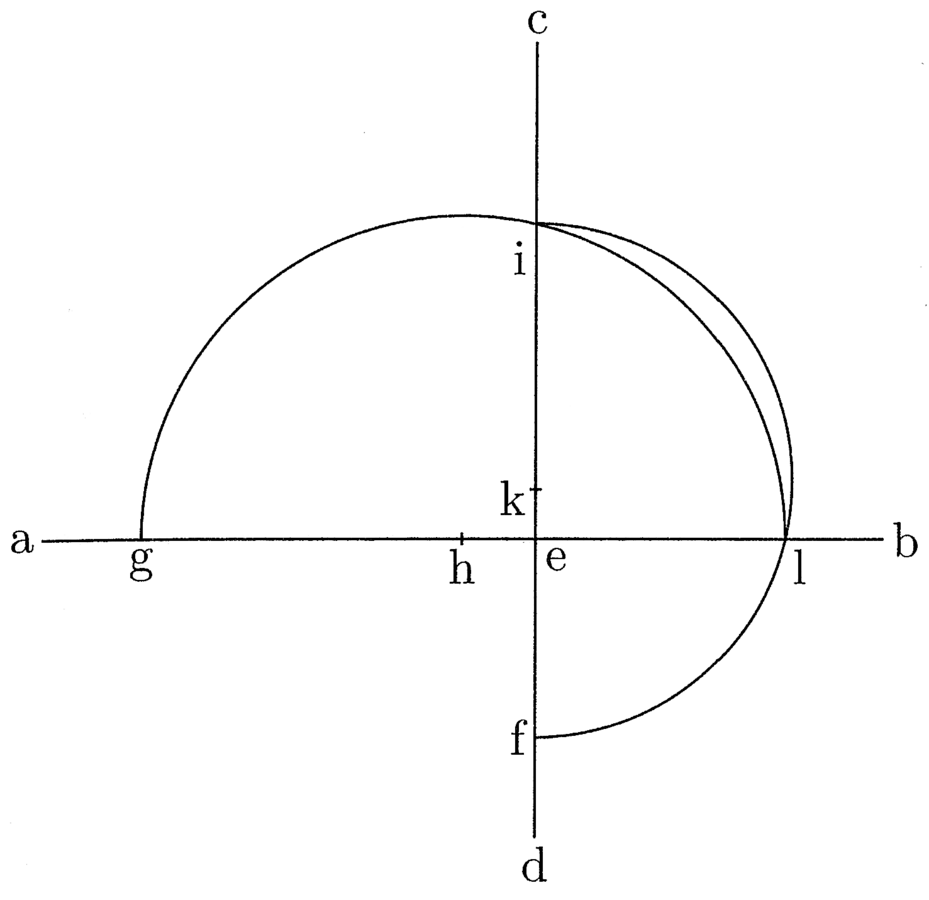
22. La terza cosa che bisogna premettere è in che modo, tra linee date, se ne possano trovare due proporzionali. Da molto tempo si sa perfettamente che, se due linee date vengono unite per formare il diametro di un cerchio e una corda le taglia ad angolo retto, allora la semicorda è il medio proporzionale tra questi, poiché è necessario che la semicorda sia il medio tra la freccia e la parte restante del diametro30.
Se dunque due linee di lunghezza indefinita come ab e cd si taglieranno ad angolo retto nel punto e, e da e verso d traccerò la linea minore, cioè ef, e da e verso a la maggiore, cioè eg, e descriverò due semicerchi, uno sulla linea ec attorno al centro, per esempio k, l’altro sulla linea ea attorno al centro, per esempio h, allora si noterà che l’arco del semicerchio il cui centro si trova sulla linea ea taglia l’arco dell’altro semicerchio sulla linea eb nel punto l e sulla linea ec nel punto i (cfr. figura 3). Nessuno può negare che ei e el, per la suddetta regola conosciutissima del medio proporzionale unico, sono i medi tra ef ed eg.
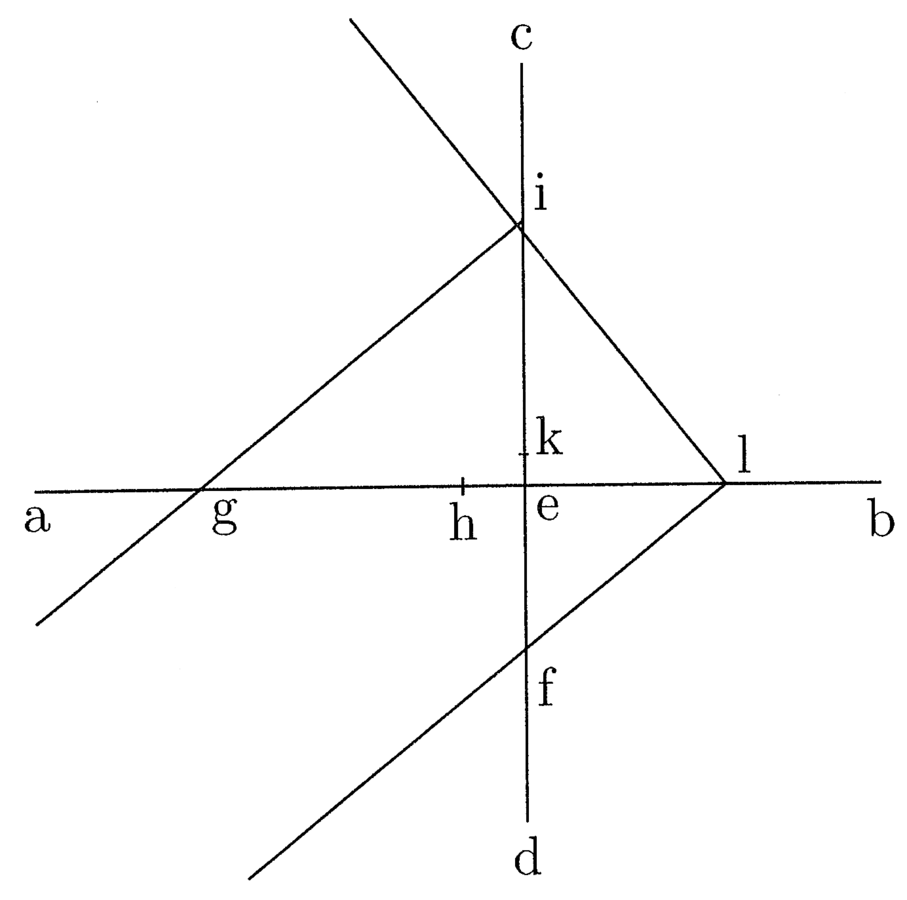
23. Per ottenere praticamente questi medi facilmente, prendi uno gnomone e una linea che, applicata al lato dello gnomone, formi un angolo retto (cfr. figura 4). Stando alla premessa, traccia due linee di lunghezza indefinita che si tagliano ad angolo retto; poni in seguito l’angolo retto dello gnomone sulla linea eb e fai passare un lato su f; nota dove il secondo lato taglia la linea ec, applica lì il regolo31 al lato di cui ho parlato in modo da ottenere un angolo retto. Se la linea condotta passerà per g, otterrai ciò che cercavi. Altrimenti, avvicina o allontana lo gnomone su eb, finché ciò si verifichi, e otterrai i due medi che cercavi. Se qualcuno lo desidererà, potrà trovare facilmente anche altri procedimenti; tuttavia, essendo il presente metodo chiaro, per il momento è sufficiente32.
24. In che modo invece si possa aggiungere a tre linee date proporzionali una quarta in proporzione continua risulta evidente da quanto già detto in precedenza33.
Quarta premessa
25. La quarta cosa [che bisogna premettere], ossia in che modo ottieni che, in rapporto a due linee date, a una terza si dia una quarta per mezzo di due triangoli aventi un angolo comune, e gli altri uguali, nella pratica risulta a tutti quasi evidente (cfr. figura 5). Infatti, se ab è una linea, cd un’altra ed ef una terza, unisci ab e cd a un angolo a piacere, ghi, e chiudi il triangolo. Quindi, prolunga il lato gh uguale ad ab finché non sarà uguale a ef, e sia questo gk. Traccia kl, parallela a hi, e prolunga gi fino ad essa, e sia questa gm. Nessuno, tranne un ignorante, può mettere in dubbio che la linea km si rapporta a gk, che è uguale a ef, come hi, che è uguale a cd, si rapporta a gh, che è uguale ad ab. Questo è quanto stabilito dalle premesse.
La trasformazione delle linee una nell’altra – capitolo primo
26. Nelle figure geometriche qualsiasi trasformazione è una trasformazione o di una linea in una linea o di una superficie in una superficie o di un solido in un solido34. Tre dunque sono i capitoli, che è opportuno trattare seriamente con l’aiuto di esempi.
27. Se intendi trasformare una linea retta in una curva di circonferenza, risolvi la linea retta in un triangolo o in un poligono regolare e, dalla prima premessa, determina il cerchio isoperimetrico la cui circonferenza è uguale alla linea retta data35.
28. Se cerchi di risolvere una linea retta in un arco qualsiasi di circonferenza, risolvila nella circonferenza del cerchio intero e, dal rapporto di quella con l’arco di circonferenza, troverai ciò che stai cercando. Infatti, il rapporto delle circonferenze è uguale a quello dei semidiametri36.
29. Se vuoi risolvere una linea retta data in un quadrante, allora ciò che cerchi è un quarto della circonferenza del cerchio il cui semidiametro è il quadruplo [di quello del cerchio la cui circonferenza è uguale alla linea retta data].
30. Se cerchi di trasformare una linea retta data in un arco di circonferenza di un cerchio dato, per prima cosa trasformala nella circonferenza del cerchio e, una volta conosciuto il rapporto dei semidiametri dei cerchi, sarà noto quanto cercato37.
31. Se vuoi trasformare una linea curva38 in una linea retta, non devi far altro che seguire la quarta premessa39, eppure so che, nel far ciò, quasi tutti si sono sbagliati. Infatti, una linea curva può essere trasformata in una linea retta solo se la si rapporta a una qualche linea retta trasformata in linea curva. Se dunque ti proponi di fare ciò, trasforma prima la linea retta in una circonferenza e prendi il semidiametro di questo cerchio come prima linea. In seguito, prendi un terzo della linea retta trasformata o un altro segmento come seconda linea; e indica come terza linea il semidiametro del cerchio la cui circonferenza è ciò che ti proponi di rettificare. Chiudi i triangoli che hanno un angolo comune e gli altri uguali; i lati opposti all’angolo comune risultano paralleli. Infatti, il secondo lato sarà una parte della linea cercata, per esempio un terzo, se il lato parallelo al primo è un terzo della circonferenza; se è altro, sarà diverso. In questo modo si conosce la trasformazione di una circonferenza in una linea retta e si conosce anche la trasformazione di un arco, che è la parte aliquota40 e conosciuta della circonferenza.
32. Se ignori il rapporto di un arco dato con la circonferenza, che cerchi di rettificare, tieni conto della seconda premessa, e fai passare una linea dal punto d’intersezione o attraverso l’arco che cerchi o una sua parte, fino all’altro arco e segna la linea compresa tra i due archi. Poi, fa’ che il semidiametro sia la prima linea, che la linea uguale al quadrante o a una sua parte aliquota sia la seconda, e chiama terza linea quella che hai tracciato tra gli archi. Dalla quarta premessa troverai la linea cercata attraverso i triangoli.
33. E si può ottenere ciò che cerchi solo in questo modo, che ti permette anche di trasformare una retta data nell’arco di una circonferenza data, anche se il rapporto dell’arco con la circonferenza non è nota. Ebbene, con questo procedimento, ciò è possibile.
Prendi il semidiametro del cerchio come primo lato del triangolo, la linea retta corrispondente alla quarta [parte] della circonferenza come secondo [lato] e chiudi il triangolo (cfr. figura 6). Così, se il semidiametro è ab e la quarta parte della circonferenza bc, la linea ca chiude il triangolo. Fa’ cadere una linea o una sua parte aliquota all’interno di questo triangolo parallelamente a bc, e sia essa de. Quindi, traccia da b verso c una linea uguale al semidiametro ab, ossia bf41; traccia af e indica con la lettera g il punto di intersezione con de. Poi torna alla seconda premessa e tira una linea dal comune punto di intersezione affinché si trovi tra gli archi un segmento uguale a dg; questo è il semiarco uguale alla linea data o la parte aliquota dell’arco cercato, se hai lavorato con una parte della linea.
34. Con questo metodo puoi anche trasformare una curva data e qualsiasi arco di una qualsiasi circonferenza in un diverso arco di un altro cerchio42, trasformando per prima cosa la curva stessa in una linea retta e in seguito questa linea retta in un arco della circonferenza data secondo il procedimento illustrato. Ciò è stato sufficientemente spiegato in questo capitolo sulla trasformazione delle linee.
La trasformazione delle superfici l’una nell’altra – capitolo secondo
35. Per spiegare sufficientemente la trasformazione delle superfici ed evitare inutili discorsi, tralascio, in quanto nota, la trasformazione delle superfici rettilinee43. Infatti, che il triangolo possa essere diviso in più triangoli e trasformato in un qualsiasi rettangolo44 e questi, a sua volta, in un qualsiasi quadrato, e più quadrati in uno solo, o che un solo triangolo possa essere diviso in più triangoli equilateri e, similmente, anche il triangolo e il quadrato e così tutti i poligoni equilateri e in non equilateri in altre figure, tutto ciò ti è noto dagli Elementi di geometria e dal rapporto di proporzionalità tra i cerchi e i quadrati, per cui tralascio tutto questo, dato che è mia intenzione accrescere quanto già si sa e non ripetere ciò che è trito e ritrito. Così, grazie a ciò che ho trattato in precedenza, questo capitolo può essere facilmente compreso.
36. Se proponi di trasformare una superficie circolare in una rettilinea, per prima cosa risolvi la sua circonferenza in una linea retta; quindi, aggiungi il semidiametro della circonferenza ad angolo retto e chiudi il triangolo; così la superficie circolare è trasformata in una superficie triangolare. Se vuoi trasformarla in un rettangolo o in un quadrato, ciò è possibile facilmente a partire dal triangolo. Infatti, si quadra il cerchio, prendendo come lato del quadrato il medio proporzionale tra il semidiametro e la metà della circonferenza. È dimostrato dalle menti più acute che dal prodotto del semidiametro per la metà della circonferenza risulta l’area di un rettangolo che non sarà né maggiore né minore dell’area del cerchio45. Infatti, il prodotto del semidiametro del cerchio inscritto per la metà del perimetro del poligono inscritto è uguale all’area del poligono inscritto46; il prodotto del semidiametro del cerchio circoscritto per la metà del perimetro del poligono circoscritto è maggiore dell’area del poligono e minore dell’area del cerchio e, parimenti, il prodotto del semidiametro del cerchio inscritto per la metà del perimetro di ogni poligono circoscritto è uguale all’area di questo e maggiore dell’area del cerchio. Di conseguenza il prodotto del semidiametro per la metà della circonferenza del cerchio non può essere né maggiore né minore [dell’area del cerchio].
37. Se tuttavia cerchi di trasformare l’area di una superficie rettilinea nell’area di una circolare47, per prima cosa risolvi quella circolare, come già detto, in un poligono, per esempio in un quadrato, e prendi il semidiametro del cerchio come [prima] linea e il lato del quadrato come [seconda] linea, e, dopo aver trasformato la superficie rettangolare in un quadrato, prendi il lato [del quadrato] come terza linea: dalla quarta premessa troverai la quarta linea che sarà il semidiametro del cerchio cercato. Nota come non si arrivi alla trasformazione di un arco di circonferenza in una linea retta se non per mezzo della trasformazione di una qualche linea retta in un arco di circonferenza; e, inversamente, non si giunge alla trasformazione di una superficie rettilinea in una circolare, se non attraverso la trasformazione di una qualche superficie circolare in una rettilinea. L’arcano che qui si nasconde non è oggetto della presente trattazione48.
38. Se tuttavia vuoi trasformare una qualsiasi porzione di superficie circolare che cade tra due raggi49, che sia o no proporzionale all’intera superficie50, lo puoi fare risolvendo in una retta l’arco compreso tra i due settori e moltiplicando il semidiametro per la metà dell’arco stesso.
39. Se cerchi di ridurre la porzione compresa tra una corda e l’arco in una superficie delimitata da lati dritti51, per prima cosa risolvi tutta la porzione compresa tra i raggi tracciati dal centro nel modo già illustrato in un cerchio. Quindi, trasforma, allo stesso modo, il triangolo compreso tra i raggi e la corda in un cerchio e, dopo averlo sottratto dal primo, resterà una porzione [di cerchio] ridotta in una superficie compresa tra le due circonferenze, che può essere ridotta nella superficie di un rettangolo attraverso la risoluzione di ciascun cerchio in quadrato e la sottrazione di ciascun quadrato dall’altro, visto che la differenza è uguale a questa porzione. Essa può dunque essere risolta nella superficie di un quadrato e attraverso questa nella superficie di un cerchio secondo i procedimenti già sufficientemente esposti. Attraverso questi esempi l’arte della trasformazione delle superfici l’una nell’altra è sufficientemente spiegata.
40. A ciò che l’arte delle trasformazioni esige come necessario si possono aggiungere molti altri punti [rimasti] finora nascosti, per esempio come fare a descrivere un angolo attorno al centro di un cerchio che si rapporta a due angoli doppi secondo il rapporto della doppia proporzionale52, in base a quanto detto nella seconda premessa. Infatti, si può dare una linea retta che si rapporta a una data come il lato [del quadrato] alla diagonale53. Entrambi possono essere ridotti nell’arco della stessa circonferenza. Da lì, tracciati i raggi fino alle estremità degli archi, si formeranno attorno al centro necessariamente gli angoli secondo il rapporto degli archi.
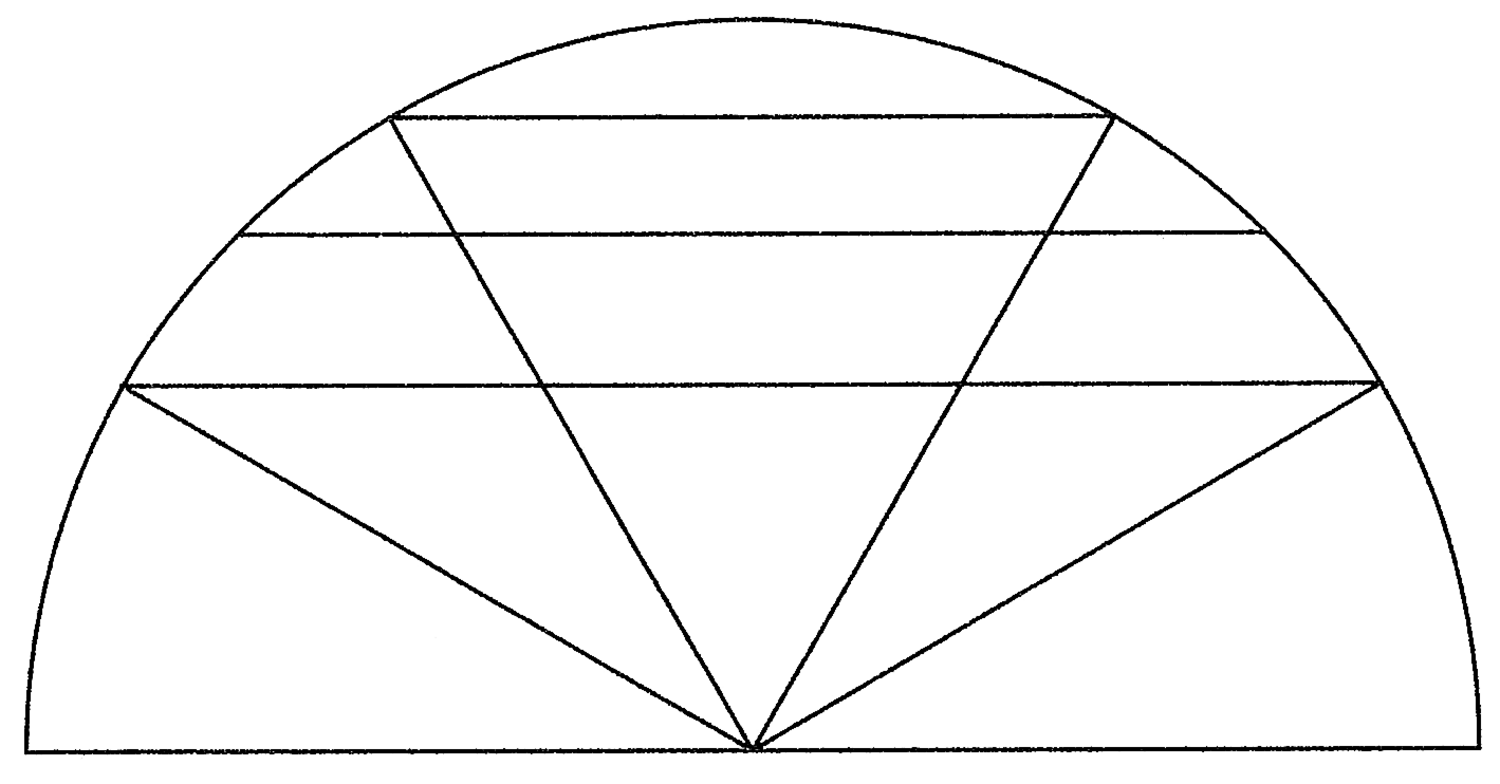
41. Se, infatti, cerchi di risolvere una superficie in altre, tante quante ne vuoi, che non sono proporzionali tra di loro né alla superficie totale, ma sono tuttavia tali che se aggiungessi l’una all’altra, risulterebbe una parte aliquota della superficie totale, anche se la superficie data non fosse semicircolare, riducila in superficie semicircolare tracciando la corda dell’arco del quadrante, parallela al diametro, chiamato “medio divisore”54(cfr. figura 7). Da questa [corda], su entrambe le parti, attraverso archi uguali, traccia, a tuo piacimento, corde [parallele] maggiori e minori. Tutte le porzioni55 non saranno proporzionali né tra di loro né al tutto. Ma se unirai due porzioni aventi la stessa distanza dal “medio divisore”, esse formeranno una parte della superficie [semicircolare] uguale a quella dell’arco sulla circonferenza. Così facendo, potrai ricavare dalla metà della superficie del semicerchio qualsiasi parte aliquota tu vorrai. La dimostrazione di ciò sta nel fatto che i triangoli compresi tra i raggi e le corde parallele al medio divisore, la cui distanza dal medio divisore è data da archi uguali, sono necessariamente uguali, ed è massimo quel triangolo compreso tra i raggi e la corda che chiamiamo medio divisore. Puoi anche dividere la superficie in parti, in modo che, unendo l’una all’altra, la superficie formata da queste parti resti non proporzionale, come accade se tracciassi le corde dal medio divisore, attraverso archi non proporzionali alla circonferenza. E da qui potrai dedurre tutto il resto a tuo piacimento56.
La trasformazione dei solidi l’uno nell’altro – capitolo terzo
42. In ultimo luogo, resta da spiegare la trasformazione dei corpi con l’aiuto di esempi. D’altra parte, i solidi si trasformano in corpi in base alle proposizioni fondamentali esposte.
43. Un parallelepipedo [rettangolo]57 si riduce in un cubo in questo modo. Si quadra la sua base, se non è già quadrata, attraverso il medio proporzionale tra i suoi due lati diversi; tra questo lato [del quadrato] e l’altezza del corpo si costituiscono due linee in proporzione continua, secondo la terza premessa; e se l’altezza è maggiore del lato del quadrato, il medio minore è il lato della base del cubo cercato. Ma se il lato del quadrato è maggiore dell’altezza, il lato della base del cubo cercato è il medio58 maggiore. Se è uguale, allora si ha il cubo. Se è un cilindro, si quadra la base e si procede secondo quanto finora stabilito.
44. Tuttavia, se vuoi trasformare un cubo in una sfera, riduci la superficie quadrata del cubo in un cerchio e fa’ di questo il cerchio maggiore della sfera59.
45. Se vuoi raggruppare più cubi in un unico cubo, posto che siano uguali, prendi come linea minore quella uguale al lato del cubo, e come linea maggiore quella uguale alla [somma di] tutti i lati [del cubo], segna quindi tra queste due linee due medi proporzionali secondo la terza premessa, poiché il minore tra questi due è il lato del quadrato, come abbiamo visto a proposito del parallelepipedo.
46. Se ti proponi di ridurre due [cubi] diversi in uno, riduci prima il più piccolo in un parallelepipedo rettangolo60, la cui altezza61 sia uguale al lato del cubo più grande, nel modo seguente: prendi il lato del più grande a cui aggiungi direttamente il lato del più piccolo cercando tra questi un solo medio proporzionale; trova un’altra linea in proporzione continua dopo il lato del più piccolo, cosicché siano quattro le linee in proporzione continua. Quest’ultima linea scoperta è il lato della base quadrata del parallelepipedo rettangolo la cui altezza è il lato del quadrato più grande, come risulta dal procedimento inverso di trasformazione del parallelepipedo. Fatta questa riduzione, cerca un quadrato uguale alla [somma di] due quadrati, ossia del quadrato del cubo più grande e della base quadrata del parallelepipedo rettangolo già menzionato, riducendo il cubo più grande e il parallelepipedo menzionato in un unico parallelepipedo rettangolo, il cui lato della base quadrata è maggiore dell’altezza. Riduci infine quest’ultimo a un cubo, seguendo la regola illustrata. Con questo metodo è evidente che si possono trasformare tutti i cubi che vuoi, siano essi uguali o diversi, in un cubo o infine in una sfera. E così facendo si possono ridurre più sfere in una sola, in un cubo o in un parallelepipedo rettangolo.
47. Ma se ti proponi di ridurre un parallelepipedo alto in uno più basso e/o viceversa, per prima cosa trasformalo in un cubo, poi traccia l’altezza [del nuovo solido] in cui ti proponi di trasformarlo. A questa aggiungi il lato del cubo cercando un solo medio proporzionale e una quarta linea in proporzione continua a queste tre. Questa quarta linea sarà [il lato] della base quadrata del parallelepipedo rettangolo avente l’altezza data62.
48. Così, se di più parallelepipedi uguali o diversi vuoi costruire uno avente una data altezza, se essi sono uguali, prendi la base quadrata uguale a tutti e riducila in cubo e questo nel parallelepipedo avente l’altezza data secondo le modalità sopra esposte; se essi sono diversi, riduci a mente tutti i parallelepipedi in uno solo e questo in un cubo, e quest’ultimo in un parallelepipedo alto o basso, a tuo piacimento. Tuttavia, in ciò bisogna fare attenzione, poiché, se il cubo deve essere ridotto in un solido che ha come base un quadrato il cui lato è maggiore della sua altezza, allora [è necessario] unire all’altezza minore data il lato della base del cubo, cercando un solo medio proporzionale. A questo punto troverai una quarta linea, che si rapporta al medio come il lato del cubo si rapporta ‹all’altezza› [del solido cercato], e questa linea sarà il lato della base quadrata del solido, in cui volevi ridurre gli altri. Ma se vuoi che l’altezza di quel solido cercato sia maggiore del lato di base quadrata, aggiungi l’altezza direttamente al lato del cubo, e cerca il medio proporzionale: la quarta linea in proporzione continua dopo il lato del cubo è il lato cercato63.
49. Se invece provi a trasformare una sfera in una piramide, fa’ che la base della piramide sia uguale alla superficie curva della sfera e che la sua altezza sia uguale al semidiametro della sfera64.
50. Se qualcuno dicesse: date due sfere di cui una è doppia dell’altra, trasformale in un cilindro, tu fa’ che l’altezza del cilindro sia uguale al diametro della sfera ‹maggiore› e la base uguale al cerchio maggiore di questa sfera. Questo cilindro sarà uguale ad entrambe le sfere. Infatti, il cilindro la cui altezza è uguale al diametro della sfera e la cui base è uguale al cerchio massimo, è una volta e mezzo la sfera65.
51. Questi e altri esempi, e tutto ciò che può avvenire nei solidi regolari mediante la trasformazione geometrica delle figure, puoi ricavarli da questi insegnamenti.
‹Appendice›
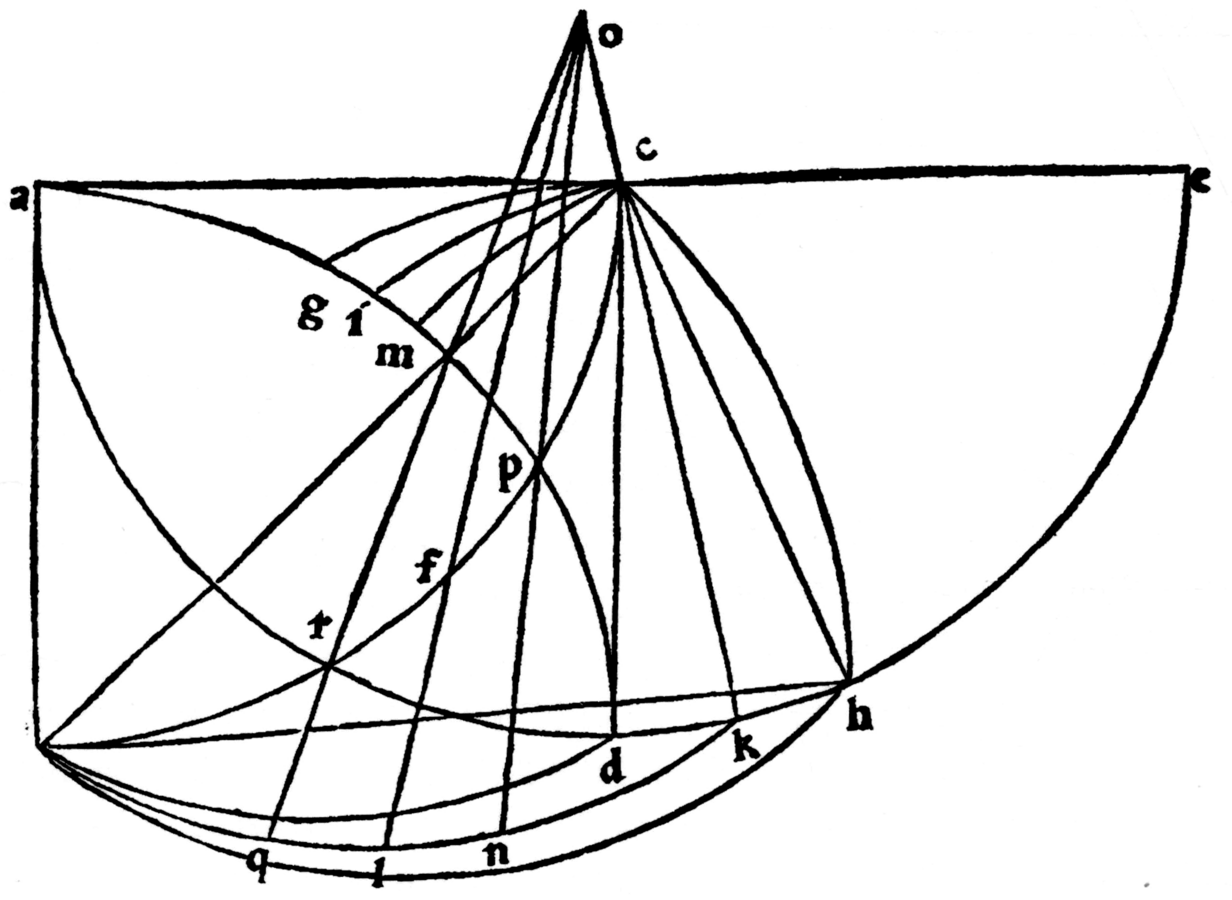
α66 Ho descritto dunque un quadrante bc intorno al punto a, e, col piede del compasso fisso in c, ho tracciato il semicerchio ade (cfr. figura 8). Ho cercato in questo genere di triangoli il più piccolo e ho notato che, se si conduce una retta dal punto c al punto d, essa descrive un angolo tangente al quadrante, e di conseguenza il terzo lato che chiude questo triangolo sarà il più piccolo, essendo l’angolo a cui è sotteso, ossia quello di tangenza, il più piccolo. Tracciato quindi ab intorno al centro b, descrivo il quadrante occulto ad, uguale a bc. Dall’altra parte, tracciato cd intorno al centro d, indico con g il punto d’intersezione con il quadrante occulto ad. Poi, posto il piede del compasso fisso in g e l’altro in b, muovo b fino al punto d; l’arco descritto, ossia bd, avrà la stessa curvatura dell’arco del quadrante bc. Poiché tutte le rette condotte dal quadrante occulto al punto b sono uguali, è necessario descrivere archi della stessa curvatura o di cerchi eguali.
β. bd sarà il lato curvo più piccolo e convesso; di conseguenza il triangolo BCD sarà il in questo genere di triangoli, contenendo il più piccolo degli angoli, ossia quello di tangenza, dato che il lato curvo bd al quale è sotteso è il più piccolo. E, poiché è il più piccolo, il lato curvo bc sarà il più grande. Infatti, non si può dare il lato bc come il più piccolo, perché, se così fosse, il lato dritto dc intersecherebbe il quadrante bc, e il triangolo che si ottiene non rientrerebbe nel genere di quelli cercati. Dunque BCD è un triangolo i cui due lati curvi sono bc e bd, e di questi uno è il più grande ed è concavo, l’altro è il più piccolo ed è convesso; questi lati curvi hanno la stessa curvatura, il cui diametro è il terzo lato dritto, ossia dc. E poiché in questo genere [di triangoli] non se ne può dare uno il cui lato più piccolo convesso sia bd, allora BCD sarà il triangolo più piccolo in questo genere di triangoli. Al contrario, poiché in questo genere di triangoli si possono dare triangoli più grandi, ossia quelli il cui lato curvo convesso è più grande dell’arco bd, si può dare correttamente il più grande, allorché il lato curvo e convesso sarà uguale a quello concavo, ossia quando è il più grande. Per descrivere tutto ciò, traccio una linea retta bd, e intorno al centro h descrivo hc e indico con m il punto d’intersezione di hc con il quadrante occulto. Al contrario, fissando il piede del compasso in m e l’altro in b, muovo b verso h: l’arco descritto, ossia bh, sarà uguale al quadrante bc. Infatti sono descritti con lo stesso diametro e le corde degli archi sono uguali; di conseguenza avranno la stessa curvatura. Da ciò risulta che il triangolo BHC – i cui due lati curvi hanno la stessa curvatura, ossia l’arco bc e l’arco bh, e il terzo lato dritto, ossia hc, è eguale al semidiametro dei cerchi degli archi – è il più grande in questo genere di triangoli; infatti, il lato più piccolo coincide con quello più grande. Al contrario, poiché nel triangolo più piccolo, ossia BCD, la linea condotta dalla metà del lato curvo alla metà dell’altro lato curvo è maggiore della metà del lato dritto, allora esso sarà in assoluto il più piccolo, dato che si tratta del triangolo più piccolo. E poiché la linea condotta dalla metà del lato curvo alla metà dell’altro lato curvo nel triangolo più grande, ossia CBH, è maggiore della metà del lato dritto (e questo perché i lati curvi sono uguali), la linea tracciata sarà in assoluto la più grande, trovandosi nel triangolo più grande. Da ciò consegue che nel triangolo intermedio ed equidistante dal massimo e dal minimo, in cui cioè il massimo e il minimo coincidono, la linea condotta dalla metà del lato curvo alla metà dell’altro lato curvo non è né maggiore né minore della metà del lato dritto, e, di conseguenza, questo triangolo intermedio sarà quello cercato.
γ. Per ottenere ciò, divido l’arco dh in due parti uguali; indico con k il punto medio e traccio kc. Intorno al centro h descrivo kc e indico con i il punto d’intersezione di kc con il quadrante occulto. Posto il piede del compasso fisso in i e l’altro in b, muovo b verso k, e così sarà descritto l’arco bk, che, insieme all’arco del quadrante bc e alla linea kc, descrive il triangolo cercato. Infatti il lato più grande e curvo è il quadrante ed è concavo, ed esso, rispetto all’altro lato curvo e convesso, ossia bk, ha la stessa curvatura; mentre il terzo lato è dritto e eguale al semidiametro del cerchio degli archi.
δ. Poiché, infatti, il triangolo più grande CBH si muove verso quello intermedio decrescendo di continuo, e il triangolo più piccolo BDC si muove verso quello intermedio crescendo di continuo, essi coincidono nel medesimo triangolo, che non può che essere BKC, che è quello cercato. Al contrario, si divida il lato curvo cb in due parti uguali con il punto medio in f e allo stesso modo si divida il lato curvo bk nel punto medio l. Sia kc di lunghezza indefinita e si conduca un’altra linea dal punto l passando per f. Poiché kc e fl non sono paralleli, convergono necessariamente in un punto, o, che sarà il punto d’intersezione delle linee kc e fl. Da ciò kc starà a fl come bl a bk o bf a bc.
ε. Di tutte le linee che, condotte dal punto d’intersezione, tagliano i due lati curvi, quelle comprese tra questi conserveranno con il lato dritto lo stesso rapporto che le parti dei lati curvi verso l’angolo b hanno con i lati curvi. Come on, che passa per p, e bp sono due terzi di bc, allo stesso modo nb sarà due terzi di bk e np due terzi di kc. Al contrario nel caso di oq, che passa per r, rb è un terzo di bc e bq è un terzo di bk e allo stesso modo qr è un terzo di kc. E così, essendo il triangolo BKC equidistante da quello più grande, ossia BHC, e da quello più piccolo, ossia BDC, nei quali si realizzano il massimo e il minimo in assoluto (come si dice); di conseguenza, in quello intermedio non ci sarà né il più né il meno, dal momento che in esso coincidono il triangolo minimo e il triangolo massimo.
Note a piè pagina
Le trasformazioni geometriche e I complementi aritmetici sono dedicati a Toscanelli, cui Cusano riconosce la massima autorità scientifica. Sarà proprio Toscanelli a criticare aspramente il primo libro de I complementi matematici, e ciò spingerà il cardinale alla stesura del secondo libro de I complementi matematici. Cusano era stato presentato al medico e astronomo Toscanelli (cfr. Uzielli 1894) durante il periodo di studi a Padova e aveva ascoltato con lui le lezioni di Prosdocimo de’ Baldomandi (cfr. Favaro 1879). Tra loro nasce una sincera amicizia, testimoniata, per esempio, dal fatto che, nel 1443, Toscanelli aveva dato a Cusano, attraverso la penna del generale camaldolese Ambrogio Traversari, la traduzione della Theologia latina dello Pseudo–Aereopagita. Sarà lo stesso Toscanelli ad accompagnare Cusano nel suo ultimo viaggio da Roma a Todi (cfr. Stinger 1977, 42–44ss.).
Per «rectus» e «curvus» si intende una linea dritta e una linea curva.
Qui «ars», di lulliana memoria, sta per sapere, conoscenza, metodo.
Cfr. Cusanus 1972b, II, 2, 82.
Cfr. Cusanus 1972a, I, 4, 11.
Sebbene, qui come altrove, Cusano abbia in mente i poligoni regolari, di essi il cardinale considera solo l’uguaglianza dei lati, non anche quella degli angoli; cfr. Cusanus 2010i, 8, 8–11. La stessa restrizione si ritrova in Busard 1980, 1, 6. Bradwardine 1495a, II, 4, concl. 4 e 5 introduce il termine «isoperimetrico» nella conclusione 1; nella conclusione 2 richiama l’attenzione sul rapporto tra l’incremento della superficie e quello del numero di angoli di un poligono, e, nelle conclusioni 3 e 4, i poligoni sono pensati sempre come regolari. Stessa considerazione si trova in Cusanus 2010i, 8, 8–11. Cfr. Hofmann e Hofmann 1980, nota 4, 190–191.
Il termine «capacitas» è qui tradotto con ampiezza; per rispettare al meglio lo spirito del linguaggio cusaniano, a differenza sia di J. E. Hofmann che traduce «capacitas» con «Fläche» (cfr. Hofmann e Hofmann 1980, 54), sia di J.M. Nicolle che traduce il termine latino con «Surface» (cfr. Nicolle 1998, 7), si è preferito qui differenziare i due termini (capacitas e superficies), utilizzati entrambi da Cusano, rendendo il latino capacitas a volte con ampiezza, altre volte, a seconda del contesto, con estensione o superficie. In linea di massima sembra che Cusano utilizzi il termine capacitas per indicare l’ampiezza in generale, mentre fa uso del termine superficies quando intraprende costruzioni geometriche specifiche o discorsi che comportano una misurazione.
Cfr. Bradwardine 1495b, II, 5, concl. 5. Sul tema, cfr. Gericke 1982, 160–187; Di Meglio 2010, 15–21; Heath 1921, 2019–2111; Porter 1933.
Cfr. Cusanus 1972a, I, 3.
Qui si presuppone tacitamente la formula dell’area 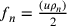 ,
esplicitata più avanti.
,
esplicitata più avanti.
La conclusione è che: a  appartiene
l’inscritto
appartiene
l’inscritto 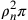 e al circoscritto
e al circoscritto 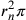 . Poiché
. Poiché 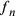 si rapporta a
si rapporta a
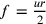 non in una proporzione razionale, allora neanche
non in una proporzione razionale, allora neanche 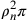 , o meglio
, o meglio
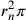 , a
, a
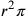 .
.
Il termine «aequalis» indica un’uguaglianza in generale e Cusano lo utilizza sia nel caso di uguaglianze tra lunghezze (come in questo caso), sia per indicare un’uguaglianza tra aree, ossia un’equivalenza.
Cfr. Cusanus 2010c, 2–6.
Come in precedenza, Cusano utilizza «isopleur» come sinonimo di equilatero.
La stessa esposizione si trova in Cusanus 2010j, 3; Cusanus 2010i, 4–8.
Questo testo si ritrova, con piccole modifiche, in Cusanus 2010c, 2.
Cusano pone, senza dimostrazione, questa proposizione
fondamentale che costituirà l’oggetto principale di tutte le
successive discussioni. Egli pone un punto e tale che, se si fa passare per e un raggio ah che
misura 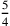 di ae, si ottiene il raggio di un cerchio
isoperimetrico al triangolo BCD.
di ae, si ottiene il raggio di un cerchio
isoperimetrico al triangolo BCD. 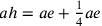 . Ciò dà
un’approssimazione di π uguale a
. Ciò dà
un’approssimazione di π uguale a 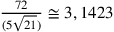 .
Secondo Hofmann, se si pone u come
perimetro del triangolo, si ha
.
Secondo Hofmann, se si pone u come
perimetro del triangolo, si ha  ,
, 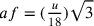 ;
; 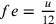 ;
;
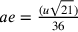 ;
; 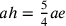 .
Questi valori sono ottenuti applicando il teorema di
Pitagora al triangolo BCD. Di conseguenza,
.
Questi valori sono ottenuti applicando il teorema di
Pitagora al triangolo BCD. Di conseguenza, 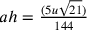 ; poiché
ah è posta come il semidiametro del
cerchio isoperimetrico al triangolo BCD, si ha l’uguaglianza
seguente:
; poiché
ah è posta come il semidiametro del
cerchio isoperimetrico al triangolo BCD, si ha l’uguaglianza
seguente: 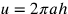 , da ciò,
, da ciò, 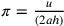 e, di conseguenza,
e, di conseguenza,
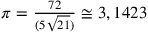 ,
un valore compreso tra i limiti di Archimede
,
un valore compreso tra i limiti di Archimede 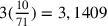 e
e 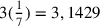 .
.
Il termine latino è «portio», che, negli scritti matematici, Cusano utilizza per indicare sia porzioni di linea retta (segmenti) sia porzioni di linea curva (principalmente archi) sia porzioni di superficie (settori circolari o segmenti di cerchio).
Il ragionamento è il seguente: se 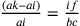 ,
allora la linea è troppo piccola. Se
,
allora la linea è troppo piccola. Se 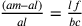 , la
linea è troppo grande. Esiste allora un punto compreso tra i e un ipotetico p
tale che:
, la
linea è troppo grande. Esiste allora un punto compreso tra i e un ipotetico p
tale che: 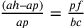 , dove
ah è il semidiametro del cerchio
isoperimetrico al triangolo. Come si legge in Hofmann e Hofmann 1980, nota 16, 192, se poniamo
, dove
ah è il semidiametro del cerchio
isoperimetrico al triangolo. Come si legge in Hofmann e Hofmann 1980, nota 16, 192, se poniamo 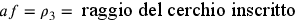 ;
; 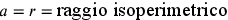 e
e
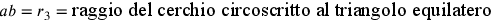 , si ha
che
, si ha
che  . Di conseguenza si dà
una posizione precisa di ah nel campo
angolare fab tale che h viene a trovarsi fuori del triangolo
rettangolo AFB e ah interseca il cateto
fb in un punto e
tra f e b. Ora
e taglia il segmento ah in un rapporto, che Cusano identifica
con un numero intero e che spera di individuare esaminando i
valori intermedi. A questo scopo egli cerca il rapporto
. Di conseguenza si dà
una posizione precisa di ah nel campo
angolare fab tale che h viene a trovarsi fuori del triangolo
rettangolo AFB e ah interseca il cateto
fb in un punto e
tra f e b. Ora
e taglia il segmento ah in un rapporto, che Cusano identifica
con un numero intero e che spera di individuare esaminando i
valori intermedi. A questo scopo egli cerca il rapporto
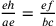 , che può
essere preso come punto di partenza della riflessione. A
questa relazione bisogna restar fedeli anche quando e è sostituito con un altro punto compreso
tra f e b, per
esempio con «i vicino a f» o con «l vicino a
b», ma in questi casi non risulterà più
il raggio isoperimetrico sul prolungamento del segmento, ma un
segmento più piccolo vicino a f e più
grande vicino a b. Cusano fissa la
corretta posizione di e attraverso una
costruzione intermedia.
, che può
essere preso come punto di partenza della riflessione. A
questa relazione bisogna restar fedeli anche quando e è sostituito con un altro punto compreso
tra f e b, per
esempio con «i vicino a f» o con «l vicino a
b», ma in questi casi non risulterà più
il raggio isoperimetrico sul prolungamento del segmento, ma un
segmento più piccolo vicino a f e più
grande vicino a b. Cusano fissa la
corretta posizione di e attraverso una
costruzione intermedia.
Cfr. Cusanus 2010c, 24. Qui Hofmann introduce nel testo della sua
traduzione un simbolismo che tuttavia, come nota Nicolle 2007, nota 7, 15, è estraneo ai matematici dell’epoca. Non soltanto
Cusano redige letteralmente i rapporti proporzionali, ma
ignora la scrittura esponenziale del quadrato. Cusano fa il
medesimo ragionamento sul lato di b e
non più su quello di f: se 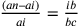 ,
allora la linea è troppo piccola; se
,
allora la linea è troppo piccola; se  ,
allora la linea è troppo grande. Esiste allora un punto
compreso tra i e l (
,
allora la linea è troppo grande. Esiste allora un punto
compreso tra i e l (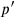 ) tale che:
) tale che: 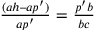 .
E’ “evidente” che
.
E’ “evidente” che 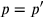 perché non c’è che un cerchio
isoperimetrico al triangolo BCD. Si ha
dunque:
perché non c’è che un cerchio
isoperimetrico al triangolo BCD. Si ha
dunque: 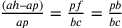 ,
e di conseguenza p non può essere che
il punto e. In questo caso si ha
,
e di conseguenza p non può essere che
il punto e. In questo caso si ha
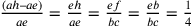 ;
;
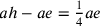 e si ottiene
e si ottiene
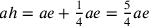 .
.
Cusano fa lo stesso ragionamento con i quadrati. Se
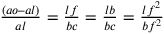 ,
allora la linea è troppo grande. Se
,
allora la linea è troppo grande. Se 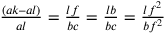 ,
allora la linea è troppo piccola. Si cerca dunque un punto e tale che
,
allora la linea è troppo piccola. Si cerca dunque un punto e tale che 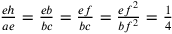 .
.
Cusano passa dal triangolo equilatero a un poligono
regolare isoperimetrico e afferma che 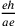 decresce con l’aumentare
del numero degli angoli. Per il suo svolgimento, cfr. Hofmann e Hofmann 1980, nota 19, 193.
decresce con l’aumentare
del numero degli angoli. Per il suo svolgimento, cfr. Hofmann e Hofmann 1980, nota 19, 193.
Cfr. Cusanus 2010b, 6, 2–3.
Per «trigonum rectilineum» si intende un triangolo delimitato da linee (lati) dritte.
La difficoltà a comprendere questo passaggio deriva dalla diversa prospettiva tra la descrizione di Cusano e ciò che noi oggi chiamiamo curva concava o convessa. Noi intendiamo per curva concava quella che presenta una superficie incavata e convessa quella che è arrotondata all’esterno, situandoci all’interno della figura. Ora Cusano descrive queste curve dall’esterno delle figure. Come riporta Nicolle 2007, nota 9, 16, si ha:
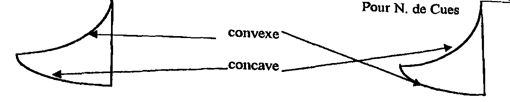
La traduzione matematica di questa relazione è ben svolta da Hofmann e Hofmann 1980, nota 22, 194, che però mostra come Cusano dimostri questa proporzione solo nel caso di semiarchi.
Cusano parla di «semicirculus occultus» e, qualche riga sotto, di «arcus occultus». È un termine di difficile traduzione, che non ci risulta utilizzata dai matematici del tempo. Essa invece si trova negli scritti matematici di fine Cinquecento e Seicento, per esempio in Christopher Clavius (Gnonomices octo libri 1588, libro VIII, cap. III), in Jean Voel (De horologiis sciothericis libri tres 1608, libro I), nel cap. XXXVII del De Usus et fabrica circini cuiusdam proportionis 1607 (traduzione latina ad opera di Baldassare Capra de Le operazioni del compasso geometrico et militare di Galileo (il termine „occulto“ si trova all’interno dell’operazione XXVI) (Padova, 1606); nel terzo Dialogo de il Dialogo sopra i due massimi sistemi di Galileo Galileo (1632).
Cfr. Bradwardine 1495b, III, 4, concl. 4 e Da Novara 2005, VI, 9. È necessario prendere il concetto di freccia nel senso più ordinario di retta perpendicolare al centro della corda dell’arco. Luca Pacioli la definisce così: «Si chiama freccia questa linea retta che parte dal punto mediano dell’arco di qualche porzione di cerchio per cadere in squadra nel mezzo della sua corda. Essa è detta freccia in relazione con la parte della circonferenza che si chiama arco, per somiglianza con l’arco materiale per il quale sono anch’esso usuali questi tre termini: corda, arco e freccia» (Pacioli 1509, 134).
La «regula» consiste nel condurre una linea perpendicolare al lato.
Questa pagina si ispira a Eutocius da Ascalona (ca. 480–ca. 540), matematico bizantino, autore (circa sette secoli dopo Archimede), del Commento della sfera e del cilindro di Archimede, tradotto da Guglielmo di Moerbeke, o Willem van Moerbeke (ca. 1215–ca. 1286). Cfr. Clagett 1964–1984a, II, 238. Secondo Clagett 1964–1984a, III, 299–301 Cusano avrebbe letto questo passaggio nel De arte mensurandi di Johannes De Muris (cfr. De Muris 1998, VII, 16).
Si tratta di determinare d dalla
proporzione continua 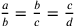 ;
c è la terza proporzionale tra a e b; d è la terza proporzionale a b e c. Cfr. Da Novara 2005, VI, 10.
;
c è la terza proporzionale tra a e b; d è la terza proporzionale a b e c. Cfr. Da Novara 2005, VI, 10.
Il termine latino è «corpus».
Cfr. Cusanus 2010d, 19.
«Curva» indica qui una curva circolare, poiché la trasformazione si può realizzare solo su una curva regolare come la circonferenza di un cerchio.
Per «aliquota» s’intende: contenuta un numero intero di volte, ossia un sottomultiplo intero. Cfr. Bradwardine 1328, 68: «pars autem aliquota est illa quae, aliquotiens sumpta, reddit aequaliter summum suum. Pars vero non aliquota est illa quae nullatenus, aliquotiens sumpta, reddit aequaliter summum suum» («Una parte aliquota è invero quella che, presa un determinato numero di volte, dà come risultato il suo tutto. Una parte non aliquota è quella che, presa un qualsiasi numero di volte, non dà come risultato il suo tutto»). La citazione si trova anche in Clagett 1964–1984a, 493.
Si deve determinare anche l’angolo (il radiante 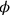 ) di ciascun arco
di circonferenza dal semidiametro ab,
che sia uguale al segmento ed (
) di ciascun arco
di circonferenza dal semidiametro ab,
che sia uguale al segmento ed (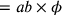 ).
Mediante la costruzione sul triangolo risulta che
).
Mediante la costruzione sul triangolo risulta che 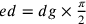 ; e così è
applicabile
; e così è
applicabile 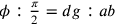 e la
costruzione della seconda premessa. Secondo Hofmann sulla
figura originale del manoscritto bf non
è uguale a ab, come invece dovrebbe
essere (Hofmann e Hofmann 1980, nota 34, 195).
e la
costruzione della seconda premessa. Secondo Hofmann sulla
figura originale del manoscritto bf non
è uguale a ab, come invece dovrebbe
essere (Hofmann e Hofmann 1980, nota 34, 195).
Per «superficies rectilinea» si intende una superficie delimitata da linee dritte. Cfr. Da Novara 2005, VI, 25 e Bradwardine 1495b, III, 6, concl. 4: «E’ possibile ridurre ogni poligono in quadrato attraverso la risoluzione in triangoli, attraverso le quadrature di questi triangoli e attraverso circoscrizioni gnomoniche».
Con rettangolo si traduce «quadrangulus». In questo, come negli altri scritti matematici, il termine «figura quadrangularis» è equivoco: Cusano lo riferisce tanto al quadrato quanto al rettangolo e al parallelogramma. Di volta in volta, a seconda del contesto, si renderà il termine «quadrangularis» con la figura corrispondente. Sull’utilizzo, da parte di Cusano, del termine «quadrangulus» e sull’influenza dalla terminologia matematica medioevale, cfr. Hofmann 1966, 98–136, spec. 105. Cfr. anche Cusanus 2010j, 2.
Cfr. Archimedes 1910a, prop. 1, ripreso da Bradwardine 1495b, III, 6, concl. 5.
La formula dell’area 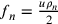 , già utilizzata
nell’introduzione, compare nell’esempio dell’ottagono nel Circ. dem., di Archimede, è ripresa da Bradwardine 1495b, II, 5, concl. 2 ed è menzionata in Cusanus 2010i, 10 per dimostrare il quadrato. La formula dell’area del
cerchio è espressa in Bradwardine 1495b, III, 6, concl. 5, ma senza riferimenti al processo dimostrativo
archimedeo.
, già utilizzata
nell’introduzione, compare nell’esempio dell’ottagono nel Circ. dem., di Archimede, è ripresa da Bradwardine 1495b, II, 5, concl. 2 ed è menzionata in Cusanus 2010i, 10 per dimostrare il quadrato. La formula dell’area del
cerchio è espressa in Bradwardine 1495b, III, 6, concl. 5, ma senza riferimenti al processo dimostrativo
archimedeo.
Cfr. Cusanus 2010l, 10.
Cfr. Cusanus 2010i, 34.
Secondo Clagett 1968, II, 302–304, Cusano ha compreso male la dimostrazione indiretta di Archimede «.. e inversamente…»: questa idea di operazione inversa gli venne dal De arte mensurandi (cap. 8, prop. 15) di Johannes De Muris (De Muris 1998).
Nel Medioevo le figure geometriche sono viste non come rette che delimitano delle superfici, ma come superfici delimitate dalle rette. Cusano vede l’angolo come una superficie e i settori come porzioni di superficie del cerchio delimitate da raggi (cfr. Nicolle 1998, nota 19, 17). Troviamo la seguente definizione in Proclo: «la natura particolare dell’angolo non consiste in una contrazione di superficie o del solido, ma in una superficie contratta in un punto e compresa tra due linee spezzate» (Proclus 1873, 117, 73).
Cfr. Cusanus 2010i, 28.
Cfr. Cusanus 2010i, 29, 4–5.
«Secundum proportionem medietatis duplae»: si tratta di
un’espressione idiomatica intraducibile in sè, utilizzata
anche ne La quadratura del cerchio
(Cusanus 2010j, 9, 8) e ne I complementi
matematici (Cusanus 2010i, 36). Considerando l’angolo come una superficie, Cusano
ritiene il rapporto tra angoli uguale al rapporto degli archi
corrispondenti allo stesso cerchio (cfr. Hofmann e Hofmann 1980, nota 42, 195–196). Vescovini 1972, nota10 sottolinea che l'espressione medietatas duplae
rimanda alla tradizione matematica medievale con cui Cusano
allude alla dimostrazione dell’irrazionalità della 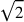 , spesso citata
in Aristotele e menzionata anche in Oresme 1966, 160 e in Bradwardine 1495b, III–1. Oresme chiama il rapporto
, spesso citata
in Aristotele e menzionata anche in Oresme 1966, 160 e in Bradwardine 1495b, III–1. Oresme chiama il rapporto  la metà di
la metà di 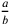 (cfr. Oresme 1966, 454). La proportio proportionum,
cioè la proporzione tra due rapporti
(cfr. Oresme 1966, 454). La proportio proportionum,
cioè la proporzione tra due rapporti 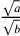 e
e 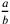 è espressa
dal rapporto
è espressa
dal rapporto 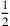 . Se la proportio dupla è il quadrato allora, la
metà, ossia la medietas duplae, è la
radice. Cusano si riferisce a questa terminologia matematica
di Bradwardine, di Oresme e di altri studiosi interessati agli
incommensurabili e ai rapporti irrazionali. Cfr. Rommevaux 2003, 401–418; Pedersen 1953, 134ss.. Questa espressione è legata al problema della
duplicazione del cubo e alla relativa doppia media
proporzionale. Secondo la leggenda l’oracolo di Delo aveva
vaticinato che per far cessare una terribile pestilenza si
doveva dedicare alla divinità un’ara cubica di volume doppio
rispetto all’ara cubica dedicata in precedenza. Un problema
semplice solo in apparenza. Era noto che, raddoppiando la
misura degli spigoli del cubo, il volume aumenta
. Se la proportio dupla è il quadrato allora, la
metà, ossia la medietas duplae, è la
radice. Cusano si riferisce a questa terminologia matematica
di Bradwardine, di Oresme e di altri studiosi interessati agli
incommensurabili e ai rapporti irrazionali. Cfr. Rommevaux 2003, 401–418; Pedersen 1953, 134ss.. Questa espressione è legata al problema della
duplicazione del cubo e alla relativa doppia media
proporzionale. Secondo la leggenda l’oracolo di Delo aveva
vaticinato che per far cessare una terribile pestilenza si
doveva dedicare alla divinità un’ara cubica di volume doppio
rispetto all’ara cubica dedicata in precedenza. Un problema
semplice solo in apparenza. Era noto che, raddoppiando la
misura degli spigoli del cubo, il volume aumenta 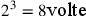 . Il
problema consisteva, quindi, dato un cubo di spigolo a, nel trovare un cubo di spigolo x tale
che
. Il
problema consisteva, quindi, dato un cubo di spigolo a, nel trovare un cubo di spigolo x tale
che 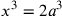 ,
ossia nel trovare due numeri tali che la terza potenza di uno
sia il doppio della terza potenza dell’altro. Ippocrate di
Chio (ca.470a.C.–ca.410a.C.) aveva proposto una via di
risoluzione riducendo il problema di Delo all’altrettanto
difficile problema delle due medie proporzionali, nel senso
che la soluzione del secondo equivale alla soluzione del
primo. ‘Due medie’ perché se tra i segmenti a e b riusciamo a
inserire due segmenti x e y tali che
,
ossia nel trovare due numeri tali che la terza potenza di uno
sia il doppio della terza potenza dell’altro. Ippocrate di
Chio (ca.470a.C.–ca.410a.C.) aveva proposto una via di
risoluzione riducendo il problema di Delo all’altrettanto
difficile problema delle due medie proporzionali, nel senso
che la soluzione del secondo equivale alla soluzione del
primo. ‘Due medie’ perché se tra i segmenti a e b riusciamo a
inserire due segmenti x e y tali che  , allora abbiamo trovato
il valore di x che risolve il problema
cioè, come diciamo oggi, che soddisfa l’equazione di terzo
grado
, allora abbiamo trovato
il valore di x che risolve il problema
cioè, come diciamo oggi, che soddisfa l’equazione di terzo
grado 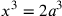 . La riduzione di
Ippocrate alle ‘due medie’ è corretta, infatti dalle due
proporzioni si ricava x e y ossia:
. La riduzione di
Ippocrate alle ‘due medie’ è corretta, infatti dalle due
proporzioni si ricava x e y ossia: 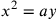
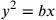 da cui elevando al quadrato
da cui elevando al quadrato
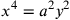 ,
sostituendo
,
sostituendo 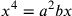 cioè
cioè 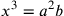 e ponendo
e ponendo  , si ottiene
l’equazione cercata
, si ottiene
l’equazione cercata 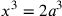 . È Eutocio che, nel suo Commento alle Sfera
e Cilindro di Aristotele (Libro II), riporta la lettera di Eratostene a re
Tolomeo, raccontando, vera o presunta che sia, la nascita del
problema del raddoppiamento del cubo. Sul tema, cfr. Gamba e Montebelli 1988, 166ss; Maracchia 2017, II, 24ss.. Fatto questo, rimane il problema di determinare x e y. Ragionando
nei termini della geometria analitica nata con Cartesio, le
relazioni
. È Eutocio che, nel suo Commento alle Sfera
e Cilindro di Aristotele (Libro II), riporta la lettera di Eratostene a re
Tolomeo, raccontando, vera o presunta che sia, la nascita del
problema del raddoppiamento del cubo. Sul tema, cfr. Gamba e Montebelli 1988, 166ss; Maracchia 2017, II, 24ss.. Fatto questo, rimane il problema di determinare x e y. Ragionando
nei termini della geometria analitica nata con Cartesio, le
relazioni 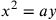 e
e 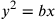 sono le equazioni di due
parabole entrambe passanti per l’origine degli assi
cartesiani, una simmetrica all’asse x,
l’altra all’asse y. Oltre che a
intersecarsi nell’origine, le due parabole si intersecano in
un punto P di coordinate (x , y), e la coordinata x risolve il problema di Delo.
sono le equazioni di due
parabole entrambe passanti per l’origine degli assi
cartesiani, una simmetrica all’asse x,
l’altra all’asse y. Oltre che a
intersecarsi nell’origine, le due parabole si intersecano in
un punto P di coordinate (x , y), e la coordinata x risolve il problema di Delo.
Cusano utilizza il termine «diameter» per indicare la
diagonale, in base a una etimologia inesatta da «δύο» e
«
Il termine latino è «medium divisionis».
Qui per porzione s’intende un segmento circolare.
Questa uguaglianza tra la porzione del cerchio e la sezione della circonferenza è ripresa da Di San Vincenzio 1647, X, 20, il quale verosimilmente aveva preso Cusano come modello. Per una chiara illustrazione del ragionamento cusaniano, cfr. Hofmann e Hofmann 1980, nota 43, 196.
Cusano usa l’espressione «columna quadrangula» o anche (alla fine del §46) «corpus altera parte longius» per indicare il parallelepipedo; più avanti (§ 50) Cusano indica il cilindro con l’espressione «columna rotunda». Anche in questa proporzione Cusano si ispira al De arte mensurandi di De Muris.
Se a è il lato della base quadrata,
h l’altezza (Cusano usa longitudo) del parallelepipedo dato, e c lo spigolo del cubo cercato, si ha:
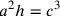 .
Questo risulta aggiungendo due rette intermedie x e y tali che
.
Questo risulta aggiungendo due rette intermedie x e y tali che
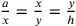 ;
se
;
se 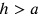 allora c è la minore delle due rette.
Se
allora c è la minore delle due rette.
Se  allora c è la maggiore. Se
allora c è la maggiore. Se 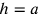 allora
allora 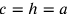 .
.
Se c è lo spigolo del cubo e r il raggio della sfera, Cusano afferma a
torto che 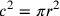 . Come riporta Nicolle 1998, nota 24, 17, Hofmann e Clagett segnalano qui un errore di
comprensione del testo di Archimede da parte di Cusano. In una lunga annotatio di Omnisanctus indica lo stesso errore in una Geometria vulgaris di quel tempo, da
un’altra annotatio all’ultimo passaggio
del 3 capitolo risulta che si tratta della geometria di Ch.
Bouvelles, in cui compare tra gli altri lo stessa formula
sbagliata (
. Come riporta Nicolle 1998, nota 24, 17, Hofmann e Clagett segnalano qui un errore di
comprensione del testo di Archimede da parte di Cusano. In una lunga annotatio di Omnisanctus indica lo stesso errore in una Geometria vulgaris di quel tempo, da
un’altra annotatio all’ultimo passaggio
del 3 capitolo risulta che si tratta della geometria di Ch.
Bouvelles, in cui compare tra gli altri lo stessa formula
sbagliata (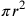 ) per la superficie della sfera. Cfr. Klibansky 1980, 358–362.
) per la superficie della sfera. Cfr. Klibansky 1980, 358–362.
Cusano utilizza la perifrasi «corpus altera parte longius» per indicare il parallepipedo rettangolo.
La lunghezza, cioè l’altezza della colonna.
Si cerca la trasformazione di un parallelepipedo di
superficie quadrata 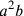 in un altro
in un altro
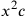 di
altezza data. Cusano costruisce non direttamente, ma
indirettamente, ciò che facilmente sarebbe possibile da
di
altezza data. Cusano costruisce non direttamente, ma
indirettamente, ciò che facilmente sarebbe possibile da
 :
determina t da
:
determina t da 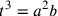 , pone poi
, pone poi 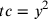 e conclude
e conclude
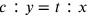 . In
realtà
. In
realtà 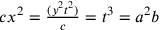 ,
c.v.d. Cfr. Hofmann e Hofmann 1980, nota 49, 197.
,
c.v.d. Cfr. Hofmann e Hofmann 1980, nota 49, 197.
Se 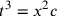 allora, per quanto detto nella nota precedente, si ha
allora, per quanto detto nella nota precedente, si ha 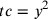 e
e 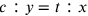 . Ora Cusano
distingue due casi:
. Ora Cusano
distingue due casi:  (e dunque
(e dunque 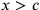 ) e
) e 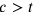 (e dunque
(e dunque
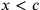 ).
Questo passaggio è oscuro e l’edizione di Omnisanctus presenta grandi differenze con il manoscritto. A
quanto pare Cusano vuole costruire nel caso
).
Questo passaggio è oscuro e l’edizione di Omnisanctus presenta grandi differenze con il manoscritto. A
quanto pare Cusano vuole costruire nel caso 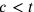 da
da 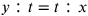 e nel caso
e nel caso
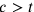 da
da
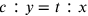 , ma
non si capisce chiaramente il perché.
, ma
non si capisce chiaramente il perché.
Cfr. Archimedes 1910a, I, 33, letto attraverso il De arte mensurandi di De Muris o il De curvis superficiebus archimenidis di Johannes De Tinemue (cfr. Clagett 1964–1984a, I, 496–500 e 502–504).
Da queste righe risulta che Cusano conoscesse la formula
corretta del volume della sfera. Se a è
il raggio della sfera maggiore, allora il suo volume è
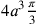 e quello della sfera
minore
e quello della sfera
minore 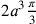 ; entrambi danno
; entrambi danno
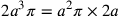 . Che il volume
del cilindro circoscritto si rapporti a quello della sfera
come
. Che il volume
del cilindro circoscritto si rapporti a quello della sfera
come 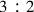 , è
detto nella Prefazione del primo libro di Archimede, Sulla sfera e sul cerchio
(cfr. Archimedes 1910a, I, 34).
, è
detto nella Prefazione del primo libro di Archimede, Sulla sfera e sul cerchio
(cfr. Archimedes 1910a, I, 34).
Questo testo si trova in b e p, tra i capitoli 20 e 21. Essa non è presente nelle traduzioni di Hofmann e Nicole.