2 Cusano e la matematica

Prima di indagare gli scritti matematici, è opportuno tener conto di alcune coordinate di fondo della filosofia della matematica elaborata da Cusano nei suoi scritti.

Nel primo capitolo del De docta ignorantia, Cusano, analizzando il modo in cui procede la conoscenza razionale¹, afferma che ogni ricerca consiste nell’istituire un confronto tra due cose, di cui una è nota e l’altra è ciò che si intende conoscere. Mediante tale comparatio si giunge a individuare un rapporto (proportio), che permette di conoscere ciò che è ignoto². Avendo carattere comparativo, la nostra conoscenza si basa fondamentale sulla misurazione, la quale non può realizzarsi senza il numero, che, afferma Cusano, costituisce la condizione necessaria di ogni comparazione³ e, in quanto tale, è il principio formale di ogni atto conoscitivo della ragione⁴. Da ciò Cusano trae due conseguenze fondamentali. La prima è che l’infinito è per l’uomo inconoscibile, in quanto si sottrae a ogni proportio e a ogni comparatio⁵: «finiti ad infinitum nulla est proportio».⁶ La seconda è che la «precisa veritas est incomprehensibilis»⁷, ossia che è impossibile conoscere perfettamente (adaequate) le cose, il che conferisce alla nostra conoscenza un carattere strutturalmente congetturale⁸.

Misurando, inoltre, l’uomo diventa consapevole dei limiti della propria conoscenza e, facendo esperienza dell’impossibilità di raggiungere la conoscenza dell’ab–solutum, acquisisce la saggezza della consapevolezza della propria ignoranza, la docta ignorantia⁹. E, poiché il processo attraverso il quale comprendiamo è lo stesso che blocca l’accesso all’infinito e ci separa abissalmente da esso, alla mente non resta che vedere l’infinito prospettivamente, nella miriade di modi in cui si manifesta nel mondo finito, ossia nella molteplicità dei particolari che, «secundum plus et minus»¹⁰, partecipano di essa¹¹. L’infinito è per l’uomo un enigma insondabile, il cui mistero è penetrabile riconoscendo il significato dei segni soprannaturali di cui il mondo è intessuto, o, come scrive Cusano nel De filiatione dei, contemplando nelle cose sensibili («che sono segni del vero espressi attraverso simboli») le realtà intellettuali e da queste ascendendo, «con una qualche comparazione senza proporzione», alle realtà eterne¹².

La sproporzione che sussiste tra finito e infinito è la stessa di quella esistente tra numero e unità o tra ciò che è curvo e ciò che è retto. Nell’infinito, nell’unità e nella rettitudine si realizza la perfetta uguaglianza, la praecisio absoluta («deus est ipsa absoluta praecisio»¹³) la quale tuttavia resta alla mente umana «inaccessibilis»¹⁴, «inattingibilis»¹⁵ o «in nullo cognoscibili cognoscitur»¹⁶ o «impossibilis [est]in omni finito»¹⁷.

Cusano vede nella ratio o unitas aequalitatis la misura dell’essere e del conoscere: ogni misurazione, infatti, presuppone necessariamente un’unità di misura, «sine qua numerus non esset numerus»¹⁸. Questa unità assoluta, costituendo il principio della numerazione, sfugge, tuttavia, ad ogni misurazione¹⁹: essa «in pluralitate contracta est»²⁰ o, detto altrimenti, «numerus est explicatio unitatis»²¹. Questo vuol dure che l’unità non è mai visibile uti est, ma solo in alteritate²². Ma, come ogni realtà, in quanto è, partecipa²³dell’uguaglianza secondo un diverso grado di proporzione, così ogni immagine, partecipando della verità nell’alterità del suo essere, è sempre lontana dalla verità del suo esemplare²⁴, che, in sé, è «imparticipabilis»²⁵.

Tuttavia, tra tutte, le figure matematiche rappresentano per Cusano lo speculum più trasparente in cui la verità (ri)splende non come in una lontana immagine (remota similitudo), ma come nella più luminosa delle approssimazioni (fulgida propinquitas)²⁶. La matematica, per Cusano, viene a configurarsi come la via regia del processo di assimilazione mediante cui il soggetto (la mente) cerca di eguagliare l’oggetto ineguagliabile (dio). Questo perché «mens nostra mathematicalia fabricat»²⁷: essendo prodotti dalla mente, gli enti matematici non sono soggetti al mutamento che contrassegna i sensibilia e sono perciò dotate di maggiore certezza, anzi di una «fermissimam atque nobis certitudinem»²⁸.

Tuttavia, proprio in quanto prodotti della ragione, gli enti matematici sono finiti e non possono essere raffigurati dall’immaginazione diversamente da come sono: «cum omnia mathematicalia sint finita et aliter etiam imaginari nequeant»²⁹. Nella scia di Boezio (ca. 480–ca. 524)³⁰, infatti, Cusano afferma che qualsiasi figura si esplica necessariamente nella grandezza (magnitudo) ed è tale perché è una certa quantità³¹, che differisce necessariamente da un’altra. In pratica il geometra vede la figura come entità separata dalla materia corporea e sensibile, ma non dalla materia intelligibile³²: «sed materia eius magnitudo est, sine qua nihil concipit mathematicus»³³. E tuttavia, mentre disegna un particolare triangolo o un particolare cerchio, il geometra guarda con la mente all’exemplar, ossia al modello infinito³⁴. Il triangolo disegnato è in realtà infinito nella mente e non è soggetto alle dimensioni: non è pensato come grande o piccolo, ma come l’atto di tutti i triangoli possibili³⁵. Nell’ambito geometrico–matematico l’infinito viene, per così dire, esperito «d[a]ll’intelletto insieme con l’immaginazione»³⁶.

Ora, se la geometria è vista da Cusano come il terreno previlegiato in cui si può, certo modo, vedere l’infinito, questo deriva dal fatto che vi è un luogo geometrico in cui si realizza la perfetta uguaglianza del principio, ossia nella linea retta. La linea retta gode, infatti, di una proprietà “limite”: in essa sparisce ogni curvità, cessano di esistere il più e il meno di ciò che può essere più o meno curvo; i concetti di aumento e diminuzione si elidono perché coincidono nell’uguaglianza assoluta.

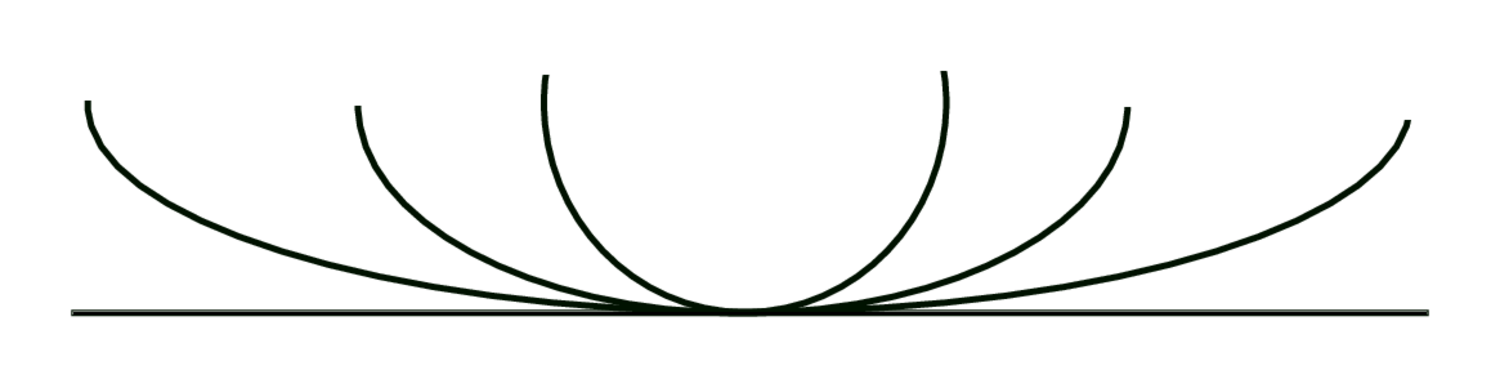
È per questa proprietà che Cusano può affermare che ciò che è retto è misura di tutto ciò che è curvo³⁷. Nel più e meno è implicito infatti un criterio di misura che postula l’esistenza di un ente uguale solo a se stesso rispetto al quale definire il più e il meno. Ciò che è curvo è più o meno curvo in base alla sua aderenza (partecipazione) alla retta, che, per definizione, è priva di curvità. E se è vero che non si può immaginare che il curvo arrivi a coincidere col retto anche dopo una successione infinita di curve sempre più aderenti ad esso, la retta resta tuttavia l’ultimo termine di riferimento, l’unità di misura per l’infinità delle linee curve.

Così, nel concetto di rectitudo («la linea infinita è rettitudine infinita»³⁸), o meglio nella paradossale soluzione del curvo nel retto, ossia nella perfetta uguaglianza della loro coincidenza, Cusano illustra geometricamente l’infinito in atto, fermo restando «l’impossibilità che esista una linea infinita in atto»³⁹.

Nell’Apologia doctae ignorantiae, nel rispondere a Wenck che non riusciva a comprendere come l’infinito potesse essere misura dei finiti, dal momento che il finito non ha con l’infinito nessuna proportio⁴⁰, Cusano riprende l’esempio della linea infinita utilizzato nella sua prima opera, per mostrare come sia possibile pervenire «ad simpliciter infinitum»⁴¹. Ogni linea (finita) è, in sé, infinita, perché, pur essendo potenzialmente divisibile all’infinito, resta sempre una linea. Questo implica che «una linea finita è indivisibile nel suo esser linea […] Ne consegue che la linea infinita è la ragion d’essere della linea finita»⁴². Allo stesso modo, ogni linea, qualunque sia la sua misura, estesa all’infinito non è più una linea, ma si identifica con l’infinità stessa⁴³. Nella linea infinita, dunque, vi è ogni linea finita, sebbene ciascuna linea finita ne partecipi in gradi diversi. In questo senso, la linea retta infinita costituisce l’esemplare di tutte le figure geometriche che si possono costruire con le linee⁴⁴.

Ora, se è vero che l’infinito semplice comprende il massimo e il minimo assoluto, va detto che, poiché solo il massimo assoluto, che contiene tutto, include il minimo; solo il massimo assoluto è uguale a se stesso, e dunque in esso solo è fondata l’uguaglianza assoluta⁴⁵. Così, nel massimo assoluto il cerchio è in ogni poligono, e ogni poligono è nel cerchio: l’uno è nell’altro, e c’è un solo perimetro infinito: la massima linea curva è uguale alla linea retta, così come lo è la minima linea curva⁴⁶. Questo vuol dire che la curva, in sè, non è nulla, ma partecipa della rettitudine secondo un certo grado⁴⁷, e dunque, comparando la curva e la retta, si conclude che la linea retta partecipa della linea infinita più di quanto ne partecipi la linea curva: «premetto che la linea retta è più semplice della linea curva, in quanto la linea curva, deviando dalla linea retta, non può essere concepita senza il concavo e il convesso»⁴⁸.

La linea infinita, a sua volta, cessa di essere linea perché essa non ha più né quantità né termine; la linea infinita non è più linea, ossia non è più un ens rationis, ma la stessa infinità, ossia uguaglianza assoluta⁴⁹. Questo vuol dire che il maximum in se non è né linea, né triangolo, né cerchio, né sfera, «ma è piuttosto infinitamente e senza alcuna proporzione al di sopra di esse»⁵⁰.

Dunque, attraverso un processo di infinitizzazione delle figure geometriche (linea, triangolo, cerchio, sfera), è possibile avvicinarsi all’«infinito semplice che è del tutto indipendente da ogni figura»⁵¹. Questo processo avviene, scrive Cusano, per additionem infinitatis⁵². Tuttavia, più che come l’attuazione dell’illimitato sviluppo di un’infinità potenziale, l’infinità si configura come rimozione del finito, ossia del limite, dal finito: «quando infinitas additur termino […] non aliud agit eius additio ad terminum quam removere terminum»⁵³. Si potrebbe dire che l’additio infinitatis altro non è che un’ablatio finitatis. Così facendo, si intuisce, in una superiore visione mentale, lo stesso infinito sine termine⁵⁴, «et tuns nostra ignorantia incomprehensibilter docebitur»⁵⁵.

Cusano sa che le figure infinite non esistono in actu. Esse sono semplicemente un «enigma intellettuale» – il più adeguato (propinquius) – per indicare Dio⁵⁶. La transumptio attuata dalla matematica intellettuale, configurandosi come assimilatio del finito alla natura infinita divina⁵⁷, costituisce un’utile manuductio all’indagine umana intorno alle cose divine (in rebus divinis⁵⁸) e rappresenta il terreno fertile per un’antropologia metafisica che cerca di conciliare il potere dell’uomo con l’infinita potenza di Dio mediante il principio della coincidentia oppositorum⁵⁹. In questo senso David Albertson afferma: «Geometry was for him (i.e. Cusanus) a kind of mathematical laboratory for speculative discoveries, or better, a kind of playground where he could observe his mind’s movements and exercise it for theological tasks»⁶⁰.

Note a piè pagina