1. Quia vidi practicum magisterium commensurationis curvi et recti deesse geometricis, ideo ipsos imperfectos et plura, quae possibilia fieri vident, ad actum deducere non posse, conatum igitur non parvum adhibui, ut ipsam artem assequerer. Quam si repperi, tu qui haec leges, iudicabis.
2. Commensurari autem curvum et rectum dico, quando una mensura mensurantur, puta quando recta linea tot pedes habet rectos quot arcus curvos.
Propositio prima
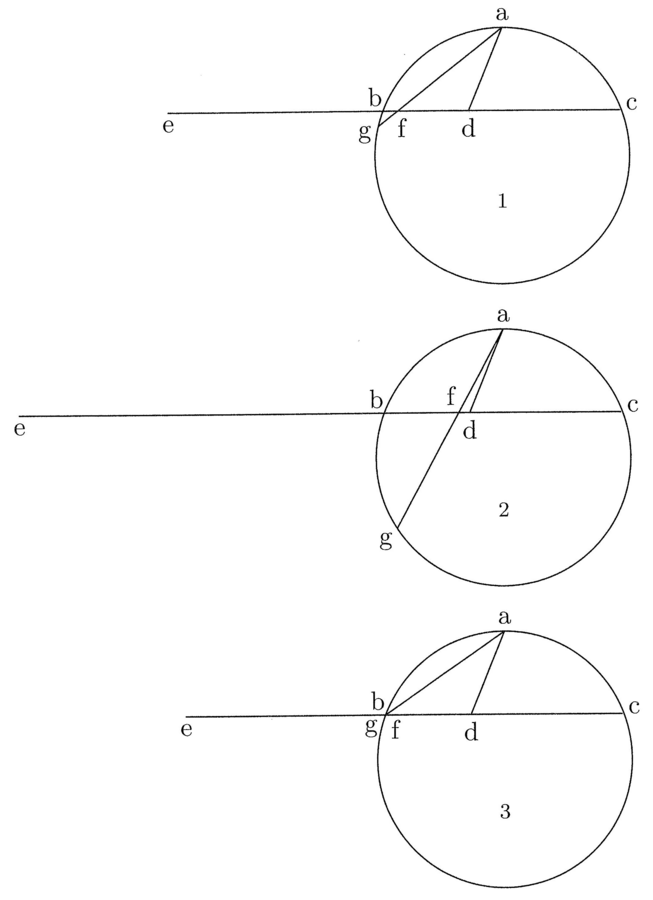
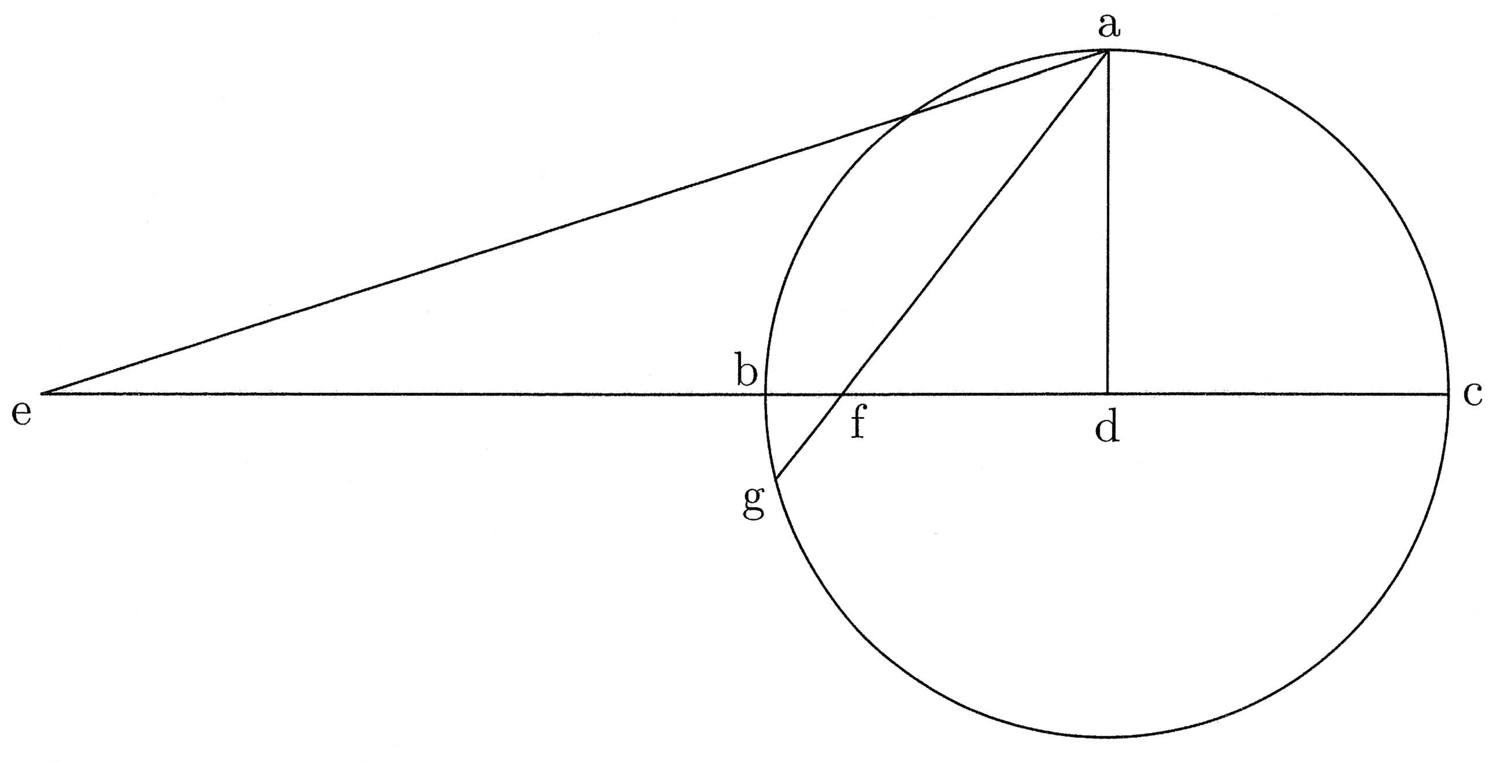
3. Dato area rectam ei commensurabilem assignare (cfr. figura 1).
Sit bc datus arcus, cuius a medium, et trahatur chorda bc et in illa punctus aequedistans de a et b, qui sit d, et hic est punctus huius magisterii. De illo igitur per b continua rectam, quae sit de, taliter, quod si de a chordam ag, quae sit ut medietas de, per de traxeris, illa chorda vadat per f punctum lineae de. Sit autem df quarta pars de. Tunc de linea recta est commensurabilis bc arcui.
4. Ad hoc probandum praesuppono duo. Primo, quod de sic signari potest, quod inter f punctum, per quam vadit chorda, ut praefertur, et e, finem lineae de, portio aequetur tribus quartis commensurabilis rectae. Patet de se. Nam certum est, quod taliter signari potest, quod fe est plus, ut in secunda figura, et taliter etiam, quod est minus, ut in tertia figura; igitur et taliter, quod nec plus nec minus. Secundo praesuppono, quod quanto de est minor, tanto fe in habitudine ad de est minor et df maior, et quanto maior, huius contrarium. Hoc etiam per se patet ad oculum in secunda et tertia figuris.
5. Dico igitur primum praesuppositum verificari, aut quando de est quaesita, scilicet commensurabilis arcui, aut quando minor aut quando maior. Si primum, habeo intentum; nam oportebit tunc df esse necessario quartam partem de. Si dicis verificari, quando de est minor commensurabili, hoc est impossibile. Nam cum tunc ex secunda suppositione fe sit minor in habitudine ad de et df maior quarta in commensurabili, et secundum te aequabitur tribus quartis commensurabilis; non erit de minor commensurabili, sed maior. Sic si dicis verificari, quando de est maior commensurabili, similiter implicat contradictionem.
Propositio secunda
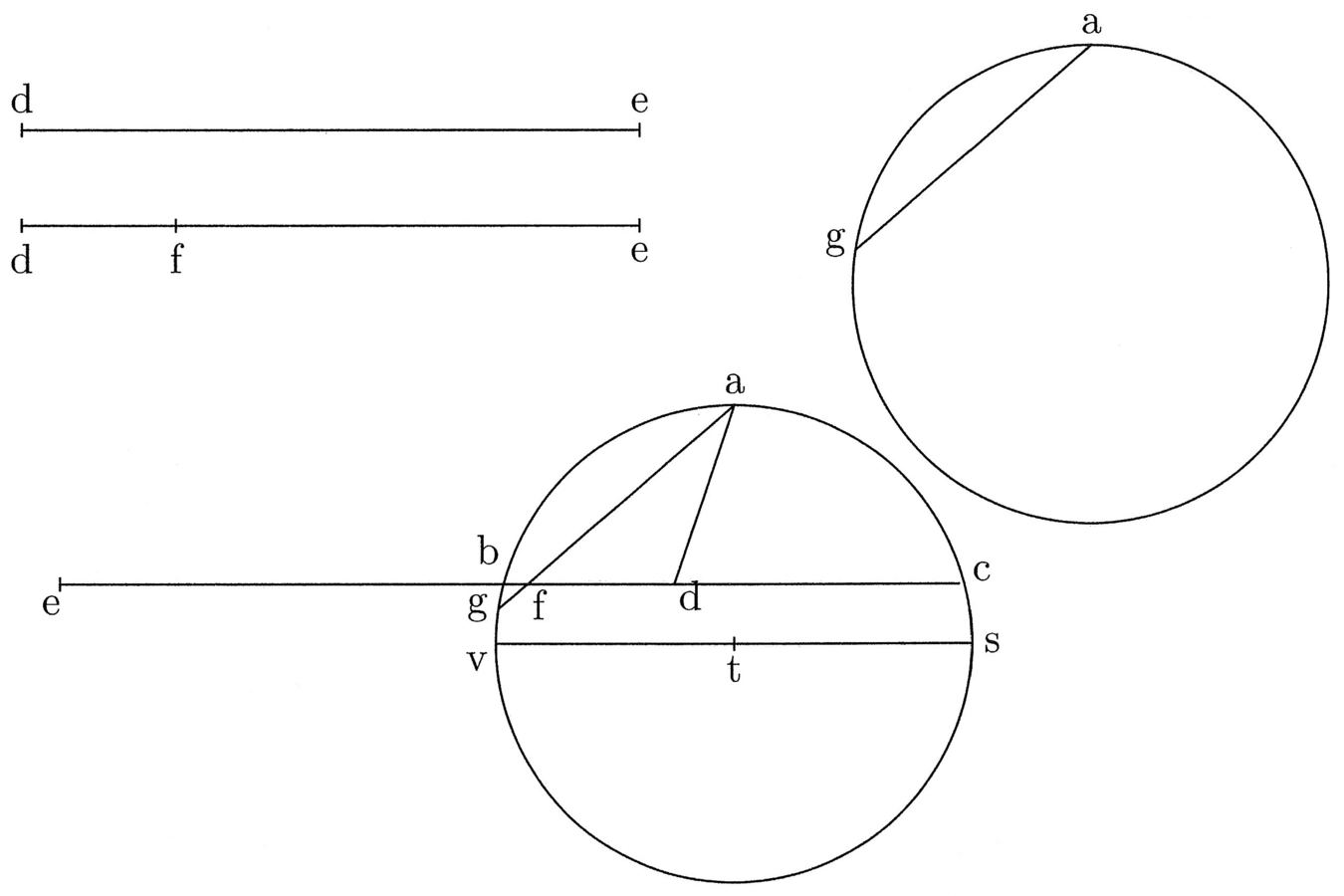
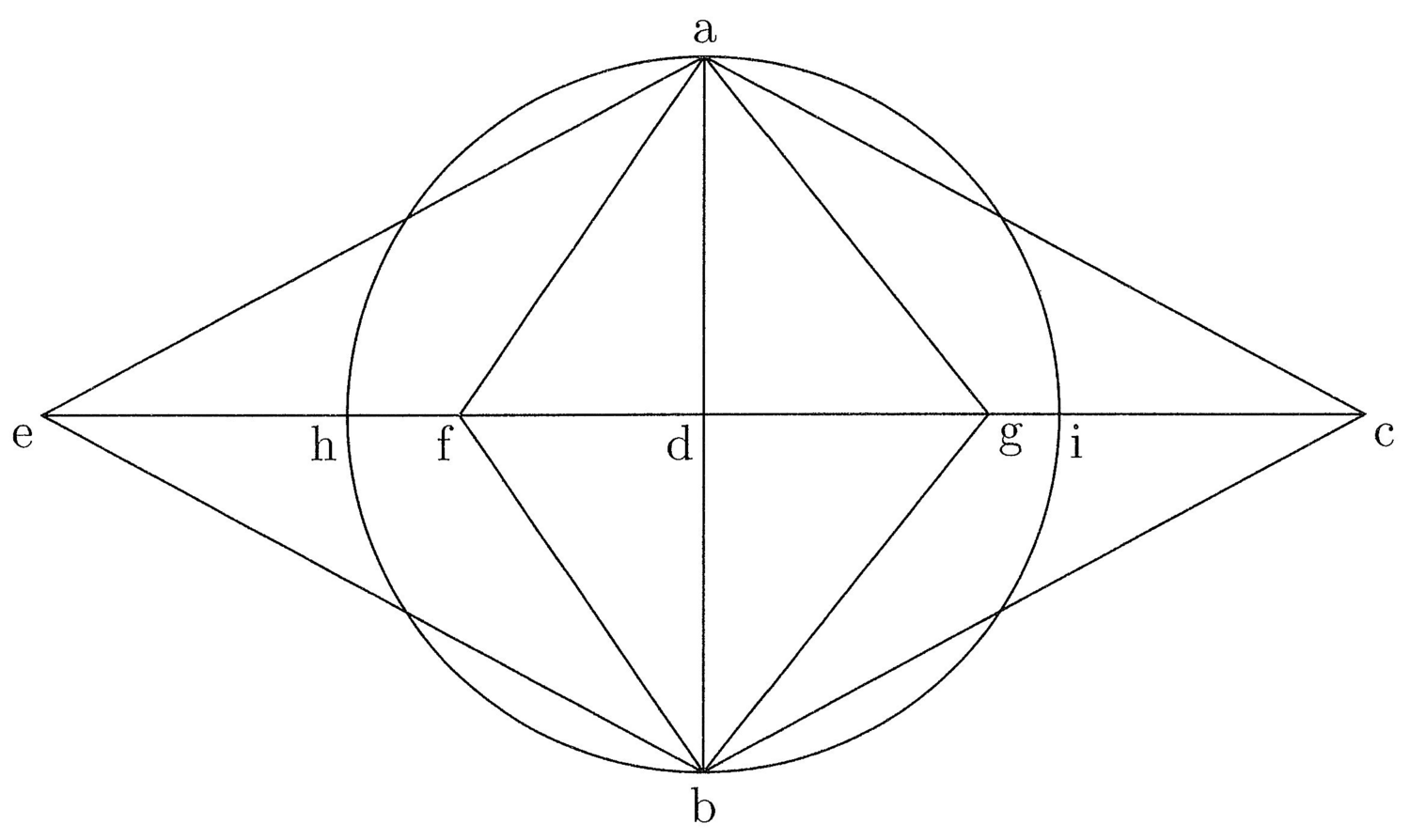
6. Datae rectae arcum dati circuli commensurabilem assignare (cfr. figura 2).
Sit data recta de et datus circulus, cuius centrum t et diameter stv et a medium omnium arcuum. De a trahe chordam ag, quae sit ut medietas de, et in de signa eius quartam, quae sit df, et applica de aequedistanter ad tv, taliter quod f cadat super ag chordam, et ubi secat circumferentiam circuli, pone b. Si tunc d aequedistat de b et a, erit ba medietas arcus quaesiti. Continua igitur bd, quousque compleatur chorda in c, et habes bc arcum commensurabilem de rectae. Totum patet ex praemissa.
7. Ut autem videas d esse punctum huius magisterii, qui si ag chorda est ba arcui commensurabilis, ab f sectione ubi ag secat bcd, ipse punctus per medietatem ag distat, considera, quod quanto bc chorda est maior, tanto d de b et a plus et de centro circuli minus distat, et quanto minor, huius contrarium; et hoc de se patet (cfr. figura 3).
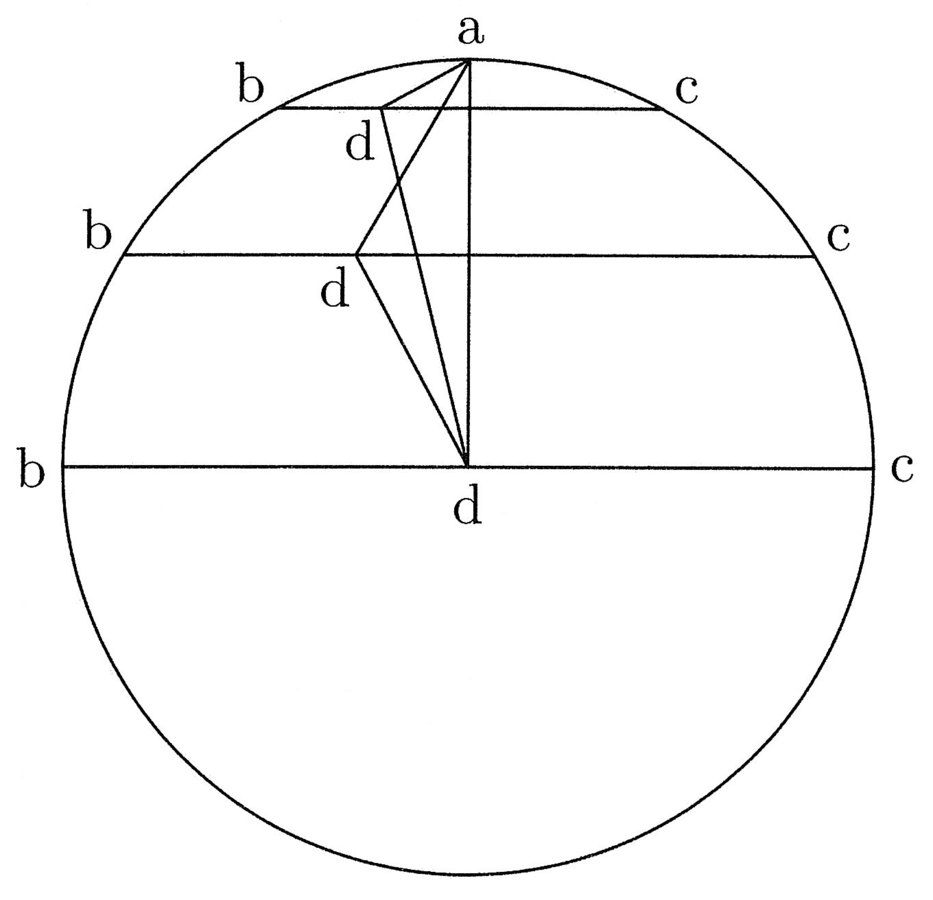
In maxima igitur chorda d minime distat a centro circuli et maxime de b et a; in minima chorda maxime distat de centro et minime de b et a. Unde d in maxima chorda est in centro circuli, et in minima in circumferentia eius. Sed certum est, quod d sive in maxima chorda sive in minima aequedistat de b et a; igitur sic in omnibus intermediis. Unde sequitur, quod si bc est chorda arcus tertiae partis circumferentiae circuli, d punctus a centro et de b et a aequedistabit.
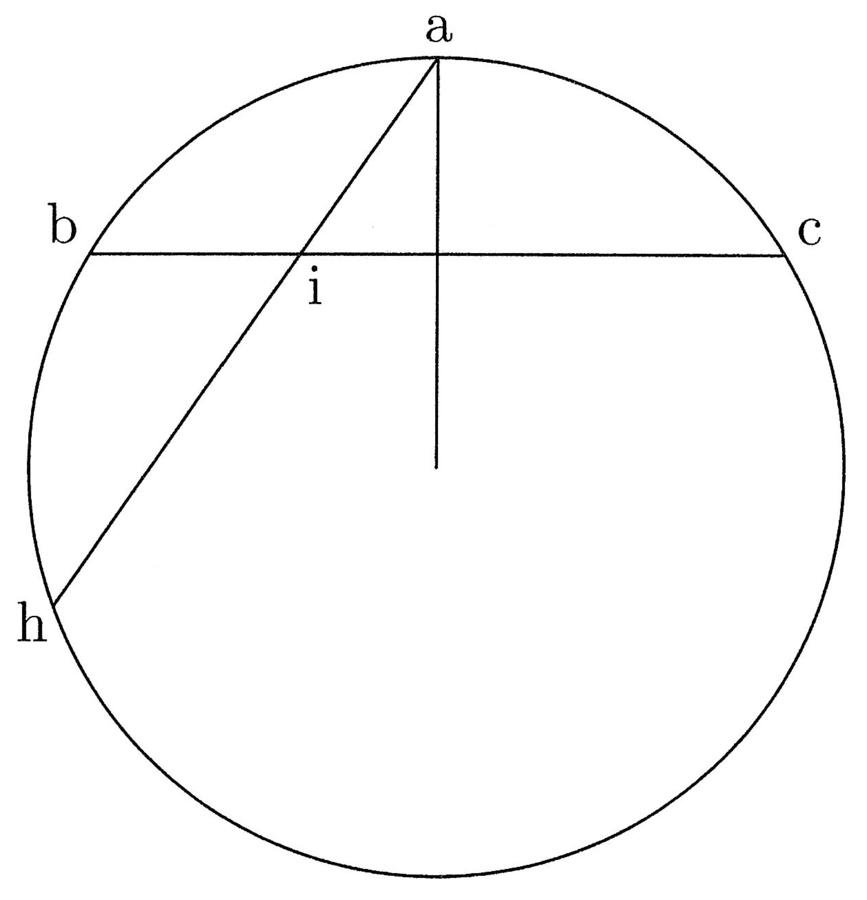
8. Adhuc sic de a potest trahi ah chorda per bc, quam in i puncto secet (cfr. figura 4). Dico aih sic potest trahi, quod ai erit distantia puncti d de a in illa chorda ah. Hoc certum.
Aut igitur hoc erit, quando ah est ut bc, et tunc i sectio aequedistabit de b et a, et erit d utriusque, et est intentum. Aut ah est minor, et hoc non est possibile, quia tunc ai esset maior quam prius, quando aequalis; aut quando maior, et est iterum impossibile, quia ai minor quam prius, quando aequalis.
Propositio tertia
9. Arcui semicirculi rectam et areae eius curvae rectilinealem commesuraliles designare (cfr. figura 5).
Sit circulus et bc arcus semicirculi, cuius medium a, et d punctus magisterii aequedistans de a et b, puta hoc casu centrum circuli. Et trahe ad lineam, deinde trahe db in continuum, et sit de, ita quod si medietatem de feceris chordam ag, quae de a per de trahitur, ipsa transeat per f punctum de, qui f punctus distet de d per quartam partem de modo quo supra. Deinde claude orthogonium per ae latus. Dico aream ade orthogonii commensurabilem areae semicirculi, et de commensurabilem arcui bc. Secundum patet ut supra. Primum patet eodem modo ut prius per duo supposita, quorum primum est: de posse signari et per ea orthogonium claudi, taliter quod si ducitur chorda, quae sit medietas de de a per de, ut sit afg, area inter afe cadens erit commensurabilis tribus quartis areae semicirculi. Patet, quia datur, ubi est plus et ubi minus, igitur et ubi nec plus nec minus. Secundo praesuppono, quod quanto de fuerit minor, tanto illa area afe est minoris habitudinis ad totam aream orthogonii ade, et quanto maior, maioris. Primum igitur praesuppositum aut verificatur, quando area orthogonii ade est commensurabili areae semicirculi, et habetur intentum; aut ubi minor seu maior, et utrumque implicat contradictionem praecise modo quo supra.
10. Palam igitur est, quod si orthogonius, cuius unum latus est semidiameter et aliud cum illo rectum angulum faciens est commensurabile toti circumferentiae circuli: area illius orthogonii est commensurabilis areae circuli. Et quia quaelibet polygonia in aliam verti potest, igitur poteris areae circuli commensurabilem aream trianguli, quadranguli, quadrati, pentagoni et cuiuscumque alterius polygoniae assignare, et cuiuslibet partis circuli etiam circulo incommensurabili. Dare etiam angulos poteris datarum linearum habitudinis et figurarum omnium unius in aliam commensurabiliter: dico mirabiles transmutationes facere salva cuiuslibet figurae capacitate et propria invariabilique natura, et ad multa occulta, quae vix enarrari possunt, hac arte pervenies, etiam in sectionibus et uniformiter difformibus curvitatibus. Etiam angulos et instrumenta componere poteris, cum quibus praemissa facillime et subito facies, quae tuae industriae relinquimus.
11. Area agbf
commensuratur medietati areae circuli et area abe commensuratur areae circuli
(cfr. figura 6). Medium proportionale inter ad semidiametrum et ed
rectam medietati circumferentiae circuli commensurabilem, quam
nona sexti Euclidis
Finis.