1. Paulo
2. Etsi veteres magno ingenio praediti sedula indagatione conati sunt milita tunc abscondita sibi et posteris nota facere perfecerintque utiliter in plerisque maximis atque optimis artibus, non tamen omne desideratum, in quibusque altioribus theoriis attigerunt, praeordinante hoc universorum optimo provisore, ut in nobis vis illa divinae intelligentiae non torpeat, sed admiratione vehementiori ad ipsa latentia et scitu possibilia feratur. Ardentius quidem in obscuri penetrationem movemur, ut quietius de mentis vigorositate delectemur. Inter ea autem, quae geometricis speculationibus insudantibus hucusque impedimento fuere, unum ab omnibus, quorum vires ingenii libri, qui ad nostram notitiam deducti sunt, curiosius observant, incognitum remansit, de recti scilicet atque curvi aequalitate aut in invicem transmutatione statuenda, ita ut non minimis, immo paene omnibus huic inquisitioni deditis post immensos labores visum sit viam ad huius notitiam acquirendam a nobis sublatam, hoc rei impossibilitate agente et natura ipsam tantae oppositionis coincidentiam repellente. Ego vero rei huius difficultatem in parvitate apprehensionis et intermissione diligentiae, non summo acumine vigilantium, ut obscuritas negotii deposcit, potius existimans dato qualicumque otio ad artem novam, qua ad quaesitum pertingerem, me contuli ei diligenter satis ob altiores fines insudando, quousque cunctarum meditationum mearum subscriptam formula facilem resolutionem efficerem. Quoniam autem in tanta et hactenus ignota arte, a qua non tantum perfectio geometricae transmutationis dependet, sed et etiam introductio ad altiora ascendendi figuratur, non erat in obscuritate et parvitate ingenioli mei confidendum, recte statui ad te, arbitrum peritissimum atque veritatis zelatorem, confugere et iamdudum probatissimo amico inventionem pandere, ut in statera aequissimi iudicis extimetur. Noli igitur, amice dilectissime, ista, etiam si in maioribus verseris, quasi cruda indigestaque abicere. Lectu enim parva, intellectu vero facillima sunt. Sed quanto me ab annis iuventutis atque adolescentiae nostrae strictiori amicitiae nodo atque cordiali quodam amplexu indesinenter constrinxisti, tanto nunc accuratius emendationi animum adhibe et in communionem aliorum nisi correctum predire non sinas.
3. Post innumeros paene modos, quibus, semper tamen deficiens, ad institutam artem pervenire contendi, tandem ad principium, quo in De docta ignorantia usus sum, respiciens via mihi patefacta existit. Exigit autem ars, quam inquiro, praeter ea iam tradita in geometricis versionem curvi in rectum ac recti in curvum. Inter quae cum nulla rationalis proportio cadat, oportet in quadam coincidentia extremorum hoc latere secretum. Quae cum in maximo sit, ut alibi traditur, et maximum sit circulus, qui ignoratur, in minimo, qui est triangulus, inquiri ipsum debere ibi ostenditur.
4. Omnium autem figurarum multorum angulorum, quae polygoniae, et aequalium laterum, quae isopleurae, et eiusdem longitudinis laterum, quae eandem habentes peripheriam isoperimetrae dicuntur, triangularem minimae capacitatis existere constat. Et cum tanto quaelibet isoperimetra sit capacior, quanto plures angulos habuerit, erit circulus isoperimeter figurarum omnium capacissima. Ad quam per angulorum multiplicationem deveniri nequit, sicut nec in numero ad maximum. Nulla igitur polygonia ad circularem isoperimetram proportionem rationalem habere potest.
5. Quia vero differentia capacitatis isoperimetrarum figurarum correspondet differentiae ‹semidiametrorum› circulorum infrascriptorum eisdem, ut iam ante hoc notum est, quare nec circulus inscriptus, qui semper minor est, nec circumscriptus, qui semper maior est, ad circulum isoperimetrum rationalem proportionem habebit. Semidiametri autem illorum iam dictorum circulorum maxime inaequales in trigono existunt, in aliis successive minus inaequales, in circulo vero ‹isoperimetro› coincidentes, cum ibi inscriptus, circumscriptus et peripheria coincidant. Hinc inquirendum, qua arte ad coincidentiam ipsam atque propositum nostrum pertingere valeamus.
6. Videtur autem ad artis quaesitae sufficientiam primum pertinere, ut datae rectae detur aequalis curva. Secundo, ut secundum habitudinem curvae ad curvam detur recta ad rectam. Tertio, ut inter datas lineas duae proportionales assignentur. Quarto, ut secundum habitudinem duarum datarum sciatur ad tertiam datam dari quarta. Primum hactenus ignotum. Secundum nondum consideratum. Tertium a paucis obscure tactum. Quartum clare a multis explicatum. Complicatur in his omne, quod transmutatoriae huic arti opportunum est, ut praemissis istis, quae circa haec necessaria sunt, in exemplaribus subsumptionibus ostendere conabor.
Primum praemittendum
7. Posse lineam curvam esse, quae datae rectae nec maior nec minor sit, ab omnibus admittitur, licet non omnes eam signari posse affirment. Potest igitur peripheriae datae polygoniae circuli alicuius peripheria nec maior nec minor esse, ut sint isoperimetrae. Sed quomodo haec detur, inquirimus.
8. Quoniam autem tanto circulus polygoniae aequilaterae seu isopleurae circumscriptus maior est quanto ipsa paucorum angulorum, et ei inscriptus tanto minor, hinc nemo negare potest, quin omnis circulus polygoniae aequilaterae inscriptus minor sit circulo isoperimetro atque quod omnis circumscriptus maior. Quare inter inscriptum atque circumscriptum isoperimeter cadens habet semidiametrum omni semidiametro cuiuscumque inscripti circuli cuicumque polygoniae isopleurae et isoperimetrae maiorem et circumscripti semidiametro minorem. Manifestabitur autem id, quod quaerimus, post multos difficiliores modos facili consequentia ex hac propositione:
9. Semidiameter circuli isoperimetri trigono inscripto se habet ad lineam a centro circuli, cui trigonus inscribitur, ad quartam lateris ductam in proportione sesquiquarta.
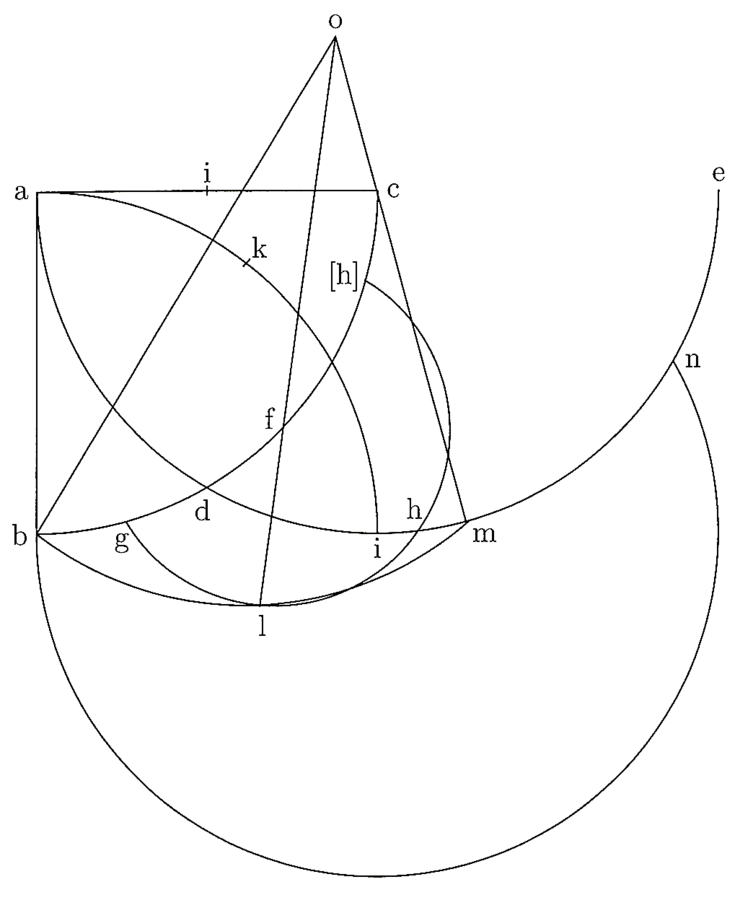
10. Sit circulus super a centro descriptus, cui bcd trigonus inscribitur, diviso bc latere in quattuor partes aequales per e, f, g signatas. Dico, si de a ad e linea ducta extendatur per quartam sui, ut sit ah, illam fore semidiametrum circuli, cuius circumferentia aequatur tribus trigoni lateribus.
11. Hoc sic facillime verum comprobatur. Nam tracta de a ad f linea illam semidiametrum circuli inscripti fore constat, quae est omnium inscriptorum polygoniis isoperimetris minima. Et similiter linea de a ad b ducta est semidiameter circumscripti, quae est omnium circumscriptorum isoperimetris polygoniis maxima (cfr. figura 1). Et si de a prope f ad i punctum lineam duxeris extendendam secundum habitudinem if portionis ad bc latus, quae extensa sit ak illam minorem esse semidiametro circuli isoperimetri manifestum, cum semidiameter circuli isoperimetri sit omnium inscriptorum polygoniis isoperimetris maxima. Similiter si de a prope b ad punctum f linea ducta extensa fuerit secundum habitudinem portionis if ad bc, quae sit am, illam esse maiorem quaesita per se clarum est, cum quaesita sit omnium ‹semi›diametrorum circulorum circumscriptorum polygoniis isoperimetris mimima. Potest igitur inter l et i ad aliquem punctum de a linea duci, quae extensa secundum habitudinem portionis inter punctum illum et f cadentis ad latus bc aequabitur quaesitae.
12. Pariformiter si fuerit linea ai extensa secundum habitudinem portionis ib ad bc, ut sit an, illam minorem fore quaesita manifestum est. Et similiter si fuerit al extensa secundum habitudinem lb ad bc, ut sit ao, illam maiorem esse quaesita certum existit. Cadet igitur inter l et i punctus, ad quem de a linea ducta et extensa secundum habitudinem portionis inter punctum illum et b cadentis ad bc latus aequabitur quaesitae. Unde uti reperitur punctus, puta i, ad quem linea ducta si extenditur secundum habitudinem ambarum portionum sive versus b sive versus f ad latus trigoni, remanet minor. Et alius punctus, videlicet l, reperitur, ad quem linea ducta sive extendatur secundum habitudinem unius sive alterius portionis ad latus trigoni, fit semper maior quaesita. Sic erit punctus e tertius, ad quem linea ducta et extensa secundum habitudinem cuiuscumque portionis ad latus trigoni non fit nec maior nec minor. Et constat alium quam e punctum esse non posse, in quo solum secundum utriusque portionis extensionem idem evenire potest.
13. Poteris pariformiter dicere: si ai linea extenditur secundum habitudinem fi ad bc, est minor, et similiter: si extenditur secundum habitudinem quadrati if ad quadratum bf, est minor. Et si al extenditur secundum habitudinem lf ad bc, est maior, et similiter: si extenditur secundum habitudinem quadrati lf ad quadratum bf, est maior. Erit igitur punctus inter l et i, ad quem linea ducta et extensa secundum habitudines duas iam dictas nec maior erit nec minor, et hoc necessario est e.
14. Poteris etiam adhuc adicere tertiam habitudinem, scilicet si ai extensa secundum habitudinem quadrati if ad quadratum bf et habitudinem if ad bc et habitudinem bi ad bc, semper est minor, et al secundum illas habitudines extensa est maior. Erit punctus ad quem linea de a ducta et secundum trinas istas habitudines extensa nec est maior nec minor, et iste est e punctus aequedistans a b et f.
15. Probatur autem idipsum hac via. Manifestum est in omni polygonia isoperimetra lineam de centro ad punctum medium lateris esse semidiametrum inscripti et continue secundum capacitatem maiorem polygoniae plus accedentem ad aequalitatem semidiametri circuli isoperimetri, et similiter lineam ductam de centro ad finalem terminum lateris esse semidiametrum circuli circumscripti et illam tanto minorem continue fieri, quanto capacior fuerit polygonia. Cadet igitur inter illa duo puncta, scilicet terminalem et medium lateris cuiuslibet polygoniae, punctus unus, ad quem si linea de centro ducitur et secundum habitudinem quadrati portionis inter punctum contactus et medium lateris ad quadratum medii lateris vel secundum habitudinem portionis ad latus extenditur, erit ut semidiameter circuli isoperimetri. Et hoc quidem nihil haesitationis habet.
16. Continget autem hunc punctum in omnibus polygoniis differenter distare ab illis duobus punctis, scilicet terminali et medio lateris, plus accedendo ad medium lateris et recedendo ab extremali, quanto capacior fuerit polygonia. Sicut igitur hic punctus continue accedit ad medialem in capacioribus, quousque in capacissima deveniatur ad coincidentiam omnium trium illorum punctorum, ita necessario in minus capacibus recedit punctus ille a mediali, quousque in minime capaci ab illis duobus punctis maxime distet. Quare e est medius punctus aequaliter maxime ab extremis distans, in quo incapacissimo trigono habetur quaesitum. Ob hoc omnis semidiameter circuli circumscripti cadit de a ad aliquem punctum lineae be secundum praefatas habitudines portionis versus b extensae, et ae sic extensa est omnium illarum minima. Hinc est semidiameter circuli isoperimetri, cum semidiameter illa sit omnium semidiametrorum talium circumscriptibilium circulorum minima, cum qua coincidit maxima semidiameter inscriptibilium. Unde in e puncto est coincidentia ascensionum de f versus e semidiametrorum inscriptibilium et descensionum de b versus e semidiametrorum circumscriptibilium, extensionibus factis secundum praefatas habitudines portionum versus b in una et versus f in alia.
Secundum praemittendum
17. Aiebam iam ante praemitti oportere, qua via habitudo attingeretur inter rectam et rectam, quae est inter curvam et curvam, quoniam, ut sequentia ostendent, perfectio transmutatoriae artis, quam inquirimus, non poterit hoc ignorato adipisci. Cumque ego inquirendo hoc ipsum ad rectilineum trigonum respicerem, ubi de portione lateris unius ad similem lateris alterius portionem linea ducta ad latus primum triangulum claudens, a quo aequedistat, eam habet proportionem qualem portio lateris alterius, per quam ducta est, ad totum latus; et simile in arcu inquirerem quale hic in latere rectilineo, vidi quod si triangulum depingerem unum latus arcuale habens et aliud rectilineale, tunc non possit linea per portionem arcualis lateris duci ad alterius lateris similem portionem, quae se ad latus rectilineum secundum quaesitam habitudinem habeat, si latus tertium fuerit rectilineum. Nam si latus curvum fuerit convexum, manifestum est de eius medio ad medium rectilineam ductam maiorem esse medietate lateris rectilinei triangulum claudentis. Si vero concavum fuerit, necessario minus erit.
18. Sic si arcuale fuerit latus, tunc si fuerit uti aliud, puta concavum si est concavum aut convexum si est convexum, erit linea maior aut minor per portionem tracta ut in genere iam statim praemisso. Sed si latus ipsum fuerit convexum alio existente concavo, et fuerint portiones arcuales eiusdem circumferentiae circularis et aequales, excedere necesse est lineam per portiones arcuales eiusdem ductam eam, quae secundum habitudinem esse debet quaesitam. Nam chordae si arcubus subtenduntur, eundem efficiunt angulum quem arcus. Et si fuerint chordae medietatum arcuum, iterum idem angulus exsurget. Et cum chordae medietatis excedant medietatem chordarum integri arcus, erit manifestum lineam de medietate ad medietatem ductam secundum excessum chordae medietatis arcus super medietatem chordae integri arcus excedere.
19. Oportet ergo alterum latus arcuale alio brevius esse. Non potest autem concavum brevius esse. Nam chordae si illis arcubus subtenderentur, angulus chordarum angulo arcuum minor esset, et ille angulo, qui ex chordis medietatis arcuum exsurgeret. Hinc linea de portione ad portionem tracta maior foret quaesita. Quare necesse erit, quod triangulus ille, quem quaerimus, sit ex tribus lateribus, quorum duo sint arcualia inaequalia, ita quod maius sit maior portio circumferentiae circuli et concave superficiem claudat, aliud vero arcuale latus minor sit portio circumferentiae eiusdem circuli et convexe superficiem trianguli terminet, tertium autem latus rectum existat. Necesse est autem, quod cum lateribus istis arcualibus chordas subtendis, quod angulus chordarum maior sit angulo arcuum et angulus chordarum medietatis arcuum maior angulo arcuum et minor angulo chordarum integrorum arcuum, tanto quidem minor, quanto excedunt chordae medietatis arcuum chordas medias integrorum. Et cum hac via conspicerem possibile fore dato triangulo iam dicto lineas per portiones ductas esse minores ac etiam esse maiores atque aequales quaesitis, quaerere proposui triangulum, cuius latus rectilineum esset ut semidiameter circuli laterum arcualium, et quod latus maius arcuale esset ut quadrans.
20. Descripsi igitur quadrantem bc super a centro ac posito pede circini in c descripsi semicirculum ade (cfr. figura 2). Divisi arcum bc per medium significando f, descripsi semicirculum super f, qui sit gh, cuius semidiameter ut medietas ac. Descripsi super b semicirculum occultum ik et in eius circumferentia quaesivi punctum, in quo posito uno pede circini et alio in b extenso arcum describerem, qui transiret per semicirculum minorem gh ad semicirculum maiorem ade, ita quod punctus arcus illius, ubi secatur semicirculus gh, puta l, sit medius totius arcus aequedistans a b puncto et a puncto contractus arcus de, puta m. Aequaliter traxi igitur lineam cm et habui triangulum cbm quaesitum. Cum autem quaererem punctum m, adverti ipsum necessario debere distare a d per medietatem arcus bc, puta medietatem quadrantis. Nam hic punctus est cadens inter propinquissimum et remotissimum possibiles. Posito enim pede circini in circumferentia occulta aki, scilicet in a, propinquissimus punctus erit d, qui est coincidens cum bc arcu. Et si posuero pedem circini in puncto, ubi arcus occultus aki secat de, puta in i, et descripsero bn arcum, erit n maxime distans. Non enim poterit in arcu de punctus reperiri plus distans a d. Manifestum est autem d n in arcu de per quadrantem distare, in cuius medio est m punctus, in quo extrema ad aequalitatem mediam reducta reperiuntur. Hac via triangulum quaesitum adinveni.
21. Post haec adverti, si cm ducerem in continuum et directum in infinitum et ducerem de l per f lineam similiter in continuum, quod necessario illae in aliquo puncto concurrerent, cum non sint aequedistantes. Notavi igitur punctum concursus per o punctum. Consideravi igitur, quod lineae omnes, quae de portione ad portionem et in continuum ducerentur, cum ambabus illis necessario concurrerent, nec citius cum una quam cum alia. Quare omnes in o puncto convenirent. Habui igitur, quod si de o puncto linea duceretur per quamcumque portionem quadrantis bc usque ad arcum bm, quod portio lineae rectae illius illos inter arcus cadens se habebit ad rectam cm sicut portio arcus de b ad sectionem lineae rectae ad totam quadrantem bc, puta eadem est proportio arcus bf ad bc quadrantem, quae est lineae fl ad lineam cm, et hoc erat quaesitum.
Tertium praemittendum
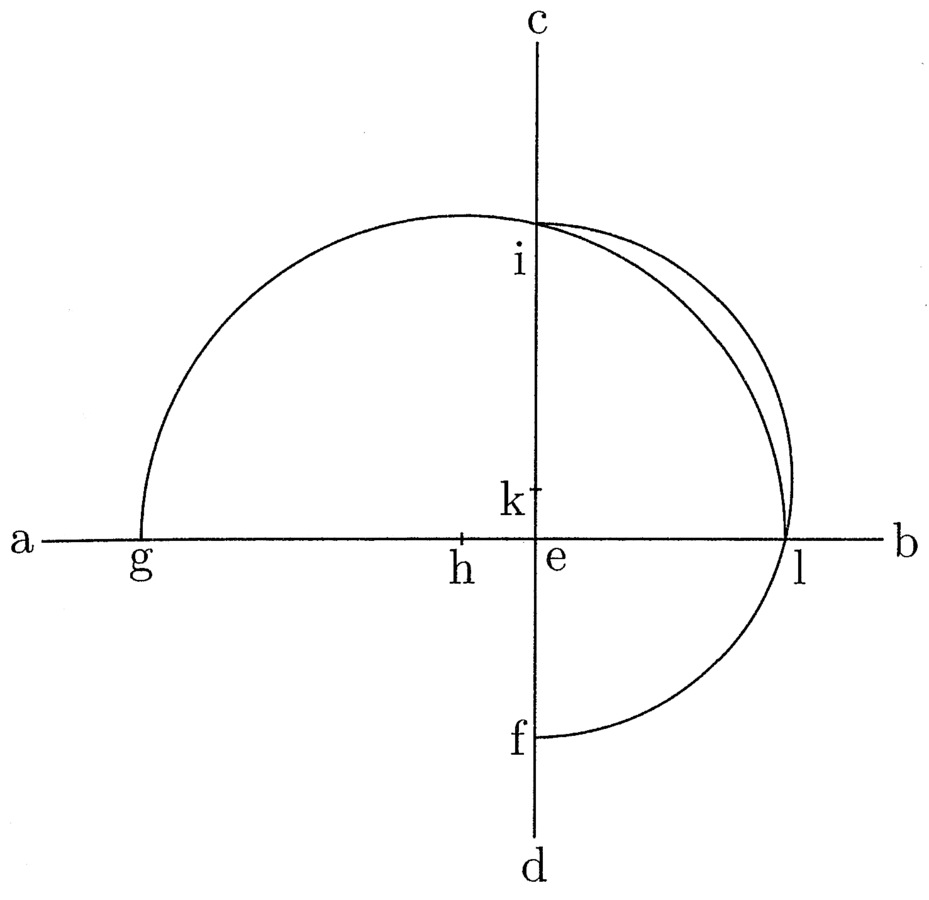
22. Tertium, quod antemittendum asserui, est quomodo inter datas lineas duae proportionales statuantur. Iamdudum notissimum fuit, si datae duae lineae simul iunctae diameter circuli fiant et eas chorda orthogonaliter separaverit, quod semichorda est medio loco inter ipsas proportionalis, quoniam semichordam inter sagittam et residuum diametri mediare necessarium est (cfr. figura 3). Si igitur duae lineae indefinitae longitudinis, ut ab et cd, se orthogonaliter secaverint in e puncto, et de e versus d minorem lineam signavero, quae sit ef, et de e versus a maiorem, quae sit eg, descripseroque duos semicirculos, unum super centro in linea ec, puta k, alium super centro in ea, puta h, existente hac quadam advertentia, quod arcus semicirculi, cuius centrum reperitur in ea linea, concurrat cum arcu alterius semicirculi in linea eb et linea ec, puta punctis i et l. Nemo haesitare potest ei et el mediare, ex praemissa notissima regula unici medii proportionalis, inter ef et eg.
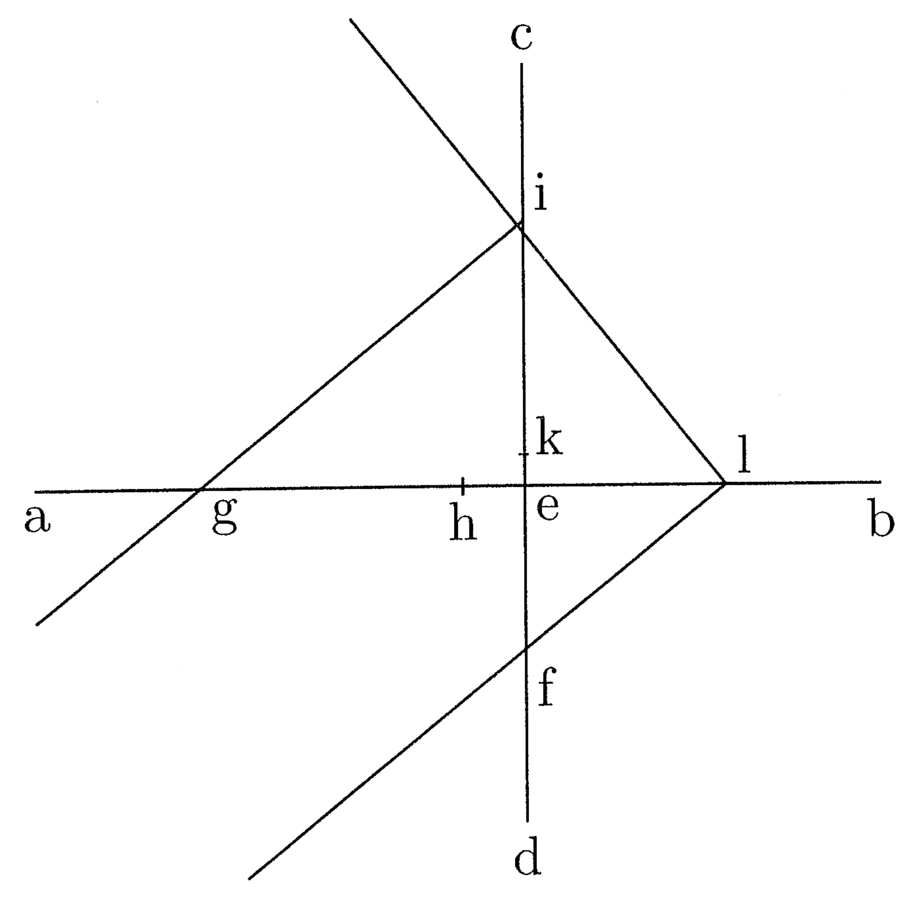
23. Unde, ut in praxi haec media facile attingas, habeto gnomonem atque lineam unam, quae ad latus gnomonis applicata rectangulum efficiat (cfr. figura 4). Et iuxta praemissa duas indefinitae quantitatis lineas sic fac orthogonaliter secare, ponas deinde rectum angulum gnomonis super lineam eb et latus unum super f, et nota, ubi reliquum latus ec secaverit, applica ibi regulam ad latus, de qua dixi, ut rectangulum efficiat. Si haec regula per g transiverit, habes quaesitum. Si non, gnomonem in eb attrahe vel elonga, quousque ita evenerit, et habes media illa duo, quae inquiris. Possunt quidem et alii plerique modi de facili inveniri per eum, qui studium adhibere voluerit. Sed hic modus cum clarus sit, ad praesens sufficit.
24. Quomodo autem ad tres datas proportionales lineas quarta continuae proportionis linea subiungi valeat, iam ante atque ex praemissis relinquo manifestum.
Quartum praemittendum
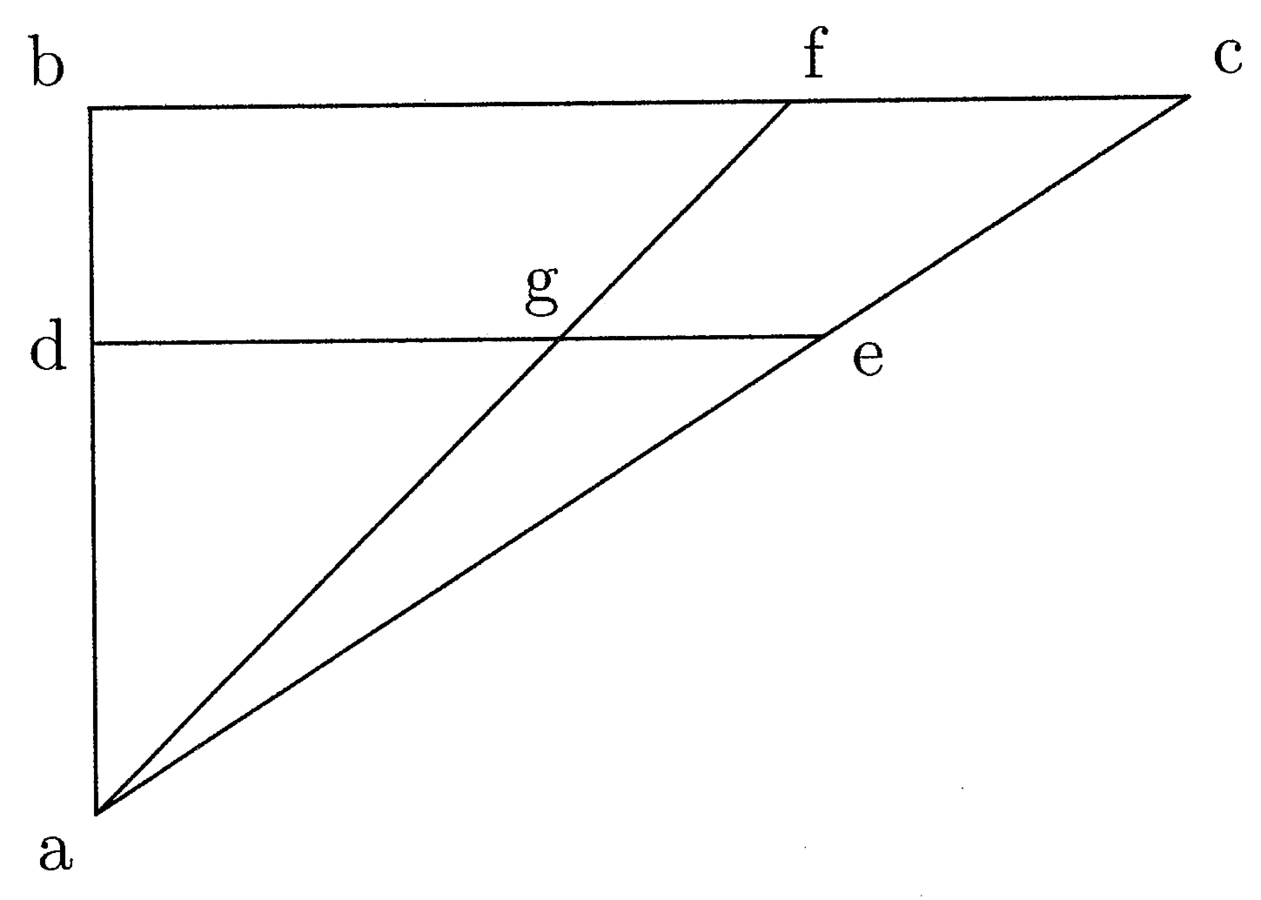
25. Quartum autem, quomodo in habitudine datarum ad tertiam datam detur quarta, omnibus paene manifestum in praxi, per duos triangulos unum angulum communem et ceteros aequales habentes inquiras (cfr. figura 5). Nam si ab est linea una, alla cd, tertia ef, iunge ad angulum quemvis ab et cd, qui sit ghi, et claude trigonum. Deinde continua gh latus aequale ab, quousque fuerit aequale ef, et sit gk. Trahe aequedistantem ad hi, quae sit kl, et continua gi usque in ipsam, et sit gm. Nulli nisi parum sciolo dubium est km lineam ad gk, quae aequatur ef, se habere ut hi, quae aequatur cd, ad gh, quae aequatur ab. Haec de praemittendis sic dicta sint.
De linearum in invicem transmutatione – capitulum primum
26. Omnis autem transmutatio in geometricis figuris est vel lineae in lineam, vel superficiei in superficiem, aut corporis in corpus. Tria igitur sunt capitula, quae seriatim per exemplari manuductione tangi convenit.
27. Si lineam rectam in circumferentialem curvam vertere cupis, ipsam rectam in triangulum aut polygoniam isopleuram resolvito et ex primo praemissorum circulum isoperimetrum elicito, cuius circumferentia datae rectae adaequabitur.
28. Si rectam in aliquotam circumferentiae portionem resolvere quaeris, ipsam in circularem integram resolvito, et ex proportione illius ad partem aliquotam pervenies ad quaesitum. Nam eadem est habitudo circumferentiarum quae semidiametrorum.
29. Si datam rectam in quadrantem resolvi optas, quarta circumferentiae circuli, cuius semidiameter est quadrupla, est quaesitum.
30. Si datam rectam in portionem circumferentiae dati circuli transferre quaeris, eam primo in circonferentiam circuli commuta, et ex nota habitudine semidiametrorum inventi et prius dati circulorum propositum notificabitur.
31. Si curvam lineam in rectam vertere studes, non alio umquam hoc facies ingenio quam ex ope quarti praemissi. In qua re paene omnes errasse comperio. Nam curva linea non potest inrectam mutari nisi ex proportione alicuius rectae in curvam versae. Dum igitur hoc agere proponis, primo rectam in circumferentialem vertito et huius circuli semidiametrum notato pro prima linea. Deinde tertiam rectae versae aut aliam portionem eius facito secundam lineam, et tertiam semidiametrum circuli, cuius circumferentiam rectilineare proponis, signato. Et triangulos claudito, quorum angulus unus communis et alii aequales, lateraque communi angulo opposita aequedistantia existant. Erit enim secundum latus portio lineae quaesitae, scilicet pars tertia, si latus aequedistans primum pars tertia circumferentiae fuerit; si alia, tunc alia. Per hoc scitur versio circumferentiae in rectam. Scitur etiam versio arcus, qui est pars aliquota et nota circumferentiae.
32. Quod si ignoraveris proportionem dati arcus ad circumferentiam, cuius rectilineationem perquiris, utere secundo praemisso et fac lineam de o puncto concursus per arcum quaesitum aut eius aliquotam usque ad arcum alium transire, et lineam inter arcus cadentem notato. Deinde fac semidiametrum esse lineam primam, et lineam aequalem quadranti aut eius aliquotam fac secundam, et lineam tertiam facito eam, quam inter arcus cadentem annotasti. Et iuxta quartum praemissum per triangulos quaesitam lineam reperies.
33. Neque alia via hoc quaesitum attingetur, qua etiam si advertis duci poteris, ut datam rectam in arcum vertas datae circumferentiae, etiam si eius arcus ad circumferentiam proportio ignota existat (cfr. figura 6). Hoc autem eo ingenio: Semidiametrum circuli fac latus primum trianguli, et lineam rectam quartae circumferentiae aliud claudendo trigonum, ut si semidiameter sit ut ab, et bc ut quarta circumferentiae, claudendo linea ca trigonum. Deinde fac lineam datam aut eius aliquotam cadere in eo trigono aequedistantem ad bc, et sit de. Post hoc de b versus c signa aequalem semidiametro ab lineam, quae sit bf, trahe af lineam et nota sectionem de, quam nota per g litteram. Deinde recurre ad secundum praemissum et lineam ducito de communi puncto concursus, quousque inter arcus cadat aequalis portio ad dg, et hic est arcus aequalis datae lineae aut portio aliquota arcus quaesiti, si cum portione lineae fueris operatus.
34. Poteris etiam ex his datam curvam et cuiuscumque circumferentiae arcum quemcumque in alium arcum alterius circuli vertere, transmutando primo ipsam datam curvam in lineam rectam et deinde illam rectam in arcum datae circumferentiae modis praetactis. Et in hoc capitulum transmutationis linearum sufficienter explicatum existit.
De superficierum in invicem transmutatione – capitulum secundum
35. Superficierum transmutati ut sufficienter explicetur et superflua resecentur, rectilinealium superficierum versionem uti notam praetergredior. Nam triangulum posse in plures scindi triangulos, et quemlibet in quadrangulum verti et illorum quemlibet in quadratum, et plura quadrata in unum, atque trigonum unum in plures aequiangulos trigonos, et triangulum similiter atque quadratum sic et omnia polygonia isopleura et non isopleura in alias figuras, haec omnia ex elementis geometricis et proportione circulorum et quadratorum tibi nota relinquo, cum intendam adicere scitis et non replicare trita. Per ea autem, quae iam ante tetigi, facilitas huius capituli aperitur.
36. Superficiem circularem si in rectilinearem transmutare proponis, primo eius peripheriam curvam in rectam resolvito, deinde semidiametrum peripheriae ad rectum angulum iungito trigonum claudendo, et versa est circularis superficies in trigonam. Si in tetragonam, quadrangulam et quadratam, hoc ex trigono facile est. Circulus enim quadratur, si inter semidiametrum et medium peripheriae lineam medio loco proportionalem costam feceris et quadraveris. Ostensum enim est a subtilioribus per multiplicationem semidiametri in medietatem peripheriae aream quadrangulam exsurgere, quae nec maior nec minor erit areae circuli. Multiplicatio enim semidiametri circuli inscripti polygoniae in medietatem peripheriae areae polygoniae inscriptae aequatur, et multiplicatio semidiametri circuli circumscripti in medietatem peripheriae polygoniae est maior area polygoniae et minor area circuli, et multipIicatio ipsius semidiametri circuli inscripti in medietatem peripheriae omnis polygoniae circumscriptae pariformiter areae eius similis est, hinc maior area circuli. Quare multiplicatio semidiametri in medietatem peripheriae circuli nec maior nec minor esse poterit.
37. Si vero quaeris aream superficiei rectilinealis in circularem transmutare, primo circularem resolvito per iam dicta in polygoniam, puta quadratam, et semidiametrum circuli facito lineam unam, costam quadrati aliam. Deinde superficiem rectangulam datam quadra, et costam eius facito lineam tertiam. Et secundum quartum praemissum quartam lineam reperies, quae erit semidiameter circuli quaesiti. Et attende, quomodo non devenitur ad versionem circumferentialis lineae in rectam nisi per versionem rectae alicuius in circumferentialem. Et e contrario non devenitur ad transmutationem superficiei rectilinealis in circularem nisi mediante versione alicuius circularis in rectilinealem. Quae hic lateant arcana, praesentis propositi non existunt.
38. Si vero quamcumque portionem superficiei circularis inter sectores cadentem, sive illa proportionalis sit ad superficiem totam sive non, vertere cupis, artem habes arcum inter sectores interceptum resolvendo in rectam et semidiametrum in medietatem eius multiplicando.
39. Sic si abscisionem ex chorda et arcu in rectam superficiem redigere conaris, primo a centro sectoribus tractis totam portionem per iam dicta resolvis in circulum, deinde triangulum ex sectoribus et chorda similiter in circulum, et subtracto illo a priori portio remanet resoluta in superficiem cadentem inter circumferentias amborum, quae resolvi potest in rectangulam superficiem per resolutionem utriusque circuli in quadratam et per subtractionem unius quadratae ab alia, quoniam differentia est uti portio illa. Poterit igitur illa in quadratam superficiem et per quadratam in circularem resolvi modis sufficienter praeexpressis. Et in hoc satis exemplificatum est ad artis sufficientiam de superficierum in invicem transmutatione.
40. Possent adiungi praeter necessitatem transmutatoriae artis alia plura occulta hactenus, quomodo scilicet angulus describi posset circa centrum circuli se habens inter duos duplos angulos secundum proportionem medietatis duplae, et hoc ex secundo praemisso. Potest enim dari linea recta ad datam se habentem ut costa ad diametrum. Possunt et ambae in arcus eiusdem circumferentiae resolvi. Unde sectores ad terminos arcuum tracti angulos circa centrum causare secundum habitudinem arcuum necesse erit.
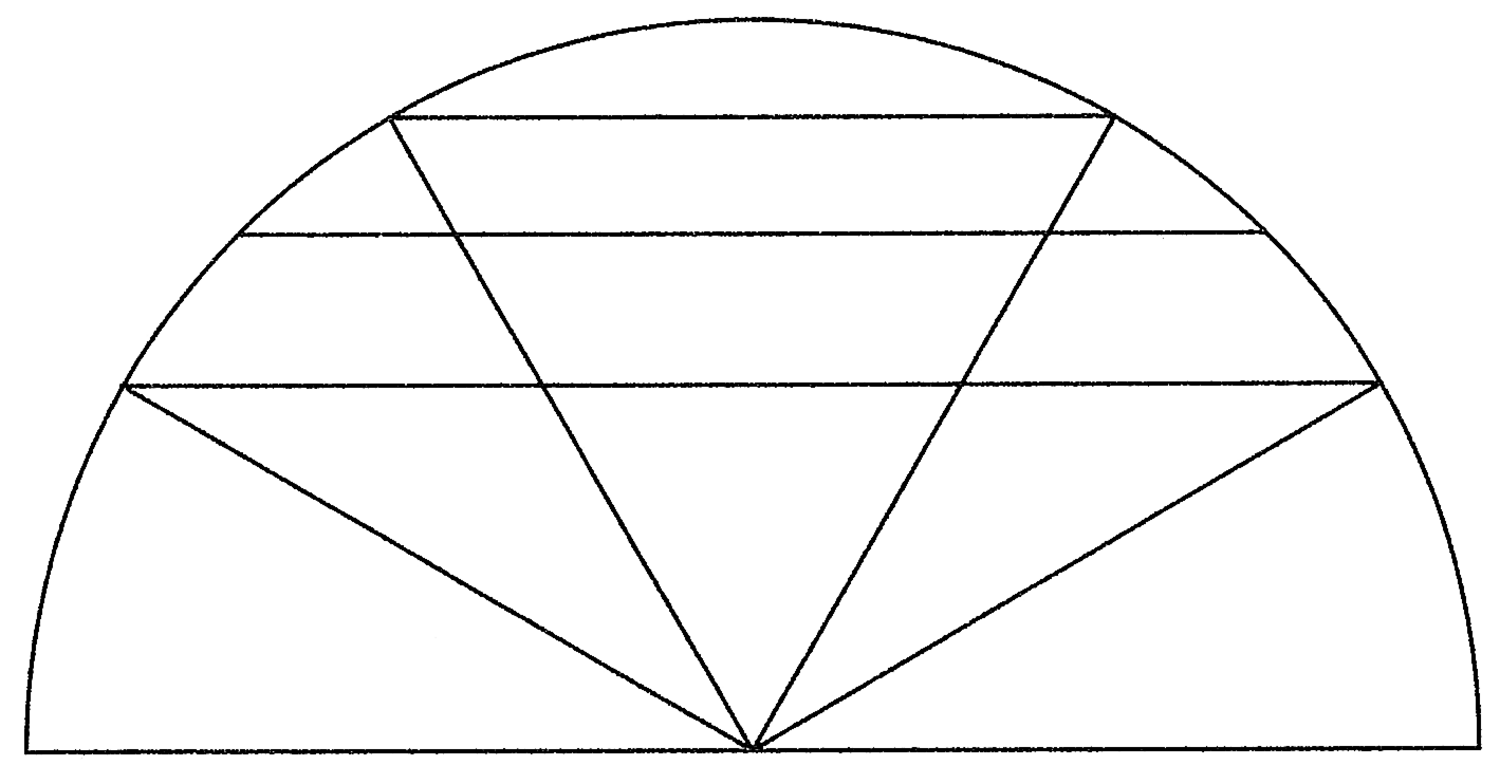
41. Si etiam superficiem unam resolvere quaeris in plures, quot volueris, quae sunt ad se et totam superficiem improportionales, ita tamen quod si addideris unam ad aliam, composita totius aliquota sit, superficiem illam, si semicircularis non fuerit, in talem resolvito trahendo chordam aequedistantem diametro arcus quadrantis, quae medium divisionis vocetur (cfr. figura 7). Ab ea ex utraque parte per aequales arcus maiores et minores chordas ducito, quot volueris. Erunt omnes portiones improportionales ad se et ad totam. Sed si duas aequedistantes a medio divisionis iunxeris, erunt talis pars superficiei, qualis circumferentiae fuerit arcus. Qua via de media superficie semicirculari abscindere poteris partem aliquotam eius, quam volueris. Huius ostensio est, cum trianguli ex sectoribus et chordis a medio divisionis hinc inde per aequales arcus distantibus sint necessario aequales et maximus sit ille triangulus, qui ex sectoribus et chorda, quae divisionis medium vocatur, constituitur. Poteris etiam superficiem dividere in partes, quarum una, si cuicumque alteri iuncta fuerit, [quod] adhuc composita ex ipsis superficies improportionalis remaneat, quando scilicet a medio divisionis per improportionales arcus ad circumferentiam chordas duxeris. Ex his alia ut libet elicias.
De corporalium figurarum in invicem transmutatione – capitulum tertium
42. Ultimo loco restat corporum transmutationem exemplari manuductione aperire. Transmutantur autem corporales figurae in corporales ex apertis fundamentis.
43. Nam columna quadrangula in cubum sic reducitur. Basis eius si quadrata non fuerit, quadretur per medium proportionale inter duo dissimilia eius latera. Inter hoc latus et longitudinem corporis constituantur duae continue proportionales lineae secundum tertium praemissum, et si longitudo 'H~'maior fuerit latere quadrati, minus medium est latus cubi quaesiti. Sed si latus quadrati fuerit maius longitudine, maius medium est quaesitum. Si aequale, iam cubus habetur. Si columna fuerit rotunda, quadretur basis et procedatur, ut iam dictum est.
44. Sed si cubum in sphaeram transmutare velis, reduc superficiem quadratam cubi in circulum et illum facito maiorem circulum sphaerae.
45. Cubos plures si in unum colligere optas, hoc efficias, si aequales fuerint, lineam unam signando pro minori, quae aequetur uni lateri unius, et aliam pro maiori, quae omnibus lateribus, duplex medium inter illos capiendo secundum tertium praemissum, quoniam minus inter illa duo latus est quadrati, uti de columna praemisimus.
46. Sed si duos inaequales ad unum conducere proponis, reduc primo minorem cubum ad corpus altera parte longius, cuius longitudo sit aequalis lateri maioris cubi, hoc modo: Accipe latus maioris, cui adiunge directe latus minoris, unum proportionale medium quaerendo inter illa, et linea alia reperiatur continue proportionalis post latus minoris, ut sint quattuor lineae continue proportionales. Et illa ultimo inventa est latus quadrati basis huius corporis altera parte longioris, et latus maioris quadrati est eius longitudo, ut ex opposito conversionis columnae patere potest. Quo reducto quaere quadratum aequale duobus, maioris cubi et basis iam dicti altera parte longioris, reducendo cubum maiorem et iam dictum corpus ad unum corpus, cuius latus basis quadratae est maius longitudine eius. Et hoc corpus ultimo ad cubum reducito per datam doctrinam. Ita patet via, quot volueris sive aequales sive inaequales cubos ad unum cubum sive denique ad sphaeram transmutandi. Ita quidem et sphaerae plures in unam et in cubum aut corpus altera parte longius reduci poterunt.
47. Sed si columnam longam in brevem vel brevem in longam reducere proponis, primo ipsam in cubum verte, deinde longitudinem signa, in quam eam transmutare proponis. Cui adiunge latus cubi quaerendo medium unum proportionale et quartam quantitatem continue proportionalem ad istas tres. Et erit datae longitudinis columnae basis quadrata linea quarta.
48. Sic si plurium columnarum aequalium vel inaequalium unam datae quaeris longitudinis, si aequales fuerint, basim unam omnibus aequalem recipito, quam in cubum reducito et cubum in columnam datae longitudinis per vias praeapertas. Si inaequales, reducito ingenio tuo omnes in columnam et columnam in cubum et illum in columnam longam vel brevem, prout placuerit. Sed in hoc opus est, ut caveas, quoniam quando cubus in corpus reduci debet, cuius latus basis quadratae est maius longitudine, tunc basis latus iungas cum longitudine dati minori quaerendo medium unum proportionale. Quo habito lineam quartam invenies se ad illam habentem sicut latus basis cubi ‹ad longitudinem›, et illa erit latus basis quadratae talis corporis, in quod alia reducere proponebas. Sed si optas, quod longitudo illius quaerendi corporis sit maior latere basis quadratae eius, iunge illam longitudinem cum latere cubi directe medium proportionale quaerendo, post latus cubi quarta linea continue proportionalis est latus quaesitum.
49. Si autem sphaeram in pyramidem transmutare quaeris, fac quod basis pyramidis aequetur curvae superficiei sphaerae et altitudo eius ‹semi›diametro sphaerae.
50. Si quis dixerit: sunt sphaerae duae, quarum maior est dupla ad minorem, transfer illas in rotundam columnam, fac quod columnae altitudo sit ut diameter sphaerae ‹maioris› et basis ut maior circulus eiusdem. Illa etenim columna ambabus aequatur sphaeris. Nam columna, cuius altitudo diametro et basis maximo circulo sphaerae aequantur, sesquialtera est ad sphaeram.
51. Talia quidem et quae in regularibus corporibus via transmutationis figurarum geometrice fieri possunt, ex his elicito doctrinis.
‹Additamentum›
In editionibus σ hic textus capitulorum 20 et 21 traditus est
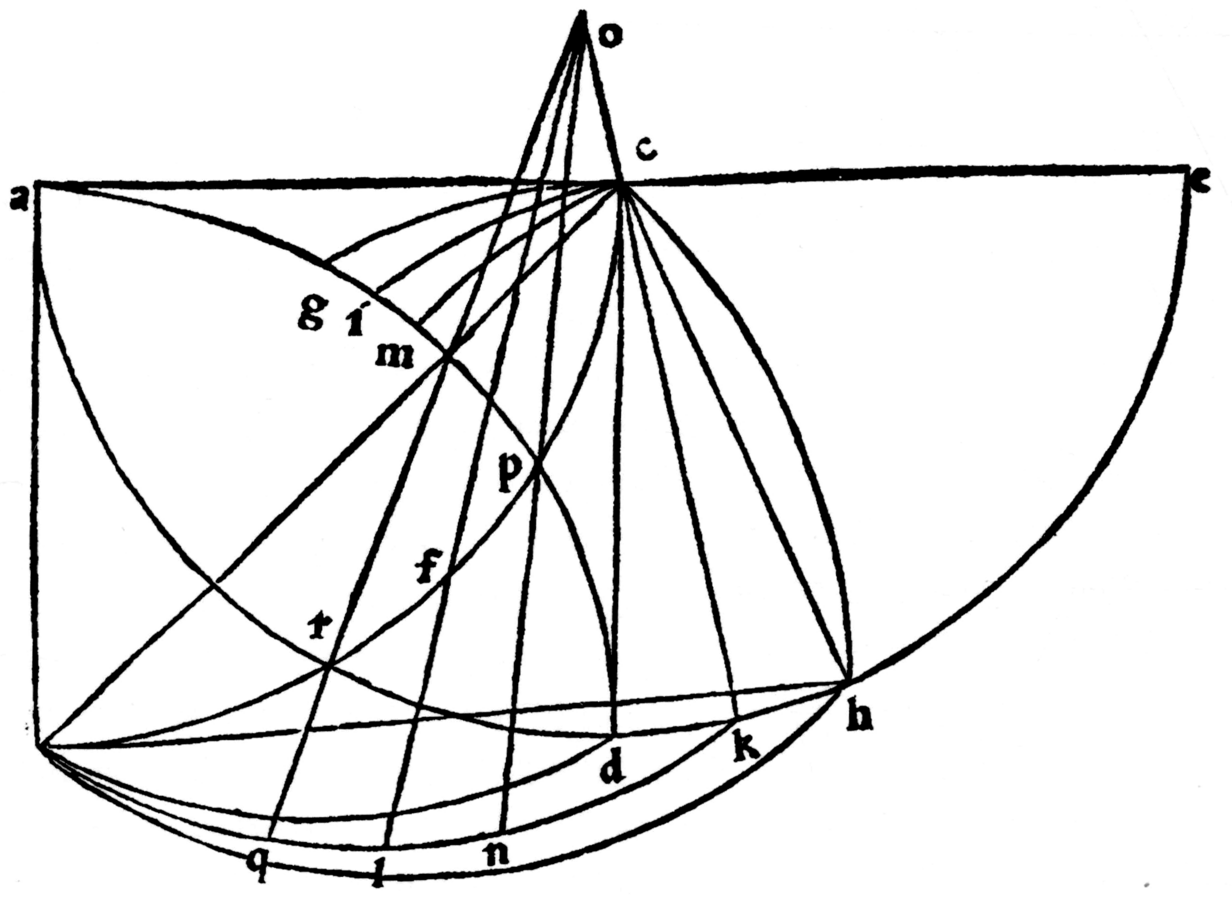
α. Descripsi igitur quadrantem bc super a centro, et posito pede circini in c descripsi semicirculum ade (cfr. figura 8). Quaesivi in dicto genere triangulorum minimum et vidi, si recta ducatur a puncto c ad punctum d, describet angulum contingentiae cum quadrante, quare tertium latus claudens istum triangulum erit minimum, cum angulus, cui subtenditur, scilicet contingentiae, minimus dicatur. Facto igitur b centro circumduco ab et quadrantem occultum describo ad aequalem quadranti bc. Rursus facto d centrum circumduco cd, et ubi secat quadrantem occultum ad, pono g. Et posito pede circini in g et alio in b moveo b usque ad punctum d; eritque arcus descriptus, scilicet bd, eiusdem circularis cum arcu quadrantis bc. Omnes quippe rectas ductas a quadrante occulto ad punctum b ‹cum sint aequales› arcus eiusdem circularis sive aequalium circulorum describere est necesse.
β. Erit bd latus arcuale minimum et convexum; quare triangulus bcd erit minimus in dicto genere triangulorum, cum contineat minimum angulum, scilicet contingentiae, ratione cuius bd arcuale latus ei subtensum minimum est. Et quia minimum, erit bc latus arcuale maximum. Non enim potest dari latus minus bd; si enim minus esset, tunc dc latus rectilineum quadrantem bc secaret, et sic triangulus iste non esset in genere quaesitorum. Est igitur bcd triangulus, cuius duo latera arcualia sunt bc et bd, et maius concavum est et quadrans, alterum convexum et minus; quae latera arcualia sunt eiusdem circularis, cuius semidiameter est tertium latus rectilineum, scilicet dc. Et quia in isto genere non potest dari triangulus, cuius latus convexum minus sit bd, erit igitur in isto genere triangulorum bcd triangulus minimus. Rursus cum in isto genere triangulorum dabiles sint maiores, quorum scilicet arcuale latus convexum maius sit arcu bd, recte maximus dabitur, ubi arcuale latus et convexum aequale erit concavo, quod est maximum. Ad quod describendum traho bc rectam, et facto b centro circumduco bc, et ubi secat semicirculum, pono h. Traho hc et facto h centro circumduco hc, et ubi secat quadrantem occultum, pono m. Rursus posito pede circini in m puncto et alio in b moveo b usque h; erit arcus descriptus, scilicet bh, aequalis quadranti bc. Nam aequali semidiametro descripti sunt, et chordae arcuum sunt aequales; quare eiusdem circularis erunt. Quo fit, ut triangulus bhc, cuius duo latera arcualia eiusdem circularis aequalia sunt, scilicet arcus bc et arcus bh, tertium vero rectilineum, scilicet hc, aequale semidiametro circulorum arcuum, sit maximus in dicto genere triangulorum; nam minimum latus cum maximo coincidit. Rursus cum in triangulo minimo, scilicet bcd, recta a medietate lateris arcualis ducta ad medietatem alterius lateris arcualis minor sit medietate lateris rectilinei, erit maxime minor, quia minimus triangulus. Et cum recta ducta a medietate lateris arcualis ad medietatem alterius arcualis lateris in maximo triangulo, scilicet cbh, sit maior medietate lateris rectilinei (eo quod latera arcualia aequalia sint), erit ipsa recta ducta maxime maior, quia in maximo triangulo. Quo fit, ut in mediali triangulo et aequidistanti a maximo et minimo, in quo scilicet maximus et minimus coincidunt, recta a medietate lateris arcualis ad medietatem alterius lateris arcualis non sit nec maior nec minor medietate lateris rectilinei; quare talis medialis triangulus erit quaesitus.
γ. Ad quem habendum divido arcum dh in duo aequa per punctum k et traho kc, factoque k centro circumduco kc, et ubi secat quadrantem occultum, pono i. Et posito uno pede circini in i puncto et alio in b moveo b usque k, et descriptus erit arcus bk, qui cum arcu quadrantis bc et recta kc describet triangulum quaesitum. Nam latus maius et arcuale est quadrans et concavum, quod cum alio arcuali et convexo, scilicet bk, eiusdem est circularis; latus vero tertium rectilineum est et aequale semidiametro circuli arcuum.
δ. Cum enim cbh maximus triangulus movetur ad medium continue decrescendo, et bdc minimus ad medium continue crescendo movetur, ipsi in aliquo coincident triangulo, et non nisi in triangulo bkc, qui est quaesitus. Rursus dividatur cb latus arcuale in duo aequa in puncto f, similiter et bk aliud arcuale in puncto l, et fiat kc indefinitae quantitatis, et ducatur alia recta a puncto l per punctum f. Quia kc et fl non sunt aequidistantes, necessario in aliquo concurrent puncto, qui sit o; erit o punctus concursus linearum kc et fl. Unde erit lf ad kc sicut bl ad bk vel bf ad bc.
ε. Et quotquot rectae a puncto concursus ductae dividentes duo latera arcualia, rectae cadentes inter ipsa ullam proportionem ad rectilineum latus servabunt, quam portiones laterum arcualium versus angulum b ad latera arcualia. Ut on, quae per p transit, et bp duae sunt tertiae de bc, erit pariter et nb ut duae tertiae de bk, et np ut duae tertiae de kc. Rursus oq, quae transit per r; et rb est ut una tertia de bc, erit pariter bq ut una tertia de bk, similiter qr ut una tertia de kc. Et hoc ideo, quia bkc triangulus aequidistans est a maximo, scilicet bhc, et minimo, scilicet bdc, in quibus est maxime plus et minus (ut dictum est); quare in isto mediali nec plus nec minus erit, cum in ipso maximus et minimus triangulus coincidant.