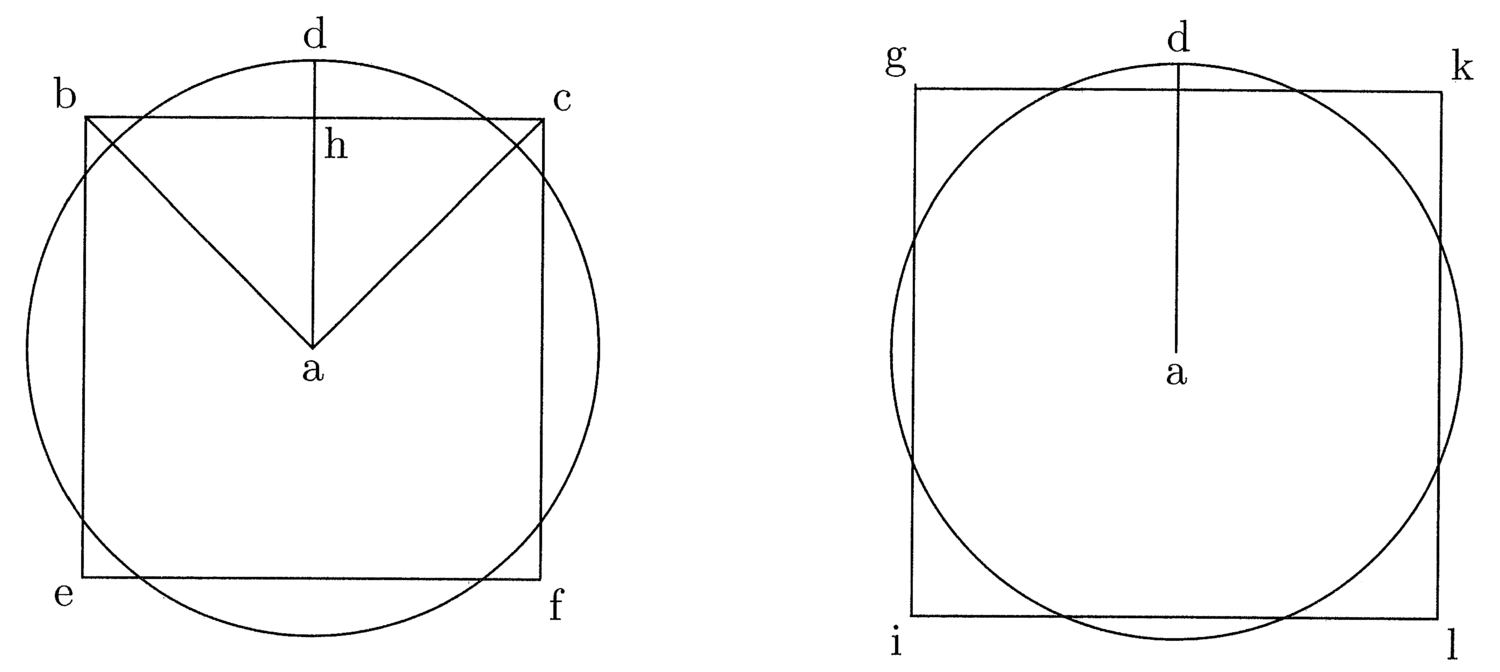
1. Tre linee tracciate da un centro che formano angoli uguali, semirette o minori, hanno lo stesso rapporto con la linea che le delimita, sia essa un arco o una corda1 (cfr. figura 1).
Se da a, centro di bdc, sono tracciate linee di lunghezza indefinita, che formano intorno ad a due angoli uguali, semirette o minori, questi angoli sono delimitati o da un arco di un qualsiasi cerchio, per esempio bdc, o dalla sua corda bhc, o dalla tangente edg: le tre linee ab, ad e ac hanno con l’arco che le delimita lo stesso rapporto che le linee ab, ah e ac hanno con la corda bhc che le delimita o che le linee ae, ad e ag hanno con la tangente edg. E’ la stessa cosa se si dicesse: se l’arco bdc è un quadrante e le tre linee ab, ad e ac i suoi semidiametri, allora edg è uguale al quadrante e ae, ad e ag sono uguali ai tre semidiametri del suo cerchio2.
2. Questo perchè se l’arco bdc dovesse essere esteso in una retta compresa tra le due linee che passano da a per b e da a per c, e le cui estremità sono equidistanti dal centro a, allora le estremità e il punto medio avrebbero necessariamente la stessa distanza dal centro a sia sulla retta sia sull’arco3. Se infatti le estremità avessero la stessa distanza [sulla retta e sull’arco], allora la distanza tra il punto medio e la retta dal centro a sarebbe minore della distanza tra il punto medio e l’arco e la retta sarebbe minore dell’arco come sulla corda bhc4. E se i punti medi avessero la stessa distanza [sulla retta e sull’arco], allora la distanza tra le estremità e le rette sarebbe maggiore [di quella tra le estremità e l’arco] come, per esempio, sulla tangente edg5, e allora questa sarebbe maggiore dell’arco bdc. Bisogna quindi che il punto medio dell’arco, mentre questo si estende, si abbassi verso il centro e, allo stesso tempo, le estremità si alzino verso il centro come su ikl, dove il punto medio dell’arco in estensione si abbassa da d verso k e le estremità b e c si alzano verso i e l; l’innalzamento delle estremità è uguale all’abbassamento dei punti medi in modo che le estremità e il punto medio della retta abbiano la stessa distanza dal centro a di quella delle estremità e il punto medio dell’arco bdc6. Se non vi fosse questa equidistanza, allora la retta non sarebbe uguale a questo arco, ma all’arco corrispondente di un cerchio maggiore se la distanza dal centro fosse maggiore, o a uno minore se essa fosse minore7.
3. E poiché più grande è il cerchio, più l’arco si avvicina alla retta, allora la mente vede che se si potesse tracciare un cerchio di grandezza infinita, allora sarebbe contemporaneamente arco e retta e la proposizione sarebbe vera8. E ancora, poiché l’angolo attorno al centro resta lo stesso, il rapporto tra ciò che delimita e ciò che è delimitato è lo stesso; ecco perché ciò che la mente vede come vero per il massimo, lo coglie anche in tutti gli altri casi9. La proposizione è, quindi, considerata la più vera in questi e altri innumerevoli casi.
4. La ragione per la quale la proposizione parla di due angoli semiretti che sommati formano un angolo retto o di due minori, e non di tutti gli angoli, è che, poiché dall’arco minimo e dalla minima porzione di cerchio fino al quadrante, il triangolo composto dai triangoli rettangoli e inscritto nella porzione di cerchio aumenta continuamente, esso [triangolo] diventa massimo nel quadrante e poi diminuisce10. Ecco perché la proposizione non può essere [parimenti] vera nel caso in cui l’arco, la porzione [di cerchio] e il triangolo aumentano [contemporaneamente] e nel caso in cui l’arco e la porzione [di cerchio] aumentano mentre il triangolo diminuisce.
5. È evidente che qualsiasi arco può essere facilmente rettificato (cfr. figura 2). Infatti se tre segmenti di una retta sono una parte aliquota di tre semidiametri, allora questa retta sarà una parte aliquota dell’arco11; la superficie delimitata dalla linea curva è pertanto maggiore della superficie delimitata dalla retta. Se togli, quindi, un terzo dei tre segmenti della retta e tracci il semidiametro descrivendo un arco, questo sarà uguale alla retta e in generale puoi trasformare un arco in una retta e una retta in un arco e l’arco di un cerchio in arco di un altro cerchio12.
6. È chiaro anche che si possono dare angoli che si rapportano tra loro come il lato e la diagonale di un quadrato e, in generale, si possono dare allo stesso modo linee, superfici e solidi. Hai anche moltissimi modi per rettificare il cerchio e trasformarlo in rettangolo e in quadrato. Questo vale per qualsiasi porzione di cerchio, che sia commensurabile o meno al cerchio13. Si scopre anche ciò che era sconosciuto sui seni e sulle corde. Tutto questo era finora sconosciuto nelle matematiche e tutto ciò che si saprà in questo campo, lo sarà grazie agli infiniti corollari non ancora trovati che derivano da questo.
7. Coloro che guardano più lontano vedono che l’uguaglianza del rapporto è il mezzo della trasformazione e del passaggio da contrario a contrario e che c’è qualcosa di divino nel fatto che tre linee tracciate da un punto siano delimitate o da un solo arco – e sono tutte uguali – o da una retta – e le estremità sono uguali e i punti medi variano fino all’incommensurabilità, come sono il lato e la diagonale di un quadrato. Il diverso modo in cui [le linee] sono delimitate rende diverse le superfici, così che una è delimitata da una curva, l’altra da una retta, mantenendo il rapporto delle linee di delimitazione uguale a quello delle linee che provengono da uno stesso punto in modo uguale. Questo non può essere vero né al di qua né al di là delle tre linee, considerate non come separate, ma come un’unica, semplice lunghezza14. Sarà compito della più alta speculazione occuparsi di questo principio unitrino e la derivazione delle cose da esso15.
Finito a Roma l’8 Agosto 1459 al tempo della legazione nella città ecc.
Note a piè pagina
Si tratta dell’ultimo trattato matematico conosciuto di Cusano, concluso a Roma l’8.8.1459, nel periodo in cui Cusano era incaricato dalla legazione romana. Esso contiene le stesse idee del De mathematica perfectione, ma introduce una formula matematica fondamentale. La denominazione “proposizione aurea” non rimanda in nessun modo al concetto di oro, ma a una proprietà preziosa e misteriosa della matematica, nella quale Cusano vede il simbolo della Trinità divina.
L’ipotesi è dunque che 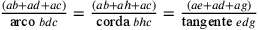 . Sulla
figura, ad è il raggio del cerchio, dm è la semicirconferenza, cioè 2 archi bc e admo è il
rettangolo avente la stessa area del cerchio.
. Sulla
figura, ad è il raggio del cerchio, dm è la semicirconferenza, cioè 2 archi bc e admo è il
rettangolo avente la stessa area del cerchio.
Questo vuol dire che, nel corso della rettificazione di un arco, le estremità si allontanano dal centro mentre il suo centro vi si avvicina. La somma delle tre distanze resta, quindi, costante.
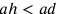 il
segmento
il
segmento 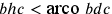 .
.
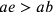 ,
, 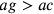 e il segmento
e il segmento 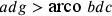 .
.
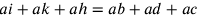 .
.
Per estendere l’arco bdc,
l’innalzamento delle estremità 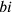 e
e 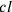 deve essere compensato con
l’abbassamento del centro dell’arco dk.
deve essere compensato con
l’abbassamento del centro dell’arco dk.
Allusione alla visio intellectualis.
Questa giustificazione del teorema con l’esempio del massimo non può essere ammesso in matematica, come anche l’esempio del minimo utilizzato nel De mathematica perfectione.
Questo vuol dire che il triangolo rettangolo (per esempio ACH) di cui l’angolo al centro del cerchio
comincia a sorpassare i 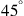 , diminuisce in superficie.
, diminuisce in superficie.
Per esempio, se 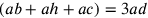 , allora
, allora 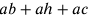 è una parte
aliquota del cerchio.
è una parte
aliquota del cerchio.
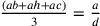 e
l’
e
l’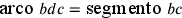 .
.
bac è un angolo retto, ad è un terzo della somma di ab, ah e ac ed è il
raggio del cerchio di cui un quarto della circonferenza è uguale
al segmento bhc. La somma dei quattro
segmenti bc, cf, be e ef forma il perimetro del quadrato
isoperimetrico al cerchio, cioè 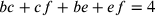 archi bdc; da ciò, tuttavia, non deriva che le
superfici sono uguali, poiché la superficie del cerchio è
maggiore di quella del quadrato. gk è e
la media geometrica tra ad ed il doppio
dell’arco dato bc, e anche il lato del
quadrato la cui superficie è uguale a quella del cerchio, per
cui il quadrato GIKL risulta uguale al cerchio, avente come
raggio ad.
archi bdc; da ciò, tuttavia, non deriva che le
superfici sono uguali, poiché la superficie del cerchio è
maggiore di quella del quadrato. gk è e
la media geometrica tra ad ed il doppio
dell’arco dato bc, e anche il lato del
quadrato la cui superficie è uguale a quella del cerchio, per
cui il quadrato GIKL risulta uguale al cerchio, avente come
raggio ad.
Nel rapporto delle tre linee in questione Cusano vede l’espressione del mistero della Trinità. Cfr. Cusanus 1972a, I, 19, 55, 37ss.; Cusanus 1972b, I, 35ss..