Capitulum primum, in quo ponuntur aliqua communia elementa in hac materia, definitiones videlicet divisionibus adiunctis
Philosophorum principis Aristotelis
Motus localis uniformis est, quo in aequalibus temporis aequalia spatia pertranseuntur rarefactione et condensatione deductis, deductis etiam aliis parvis quisquiliis, cuiusmodi est contra, mutatio spatii vel [id], quod non sit aliquod spatium, sufficit enim verum vel imagina[t]um spatium. Exemplum, ut si mobile in hora adaequate pertranseat leucam. Et in prima parte proportionali horae primam partem proportionalem leucae, in secunda secundam et sic consequenter. ¶ Motus vero difformis est, quando in aequalibus partibus temporis non aequalia spatia pertranseuntur ceteris paribus deductis deducendis, ut si mobile pertranseat in hora adaequate leucam, in prima medietate unam quartam et in secunda tres quartas, talis motus est difformis. ¶ Motus difformis dividitur, quia quidam est uniformiter difformis, quidam vero difformiter difformis. Motus uniformiter difformis – ut communiter definitur – est triplex, quidam est uniformiter difformis quoad subiectum tantum, quidam quoad tempus tantum, quidam vero quoad subiectum et tempus similiter. ¶ Motus uniformiter difformis quoad subiectum – ut communiter definitur – est, quando cuiuscumque partis subiecti dimidium tantum exceditur in velocitate ab extremo velociori illius, quantum excedit extremum tardius motum in velocitate. Exemplum ut motus rotae figuli, et per dimidium intelligas punctum in medio vel [eum], qui imaginarie est, ibi termin[]ando. ¶ Motus vero uniformiter difformis quoad tempus est, quando cuiuscumque partis acceptae secundum tempus, in qua adaequate est in aliqua parte temporis gradus medius, qui est in medio talis partis, tanto excedit extremum remissius, quanto exceditur ab intensiori. Exemplum, ut si aliquod mobile incipiat moveri a non gradu continuo intendendo uniformiter motum suum per aliquod tempus, tunc talis motus est uniformiter difformis quoad tempus. ¶ Motus autem uniformiter difformis quoad tempus et quoad subiectum definitur coniungendo definitiones motus uniformiter difformis quoad tempus et quoad subiectum. ¶ Motus autem difformiter difformis consimiliter dividi potest, videlicet motuum difformiter difformium, alius est difformiter difformis quoad tempus, alius quoad subiectum, alius quoad tempus et subiectum simul. Et similiter potest dividi motus uniformis, quamvis proprie secundum definitionem datam ille motus sit uniformis, quo in aequalibus partibus temporis aequalia spatia pertranseuntur, et in nullis aequalibus inaequalia, sive talis
motus sit uniformis quoad subiectum, sive difformis. ¶ Sed quam definitio motus uniformiter difformis quoad subiectum, quae communiter datur, mihi sufficiens non videtur. Ideo ut definitio motus uniformiter difformis adinveniatur, ut possibile erit. Quaeritur, an definitio illa motus uniformiter difformis quoad subiectum sit bene assignata.
Et arguitur primo quod non, quia secundum illam nullus est motus uniformiter difformis quoad subiectum, igitur. Arguitur antecedens, quia si esset aliquis motus uniformiter difformis quoad subiectum, maxime esset motus rotae, quo movetur circulariter, sed talis motus non est uniformiter difformis quoad subiectum, igitur consequentia patet cum maiore, et arguitur minor, quia si talis motus est uniformiter difformis, capio unam rotam, quae moveatur uniformiter difformiter a non gradu in centro usque ad octavum in circumferentia, et arguo sic: talis motus per te est uniformiter difformis a non gradu usque ad octavum, ergo velocitas eius correspondet gradui medio, puta ut 4, qui medius gradus ut 4 est in puncto medio talis rotae, sed consequens est falsum, igitur illud, ex quo sequitur, consequentia patet supposita opinione tenente motum uniformiter difformem correspondere motui existenti in medio corporis mobilis. Falsitas consequentis probatur, quia aliquis punctus, qui tardius movetur quam punctus existens in medio illius rotae, movetur velocitate ut 4, ergo sequitur, quod alter punctus, puta medius talis rotae, velocius movetur quam ut 4. Consequentia patet, et arguitur antecedens, quia punctus existens in medio semidiametri inter centrum et circumferentiam movetur velocitate ut 4, et talis punctus tardius movetur quam punctus existens in medio rotae, igitur propositum. Arguitur maior, capio unam rotam ABC, et volo, quod intra illam describatur unus circulus ei concentricus, cuius diameter sit subdupla ad diametrum totius rotae, et transeat talis circulus per medium puncti semidiametri, qui circulus sit FGH, ut scribitur in figura.
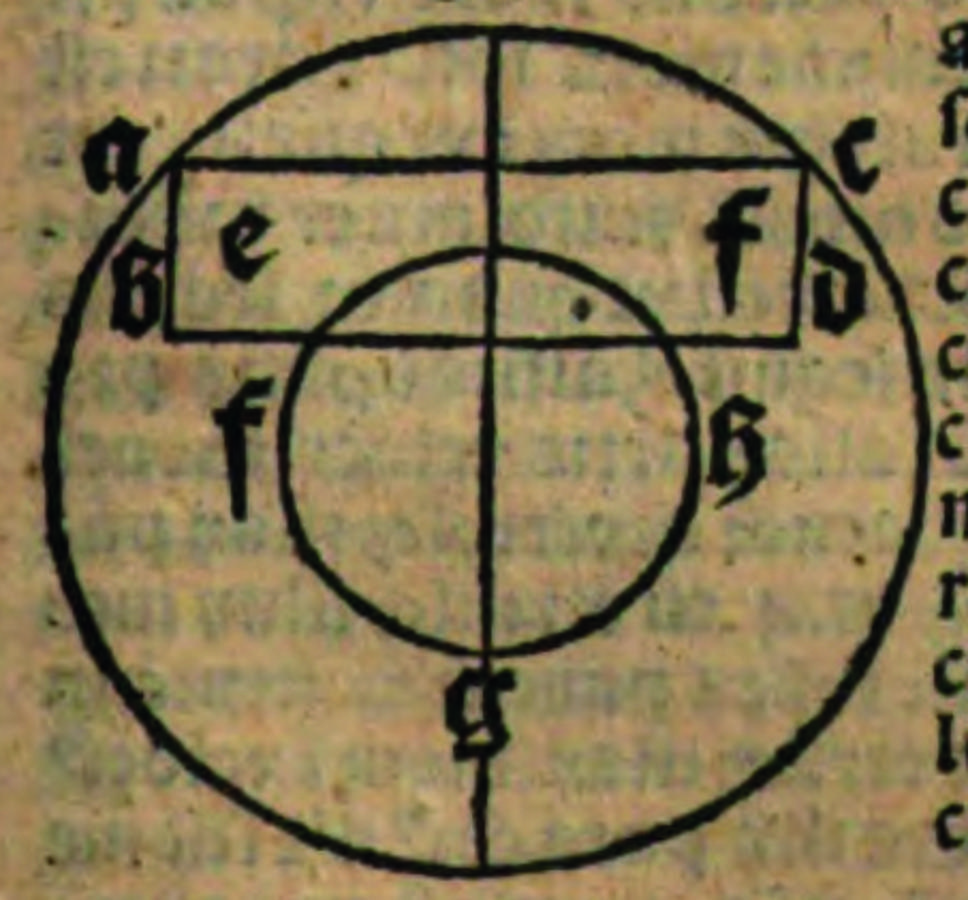
Abb. 2: Alvarus Thomas, Liber de triplici motu, S. 127.
Quo posito sic argumentor: punctus medius semidiametri describit circulum FGH, et talis circulus sive talis linea circularis est subdupla ad circulum ABC sive ad lineam circumferentialem talis rotae, quae describitur a puncto velocissime moto talis rotae, quia circumferentia circuli, cuius diameter est dupla ad diametrum alterius circuli minoris, est dupla ad circumferentiam minoris circuli. Modo sic est in proposito de diametris, et per consequens de circumferentiis illorum duorum circulorum, igitur ille punctus semidiametri movetur velocitate ut 4. Probatur haec consequentia, quia subduplam lineam describit ad lineam descriptam a puncto velocissime moto, et talis punctus movetur velocitate ut 8, ut positum est, igitur ille punctus medius semidiametri, (quam movetur subdupla velocitate), movetur ut 4. Quod fuit probandum. Sed iam probatur minor videlicet, quod talis punctus tardius movetur quam punctus existens in medio rotae, (et non loquor hic de medio centrali, quia tale medium non movetur, sed de medio, quod est inter centrum et circumferentiam), et arguo sic: talis punctus medius semidiametri est in fine tertiae quartae totius corporis illius rotae et in principio ultimae quartae procedendo versus centrum, igitur punctus existens in medio totius magnitudinis ipsius rotae est proximior circumferentiae, quam ille punctus medius semidiametri, et per consequens movetur velocius quam ille punctus medius semidiametri, quod fuit probandu[m]. Patet consequentia intelligenti naturam motus uniformiter difformis. ¶ Dices forte et bene negando antecedens et ad probationem concedendo maiorem et negando minorem, et cum probatur, admitto casum cum his, quae ibi supponuntur, et concedo antecedens et consequentiam et distinguo consequens quantum ad illam particulam, in qua dicitur, quod talis gradus medius est in | puncto existenti in medio talis rotae, quia aut tu intelligis de medio magnitudinis illius rotae, quod quidem medium est in medio inter centrum et circumferentiam talis rotae dividendo illam rotam in duas rotas concentricas aequalis magnitudinis, quamvis sint inaequal[e]s ambitus et circumferentiae, ut patet in figura, et sic nego, aut loqueris de puncto existente in medio longitudinis inter centrum et circumferetiam, et sic bene concedo, quod ibi est gradus medius, ut bene probat argumentum. Unde dico, quod quamvis in qualitate uniformiter difformi medius gradus debeat esse in medio corporis quantum ad magnitudinem, in motu tamen uniformiter difformi non oportet, quod gradus medius sit in medio corporis quantum ad magnitudinem, sed oportet, quod sit in medio corporis quantum ad longitudinem (sumendo longitudinem eius a puncto non moto sive tardissime moto usque ad punctum velocissime motum), quia secundum illum modum praecedit ille motus uniformiter difformis.
Sed contra arguitur sic, quia aliqua pars illius rotae non movetur uniformiter difformiter, ergo sequitur, quod ipsa tota rota non movetur uniformiter difformiter. Consequentia patet secundum hanc opinionem, quia oportet, quod in motu uniformiter difformi cuiuslibet partis gradus medius, (id est, qui est in medio longitudinis, ut dictum est), tantum excedat infimum, quantum exceditur a summo, (ut patet ex definitione.) Probatur antecedens, quia datur ibi una pars in illa rota, cuius punctus medius secundum longitudinem non tantum excedit unum extrem[u]m, quantum exceditur ab altero in velocitate, igitur talis pars non movetur uniformiter difformiter. Probatur antecedens, et signo in tali rota unum quadratum non aequalium laterum, cuius punctus medius sit punctus medius semidiametri inter centrum et circumferentiam, et tangat tale quadratum extremitates circumferentiae ex utroque latere, ut patuit in in figura supra posita, sitque illud quadratum ABCD, et arguo sic: punctus existens in medio illius quadrati movetur ut 4, cum sit punctus medius semidiametri inter centru, et circumferentiam illius rotae, quem superius probavimus moveri velocitate ut 4, et puncta extrema, quae tangunt extremitates rotae, moventur velocitate ut 8. Ergo gradus medius neutrum extremorum excedit, et per consequens non tantum, quantum exceditur ab uno, excedit reliquum. Quod fuit probandum. ¶ Dices forte negando antecedens, et ad probationem negando iterum antecedens, et cum probatur, concedo, quod punctus medius illius quadrati movetur velocitate ut quatuor, et concedo etiam, quod duo puncta extrema talis quadrati applicata circumferentiae rotae moventur velocitate ut 8. Sed non debent capi extrema motus illius partis secundum talem longitudinem, quamvis de facto illa sit longitudo talis partis, sed debet sumi in tali parte procedendo secundum latitudinem per lineam rectam a centro rotae procedentem per medium talis partis usque ad circumfetiam, ut patet in figura superius posita. Modo potest dici, immo de facto ita est, quod quanto gradus medius exceditur a gradu velocissime moto illius partis existentis in tali linea, tantum excedit tardissimum existentem in tali parte.
Sed contra, quia utraque medietas illius quadrati ABCD movetur velocius quam ut 4, ergo sequitur, quod totum illud quadratum movetur velocius quam ut 4, consequentia patet, quia totius velocitas conficitur ex partium velocitatibus, et velocitatis denominatio ex utriusque medietatis denominationibus constatur. Sed probatur antecedens, quia utraque medietas illius quadrati aequaliter movetur, puta medietas E et medietas F cum aequaliter distent a centro illius rotae, et utraque illarum velocius movetur quam ut 4, igitur propositum. Cons[e]quentia patet, et arguitur minor, quia utriusque medietatis punctus medius movetur velocius quam ut 4, cum utriusque medietatis tam E quam F punctus medius plus distet a centro quam punctus medius totius, ut patet in figura, igitur utraque illarum medietatum F et E velocius movetur quam ut quatuor. Quod fuit probandum.
¶ Et confirmatur, quia cuiuslibet motus uniformiter difformis gradus velocissimus, [...] quo movetur punctus velocissime motus, tantum excedit gradum medium, quantum gradus medius excedit gradum, quo movetur punctus tardissime, motus, ut concedit haec opinio et communis sc[h]ola, sed motus talis quadrati ABCD non est huiusmodi, igitur talis motus non est uniformiter difformis. Minor probatur, quia gradus velocissimus illius partis est gradus octavus, cum quadratum illud applicetur circumferentiae rotae, et medius est ut quatuor, et motus illius non terminatur ad non gradum, ergo sequitur, quod gradus velocissimus per maiorem latitudinem excedit medium, quam medius excedat infimum. Quod fuit probandum.
¶ Confirmatur secundo principale argumentum, quia si motus talis rotae esset uniformiter difformis a non gradum usque ad octavum, sequeretur, quod adaequata velocitas illius rotae esset ut quatuor, sed consequens est falsum, igitur illud, ex quo sequitur. Consequentia est nota, et falsitas consequentis arguitur, quia velocitas totius illius partis, quae clauditur circulo minori DEF, est ut duo, cum sit a quarto usque ad non gradum, et velocitas totius residui est ut sex, cum sit a quarto usque ad octavum, et si esset in medietate adaequate faceret ad denominationem totius motus ut tria, modo est in sexquialtero maiori parte medietate, ergo sequitur, quod motus eius facit ad denominationem totius in sesquialtero magis, et per consequens ut quatuor cum dimidio, (cum quatuor cum dimidio ad tria sit proportio sesquialtera), ergo sequitur, quod talis motus adaequate est velocior quam ut quatuor cum dimidio, et per consequens velocior quam ut quatutor. Quod fuit probandum. Sed iam probo, quod illa pars rotae, quae est totum residuum a minori circulo, est in sexquialtero maior medietate, quia illa pars est tres quartae totius rotae, igitur in sesquialtero est maior medietate. Probatur, quia medietas est duae quartae, modo trium quartarum ad duas quartas est proportio sesquialtera. Sed iam probo antecedens videlicet, quod residuum illius rotae a minori circulo sit tres quartae illius rotae, quia totius rotae ad minorem totum circulum est proportio quadrupla, ergo totum residuum a minori circulo, qui est una quarta, est tres quartae, sed illa pars est totum residuum a minori circulo, ut notum est, ergo illa est tres quartae totius rotae. Quod fuit probandum. Sed iam probo, quod totius rotae ad minorem circulum ei concentricum sit proportio quadrupla, quia – ut demonstrat Bravardinus
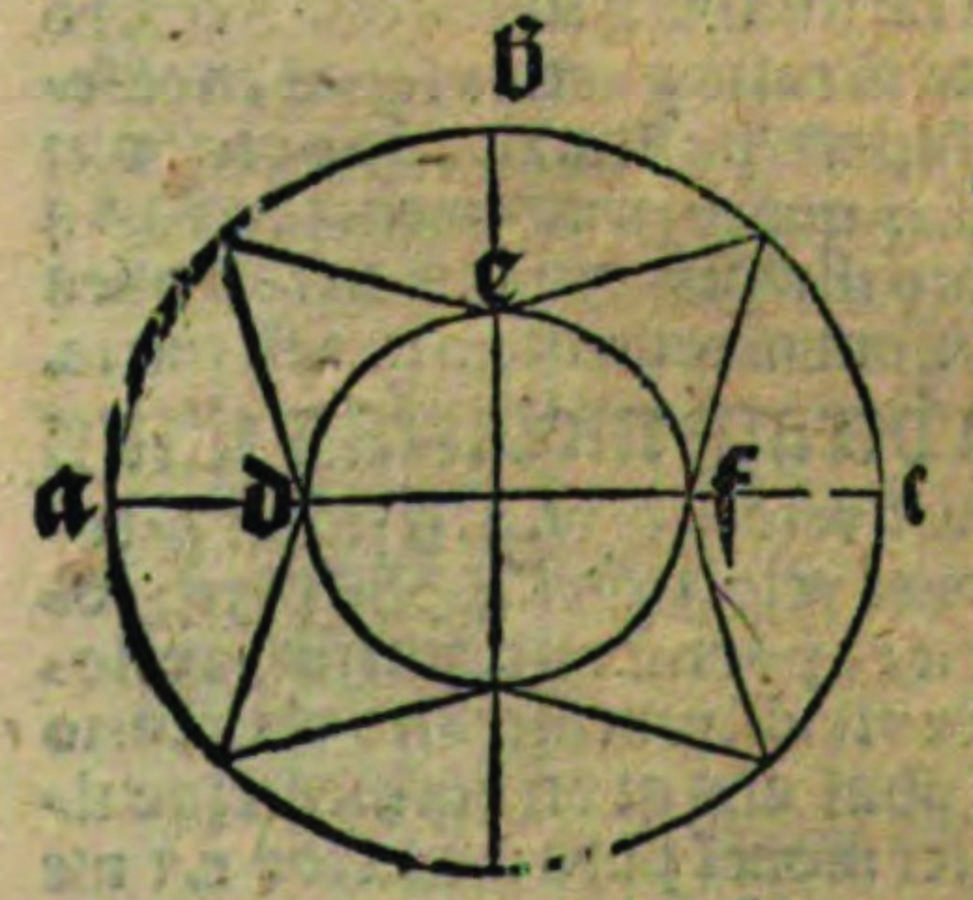
Abb. 4: Alvarus Thomas, Liber de triplici motu, S. 128.
Quod vero diametri ad diametrum sit proportio dupla, patet ex casu principalis argumenti. Et sic ex hac deductione patet, quod totus ille motus est ut quinque, quia illae tres quartae denominant ut quatuor cum dimidio, et alia quarta, quod est minor circulus, denominat ut dimidium, (cum sit ut duo), igitur totus motus est ut quinque et sic non est adaequate ut quatuor. Quod fuit probandum.
Secundo principaliter arguitur sic: si illa definitio esset bona, sequeretur, quod motus caeli non esset uniformiter | difformis quoad subiectum, sed consequens est falsum, et contra communiter opinantes. Igitur illud, ex quo sequitur. Sequela probatur: et divido primum mobile in duas medietates per colurum, videlicet procedentem a polo artico per polum antarticum et per capita arietis et librae. Quo posito arguo sic: nulla illarum medietatum movetur uniformiter difformiter, igitur nec caelum movetur uniformiter difformiter. Consequentia patet, et arguitur antecedens, quam neutrius illarum medietatum punctus, qui est in medio, tantum exceditur in velocitate a puncto velocissime moto, quantum excedit punctum tardissime motum sive non gradum, cum punctus existens in medio sit punctus existens in circulo aequinoctiali, qui est punctus velocissime motus, igitur a nullo exceditur in velocitate, et per consequens non tantum excedit a puncto velocissime moto, quantum excedit punctum tardissime motum vel non gradum velocitatis. Quod fuit probandum.
¶ Et confirmatur, quia si esset aliquis motus uniformiter difformis quoad subiectum, maxime esset motus localis, quo per rarefactionem movetur unum quadratum, quod rarefit uniformiter a non gradu in extremo quiescente usque ad octavum in altero extremo, sed haec non, igitur. Maior est nota cum consequentia, et probatur minor, quia non cuiuslibet partis illius gradus medius tantum exceditur a velocissimo, quanto excedit gradum tardissimum illius partis vel non gradum, igitur totum illud quadratum non movetur uniformiter difformiter quoad subiectum. Consequentia patet ex definitione, et arguitur antecedens, et signo unam partem in medietate illius quadrati, quae velocius rarefit, et sit illa pars figurata per modum duorum laterum unius trianguli facientis unum angulum supra punctum medium ex uno latere et ex alio infra, ut apparet in figura hic infra scripta.

Abb. 5: Alvarus Thomas, Liber de triplici motu, S. 128.
Tunc sic arguitur, illa pars est pars illius quadrati, et tamen ipsa non movetur uniformiter difformiter, igitur propositum. Arguitur antecedens, quia punctus existens in medio illius partis in linea procedente a puncto non moto usque ad punctum velocissime motum ipsius quadrati est punctus medius totius quadrati, qui movetur ut quatuor, ut patet in figura, igitur si talis movetur uniformiter difformiter, sequitur, quod totus motus eius est ut quatuor, sed consequens est falsum, igitur illud, ex quo sequitur. Falsitas consequentis probatur, quia utraque medietas talis partis velocius movetur per rarefactionem quam ut quatuor, quia utriusque illarum punctus medius est intensior quam ut 4, cum utriusque illarum medietatum punctus medius sit supra punctum existentem in medio illius quadrati, et sic utraque illarum movetur velocius quam ut quatuor, ergo per consequens tota illa pars, cuius illae sunt medietates, movetur velocius quam ut quatuor, quod est oppositum, aut saltem infert oppositum consequentis, quod erat probandum falsum.
In oppositum tamen arguitur per communem auctoritatem recentium philosophorum hanc definitionem ponentium.
Pro solutione et enodatione huius quaestionis pono aliquas conclusiones, quibus mediantibus adinveniatur definitio motus uniformiter difformis quoad subiectum.
Prima conclusio: motus uniformiter difformis quoad subiectum non bene definitur isto modo: motus uniformiter difformis quoad subiectum est, cuius omnes partes immediatae secundum extensionem sunt immediatae secundum intensionem motus sive velocitatum, ita quod remississimus gradus velocitatis, qui est in intensiori, sit remississimus, qui non est in remissiori illarum duarum partium sibi immediatarum. Probatur haec conclusio, quia pono casum, quod sit una rota, quae [...] movetur a non gradu usque ad certum gradum, ita quod a centro eius quiescente usque ad medium semidiametri sit motus uniformiter difformis a non gradu usque ad quatuor, et a puncto medio semidiametri usque ad circumferentiam sit motus uniformiter difformis
a quarto usque ad duodecimum – volo enim, quod talis rota sit flexibilis, quia alias non video quomodo, hoc esset possibile. Quo posito arguitur sic: motus ille non est uniformiter difformis, et tamen omnes partes immediate secundum extensionem sunt immediate secundum intensionem, igitur illa definitio convenit aliis a diffinito, et per consequens non est bona. Minor est nota ex casu, et maior probatur, quia si esset uniformiter difformis, cum incipiat a duodecim et terminatur ad non gradum, punctus medius semidiametri moveretur velocitate, quae est gradus medius inter duodecim et non gradum, sed hoc est falsum, ut patet ex casu, quam talis punctus movetur ut quatuor, ut ponitur.
Secunda conclusio: motus uniformiter difformis quoad subiectum non bene definitur isto modo: motus uniformiter difformis quoad subiectum est, quando cuiuscumque partis subiecti punctus, qui est in medio, (loquor de puncto vero vel imaginario) tanto exceditur in velocitate ab extremo illius partis velocissime moto, quantum excedit extremum remississime motum eiusdem partis sive non motum, (quod dico propter motum terminatum ad non gradum.) Haec conclusio bene probatur per primum argumentum principale ante oppositum et per secundam confirmationem eius. Illud enim argumentum et confirmatio ostendunt, quod non oportet medium gradum motus uniformiter difformis quoad subiectum esse in medio magnitudinis corporis moti uniformiter difformiter quo ad subiectum, sed bene oportet, quod sit in medio longitudinis talis corporis modo exposito in argumento.
Tertia conclusio: motus uniformiter difformis quoad subiectum non bene definitur sic: motus uniformiter difformis quoad subiectum est, quando cuiuscumque partis subiecti dimidium sive punctus, qui est in medio talis partis, (in medio inquam secundum longitudinem) tantum exceditur in velocitate a puncto sive ab extremo velocissime moto, quantum excedit punctum sive extremum tardissime motum in velocitate sive extremum non motum (quod dico propter motum terminatum ad non gradum). Probatur haec conclusio per ultimam replicam primi argumenti huius dubitationis et per secundum argumentum. Nam si illa definitio esset bona, sequeretur, quod quaelibet pars illius, quod uniformiter difformiter movetur quo ad subiectum, etiam uniformiter difformiter moveretur quo ad subiectum, ut facile deducitur ex illa definitione, sed tenendo illam definitionem sequitur oppositum videlicet, quod non quaelibet pars illius, quod uniformiter difformiter movetur et cetera, ut probat ultima replica primi argumenti et secundum argumentum.
Quarta conclusio: motus uniformiter difformis quoad subiectum – ut pro nunc mihi apparet – bene definitur sic: motus uniformiter difformis quoad subiectum est, quando quilibet punctus subiecti intrinsecus et etiam extrinsecus velocissime motus in ea proportione velocius movetur, in qua magis distat a centro talis motus. Exemplum, ut si rota moveatur uniformiter difformiter, requiritur, quod in quacumque proportione puncta magis distant a centro ipsius rotae, in ea proportione velocius moveantur. Et per centrum in proposito ego intelligo punctum quiescens existens in illo corpore, quod sic movetur uniformiter difformiter, vel a quo imaginarie procedit talis motus. Et volo dicere, quod si corpus moveatur uniformiter difformiter quo ad subiectum a non gradu usque ad certum gradum, oportet, quod in | quacumque proportione puncta magis distant a puncto illius subiecti, in quo est non gradus motus, in ea [proportione] velocius moveantur. Si vero tale corpus, quod movetur uniformiter difformiter quo ad subiectum, ita se habeat, quod quilibet punctus eius moveatur, ita quod motus eius incipiat a certo gradu remissiori et terminetur ad certum gradum intensiorem, ut verbi gratia incipiat a quarto et terminetur ad octavum, sicut est de motu totius residui a circulo minori existente intra rotam in casu primi argumenti, tunc ad inveniendum centrum talis motus oportet addere corpori aliquod corpus, quod moveatur uniformiter difformiter a non gradu ad gradum ut quatuor, vel remissimum, quo movetur aliud corpus, cuius motus utrimque terminatur ad gradum, et si tunc omnia puncta illius corporis, cuius motus in utroque extremo terminatur ad gradum, in ea proportione velocius moveantur, in qua plus distant a puncto non moto corporis dati, qui quidem punctus tunc est centrum illius motus, tunc tale corpus uniformiter difformiter movetur quo ad subiectum. Probatur haec conclusio, quia illa definitio convenit omni et soli et cetera, igitur est bona, et antecedens pro nunc alio modo non probatur, nisi quia omni motui, qui communiter conceditur uniformiter difformis quo ad subiectum, convenit illa definitio, et soli tali, igitur propositum.
¶ Ex hac conclusione et praedictis sequitur, quod cuiuslibet, quod uniformiter difformiter movetur quoad subiectum, quaelibet pars quantitiva uniformiter difformiter movetur quoad subiectum. Probatur, quia cuiuslibet talis partis quilibet punctus in ea proportione velocius movetur, in qua plus distat a centro illius motus, ergo sequitur, quod quaelibet pars quantitatiua illius, quod uniformiter difformiter movetur quo ad subiectum, etiam uniformiter difformiter movetur quoad subiectum. Consequentia patet ex definitione, et antecedens patet, quoniam sicut illa puncta moventur in toto, ita etiam in illa parte totius, in qua sunt, ut notum est. ¶ Sequitur secundo, quod non oportet, quod motus uniformiter difformis quoad subiectum correspondeat gradui motus existenti in medio magnitudinis talis corporis, nec in medio longitudinis. Probatur hoc correlarium quoad primam partem ex primo argumento et eius secunda confirmatione et quoad secundam partem ex confirmatione secundi argumenti.
¶ Sequitur tertio, quod motus uniformiter difformis quoad subiectum commensurari habet penes gradum medium inter summ[um] et infimum vel non gradum, ubicumque sit talis gradus. Patet, quia non videtur alius modus cognoscendi totalem velocitatem motus uniformiter difformis quoad subiectum. Et per hoc patet conclusio responsiva ad dubitationem, quae talis est:
Definitio illa, quae communiter datur de motu uniformiter difformi quoad subiectum, non est sufficienter assignata, quoniam nec valet, si intelligatur de medio magnitudinis, nec [valet], si intelligatur de medio longitudinis, ut declaratum est in secundo correlario.
His positis respondeo ad argumenta ante oppositum, quod illa sunt pro conclusione respo[n]siva. Quia tamen in primo argumento quaeritur, an in motu uniformiter difformi quoad subiectum gradus medius debeat esse in medio corporis quoad magnitudinem vel quoad longitudinem, dico, quod neuter illorum {modorum}1 requiritur, quod sit in medio corporis, ut dicit secundum correlarium. ¶ Ad replicam tamen respondetur negando antecedens, ut ibi dicitur, quamvis
talis replica sit pro conclusione. Quia tamen inquirit[ur], penes quem punctum debeat ibi attendi motus illius quadrati, dico, quod debet attendi penes punctum, qui movetur gradu medio inter gradum octavum, quo movetur punctus velocissime motus, illius partis et gradum, quo movetur punctus tardissime motus, eiusdem quadrati, ubicumque talis punctus fuerit, de situ enim eius non est curandum. Sed ad videndum an tale quadratum moveatur uniformiter difformiter oportet aspicere an in quacumque proportione quilibet punctus eius magis distet a centro in ea velocius moveatur. Et hoc sufficit et requiritur ad motum uniformiter difformem, ut ibi dictum est, et quia sic est de illo quadrato. Ideo dico illud moveri uniformiter difform[i]ter. ¶ Ad secundam confirmationem concedo sequelam, et nego falsitatem consequentis, et ad probationem dico, quod denominatio motus non debet attendi penes denominationem partium ita quod quantocunque motus fuerit in maiori parte subiecti tanto plus denominat. ut bene probat argumentum, quamvis hoc oporteat in qualitate, ut postea dicetur. Sed quomodo debeat cognosci velocitas talis motus dictum est, et postea latius. dicetur.
Ad secundum argumentum cum sua confirmatione dico, quod sunt pro conclusione resp[o]nsiva, quia impugnant definitionem communem. Dico tamen, quod motus caeli est uniformiter difformis, ut postea dicetur, quia quodlibet punctum eius in ea proportione, in qua plus distat a polo proximiori vel aeque propinquo, in ea velocius movetur. Dico „aeque propinquo“ propter puncta existentia in aequinoctiali, de hoc postea dicetur. ¶ Quantum ad confirmationem dico, quod illud quadratum uniformiter difformiter movetur per rarefactionem, et similiter illa pars, quae signatur in eo. Et cum probatur, quod non dico, quod illa probatio est pro me et contra definitionem, quam impuggno. Et haec de dubitatione. ¶ Sed de velocitate motus penes effectum est difficultas, per quid habeat attendi Ideo recitande sunt opiniones in hac materia communiter occurrentes. Unde duplex est opinio communis tam de motu uniformiter difformi quoad tempus, quam de motu uniformiter difformi quoad subiecum et quoad subiectum et tempus simul.
Prima opinio est Guillermi Hentisberi
¶ Advertendum tamen, quod quando dicimus, quod velocitas motus uniformiter difformis debet attendi penes gradum medi[]um voluminis, dicere, quod tale mobile uniformiter difformiter motum movetur adaequate ita velociter, sicut movetur punctus, in quo est gradus medius talis latitudinis. Et quando dicitur, quod motus uniformiter difformis quoad tempus velocitas debet attendi penes gradum medium, qui est in medio temporis, volumus dicere, quod tam velociter movetur in illo tempore adaequate illud mobile, ac si per totum illud tempus moveretur illo gradu, quem habet in medio illius temporis. |
¶ Advertendum est ulterius, quod velocitas motus quoad effectum debet attendi penes spatium pertransitum, ita quod quanto spatium pertransitum fuerit maius in aequali tempore, tanto motus erit velocior. Dico tamen, quod non debet attendi velocitas motus localis penes spatium corporale nec penes spatium superficiale, sed penes spatium lineale descriptum a certo puncto, quia tunc si unus equus traheret duas trabes inaequales aeque velociter, tamen sequeretur, quod maior velocius moveretur, cum describat maius spatium corporale et superficiale quam minor, quod tamen falsum, quia aequaliter moventur, cum in utraque punctus medius aequale spatium describat. Et sic etiam dicendum est de motu circulari uniformiter difformi quoad subiectum, quod velocitas eius habet attendi penes lineam circularem descriptam a puncto, in quo est gradus medius illius latitudinis motus uniformiter difformis. Velocitas motus uniformiter difformis quoad tempus et quoad subiectum debet attendi penes lineam descriptam a puncto, in quo est medius gradus talis latitudinis. Et similiter dicendum est de motu difformiter difformi quoad tempus, quod velocitas eius debet attendi penes spatium pertransitum in tali tempore. Qualiter autem quantitas talis spatii debeat cognosci, quia ibi est huius materiae praecipua inquisitio, in sequent[]ibus suo loco declarabitur. ¶ Ex his tamen infertur istam consequentiam non valere. Ista rota uniformiter difformiter mota quoad subiectum describit maiorem lineam quam punctus, in quo est gradus medius totius latitudinis motus, igitur movetur velocius quam ille punctus, quia antecedens est verum, cum punctus existens in circumferentia sive peripheria ipsius rotae describat maiorem lineam quam punctus, in quo est gradus medius latitudinis motus, et utraque illarum linearum per motum rotae describitur. Similiter arguendo de caelo dabitur antecedens verum et consequens falsum, ut aliqualiter visum est, et postea videbitur. ¶ Secundo sequitur, quod ista consequentia non valet: ista rota uniformiter difformiter movetur quoad subiectum et citius transibit lineam circularem aequalem lineae descriptae a puncto, in quo est medius gradus latitudinis, quam talis punctus, in quo est gradus medius latitudinis motus, describat suam lineam, ergo rota citius movetur quam talis punctus. Manifestum est enim, quod rota secundum se totam, quantocumque [...] tempore moveatur, describit talem lineam, punctus vero non. Et ideo dictum est, quod debet attendi penes lineam ab uno puncto continuo descriptam, de quo tamen latius in sequentibus [dicitur]. ¶ Tertio sequitur, quod ista consequ[e]ntia non valet, istud lignum maius spatium pertransibit quam illud in eodem tempore, igitur velocius movebitur in eodem tempore. Probatur captis, ut iam dictum est, duobus lignis in aequalis crassitudinis et longitudinis, quae ab uno equo aequaliter trahantur, et manifestum est, quod maius spatium corporale superficiale et etiam lineale – non tamen ab eodem puncto continuo descriptum – pertransit quam aliud lignum minus, nihilominus tamen talia ligna aequaliter moventur. ¶ His superficie tenus dictis, ut intelligatur ordo procedendi in hac materia: primo disceptabo, penes quid habeat attendi velocitas motus difformis q[u]oa[d] subiectum, hoc est tam uniformiter difformis quam difformiter difformis quo ad subiectum. Et secundo disputabo, penes quid habeat attendi velocitas motus difformis quoad tempus tam uniformiter difformis quam difformiter difformis, quantum ingenioli nostri capacitas
se extendit. In ea enim parte est abyssus multa et huius materiae labyrinthus a capacitate intellectus finita in extricabilis et incomprehensibilis, ut ibi videbitur in positione variorum casuum varia monstra et difformitates motuum difformiter difformium ad tempus ponentium. Et postremo aliquid, quam brevissime potero, de velocitate motus difformis quoad tempus et quoad subiectum simul et etiam motus mixti determinabo. Et sic trimembris dumtaxat erit huius materiae disceptatio, et inquisitio quibus determinatis absoluta fere erit.





