Capitulum quintum, in quo ponuntur regulae sive conclusiones velocitatis et tarditatis motus penes proportionem proportionum conformiter ad intentionem calculatoris
Ad inducendas seriatim mathematico more conclusiones docentes velocitatem et tarditatem motus penes causam iuxta opinionem quartam sit:
Prima suppositio: ab aequalibus proportionibus aequales velocitates proveniunt, et ab inaequalibus inaequales, et a rationalibus rationales, et ab incommensurabilibus incommensurabiles. Patet haec suppositio ex opinione, quae ponit velocitatem sequi proportionem proproportionum.
Secundua suppositio: ab aequalibus proportionibus, quae sunt partes aliarum proportionum sive aequalium sive inaequalium, aequales velocitates proveniunt. Declaro hanc suppositionem et capio proportionem triplam et duplam, et manifestum est, quod utriusque proportio sexquialtera est pars. Dico tunc, quod quantam velocitatem producit sexquialtera quae est pars duplae, tantam velocitatem producit sexquialtera, quae est pars triplae. Probatur ex priori suppositione, quia sexquialtera, quae est pars duplae, et sexquialtera, quae est pars triplae, sunt aequales proportiones.
Tertia suppositio: per additionem aequalium proportionum super proportiones aequales vel inaequales velocitates aequaliter intenduntur. Declaro hoc in terminis et capio proportionem duplam et quadruplam, et volo, quod vtrique addatur proportio sexquialtera, qua addita dico, quod aequaliter intendunt proportiones illae, sive illae potentiae motum suum intendunt, et tantam velocitatem acquirit proportio maior sicut et minor supra velocitatem habitam ante additionem proportionis sesquialterae. Probatur haec suppositio ex secunda, quia illa proportio sexquialtera efficitur pars duarum proportionum inaequalium, igitur cum utraque aequalem velocitatem producet.
Quarta suppositio: per decrementum duarum proportionum aequalium, quae sunt partes duarum proportionum, sive aequalium sive inaequalium, aequales velocitates perdentur. ¶ Declaratur haec suppositio, et capio proportionem duplam et triplam, et volo, quod utraque deperdat proportionem sexquialteram, tunc dico, quod si proportio dupla perdat duos gradus velocitatis, etiam duos adaequate perdit proportio tripla. Patet haec suppositio ex priori, quoniam illae duae proportiones deperditae, cum essent aequales, aequalem velocitatem producebant, igitur per decrementum illarum aequales velocitates perduntur, quia perduntur ipsaemet, quas ipsae producebant.
Quinta spupositio: per additionem aequalis quantitatis maiori et minori quantitati maior proportio acquiritur minori quantitati quam maiori. ¶ Haec est octava suppositio quarti capitis secundae partis.
Sexta suppositio: aeque velociter intendere motum est in aequali tempore aequales partes adaequate acquirere, et aeque proportionabiliter intendere est in aequali tempore aequales proportiones acquirere. Et similiter dicendum est de aeque velociter remitte[ndo] et aeque proportionabiliter, ut si numerus
senarius aequirit binarium, et numerus quinarius in eodem tempore etiam binarium, dico, quod aeque velociter intenduntur, sed non aeque proportionabiliter. Sed si numerus ternarius acquirat unitatem, et numerus senarius acquirat in eodem tempore dualitatem, dico, quod tunc aeque proportionabiliter acquirunt et non aeque velociter, quoniam tam ternarius numerus quam senarius proportionem sexquitertiam acquirit, ut facile est intueri. Haec definitio est.
His suppositis praemissis sit prima conclusio: si aliqua potentia crescit respectu resistentiae non variatae, tantam proportionem acquirit supra se, quantam supra suam resistentiam et eocontra. Probatur haec conclusio auxiliante septima conclusione octavi capitis praecedentis partis.
Nam potentia se habet ut quantitas maior, et resistentia ut minor, si activitas prodeat.
Secunda conclusio: si aliqua virtus decrescat respectu resistentiae non variatae, tantam proportionem deperdit respectu suae resistentiae, quantam respectu sui ipsius ut capta potentia ut 4 et resistentia ut 2, si potentia ut quatuor efficiatur in sexquitertio minor perdendo unitatem sive proportionem sexquitertiam, eandem proportionem sexquitertiam perdit respectu suae resistentiae ut duo. Probatur haec conclusio ex septima conclusione octavi capitis praeallegata eo modo, quo prior.
Tertia conclusio: si aliqua resistentia crescat vel decrescat respectu potentiae non variatae, tantam proportionem acquiret vel deperdet respectu sui ipsius, quantam acquiret vel deperdet respectu talis potentiae. Hoc est: tantam acquirit vel deperdit talis potentia respectu eiusdem resistentiae. Patet haec conclusio ex octava conclusione octavi capitis praeallegati et suo primo correlario.
Quarta conclusio: si potentia crescat vel decrescat respectu potentiae non variatae, tantam proportionem acquirit vel deperdit respectu suae resistentiae, q[u]antam acquirit vel deperdit respectu sui ipsius. Probatur haec conclusio ex primo correlario septimae conclusionis capitis praeallegati, et facile ex prima et secunda huius deducitur.
Quinta conclusio: si aliqua potentia aeque velociter crescit vel decrescit respectu duarum resistentiarum sive aequalium sive inaequalium, aeque velociter cum utraque illarum intendet vel remittet motum suum. Probatur haec conclusio, quoniam illa potentia aequalem proportionem acquirit vel deperdit respectu utriusque resistentiae, ut patet ex prima conclusione huius et secunda parte septimae conclusionis octavi capitis praeallegati et suo secundo correlario, igitur aequalem velocitatem acquirit vel deperdit respectu utriusque resistentiae.
Patet consequentia ex tertia suppositione.
Sexta conclusio: si aliqua resistentia crescat vel decrescat respectu duarum potentiarum sive aequalium sive inaequalium non variatarum, utraque potentia aeque velociter cum illa resistentia intendet vel remittet motum suum. Probatur haec conclusio, quoniam respectu utriusque potentiae aequalem proportionem acquirit vel deperdit, ut patet ex secundo correlario octavae conclusionis octavi capitis praeallegati, igitur utraque potentia aequalem velocitatem acquirit vel deperdit. |
Septima conclusio: si duae potentiae inaequales aeque velociter crescant vel decrescant respectu eiusdem resistentiae non variatae, potentia minor velocius intendet vel remittet motum suum. Probatur haec conclusio, quoniam semper potentia minor per aequale crementum vel decrementum additum sibi vel deperditum et maiori maiorem proportionem acquiret vel deperdet quam maior, ut patet ex quinta suppositione huius capitis, igitur talis potentia velocius intendet vel remittet motum suum. Consequentia patet ex prima suppositione. Ab aequalibus enim proportionibus acquisitis sive deperditis inaequales velocitates acquiruntur sive deperduntur, et per idem sequitur, quod ad acquisitionem vel deperditionem maioris maior velocitas acquiritur vel deperditur.
Octava conclusio: si duae resistentiae inaequales aeque velociter crescant vel decrescant respectu eiusdem potentiae non variatae, illa potentia velocius intendet vel remittet motum suum cum minori resistentia quam cum maiori. Probatur haec conclusio, quoniam semper minor resistentia maiorem proportionem acquirit vel deperdit per aequalem deperditionem vel additionem ipsi et maiori, igitur potentia cum ea velocius intendet vel remittet motum suum. Patet consequentia auxilio duarum primarum suppositionum.
Nona conclusio: si duae potentiae inaequales aeque velociter crescant vel decrescant respectu duarum resistentiarum sive aequalium sive inaequalium, potentia minor semper velocius intendet vel remittet motum suum, sive agat cum resistentia maiore sive minore. Patet haec conclusio ex septima huius.
Decima conclusio: si duae resistentiae inaequales crescant vel decrescant respectu duarum potentiarum sive aequalium sive inaequalium, potentia agens cum minore velocius intendet vel remittet motum suum. Haec patet ex octava.
Undecima conclusio: si duae potentiae aequales vel inaequales aeque propor[t]ionabiliter crescant vel decrescant respectu eiusdem resistentiae non variatae, tales potentiae aeque velociter intendent vel remittent motus suos. Patet haec conclusio ex sexta suppositione, quae definit istum terminum aeque proportionabiliter auxilio primae suppositionis.
Duodecima conclusio: si duae resistentiae aequales sive inaequales aeque proportionabiliter crescant vel decrescant respectu eiusdem potentiae non variatae, talis potentia cum utraque illarum resistentiarum aeque velociter intendet vel remittet motum suum. Haec cum praecedente eandem sortitur demonstrationem.
Tridecima conclusio: si duae potentiae inaequales aeque proportionabiliter crescant vel decrescant respectu duarum resistentiarum sive aequalium sive inaequalium non variatarum, ipsae aequevelociter intendent vel remittent motus suos. Patet haec conclusio ex prima suppositione auxiliante ultima definiente aeque velociter et aeque proportionabiliter.
Quartadecima conclusio: si duae resistentiae inaequales crescant vel decrescant aeque proportionabiliter respectu duarum potentiarum sive aequalium sive in[ae]qualium, tales potentiae aequevelociter
intendent vel remittent motus suos. Ex probatione prioris haec probata evadit.
Quindemica conclusio: si duae potentiae per earum intensionem aeque velociter intendunt motus suos cum eadem vel diversis resistentiis non variatis, ipsae aeque proportionabiliter crescunt, et si per earum remissionem et cetera aeque velociter remittunt motus suos, ipsae aeque proportionabiliter decrescunt. Haec patet ex undecima. Et dicit calculator
Decimasexta conclusio: si per crementa aliquarum resistentiarum vel decrementa potentia vel potentiae cum illis resistentiis moventes uniformiter moveantur, tales potentiae aeque proportionabiliter crescunt vel decrescunt cum suis resistentiis. Patet conclusio, quia ad hoc, quod proportio maneat semper aequalis, et [quod] numeri eius crescunt vel decrescunt, necesse est, quod quantamcu[m]que proportionem numerus maior acquirat vel deperdat, tantam proportionem acquirat vel deperdat numerus minor, ut patet ex primo correlario quartae conclusionis octavi capitis secundae partis, igitur.
Decimaseptima conclusio: si potentia crescens vel decrescens uniformiter movetur et aeque velociter, necesse est resistentiam aeque proportionabiliter crescere vel decrescere et eocontra. Haec ex primo correlario quartae conclusionis praeallegato patrocinio primae suppositionis huius manifesta evadit.
Decimaoctava conclusio: si resistentia crescat vel decrescat, et potentia aeque velociter movetur, ipsa potentia aeque proportionabiliter crescit vel descrescit cum sua resistentia et eocontra. Haec praecedentis probationem assumit.
Decimanona conclusio: si potentia aeque velociter moveatur, et ipsa difformiter crescit vel decrescit, necesse est suam resistentiam difformiter crescere vel decrescere. Patet hoc ex probatione aliarum.
Vigesima conclusio: si aliqua resistentia uniformiter crescat vel decrescat potentia aeque velociter movente, necesse eandem potentiam crescere vel decrescere uniformiter. Patet conclusio, quia alias non maneret eadem proportio, ut patet ex correlario praeallegato, et per consequens nec eandem velocitas.
Vigesimaprima conclusio: si aliqua potentia uniformiter crescat respectu resistentiae non variatae, talis potentia tardius et tardius intendit motum suum. Probatur haec conclusio ex sexta suppositione. Continuo enim eadem latitudo addetur maiori et maiori numero, igitur continuo acquiretur minor proportio, et sic continuo motus tardius et tardius intendetur.
Vigesimasecunda conclusio: si aliqua potentia uniformiter decrescat resistentia non variata, ipsa continuo velocius et velocius remittet motum suum. Haec itidem patet ex sexta suppositione.
Vigesimatertia conclusio: si aliqua resistentia uniformiter crescat respectu potentiae non variatae, talis potentia tardius et tardius remittet motum suum. Haec modo quo praecedens probatur. |
Vigesimaquarta conclusio: si aliqua resistentia uniformiter decrescat potentia non variata, talis potentia velocius et velocius intendet motum suum. Patet, quoniam continuo maiorem proportionem acquirit, ut patet ex sexta suppositione.
Vigesimaquinta conclusio: si aliqua potentia tardius et tardius crescat respectu resistentiae non variatae, ipsa tardius continuo et tardius intendet motum suum. Patet haec conclusio ex vigesimaprima per locum a maiori, quoniam si semper uniformiter cresceret, tardius continuo et tardius intenderet motum suum. Igitur si continuo tardius crescat, a fortiori tardius et tardius i[n]tendet motum suum.
Vigesimasexta conclusio: si aliqua potentia velocius continuo decrescat respectu resistentiae non variatae, ipsa conti[n]uo velocius remittet motum suum. Patet ex vigesimasecunda suffragante loco a maiori.
Vigesimaseptima conclusio: si aliqua resistentia tardius continuo crescat respectu potentiae non variatae, ipsa potentia continuo tardius remittet motum suum. Patet ex vigesimatertia auxilio loci a fortiori.
Vigesimaoctava conclusio: si aliqua resistentia continuo velocius decrescat respectu potentiae non variatae, talis potentia continuo velocius intendet motum suum. Patet ex vigesima quarta.
Vigesimanona conclusio: si duae vel tres vel quatuor aut quotlibet potentiae inaequales aeque velociter crescant vel decrescant respectu eiusdem resistentiae non variatae, minima illarum velocius intendet vel remittet motum suum. Patet haec conclusio ex sexta suppositione, quoniam illi minori potentiae per additionem vel remotionem aequalis latitudinis semper accrescit vel decrescit maior proportio.
Tricesima conclusio: si duae aut tres aut quatuor, aut quotlibet resistentiae aeque velociter crescant vel decrescant respectu eiusdem potentiae non variatae, semper talis potentia cum minima illarum velocius intendet vel remittet motum suum. Haec et praecedens aequalem subeunt demonstrationem. ¶ Nunc modicum a serie discedentes opere pretium est aliquas conclusiones his a[d]ducere.
Tricesimaprima conclusio: si duplum et subduplum aeque velociter ad non gradum remittantur, in maiori tempore remittitur duplum quam subduplum. Probatur haec conclusio, quoniam capto quaternario et binario, si aeque velociter et uniformiter remittantur, quando duae unitates quaternarii remissae sunt, restant duae, et binarius est complete remissus. Igitur oportet, quod in tempore sequenti remittantur aliae duae unitates quater[n]arii, postquam binarius est ad non gradum deductus, et per consequens conclusio vera.
Tricesimasecunda conclusio: si duplum et subduplum uniformiter remittantur et continuo aeque velociter, tempus remissionis dupli est duplum ad tempus remissionis subdupli. Et consimiliter dicatur de triplo, quadruplo, sexqualtero et sic in infinitum, quoniam tempus tripli erit
triplum, et quadrupli quadruplum, et sexquialteri sexquialterum et sic deinceps. Probatur haec conclusio, quoniam duplum continet bis subduplum, et triplum ter subtriplum et sic in infinitum, ergo si remittantur uniformiter et aeque velociter continuo, necesse est, cum subduplum fuerit remissum, restat tantum de duplo remittendum, quantum erat subduplum, et cum subtriplum fuerit remissum, restet bis tantum remittendum et cetera.
Tricesimatertia conclusio: si duplum et subduplum uniformiter et aeque velociter remittantur ad non gradum, et quodlibet illorum continuo tardius et tardius, subduplum in minori tempore quam []duplum remittetur, ita quod, si duo remittantur in una hora, 4 remittentur in maiori tempore, quam sit tempus duarum horarum. Probatur haec conclusio, et capio 4 et 8, et volo, quod uniformiter et aeque velociter remittantur, sed continuo tamen quodlibet illorum tardius et tardius. Volo dicere, quod semper, quando remittitur unitas unius, puta subdupli, remittatur unitas alterius, sed continuo tardius et tardius. Hoc est, quod si utriusque unitas prima fuerit remissa in media hora, alia unitas in maiori tempore adaequate remittatur. Quo posito manifestum est, quod si in una hora fuerit remissus quaternarius, etiam in eadem hora remissus est quaternarius ab octonario, et ab ipso octonario restat remittendus quaternarius, et continuo tardius remittetur. Igitur in maiori tempore quam alter quaternarius, igitur totum tempus, in quo duplum remittitur adaequate, est maius quam duplum ad tempus, in quo remittitur subduplum.
Tricesimaquarta conclusio: si duplum et subduplum remittantur aeque velociter et continuo velocius et velocius, totale tempus remissionis dupli est minus quam duplum ad tempus totalis remissionis subdupli. Et volo dicere, quod si duo et quatuor remittantur, ita quod quando remittitur unitas binarii, tunc adaequate remittatur uni[t]as quaternarii, sed tamen velocius, sic quod si prima unitas binarii et quaternarii remittatur in hora, secunda unitas in minori tempore remittatur. Dico, quod tempus totale, in quo remittuntur ipsa 4, est minus quam duplum ad tempus totalis remissionis ipsorum 2. Probatur haec conclusio, quia si aequevelociter et uniformiter remittentur quo ad tempus, tunc tempus remissionis dupli esset adaequate duplum ad tempus remissionis subdupli, ut dicit tricesimasecunda conclusio, sed modo continuo velocius remittuntur duplum et subduplum, igitur duplum in minori tempore quam duplum ad tempus remissionis ipsius subdupli totaliter remittetur. ¶ Et confirmatur, quia quando 2 et 4 remittuntur aeque velociter et continuo velocius et velocius, tempus, in quo remittetur prima medietas ipsorum 4, erit aequale tempore, in quo remittuntur 2, et tempus remissionis alterius medietatis ipsorum 4 est minus tempor[e] remissionis primae medietatis, ergo totum tempus remissionis ipsorum 4 est minus quam subduplum ad tempus remissionis ipsius dualitatis.
Tricesimaquinta conclusio: aliquid alio plusquam in duplo citius remittitur, et tamen quamdiu manent ambo aeque velociter, continuo remittuntur. Probatur haec conclusio, et capio pedale et bipedale, sive albedinem unius gradus et albedinem duorum graduum, et volo, quod incipiant remitti et continuo taliter remittantur, quod in aequalibus temporibus | aequales partes deperdant, continuo tamen tardius et tardius. Quo posito sic arguo: unus gradus plusquam in duplo citius remittetur quam duo gradus, ut patet ex tricesimatertia conclusione, et tamen continuo aeque velociter, quamdiu simul mament remittuntur, ut patet ex casu, igitur conclusio vera.
Tricesimasexta conclusio, quod ista consequentia nihil valet: A est duplum, et B subduplum, et plusquam in duplo citius deperditur B subduplum quam A duplum. Igitur velocius deperditur B subduplum quam duplum. Stat enim cum ante[cedente], quod A duplum in aliquo tempore ita velociter movetur sicut B subduplum ex anteriori conclusione, quod est oppositum tertiae exponentis ipsius consequentis. Sed haec consequentia est bona: B est subduplum et A duplum eius et plusquam in duplo velocius deperditur sive remittitur quam B, et utrumque illorum semper remittitur uniformiter, ergo A velocius remittetur quam B, sed antecedens talis consequentiae est impossibile, ut patet ex tricesimasecunda conclusione. Partes enim antecedentis repugnant.
Tricesimaseptima conclusio: si aliqua potentia invariata movetur per medium uniformiter difforme invariatum a remissiori extremo incipiendo, talis potentia continuo tardius et tardius acquirit sibi resistentiam. Probatur haec conclusio supponendo, quod omnium duarum partium aequalium corporis uniformiter difformis extremum intensius per aequalem latitudinem excedit extremum remissius, ut capta latitudine uniformiter difformi a quarto usque ad octavum primae quartae extremum intensius, puta ut 5, excedit remissius per unum gradum, et secundae quartae extremum intensius, puta ut sex, excedit extremum remissius eiusdem quartae, ut 5, etiam per unum gradum et sic consequenter. Et hoc non solum habet verum de partibus aequalibus immediatis, verum etiam de mediatis, ut facile est intueri, et etiam hoc in capite decimo huius tractatus probabitur. Isto supposito probatur conclusio, quoniam continuo pertransitionem duarum partium aequalium aequaliter acquiret de resistentia. Quando enim pertransibit secundam quartam, tantam resistentiam acquiret super resistentiam habitam, quantam transeundo primam quartam adaequate, et tantam resistentiam acquiret adaequate transeundo primam octavam sicut secundam et sicut tertiam et sicut quartam et sic de quibuscunque partibus aequalibus, et continuo tardius et tardius talis potentia movetur, quia semper sibi accrescet resistentia ipsa invariata, igitur tardius continu[o] acquiret sibi resistentiam.
Tricesimaoctava conclusio: si aliqua potentia non variata continuo moveatur per medium uniformiter difforme implendo ab extremo intensiori, continuo velocius et velocius decrescet sibi de resistentia. Patet, quia continuo velocius et velocius movetur et continuo aequalem partem transeundo aequalem resistentiam deperdit, igitur continuo velocius et velocius decrescit sibi de resistentia.
Tricesimanona conclusio: si aliqua potentia non variata movetur per medium uniformiter difforme ab extremo remissiori incipiendo, talis potentia continuo tardius et tardius remittit motum suum. Patet, quia tardius et tardius accrescet sibi de resistentia, igitur continuo tardius et tardius remittit motum suum. Patet consequentis
ex vigesimaseptima conclusione.
Quadragesima conclusio: si aliqua potentia non variata movetur per medium uniformiter difforme incipiendo ab extremo intensiori, talis potentia continuo velocius et velocius intendit motum suum. Patet, quia continuo velocius et velocius decrescit sibi de resistentia, igitur continuo velocius et velocius intendit motum suum. Patet consequentia ex vigesimaoctava conclusione.
Quadragesimaprima conclusio: stat duas potentias aequales moveri per medium uniformiter difforme incipiendo ab extremo remissiori eiusdem medii ipsis et medio simplicter invariatis et tamen unam moveri velocius altera. Probatur haec conclusio, et capio unum medium quadratum uniformiter difforme a non gradu usque ad octavum vel a certo gradu (in idem redit), et volo, quod A et B sint duae potentiae aequales, et incipiat una moveri ab extremo remissiori per diametrum, et alia per lineam rectam ab eodem extremo, quo posito sic arguo: A et B movebuntur, et A non movebitur tardius ipso B nec aeque velociter adaequate, ergo velocius. Maior patet cum co[n]sequentia, et minor probatur, quia si moverentur aequaliter, sequeretur, quod aequales potentiae cum inaequalibus resistentiis aequaliter moverentur, et per consequens ab inaequalibus proportionibus aequales motus proveniunt, quod est contra primum suppositionem huius capitis et directe contra opinionem. Sequ[a]la tamen probatur, quoniam capto quocumque puncto diametri aequaliter distante ab angulo quadrati, hoc est a linea quadrati faciente angulum, sicut certus punctus est minoris resistentiae quam punctus existens in linea recta aequaliter distante cum ipso. Ergo sequitur, quod semper A habebit minorem resistentiam et per consequens maiorem proportionem ad talem punctum quam B in puncto sibi correspondente, et tamen per te A et B moventur aequaliter, igitur propositum. Q[uod] autem in tali puncto diametri sit semper resistentia minor quam in puncto sibi correspondente in linea directe, et perpendiculariter procedente probatur, quoniam semper talis punctus plus distat a gradu summo illius corporis quam punctus sibi correspondens in linea directe et perpendiculariter procedente. Igitur semper in eo est minor resistentia, et per consequens proportio maior. Patet haec demonstratio aspicienti figuram quadratam uniformiter difformem quoad resistentiam, quae sit AB et CD, et extremum remississimum sit AC, et linea diametralis, per quam A movetur, sit AD, et linea, per quam movetur B, sit CD.
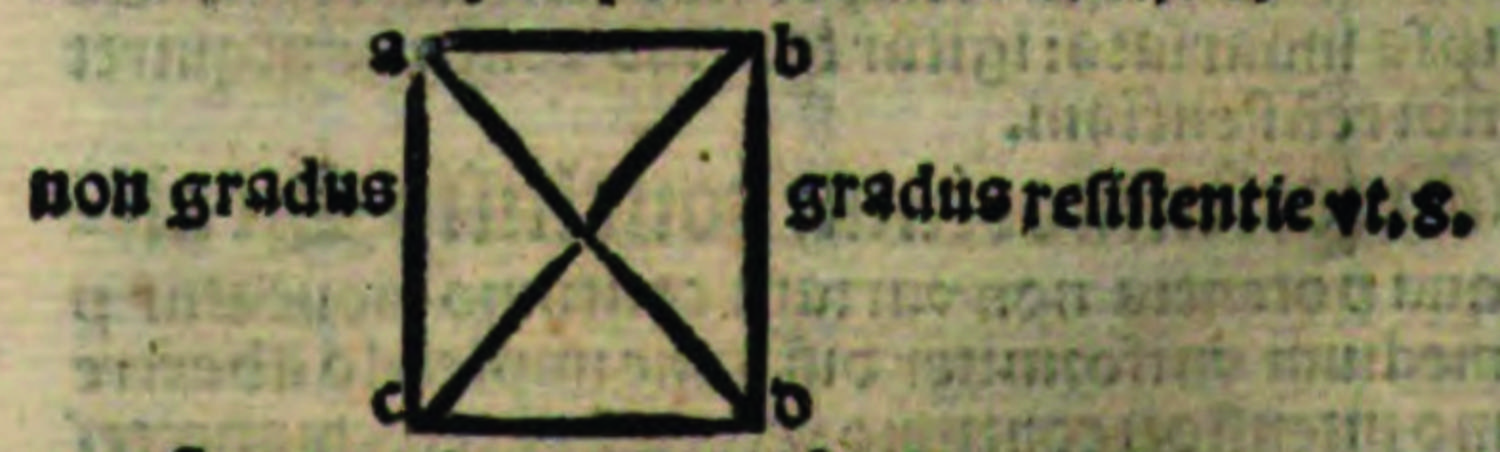
Abb. 5: Alvarus Thomas, Liber de triplici motu, S. 64.
Qua figura inspecta patet facile propositum. Et haec de his conclusionibus, in quibus ferme secutus sum calculatorem




