Capitulum sextum, in quo datur modus dividendi corpus in partes proportionales proportione irrationali
Quemadmodum quodlibet corpus dividi potest proportione rationali infinitisque speciebus eius, ut caput praecedens ostendit, ita etiam proportione irrationali infinitisque speciebus eius quodlibet corpus dividi potest. Pro cuius divisionis notitia sit.
Prima conclusio: quodlibet corpus divisum aliqua proportione irrationali se debet habere ad aggregatum ex omnibus partibus proportionabilibus tali proportione sequentibus primam in ea proportione, qua totum dividatur. Haec conclusio claram et evidentem ex prima praecedentis capitis demonstrationem sortitur.
Secunda conclusio: ad dividendum corpus infinitis proportionibus irrationabilibus minoribus dupla, ut puta proportione diametri ad costam, aggregati ex medietate excessus, quo diameter excedit costam, et ipsa costa [ad] ipsammet costam
et sic consequenter, ut capite quarto ostensum est, debet pro prima parte capi excessus, quo maior quantitas excedit minorem, ita quod residuum a prima sit minor quantitas, et totum corpus sit maior quantitas talis proportionis. Probatur haec conclusio ex praecedenti, quoniam totum corpus divisum proportione aliqua irrationali se debet habere ad aggregatum ex omnibus sequentibus primam tali divisione in ea proportione, qua ipsum corpus dividitur, igitur oportet, quod totum corpus se habeat ut maior quantitas talis proportionis, et aggregatum ex omnibus sequentibus primam [se habeat] ut minor quantitas, et per consequens excessus, quo totum corpus excedit aggregatum ex omnibus sequentibus primam, erit prima pars proportionalis tali proportione. Patet consequentia, quia residuum est aggregatum ex omnibus aliis a prima, ille igitur excessus erit prima. Quod fuit probandum. ¶ Ex hac conclusione sequitur primo, quod ad dividendum corpus proportione irrationali diametri ad costam oportet pro prima parte proportionali capere excessum, quo diameter excedit costam, et pro secunda capere etiam excessum, quo illa costa, cum est diameter quadrati, excedit costam illius quadrati, et sic consequenter. Et ad dandam primam partem proportionale proportionis irrationalis, quae est aggregati ex costa et medietate excessus diametri ad ipsam costam, capiatur pro prima parte proportionali illa medietas excessus, et pro secunda parte proportionali capiatur tanta pars residui, ad quam prima habeat illam proportionem, quae est totius corporis ad aggregatum ex omnibus sequentibus primam, et iterum in residuo a prima parte et secunda pro tertia parte capiatur tanta pars, ad quam secunda habeat illam proportionem, quam prima habet ad ipsam, et sic consequenter. Et simili modo operandum esset, si divideretur corpus proportione irrationali, quae est aggregati ex costa et quarta parte vel octava vel decimasexta excessus, qu[o] diameter excedit costam, ad ipsam costam. Patet correlarium ex conclusione addita suppositione secunda praecedentis capitis, illae enim partes infinitae continuae se habent in proportione divisionis, et totum absolvunt. ¶ Sequitur secundo, quod diviso corpore per partes proportionales proportione irrationali, quae est diametri ad costam, omnes partes impares continuo se habent in proportione dupla, et omnes pares similiter, et omnes duae, inter quas mediant duae, se habent continuo in proportione sesquialtera ad duplam, et omnes, inter quas mediant tres, se habent in proportione quadrupla et sic consequenter. Probatur, quia proportio, quae est primae partis proportionalis ad tertiam, componitur ex duabus proportionibus aequalibus, quarum utraque est medietas duplae, ergo sequitur, quod illa est dupla. Patet consequentia, et probatur antecedens, quia componitur illa proportio ex proportione primae partis ad secundam, quae est medietas duplae, et ex proportione secundae ad tertiam, quae etiam est medietas duplae, quoniam proportio diametri ad costam est medietas duplae, ut patet ex tertia suppositione tertii capitis. Et sic probabis de quibuscunque duabus partibus paribus immediatis et etiam imparibus. Sed iam probo partes, inter quas mediant duae, se habere in proportione sexquialtera ad duplam, quia proportio inter tales partes componitur | ex proportione primae ad secundam et secundae ad tertiam et tertiae ad quartam, sed proportio primae ad tertiam est dupla, ut patet ex probatione praecedentis partis, et proportio tertiae ad quartam est proportio, quae est medietas duplae, ut constat, ergo proportio primae ad quartam continet duplam et medietatem duplae adaequate, et per consequens talis proportio, quae est primae ad quartam, est sexquialtera ad duplam. Patet haec consequentia ex definitione sexquialterae. Et sic probabis de aliis huiuscemodi partibus. Sed iam probo tertiam partem, quia proportio partium, inter quas manent tres cuiusmodi, est proportio primae partis ad quintam, componitur ex duabus duplis, puta ex proportione, quae est primae ad tertiam et tertiae ad quintam, quae sunt duplae, ut patet ex prima parte huius correlarii, et per consequens talis proportio primae ad quintam est dupla ad duplam, cum contineat ipsam duplam bis, et per consequens quadrupla. Patet consequentia ex definitione duplae et secunda parte. Et hoc modo probabis de omnibus similibus. Patet hoc correlarium sensui in figura sequenti, in qua prima pars est diameter quadrati maioris ibidem positi, et secunda est costa eiusdem quadrati, et tertia est costa quadrati sequentis, et tertia est costa tertii quadrati, et diameter quarti, et quarta est costa quarti quadrati, et diametri quinti, et quinta est costa ipsius quinti quadrati, et sic in infinitum poteris procedere, ibi enim conspicies, quod primae ad tertiam est proportio dupla et secundae ad quartam etiam dupla, et primae ad quintam est quadrupla.
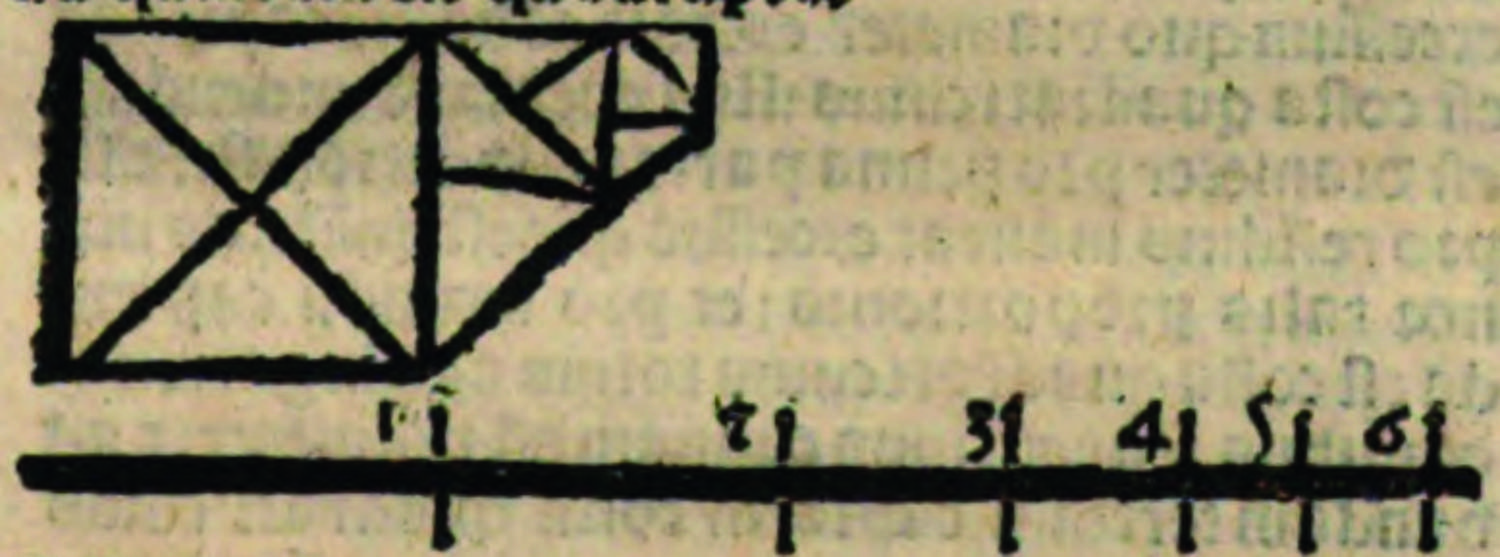
Abb. 2: Alvarus Thomas, Liber de triplici motu, S. 13.
¶ Ex quo sequitur tertio, quod in tali divisione aggregatum ex omnibus imparibus a prima impari est aequale primae, et aggregatum ex omnibus paribus a secunda, quae est prima par, est aequale secundae, et aggregatum ex omnibus imparibus se habet ad aggregatum ex omnibus paribus in proportione, quae est medietas duplae. Probatur prima pars huius correlarii, quia partes impares continuo se habent in proportione dupla, ut patet ex proximo correlario, igitur residuum ex omnibus imparibus sequentibus primam imparem est aequale primae impari. Patet consequentia ex secundo correlario tertiae conclusionis quinti capitis. Et eodem modo probabis secundam partem. Sed iam probatur tertia, quoniam medietas aggregati ex omnibus imparibus se habet ad medietatem aggregati ex omnibus paribus in proportione, quae est medietas duplae, ergo totum aggregatum imparium se habet ad totum aggregatum parium in proportione dupla. Patet consequentia, per hanc regulam in quacumque proportione se habent partes aliquotae aliquarum quantitatum eiusdem denominationis, in eadem se habent et illae quantitates totales, et per consequens in proportione, qua se habent duae medietates aliquorum, in eadem se habent tota illarum medietatum. Sed probatur antecedens, quia prima pars proportionalis impar se habet ad primam parem, quae est secunda,
in proportione quae est medietas duplae ut constat, quia illa est proportio divisionis, et prima pars proportionalis impar est medietas totius aggregati ex omnibus imparibus, et prima par, quae est secunda est medietas aggregati ex omnibus paribus, ut patet ex duabus primis partibus correlarii, ergo medietas omnium imparium se habet ad medietatem omnium parium in proportione, quae est medietas duplae. Quod fuit probandum.
¶ Sequitur quarto, quod diviso corpore per partes proportionales proportione irrationali, quae est medietas triplae, omnes partes impares talis divisionis se habent in proportione tripla, et etiam omnes pares, et omnes, inter quas mediant tres, in proportione novocupla, et aggregatum ex omnibus imparibus se habet ad aggregatum ex omnibus paribus in proportione, quae est medietas triplae. Hoc correlarium cum praecedenti similem demonstrationem admittit.
Tertia conclusio: ad dividendum corpus in partes proportionales infinitis speciebus proportionis irrationalis maioris dupla, ut puta proportione, quae est totius diametri ad excessum, quo ipsa diameter excedit costam, et totius diametri cum medietate excessus, quo excedit costam, vel ad quarta[m] [...] vel ad quintam vel ad sextam, ut superius dictum est, pro prima parte proportionali capiendus est excessus, quo quantitas maior excedit minorem in tali proportione, et quantitas minor [capienda est] pro residuo, ut si velis partiri corpus in partes proportionales proportione, quae est totius diametri ad excessum, quo diameter excedit costam, capienda est costa quadrati, cuius illud corpus dividendum est, diameter pro prima parte proportionali, et sic pro residuis maneat excessus, qu[i] est quantitas minor talis proportionis, et pro secunda capienda est costa quadrati, cuius totum aggregatum ex omnibus sequentibus primam est diameter, et ad dandam tertiam capiatur costa quadrati, cuius est diameter aggregatum ex omnibus sequentibus primam et secundam. Et ad dividendum aliquod corpus proportione, quae est totius diametri ad medietatem excessus, quo excedit costam, pro prima parte proportionali capiendus est excessus, quo maior quantitas excedit minorem tali proportione. Constituendum enim est totum corpus, diameter alicuius quadrati, et tunc pro prima parte proportionali capienda est tanta pars illius corporis, quod pro omnibus sequentibus non maneat nisi medietas excessus, quo tale corpus existens diameter excedit costam eiusdem quadrati, et addandam secundam partem proportionalem constituatur totum, quod sequitur primam diameter alicuius quadrati, et pro secunda parte capiatur tantum, quod pro sequentibus non maneat nisi medietas excessus, quo talis diameter excedit suam costam, et sic consequenter. Patet haec conclusio eo modo, quo secunda huius capitis. Hic poteris multa correlaria inferre, sed iam ad ea inferenda ex praedictis facilem haberes aditum. Et haec de proportione irrationali et de divisione corporum eadem irrationali proportione, de qua non est facile cum r[a]tione loqui.


