3 The Present Position of Classical Relativity Theory and Some of its Problems

We are here to consider an extraordinary topic, one that ranges from the infinitely large to the infinitely small. We want to find what general relativity and gravitation physics have to do with the description of nature. This task imposes a heavy burden of judgement and courage on us, for never before has theoretical physics had to face such wide subject matter, assisted by so comprehensive a theory but so little tested by experiment.

Our problems fall under three heads. First: What checks do we have today of Einstein's general relativity theory, and what can be done to improve our tests? Second: What ways can we see to draw new richness out of the theory? And third: What connection can we foresee between this theory and the quantum world of the elementary particles?

Without going over all the evidence from observational tests of general relativity, it is perhaps worthwhile to set down a few numbers relating to the three traditional tests of the theory.

Planet	Observed Value	Prediction from General Relativity
Mercury		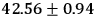43.15
Earth		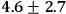3.84
Mars	—	1.35

Tab. 3.1: Precession in seconds of arc per century

Table 3.1 compares the predicted and observed values of the precession of the perihelion of Mercury and the Earth; for Mars there are not yet data to give a check. The predicted effects are well within the experimental error.

The second well-known test is the deflection of light in passing the sun, which shows itself as the difference between photographs of the star field taken when the sun is in its midst and those taken when the sun is elsewhere. The expected effect is 1.751 seconds of arc deflection for a ray which passes the sun at grazing incidence. Although there has been some disagreement among astronomers, the careful review of the evidence by McVittie leads to acceptance of Mitchell's result, based on the 1919, 1922, and 1929 eclipses, of 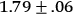seconds of arc, which value has since been confirmed by observations of the 1952 eclipse. The theoretical prediction is thus in agreement with the data.

The third observational test of general relativity, the gravitational red shift of spectral lines emitted on the surface of a massive star, presents insuperable difficulties in the case of the sun, owing to the fact that spectral shifts originating in atmospheric currents and turbulence completely mask the effect. On the other hand, white dwarf stars have mass to radius ratios large enough to make these Doppler effects negligible in comparison with the gravitational red shift. Observations are available on two stars, and are summarized in Table 3.2.

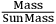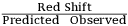40 Eri B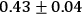
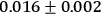Sirius B	1	0.008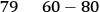

Tab. 3.2: Observed and Predicted Gravitational Red Shifts

It appears from these three traditional tests that general relativity is not in disagreement with the observations.

The chief possibilities of improvement exist in the second and third effects - that is, the bending of light and the gravitational red shift. We hope to hear from Professor Dicke later what prospects there are for new experiments. In particular, the development of the “atomic clock” may begin to make feasible detection of gravitational red shift on the earth itself.

To go on to the second general problem, namely, how to draw new richness out of the theory on the classical level: there is a far-reaching analogy between the equations of general relativity on the one hand and those of Maxwell's theory on the other; they are both second order partial differential equations, and the future can be predicted from the knowledge of initial conditions. From Maxwell's equations, which are quite simple, a wealth of information can be obtained: dielectric constants, scattering of waves, index of refraction, and so on; the equations of general relativity have, however, scarcely been explored, and much remains to be done with them. Another task ahead of us is the construction of the curve giving the spectrum of gravitational radiation incident on the earth, analogous to the known curve of the electromagnetic radiation spectrum; or at least the determination of upper limits on it. Until something is known about this, we can scarcely be said to know what we are talking about.

We can, however, go on to explore some of these analogies on a deeper level. First among the problems is the “initial value problem.” If I make a diagram similar to a shuffleboard court, with different squares corresponding to the various unsolved problems, and with scores attached to the various squares, we should assign a very high score - say 100 points - to this problem. We know that in electromagnetic theory, if and 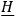are given at time 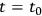, their values at later times can be predicted. However, they may not be specified arbitrarily on the initial time-like surface, but must obey certain conditions - namely the vanishing of their divergences. Through the work of Professor Lichnerowicz, 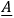we now know the analogous conditions in the case of relativity theory. They are non-linear conditions, rather than linear ones as in the Maxwell theory. Unfortunately, however, we do not know yet any “super-potentials,” analogous to in electromagnetic theory, which can be specified arbitrarily and whose derivatives give the field quantities while automatically satisfying the supplementary conditions. This is one of the most important problems of relativity theory, and one may well believe that it must be solved before further progress with quantization of the theory can be made. The further problem of the “time-symmetric” specification of initial conditions, which we know can be done in electromagnetic theory by specifying 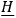on two time-like surfaces instead of specifying both and on one surface, and which is the appropriate form for quantization, is also yet to be solved in relativity theory.

Now this is a local condition; but boundary conditions in the large must be considered, especially when considering systems with closed topology - and to this problem we may assign a score of, say, 25.

A third problem is that of translating Mach's principle - that the distribution of matter in the universe should specify the inertial properties at any given point of space - into concrete, well defined form. We know from the work of Dr. Sciama that one can translate the differential equations of the Einstein theory into integral equations, and that one has an analogy between the solutions of the equations of static and radiative type, respectively, and the corresponding types of solutions of Maxwell's equations: namely, inverse square behavior of the static solutions, but inverse first power behavior at large distances, arising from the radiative terms. If one sums these interactions over all masses in the universe, one sees something of the connection between the inertia of one particle and the distribution of the rest of matter in space. This problem of spelling out Mach's principle in a better-defined way we may assign a score of, say, 25. It is of course related also to the problem of specification of conditions in the large, which we mentioned earlier; it is also related to another issue: that of uniqueness of solutions of the gravitational field equations, to which we may assign, say, 10 points.

To pass on from these issues, let us consider some further analogies with electromagnetic theory. We know that if we have in a given frame of reference a specified field, there exists another frame of reference moving with velocity

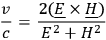
in which 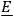and 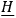have been reduced to parallelism. We then have a canonical situation in which, if we chose the 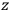-axis as the direction of 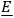and 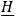, any rotation in the 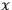- 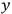plane leaves the situation unchanged, and any Lorentz transformation in the 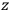- 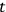plane also leaves the situation unchanged. Thus what Schouten has called a “two-bladed” structure of the space-time continuum at any point is defined by the electromagnetic field. This is then a geometrical interpretation of what we have to deal with in the electromagnetic case, and we would like to understand what the analogous situation is in the gravitational case. Here we have to deal with the quantities 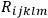that measure the curvature of space - geometrical quantities much more elaborate than the electromagnetic field tensor, of course. We would like to understand what kinds of invariance this quantity defines. We have the remarkable work of Géhéniau and Debever on this problem, but there are still issues to be defined in giving a clear understanding of what geometrical quantities are specified by the existence of the gravitational field. I would attach a score of, say, 15 to this problem of the geometrical interpretation of the gravitational field quantities.

This in turn leads us to another issue. Einstein has taught us to think in terms of closed continua, rather than the open continua such as Euclidean space; but since the differential equations are purely local and say nothing about the topology in the large, we are obliged to consider what the possibilities are. Recently we have become aware, for example, of one way of understanding, in terms of topological notions, such a concept as that of electric charge. Figure 3.1 below shows one intriguing kind of topological connectedness in the small.

If one thinks of the upper region 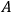as a two-dimensional space, there exists the possibility of connecting two regions 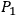and 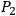by a “wormhole” 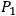so that for instance an ant coming to , would emerge at 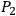without ever having left the two-dimensional surface on which he started out. Now ordinarily, if we have electric lines of force converging on some point in space, we think of two possibilities: either Maxwell's equations break down near the point, or there exists a mysterious entity called electric charge at the point. Now a third possibility emerges: the topology in the neighborhood of the point may be such as to give a space-like binding to the lines of force; they may enter the “wormhole” at 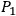and emerge at (see Fig. 3.2). Misner has shown, in fact, that the flux through such a “wormhole” is invariant, giving one a possibility of identifying this flux with the notion of charge. Actually, there are strong reasons why this cannot be identified with an elementary charge; our purpose is to classify and try to understand the topological possibilities of the classical theory. I would give this problem a rather high score, say 50 points.

An objection one hears raised against the general theory of relativity is that the equations are non-linear, and hence too difficult to correspond to reality. I would like to apply that argument to hydrodynamics - rivers cannot possibly flow in North America because the hydrodynamical equations are non-linear and hence much too difficult to correspond to nature! We need to explore the analogies between the gravitational and the hydrodynamic equations; are there gravitational counterparts of such hydrodynamic phenomena as shock waves, cavitation, and so on? A fairly high score, say 40 points, should be given to this problem of the physics of non-linear fields, and analogies with hydrodynamics.

The non-linear couplings between gravitation and electromagnetism also give rise to new structures such as “geons,” which should be studied further to enrich one's understanding on the physical side.

The last topic to be covered under the classical aspects of general relativity is the topic of unified field theory - namely, what can one find in the way of a description of electromagnetism which has the same purely geometrical character as that which Einstein gave to gravity? Although the various attempts to modify Einstein's theory in such a direction are well known, it does not seem to be so well known that within the framework of Einstein's theory one can construct, so to speak, an “already unified” theory, as Misner and earlier Rainich have shown, based on the role of the electromagnetic field as a source of the gravitational field through its stress-energy tensor.

The result is that one can write the equations of both electromagnetism and gravitation in a form in which only purely metric quantities enter, as in Einstein's theory. It is a system of fourth order equations which contain all the content of the two coupled second order equations of electromagnetism and gravity. Further investigation of theories of this kind deserve a score of, say, 25 points on our “shuffleboard” court.

In summarizing, let me remark that we have here, in the “already unified theory,” electromagnetism without electromagnetism, just as we have, in geons, “mass without mass,” and in connection with multiply connected topologies, “charge without charge.” This then is just one man's start at listing some of the problems with which we will be occupied in the coming days.