24 Divergences in Quantized General Relativity

The possible physical effects of general relativity on the elementary problem have usually been considered as negligible in view of the fact that energies at which the former might have a bearing are much too high. It is added that the effects of the new particles and the energies at which current theory loses its validity occur very much below this range and therefore a correct future theory will have solved the present difficulties in a much lower domain. In any case, field theory will have been altered so radically that arguments from the present one will lose their validity. Further, it is sometimes felt that general relativity is a purely macroscopic theory which loses its meaning in microscopic domains, where the concept of metric is not very transparent.

To these “classic” objections there exist several levels of replies. On a general level, it may be pointed out that the effect of a theory is not always first felt through its gross direct dynamical contributions (as, for example, spin). Since general relativity is needed, at least in a formal way, to provide a correct definition of the energy-momentum tensor, it underlies any theories which deal with the energies of fields and particles. The principle of general covariance on which the general theory is based is not in any way restricted a priori to macroscopic considerations and it is thus necessary to explore its consequences for any theory. The fact that the metric may not be so simply measurable in microscopic domains (say “within” an elementary particle) is no more an argument against the relevance of relativity than the definition of position measurement in a hydrogen atom is an argument against the use of coordinates in quantum mechanics. Finally, that a future correct theory will exclude the relevance of relativity is not an argument but a wish.

To these arguments of general principle, some very considerable quantitative ones can be added. The whole scheme of local field theory is plagued with divergences occurring because there is no upper limit to the energies involved in it. No satisfactory cutoff method is known which preserves the basic requirements of physical meaningfulness and there is no strong doubt that any can be found within a Lorentz-covariant framework. At this point general relativity may be invoked. Classical considerations show that for any kind of “matter” coupled to the metric field in the Einstein way, there are limitations to the energy densities and masses which can be concentrated or built up in a given region. Similarly, lower bounds exist on the sizes of wave-packets built up from linear wave equations.

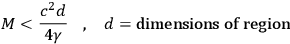
For a high frequency wave packet one has roughly

Therefore, the dimensions of the wave packet must be greater than the fundamental length ( 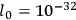cm). In all these investigations it appears that space-time loses its physically meaningful character beyond such limits. It is true that these limits always involve and are thus quite small, but they do occur at finite energies and their effects may well be felt sooner.

A still more significant point is the following. It is known that under very wide assumptions any theory of coupled fields leads, near the light cone, to singularities in the propagators of the “clothed” particles and to the existence of at least some infinite renormalization constants, independent of perturbation theory. All the known Lorentz-invariant field couplings are of this type, in particular electrodynamics and the renormalizable meson theories. It is just here that the coupling of the gravitational field differs so profoundly from the usual couplings between matter fields. First of all a basic condition for the proof of these theorems in flat space-time is that there exists an energy-momentum vector , and that the usual commutation relations hold for any operator.

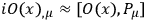
This is not the case in the general theory, and it is a very basic point there. In fact, a 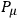can, as is well known, only be defined so as to be independent of any inner coordinates and therefore it cannot tell one the change of a quantity that is located somewhere in that region in question. It is connected with the non-linearity of the system and the lack of translational properties of parts of the system by themselves. One cannot simply fix the position of an arbitrary component of the total system, for this would clash with the energy density bounds mentioned above. Furthermore, matter and gravitational energies are not invariantly separable.

A second related departure from usual couplings is the form of the interaction terms. Contrary to normal field theory, there simply is no “free-particle” part of the matter Lagrangian. Here, the coupling enters in the kinetic energy, in a multiplicative fashion, and one cannot really disentangle a non-interacting particle here. This is rightly so, since the particle's mass and energy are defined precisely by the coupling. The equal time matter commutation relationships also would depend upon the positions in space-time involved. This fundamentally different mode of coupling will occur most critically at high energies and forbid any approximation from “free-particles.” In particular, each matter field by itself will no longer be represented by a linear wave equation in this domain. Free motion varies with the geometry of the space involved, which is in turn conditioned by the matter present which is doing the moving. Later, it will be seen that the arguments obtained in this investigation for convergence and non-singularity of propagators are based in good part on just this type of coupling, it may well be that a more adequate future theory of particles will incorporate some of these aspects of the non-linear gravitational coupling. Certainly, if it is a field theory, it must escape the pessimistic conclusions for the current theories by some such channel. If so, it may be all the more instructive to see how an improvement seems to emerge in this case.

Before one proceeds to further treat the extended theory, he must decide whether it is necessary to quantize the gravitational field. This will not be discussed here; and the Feynman method will be used, in which the question of which components of the gravitational field are to be quantized seems to be solved by itself. In any case, one need write down whatever physical quantities are of interest as functional integrals, which in principle go over only independent classical configurations of the system and yield the quantum result.

This method will be used to determine the behavior of the matter fields as modified by gravitational interactions. It may be expected, roughly, that the contributions of the “scalar” and “transverse” parts of the gravitational field, though not really separable will limit the density of matter in a given region for the former, while for the latter will “smear out the light cone.” This phrase refers to the expectation that the summation over all possible Riemann spaces (corresponding to the various transverse modes) will average away the uniqueness of the Minkowski light cone, and with it the singularities of the matter propagators of such a cone.

The effects of gravitation on propagators of various matter fields will now be considered. Rigorously one should treat, for example, the Feynman function for an electron interacting with the electromagnetic and metric fields. However as is known, in ordinary electrodynamics in flat space the behavior of this propagator cannot be less singular on the light cone than the free one, .

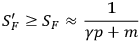
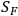is already singular enough to give the infinite renormalization 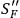constants of electrodynamics. Therefore, if one can show that , the propagator of the electron modified by gravitation alone, behaves better than 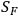, this is a step in the right direction and is an indication that the three-field problem will stay good. This is due to the fact that the three-field interaction energy, which has been omitted, presumably would not make things worse. If one gets promising results here then the whole problem should be investigated. Alternately, the use of electrons and photons “clothed” by gravitation as the “non-interacting” elements of quantum electrodynamics seems to be a very good approximation to the total problem. If one calls the functions the matter field functions corrected only for the gravitational field, and if 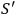reduces to 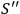this is all right. It may also be expected that many-particle propagators will behave, if anything, better than the one-particle ones since there will be a bias against too close approach. Gravitational field propagators themselves should also behave non-singularly, i.e., the Schwarzschild type of singularities should vanish (the matter now being “regularly” spread) while the “transverse” propagation should also be free of singularity, just as the photon Green's function is expected to be. Also, it seems that the question of renormalization of gravitational coupling should never appear since the mass, , plays the double role of “charge” and mass, and the two renormalizations, if any, must be equal. 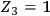Now, since all “charges” are positive, we expect no vacuum polarization, , and 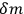should also be zero in view of the absolute definition of mass and energy levels in the gravitational theory, and of the fact that the mass is defined automatically from the gravitational coupling.

From the above arguments it would appear that the simplest case of a scalar field coupled to the metric is a sufficient example to consider. In the usual field theory the vacuum expectation value

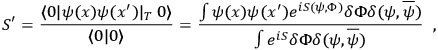
where 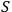is the total action and the integration is over the meson, electron, and positron fields. The action,

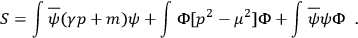
Now, one can eliminate the electron field and the vacuum expectation value becomes equal to

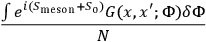
where is due to the pure meson field and 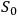is due to closed loops. The Green's function 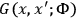satisfies 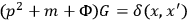, if we replace the spinors 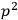by to simplify the calculation. Now one knows how 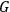behaves near the light cone.

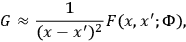
where 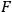is a well behaved function (aside from possible “harmless” logarithmic terms). Thus one finds, near the light cone, that varies essentially as . This, propagation function, 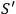, is singular enough to give one divergences.

Now consider the parallel problem when a matter field is interacting with the gravitational field. The Lagrangian is

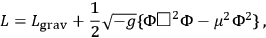
where the D'Alembertian depends upon the metric. The mass term will, as usual, not be relevant to the singularity questions. One wants to compute

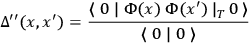
where and are to be defined with respect to a flat background frame which is used to make a classical measurement. The functional integration used to define 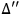is

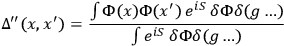
where 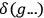means a summation over all Riemann spaces which preserve the signature of . Now, as before, the matter variables are eliminated giving

where

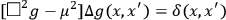
and 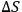comes from integration over matter variables. One is interested only in the solution for two points which are on each other's light cones. Again, the general theory of differential equations tells one that near the light cone

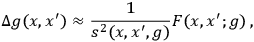
where 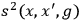is the square of the interval between the two points and 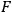is a regular function. Here the difference between these propagators and the usual ones of field theory is obvious since the 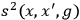depends upon the variables. Now,

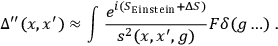
At this point the more or less rigorous mathematical treatment stops and things that are said cannot be proved mathematically.

There will be “very few” spaces where null geodesics will connect 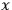and 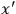in comparison to the number of integrations possible. It is possible to make a vague analogy to the usual theory of poles in a finite number of dimensions and in such cases one expects the singularities to be smoothed out - with any “measure” which makes sense. For large distances, on the other hand, the exponential may be expected to vary wildly and thus cancel the effects of the various spaces summed over. It is felt that one should not make the linear approximation in the action since this will reinstate the privileged character of the Minkowski metric and the whole point of non-linear gravitation is that the propagator depends upon the space one is in.

A corroborative argument from quite a different direction, which was mentioned earlier, is the 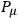commutation relation. In a flat space-time, and effectively (by suitable modification) in a non-flat but externally given geometry this commutation rule holds. determines the translation of the system as a whole and, because of superposition, of any part of it. In a space-time which interacts with matter, however, this relation no longer holds. 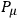does have as a canonical conjugate the center of mass, 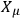, of the system with respect to the flat external frame. However, it cannot be used to locate closely any component of the system. The existence of a in Minkowski space-time is essential to the pessimistic theorems mentioned before. It is obvious that if P does not have all the properties required there, the proof that any component field, if sufficiently focused on, acts as if it is uncoupled, loses support. It may be argued that the propagators, 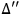, mentioned above, also lose some of their meaning by the same argument. This is true only to the extent that physical quantities always involve space-time integrals of such functions. The fact that the 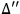are now non-singular is merely due to the fact that one can never force a field to behave as if it is too concentrated - the induced geometry would force a repulsion.

If it is granted that this action introduces an effective cutoff, at about 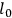, then such high energy approximations as Landau's could be examined again. As Landau has noted, using 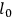as a cutoff, theory predicts roughly the experimental charge regardless of the value of the bare charge and similarly for the mass. Of course, our results, being generally covariant, cannot be directly translated into flat spacetime language without apparent paradoxes.

One thing that should be done is to look into the vacuum expectation value of the total energy-momentum of the system since this should be zero in general relativity due to the absolute definition of energies; similarly, should be nowhere singular.

In the discussion which followed DESER's 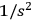presentation, LICHNEROWICZ and FOURES commented on the need for an exact definition of the measure. ANDERSON suggested that the integration difficulties might be circumvented by first solving the classical problem of motion of two matter fields. Then, one can eliminate the non-physical variables from the action. WHEELER first brought up the point that the fluctuation of the metric at very small distances, which brings about change in the topology of the space, may make a flat space-time unusable, even as a first approximation. In reference to the work he previously discussed, the use of a matter propagator as a starting point is foreign to that point of view. Also, the whole nature of quantum mechanics may be different in general relativity since in every other part of quantum theory, the space in which physics is going on is thought of as being divorced from the physics. General relativity, however, includes the space as an integral part of the physics and it is impossible to get outside of space to observe the physics. Another important thought is that the concept of eigenstates of the total energy is meaningless for a closed universe. However, there exists the proposal that there is one “universal wave function.” This function has already been discussed by Everett, and it might be easier to look for this “universal wave function” than to look for all the propagators. FEYNMAN said that the concept of a “universal wave function” has serious conceptual difficulties. This is so since this function must contain amplitudes for all possible worlds depending on all quantum-mechanical possibilities in the past and thus one is forced to believe in the equal reality of an infinity of possible worlds. The following argument was proposed to challenge the conclusions of Deser. If one started to compute the mass correction to, say, an electron, one has two propagators multiplying one another each of which goes as and are singular for any value of the 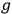's. Therefore, do the spatial integrations first for a fixed value of the 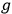's and the propagator is singular, giving . Then the superposition of various values of the 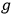's is still infinite. DESER replied that this is partly due to an unallowed interchange of limits.

A resolution was passed at this conference to the effect that there is to be another gravitational conference in Europe during the summer of 1958.

ERNST reported on a paper on Corinaldesi¹ Here, higher order terms are obtained through a quantum treatment of the linearized theory.

Footnotes