This is a survey of the main results on the integration of the Einstein equations and the problems which remain open.
5.1 The Space-Time Manifold
In any relativistic theory of the gravitational field, the main element is a differentiable manifold of four dimensions, the space-time
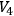 . To be precise: I assume that this differentiable structure is “
. To be precise: I assume that this differentiable structure is “
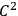 , piecewise
, piecewise
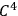 .” This means that in the intersection of the domains of two admissible systems of local coordinates the local coordinates of a point for one system are functions of class
.” This means that in the intersection of the domains of two admissible systems of local coordinates the local coordinates of a point for one system are functions of class
 , i.e., possess continuous derivatives up to second order, with non-vanishing Jacobian, of the coordinates of the point in the other system. Third and fourth derivatives also exist, but are only piecewise continuous.
, i.e., possess continuous derivatives up to second order, with non-vanishing Jacobian, of the coordinates of the point in the other system. Third and fourth derivatives also exist, but are only piecewise continuous.
On
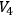 we have a hyperbolic normal Riemannian metric
we have a hyperbolic normal Riemannian metric
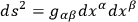
|
5.1 |
which is everywhere “
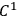 , piecewise
, piecewise
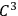 .” This metric is said to be regular on
.” This metric is said to be regular on
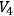 . Note that the manifolds which admit hyperbolic metrics are precisely those on which there exist vector fields without zeros. Such a manifold admits global systems of time-like curves, but generally does not admit global systems of space-like hypersurfaces.
. Note that the manifolds which admit hyperbolic metrics are precisely those on which there exist vector fields without zeros. Such a manifold admits global systems of time-like curves, but generally does not admit global systems of space-like hypersurfaces.
We suppose that no further specification of the differentiable structure of the manifold or of the metric has any physical meaning.
For the study of global problems assumptions belonging to the differential geometry in the large are often needed. Frequently
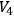 is identified with a topological product
is identified with a topological product
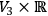 ,
,
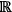 being the real numbers, where straight lines are time-like curves and thus trajectories of a unitary vector field
being the real numbers, where straight lines are time-like curves and thus trajectories of a unitary vector field
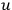 . The space sections defined by
. The space sections defined by
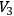 are then generally either closed manifolds or complete Riemannian manifolds for the metric defined on them by
are then generally either closed manifolds or complete Riemannian manifolds for the metric defined on them by
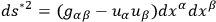
|
5.2 |
moreover, in this case
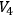 admits a Minkowskian asymptotic behavior at infinity.
admits a Minkowskian asymptotic behavior at infinity.
The problem whether these assumptions are necessary or sufficient is open.
5.2 The Cauchy Problem for the Gravitational Field
In general relativity the metric
 satisfies the Einstein equations:
satisfies the Einstein equations:

|
5.3 |
where the energy-momentum tensor
 is piecewise continuous. It defines the sources of the field. In the regions where
is piecewise continuous. It defines the sources of the field. In the regions where
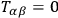 we have the “exterior case.”
we have the “exterior case.”
Let
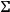 be a local hypersurface of
be a local hypersurface of
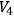 which is not tangent to the cones
which is not tangent to the cones
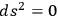 . If
. If
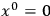 defines
defines
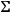 locally, we have
locally, we have
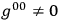 . The Einstein equations can then be written as1
. The Einstein equations can then be written as1
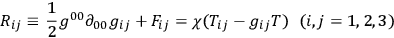
|
5.4 |

|
5.5 |
where
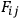 and
and
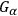 are known functions on
are known functions on
 if we know the values of the potentials
if we know the values of the potentials
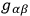 and their first derivatives (“Cauchy
and their first derivatives (“Cauchy
Eq.(5.5) links the Cauchy data to the sources. Eq.(5.4) gives the values on
 of the six second derivatives
of the six second derivatives
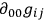 which I have called the significant derivatives. The four derivatives remain unknown and may be discontinuous at
which I have called the significant derivatives. The four derivatives remain unknown and may be discontinuous at
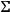 . But, according to our differentiable structure, these discontinuities have no physical or geometrical meaning. We grasp here the connection between the covariance of the formalism and the assumptions on the structure.
. But, according to our differentiable structure, these discontinuities have no physical or geometrical meaning. We grasp here the connection between the covariance of the formalism and the assumptions on the structure.
From Eq.(5.4) one sees that the significant derivatives for
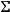 can have discontinuities only if
can have discontinuities only if
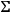 is tangent to the fundamental cones, or if the energy-momentum tensor is discontinuous at
is tangent to the fundamental cones, or if the energy-momentum tensor is discontinuous at
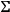 . Gravitational waves
. Gravitational waves 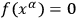 , tangent to the fundamental cone, i.e., such that
, tangent to the fundamental cone, i.e., such that

|
5.6 |
(WHEELER , or as the singular geodesics of the metric.
, or as the singular geodesics of the metric.
In the hydrodynamic interior case the exceptional hypersurfaces are (1) the gravitational waves,
5.3 Local Solutions for the Exterior Case
In the exterior case,
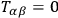 , the system of Einstein equations has the involution property:
, the system of Einstein equations has the involution property: 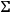 only, the equations
only, the equations
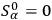 , then it satisfies these equations also outside of
, then it satisfies these equations also outside of
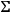 . This is a trivial consequence of the conservation identities. Thus, for a space-like hypersurface the Cauchy
. This is a trivial consequence of the conservation identities. Thus, for a space-like hypersurface the Cauchy
1The search for Cauchy data satisfying the system
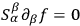 on
on
 . This is the problem of the initial values.
. This is the problem of the initial values.
2The evolutionary problem of integrating Eq.(5.4) subject to these Cauchy data.
Assuming only differentiability, Mme. Fourès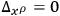 ) and thus proves the local existence and physical uniqueness theorem for the solution of the Cauchy
) and thus proves the local existence and physical uniqueness theorem for the solution of the Cauchy 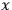 plays the essential part, and it is clear that the values of the solution in
plays the essential part, and it is clear that the values of the solution in
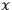 depend only on the values of the Cauchy data in the part of
depend only on the values of the Cauchy data in the part of
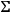 interior to the characteristic conoid. We obtain thus all the results of a classical wave propagation theory.
interior to the characteristic conoid. We obtain thus all the results of a classical wave propagation theory.
5.4 The Problem of the Initial Values
This, most interesting, problem is simple if
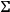 is a minimal hypersurface. If
is a minimal hypersurface. If

|
5.7 |
we take
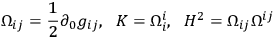
|
5.8 |
and we obtain for the exterior case
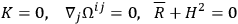
|
5.9 |
where
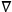 is the operator of covariant differentiation, and
is the operator of covariant differentiation, and
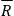 the scalar curvature of
the scalar curvature of
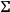 . If we set
. If we set
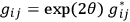
|
5.10 |
where we assume the metric
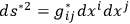 to be known on
to be known on
 , then it is possible to introduce the functions
, then it is possible to introduce the functions

|
5.11 |
For these functions a very simple system of equations holds:
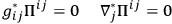
|
5.12 |
and the elliptic equation:

|
5.13 |
The Dirichlet problem 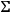 is sufficiently small or if
is sufficiently small or if
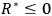 and if
and if
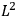 is sufficiently small. This study can be extended to some hydrodynamic interior cases, and it is thus possible to construct examples of Cauchy data corresponding to the motion of
is sufficiently small. This study can be extended to some hydrodynamic interior cases, and it is thus possible to construct examples of Cauchy data corresponding to the motion of
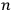 bodies. For the two-body problem, Newton’s law is obtained approximately.
bodies. For the two-body problem, Newton’s law is obtained approximately.
Recently Mme. Fourès
It would be important to obtain new global theorems for this problem, currently perhaps the most important problem of the theory.
5.5 The Cauchy Problem for the Asymmetric Theory
The Cauchy
On the differentiable manifold
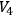 we have:
we have:
1An asymmetric tensor field
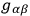 of class “
of class “
 , piecewise
, piecewise
 ,” with a non-vanishing determinant
,” with a non-vanishing determinant
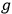 , the associated quadratic form defined by
, the associated quadratic form defined by
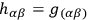 being hyperbolic normal.
being hyperbolic normal.
2An affine connection of class “
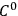 , piecewise
, piecewise
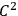 ;”
;”
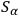 is the torsion vector of the connection.
is the torsion vector of the connection.
If we substitute into this connection the connection
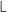 without torsion vector, which admits the same parallelism, the field equations deduced from the classical variational principle
without torsion vector, which admits the same parallelism, the field equations deduced from the classical variational principle  from
from
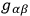 and the first derivatives of the tensor. The field is now defined by
and the first derivatives of the tensor. The field is now defined by
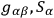 which satisfy the equations
which satisfy the equations
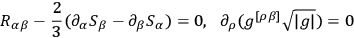
|
5.14 |
where
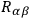 is the Ricci tensor of
is the Ricci tensor of
 . In addition we have a normalization condition for
. In addition we have a normalization condition for
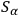 :
:
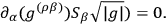
|
5.15 |
The Cauchy
• (a): If
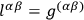 we have the cone
we have the cone
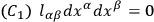
|
5.16 |
where
 is dual to
is dual to
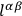 .
.
• (b): If
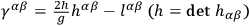 we have the cone
we have the cone
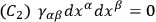
|
5.17 |
where
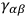 is dual to
is dual to
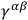 .
.
If the skewsymmetric part of
 is small compared to the symmetric part, then
is small compared to the symmetric part, then
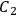 contains
contains
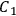 .
.
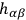 itself has no wave properties in the unified field theory.
itself has no wave properties in the unified field theory.
The evolutionary problem of the asymmetric theory remains unsolved.
5.6 Global Solutions and Universes
I now return to general relativity. The main question of the theory is the following: When is a gravitation problem effectively solved?
A model of the universe - or shortly, “a universe” - is a
 with a regular metric satisfying the Einstein equations and certain asymptotic conditions. When
with a regular metric satisfying the Einstein equations and certain asymptotic conditions. When
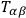 is discontinuous through a hypersurface
is discontinuous through a hypersurface
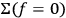 we assume that
we assume that
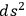 is always “
is always “
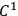 , piecewise
, piecewise
 ” in the neighborhood of
” in the neighborhood of
 . The joining of the different interior material fields with the same field causes the interdependence of the motions, and the classical equations of motion are due to the continuity through
. The joining of the different interior material fields with the same field causes the interdependence of the motions, and the classical equations of motion are due to the continuity through
 of the four quantities
of the four quantities
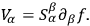
|
5.18 |
In this view the main problem is to construct and study universes. This being a hyperbolic non-linear global problem, it is very difficult to do this. Clearly global solutions of the problem of the initial values would be very helpful here.
Another approach might be the study of some elementary global solutions of the Einstein equations. It appears that such solutions are connected with the solutions with singularities introduced by various authors.
5.7 Global Problems
This view of the universe leads us to the following question: Is it possible to introduce in a universe new energy distributions, the interior fields of which are consistent with the exterior field of the universe? Furthermore, if a universe model is defined by a purely exterior field, regular everywhere, is the universe empty and thus locally flat?
The regularity problem is the study of the exterior fields regular everywhere under some general topological or geometrical assumptions. Good results are known only in the stationary case. We assume
 , and we use the explicit assumptions made at the beginning of this survey. Then we have the following results:
, and we use the explicit assumptions made at the beginning of this survey. Then we have the following results:
An exterior stationary field which is regular everywhere is locally flat
(a) if
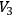 is compact, or
is compact, or
(b) if
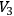 is complete and has a Minkowskian asymptotic behavior.
is complete and has a Minkowskian asymptotic behavior.
In a stationary universe the exterior field extended through continuity of the second derivative into the interior of the bodies is singular in the interior.
A stationary universe which admits a domain surrounding infinity and which in this domain has a Minkowskian asymptotic behavior and for which the streamlines are time lines, is static. There exist space sections orthogonal to the time lines.
This is of interest in the Schwarzschild
Much less is known in the non-stationary case, which is of course more interesting. Concerning the regularity problem,
However, the results on the problem of the initial values give new theorems under the following assumptions:
It is possible to diagonalize the matrix
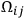 which defines the second fundamental quadratic form of
which defines the second fundamental quadratic form of
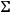 and there exist foliations of
and there exist foliations of
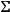 by the corresponding system of curves, that is to say by curvature lines.
by the corresponding system of curves, that is to say by curvature lines.
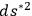 has a flat asymptotic behavior.
has a flat asymptotic behavior.
The tensor
 has a summable square on
has a summable square on
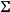 .
.
If these assumptions are satisfied on
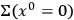 and also on the sections corresponding to arbitrarily small
and also on the sections corresponding to arbitrarily small
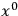 , the universe is static and thus locally flat.
, the universe is static and thus locally flat.
***
MISNER
“This comes about because, according to work of
“We have studied a certain class of solutions to the problem of initial values. These solutions are global but by no means the most general. They serve as examples. These solutions are always continuous and instantaneously static. We find that there exist exact solutions of the Einstein-Maxwell equations for which the fields on a certain surface
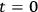 are given by:
are given by:

|
5.19 |
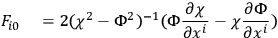
|
5.20 |
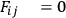
|
5.21 |
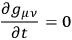
|
5.22 |
where
 satisfy
satisfy
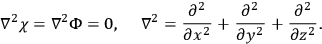
|
5.23 |
This metric together with the electric field
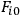 gives a solution of the initial value equations. In the neighborhood of the surface
gives a solution of the initial value equations. In the neighborhood of the surface
 we have a solution of the time-dependent equation but do not know what it is. Perhaps one should use a high speed computing machine.
we have a solution of the time-dependent equation but do not know what it is. Perhaps one should use a high speed computing machine. 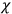 and
and
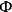 can only have the form:
can only have the form:
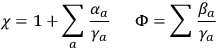
|
5.24 |
where
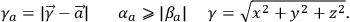
|
5.25 |
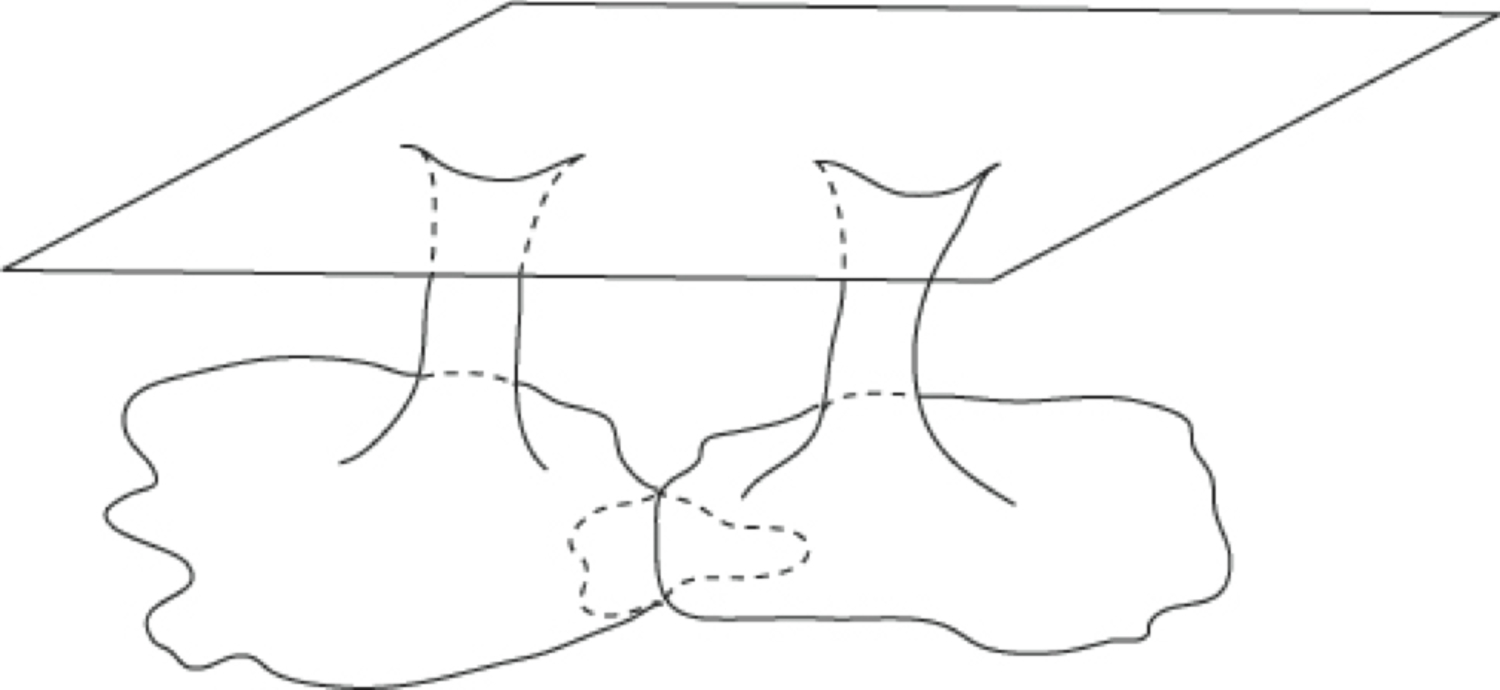
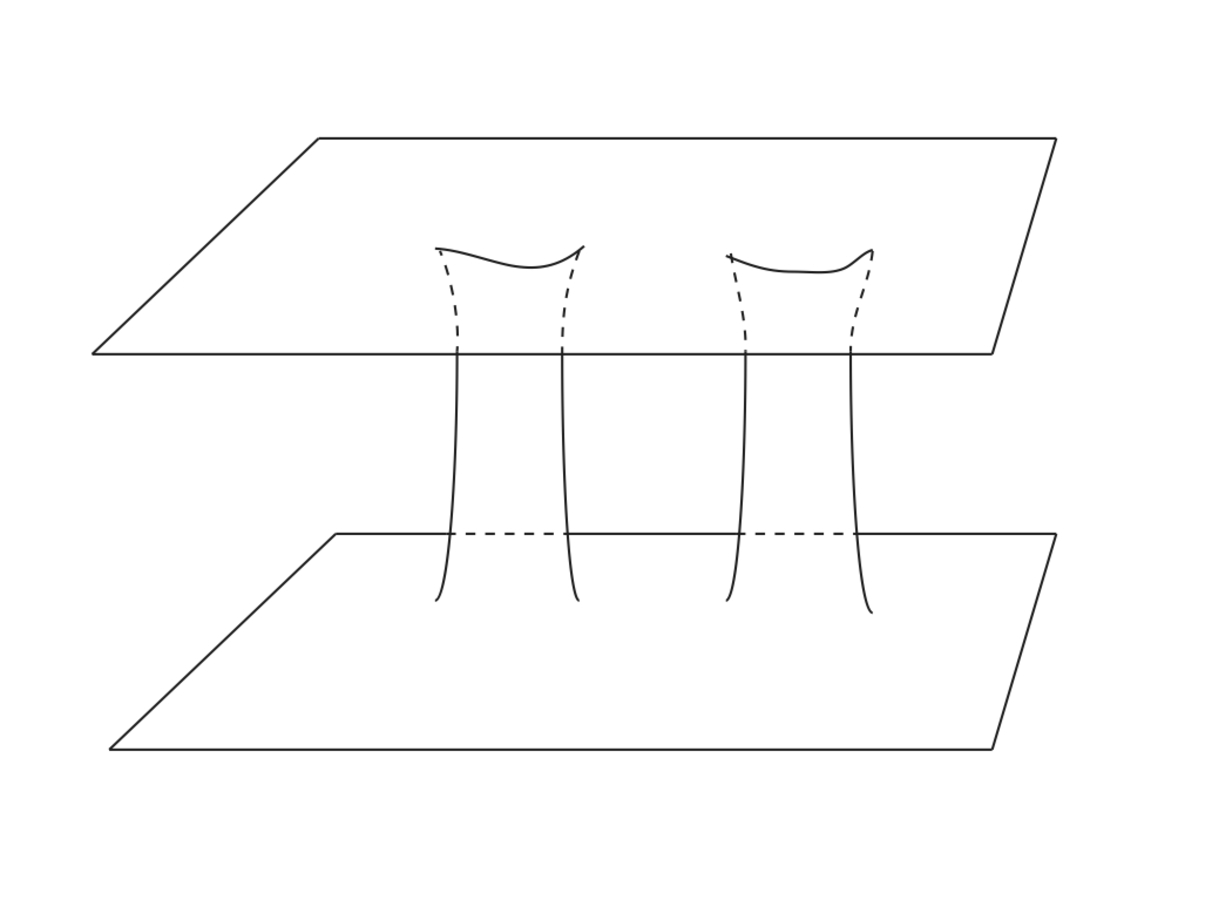
These functions appear to contain singularities, but they really do not. This brings us into the study of the topology of this situation. The point at which the metric seems to become singular can be thrown away. This is consistent with the requirement of completeness, but would not be consistent if the point which is thrown away were one at which the metric did not become singular. A picture can be drawn to indicate what the space so obtained looks like. Near the point
 the space, which is flat further away, curves and flares out and goes over into another roughly flat portion like this:
the space, which is flat further away, curves and flares out and goes over into another roughly flat portion like this:
We have here as many regions where the space is asymptotically flat as we have particles. The next problem is to put these portions together. One should then try to construct the initial values which would give rise to the wormhole
“One additional advantage of the solutions exhibited here over introducing point singularities into the theory is that by using Lichnerowicz’s regularity conditions you eliminate automatically all negative masses, mass dipoles and higher multipoles. It also, unfortunately, implies that for any particle or cluster of particles described by these deformities the total charge and mass have a ratio
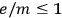 , while for an electron in these units, where
, while for an electron in these units, where
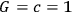 ,
,
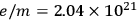 . The reason for this too large mass, for a given electron charge, is that you don’t have enough of a cut-off for the electromagnetic mass. Perhaps one might hope that quantum mechanics might help here. In any event, we have here strong indications that the Einstein-Maxwell theory is a good model for a unified field theory.
. The reason for this too large mass, for a given electron charge, is that you don’t have enough of a cut-off for the electromagnetic mass. Perhaps one might hope that quantum mechanics might help here. In any event, we have here strong indications that the Einstein-Maxwell theory is a good model for a unified field theory.
In the discussion, PIRANI
BERGMANN
DE WITT
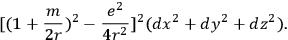
|
5.26 |
MlSNER then added some remarks on global solutions.


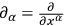 ,
,
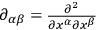 .
.