20 The Three-Field Problem

F. J. BELINFANTE 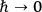opened with an examination of the three-field problem: gravitational and electromagnetic fields plus the Dirac electron field. He considered first the “classical” theory, defined by him as the limit of the quantum theory as so that gravitational and electromagnetic fields commute and spinor fields purely anticommute. The notational developments which he then proceeded to outline go something like this:

He defines a “modernized” Poisson bracket with 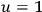for Fermi-Dirac fields and 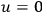for Bose-Einstein fields. He also distinguishes 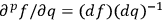and 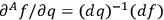, which is a refinement necessitated by factor ordering difficulties.

He then uses vierbeine 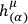to describe the gravitational field, and introduces local 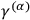components independent of 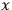for the spinor fields so that

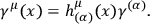
The canonical formalism can be developed following the method of Dirac¹ There are 11 first-class primary constraints 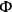, , 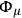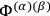arising from gauge, coordinate, and vierbein-rotational invariance of the theory, which lead to five first-class secondary constraints 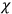, 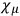. In addition there are eight second-class constraints

arising from redundancy in the variables used to describe the spinor field.

One finds

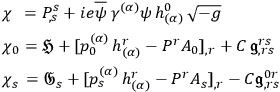
where 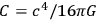, and is canonically conjugate to 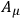, while 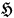with is integrated over space to give the energy-momentum (free-) fourvector, if one assumes vanishing fields and flat space-time at infinity.

In passing to the quantum theory one makes use of the modified Poisson bracket due to Dirac, which is defined by

with

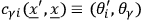
and

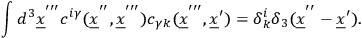
One sets

The dynamical equations then become

where the symbol 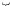means place the 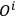factor where 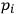is taken out. The 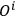factor is given by

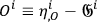
where the .

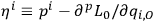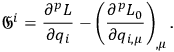
Also

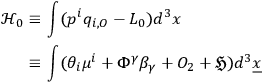
the 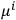and 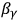being certain coefficients and 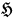a function of the 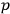’s, ’s, and their space derivatives only. 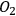is quadratic in the . The constraint expressions and 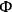here are meant as functions of the and 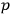and therefore are expressions in the 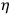partially linear in them. (Note that the constraints are identities when expressed in terms of and 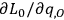, but through the 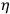vanish only weakly when expressed in the and 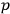as we do.) If one works only with modified Poisson brackets the 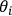may be set to zero, and then

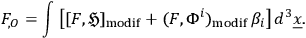
Kennedy has verified the consistency of this scheme by direct computation of the modified Poisson brackets 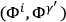, , 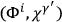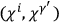. They all reduce to linear combinations of the 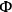’s and ’s alone.

The modified Poisson brackets for the spinor variables lead to some unwanted peculiarities which can be removed by redefining the spinor variables according to

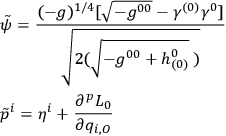
One then finds

Thence, modified Poisson brackets defined by partial derivatives with respect to 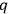and 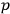equal ordinary (though modernized) Poisson brackets defined by partial derivatives with respect to 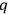and 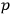. Thus working with 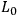in terms of the 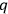and from the beginning makes it possible to quantize without ever mentioning modified Poisson brackets.

BELINFANTE pointed out that in its present form his theory seems to be incovariant. This is related to the fact that the do not vanish in the strict sense. (They only vanish “weakly,” in Dirac’s terminology.) However he proposed simply to bypass this problem for the time being, and, for the sake of being able to make practical computations, pass over to what he calls a “muddified theory,” i.e., a theory obtained by throwing in “mud.” In electrodynamics this is just Fermi’s procedure of adding a non-gauge invariant quantity to the Lagrangian. The first-class constraints then disappear and one must replace them by auxiliary conditions (e.g. the Lorentz condition). There is a certain arbitrariness here, since the forms of the auxiliary conditions depend on the precise form of the “mud” which has been thrown in. 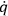However, if the ’s are replaced by their expressions in terms of the 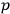’s then the auxiliary conditions must reduce to the original constraints. BELINFANTE has made certain special choices for these conditions (e.g., De Donder condition), based on convenience, and he hopes he can then do meaningful practical calculations, just as the Fermi theory was long used for practical calculations in electrodynamics before all the mathematical subtleties of various constraints were precisely understood. BELINFANTE has shown by explicit computation that the constraints of his “muddified” theory are conserved, and has calculated explicitly the .

With the “muddified” theory 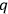the commutation relations are covariant. However, the equations of motion are no longer covariant. This means that the ’s and 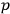’s at time will depend not only on the ’s and 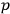’s at a time 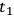, but also on the coordinate system chosen to link 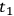and . On the other hand, differences in results of going from 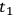to are merely accumulated mud; so, if a “true” theory is later developed in which the mud can be made identically zero by altering the commutation relations as proposed by Bergmann and Goldberg, the covariance will be restored. (In the muddified theory, covariance will exist “weakly” unless the positions of the weakly vanishing factors in products due to noncommutativities would cause troubles.)

One can introduce annihilation and creation operators (for photons, gravitons, etc.), although the Fourier transformation procedure on which they are based is a non-covariant procedure.

BELINFANTE has gone on to see if he can find the unitary transformations which will separate the gravitational and electromagnetic fields into their so-called “true” and “untrue” parts (e.g., transverse and longitudinal parts). This is rather difficult, particularly when spinor fields are present. But there is also a more serious problem, connected with the -constraints (above). “True observables” have been defined by Bergmann and Goldberg as those which commute with the first-class constraints as well as with the canonical conjugates to the first-class constraints. BELINFANTE prefers to call them true “variables.” If the constraints are only linear in the momenta it is not difficult to find the “true variables.” However, the constraint involves the quantity 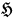which is quadratic in the momenta, being essentially the energy density of the combined fields. This means that the only “true variables” which will be easy to find are the constants of the motion. (Since differs from 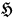by a divergence one might at first sight conclude, by integrating 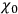over all space, that the total energy must always be zero. However, the surface integrals cannot be ignored here – Ed.)

BELINFANTE concluded by suggesting that a theory in which only “true variables” appear may be mathematically nice but somewhat impractical. From the point of view of a scattering calculation, for example, there may be some truth even in an almost true “untrue variable.” In any event the “true” theory still eludes us at present.

Following BELINFANTE’s remarks, there was considerable discussion as to whether or not all true observables are necessarily constants of the motion in a generally covariant theory. No progress was made on this question, however, and the answer is still up in the air as of this moment.

NEWMAN next reported on some work he has been doing to try to obtain the true observables by an approximation procedure. Instead of dealing directly with the gravitational field he considered a “particle” Lagrangian of the form

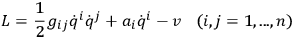
for which the equations of motion are nonlinear but invariant under a transformation group analogous to the gauge group of electrodynamics or the coordinate transformation group of general relativity. The gravitational field is embraced by this example when becomes transfinite. In a linear theory the true observables are easy to find. In NEWMAN’s approximation procedure the search for the next higher order terms (with respect to some expansion parameter) in the true observables is no worse than finding the exact expression in the linear case, and can actually be carried out, even when some of the constraints are quadratic in the momenta. In the case of the gravitational field the true observables evidently become more and more nonlocal (i.e., involving higher order multiple integrals) at each higher level of approximation. NEWMAN could say nothing about the convergence of his expansion procedure.

BERGMANN remarked that NEWMAN’s procedure was quite different from the more common differential-geometric approach which is specifically tailored to the gravitational case. He mentioned in this connection the work of Komar and Géhéniau on metric invariants constructed out of the curvature tensor. It is thought that these invariants have some close connection with the “true observables.”

MISNER advocated at this point that one simply forget about the true observables, at least as far as quantization is concerned. He suggested starting with a metricless, field-less space, defined simply in terms of quadruples of real numbers, then performing certain formal mathematical operations and finding the true observables later, if one desires them.

SCHILLER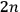 outlined still another way of looking at the problem of finding the true observables: The field equations of Einstein are not of the Cauchy-Kowalewski type. That is, the metric field variables and their time derivatives cannot all be specified on an initial space-like surface. However, Einstein’s equations can be replaced by a Cauchy-Kowalewski set provided one imposes coordinate conditions. A standard canonical formalism can then be set up in which the coordinates and momenta are expressed as functions of constants of the motion 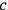and the time ( 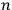is transfinite). In the canonical formalism the coordinate conditions take the form 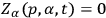for certain functions . These three sets of equations can then (in principle) be solved to eliminate some of the constants from the theory. The remaining constants, when, reexpressed as functions of the 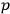’s, 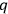’s and 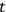, will be the true observables. This, of course, assumes that the true observables are constants of the motion.

WHEELER remarked that all of these discussions lead to the conclusion that the problems we face are problems of the classical theory.

BERGMANN agreed, and expressed his conviction that once the classical problems are solved, quantization would be a “walk.”

WHEELER, however, still felt that in the Feynman quantization procedure the whole problem is already solved in advance.

GOLDBERG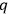 and ANDERSON concluded the afternoon session with a discussion of “Schwinger quantization,” that is, the procedure which uses a -number Lagrangian as a starting point. In making variations of such a Lagrangian one must pay careful attention to the ordering of factors.

GOLDBERG outlined a problem of trying to find the unitary operators which generate various invariant transformations, within the subspace defined by the constraints.

ANDERSON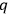 pointed out some difficulties, connected with the factor ordering problem, of defining a unique -number Lagrangian.

BELINFANTE suggested that, if an interaction representation could be found, at least some of the factor ordering problems might be avoided with the use of “Wick brackets” which reorder the annihilation and creation operators, even though these brackets, being defined with respect to a flat space, would have no generally covariant significance.

Footnotes