9.1 Static Cylinder
The general external solution may be reduced to
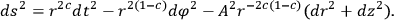
|
9.1 |
This is equivalent to Wilson’s result (1920), who finds
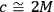 by considerations of geodesic motion.
by considerations of geodesic motion.
Consider solutions inside the cylinder (radius
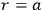 ) corresponding to metrics of the type (not the most general)
) corresponding to metrics of the type (not the most general)
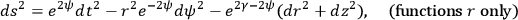
|
9.2 |
of which (9.1) is a particular case.
Suppose we take
 ,
,
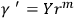 , where
, where
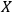 and
and
 are constants determined by boundary conditions. Field equations give
are constants determined by boundary conditions. Field equations give
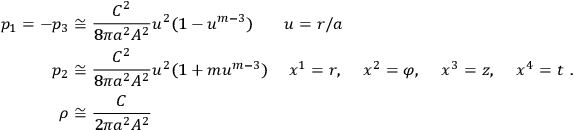
|
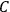 is small (
is small (
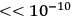 , say) since
, say) since
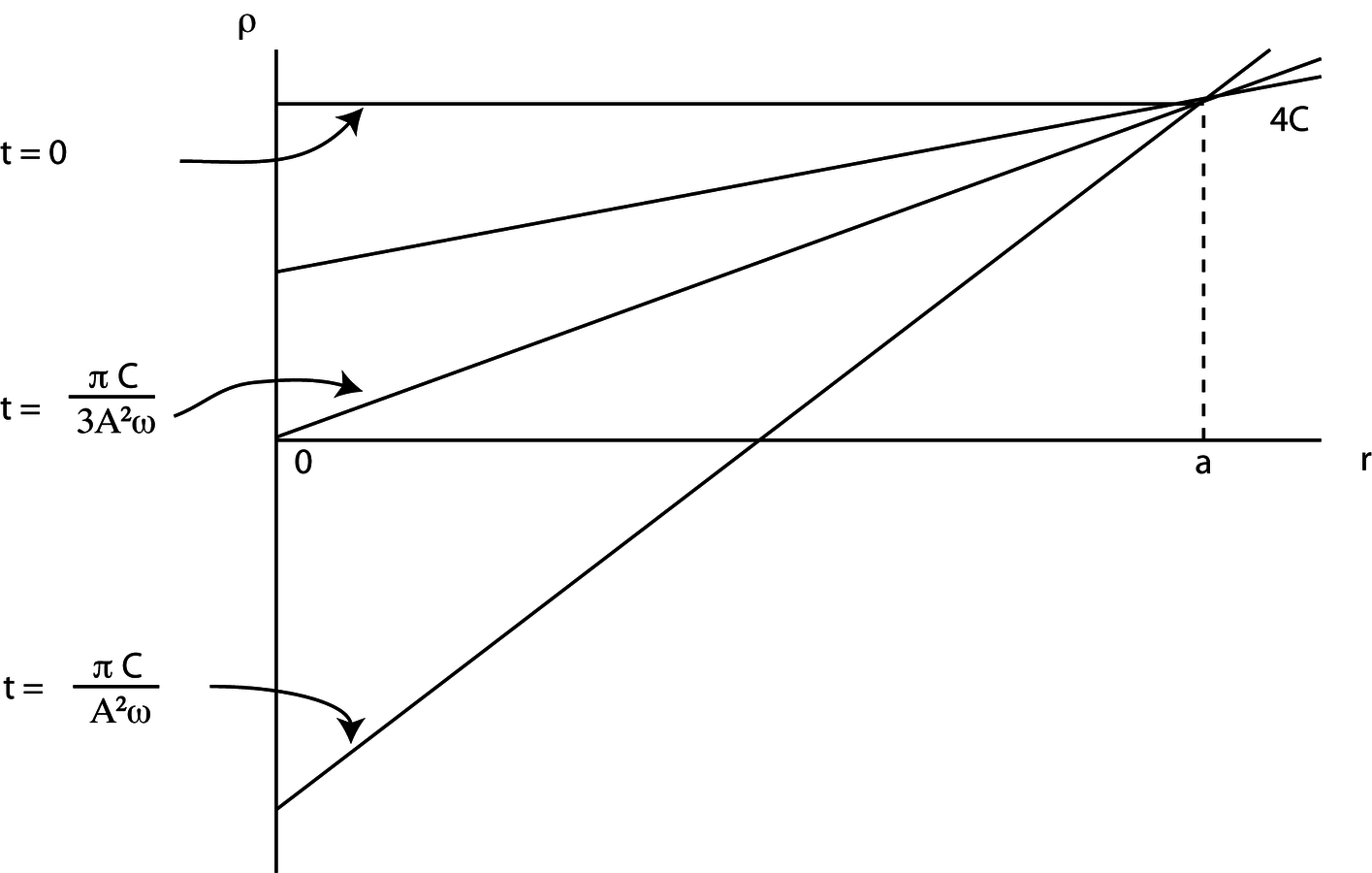
 . Pressures are therefore small compared with density which is positive and approximately constant.
. Pressures are therefore small compared with density which is positive and approximately constant.
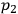 is larger than other pressures and balances gravitational attraction. Integrating
is larger than other pressures and balances gravitational attraction. Integrating
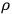 gives
gives
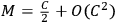 where
where
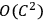 depends on distribution. Considerations of periodicity of
depends on distribution. Considerations of periodicity of
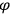 show
show
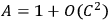 . Other solutions for
. Other solutions for
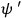 ,
,
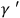 give alternative but less interesting solutions. Geodesic motion shows that free particles outside the cylinder have, in general, an acceleration in the
give alternative but less interesting solutions. Geodesic motion shows that free particles outside the cylinder have, in general, an acceleration in the
 -direction.
-direction.
9.2 Periodic Waves
Take metric of form

|
9.3 |
with
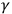 ,
,
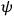 ,
,
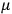 functions
functions
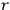 ,
,
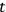 (not to be confused with previous
(not to be confused with previous
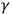 ,
,
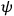 ). Rosen
). Rosen 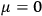 [field equations
[field equations
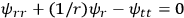 ,
,
 ,
,
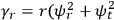 )] in free space, and takes as periodic wave solution (denoted by
)] in free space, and takes as periodic wave solution (denoted by
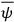 , 8 on detailed paper).
, 8 on detailed paper).
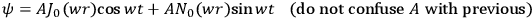
|
and a corresponding
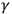 which has a factor
which has a factor
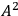 and contains an aperiodic term,
and contains an aperiodic term,
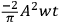 . We have superimposed the static exterior solution (transformed) on to Rosen’s
. We have superimposed the static exterior solution (transformed) on to Rosen’s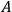 of order
of order
 . The aperiodic term makes the system unphysical by changing the sign of the density at
. The aperiodic term makes the system unphysical by changing the sign of the density at
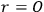 . This is the first unphysical behavior of the system. The mass of the cylinder/unit length is initially
. This is the first unphysical behavior of the system. The mass of the cylinder/unit length is initially
 , showing that
, showing that
 vanishes at
vanishes at
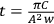 . The density changes sign at
. The density changes sign at
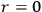 at
at
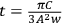 .
.
9.3 Pulse Waves
A solution of field equations relating to (9.3) is
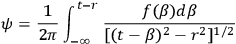
|
where
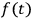 represents the source of the pulse.
represents the source of the pulse.
• If: (1)
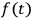 is of finite duration
is of finite duration
• or: (2)
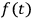 is of infinite duration with a finite number of sign changes,
is of infinite duration with a finite number of sign changes,

|
• or: (3)
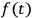 is of infinite duration with an infinite number of sign changes,
is of infinite duration with an infinite number of sign changes,
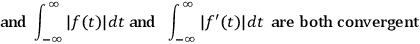
|
then
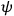 ,
,
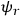 ,
,
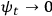 ,
,
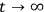 , for fixed
, for fixed
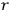 , showing, by boundary conditions, etc., that when the pulse has travelled to infinity the mass of the cylinder reverts to its value prior to the pulse. Considerations of a particular form of pulse show that the mass does change during early motion of the pulse. It is clear that
, showing, by boundary conditions, etc., that when the pulse has travelled to infinity the mass of the cylinder reverts to its value prior to the pulse. Considerations of a particular form of pulse show that the mass does change during early motion of the pulse. It is clear that
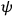 and derivatives are not of such a form as to allow the mass to return to its original value whatever the form of
and derivatives are not of such a form as to allow the mass to return to its original value whatever the form of
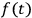 , as such functions as
, as such functions as
 do not correspond to true pulses, but to travelling waves such as those considered above, which clearly radiate mass.
do not correspond to true pulses, but to travelling waves such as those considered above, which clearly radiate mass.
***
DE WITT asked, “If the mass eventually returns to its original state, are there any waves left out in space?”
BONDI
In answer to a question as to why it was necessary for the process of emission of gravitational waves
DE WITT added, “In other words, if I know at an initial time that I am going to give you a yes answer, then the field already contains it.”
BELINFANTE
BELINFANTE
WHEELER
BONDI
BONDI
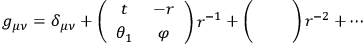
|
The coefficients are functions of the variables in the brackets. He investigates what one gets if one proceeds to the approximation which includes the
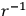 term. His strong impression is that this coefficient is independent of time. If we again consider the transmitter, only this time a much more general one (the system is three-dimensional) - but suppose the system to be spherically symmetrical both before and after emission - the “
term. His strong impression is that this coefficient is independent of time. If we again consider the transmitter, only this time a much more general one (the system is three-dimensional) - but suppose the system to be spherically symmetrical both before and after emission - the “
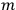 ” of the two Schwarzschild solutions
” of the two Schwarzschild solutions
The next speaker was WEBER, and
and
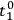 , he finds that they vanish everywhere. This has the consequence that energy cannot be transferred around as long as one has this type of symmetry and the above metric.
, he finds that they vanish everywhere. This has the consequence that energy cannot be transferred around as long as one has this type of symmetry and the above metric.
BONDI: “Where did you feed in the condition that the solution is well behaved at infinity?”
WEBER
BONDI remarked that it is vital, in this confusing subject, to make sure that one can physically detect what one is talking about. Also a single particle is a very poor absorber of any sort of energy.
WEBER
BERGMANN
The next speaker was PIRANI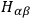 of a skew tensor, regarding it as a six dimensional vector. The curvature tensor
of a skew tensor, regarding it as a six dimensional vector. The curvature tensor
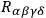 can be similarly cast in the six dimensional formalism, appearing as a symmetric 6-tensor. If one imposes the empty space-time field equations one finds that its form must be
can be similarly cast in the six dimensional formalism, appearing as a symmetric 6-tensor. If one imposes the empty space-time field equations one finds that its form must be
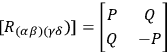
|
where
 and
and
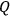 are symmetric
are symmetric
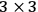 arrays. The spurs of both
arrays. The spurs of both
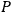 and
and
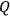 are zero. Lichnerowicz’s
are zero. Lichnerowicz’s 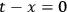 ):
):
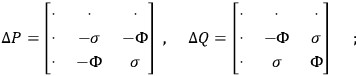
|
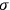 and
and
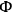 are independent numbers. This form is obtained by taking a particular choice of
are independent numbers. This form is obtained by taking a particular choice of
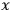 and
and
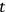 axes. Here
axes. Here
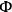 can be made to vanish by a suitable choice of
can be made to vanish by a suitable choice of
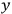 and
and
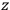 axes. The above array, using the preceding definition, characterizes a gravitational wave
axes. The above array, using the preceding definition, characterizes a gravitational wave
In the electromagnetic case, one can define an invariant Poynting vector
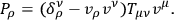
|
If the field is not of the self conjugate type, then an observer following the field can make the Poynting vector vanish by acquiring a suitable 4-velocity. If it is self-conjugate, then the field contains pure radiation, and the Poynting vector vanishes only if the observer acquires the velocity of propagation of the wave.
Similarly, in the gravitational case one can define a certain timelike eigenvector, in terms of the Riemann tensor. This vector is interpreted as the 4-velocity of an observer following the field, and if for some field this vector collapses onto the null cone, one has radiation. The eigenvectors of the gravitational field are defined with the aid of Petrov’s classification
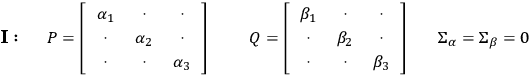
|
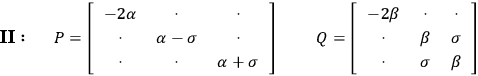
|
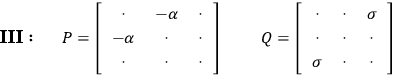
|
The
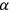 ’s and
’s and
 ’s are independent scalar invariants
’s are independent scalar invariants
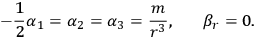
|
The Einstein-Rosen
Next, SCHILD
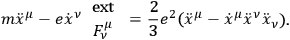
|
One proceeds by analogy and attempts to write the geodesic equations in the gravitational case as
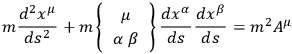
|
where, in analogy with the electromagnetic case

|
A procedure like this does not work in principle, and this for the following reasons: For an equation like this to make sense, one must go to a limiting background field, letting the mass tend to zero. That is, what one really is considering is the limit of the field containing mass as the mass goes to zero:

|
This means that we are considering different Riemannian 4-spaces, with no natural one-to-one correspondence between the points of any two spaces. Thus we must demand invariance under independent transformations in different spaces:
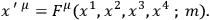
|
Since the equations are tensorial under
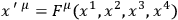
|
it remains to demand (to order in
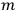 considered) invariance under
considered) invariance under
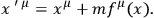
|
However, the equations are not invariant under such a transformation. It appears from an investigation still in progress that any right hand side
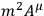 can be wiped out by a suitable choice of such a transformation.
can be wiped out by a suitable choice of such a transformation.
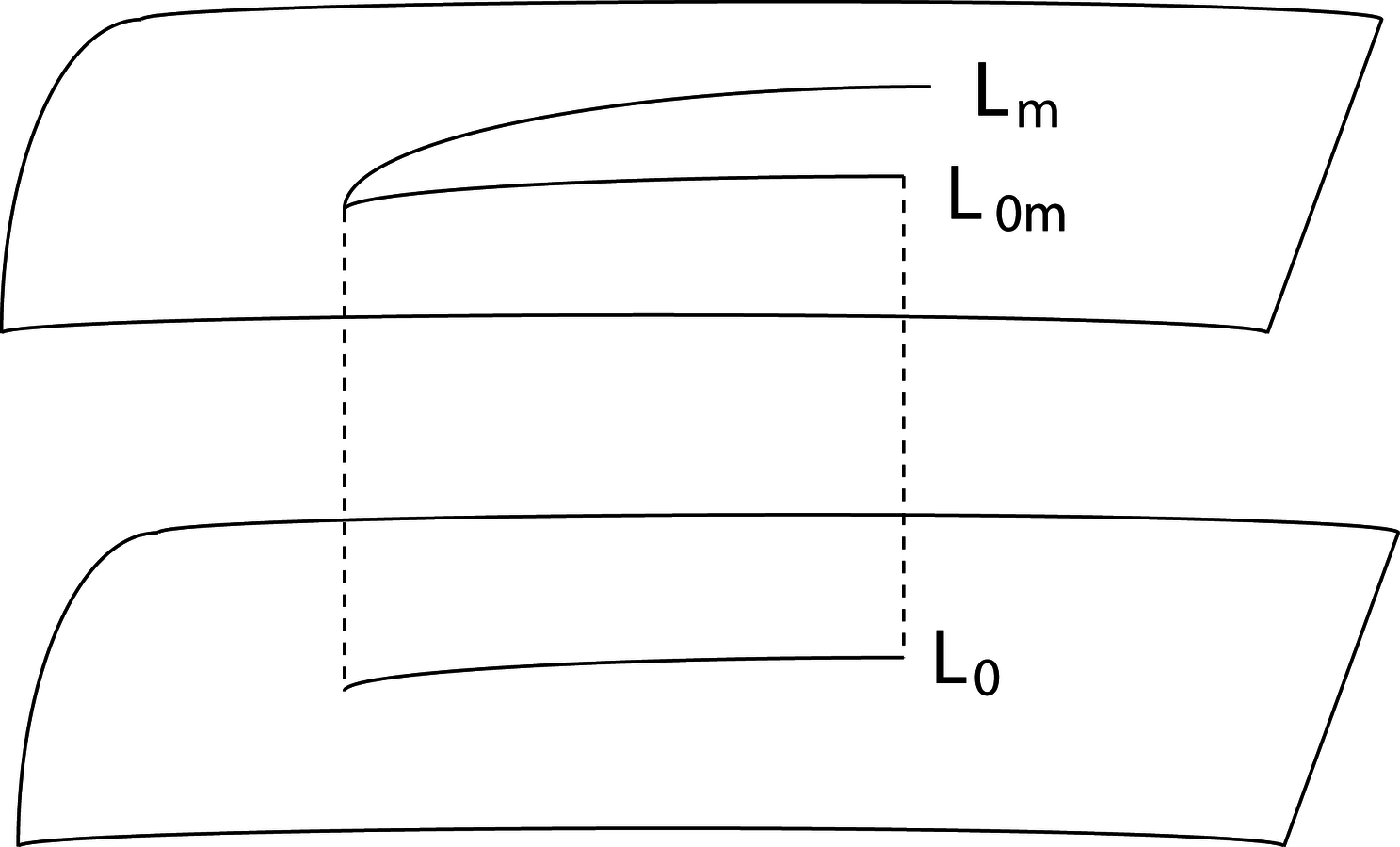
Geometrically one may picture this as follows:
If one changes coordinate systems in
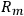 (or equivalently, a one-to-one correspondence
(or equivalently, a one-to-one correspondence
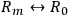 ) one can move
) one can move
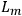 into coincidence with
into coincidence with
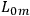 .
.
PIRANI