The real problems in gravitational theory are:
1To understand classical relativistic gravity without the complications of other things.
2The general theory of cosmology because we may be able to work out the shape of the world.
3To study the theory to see if anything new is in it which is not contained at first sight.
4To learn from the philosophy of gravity something to use in other fields such as we have made use of the invariance principles and the ideas of Einstein.
5Curiosity
There exists, however, one serious difficulty, and that is the lack of experiments. Furthermore, we are not going to get any experiments, so we have to take a viewpoint of how to deal with problems where no experiments are available. There are two choices. The first choice is that of mathematical rigor. People who work in gravitational theory believe that the equations are more difficult than in any other field, and from my viewpoint this is false. If you then ask me to solve the equations I must say I can't solve them in the other fields either. However, one can do an enormous amount by various approximations which are non-rigorous and unproved mathematically, perhaps for the first few years. Historically, the rigorous analysis of whether what one says is true or not comes many years later after the discovery of what is true. And, the discovery of what is true is helped by experiments. The attempt at mathematical rigorous solutions without guiding experiments is exactly the reason the subject is difficult, not the equations. The second choice of action is to “play games” by intuition and drive on. Take the case of gravitational radiation. Most people think that it is likely that this radiation is emitted. So, suppose it is and calculate various things such as scattering by stars, etc., and continue until you reach an inconsistency. Then, go back and find out what is the difficulty. Make up your mind which way it is and calculate without rigor in an exploratory way. You have nothing to lose: there are no experiments. I think the best viewpoint is to pretend that there are experiments and calculate. In this field since we are not pushed by experiments we must be pulled by imagination.
The questions raised in the last three days have to do with the relation of gravity to the rest of physics. We have gravity - electrodynamics - quantum theory - nuclear physics - strange particles. The problem of physics is to put
them all together. The original problem after the discovery of gravity was to put gravity and electrodynamics together since that was essentially all that was known. Therefore, we had the unified field theories.
Quantum mechanics and gravity do have something in common. The energy in quantum mechanics is best given by describing how the wave function changes if one solves the coordinate system a little bit, and gravity is connected with just such transformations of coordinates. Thus, the group-theoretic definition of energy and momentum in quantum theory is not very far away from the geometric connection between energy and what happens when you move the coordinate system.
The connection of gravity with the other parts of physics (nuclear and strange particles) was not mentioned here. This is interesting and strange because from the point of view of a non-specialist there is just as much physics in these other fields. From the experimental side we have much more detail there but have no beautiful theory.
Instead of trying to explain the rest of physics in terms of gravity I propose to reverse the problem by changing history. Suppose Einstein never existed, and his theory was not available, but the experimenters began to discover the existence of the force. Furthermore, suppose one knows all the other laws known now including special relativity. Then people will say we have something new, a force like a Coulomb force. Where did it come from? There will be two schools of thought. First, some people will say this force is due to a new field and second some people will say that it is due to some effect of an old field which we do not recognize. I have tried to do this forgetting about Einstein.
First I will do the case of the new field. The force is proportional to
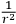 and thus it must be mass zero field. Also, I assume that later one gets experiments about the precession of orbits so that the rate of motion does not appear to be proportional to the mass. Someone would try scalar fields, vector fields, ..., and so on. Sooner or later one would get to a spin two field and would say perhaps it is analogous to electrodynamics. Then he would write down
and thus it must be mass zero field. Also, I assume that later one gets experiments about the precession of orbits so that the rate of motion does not appear to be proportional to the mass. Someone would try scalar fields, vector fields, ..., and so on. Sooner or later one would get to a spin two field and would say perhaps it is analogous to electrodynamics. Then he would write down
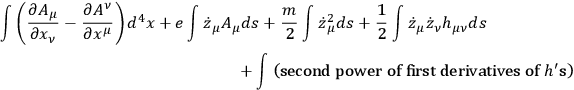
|
or in place of the second term
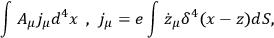
|
and in place of the fourth term
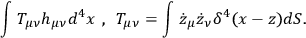
|
In all this
 is the new field under investigation.
is the new field under investigation.
From this one gets some second order equations roughly of the form
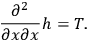
|
Also the equation of motion of the particles is
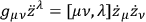
|
where
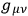 is just a shorthand for
is just a shorthand for
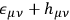 . The field equations of electrodynamics
have a property that the current conservation is an identity from the field equations.
. The field equations of electrodynamics
have a property that the current conservation is an identity from the field equations.
Now one asks what is
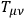 equal to such that we get automatically
equal to such that we get automatically
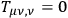 ?
Now, when one puts in the second power of the first derivatives of
?
Now, when one puts in the second power of the first derivatives of
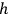 in the action he gets something definite. Incidentally, one gets the linearized form of the gravity
equations. If now these equations are solved to see if any progress has been made, one deduces that light is deflected by the sun. One at this point might say that we know too much, that a field theorist would never have thought of this
important conservation theorem. This is not true. Pauli deduced this equation without looking for gravity, but by asking himself what must the field equations be for fields of arbitrary spin. Soon someone would realize that something is wrong, for if particles move according to the equation of motion, which they must do from the given action, then the
in the action he gets something definite. Incidentally, one gets the linearized form of the gravity
equations. If now these equations are solved to see if any progress has been made, one deduces that light is deflected by the sun. One at this point might say that we know too much, that a field theorist would never have thought of this
important conservation theorem. This is not true. Pauli deduced this equation without looking for gravity, but by asking himself what must the field equations be for fields of arbitrary spin. Soon someone would realize that something is wrong, for if particles move according to the equation of motion, which they must do from the given action, then the
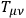 doesn't satisfy the correct equations. A suggestion, then, would be to add the field energy into the stress energy tensor and say that this also is a source of gravity. Then,
doesn't satisfy the correct equations. A suggestion, then, would be to add the field energy into the stress energy tensor and say that this also is a source of gravity. Then,
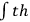 would become
would become
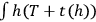 . However, this would not work because a variation of the
. However, this would not work because a variation of the
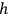 's gives not only what one wants, but some new terms. Finally one asks if there exists an expression of third order
in the
's gives not only what one wants, but some new terms. Finally one asks if there exists an expression of third order
in the
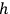 's which can be used in the action of the form
's which can be used in the action of the form
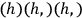 and will give any relief from the difficulty. It is possible to prove from the definition of
and will give any relief from the difficulty. It is possible to prove from the definition of
 and the equation of motion that the true
and the equation of motion that the true
 must satisfy some equation of the form
must satisfy some equation of the form
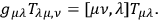
|
Then one can go to the next higher order of approximation and this approximation will explain the perihelion of Mercury. Although one is on the right track this process is just an expansion. It is possible, however, to solve the problem mathematically by finding an expression which is invariant under
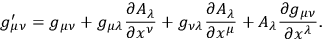
|
To get the solution of this problem one asks a mathematician. However, it could have been solved by noticing that it is a geometric transformation in a Riemannian space. Finally, someone might suggest that geometry determines the metric. This would be a marvellous suggestion but it would be made at the end of the work and not at the beginning.
What does one gain by looking at the problem in this manner? Obviously, one loses the beauty of geometry but this is not primary. What is primary is that one had a new field and tried his very best to get a spin-two field as consistent as possible.
I think quantization would proceed in the same direction as the original solution of the problem. One would consider this just another field to be quantized. From the other viewpoint the geometry is important, but from this viewpoint gravity is just another field. I am sure that an enormous amount of formulae would be collected without having the generally covariant quantum theory. I advertise that this new point of view may, in fact, succeed in the end. Certainly people would not think that the rest of physics could be deduced from gravity. They may well be wrong, but it also may be true that gravity is just one more of a long list of difficult things that some day have to be put together.
Now let us go to the second possibility, old fields. The physicists might try to explain the new force on the basis of the incomplete cancellation of electric charges of the order (number of particles)
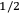 or some such scheme. However, there are a number of interesting possibilities which are not completely impossible. One
important fact is that this field has an infinitesimal coupling constant and already one knows about one weakly coupled field, the neutrino. Also, the neutrino has zero
rest mass which is needed for
or some such scheme. However, there are a number of interesting possibilities which are not completely impossible. One
important fact is that this field has an infinitesimal coupling constant and already one knows about one weakly coupled field, the neutrino. Also, the neutrino has zero
rest mass which is needed for
 dependence. The neutrino equation is modified, for convenience, to read
dependence. The neutrino equation is modified, for convenience, to read
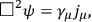
|
and the neutrino propagators are assumed to be
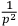 . A first trial might be the single exchange of a neutrino between the two interacting bodies. In this case,
however, a
. A first trial might be the single exchange of a neutrino between the two interacting bodies. In this case,
however, a
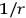 law does not result because the initial and final states are orthogonal. Another possibility is a two neutrino exchange, but this gives a potential which falls off faster than
law does not result because the initial and final states are orthogonal. Another possibility is a two neutrino exchange, but this gives a potential which falls off faster than
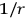 . Next, one could try one neutrino exchange between the two bodies with each body exchanging one neutrino with the rest of the universe. The rest of the universe is assumed to be at some fixed distance,
. Next, one could try one neutrino exchange between the two bodies with each body exchanging one neutrino with the rest of the universe. The rest of the universe is assumed to be at some fixed distance,
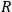 . This does give rise to a potential which varies as
. This does give rise to a potential which varies as
 . However, the amount of matter varies as
. However, the amount of matter varies as
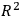 so that upon integration over the universe one gets a logarithmic divergence. The most serious difficulty with this approach is, however, the large effect the sun would have on the earth-moon system. This last trial was so much better than
the others one can go a step further and try a four neutrino process with the additional neutrino being exchanged in the rest of the universe. This will also give a
so that upon integration over the universe one gets a logarithmic divergence. The most serious difficulty with this approach is, however, the large effect the sun would have on the earth-moon system. This last trial was so much better than
the others one can go a step further and try a four neutrino process with the additional neutrino being exchanged in the rest of the universe. This will also give a
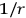 potential and a higher order divergence and one must worry about the
density of matter, etc. Higher order terms are possible but they are much more difficult to handle. Therefore, the possibility exists that the material from the outside is making the source of gravitation here through the exchange of well
known particles, the neutrinos.
potential and a higher order divergence and one must worry about the
density of matter, etc. Higher order terms are possible but they are much more difficult to handle. Therefore, the possibility exists that the material from the outside is making the source of gravitation here through the exchange of well
known particles, the neutrinos. 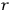 dependence. If one did put in things correctly and got a finite amount for a result, then this is very curious and has not been noticed before. That is one of the advantages of looking at something from a different direction. Anyway, this is what the people who believe in old theories would do.
dependence. If one did put in things correctly and got a finite amount for a result, then this is very curious and has not been noticed before. That is one of the advantages of looking at something from a different direction. Anyway, this is what the people who believe in old theories would do.
This different point of view has been advertised in the hope that a few people will start looking at gravitation from a different direction. I think really that it is more likely and more interesting to go from the geometric side, but if a few investigations change directions we may get somewhere.
ROSENFELD
