This session opened the second half of the conference, devoted to discussion of the problems of quantizing the gravitational field, previous sessions having been restricted to the classical domain. The first contribution was an introduction by P. G. BERGMANN outlining the present position of the infant subject of quantum gravidynamics, indicating why one is interested in it in the first place, and stating some of its outstanding problems. The following is a summary of BERGMANN's introduction:
BERGMANN first asked the question, “Why quantize?” His reply was that physical nature is an organic whole, and that various parts of physical theory must not be expected to endure in “peaceful coexistence.” An attempt should be made to force separate branches of theory together to see if they can be made to merge, and if they cannot be united, to try to understand why they clash. Furthermore, a study should be made of the extent to which arguments based on the uncertainty principle force one to the conclusion that the gravitational field must be subject to quantum laws: (a) Can quantized elementary particles serve as sources for a classical field? (b) If the metric is unquantized, would this not in principle allow a precise determination of both the positions and velocities of the Schwarzschild singularities of these particles?
These aims have not yet been achieved, but BERGMANN expressed certain hopes as to the results of such a program: Quantization of the gravitational field is likely to have a profound effect on our notions of space and time, making all distance and volume concepts subject to uncertainty relations. Thus, in spite of the quantitatively negligible character of the gravitational forces between elementary particles, it is conceivable that (a) the gravitational field may help to eliminate the divergences of quantum field theory (which result from the compounded effect of singularities in particle propagators) by smearing out the light cone, and (b) it may somehow contribute to the structure of elementary particles. In regard to the latter point, however, BERGMANN expressed his opinion that one cannot hope to get
the complete structure of the elementary particles from any quantized unified field theory that is principally motivated by the desire to unify just the gravitational and electromagnetic fields.
BERGMANN emphasized the formidable nature of the problem of quantizing generally covariant theories and expressed the conviction that one will first have to have a thorough clarification of the underlying conceptual problems in the classical theory. He then went on to outline the principal methods of approach to the purely technical problems of quantization which we now possess: (1) The canonical Hamiltonian method (Dirac); (2) The Lagrangian method (Schwinger); (3) The path-summation method (Feynman). It appears that the need to identify the so-called “true observables,” or coordinate-invariant quantities, arises in all three schemes. Furthermore, this identification will be intimately related with the structure of the transformation groups under which the classical theory remains invariant.
In the quantum theory the state vector of a generally covariant system will be subject to various constraints which must, of necessity, be imposed owing to the existence of the invariant transformation groups. A “true observable” will be described by an operator which, when applied to the state vector, produces another
vector which satisfies the same constraints as the original vector. A reduced Hilbert space is envisaged in which the only canonical transformations which are physically meaningful are those generated by true observables. The constraint operators
themselves qualify as true observables under this definition, but they are trivial, being simply “null generators.” BERGMANN believes that it is immaterial whether the Lagrangian or Hamiltonian approach is used to discover the nontrivial true observables; the results will be the same in either case.
As remaining problems which must eventually be looked at, BERGMANN gave the following partial list:
1The hyperquantized particle field vs. the treatment of particles as singularities in a quantized gravitational field.
2The interaction of the gravitational field with fermions.
3The interaction of the gravitational field with other quantized fields.
4The relation of elementary particle theory to unitary field theories.
5The relation of the law of conservation of energy and momentum arising from the coordinate transformation invariance of general relativity to other strong conservative laws of physics with their associated invariance
groups.
Discussion then turned to the problems of measurement of the gravitational field. This item was placed first on the agenda in an attempt to keep physical concepts as much as possible in the foreground in a subject which can otherwise be quickly flooded by masses of detail and which suffers from lack of experimental
guideposts. The question was asked: What are the limitations imposed by the quantum theory on the measurements of space-time distances and curvature? Since the curvature is supposed to be affected by the presence of gravitating matter, an equivalent question is to ask: What are the quantum limitations imposed on the
measurement of the gravitational mass of a material body, and, in particular, can the principle of equivalence be extended to elementary particles?
(In the interest of clarifying the importance of some of the following
discussion, the editors would like to point out at least one reason, which was not given sufficient attention at the conference, why the answer to the latter question is not a simple matter of dimensional arguments. In quantum gravidynamics there exists a natural unit of mass, namely
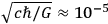 g. One might be tempted to suppose that this represents a lower limit on the mass of a particle whose gravitational effect can in principle be measured. That this conclusion is wrong can be shown by the following arguments:
g. One might be tempted to suppose that this represents a lower limit on the mass of a particle whose gravitational effect can in principle be measured. That this conclusion is wrong can be shown by the following arguments:
The gravitational field strength is given by
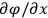 and can immediately be determined by a measurement of
and can immediately be determined by a measurement of
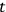 and
and
 . If however the particle is subject to quantum laws its initial position and velocity are subject to (root mean square) uncertainties related by
. If however the particle is subject to quantum laws its initial position and velocity are subject to (root mean square) uncertainties related by
leading to an uncertainty in position at time
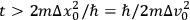 of amount
of amount
The initial position measurement may be made by a photon of momentum uncertainty
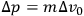 (or, in principle, by a graviton having the same momentum uncertainty if
one prefers to deal with absolute electrically neutral test particles!). The resulting uncertainty in the initial time may be ignored since it is given by
(or, in principle, by a graviton having the same momentum uncertainty if
one prefers to deal with absolute electrically neutral test particles!). The resulting uncertainty in the initial time may be ignored since it is given by
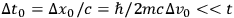 (assuming
(assuming
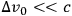 ). The final position and time measurements may be made with arbitrarily high precision, using energetic photons, since the experiment is then over.
). The final position and time measurements may be made with arbitrarily high precision, using energetic photons, since the experiment is then over.
The gravitational field can now be determined from the classical equation if
However, one must be able to choose
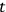 small enough so that
small enough so that
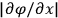 does not change appreciably during the course of the motion. This imposes a condition on the gravitational field, namely
does not change appreciably during the course of the motion. This imposes a condition on the gravitational field, namely
It is, however, still a matter of basic interest to determine whether or
not the measurement could be carried out on a single elementary particle. Here the main practical problem concerns the measurement of time. One has the restriction
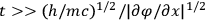 or
or
If both the test particle and source has protonic mass then
and all conditions may seemingly be satisfied by choosing
 to have the not unreasonable value
to have the not unreasonable value
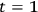 sec. Moreover, no complications should arise due to the nonlinear character of the gravitational field (the linear Newtonian approximation should be
masses as small as a proton).
sec. Moreover, no complications should arise due to the nonlinear character of the gravitational field (the linear Newtonian approximation should be
masses as small as a proton).
Nevertheless, a number of subtleties enter the problem at this point, chiefly concerning the nature of the recording apparatus, or clock, which measures the requisite time intervals (independently of the photons which interact with the test particle) and how the presence of the clock's mass in the neighborhood may influence results of the experiment.)
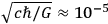 g.
g.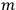 which is initially at rest at the point
which is initially at rest at the point
 (we restrict ourselves to one dimension) in a gravitational potential
(we restrict ourselves to one dimension) in a gravitational potential
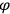 . At the time
. At the time
 the position of the particle will be
the position of the particle will be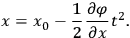
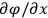 and can immediately be determined by a measurement of
and can immediately be determined by a measurement of
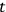 and
and
 . If however the particle is subject to quantum laws its initial position and velocity are subject to (root mean square) uncertainties related by
. If however the particle is subject to quantum laws its initial position and velocity are subject to (root mean square) uncertainties related by
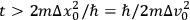 of amount
of amount
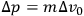 (or, in principle, by a graviton having the same momentum uncertainty if
one prefers to deal with absolute electrically neutral test particles!). The resulting uncertainty in the initial time may be ignored since it is given by
(or, in principle, by a graviton having the same momentum uncertainty if
one prefers to deal with absolute electrically neutral test particles!). The resulting uncertainty in the initial time may be ignored since it is given by
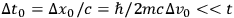 (assuming
(assuming
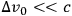 ). The final position and time measurements may be made with arbitrarily high precision, using energetic photons, since the experiment is then over.
). The final position and time measurements may be made with arbitrarily high precision, using energetic photons, since the experiment is then over.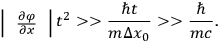
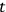 small enough so that
small enough so that
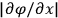 does not change appreciably during the course of the motion. This imposes a condition on the gravitational field, namely
does not change appreciably during the course of the motion. This imposes a condition on the gravitational field, namely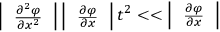
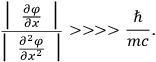
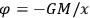 ,
,
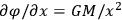 ,
,
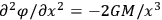 , and the required condition becomes
, and the required condition becomes
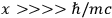 which can always be satisfied. Evidently the gravitational field of any mass is measurable in principle because of the long “tail” in the Newtonian force law. In fact, the long tail is what permits us to “measure” the
which can always be satisfied. Evidently the gravitational field of any mass is measurable in principle because of the long “tail” in the Newtonian force law. In fact, the long tail is what permits us to “measure” the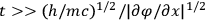 or
or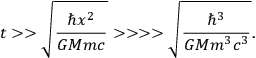
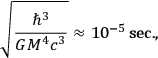
 to have the not unreasonable value
to have the not unreasonable value
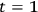 sec. Moreover, no complications should arise due to the nonlinear character of the gravitational field (the linear Newtonian approximation should be
masses as small as a proton).
sec. Moreover, no complications should arise due to the nonlinear character of the gravitational field (the linear Newtonian approximation should be
masses as small as a proton).