8 Some Remarks on Cosmological Models

It is unusual to hypothesize that the four-dimensional space-time universe of general relativity is compact (i.e., “finite”). But in such a case several interesting conclusions can be drawn. In the first place, if the mass distribution is assumed to be continuous, so that the metric tensor has no singularities, then the Euler-Poincaré characteristic of the universe must be zero [1]. This implies, for example, that the universe cannot be a four-dimensional sphere. It also implies that a finite universe cannot be simply-connected, in the sense that the first Betti number cannot vanish. This is reminiscent of Professor J.A. Wheeler’s non-simply connected models.)

In the second place, it seems to be generally known that in a finite cosmology there must exist a closed curve in space-time whose tangent vector at every point is time-like. Professor L. Markus has indicated a proof to us. Let denote the 4-manifold of the universe. Now, on 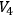construct a continuous, nowhere vanishing field of time-like vectors ([1], pp. 6-7; cf.[2], p. 207). By Birkhoff’s fundamental theorem on the existence of recurrent orbits in compact dynamical systems [3], there must exist either an orbit of the type sought or else an “almost-closed” time-like orbit which can serve for the construction of such a closed orbit by an obvious procedure.

A more standard hypothesis, however, is that the universe 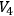is not compact, but is the topological product of the infinite real line (a time axis) with a 3-manifold 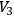. The manifold 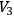is often assumed to be compact, and any local (hence experimentally verifiable) condition which implies compactness is of much interest. For example, if 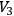has constant curvature 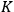then 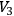is compact if, and only if, is positive ([4], pp. 84 and 203), and in this case is a 3-sphere if its first Betti number vanishes, and in general admits the 3-sphere as a covering space.

We wish to point out a new method for studying the topology of manifolds such as 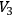and 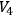. This method consists of the construction of a continuous, nowhere vanishing, irrotational vector field on the manifold under consideration. Once such vector field has been constructed, we can assert that either the manifold is non-compact (i.e., open or “infinite”), or that it cannot be simply-connected.

We shall prove a slight generalization of this theorem; but first, let us note that a similar, but more restrictive and less easily applicable condition is a trivial consequence of Hodge’s well-known theorem that the number of linearly independent harmonic vector fields on a compact Riemannian manifold is equal to its first Betti number. For if after constructing on our manifold an irrotational vector field (which is non-trivial but may vanish at more than one point), we then ascertain that it is also solenoidal (i.e., of vanishing divergence), then the vector field must be harmonic ([5], p. 56).

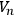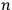• Theorem 1 (Hodge):: Let be an -dimensional Riemannian manifold (with positive definite metric tensor), and let 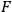denote a non-trivial class 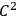vector field defined on 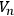. Suppose that the curl and the divergence of 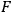both vanish identically; or equivalently, suppose that the field 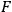satisfies the generalized Laplace equation for harmonic vector fields. Then, if 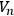is compact, its first Betti number is not zero.

• Corollary (Bochner-Myers):: If 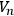is orientable and has positive definite Ricci curvature throughout, then its first Betti number vanishes. ([5], p. 37).

Recall that the curl tensor of a vector field is independent of the metric tensor, and so is a non-metric notion. Accordingly, the following theorem applies equally well to with its indefinite hyperbolic metric as to 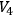with its positive definite Riemannian metric.

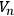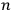• Theorem 2:: Let be an -dimensional differentiable manifold, and let 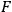be a continuous, class 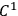vector field defined on 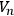. Suppose that F vanishes at most once and that its curl vanishes identically on 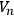. Then either 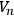is non-compact, or 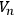is compact and its first Betti number does not vanish. In either case, of course, if actually vanishes nowhere, the Euler-Poincaré characteristic of 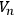is zero.

For non-vanishing 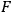this theorem is a consequence of a more general theorem [6] which applies, for example, to manifolds with boundary. In fact, by a generalization to arbitrary flows of a theorem proved by Lichnerowicz 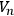for a very special class of flows ([7], p. 79), we can prove [8] that is homeomorphic to the product of the real line with an 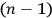-dimensional space which is a connected subset of a 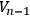. But in the present case, because we are dealing with a manifold, there is a much simpler proof. We wish to thank Professor Kervaire 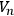for pointing out to us this simpler proof during the Conference on the Role of Gravitation in Physics. The proof runs as follows. If is simply connected, then the generalized Stokes Theorem assures us that there exists on 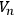a single-valued scalar potential function of which 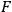is the gradient field. (See the survey of vector analysis in [9].) But if 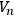is compact, this potential function must assume both its maximum and minimum values on 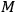, and at these extreme points the gradient must vanish. This contradicts the hypothesis that 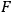has at most one zero on 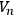, and so proves the theorem.

It is possible that Theorems 1 and 2 have applications to the study of specific cosmological models. In fact, there are many ways of constructing on 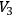, or on continuous vector fields which are unique once the indefinite metric (or set of gravitational potentials) for 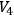has been specified.

Professor J.A. Wheeler has pointed out to us an application of Theorem 2 to .

• Theorem 3:: Consider the combined Einstein-Maxwell field theory on 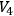. If the vector field

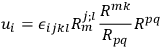
is defined everywhere and of class 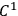on 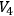, and if 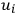does not vanish more than once, then the universe 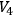cannot be compact.

The vector field 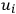, which was defined by Dr. C. W. Misner, 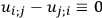is essentially the gradient of the ratio (in a certain coordinate system) of the electric to the magnetic field strength. Dr. Misner has shown that Maxwell’s equations imply that . Hence, Theorem 3 follows from Theorem 2.

References