27 An Expanded Version of the Remarks by R.P. Feynmanon the Reality of Gravitational Waves

I think it is easy to see that if gravitational waves can be created they can carry energy and can do work. Suppose we have a transverse-transverse wave generated by impinging on two masses close together. Let one mass carry a stick which runs past touching the other . I think I can show that the second in accelerating up and down will rub the stick, and therefore by friction make heat. 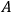I use coordinates physically natural to , that is so at there is flat space and no field (what are they called, “natural coordinates”?). 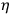Then Pirani at an earlier section gave an equation for the notion of a nearby particle, vector distance from origin , it went like, to order in

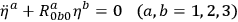
is the curvature tensor calculated at 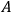. Now we can figure directly, it is not reasonable by coordinate transformation for it is the real curvature. It does not vanish for the transverse-transverse gravity wave but oscillates as the wave goes by. So, 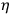on the RHS is sensibly constant, so the equation says the particle vibrates up and down a little (with amplitude proportional to how far it is from 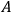on the average, and to the wave amplitude.) Hence it rubs the stick, and generates heat.

I heard the objection that maybe the gravity field makes the stick expand and contract too in such a way that there is no relative motion of particle and stick.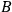 But this cannot be. Since the amplitude of 's motion is proportional to the distance from 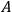, to compensate it the stick would have to stretch and shorten by certain ratios of its own length. Yet at the center it does no such thing, for it is in natural metric - and that means that the lengths determined by size of atoms etc. are correct and unchanging at the origin. In fact that is the definition of our coordinate system. Gravity does produce strains in the rod, but these are zero at the center for and its gradients are zero there. I think: any changes in rod lengths would go at least as 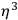and not as 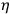so surely the masses would rub the rod.

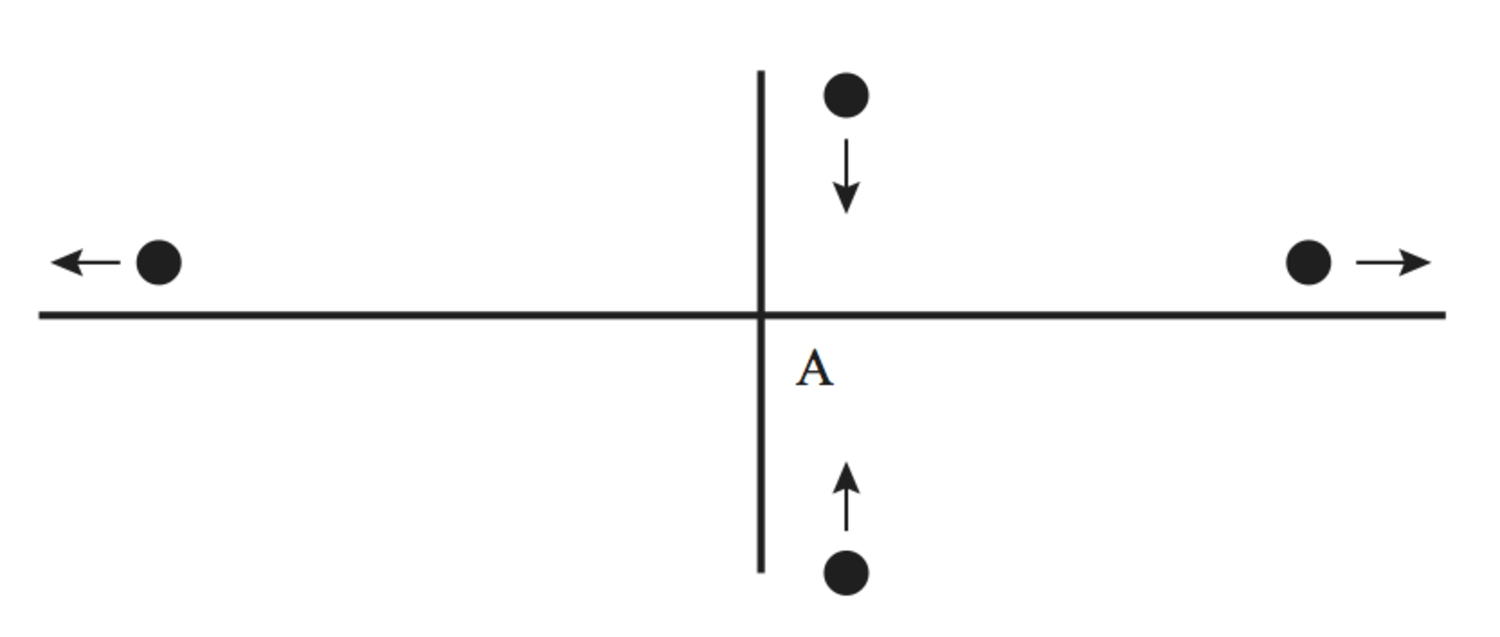
Incidentally masses put on opposite side of 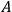go in opposite directions. If I use 4 weights in a cross, the motions at a given phase are as in the figure:

Thus a quadrupole moment is generated by the wave.

Now the question is whether such a wave can be generated in the first place. First since it is a solution of the equations (approx.) it can probably be made. Second, when I tried to analyze from the field equations just what happens if we drive 4 masses in a quadrupole motion of masses like the figure above would do - even including the stress-energy tensor of the machinery which drives the weights, it was very hard to see how one could avoid having a quadrupole 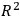source and generate waves. Third my instinct is that a device which could draw energy out of a wave acting on it, must if driven in the corresponding motion be able to create waves of the same kind. The reason for this is the following: If a wave impinges on our “absorber” and generates energy - another “absorber” place in the wave behind the first must absorb less because of the presence of the first, (otherwise by using enough absorbers we could draw unlimited energy from the waves). That is, if energy is absorbed the wave must get weaker. How is this accomplished? Ordinarily through interference. To absorb, the absorber parts must move, and in moving generate a wave which interferes with the original wave in the so-called forward scattering direction, thus reducing the intensity for a subsequent absorber. In view therefore of the detailed analysis showing that gravity waves can generate heat (and therefore carry energy proportional to with a coefficient which can be determined from the forward scattering argument). I conclude also that these waves can be generated and are in every respect real.

I hesitated to say all this because I don't know if this was all known as I wasn't here at the session on gravity waves.