It is hoped that a reconciliation of quantized gravitational fields, the
matter field, and electromagnetic field might induce a further structure on the elementary particles, and might result in softening the divergences, or eliminating them altogether. It is well known that the gravitational field has a non-local character, so it probably would not be possible by quantizing the gravitational field to find a 4-vector momentum giving a particle property to gravity. One tries the approach of generalizing Einstein's theory, making it more complicated than it is, hoping to get some more physics out of it. Since there is no physical basis in unified field theory, as there is in general relativity, one proceeds in a more mathematical fashion. Nature must be described by a complete tensor with symmetric and antisymmetric fields. One then constructs all of the quantities recognized in general relativity and obtains, for example, Bianchi identities and Maxwell identities. In order to compare the theory with general relativity, we have a conservation law in the absence of charges and this introduces a fundamental length
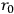 . The real motivation for this procedure is the development of a correspondence argument in order to identify the formalism with a theory. The question arises what happens if we assign no structure
to the theory and
. The real motivation for this procedure is the development of a correspondence argument in order to identify the formalism with a theory. The question arises what happens if we assign no structure
to the theory and
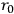 approaches 0. We obtain the equations of general relativity with the electromagnetic field as the source of gravitation plus Maxwell's equations for charge-free fields. The existence of charges is linked up with a non-vanishing fundamental length just as the existence of spin arises from a finite
approaches 0. We obtain the equations of general relativity with the electromagnetic field as the source of gravitation plus Maxwell's equations for charge-free fields. The existence of charges is linked up with a non-vanishing fundamental length just as the existence of spin arises from a finite
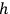 .
.
Now, the metrics depends on length. We have calculated the propagation of light in the presence of very strong background fields; the result is in agreement with those of Schrödinger from non-linear optics. One may also change the sign of
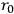 , but we cannot find a way of measuring negative length. The concept of negative length may be linked up with negative mass (or antimatter).
, but we cannot find a way of measuring negative length. The concept of negative length may be linked up with negative mass (or antimatter).
DE WITT: Can you state any conclusions about matter and antimatter?
KURSUNOGLU: I cannot state any conclusions because I must solve the equations and show that solutions involving a negative and a positive length will give repulsion.
KURSUNOGLU: Firstly, I don't believe in the Born-Infeld theory; secondly, equations of motion are a difficult concept in this theory because one has to define what a particle is first. Usually the field variables are singular at the point of a particle; here what can I let move if I don't have a particle yet?
SALECKER: Can you not quantize this theory to get the results for elementary forces?
KURSUNOGLU: One develops a unified theory in order not to do anything with quantum theory. If there are any quantum effects, they must be contained in the non-linearity which is caused by the finite value that we have introduced for the electromagnetic field. Quantization is out of the question.
LICHNEROWICZ: It seems to me that many physicists do not like this type of unified field theory. We have a very good theory of propagation, but it is difficult to find physical interpretations, because the theory is in a sense too unified. We have a good interpretation for the metric or the gravitational part, but it is difficult
to obtain a good interpretation for the electromagnetic part. The first
problem is not to obtain the equations of motion; the first problem is to obtain by a process of approximation a good identification.
BERGMANN: I believe that we have the following principal problems: Firstly, the identification, I agree with you. Secondly, the actual finding of the solutions which are free of singularities. If one believes in the unified field theory approach, he must face the question: does the theory lead to solutions which can be interpreted as particles? The equations of motion are a subsidiary problem. If
there are such solutions, are they stable?
WHEELER: Perhaps the first question to be asked about unified field theory is “why?”. We have non-singular solutions in geons in the present theory.
BERGMANN: All of the geons involve stochastic methods. A rigorous solution would be one in which no averaging operation were performed, where you can tie down a single solution.
WHEELER: A geon has exactly the property of being only an approximate solution; or rather, an accurate solution which is not fully stable with time - it leaks energy. Thus it is not in agreement with one's preconceived idea that there should be a particle-like solution that is fully stable; but aren't we being very brash if we
say that the world isn't built that way? How do we know that the leakage of energy is not a property of high mass particles which leak energy and drop down to lower mass particles? Perhaps the stability of the particles we know is due to some intrinsically quantum character, which we cannot expect to show up before we have gone to the quantum level.
BERGMANN: The original motivation of unified field theory is get a theory of elementary particles, which includes electrons and not only hyperfragments, and furthermore to obviate the need for quantization which would result from the intrinsic non-linearity.
FEYNMANN: Historically, when the unified field theory was first tackled, we had only gravitation, electrodynamics, and a few facts about quantization, so it was natural to try to write down equations which would only unite the Maxwell equations with the gravity equations and leave out of account the strange quantum effects, with the hope that the non-linearity would produce this business. In the meantime, the rest of physics has developed, but still no attempt starts out looking for the quantum effects. There is no clue that a unified field theory will give quantum effects.
ROSENFELD: We know that there are forces which are certainly not reducible to electromagnetic and gravitational forces; forces of finite range. It seems that this unification program is anachronistic. I think that it is an illusion to hope that the particle can be reduced to some distinct distribution, either singular or non-singular, for the particle must be regarded as a field itself in quantum theory.
LICHNEROWICZ: We have here a theory which has a definite mathematical meaning. In quantum theory, there are many good experiments, but many parts of quantum theory are not good theories. There are various difficulties with mathematical consistency in a large part of the quantum theory.
BONDI: We should regard general relativity not as a supertheory, but as the best theory of gravitation we have got, which describes a certain set of phenomena better than any other theory we have.
KURSUNOGLU: In unified field theory, one tries to make particles, sort of mass, out of the electromagnetic field. This is also the case in quantum electrodynamics; the field creates mass, the electron-positron pairs.
FEYNMAN: Let's ask ourselves the question: If we looked at things on a large scale, and saw them gravitating, we should discuss the character of the singularities; but, gentlemen, look at one of the singularities: we're sitting on it. Look at the degree of complexity that it has; the lights and the colors, and the trees, and the particles that it's made out of. Can you believe that in the fact that they gravitate there lies the key to all this confusion? Wouldn't it be more reasonable that gravity were a result of something on the small scale?
ANDERSON: To describe elementary particles, we must adopt a space-time description; you must say something about the metric. Relativity is not only a theory of gravity, but also a theory of space structure.
WITTEN: There may be another reason to look for a unified
field theory, as a step toward quantization. Now we quantize a lot of fields, and it might be easier to quantize just one unified field.
BONDI: One important point: gravitational forces are not self-compensating and that is why they predominate on the large scale. I think that's a side that should be looked at more, in the large.
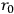 .
. 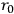 approaches 0. We obtain the equations of general relativity with the electromagnetic field as the source of gravitation plus Maxwell's equations for charge-free fields. The existence of charges is linked up with a non-vanishing fundamental length just as the existence of spin arises from a finite
approaches 0. We obtain the equations of general relativity with the electromagnetic field as the source of gravitation plus Maxwell's equations for charge-free fields. The existence of charges is linked up with a non-vanishing fundamental length just as the existence of spin arises from a finite
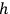 .
.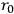 , but we cannot find a way of measuring negative length. The concept of negative length may be linked up with negative mass (or antimatter).
, but we cannot find a way of measuring negative length. The concept of negative length may be linked up with negative mass (or antimatter).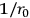 into the Lagrangian itself in order to obtain
into the Lagrangian itself in order to obtain
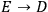 ,
,
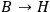 when
when
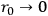 , because it is a conclusion of the Born-Infeld
, because it is a conclusion of the Born-Infeld 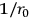 or something else, in order to obtain equations of motion.
or something else, in order to obtain equations of motion.