Because of the principle of equivalence, one cannot ascribe a direct physical interpretation to the gravitational field insofar as it is characterized by Christoffel symbols 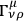 . One can, however, give an invariant interpretation to the variations of the gravitational field. These variations are described by the Riemann tensor; therefore, measurements of the relative acceleration of neighboring free particles, which yield information about the variation of the field, will also yield information about the Riemann tensor.
. One can, however, give an invariant interpretation to the variations of the gravitational field. These variations are described by the Riemann tensor; therefore, measurements of the relative acceleration of neighboring free particles, which yield information about the variation of the field, will also yield information about the Riemann tensor.
Now the relative motion of free particles is given by the equation of geodesic deviation
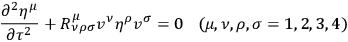
|
14.1 |
Here
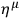 is the infinitesimal orthogonal displacement from the (geodesic) worldline
is the infinitesimal orthogonal displacement from the (geodesic) worldline
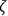 of a free particle to that of a neighboring similar particle.
of a free particle to that of a neighboring similar particle.
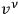 is the 4-velocity of the first particle, and
is the 4-velocity of the first particle, and
 the proper time along
the proper time along
 . If now one introduces an orthonormal frame on
. If now one introduces an orthonormal frame on
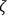 ,
,
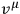 being the timelike vector of the frame, and assumes that the frame is parallelly propagated along
being the timelike vector of the frame, and assumes that the frame is parallelly propagated along
 (which insures that an observer
using this frame will see things in as Newtonian a way as possible) then the equation of geodesic deviation (14.1) becomes
(which insures that an observer
using this frame will see things in as Newtonian a way as possible) then the equation of geodesic deviation (14.1) becomes
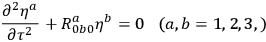
|
14.2 |
Here
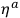 are the physical components of the infinitesimal displacement and
are the physical components of the infinitesimal displacement and
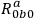 some of the physical components of the Riemann tensor, referred to the orthonormal
frame.
some of the physical components of the Riemann tensor, referred to the orthonormal
frame.
By measurements of the relative accelerations of several different pairs of particles, one may obtain full details about the Riemann tensor. One can thus very easily imagine an experiment for measuring the physical components of the Riemann tensor.
Now the Newtonian equation corresponding to (14.2) is
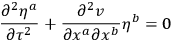
|
14.3 |
It is interesting that the empty-space field equations in the Newtonian and general relativity theories take the same form when one recognizes the correspondence
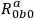
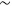
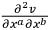 between equations (14.2) and (14.3), for the respective empty-space equations may be written
between equations (14.2) and (14.3), for the respective empty-space equations may be written
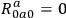 and
and
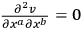 . (Details of this work are in the course of publication in Acta Physica Polonica.)
. (Details of this work are in the course of publication in Acta Physica Polonica.)
BONDI: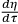 term, to learn what part of the Riemann tensor would be the energy producing one, because it is that part that we want to isolate to study gravitational waves?
term, to learn what part of the Riemann tensor would be the energy producing one, because it is that part that we want to isolate to study gravitational waves?
PIRANI: I have not put in an absorption term, but I have put in a “spring.” You can invent a system with such a term quite easily.
LICHNEROWICZ: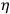 ?
?
PIRANI: It is the same as the stability problem in classical mechanics, but I haven't tried to see for which kind of Riemann tensor it would blow up.
Interaction of Neutrinos with the Gravitational Field D. Brill
The wave equation of a neutrino in a centrally symmetric gravitational field was derived, using the formalism of Schrödinger and Bargmann
BERGMANN:
WHEELER:
DE WITT:
WHEELER:
DE WITT:
WHEELER: This already comes up in the electromagnetic case; what should one use for the stress energy tensor? One counts as gravitation producing only the excitations above the vacuum state, in order to avoid infinities. Here the only neutrino states one considers are the positive energy states; the negative energy states are all filled.
BELINFANTE:
WHEELER.
Linear and Toroidal Geons F. J. Ernst
Unified, Non-Symmetrical Field Theory M. Tonnelat
In order to avoid a point singularity, it is necessary in the static case to define an electric field which is finite at the origin. The formalism of the unified and non-symmetrical field theory immediately introduces the characteristic expressions of Born-Infeld theory.
By writing the fundamental tensor as the sum of two parts, we can relate it to the invariant Lagrangian that appears in the Born-Infeld electrodynamics and the two invariants of the Maxwell theory.
On the other hand, the Einstein theory introduces the contravariant tensor, which may also be written as a sum of symmetric and skew symmetric parts, which shall be called inductions. The relations foreseen partly by the Born-Infeld
We apply the equations of the field to the calculations of a static and
spherically symmetric solution of the form chosen by Papapetrou. We can then deduce the radial component of the electrostatic field,
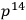 . Now introducing like Born-Infeld a field
. Now introducing like Born-Infeld a field
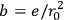 , we set
, we set
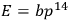 . Then, when
. Then, when
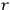 approaches 0,
approaches 0,
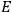 approaches
approaches
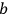 , a finite value. The originality of this conclusion comes from the fact that the values of the field and of the metric are not given a priori, but result from the field equations in the particular case of the Schwarzschild solution. We are now led to define a current following the principles of the Born-Infeld theory.
We find the charge density, after substitution of the values obtained in the
, a finite value. The originality of this conclusion comes from the fact that the values of the field and of the metric are not given a priori, but result from the field equations in the particular case of the Schwarzschild solution. We are now led to define a current following the principles of the Born-Infeld theory.
We find the charge density, after substitution of the values obtained in the  . So from the very principles of the unitary and non-symmetric
. So from the very principles of the unitary and non-symmetric
FEYNMAN: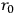 for an electron?
for an electron?
TONNELAT: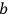 ;
;
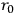 is a fundamental length.
is a fundamental length. 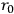 and mass, but there is a further arbitrariness in the choice of
and mass, but there is a further arbitrariness in the choice of
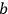 , so that the charge
, so that the charge
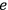 is not determined by the choice of
is not determined by the choice of
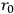 and
and
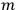 .
.
DAVIS: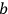 can be regarded as the ratio of the ordinary electromagnetic field to the natural electromagnetic field. It appears that
can be regarded as the ratio of the ordinary electromagnetic field to the natural electromagnetic field. It appears that
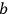 , as in the Born-Infeld theory could depend on the sign of the charge. Is this correct?
, as in the Born-Infeld theory could depend on the sign of the charge. Is this correct?
TONNELAT: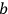 appears like the quotient of the physical field and the mathematical field.
appears like the quotient of the physical field and the mathematical field.
