WHEELER opened the session with a presentation of some conclusions reached by members of his group. Komar has investigated the interpretation of Mach's Principle and has found great difficulties, which are ascribed to the lack of understanding of the initial value problem. The stability of a Schwarzschild singularity in empty space to small disturbances was investigated with T. Regge. It was concluded that the Schwarzschild singularity is, to the extent investigated, stable against small disturbances away from its normal spherical form. Thermal geons were investigated with E. Power. A self-consistent problem was set up for the motion of photons of thermal radiation in a spherically symmetric gravitational field produced by these photons. It was found that a region existed in which photons would be trapped; there is a stable circular orbit in this region, and the other orbits consist of oscillations about the circular orbit. The limiting orbit is a spiral which is asymptotic to the outer boundary.
Ambiguity in a Gravitational Stress Energy Pseudotensor Interpreted in Terms of Arbitrariness in a `Base Line Coordinate System' W. R. Davis
In order to avoid the non-localizability to transform the stress energy pseudotensor, Kohler attempts to transform the stress energy pseudotensor in the given coordinate system, introducing in addition to the
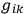 another set of quantities,
another set of quantities,
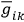 , such that the artificial metric described by the
, such that the artificial metric described by the
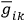 's possesses a zero curvature. He then shows that the difference between the gravitational pseudotensor defined by the
's possesses a zero curvature. He then shows that the difference between the gravitational pseudotensor defined by the
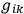 and
and
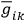 itself transforms like a tensor under coordinate changes. This result might seem to give a certain uniqueness to the definition of a gravitational stress energy tensor if one could imagine that the quantities,
itself transforms like a tensor under coordinate changes. This result might seem to give a certain uniqueness to the definition of a gravitational stress energy tensor if one could imagine that the quantities,
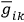 , were unique. However, a simple investigation shows that
the
, were unique. However, a simple investigation shows that
the
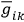 's are highly arbitrary. In fact, for every coordinate system,
's are highly arbitrary. In fact, for every coordinate system,
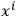 , that is asymptotically straight at infinity one can introduce a set of
, that is asymptotically straight at infinity one can introduce a set of
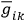 's which have the
normal Lorentz values everywhere. By this procedure the
's which have the
normal Lorentz values everywhere. By this procedure the
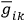 's are of course defined in any other coordinate system. The ambiguity in the choice of the
's are of course defined in any other coordinate system. The ambiguity in the choice of the
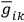 's in some specific coordinate system is therefore as great as the ambiguity in the choice of the original coordinate system which becomes asymptotically flat - an ambiguity can be regarded as a base line. Motions with respect to this base line can be thought of as due to “gravitational” forces. These gravitational forces define a gravitational stress energy tensor. This point of view has the following usefulness: One is in this way easily able to extend the discussions of the equivalence principle from the domain of equivalence between gravitation and acceleration at a point to the question of equivalence in the large. At a point the magnitude and direction of the acceleration are arbitrary. For discussing the equivalence principle in the large, the choice of the base coordinate system is arbitrary. Once one has selected this base coordinate system all else is uniquely determined.
's in some specific coordinate system is therefore as great as the ambiguity in the choice of the original coordinate system which becomes asymptotically flat - an ambiguity can be regarded as a base line. Motions with respect to this base line can be thought of as due to “gravitational” forces. These gravitational forces define a gravitational stress energy tensor. This point of view has the following usefulness: One is in this way easily able to extend the discussions of the equivalence principle from the domain of equivalence between gravitation and acceleration at a point to the question of equivalence in the large. At a point the magnitude and direction of the acceleration are arbitrary. For discussing the equivalence principle in the large, the choice of the base coordinate system is arbitrary. Once one has selected this base coordinate system all else is uniquely determined.
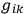 another set of quantities,
another set of quantities,
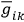 , such that the artificial metric described by the
, such that the artificial metric described by the
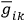 's possesses a zero curvature. He then shows that the difference between the gravitational pseudotensor defined by the
's possesses a zero curvature. He then shows that the difference between the gravitational pseudotensor defined by the
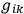 and
and
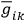 itself transforms like a tensor under coordinate changes. This result might seem to give a certain uniqueness to the definition of a gravitational stress energy tensor if one could imagine that the quantities,
itself transforms like a tensor under coordinate changes. This result might seem to give a certain uniqueness to the definition of a gravitational stress energy tensor if one could imagine that the quantities,
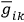 , were unique. However, a simple investigation shows that
the
, were unique. However, a simple investigation shows that
the
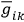 's are highly arbitrary. In fact, for every coordinate system,
's are highly arbitrary. In fact, for every coordinate system,
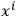 , that is asymptotically straight at infinity one can introduce a set of
, that is asymptotically straight at infinity one can introduce a set of
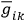 's which have the
normal Lorentz values everywhere. By this procedure the
's which have the
normal Lorentz values everywhere. By this procedure the
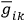 's are of course defined in any other coordinate system. The ambiguity in the choice of the
's are of course defined in any other coordinate system. The ambiguity in the choice of the
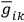 's in some specific coordinate system is therefore as great as the ambiguity in the choice of the original coordinate system which becomes asymptotically flat - an ambiguity can be regarded as a base line. Motions with respect to this base line can be thought of as due to “gravitational” forces. These gravitational forces define a gravitational stress energy tensor. This point of view has the following usefulness: One is in this way easily able to extend the discussions of the equivalence principle
's in some specific coordinate system is therefore as great as the ambiguity in the choice of the original coordinate system which becomes asymptotically flat - an ambiguity can be regarded as a base line. Motions with respect to this base line can be thought of as due to “gravitational” forces. These gravitational forces define a gravitational stress energy tensor. This point of view has the following usefulness: One is in this way easily able to extend the discussions of the equivalence principle 