In order to investigate the possibility of a physical system radiating gravitational waves, 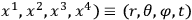 , then by a suitable choice of coordinates one can satisfy two conditions:
, then by a suitable choice of coordinates one can satisfy two conditions:
(a) The metric tensoris independent of the angle
.
(b) It is diagonal.
If one writes down the field equations in the empty space surrounding the system

|
one obtains a set of 7 equations (since
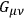 vanishes identically if one index is equal to 3) for the 4 diagonal components of
vanishes identically if one index is equal to 3) for the 4 diagonal components of
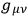 . Among these there exist 3 identities (the Bianchi identities,
. Among these there exist 3 identities (the Bianchi identities,
The field equations are non-linear and difficult to solve. It is proposed to investigate them by the method of successive approximations. As a beginning, the first approximation can be calculated. Let us write the line element in the form

|
where
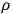 ,
,
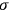 ,
,
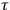 , and
, and
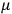 are regarded as small of the first order. The linear approximation of the field equations has the following form (indexes denoting partial differentiation):
are regarded as small of the first order. The linear approximation of the field equations has the following form (indexes denoting partial differentiation):
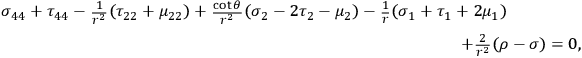
|
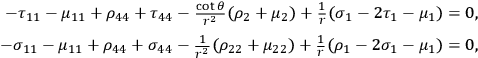
|
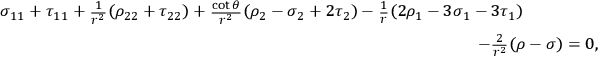
|
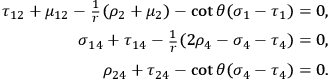
|
From these equations it is possible to derive the wave equation for
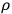 ,
,
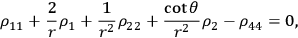
|
and to express the other unknowns in terms of the solution for
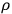 .
.
If we represent the radiating system by a quadrupole  , then the solution describing outgoing monochromatic waves can be written in terms of the frequency
, then the solution describing outgoing monochromatic waves can be written in terms of the frequency
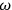 and the amplitude of the moment
and the amplitude of the moment
 ) as follows:
) as follows:

|
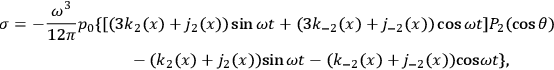
|
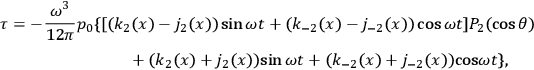
|
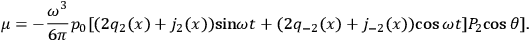
|
Here
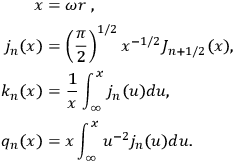
|
It is planned to use this solution as the starting point for a more accurate calculation. The interesting question, of course, is whether the exact equations have a solution going over into the above for sufficiently weak fields.
***
J. N. GOLDBERG
TONNELAT:
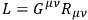
|
in which
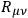 is the Ricci tensor built from an arbitrary affine connection
is the Ricci tensor built from an arbitrary affine connection
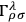 .
The variations
.
The variations
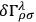 ,
,
 lead to the field equations. However, if one
tries to apply the Einstein, Infeld, Hoffmann method to these equations, one obtains merely the results of general relativity, and one does not obtain the equations for a charged particle. This result stems from the condition
lead to the field equations. However, if one
tries to apply the Einstein, Infeld, Hoffmann method to these equations, one obtains merely the results of general relativity, and one does not obtain the equations for a charged particle. This result stems from the condition
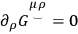
|
which is imposed by the theory.
To avoid this situation, one can start from an affine connection
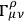 with vanishing torque
with vanishing torque
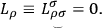
|
Lagrange multipliers are needed in the variations of
 because the 64
because the 64
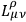 are not independent and, moreover, the vector
are not independent and, moreover, the vector
 related to the torque is introduced. In this case, one obtains
related to the torque is introduced. In this case, one obtains
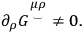
|
Introducing the metric
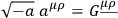
|
one obtains
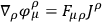
|
with
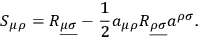
|
Setting
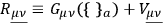
|
defines a tensor
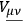 whose divergence gives a Lorentz force. This tensor plays in the field equations the role of a Maxwell tensor and leads, with the use of an extension of the Einstein, Infeld, Hoffmann method, to a Coulomb force.
whose divergence gives a Lorentz force. This tensor plays in the field equations the role of a Maxwell tensor and leads, with the use of an extension of the Einstein, Infeld, Hoffmann method, to a Coulomb force.
