H. SALECKER
The method by which a clock can be used to determine a space-like distance between two events A and B is as follows:
Let the geodesic world line of the clock pass through the event A at time
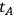 , and suppose that the clock emits a continuously
modulated light signal, e.g., monotonically changing color.1 Let this signal be reflected
at event B by a briefly exposed mirror. The time of emission
, and suppose that the clock emits a continuously
modulated light signal, e.g., monotonically changing color.1 Let this signal be reflected
at event B by a briefly exposed mirror. The time of emission
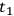 of the reflected portion of the signal will be determined by inspection of the color of this portion when it eventually returns to the
clock at time
of the reflected portion of the signal will be determined by inspection of the color of this portion when it eventually returns to the
clock at time
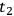 . The invariant distance S between A and B is then given by
. The invariant distance S between A and B is then given by
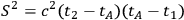
|
provided
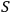 is small compared to the radius of curvature of the space-time neighborhood of the two events.
is small compared to the radius of curvature of the space-time neighborhood of the two events.
A time-like distance can of course be measured by the obvious method of letting the clock pass along a geodesic between the two events.
SALECKER
One must first ask the question: What is the accuracy with which a clock can be read, independently of inherent inaccuracies of the clock itself? At the beginning of a time interval an observer may emit a light signal to read the clock. If the length of the signal’s train is
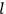 and if the pulse is properly shaped, the root mean square uncertainty in the initial time measurement will be
and if the pulse is properly shaped, the root mean square uncertainty in the initial time measurement will be
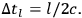
|
The clock may simultaneously be made to emit a photon to compensate for recoil. However, an inevitable uncertainty in the clock’s momentum will remain, of amount
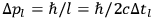
|
corresponding to an energy uncertainty in the light signal of amount
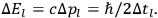
|
The clock will generally have also an initial position uncertainty
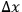 giving rise to a momentum uncertainty
giving rise to a momentum uncertainty
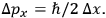
|
The total momentum uncertainty after the first reading is therefore
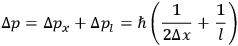
|
corresponding to a velocity uncertainty of amount

|
where
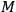 the mass of the clock. (We neglect here certain relativistic corrections which SALECKER
the mass of the clock. (We neglect here certain relativistic corrections which SALECKER 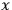 is the mean distance from the observer to the clock
then the time at which the observer receives the initial reading from the clock will be
is the mean distance from the observer to the clock
then the time at which the observer receives the initial reading from the clock will be
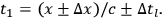
|
The time at which the observer receives a second reading at the end of a (clock’s) time interval
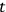 will be
will be
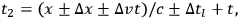
|
giving for the total inaccuracy in the reading of the time interval
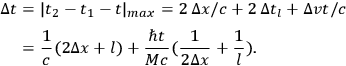
|
The minimum uncertainty is achieved by choosing
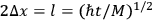 , which yields
, which yields
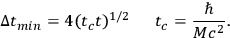
|
Evidently the accuracy of reading is greater the larger the mass of the clock. On the other hand, the gravitational field of the clock will be disturbing if its mass is made too large. One has therefore to consider the problem of how to construct a clock which shall be as light and as accurate as possible. One must at this point take into account the inherent inaccuracies in the clock itself, by considering its atomic structure.
A single atom by itself represents to a very high degree of accuracy an oscillator, but in spite of this it is not possible to take a single atom emitting radiation as a clock. Before an oscillator can be considered to be a clock it must be possible to register its information; i.e., the atom must be coupled with a device to count the number of times the emitted electromagnetic field strength reaches a certain value. Such a counting device would be in contradiction with the principles of quantum mechanics.
As his first model, therefore, SALECKER 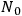 of elementary systems initially in an excited state. The systems were assumed to go over directly to a ground state and to be sufficiently
well separated so as not to reexcite one another. If the decay rate is
of elementary systems initially in an excited state. The systems were assumed to go over directly to a ground state and to be sufficiently
well separated so as not to reexcite one another. If the decay rate is
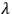 , then the probability of finding
, then the probability of finding
 systems remaining in the excited state after a time
systems remaining in the excited state after a time
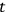 is
is

|
where
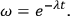
|
The average value of
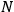 and the root mean square deviation at time
and the root mean square deviation at time
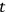 are given respectively by
are given respectively by
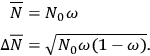
|
The registering device in the clock has only to count the number of atoms remaining in the excited state (or, alternatively, the number of systems which have decayed) in order to record a statistical time given by
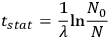
|
which has an uncertainty of amount
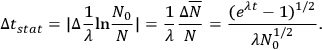
|
The minimum uncertainty is achieved by choosing
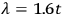 , which yields
, which yields
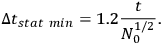
|
A final uncertainty arises from the fact that the registering device must distinguish between excited and unexcited systems, and for this purpose a time
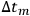 at least as great as
at least as great as
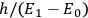 is required, where
is required, where
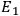 and
and
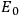 are respectively
the elementary excited and ground state energy levels. In the most favorable case the decaying systems would undergo complete disintegration with, for example, the emission of two photons in opposite directions so as to eliminate recoil. The registering
device might then be a counter to detect the photons, but however
constructed it would have an absolute minimum time inaccuracy of amount
are respectively
the elementary excited and ground state energy levels. In the most favorable case the decaying systems would undergo complete disintegration with, for example, the emission of two photons in opposite directions so as to eliminate recoil. The registering
device might then be a counter to detect the photons, but however
constructed it would have an absolute minimum time inaccuracy of amount
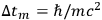 , corresponding
to photon energies of order
, corresponding
to photon energies of order
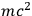 where
where
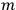 is the mass of a decaying elementary component of the clock.
is the mass of a decaying elementary component of the clock.
The total inaccuracy in the measurement of a time interval
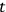 by means of a statistical clock is therefore at least
by means of a statistical clock is therefore at least
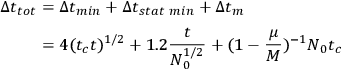
|
where
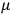 is the mass of the registering device plus the framework of the clock, and
is the mass of the registering device plus the framework of the clock, and
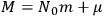 is the total clock mass. If one is clever enough in the construction
of the clock the number
is the total clock mass. If one is clever enough in the construction
of the clock the number
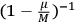 may be kept from being excessively large. The minimum total inaccuracy for a given total mass
may be kept from being excessively large. The minimum total inaccuracy for a given total mass
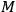 is achieved by choosing
is achieved by choosing

|
which yields

|
SALECKER 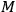 and
and
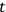 (e.g., suitable for a certain experiment) it may be utterly impossible to choose the optimum value of
(e.g., suitable for a certain experiment) it may be utterly impossible to choose the optimum value of
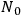 , because of the very limited range of elementary-system masses
, because of the very limited range of elementary-system masses
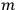 occurring in nature. SALECKER therefore considered, as a third model, a very hypothetical type of clock, consisting of a single elementary harmonic oscillator, but
operating at sufficiently high quantum numbers for it to be “read” like a classical device. Permitting himself to imagine an elementary oscillator which could function even at relativistic energies, he found for the minimum total uncertainty
occurring in nature. SALECKER therefore considered, as a third model, a very hypothetical type of clock, consisting of a single elementary harmonic oscillator, but
operating at sufficiently high quantum numbers for it to be “read” like a classical device. Permitting himself to imagine an elementary oscillator which could function even at relativistic energies, he found for the minimum total uncertainty
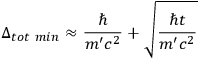
|
where
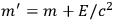 ,
,
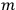 being the rest mass of the oscillator and
being the rest mass of the oscillator and
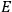 is its excitation energy.
is its excitation energy.
The quantity
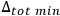 is seen generally to depend on the time interval itself. When
is seen generally to depend on the time interval itself. When
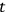 becomes of the order of
becomes of the order of
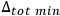 then the time interval can no longer be measured.
In every case the smallest time interval which can be measured
is roughly
then the time interval can no longer be measured.
In every case the smallest time interval which can be measured
is roughly

|
That is, the time associated with the mass of one of the elementary systems out of which the clock is constructed represents an absolute minimum for measurable time intervals. This minimum arises, of course, from the coupling between the registering device and the elementary systems, and would exist even if the registering device were removed from the immediate vicinity of the clock proper. (For example, the registering device might be the observer himself, but then, in the case of the statistical
clocks, the observer would have to send out a large number of photons so as to “read” each elementary system separately, thus raising the reading error from
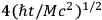 to
to
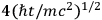 .) Since, for existing elementary systems,
.) Since, for existing elementary systems,
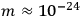 g, the corresponding time
g, the corresponding time
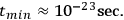 may, presently at least, be regarded as an
absolute lower limit to measurable time intervals.
may, presently at least, be regarded as an
absolute lower limit to measurable time intervals.
SALECKER
1The direct measurement of
 .
.
2The measurement of
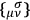 through the observation of geodesics.
through the observation of geodesics.
3The measurement of the scalar curvature of a three-dimensional space-like cross section of a quasi-static region of space-time. This is defined by
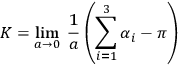
|
where
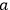 is the area of a small triangle (or prism, in space-time) around which a test body is passed, and the
is the area of a small triangle (or prism, in space-time) around which a test body is passed, and the
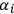 are its angles. (He also proposed that a direct measurement of the Riemann tensor should be carried out, by the method suggested in a previous session by Pirani
are its angles. (He also proposed that a direct measurement of the Riemann tensor should be carried out, by the method suggested in a previous session by Pirani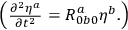 He had not been aware of this possibility prior to the conference.)
He had not been aware of this possibility prior to the conference.)
Carrying out these conceptual measurements on the gravitational field of a particle of protonic mass, using a particle of electronic mass as a test particle, and choosing the most favorable clock model to serve as measuring apparatus, SALECKER
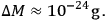
|
That is, the uncertainty is of the same order as the mass itself. From this, he concluded that the gravitational mass of a single proton is not strictly an observable quantity.
FEYNMAN 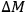 in terms of fundamental constants, omitting dimensionless factors. SALECKER replied that this would be
quite difficult. The difficulty seems to be that one has to account for the perturbing effect of the clock and, in effect, solve a two-body problem. The uncertainty in the measurement of time increases proportionally to some fractional power (
in terms of fundamental constants, omitting dimensionless factors. SALECKER replied that this would be
quite difficult. The difficulty seems to be that one has to account for the perturbing effect of the clock and, in effect, solve a two-body problem. The uncertainty in the measurement of time increases proportionally to some fractional power (
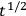 or
or
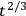 ) of the interval being measured, and decreases with increasing clock mass. On the other hand the bigger the clock the greater its perturbing (or masking) effect. One has to carry out a minimizing procedure in which the interval
) of the interval being measured, and decreases with increasing clock mass. On the other hand the bigger the clock the greater its perturbing (or masking) effect. One has to carry out a minimizing procedure in which the interval
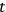 , the
protonic mass under observation, the clock mass
, the
protonic mass under observation, the clock mass
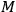 , and, in the case of statistical clocks, the number
, and, in the case of statistical clocks, the number
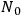 are all involved. In the resulting numerical computations the fundamental constants get mixed up in a very complicated way. SALECKER did say, however, that
are all involved. In the resulting numerical computations the fundamental constants get mixed up in a very complicated way. SALECKER did say, however, that
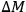 is proportional to the mass being measured, the factor of proportionality depending on the ratio of the gravitational radius of this mass to that of the clock.
is proportional to the mass being measured, the factor of proportionality depending on the ratio of the gravitational radius of this mass to that of the clock.
(The editors would like to suggest that, in view of the long range character of the gravitational force, discussed previously, the gravitational constant may, in the last analysis, not enter into the factor of proportionality. Furthermore, the value actually found for
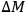 may in some way reflect the fundamental limitation in the clock, viz. that it cannot be constructed out of elementary systems having masses smaller than those found in nature, i.e., protonic.)
may in some way reflect the fundamental limitation in the clock, viz. that it cannot be constructed out of elementary systems having masses smaller than those found in nature, i.e., protonic.)
FEYNMAN
SALECKER
ROSENFELD 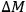 depends on
depends on
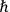 .
.
SALECKER g for the proton mass, etc.).
g for the proton mass, etc.).
ROSENFELD
Roughly speaking, the inaccuracy in the measurement of a gravitational potential - say
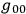 - will be proportional to the inaccuracy in the determination of lengths. Therefore, if you can determine lengths with any accuracy, then you can also determine the potential with any accuracy. However, quantum considerations tell you that if the position of the measuring rod or clock is known to an accuracy
- will be proportional to the inaccuracy in the determination of lengths. Therefore, if you can determine lengths with any accuracy, then you can also determine the potential with any accuracy. However, quantum considerations tell you that if the position of the measuring rod or clock is known to an accuracy
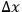 then its momentum is uncertain by an amount
then its momentum is uncertain by an amount
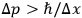 . This gives rise to an uncertainty in the value of the gravitational field produced by the measuring instrument.
. This gives rise to an uncertainty in the value of the gravitational field produced by the measuring instrument.
The factors which saved Bohr and Rosenfeld
1Because of the existence of both negative and positive charge the perturbing field of the measuring instrument could be reduced to a dipole field.
2The charge to mass ratio of the measuring instrument could be controlled.
Therefore, Bohr and Rosenfeld came to the conclusion that the measurement of any component of the electromagnetic field could be carried out with arbitrarily high precision in spite of the quantum restrictions.
These saving features are not present in the gravitational case. Wheth-er one takes the measuring instrument heavy or light its perturbing effect will be roughly the same (proportional to
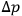 ). Therefore ROSENFELD
). Therefore ROSENFELD
WHEELER
He then went on to imagine what sort of ideas scientists might come up with if they were “put under torture” to develop a theory that would explain all the elementary particles and their interactions solely in terms of gravitation and electromagnetism alone! He first took a look a magnitudes and dimensions. In the
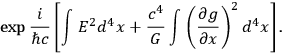
|
Therefore if one is making measurements in a space-time region of volume
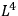 , contributions to this sum will be more or less in phase until variations in the electromagnetic
and gravitational field amplitudes from their classical values become as large as
, contributions to this sum will be more or less in phase until variations in the electromagnetic
and gravitational field amplitudes from their classical values become as large as
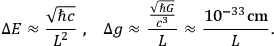
|
These represent the quantum fluctuations of the electromagnetic and gravitational fields. In the gravitational case, owing to the nonlinearity of the field equations truly new effects come into play at distances as small as
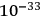 cm where
cm where
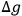 becomes of the order of unity. WHEELER
becomes of the order of unity. WHEELER
In this way he has been led to the concept of “wormhole” in space.
WHEELER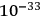 cm could be arrived at, by considering only the fluctuations in the electromagnetic field. A fluctuation of amount
cm could be arrived at, by considering only the fluctuations in the electromagnetic field. A fluctuation of amount
 would correspond to an energy fluctuation of
amount
would correspond to an energy fluctuation of
amount
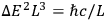 in a region of dimension
in a region of dimension
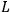 . The gravitational energy produced in this region by this fluctuation would be of the order of
. The gravitational energy produced in this region by this fluctuation would be of the order of
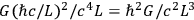 . The two energies become comparable when
. The two energies become comparable when
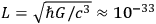 cm. In WHEELER’s “dream of the tortured scientists” the wormholes
cm. In WHEELER’s “dream of the tortured scientists” the wormholes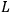 would yield a value of the order of
would yield a value of the order of
 which would represent a rough average of the apparent charge associated with each wormhole. No quantization of charge is implied here. In fact the wormholes themselves have nothing directly to do with
elementary particles. WHEELER envisaged an elementary particle as a vast structure (
which would represent a rough average of the apparent charge associated with each wormhole. No quantization of charge is implied here. In fact the wormholes themselves have nothing directly to do with
elementary particles. WHEELER envisaged an elementary particle as a vast structure (
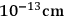 ) compared to a wormhole. However, he left open the possibility that elementary particles might somehow be constructed out of wormholes. He compared the
wormholes to “undressed particles,” their continual formation corresponding to pair production which is going on in the vacuum at all times. The electromagnetic mass associated with each wormhole is of the order of
) compared to a wormhole. However, he left open the possibility that elementary particles might somehow be constructed out of wormholes. He compared the
wormholes to “undressed particles,” their continual formation corresponding to pair production which is going on in the vacuum at all times. The electromagnetic mass associated with each wormhole is of the order of
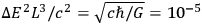 g, but this huge mass is almost entirely
compensated by an equivalent amount of negative gravitational energy.
g, but this huge mass is almost entirely
compensated by an equivalent amount of negative gravitational energy.
(Editor’s Note: No one at the conference thought to ask Wheeler
WHEELER
• (1) Electromagnetism without electromagnetism.: By this, WHEELER
• (2) Mass without mass.: This concept is illustrated by geons,
• a) Electromagnetic geons.:
• b) Geons built out of neutrinos.:
• c) Geons built out of pure gravitational radiation alone.:
• (3) Charge without charge.: Wormholes.
• (4) Spin without spin.:
• (5) Elementary particles without elementary particles.:
As for the last two ideas, WHEELER which occurs in the action.
which occurs in the action.
FEYNMAN is positive,
is positive,
 is always of the same sign. A much more serious problem, he felt, would be to determine what happens if
is always of the same sign. A much more serious problem, he felt, would be to determine what happens if
 changes sign.
changes sign.
BELINFANTE
WHEELER
WEBER
As for “elementary particles without elementary particles,” WHEELER
Over a tremendous range the wave satisfies the simple relation
 . When the wavelength becomes of the order of the size of the universe (
. When the wavelength becomes of the order of the size of the universe (
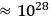 cm), however, the phase velocity is greater than
cm), however, the phase velocity is greater than
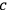 , as has been shown long ago by Schrödinger (Papal Acad.). On the other hand, when the wavelength becomes of the order of
, as has been shown long ago by Schrödinger (Papal Acad.). On the other hand, when the wavelength becomes of the order of
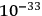 cm the disturbance will be slowed down by the foam-like structure of the vacuum (and also by having always to climb over the metric bump which it is itself
continuously creating due to its large energy concentration - Ed.).
WHEELER
cm the disturbance will be slowed down by the foam-like structure of the vacuum (and also by having always to climb over the metric bump which it is itself
continuously creating due to its large energy concentration - Ed.).
WHEELER
GOLD
WEBER ) could give rise to such a well-defined quantity as the observed charge on an electron, except possibly by some statistical means.
) could give rise to such a well-defined quantity as the observed charge on an electron, except possibly by some statistical means.
FEYNMAN
WHEELER associated with an undressed particle and the observed charge
associated with an undressed particle and the observed charge
 on an electron could be accounted for by vacuum polarization.
on an electron could be accounted for by vacuum polarization.
ROSENFELD
FEYNMAN
ROSENFELD 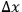 and
and
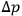 in the measuring instrument affect different components of the gravitational potential, leading to reciprocal relations of the form
in the measuring instrument affect different components of the gravitational potential, leading to reciprocal relations of the form

|
which would not, however, prevent the precise determination of the value of a given component.
ANDERSON 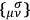 which have neither invariance nor tensor properties.
which have neither invariance nor tensor properties.
BARGMANN
ANDERSON
BERGMANN
PIRANI remarked that, in any case, if you are clever enough you should be able to construct true invariants or tensors (which don’t depend on your gadgets) from the results of reading your gadgets.
This concluded the discussion of the problems of measurement. Attention next turned to the technical aspects of the purely formal problems which arise when the attempt is made to apply mathematical quantization procedures to the gravitational field.

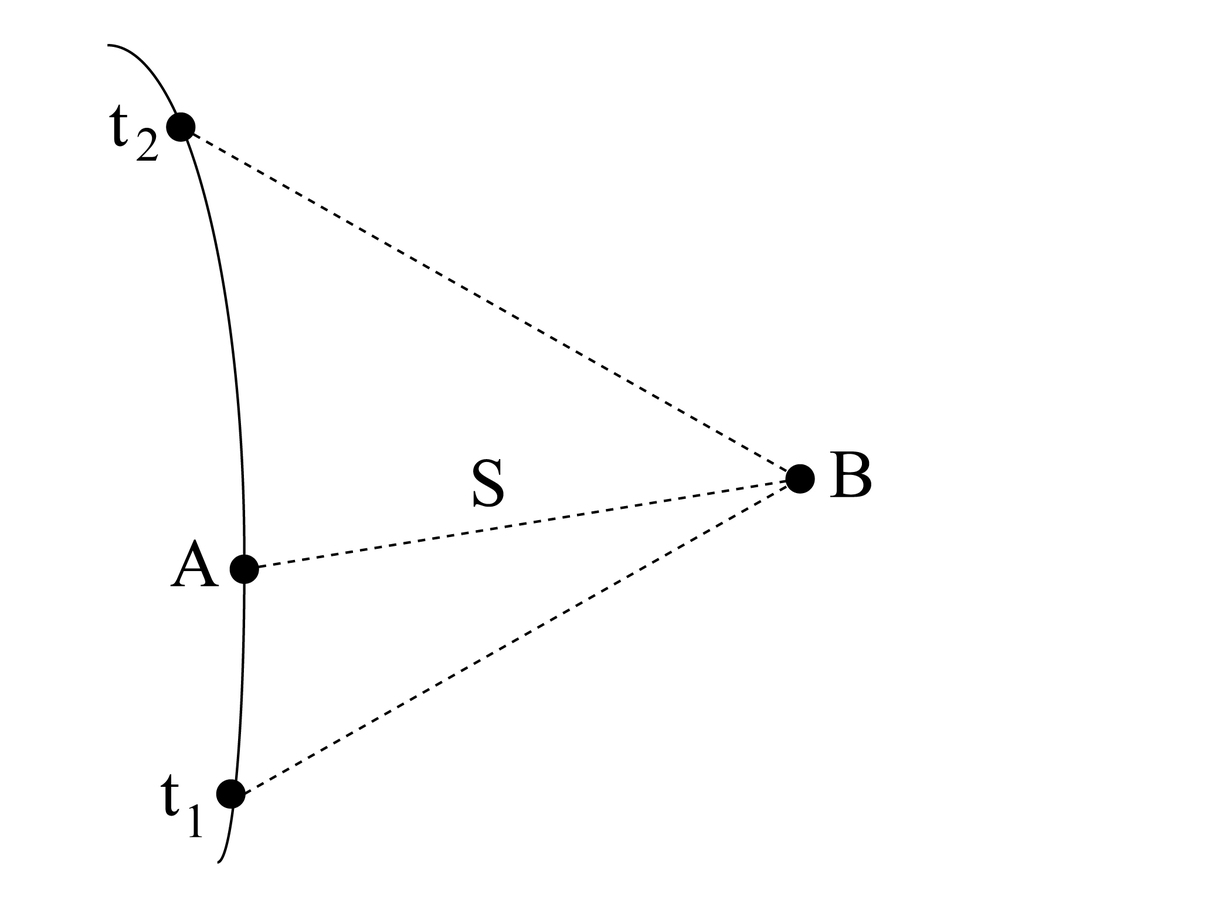



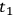 of a pulsed signal. The editors have inserted the idea of color modulation in order to avoid objections based on the principle of causality.
of a pulsed signal. The editors have inserted the idea of color modulation in order to avoid objections based on the principle of causality.