22 The Possibility of Gravitational Quantization

KURSUNOGLU began by asking that those who had presented techniques for quantizing the gravitational field in the morning session make it clear whether or not it has been decided that quantization is possible according to these techniques. He suggested that before one builds a house, he should buy the ground first. WHEELER asked, “Don't we believe that the that the theory should be quantized?” BARGMANN asked if Kursunoglu's question had to do with matters of convergence. He pointed out that it is not easy to decide whether or not one can quantize, because many things may be meant by this question. WHEELER said in a quantum theory of gravitation we would expect new, fascinating physics to come out, because the physical constants that appear in the quantum theory are the gravitation constant , the velocity of light , and the Planck's constant , but whether the results of such a theory would agree with experiment is another question. In the classical theory we have no natural mass or length. BONDI suggested that, when one does construct natural units of mass and length from these constants they may turn out to be much smaller than anything present-day physics is interested in. WHEELER replied that in a session of the day before, he had suggested a way in which one could get quantities which have a range of size inside the interesting realm. GOLD said the theory of electrodynamics required quantization because there was a broad range of phenomena that had to be accounted for; for example, the infrared catastrophe had to be somehow explained. With gravitation, one could say that either it must be quantized because otherwise one might get into a contradiction with the logical structure of quantum theory, or else that there exists a broad range of phenomena which the classical theory (without quantization) is unable to explain. But this latter range of phenomena seems to be missing, unless there is gravitational radiation and some kind of “infrared” divergence occurs there. WHEELER said that it might turn out that the elementary particles depend on gravitational fluctuations for their stability. GOLD said that this was only a hope, and WHEELER agreed that a proof was missing. ANDERSON asked if there was anything wrong with the argument that if it were possible to measure all gravitational fields accurately, that one would have enough information to violate the uncertainty principle. WHEELER answered that this was Gold's first point. GOLD said that he wanted still to be convinced that one gets into a contradiction by not quantizing the gravitational field. DE WITT said that that there is a conceptual problem here in that if the matter fields are quantized, one must decide what to use as the source of the gravitational field. If our experiments lead us to believe that the gravitational field is produced by what one may call the expectation value of the stress-energy tensor, there is still a difficulty because the expectation value depends on the measurements we make on the system. After the system has been prepared in a definite state, a measurement can change the expectation value and so the gravitational field suddenly changes because of a measurement performed on the system. Classical gravitation theory works only because the experimental fluctuations are so small on the scale at which gravitational effects become noticeable.

FEYNMAN then proposed the following experiment.

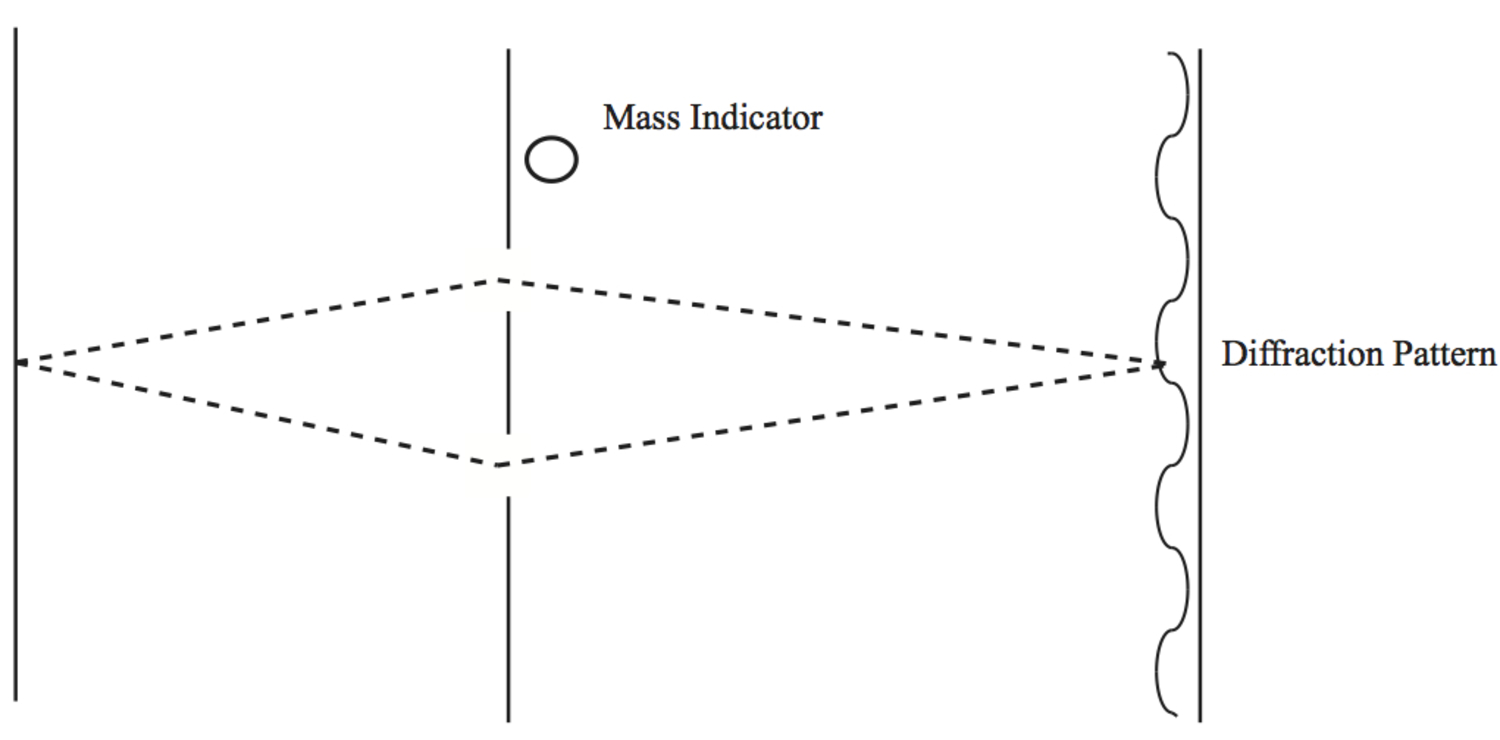
If one works in space-time volume of the order of 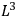in space and 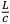in time, then the potentials are uncertain by an amount

and 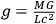is the potential produced by a mass 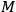in the region . An uncertainty in the potential is then equivalent to an uncertainty in the measurement of 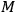, and one gets 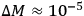grams. This means that if the time of observation is restricted to be less than 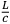, then the mass can't be determined to better accuracy than this. Of course, if one is allowed an infinite time, 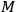can be determined as accurately as one wants. If, however, this is not possible because the particle must be allowed to pass through the equipment, then unless the mass is at least of the order of 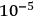, the apparatus will be unable to discover the difficulty (no contradiction). One can conclude that either gravity must be quantized because a logical difficulty 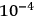would arise if one did the experiment with a mass of order grams, or else that quantum mechanics fails with masses as big as 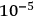grams.

UTIYAMA 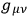then presented a technique for quantizing the gravitational field using Gupta's method. “One of the most attractive points of Einstein's theory of general relativity seems to be that the fundamental tensor can be interpreted as a potential of the gravity on the one hand, and as a metric tensor of the space-time world on the other hand. In trying to quantize the gravitational field, however, the metric interpretation of will cause some troubles, especially from the observational viewpoint. Therefore, contrary to Einstein's original intention, the separation of this geometrical concept from the interpretation of seems convenient for the quantization of the gravitational field. Gupta's [1] approach seems adequate to this line of thought.

We have investigated the cancellation between contributions from the electromagnetic and the gravitational interactions by using Gupta's method of quantization of the weak gravitational field [2].

Under the assumption of the weak field, we can put

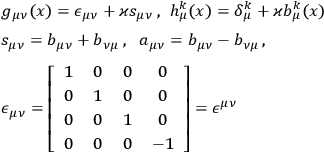
where 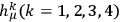is the so-called 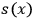“vierbeine”. or 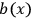is, in our approximation, considered as a field quantity in Minkowski-space, and the dual interpretation of 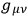is abandoned. The quantization of 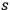or is made by following Gupta's method [2].

Let us consider a system of electrons, photons and gravitons interacting with each other. The interaction Lagrangian is

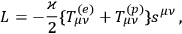
where the energy-momentum tensor of the electron-field includes the interaction between the electron and the photon fields, and 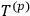is the energy-momentum tensor of the photon field. In order to avoid the formal difficulties due to the derivative couplings appearing in 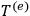and 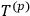, Schwinger's dynamical principle [3,4] is suitable to derive the S-matrix in the interaction representation. The S-matrix is written in the form

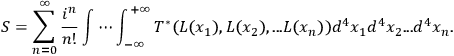
Following Dyson's analysis of the divergences appearing in any element of S-matrix, we see that there occur so many types of primitive divergences owing to the derivative couplings that this system is unrenormalizable.

In our present treatment the most essential feature of the gravitational field, namely, the non-linearity is not taken into account. Accordingly it is not clear how far our conclusion is reliable.”