Chapter structure
- 3.1 The long-term transmission of mechanical knowledge
- 3.2 The ancient roots of mechanics
- 3.3 Preclassical mechanics
- 3.4 The ancient and medieval origins of the equilibrium controversy
- 3.5 Jordanus' approach to positional heaviness
- 3.6 Tartaglia's approach to positional heaviness
- 3.7 Cardano's approach to positional heaviness
- 3.8 Guidobaldo's approach to positional heaviness
- 3.9 Benedetti's approach to positional heaviness
- 3.10 Benedetti, Guidobaldo, and Galileo
- 3.11 Theoretical excursus: mental models in the transmission of knowledge
- Footnotes
3.1 The long-term transmission of mechanical knowledge
The context of this discussion of the equilibrium controversy, based on Guidobaldo's marginalia, is the long-term development of mechanical knowledge, in particular from the origin of theoretical mechanics in antiquity to the dawn of classical mechanics in the late Renaissance, when the controversy first became a central issue of contemporary discussions. It may be helpful therefore to begin with a brief survey of the history of mechanics, a history that extends over more than two millennia. This long period can be divided into six more or less coherent periods:
1The first period may simply be called the prehistory of mechanics; it comprises the long period in which human cultures accumulated practical mechanical knowledge without documenting this knowledge in written form and without developing theories about it. Although the origin of other sciences such as mathematics and astronomy can be traced back to ancient urban civilizations such as those of Babylonia and Egypt, this, surprisingly, is not the case for mechanics. Although there are numerous sources testifying to the large construction projects of these civilizations, there is in fact not one single document referring to the mechanical knowledge that must have been involved in these endeavors.
2The next period properly merits the label origin of mechanics. It saw, in particular, the formulation and proof of the law of the lever. More generally, it is characterized by the appearance of the first written treatises dedicated to physics and mechanics in ancient Greece, associated in particular with names such as Aristotle, Euclid, Archimedes, and Heron.1 These works had an enormous impact on the subsequent development of mechanical knowledge. Aristotelian physics focused on the role of forces on moving bodies, and Aristotelian and Archimedean mechanics, based on the law of the lever, provided two fairly independent points of reference for the development of theoretical mechanics. They finally merged into one common conceptual basis for a new coherent theory of mechanics only with the advent of classical physics in the late seventeenth and eighteenth centuries.
3The third period is, at the beginning, characterized by the transformation of mechanics into a science of balances and weights and the enrichment of Aristotelian physics by a theory of impetus and a mathematical extension of the Aristotelian doctrine of generation and corruption to a theory of changing qualities. This period covers the Arabic and Latin Middle Ages, which saw the production of a substantial literature on mechanics focused on a relatively small range of subjects, in particular, the behavior of the balance and the justification of the law of the lever, and the changing qualities of mechanical bodies such as heaviness and velocity.
4The fourth period is that of preclassical mechanics, ranging from the sketches of Renaissance engineers such as Leonardo da Vinci2 to the mature works of Galileo Galilei. In contrast to the preceding period, it deals with an increasingly large number of subjects, including the inclined plane, the pendulum, the stability of matter, and the spring, in attempts to integrate the science of weights with the effect of forces on moving bodies, which necessarily transformed the inherited theoretical building blocks.
5The fifth period is that of the rise of a mechanistic world view. The successful integration of earlier traditions into the fundament of classical physics appeared without alternatives. From the first comprehensive vision of a mechanical cosmos, such as that of Descartes, via the establishment of classical and later analytical mechanics, this process led to the attempts of nineteenth-century scientists to build physics on an entirely mechanical foundation, which was conceived as an ontological basis of the natural sciences.
6The sixth period comprises the decline of the mechanistic world view and the disintegration of mechanics at the turn of the nineteenth to the twentieth century, resulting in the emergence of modern physics and its conceptual revolutions represented by the relativity and quantum theories.
This schematic overview of the long-term development of mechanics raises a number of puzzling questions. For example: How did theoretical mechanics originate in ancient Greece and why did this not happen earlier? What kind of knowledge made the formulation of the law of the lever possible, and what knowledge was required for its proof? What accounts for the remarkable differences between the medieval science of weights and preclassical mechanics? What kind of empirical knowledge made the emergence of classical mechanics possible and what accounts for its remarkable stability over the more than 200 years of classical physics? What explains the steady development, consolidation, and stabilization of Aristotelian physics over more than 2000 years? How can one explain the disintegration of mechanical concepts around the turn from the nineteenth into the twentieth century and the creation of revolutionary theories such as general relativity and quantum theory, which proved to be an adequate foundation for today's physical and cosmological knowledge, although that knowledge was not available when they emerged? How did the law of the lever survive all these changes? And finally the question that will come under closer scrutiny in the present volume, how did the concept of positional heaviness emerge and, under varying labels, become an integral part of preclassical and, after a substantial transformation, of classical mechanics?
3.2 The ancient roots of mechanics
The development of mechanical knowledge sketched here was a non-linear and multi-layered historical process. In particular, the following analysis of the specific process of the transmission of mechanical knowledge from antiquity to the Arabic and Latin Middle Ages and finally to the Renaissance makes it clear that the development of mechanics was anything but a successive accumulation and theoretical integration of a growing body of mechanical knowledge. Theoretical mechanics had a twofold root in the ancient Greek reflection on practical experiences. On the one hand, there was the intuitive experience that in order to move a body a certain effort is required depending on its weight. This experience became the basis of the concept of force as the cause of terrestrial and celestial motion in Aristotelian dynamics. On the other hand, the reflection on the potential of mechanical devices to reduce the force required to move a body became the basis of the Archimedean theory of equilibrium and its generalization in the concept of the center of gravity.
In ancient Greece the development of these basic concepts of mechanics was an issue of highly personalized communication between the members of a relatively small group of experts, for which the correspondence of Archimedes is typical.3 There was a strong relation between authors, their theoretical biases, and their specific subjects. Following the model of Euclid's compilation of the mathematical knowledge of his time, Archimedes tried to present his insights in the form of deductive treatises.4 Thus, the concept of center of gravity became the core concept of deductive mechanics. Aristotle, in contrast, presented his account of natural phenomena in a network of categorizations linked by syllogisms. Originally, there was no intimate relation between Aristotelian dynamical explanations of motion and gravity, on the one hand, and the deductive mathematical method, on the other. Similarly, Aristotelian explanations of mechanical devices merely followed the tradition of the literature presenting issues in form of problems and their solutions, without exposing an immanent necessity constituted by its subject. Finally, the shift from a personalized to a more institutionalized representation of knowledge in late antiquity contributed much to the historical transfer of the ancient heritage, but resulted in a compilation rather than an integration of the various elements of mechanics developed in the ancient Greek tradition.
3.3 Preclassical mechanics
Preclassical mechanics of the sixteenth and early seventeenth centuries was characterized by an elaboration of the knowledge resources available in light of challenging objects such as labor-saving machinery, ballistics, the stability of architecture, or ship-building provided by contemporary technology. Preclassical mechanics was a historical stage in its own right in the development of mechanics. It was pursued by a class of engineer-scientists who addressed these technical challenges by drawing on heterogeneous bodies of knowledge, which comprised the growing set of recovered ancient scientific and technical texts. The heterogeneity as well as the fragmentary nature of the shared knowledge of early modern science, especially with regard to the heritage of ancient science and its subsequent transformation, is well illustrated by the conflictual integration of Aristotelian and Archimedean knowledge resources on mechanics as it can be traced in the works of Tartaglia, Cardano, Guidobaldo, Benedetti, Galileo, and many others, and in particular also in the conflicting approaches of Guidobaldo and Benedetti documented in this volume.
No simplistic division of the protagonists of preclassical mechanics into followers of Aristotelian dynamics and Archimedean statics, into northern and central Italian schools, into Aristotelians and anti-Aristotelians, will be able to do justice to the complex interlocking of the diverse components of the shared ancient heritage.5 For instance, the works of Archimedes on statics and hydrostatics provided not only a model for a deductive theory of physics emulating the structure of Euclid's Elements, but also assets to modify specific explanations within an Aristotelian conceptual framework, in particular, the Aristotelian explanation of free fall in media with the help of the Archimedean concept of extrusion. Conversely, Aristotelian natural philosophy provided a physical underpinning to the Archimedean theory of equilibrium of planes, fostering its extension to a more comprehensive treatment of mechanics. Although discussions about mechanics in the early modern period were often shaped by questions of the superiority or compatibility of the diverse bodies of knowledge inherited from antiquity, in the end everyone drew from the same sources so that Aristotelian and Archimedean elements are found alongside each other, albeit in different constellations, in the works of authors as diverse as Tartaglia, Cardano, Guidobaldo, Benedetti, and Galileo.
The integration of these elements took place under the new conditions of the early modern period for the development of mechanical knowledge that were given not only by the emergence of challenging objects, but also by an intellectual context that involved many more actors intervening simultaneously than had ever been the case since antiquity. Accordingly, the inherent potential of the traditional bodies of knowledge was much more intensely exploited than ever before – in directions shaped, but not uniquely determined, by the concrete material at hand, that is, by the challenging objects that represented focal points of attention.
As a consequence, a multiplicity of different pathways developed, sometimes leading to the same insights into a given problem, sometimes to diverging opinions on it. At the same time, intrinsic tensions within a given traditional body now emerged more clearly, due to the fact that it was no longer, as was typically the case in antiquity, one single author or a string of authors separated by generations who were involved in its elaboration. Instead, one and the same problem was now often addressed from distinctive perspectives, thus becoming a borderline problem of different knowledge traditions and catalyzing their conflictual integration.6
The traditional image of this period, which still often lurks behind even the most sophisticated historical reconstructions, whereby single authors studied single problems with greater or lesser success as judged in hindsight, thus preparing the eventual combination of the pieces of a puzzle into one coherent whole, is fundamentally mistaken. In fact, strictly speaking, all solutions proposed in preclassical mechanics are untenable from the viewpoint of classical mechanics since they were articulated in conceptual frameworks incompatible with those of later science, making use of alien concepts such as positional heaviness, natural and violent tendencies, or impetus.
Thus, the emergence of classical mechanics from preclassical mechanics cannot have been an essentially cumulative process of selecting from ancient sources isolated pieces of knowledge that were deemed valuable, separating the wheat from the chaff, and then gradually adding new insights. Rather, the emergence of classical mechanics from its ancient roots must have amounted to the structural transformation of a system of knowledge, which involved a reorganization of conceptual systems on the basis of results achieved within traditional frameworks. Such a transformation would not have been possible without the interaction of the authors and a confrontation of their proposed solutions to mechanical problems, and can neither be described in terms of a linear accumulation of knowledge nor in terms of a competition between distinct schools or traditions.
When was a problem actually solved? With hindsight, we may claim, for instance, that Aristotle was the first to analyze the equilibrium of the balance, that Archimedes proved the law of the lever, that Jordanus solved the problem of the inclined plane, and that Galileo discovered the law of fall. With hindsight, it may indeed seem that these insights could have been achieved as isolated contributions, independent of the establishment of a larger, stable conceptual framework. From the perspective of preclassical mechanics, however, it is remarkable how far these solutions actually were from being evident or uncontroversial among the contemporaries. Some of these became the topic of heated debates, such as the question of the equilibrium of the balance. In particular, as will be seen in the following, the question of whether or not a balance with equal arms would, when deflected from the horizontal position, return to its original state, was controversially discussed by authors such as Tartaglia, Cardano, Guidobaldo, and Benedetti. The issue arose because partly different conceptual frameworks seemed to suggest different answers, since the exact relation between concepts such as center of gravity and positional heaviness had not yet been definitively established.
Solutions that appear to come close to the correct solution in classical mechanics, such as Jordanus' analysis of the inclined plane, were rather isolated and in part disregarded by contemporary authors. But an isolated solution, a solution that is not taken up, discussed, contradicted, reformulated, supported by new arguments, or used in novel contexts, fails to be a convincing solution. A broadly shared acceptance of the solution to a particular problem typically presupposes controversy and only results from embedding the solution within an extended network of arguments, eventually connecting it with everything else within a system of knowledge. A progressive accumulation of established results remained, however, illusionary as long as the argumentative networks developed in preclassical mechanics were neither comprehensive in the sense of being adequate to deal with the entire scope of shared mechanical knowledge nor coherent in the sense of yielding an unambiguous solution, at least to those problems within their range of extension. The eventual emergence of more or less stable solutions to such basic mechanical problems only emerged in the course of the transformation of preclassical into classical mechanics, and represented an outcome rather than a precondition of this development.
From a traditional perspective, it may come as a surprise that not only new discoveries of dynamics such as the law of fall and the parabolic shape of the projectile trajectory, but even elementary insights from statics such as the indifferent equilibrium of a balance suspended from its center of gravity, the equilibrium of a body on an inclined plane, or the principle of the bent lever were still not definitively established toward the end of the sixteenth century, although it seems that these results could easily have been inferred from known ancient and medieval sources. But from the perspective sketched above, the seemingly fruitless contemporary debates about such problems take on a new significance. Rather than representing encounters between blind men sometimes hitting the mark and sometimes not, they were a medium of the dialogical transformation of a system of knowledge.7
But how did this dialogical transformation of knowledge actually take place and how in the end did more or less stable solutions to basic mechanical problems result? Although we have claimed that this stabilization did not happen in a piecemeal fashion, but rather in the context of a more holistic process of conceptual reorganization, it is also clear that the transformation of preclassical into classical mechanics did not happen in one fell swoop. Rather, within the developing network of mechanical arguments, some more or less stable nodes gradually emerged which did not correspond to the original roots from which the network was growing, such as the principles of Aristotelian physics and of Archimedean mechanics. These nodes resulted instead from an elaboration of the consequences of the traditional framework triggered by the confrontation with challenging objects. Some of these consequences constituted indeed the starting points for the reorganization of the accumulated knowledge, eventually yielding the new principles of classical mechanics, such as the principle of inertia, the principle of work, or the understanding of the directional character of force and of the relation between force and torque. Thus, the principle of inertia, for instance, could be obtained by reflecting on Galileo's results concerning projectile motion which had still been achieved within a preclassical conceptual framework.8 In turn, these results were related to a stabilization of the knowledge on mechanical devices such as the inclined plane, the bent lever, and the deflected balance, also resulting from a tedious process of the elaboration and integration of different knowledge resources. This process was typically accompanied by controversies over the conceptual foundations of mechanics, for instance about the role of such concepts as that of positional heaviness, center of gravity, or momento as it can be traced in the works of Guidobaldo, Benedetti, and Galileo, and as they are illustrated in an exemplary way by Guidobaldo's annotation of Benedetti's book.
3.4 The ancient and medieval origins of the equilibrium controversy
Whether and under what circumstances an equilibrated balance deflected into an oblique position returns into the horizontal is a question that goes back to the second problem of the Aristotelian Mechanical Problems. This, however, deals with balances having a beam of finite thickness so that it makes a difference whether they are supported from above or from below. But the seemingly simple case of the beam being supported at its center of gravity is not discussed. The concept of a center of gravity in fact was unknown to the Aristotelian author. As far as we know, this concept, which immediately suggests one stance in the later controversy, was not introduced before Archimedes.9 As will become clear below, it was Guidobaldo who revived and applied this concept in the context of the controversy about the deflected balance.
An understanding of the positional dependence of the effect of a weight under the constraints of its attachement to the beam of a balance was, as far as we know, expressed in geometrical terms for the first time in the Aristotelian Mechanical Problems.10 The issue was clarified by Archimedes who formulated the law of the lever, supplying a convincing deductive proof.11
The question of why the deflected balance nevertheless caused a vivid controversy in the early modern period is obviously related to the question of which parts of the ancient mechanical knowledge were transmitted when, where, and how to early modern scholars.12 As will be shown below, the ignorance of the concept of the center of gravity in fact led to the introduction of the concept of positional heaviness.
3.4.1 The Aristotelian context
Throughout the entire period under consideration, from antiquity via the Arabic and Latin Middle Ages to the early modern period, core ideas of Aristotelian dynamics were evidently known to scholars dealing with mechanical problems.
According to Aristotle the velocity of a body in natural descent is proportional to its weight while that of a body in violent motion is proportional to the moving force. In his Physics he wrote:
[…] as to differences that depend on the moving bodies themselves, we see that of two bodies of similar formation the one that has the stronger trend (ῥοπή) downward by weight (βάρος) […] will be carried more quickly than the other through a given space in proportion to the greater strength of this trend.13
A passage from On the Heavens dealing with the effect of a moving force sheds light on what he means by the term more quickly:
[…] if there is a moving body which is neither light nor heavy (βάρος), its motion must be enforced, and it must perform this enforced motion to infinity. That which moves it is a force (δύναμις), and the smaller, lighter body will be moved farther by the same force. […] For as the greater body is to the less, so will be the speed of the lesser body to that of the greater.14
This passage contains in essence the core idea of the Aristotelian dynamics of violent, that is, enforced motion. The same force exerts a greater effect on a lesser than on a greater body. The effects are measured by the speeds in the sense of distances traversed in the same time which are inversely proportional to the sizes of the bodies.
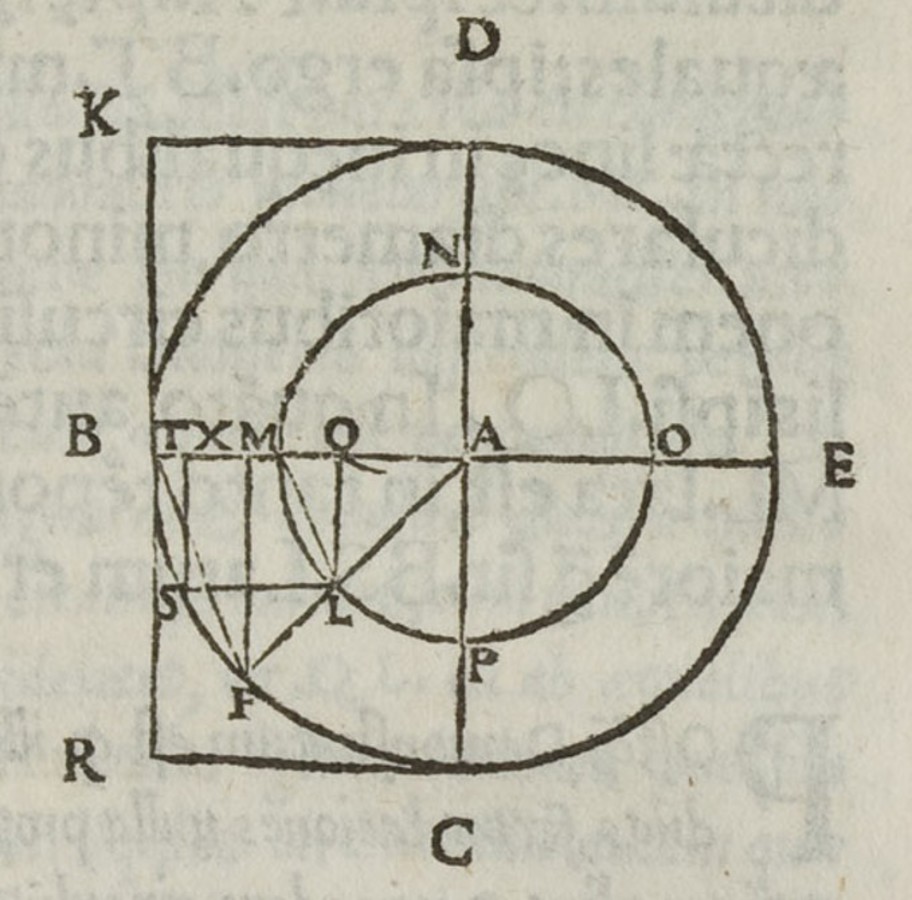
Fig. 3.1: Drawing by Tomeo in his 1525 translation Aristotelis quaestiones mechanicae illustrating that the arc BS of the larger circle is less bent than the arc ML of the smaller circle. According to Aristotle, the interference of the violent constraint on the natural downward motion must thus be greater on the smaller than on the greater circle.
The proportionality between force and effect, however, seems to contradict experiences gained from levers and balances. Applied to such tools, the same force has different effects depending on the position where it acts on a beam. The Aristotelian Mechanical Problems can be interpreted as an attempt to avoid this contradiction. The resolution of this contradiction in the Mechanical Problems relies on a basic explanatory principle interpreting the balance in terms of motions of weights along circles of different radii.15 This principle states that the part of the radius of a circle that is farther from the center moves more quickly than the part that is closer to the center being moved by the same force. The greater effect of a weight moving on the greater circle described by a larger beam is explained by the lesser interference of that violent constraint with the natural motion downward when compared to the motion along a smaller radius. In the Latin translation by Tomeo, the relevant passage reads:
Si autem duobus ab eadem potentia latis hoc quidem plus repellatur, illud vero minus, rationi consentaneum est tardius moveri id quod plus repellitur eo quod repellitur minus: quod videtur accidere maiori et minori illarum quae ex centro circulos describunt: quoniam enim proprius est manenti, eius quae minor est extremum, quam id quod est maioris, veluti retractum in contrarium ad medium tardius fertur minoris extremum. Omni quidem igitur circulum describenti istuc accidit: ferturque eam quae secundum naturam est lationem secundum circunferentiam: illam vero quae praeter naturam, in transversum et secundum centrum: maiorem autem semper eam quae praeter naturam est ipsa minor fertur: quia enim centro est vicinior quod retrahit vincitur magis.
Now if of two objects moving under the influence of the same force one suffers more interference, and the other less; it is reasonable to suppose that the one suffering the greater interference should move more slowly than that suffering less, which seems to take place in the case of the greater and the less of those radii which describe circles from the centre. For because the extremity of the less is nearer the fixed point than the extremity of the greater, being attracted towards the centre in the opposite direction, the extremity of the lesser radius moves more slowly. This happens with any radius which describes a circle; it moves along a curve naturally in the direction of the tangent, but is attracted to the centre contrary to nature. The lesser radius always moves in its unnatural direction; for because it is nearer the centre which attracts it, it is the more influenced.16
The author thus introduced the idea of explaining the dependence of the effect of a weight on its position by considering factors such as the natural and violent components of the motion and the lesser or greater deviation of the motion from its natural course.
The Aristotelian analysis left much room for interpretation. In any case, the Aristotelian Mechanical Problems could have become the starting point for formulating a concept of positional heaviness and were indeed brought into connection with it by early modern writers on this subject such as Tartaglia.17 Positions taken in the early modern period on this issue such as those of Guidobaldo and his adversaries can be considered as elaborating one or the other alternative implicit in the Aristotelian analysis.18 However, it is rather unlikely that this was how the concept of positional heaviness actually came into being in the thirteenth century, since at that time the text of the Aristotelian Mechanical Problems had probably not yet circulated in the Latin West.19 However, once it became available it was printed, translated, and commented upon by numerous early modern scholars and became a standard point of reference for mechanical arguments in the sixteenth century.20
3.4.2 The transmission of ancient mechanics
The concept of positional heaviness was, as discussed in section 2.1, explicitly introduced by the medieval scholar Jordanus de Nemore. Its historical roots can only be determined, however, by a closer look at the milestones of ancient mechanics represented in the works of Aristotle, Archimedes, and Heron, and at the vexing history of the transmission and transformation of this heritage by scholars in the Arabic world.21
From the viewpoint of the transmission of ancient knowledge, the first milestone of the development of the science of mechanics is the work of Aristotle. As mentioned above, the backbone of the long-term transmission of mechanical knowledge was Aristotelian dynamics, known in the Arabic world, in the medieval Latin period, and in early modern times. It was used throughout as a point of reference for arguments on balances and other mechanical devices.
The Aristotelian Mechanical Problems had a somewhat less continuous history as they were probably unknown when the science of weights first emerged in the Latin Middle Ages.22 The treatise has been transmitted as part of the Aristotelian corpus, but its attribution to Aristotle has been called into question although there is a consensus that it dates back to the third century BCE and has emerged from the immediate context of his work.23 With the exception of an earlier Arabic epitome,24 all extant Greek manuscripts and later printings are based on one archetype Byzantine codex, the codex Z.Gr.214 of the Biblioteca Marciana.25 Altogether twenty-nine Greek manuscripts survived.26 The three oldest manuscripts, that is, all extant manuscripts written before the fifteenth century, were written in Byzantium and only later transferred to Italy, whereas the majority of later manuscripts were certainly written in the West. The fifteenth century is marked by an extreme increase in copying activities.27 Thus twenty-one of the later manuscripts were written in the fifteenth century, four in the sixteenth, and one in the seventeenth century.28 The situation is further confused by the widely overlooked fact that the treatise was also covered by Pachymeres' Philosophia which contains paraphrases and commentaries on most of Aristotle's works. Pachymeres29 was a Greek scholar who spent most of his life in Constantinople. The extant manuscripts of Philosophia show a similar distribution as the “normal” manuscripts with a peak in the sixteenth century.30
Thus, the Aristotelian Mechanical Problems only became widely available to the scholars of the Latin tradition at the beginning of the early modern period through Greek manuscripts and their Latin translations, all of which derived from a single Byzantine source from the late eleventh or early twelfth century.31 In the Arabic context, however, the core text of the Aristotelian Mechanical Problems was known, but not the deductive justification of its basic explanatory principle32 which in the early modern period served as an important background for arguments concerning positional heaviness. The Mechanical Problems contain with this principle a precursor formulation of the law of the lever, knowledge of which was hence transmitted with the text. They also constitute, as mentioned above, a bridge between Aristotelian dynamics and the characteristics of mechanical devices to save force, a bridge that is sustained mainly by the proof of the basic explanatory principle.
The second milestone is the work of Archimedes on mechanical problems, without doubt a culmination of ancient mechanical knowledge. However, this was only partially transmitted. In particular, his writings on mechanics, apart from a fragment of On floating bodies, became known to the Arab world only indirectly, e.g., through the works of Heron and Pappus. In the Latin world they only became known through the translations from the Greek by Willem of Moerbeke33 after 1269.34 However, the law of the lever and the tradition of deductive proofs associated with his work were known in all the periods in question. But his key concept of a center of gravity seems to have been unknown in the Latin Middle Ages until the translations of Moerbeke and those produced later.
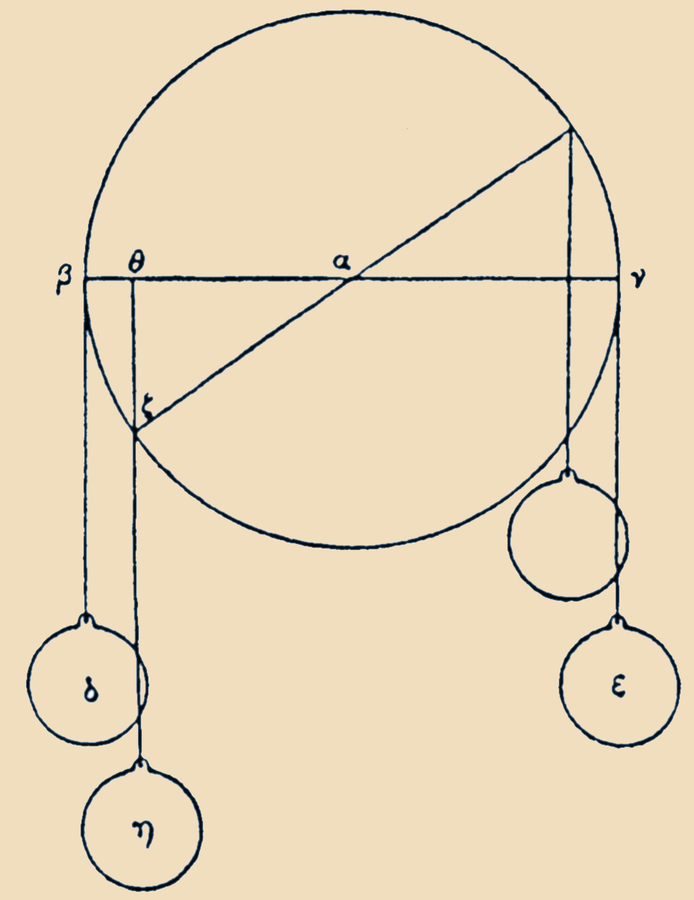
Fig. 3.2: The law of the bent lever is an implicit consequence of a theorem in Heron's Mechanics. Two ropes are fixed at points β and γ to the border of a pulley. If unequal weights are attached to the ropes, the rope of the smaller weight will be rolled up while the greater weight will move downwards to a certain point ζ until the weights are in equilibrium. Thus the pulley with the ropes acts as if it were a bent lever ζαγ.
The third milestone is the work of Heron of Alexandria. Heron of Alexandria evidently knew all of the Greek sources representing mechanical ideas but used them eclectically in his reduction of mechanical devices to a classification of simple machines. In particular, Heron's Mechanics refers to parts of Archimedes' works on mechanics, some of which have been lost. Heron introduced the concept of center of gravity and applied it several times. Moreover, he used the concept implicitly when he dealt with the equilibrium of arbitrarily shaped beams of balances.35 Furthermore, in an added proposition concerning a beam in form of a pulley, he introduced a from a modern viewpoint correct solution which covered the bent lever as a special case (see figure 3.2).36
Heron's Mechanics as a whole was, as far as we know, only transmitted to the Arabic world, while excerpts relating mainly to the simple machines were also transmitted in Greek to the West by Pappus' selection, in particular by the Latin translation of Alexandria 1588.
Further achievements of ancient mechanics regarding the balance are known to us only through fragments, probably either transmitted directly from the Greek or indirectly to the Arabic and subsequently to the Latin world. One example is a proof of the law of the lever in a Book of the Balance ascribed to Euclid. This proof is preserved only in Arabic and its ascription to Euclid is somewhat doubtful.37 The most remarkable aspect of Euclid's proof, if compared to that of Archimedes, is the fact that it proceeds without involving the concept of center of gravity, using instead a concept characterizing the positional effect of a weight on a balance, designated as the force of heaviness. Another achievement of ancient mechanics with unclear origins is the treatment of the material beam of the balance in the Liber de canonio.38
A fourth milestone in the transmission of the ancient heritage of mechanics was its reception and transformation by scholars in the Arabic world. As mentioned earlier, the Arabic world had access to Aristotelian dynamics as well as to the Aristotelian Mechanical Problems, but without the proof of the main principle. In addition, the full text of Heron's Mechanics as well as the selection made by Pappus were available.39 Furthermore, the law of the lever was known, including a proof in a text ascribed to Euclid,40 and on this basis the material beam was correctly treated.41
Arabic treatises, probably composed on the basis of Greek material by authors such as Thābit and al-Isfizari,42 focused on the proof of the law of the lever on the basis of Aristotelian dynamics, including a treatment of the material beam, and knowledge about the bent lever.43 In particular, a scholium to the treatise of Thābit contains the idea, crucial for an understanding of the bent lever, that the effect of a weight suspended not directly from the beam of a balance but from the end of a rod that is rigidly connected to the beam at an oblique angle, will be as if it were suspended at the foot of the perpendicular drawn from the weight to the beam.44 On the other hand, Thābit, contrary to later Arabic authors, did not make use of the concept of the center of gravity, a circumstance which may have motivated his attempt to justify the equilibrium of the balance instead on the basis of Aristotelian dynamics.
In his Book on the Balance of Wisdom, completed 1121–1122, al-Khāzini45 treated the question of what happens if the balance beam is supported from above or from below, which was raised in the Aristotelian Mechanical Problems. He explicitly considered the case in which the balance is supported at the center of gravity of the beam and claimed correctly that it remains at rest in whatever position it is left.46
In the course of the translation movement of the twelfth century, only a fraction of the Arabic material was transmitted to the Latin world. In particular, a treatise by Thābit entitled Liber karastonis was transmitted in a Latin version, probably translated by Gerard of Cremona47 from a lost Arabic version. However, this treatise did not contain a treatment of the bent lever and states in contrast to al-Khāzini's Book on the Balance of Wisdom that the deflected balance returns to the horizontal:
Dico ergo quod linea sit veniens super equidistantiam orizontis, ita quod si nos inclinemus punctum A ad punctum T et elevetur punctum B ad punctum D, sufficiet pondus a donec redeat linea AB ad locum suum ex equidistantia orizontis.
Then I say the line is in horizontal equilibrium, so that if we incline point A to point T and elevate point B to point D, the weight a is sufficient for line AB to return to its place of horizontal equilibrium.48
When Jordanus took up the subject of the science of weights at some point in the thirteenth century, the main sources he probably had at his disposal were, apart from Aristotelian dynamics, in particular the Liber karastonis and the Liber de canonio. Most likely he did not yet have access to Archimedes' achievements, nor to any part of Heron's work. In a sense, Jordanus was thus in a position similar to Thābit in the ninth century, confronted with the challenge to provide a deductive treatment of the science of weights on the basis of Aristotelian dynamics, without having the concept of center of gravity or other Archimedean achievements at his disposal. The further elaboration of the framework he built was evidently guided by taking into account new challenging objects beyond the balance such as the inclined plane.
A more extensive access to the ancient heritage did not become possible before the fifteenth century. Among the first to refer to the Archimedean concept of center of gravity was Leonardo da Vinci who used it in his work on mechanical devices. In particular, he applied the concept to the problem of the bent lever (see figure 3.3):

Fig. 3.3: Leonardo argued correctly that a bent lever will be in equilibrium if the weights of the two parts of the beam are equal and their centers of gravity have the same distance from the vertical through their common center of gravity.
S'e centri de' pesi saranno equidistanti al loro centro comune, essi pesi staranno equali in equilibra. S'e perpendiculari de' centri de' pesi saranno equidistanti al perpendicolare del lor centro commune, essi pesi staranno equali in equilibra, se essi pesi sieno equali. Per tal ragione il centro del mondo è sempre mobile per la mutazione della inondazione dell'Oceano.
When the centers of the weights are equally distant from their common center, these weights will be equal in equilibrium. When the perpendiculars of the centers of the weights are equidistant from the perpendicular of their common center, these weights will be equal in equilibrium, if these weights are equal. For this reason, the center of the world is always mobile because of the change of the tides of the ocean.49

Fig. 3.4: Leonardo correctly assumed that an equilibrated balance deflected into an oblique position will not return into the horizontal. He explained the common experience that the balance nevertheless seems to return into the horizontal as resulting from the difficulty in constructing a balance whose fulcrum matches precisely the center of gravity.
Leonardo also treated the behavior of an equilibrated balance deflected into an oblique position (see figure 3.4). He argued that the observable fact that such a balance tends to return to the horizontal is a consequence of the imprecision of the fulcrum:
La gravità è tutta per tutta la lunghezza del suo sostentaculo e tutta in ogni parte di quello. Per che causa accade in isperienzia che quando l'aste istando per obbliqua linia e restando colle sue parti equalmente distante a la linia centrale, essa non resta obliqa, anzi si fa equidiacente e componente colla detta linia centrale con 4 angoli retti? Risponda nascere dalla imperfezzione del polo.
The heaviness is whole for the whole length of its carrier and whole in each part of it. Why does it happen in experience that, when the beam is along an oblique line and with its parts equally distant from the central line, it does not remain oblique, but rather makes itself horizontal and forming with the said central line 4 right angles? Answer that this comes from the imperfection of the fulcrum.50
As is well known, the impact of such insights found in Leonardo's manuscripts on the subsequent scientific development is difficult to assess. From our point of view, there can be no question of singular discoveries that may have been lost or found in a scientific relay race as long as such insights are not integrated into a wider network of knowledge.51
Another striking instance in which significant contributions to a further development of mechanics based on Archimedean principles can be attributed to an author in hindsight, while in fact the contemporary impact remained rather limited, is the extraordinary work of Francesco Maurolico.52 By early 1548 Maurolico completed a major work composed of four books, entitled De momentis aequalibus.53 In this work he systematically defined the concept of momentum as the positional effect of weights responsible for their equilibrium. His work was first published, however, more than a century later when knowledge of Archimedes' work had become widely available.54
3.4.3 The unreconciled ancient heritage
The preceding overview shows that the transmission of the ancient knowledge about mechanics was neither cumulative nor a linear process. From the Hellenistic world there were essentially two pathways of transmission to the Latin scholarly tradition. The first was the transmission to the Arabic world and from there through the boundary areas of Arabic and Latin cultures in Spain and Sicily to the rest of Europe. The second was the transmission to the Eastern Roman Empire centered around the city of Constantinople and from there first to Italy and later to other Westeuropean regions.
The result was a patchwork of partly incompatible conceptual networks of mechanical knowledge, embedded in quite distinct cultural and social settings. Consequently, the intermittent and scattered transmission of the concept of center of gravity led in particular to the emergence of an alternative conceptualization of the way in which equilibrium results from the functioning of weights depending on different mechanical constellations, and this focused on the concept of positional heaviness.
Using the concept of center of gravity the equilibrium can be conceptualized in terms of the relation of the center of gravity and the point of suspension. Such a conceptualization leads directly to the concept of torque in classical mechanics if the equilibrium is expressed as an equality of physical magnitudes. However, as shown above, the concept of center of gravity, introduced by Archimedes and taken up by Heron and Pappus, was known in principle in the Arabic scholarly community but evidently had only a limited and rather late impact on Arabic mechanical knowledge. In any case, it did not become part of the Arabic treatises on mechanics which were translated in the twelfth century into Latin. It became known to the Latin scholarly world only in the later thirteenth century through the translation of works of Aristotle by William of Moerbeke who had access to now lost Greek manuscripts probably transmitted from Byzantium.
Thus, the early medieval Latin scholars were familiar with Aristotelian dynamics through works such as Aristotle's Physics or De caelo, but with the tradition of ancient mechanics only through the selective translation of Arabic sources. In this situation the attempt to solve the problem of explaining the causes for the equilibrium of balances resulted in the idea that the actual weight of a body changes according to the mechanical context. This idea, however, is ambiguous in itself. If it is the weight that really changes, what then is the magnitude that has been determined since millennia using the balance as a weighing device? But if the real weight does remain the same, what kind of weight is it that changes according to the context? How can one explain that two bodies holding a balance in equilibrium may nevertheless have different weights?
This ambiguity is reflected in the conceptual fuzziness of the terms used to express the effect of a weight under different mechanical conditions. The most advanced attempt to eliminate this ambiguity was offered by Jordanus. In accordance with the growing role of Aristotelian methodology for structuring knowledge, his solution made use of Aristotelian logic in order to avoid the apparent fallacies related to the mechanical problems associated with weights in different positions on a balance. Aristotle had introduced the term fallacia a dicto simpliciter ad dictum secundum quid to denote the fallacy of ignoring a qualification such as the position of a weight, supposing that what is true under certain circumstances,55 e.g. the equilibrium of equal weights on a balance, is true also in general, e.g. generalizing the statement of equilibrium for the positions of weights on an equal-armed balance to all positions of the counterpoise of a steelyard. Thus, Jordanus introduced the term gravitas secundum situm in contrast to the pondus of a body, translated here as positional heaviness and weight respectively. In this way a historically consequential concept of mechanics had been shaped by a reflection suggested by the intellectual context of early scholasticism (see section 2.1).
With the revival of the work of Jordanus in the early modern period this solution was widespread, but now became confronted with the alternative conceptualization of the equilibrium of balances by means of the concept of center of gravity revived with the translation of works by Archimedes and Pappus and indirectly through quotations of Heron's work in Pappus' Collectiones.
Thus, Renaissance and early modern scholars stumbled upon an unreconciled part of the ancient conceptual heritage. This eventually led to the equilibrium controversy on which the present study is focused.
3.5 Jordanus' approach to positional heaviness
The treatise Liber de ponderibus is, as discussed in section 2.1, another representation of Jordanus' core theory with an extended set of propositions, but here the postulates are preceded by a prologue. This prologue introduces Jordanus' concept of positional heaviness as a new technical term together with a justification of its introduction:
Quia si sumantur de circulo maiori et minori arcus equales, corda arcus maioris circuli longior est. Propterea possum ex hoc ostendere, quod pondus in libra tanto fit levius, quanto plus descendit in semicirculo. Incipiat igitur mobile descendere a summo semicirculi, et descendat continue. Dico tunc quod, cum maior arcus circuli plus contrariatur recte linee quam minor, casus gravis per arcum maiorem plus contrariatur casui gravis qui per rectam fieri debet, quam casus per minorem arcum. Patet ergo quod maior est violentia in motu secundum arcum maiorem, quam secundum minorem; alias enim non fieret motus magis contrarius. Cum ergo apparet plus in descensu adquirendum impedienti, patet quia minor erit gravitas secundum hoc. Et quia secundum situationem gravium sic fit, dicatur gravitas secundum situm in futuro processo.
If equal arcs are taken on a greater circle, and on a smaller one, the chord of the arc of the greater circle is longer. From this I can then show that a weight on the arm of a balance becomes lighter to the extent that it descends along the semicircle. For let it descend from the upper end of the semicircle, descending continuously, I then say that since the longer arc of the circle is more contrary to a straight line, than is the shorter arc, the fall of the heavy body along the greater arc is more contrary to the fall which the heavy body would have along the straight line, than is a fall through a shorter arc. It is therefore clear that there is more violence in the movement over the longer arc, than over the shorter one; otherwise the motion would not become more contrary (in direction). Since it is apparent that in the descent (along the arc) there is more impediment acquired, it is clear that the gravity is diminished on this account. But because this comes about by reason of position of the heavy bodies, let it be called positional heaviness in what follows.56

Fig. 3.5: Title vignette of Apianus' edition of Jordanus' Liber de ponderibus displaying a scholar and a practitioner. The scholar explains the functioning of a steelyard according to Aristotelian principles.
The justification seems to echo an argument in the Aristotelian Mechanical Problems but could also have been inspired in a more general way by Aristotelian physics. At the very least, Aristotelian scholars must have faced a contradiction. On the one hand, according to Aristotelian dynamics, the moving force or weight of a body is proportional to the resulting swiftness. On the other hand, according to the principle of Aristotelian mechanics, in circular motion the swiftness, as discussed in section 3.4.1, caused by equal forces does not stay the same but rather becomes proportional to the distance from the center (see figure 3.5). As shown above, the Aristotelian explanation for this principle was based on the assumption that the interference of the center forcing the motion into a circular path impedes the motion toward the center of the world in dependence on the degree to which the path is curved. This is similar to the argument used by Jordanus to justify for the seemingly changing weight the designation as positional heaviness (gravitas secundum situm), applying, as is claimed in section 3.4.3, an Aristotelian strategy for avoiding the secundum quid fallacy to the science of weights.
The term positional heaviness thus became the core concept in the postulates and the propositions of Jordanus' treatises on the science of weights. First he attempted in the postulates to provide a precise definition of the term on the basis of the Aristotelian assumptions. In Apianus' edition of the Liber de ponderibus, the first to the fifth postulate are formulated accordingly:
Prima est: Omnis ponderosi motum ad medium esse.
Secunda: Quanto gravius tanto velocius descendere.
Tertia: Gravius esse in descendendo, quanto eiusdem motus ad medium est rectior.
Quarta: Secundum situm gravius esse, quanto in eodem situ minus obliquus est descensus.
Quinta: Obliquiorem autem descensum minus capere de directo, in eadem quantitate.
The first is: The motion of every weight is toward the center [of the world].
The second: The heavier it [the weight] is, the faster it descends.
The third: It is heavier in descending, insofar as its movement toward the center [of the world] is straighter.
The fourth: It is positionally heavier, insofar as its descent, in that same position, is less oblique.
The fifth: But a more oblique descent partakes less of the straight [descent], for the same quantity [of the path].57
The second postulate simply asserts the basic principle of Aristotle that the velocity of a moving body depends on the exerted force, in this case the heaviness of a falling body (see section 3.4.1). The third postulate also refers to the Aristotelian tradition, but now to the consequences of the relation between natural motions and what acts contrary to them. The fourth postulate introduces the term positional heaviness as resulting from the obliqueness of descent. Finally, the term obliqueness is explained in the fifth postulate by the amount of straight descent covered by it for equal quantities of the path. This fifth postulate had, as will be shown below, the greatest influence on all attempts to quantify the concept of positional heaviness.

Fig. 3.6: Figure added by Tartaglia to the proof of the second proposition of Jordanus' De ratione ponderis. Jordanus argued that the positional weight at C is greater than at B because the vertical descent ZM is greater than the vertical descent KY.
Having stated his postulates, Jordanus started with a proposition related to the Aristotelian doctrine that velocity is proportional to weight respectively to the exerted force:
Propositio prima.
Inter quaelibet duo gravia est velocitas descendendo proprie, et ponderum eodem ordine sumpta proportio, descensus autem, et contrarii motus, proportio eadem, sed permutata.
First proposition
Between any two heavy bodies, the proper velocity of descent is directly proportional to the weight; but the proportion of descent and of the contrary movement of ascent is the inverse.58
Then, with his second proposition, Jordanus presented the claim which later became the issue of the equilibrium controversy triggered by the inherent ambiguity of the concept of positional heaviness (see figures 3.6 and 3.7:
Propositio secunda.
Cum fuerit aequilibris positio aequalis, aequis ponderibus appensis, ab aequalitate non discedet, et si ab aequidistantia separetur, ad aequalitatis situm revertetur.
Primum patet, quia sunt equae gravia. Secundum patet per suppositionem quartam, vocatur autem illud situs, quod circulus dicitur, sicut patet per praedicta.
Second proposition.
If an equilibrated [balance] is in horizontal position [positio aequalis], with equal weights suspended, it will not leave the horizontal position [aequalitate]; and if it is removed from the horizontal position [aequidistantia], it will return to the horizontal position [aequalitatis situm].
The first [part] is evident because the weights are equally heavy. The second is clear from the fourth postulate; but it [the weight] is called positionally [heavy] because one speaks about the circle as is evident from the preceding.59
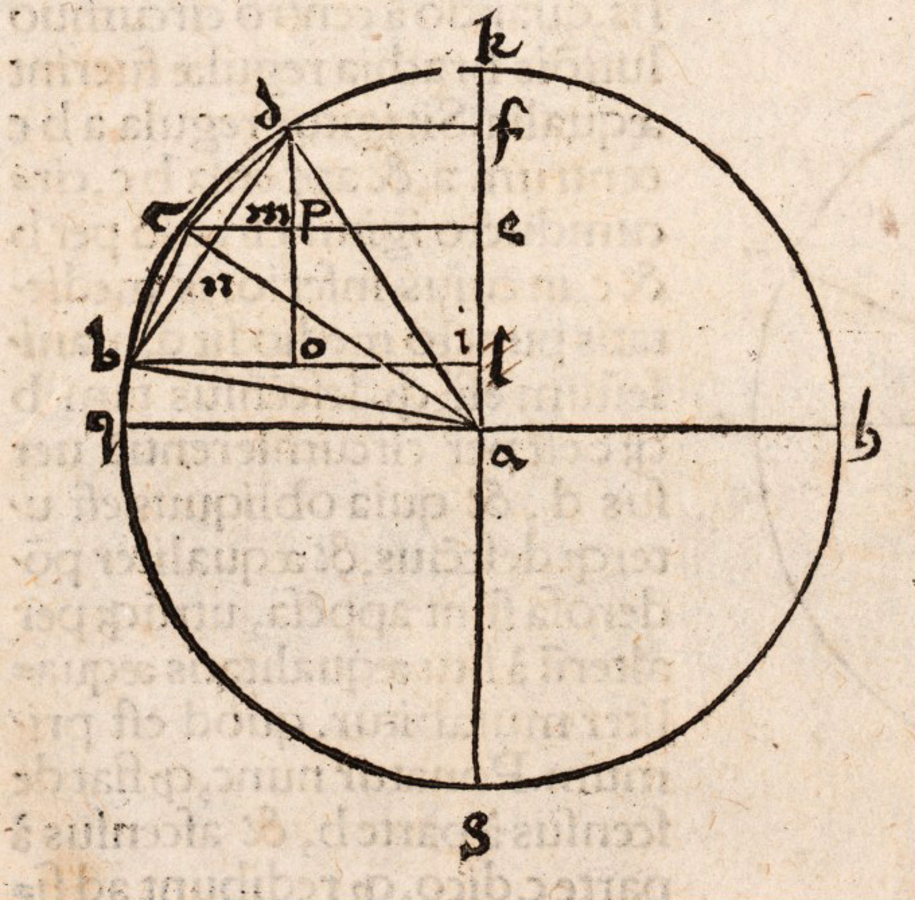
Fig. 3.7: Figure added in Apianus' edition to the proof of the second proposition of Jordanus' Liber de ponderibus. The commentary argues that equal arcs along a circle correspond to unequal vertical descents depending on the distance from the horizontal. Thus, the upper arc CD corresponds to a smaller vertical descent, i.e. FE, than the lower but equal arc BC corresponding to the vertical descent EI.
The short argument in Apianus' edition of Jordanus' Liber de ponderibus as well as the detailed proof in Tartaglia's edition of Jordanus' De ratione ponderis make essential use of the fourth postulate. The argument specifies the positional heaviness of the weights at the deflected balance by identifying the vertical components corresponding to their respective descents. Jordanus' result is the erroneous claim that the deflected balance returns into the horizontal position because the upper weight acquires a greater positional heaviness than the lower weight.
Several of the following propositions are concerned with the influence of various circumstances on the positional heaviness of a weight. The fourth proposition of Apianus' edition of the Liber de ponderibus,60 for example, concerns the dependence of the positional weight on the deflection of the beam of a balance:
Propositio quarta.
Quodlibet pondus in quamcumque partem discedat secundum situm sit levius.
Fourth proposition.
In whichever direction any weight departs [from the position of equality], it becomes positionally lighter.61
As in the case of the second proposition, the proofs of all further propositions that concern the magnitude of the positional heaviness are essentially based either on the fourth postulate, thus relating the positional heaviness to the obliqueness of the downward tendency or motion and, in consequence, to the vertical descent, or directly on the Aristotelian dynamics as it is formulated with some variations in the first theorem of all three treatises ascribed to Jordanus.
Accordingly, Jordanus presented as the eighth proposition62 the law of the lever by expressing the equilibrium of two unequal weights as equality of their positional heaviness (see figure 3.8):
Propositio octava.
Si fuerint brachia librae proportionalia ponderibus appensorum, ita, ut in breviori gravius appendatur, aeque gravia erunt secundum situm.
Eighth proposition.
If the arms of the balance are proportional to the weights suspended in such a manner that the heavier [weight] is suspended on the shorter [arm], positionally they will be equally heavy.63
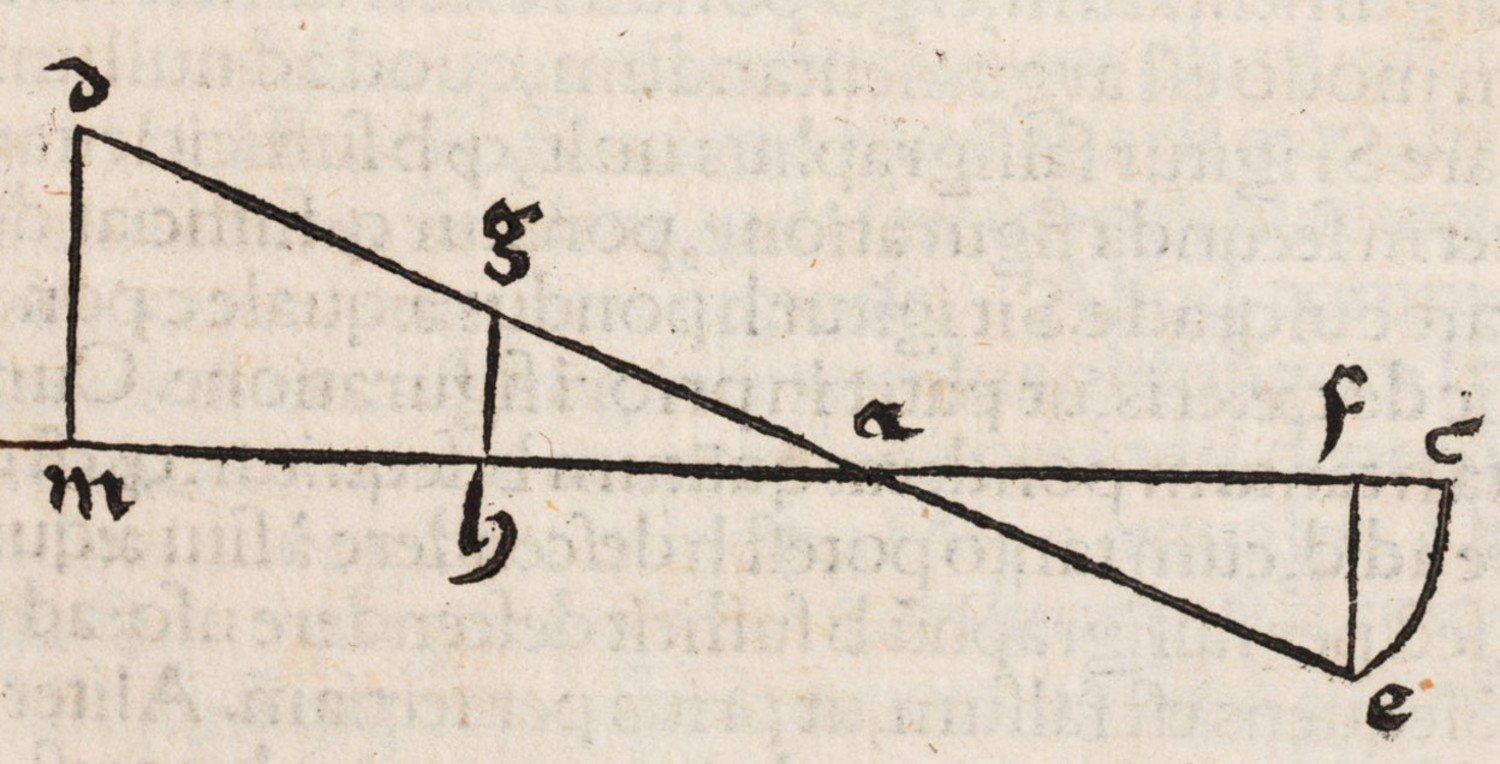
Fig. 3.8: Jordanus' proof of the law of the lever and Apianus' commentary are based on the establishment of a relationship between the motion of unequal weights D and E on a balance and upward motions MD and HG of similar weights caused by the same force treated according to Aristotelian dynamics.
The proof of this proposition is based directly on Aristotelian dynamics as formulated in the first proposition. Jordanus made particular use of the assumption, which is summarized succinctly in the passage from On the Heavens quoted above:64 distances and weights are inversely proportional when the same force is applied to them. In order to apply this assumption to the equilibrium of a balance with unequal weights he argued that the descent of the heavier weight on one side of the balance can be considered as being equivalent to an upward motion of the same weight on the other side. He could thus compare ascents of different weights over different distances, inversely proportional to the weights, which according to Aristotelian dynamics can be achieved by the same force. This then serves to show that the balance is in equilibrium.
Apianus not only reported Jordanus' proof, but also extended it with commentaries. He made explicit use of the concept of positional heaviness, exploiting the vertical component of the path of the beam as a measure (see figure 3.7).
For our context it is important to note that both the Elementa and the De ponderibus, that is, the present text, are distinguished from De ratione ponderis by the fact that the latter omits two incorrect propositions on the bent lever, propositions 6 and 7. In Apianus' edition proposition 6 reads:
Propositio sexta.
Cum unius ponderis sint appensa, et a centro motus inaequaliter distent, et si remotum secundum distantiam propinquius accesserit ad directionem, alio non moto secundum situm, illo levius fiet.
Sixth proposition
When equal weights are suspended at unequal distances from the center of movement, and if the longer arm is bent so that its end is at the same distance from the vertical as is the shorter arm, then, if the latter remains unmoved, the weight on the longer arm will become positionally lighter than the other weight.65
This incorrect proposition on the bent lever was replaced in Jordanus' treatise De ratione ponderis by a correct theorem (numbered as proposition 8) which indirectly states the measure of positional heaviness by means of vertical projections on the horizontal, and which later became central to Benedetti's work (see figure 3.15):
Si inequalia fuerint brachia librae, et in centro motus angulum fecerint: si termini eorum ad directionem hinc inde aequaliter accesserint: aequalia appensa in hac dispositione aequaliter ponderabunt.
If the arms of a balance are unequal, and form an angle at the axis of support, then, if their ends are equidistant from the vertical line passing through the axis of support, equal weights suspended from them will, as so placed, be of equal heaviness.66
It seems that the De ratione ponderis was an improved version of the Elementa, probably due to Jordanus himself.67 In particular, the distance between the weight and the vertical through the point of suspension of the beam of a balance is used as a measure of its positional heaviness, also in other theorems.68 But in spite of this improvement, other issues involving positional heaviness, such as the claim that a balance would always return to its horizontal position, still received the same problematic treatment as they had in the Elementa.69 Thus, the new insight expressed in proposition 8 did not lead to a thorough conceptual revision of the theory of the balance expounded by Jordanus and in particular not to a revision of the concept of positional heaviness. A similar situation holds for the later treatise on weights by Blasius of Parma,70 who also stuck to the erroneous assumption that a deflected balance returns to the horizontal. The bent lever, however, is correctly treated by taking the projections on the horizontal as a measure of positional heaviness.71
The erroneous claim that the deflected balance spontaneously returns to the horizontal was later criticized by Leonardo da Vinci with direct reference to the science of weights.72 Leonardo critically discussed the explanation of the balance by “Pelacani,” i.e., Blasius of Parma. According to Leonardo, Blasius had claimed that the longer arm of the balance will fall more quickly than the shorter arm because its descent traverses the quarter circle more directly than the shorter arm. Since the weights tend to fall along the perpendicular, the motion will be slower the more the circle is curved. In the proof of the seventh proposition of Part I of his treatise on weights, Blasius indeed claimed that a heavy body seeks to move along a straight line and that the slower it moves the more it deviates from its natural path.73 Leonardo argued against this by considering a case in which the weights are attached by ropes and fall perpendicularly without being impeded by the curvature of the circle described by the balance. He concluded that what is more distant from its suspension will be carried less by it. Since it is carried less, it acquires more freedom, and since a free weight will always descend, the end of the beam which is more distant from the fulcrum will sink more quickly than any other part as it carries a weight.
It remains unclear whether Leonardo's insights into the behavior of a deflected balance had any impact on the scholarly discussion of this problem in the early modern period. With certainty we only know that the De ratione ponderis was published in 1565 in Venice by Curtius Trojanus at the instigation of Niccolò Tartaglia.74 In this form it may have become one of the starting points for Benedetti's treatment of positional heaviness. He could have indeed taken the result that Jordanus had formulated in proposition 8, transforming it into a general principle for analyzing the positional effect of weight. Remarkably, the controversy in the sixteenth century between Tartaglia, Cardano, Guidobaldo, and Benedetti on the notion of positional heaviness was triggered by a conundrum that had remained unsettled for centuries, as the different versions of Jordanus' work testify.
3.6 Tartaglia's approach to positional heaviness
Compared to the situation of Jordanus, the availability of sources on mechanics was significantly different in the early modern period (see sections 3.4.1 and 3.4.2). In particular, the Aristotelian Mechanical Problems had become widely known through the transmission and translation of the Byzantine manuscript. As mentioned above, part of Heron's work had become available through Pappus. In addition, Archimedes' work on the equilibrium of planes made available the knowledge of how to treat the problems of the balance in a deductive way on the basis of the concept of center of gravity.
This broad availability of ancient sources brought about a novel situation for discussions of the dependency of the effect of a weight on its position. In particular, it now became relevant to establish connections between the different conceptual frameworks embodied in these sources. One of the key protagonists to contribute both to the spread of ancient and medieval sources and to the creation of a new synthesis was the engineer-scientist Niccolò Tartaglia. Following Jordanus, he formulated the law of the lever in Quesiti, et inventioni diverse75 in terms of positional heaviness:
Se li brazzi della libra saranno proportionali alli pesi in quella imposti, talmente, che nel brazzo più corto sia appeso il corpo più grave, quelli tai corpi, over pesi seranno equalmente gravi, secondo tal positione, over sito.
If the arms of the balance are proportional to the weights imposed on them, in such a way that the heavier weight is on the shorter arm, then those bodies or weights will be equally heavy positionally.76
Tartaglia's book became a point of reference – and a target of severe criticism – both for Guidobaldo and Benedetti and shall therefore be considered here in further detail. Tartaglia also followed Jordanus in claiming in his Third Petition that
[…] un corpo grave esser in el discendere tanto più grave, quanto che il moto di quello è più retto al centro del mondo.
[…] a heavy body in descending is so much the heavier as the motion it makes is straighter toward the center of the world.77
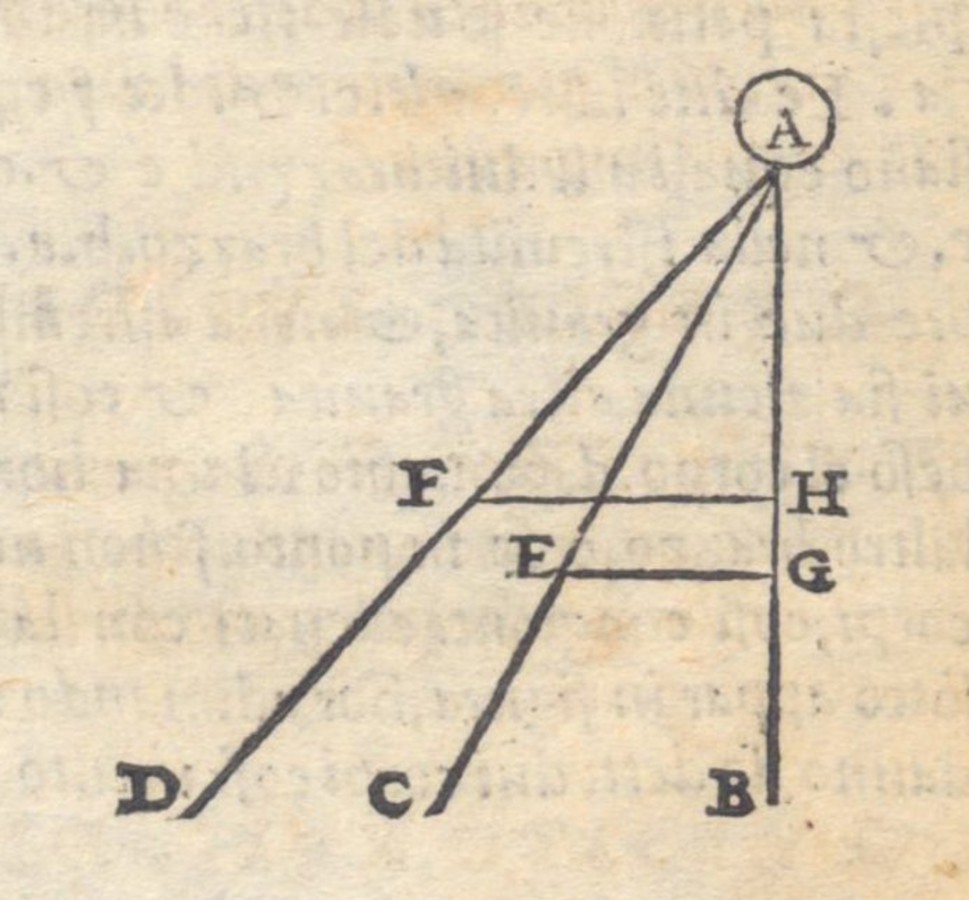
Fig. 3.9: According to Tartaglia, the descent of a body from A to D is more oblique than the descent from A to C since the projection AH on the line of descent to the center of the world is shorter than the projection AG.
He substantiated the idea by the defining concepts of line of direction to the center of the world and obliqueness:
La linea della direttione è una linea retta imaginata venire perpendicolarmente da alto al basso, e passare per il sparto, polo, over assis de ogni sorte libra, over bilancia.
The line of direction is a straight line imagined to come perpendicularly from above to below and to pass through the support or axis of any kind of scale or balance.78
…
Più obliquo se dice essere quel descenso, d'un corpo grave, il quale in una medesima quantita, capisse manco della linea della direttione, overamente del descenso retto verso il centro del mondo.
The descent of a heavy body is said to be more oblique when for a given quantity it contains less of the line of direction, or of straight descent toward the center of the world.79
Thus, Tartaglia measured the straightness of the given descent by its projection on the vertical line of direction (see figure 3.9).
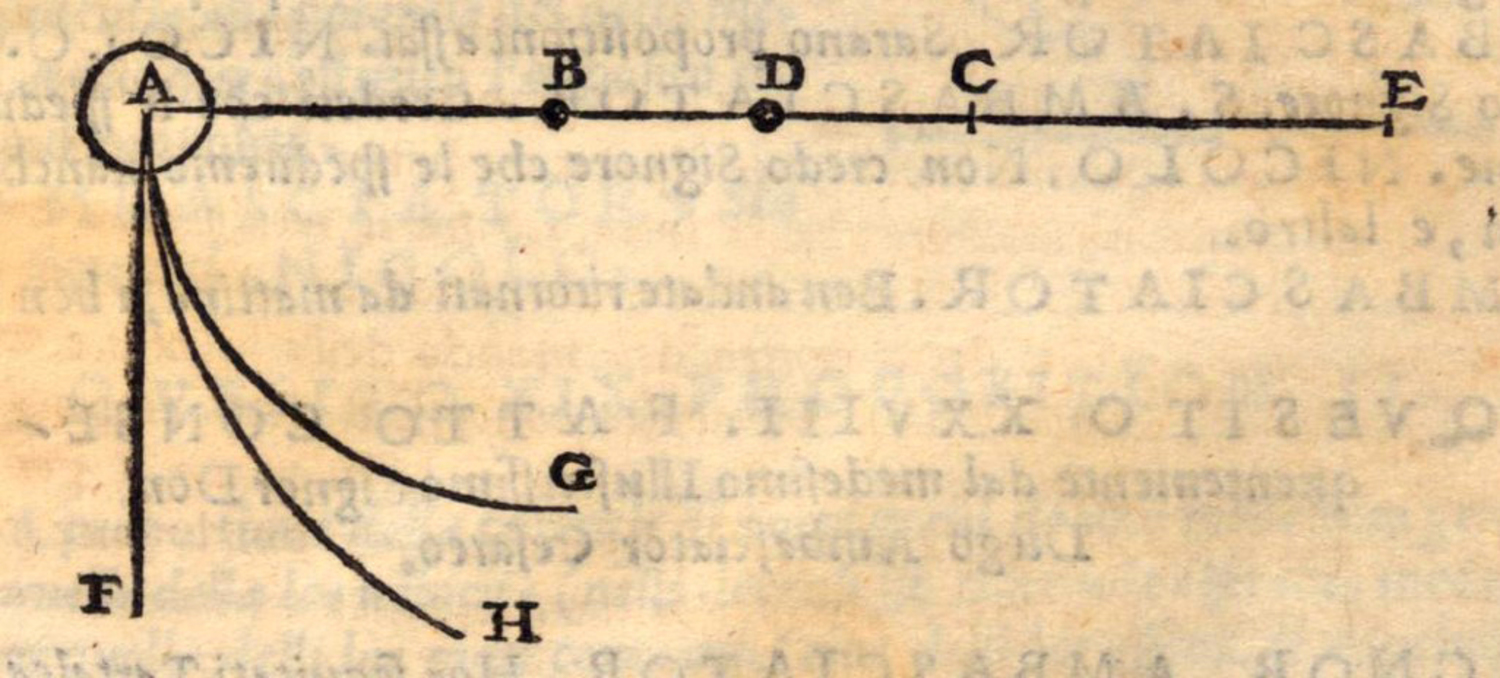
Fig. 3.10: According to Tartaglia, the descent of a body from A to G is more oblique than the descent from A to H since its curvature is greater.
Alternatively, he measured the straightness of descent also with reference to the more or less acute angle with the path of straight and direct descent to the center of the world (see figure 3.10).80 He thus followed a procedure introduced by Jordanus in De ratione ponderis which Tartaglia later edited,81 a procedure, however, that was absent in Jordanus' other works. In the case of a curved descent in particular, for instance along a circular arc, Tartaglia determined straightness by the lesser or greater curvature of the path of descent, making use of the idea of angles of contact (also referred to as curvilinear angles or as mixed angles in the following), formed not by straight lines but by circles or by a straight line and a circle.82
Tartaglia treated the case of a scale or balance of equal arms with equal weights attached to them following Jordanus. Taking the latter's stance in the equilibrium controversy, he also concluded that, when the scale is moved from its initially horizontal equilibrium position by an external intervention so that one weight is above, the other below the horizontal, the scale will return to the horizontal position by itself because the weight that has been raised has become positionally heavier than the weight that has been lowered (see figure 3.11). On the other hand, he claimed that the greater positional heaviness cannot be compensated by adding a weight to the lower weight since even the smallest weight attached to this side would move the scale to a vertical position.

Fig. 3.11: According to Tartaglia, the body at I is positionally heavier than the body at V since the projection XY is greater than WF.
To justify the first claim, Tartaglia considered the balance in any position outside the horizontal and now compared, following Jordanus, the descents of the two weights with the aim of establishing which of them is more direct. For this purpose, he compared descents through equal parts of the circle described by the arms of the balance, i.e. descents through equal angles taken downward from the given position of the beam. Due to geometrical reasons, it now turns out that the descent of the upper weight is always straighter than that of the weight that has been lowered so that the upper weight becomes, according to the definition, positionally heavier. As a consequence, the balance will return to its original horizontal position.83
In his discussion of this result Tartaglia actually employed two different measures of straightness, both of which were in agreement with his definition quoted above. In the proof of his proposition, he made use of the projection of a finite circular descent on the vertical line of direction, comparing those projections for descents of equal angles. Later, however, he compared instead more directly the angles between the curved path of descent and a straight perpendicular line to the center of the world.84 For this purpose he actually compared angles of contact, just as Jordanus had done in De ratione ponderis (see figure 3.12). In this way Tartaglia concluded that the angle between the circular descent of the lower weight and the vertical line to the center of the world is larger than the angle between the circular descent of the higher weight and the said line.
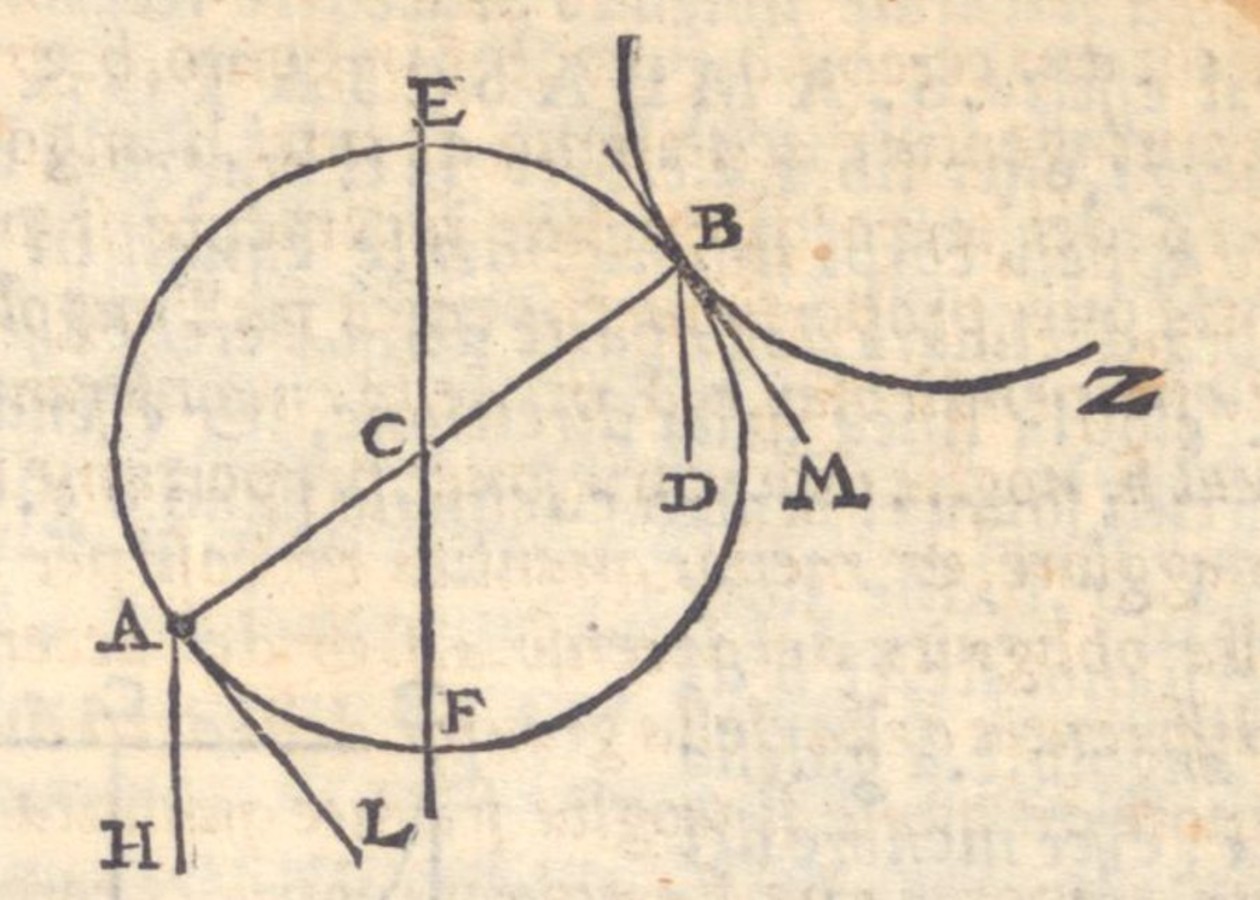
Fig. 3.12: According to Tartaglia, the body at B is positionally heavier than the body at A since the angle of contact between BD and BF (taken along the periphery) is smaller than the angle between AH and AF (taken along the periphery).
He thus again obtained the result that the descent of this higher weight is more direct and the weight itself positionally heavier. Had he just compared the ordinary angles between the tangents to the circular paths of descent and the vertical, the two angles would have simply been equal. It is thus the difference or ratio between the angles of contact, themselves less than any difference or ratio you please which can occur between any large and small quantities85 that is responsible for the difference in positional heaviness. Therefore, this difference cannot be compensated by any finite weight placed on the side of the scale that happens to be positionally lighter.
Following and improving upon Jordanus, Tartaglia also treated the inclined plane with the help of the concept of positional heaviness.86 He considered two adjacent inclined planes of different inclinations but of equal height (see figure 3.13). He then took two weights which may be imagined to be connected by a weightless rope making sure that if one weight moves up, the other moves down. He claimed that when the weights are in the same proportion as the lengths of these planes with the greater weight being placed upon the more oblique plane, equilibrium will result. This is, in fact, a correct proposition about bodies placed on inclined planes.
In his proof, Tartaglia, following Jordanus, managed to compare ascents of equal lengths along the differently inclined planes, but starting from the same height. From the larger vertical projection of the displacement along the steeper ascent he concluded that the corresponding weight must have a larger positional heaviness. By means of a geometrical argument he showed that the ratio between the positional heaviness of two weights equals the inverse relation between the lengths of the inclined planes. As a consequence, the weight on the steeper plane – due to its proportionally increased positional effectiveness – is able to equilibrate the larger weight on the more oblique plane.
Tartaglia thus employed the concept of positional heaviness in his proof of the law of the lever, in his problematic conclusion that a balance with equal arms always returns to the horizontal position although the infinitely small driving force cannot be compensated by any weight, and as well in demonstrating the equilibrium of an inclined plane. In each case, his analysis was based on evaluating the straightness of descent, either by determining the projection of the descent on the vertical, or by its angle with the line connecting a heavy body to the center of the world. Some of these achievements and the conceptual framework on which they depend were both further elaborated and criticized by Benedetti and Guidobaldo.
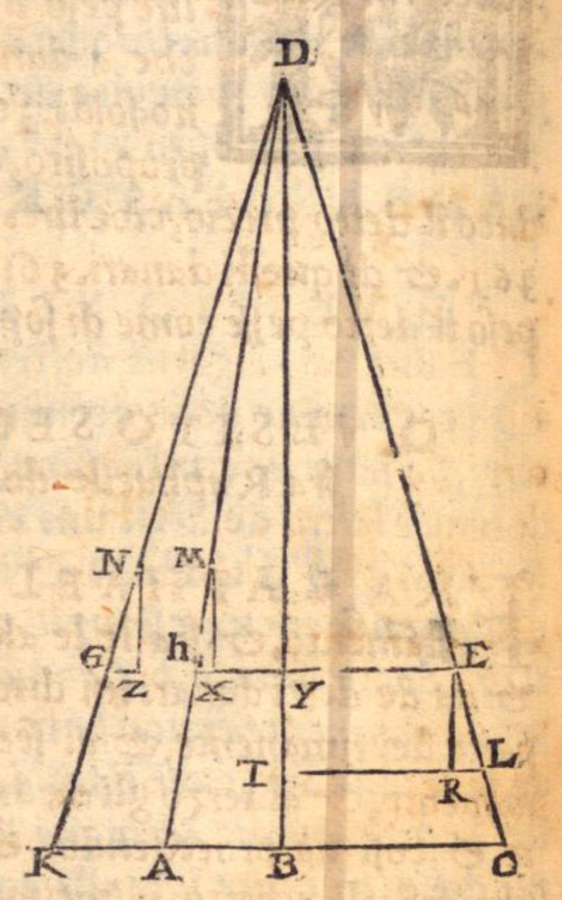
Fig. 3.13: According to Tartaglia, given that MH equals NG, the lines MX and NZ represent the different positional heaviness of a body on the corresponding inclined planes. A body at H is thus positionally heavier than the same body at G in proportion to the length of the lines MX and NZ which for geometrical reasons equals the proportion between the lengths of the inclined planes DK and DA.
Tartaglia's systematic use of the concept of positional heaviness adopted from Jordanus became a starting point for numerous attempts to apply Archimedes' law of the lever to challenging new objects of preclassical mechanics. The way Tartaglia applied the concept already shows its inherent difficulties, which puzzled scholars in the early modern period. The concept was supposed to provide an answer to the problem that the effect of a weight depends somehow on material conditions which hindered its straight movement toward the center of the world. But precisely how this effect came about remained ultimately undetermined. In particular, Tartaglia was unable to convincingly eliminate the resulting ambiguity of the concept. As we shall see in the following, this ambiguity triggered several contradicting interpretations which became stumbling blocks of preclassical mechanics and resulted in acrimonious struggles between their adherents.
3.7 Cardano's approach to positional heaviness
Girolamo Cardano was born in Pavia in 1501. His father was a lawyer and a friend of Leonardo da Vinci. He studied and practiced medicine, a subject on which he published extensively. Later, he published also on mathematics, contributing significantly to the development of algebra. On the issue of solving third-degree equations he had an intense priority dispute with Tartaglia. He also made major contributions to mechanics. In 1570 he was imprisoned by the Inquisition for heresy, in particular for having casted the horoscope of Christ. In the same year, Cardano published his Opus novum de proportionibus in which he returned to a consideration of mechanical problems, in particular, of weights on a balance and their displacements along horizontal and vertical components.
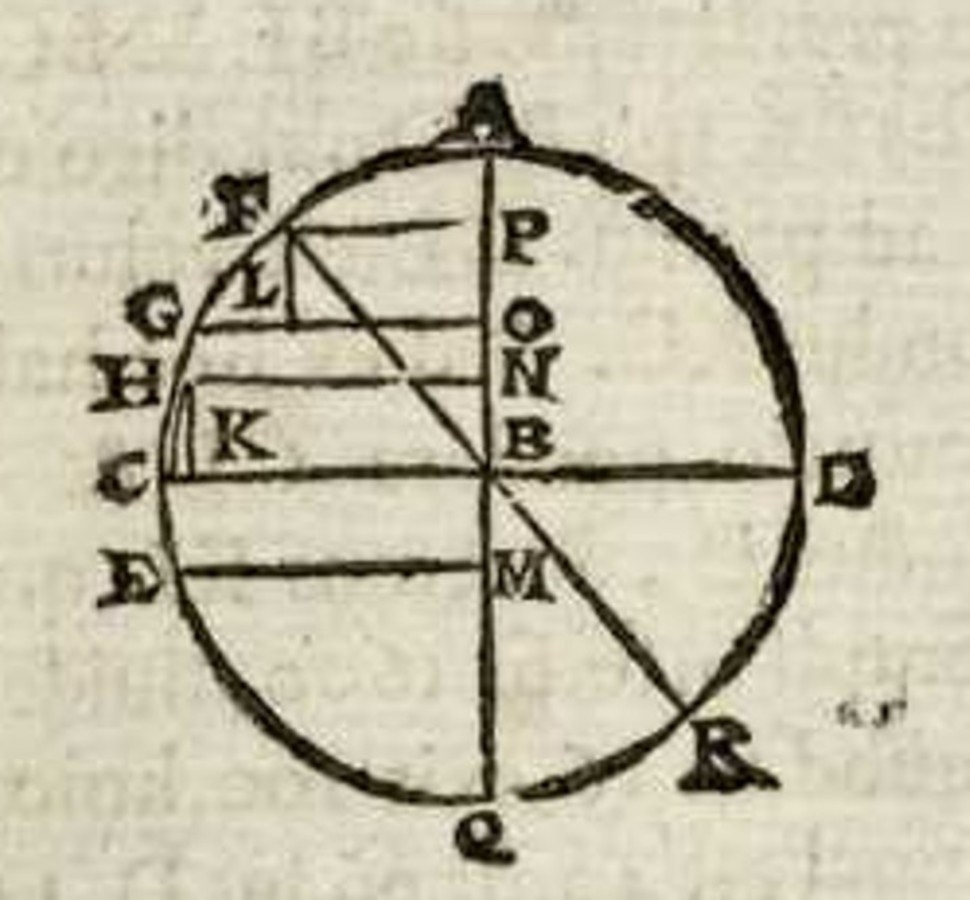
Fig. 3.14: According to Cardano there are three ways to determine positional heaviness. The positional heaviness in point F, for instance, may be determined by the horizontal FP, by the vertical FL, or by the angle QBF.
Cardano first treated the balance on a few pages of the first book of De subtilitate, published in 1550.87 At that time he may have been familiar with Jordanus' work through Apianus' edition of Liber de ponderibus printed 1533.88 It is also possible that he knew the work of Jordanus through Tartaglia's Quesiti89 published 1546, four years before his own publication. In any case, the first part of his text is substantially based on Jordanus's treatment of the medieval doctrine of the science of weights.
Cardano began his treatment of the balance with the figure of a balance deflected from the horizontal equilibrium into an oblique position (see figure 3.14). He claimed that a weight placed at the end of the beam of the balance will be heavier in the horizontal position than in any oblique position:
Dico quod pondus in C constitutum erit gravius quam si lanx collocetur in quocunque alio loco, ut pote quod constitueretur lanx in F. Ut autem cognoscamus quod C sit gravius in eo situ quam in F, necessarium est ut in aequali tempore movetur per maius spacium versus centrum. Videmus enim graviora pari ratione in reliquis existente velocius ad centrum ferri.
I say that the weight placed at C will be heavier than when the scale beam is placed in any other position, like when for instance the beam is located in F. But in order to recognize that C is heavier in this position than in F, it is necessary that it is moved in the same time through a greater distance toward the center. We see namely that the heavier bodies, everything else being equal, are more quickly carried toward the center.90
The claim that a weight will be heaviest if the beam is in horizontal position corresponds precisely to the way in which Jordanus introduced the technical term positional heaviness in the Proemium to the Liber de ponderibus91 and how he formulated the claim in his fourth proposition using the term. In Tartaglia's Quesiti, which Cardano may have known, there is no explicit proposition with the same claim, but it is implicitly contained in the proof of his fifth proposition and explicitly formulated as the first corollary to this proposition:
Dalle cose dette, et dimostrate di sopra, se manifesta qualmente un corpo grave in qual si voglia parte, che lui se parta, over removi dal sito della equalità lui si fa più leve, over leggiero secondo il sito, over luoco, et tanto più quanto più sara remosso da tal sito […]
From the things said and demonstrated above, it is manifest how a heavy body, whenever parted or removed from the position of equality, is made positionally lighter, and the more so, the more it is removed from that position.92
The first step of the justification of Cardano's claim refers to Aristotelian dynamics associating the heaviness of a body with the velocity of its descent as it was formulated in Jordanus' second comments and in a sequence of definitions and postulates of Tartaglia's Quesiti leading to his second postulate. Jordanus' postulate reads:
Secunda, quanto gravius tanto velocius descendere.
Second: That which is heavier descends more quickly.93
Tartaglia's postulate reads:
Simelmente adimandamo, che nasia concesso quel corpo, ch'è di maggior potentia debbia anchora discendere più velocemente, et nelli moti contrarii, cioè nelli ascensi, ascendere più pigramente, dico nella libra.
Likewise we request that it be conceded that that body which is of greater power should also descend more swiftly; and in the contrary motion, that is, of ascent, it should ascend more slowly – I mean in the balance.94
Cardano then announced two reasons for his claim that positional heaviness at the end of a deflected beam is greater the closer the beam is to the horizontal (see figure 3.14):
Quod autem hoc contingat magis pondere et libra in C collocata quam in F, ostendo duabus rationibus.
Prima, quod si in aliquo tempore moveatur ex C in E, et sit arcus CE aequalis FG, quod tardius descendet ex F in G, quam ex C in E, et ita erit levius in F, quam in C.
Secundo, quod posito quod in aequali spatio temporis moveretur ex C in E, ex et F in G, adhuc per arcum CE aequalem FG, magis appropinquaret centro quam per motum factum in arcu FG.
Ideo ergo duplici ratione magis gravabit pondus lance posita ad perpendiculum cum trutina, quam in quoque alio loco.
But that it is heavier when the balance is placed at C than at F, I demonstrate with two reasons.
First, because, insofar as [the weight at the end of the beam] is moved in some time from C to E, the arc CE being equal to FG, it descends more slowly from F to G than from C to E, and so it will be lighter at F than at C.
Second, because, insofar as it is assumed that [the weight at the end of the beam] is moved in the same amount of time from C to E, and from F to G, up to this point through the same arc CE equal to FG, it approaches the center more than through the motion made along the arc FG.
Hence for this double reason the weight placed on the scale beam perpendicularly with respect to the support will be heavier than in any other position.95
Cardano's first reason considers the case that equal arcs are traversed in different times and infers that the speed through the arc further away from the horizontal must be smaller and thus that the weight in this position must be lighter. His second reason considers the case that equal arcs are traversed in equal times and infers that the weight closer to the horizontal approaches the center of the world more.
The following main part of the argument explains the two cases. The first explanation reads (see figure 3.14):
Primum igitur sic declaratur. Manifestum est in stateris, et in his qui pondera elevant, quod quanto magis pondus a trutina, eo magis grave videtur: sed pondus in C distat a trutina quantitate BC lineae, et in F quantitate FP, sed CB est maior FP, ex decimaquinta, tertii elementorum Euclidis: igitur lance posita in C, gravius pondus videbitur quam in F, quod erat primum.
Ex hac etiam demonstratione manifestum est, libram quanto magis discendit versus C ex A, tanto gravius pondus reddere, et eo velocius moveri: at ex C versus Q, contraria ratione pondus reddi levius, et motum segniorem, quod et experimentum docet.
The first is thus explained in the following way. It is manifest in steelyards and in those [instruments] that lift weights, that the more the weight is [removed] from the support, the heavier it appears: but the weight at C is removed from the support by the quantity BC of the line, and at F by the quantity FP, but CB is larger than FP, from the fifteenth [proposition] of the third [book] of Euclid: hence when the beam is placed at C, the weight will appear heavier than at F, which was the first.
From this demonstration it is also manifest that the more the balance descends from A toward C, the heavier the weight will be rendered, and the quicker it will be moved: but from C to Q, for the contrary reason, the weight will be rendered lighter, and the motion slower, as also the experiment shows.96
This explanation is puzzling and not only because the last sentence refers to an experiment that relates the equilibrium controversy to the motion along a circular arc, as in the case of a pendulum. Cardano's text introduces an idea that cannot be found in Tartaglia's Quesiti, that is, the idea that if the beam is in a deflected position, the horizontal distance to the vertical through the center of the balance is a measure of the positional weight. It is, however, as discussed earlier, implicitly contained, among others, in the eighth proposition of Jordanus' De ratione ponderis, which is the proposition that has been corrected from proposition six of Elementa and Liber de ponderibus (see section 3.5). It is thus also contained in the eighth proposition of Tartaglia's later edition of Jordanus' corrected and extended treatise, which is supplemented by improved drawings (see figure 3.15).
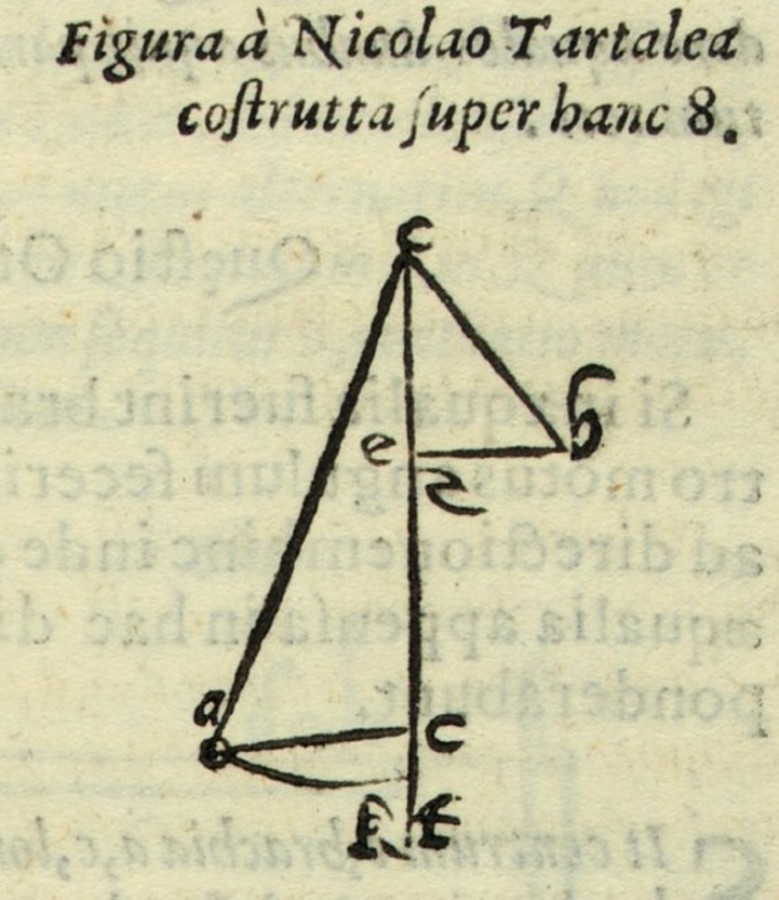
Fig. 3.15: Tartaglia's figure added to the text of Jordanus in order to explain the idea that in the case of a bent lever ACB with equal weights attached, the equilibrium is characterized by equal horizontal distances EB and AC.
The conclusive part of Cardano's second explanation reads (see figure 3.14):
Secundum vero sic demonstratur. […] Dum igitur libra movetur ex C in E pondus descendit per BM lineam, seu propinquius centro redditur quam esset in C, et dum movetur per spatium arcus FG, descenditque per OP, et BM, maior est OP.
Igitur suppositio etiam quod in aequale tempore transiret ex C in E, et ex F in G, adhuc velocius descendit ex C, quam ex F. Igitur gravius est in C, quam in F. Ex hoc autem demonstratur quod dicit Philosophus, quod si aequalia sint pondera in F et R, libra tamen sponte redit ad situm CD, ubi trutina sit AB. Nec hoc demonstrat Iordanus, nec intellexit.
But the second will be thus demonstrated. […] When thus the balance is moved from C to E the weight descends through the line BM, that is, it is rendered closer to the center than when it was in C, and when it is moved through the space of the arc FG, it will descend through OP, and BM [is] larger than OP.
Hence also the supposition that when [the weight] traverses in the same time from C to E, and from F to G, it thus descends more quickly from C than from F. Hence, it is heavier at C than at F. But from this it is demonstrated what the Philosopher says, that when the weights at F and R are equal, the balance will nevertheless spontaneously return to the position CD, where the support is AB. And this Jordanus neither demonstrates nor understands.97
In this case Cardano again closely followed the fourth and fifth postulates of Jordanus by which the vertical descent is taken as a measure of the positional heaviness (see section 3.5). His argument also parallels Tartaglia's line of argument in the Quesiti where the twelfth in combination with the seventeenth definition completely determines his further reasoning (see section 3.6).
Tartaglia's twelfth and seventeenth definitions read:
Diffinitione XII:
Un corpo se dice essere più, over men grave d'un'altro nel descendere, quando che la rettitudine, obliquita, over dependentia del luoco, over spacio dove descende lo fa descendere più, over men grave dell'altro, et similmente più, over men veloce dell'altro, anchor che siano ambidui simplicemente eguali in gravità.
Definition XII:
A body is said to be more or less heavy in descent than another when the straightness, obliquity, or pendency of the place or space where it descends makes it descend more or less heav[il]y than the other, and similarly more or less rapidly than the other, though both are simply equal in heaviness.98
Diffinitione XVII:
Più obliquo se dice essere quel descenso, d'un corpo grave, il quale in una medesima quantità, capisse manco della linea della direttione, overamente del descenso retto verso il centro del mondo.
Definition XVII:
The descent of a heavy body is said to be more oblique when for a given quantity it contains less of the line of direction, or of straight descent toward the center of the world.99
Consequently, Cardano, like Jordanus and Tartaglia, also arrived at the erroneous conclusion that an equilibrated balance, deflected into an oblique position, will spontaneously return to the horizontal. Strictly speaking, this conclusion does not follow from his first measure of positional weight, but Cardano evidently failed to notice the fact that his different measures have different implications. In particular, he failed to recognize the potential of the first measure to lead to the correct solution of later classical physics.
Remarkably, Cardano ascribed the traditional stance in the equilibrium controversy to Aristotle himself. While he disputed that the claim that a deflected balance returns to the horizontal had been properly demonstrated by Jordanus, he referred to the Aristotelian Mechanical Problems for further support of this claim and introduced, on this basis, a third measure of positional weight, the angle with regard to what he called the meta, the direction of the line of support in the sense that, when the support is from above, the meta is represented by the lower half line, and when the support is from below, the meta is represented by the upper half line (see figure 3.14):
Aristoteles dicit hoc contingere, quum trutina est supra libram, quia angulus QBF metae, maior est angulo QBR. Et similiter quum trutina fuerit QBQB, erit meta AB, et tunc angulus RBA, maior erit angulo FBA, sed maior angulus reddit gravius pondus.
[…]
Generalis igitur ratio haec sit: pondera quo plus distant a meta seu linea descensus per rectam aut obliquum, id est, per angulum, eo sunt graviora.
Aristotle says that this happens when the support is above the balance, because the angle QBF of the meta is larger than the angle QBR. And similarly when the support is QB, the meta will be AB, and thus the RBA will be larger than the angle FBA, but the larger angle will render the weight heavier.
[…]
The general reason is hence this: the more the weights are removed from the meta or from the line of descent along a straight or an oblique line, that is, [as measured] by an angle, the heavier they are.100
Many years later, in 1570, Cardano published his Opus novum de proportionibus where he once again returned to a consideration of mechanical problems, in particular also of weights on a balance and their displacements along horizontal and vertical components without, however, proposing a new approach to the question of the stability of the balance.101
3.8 Guidobaldo's approach to positional heaviness
In his Mechanicorum liber of 1577102 Guidobaldo del Monte made considerable efforts to criticize the concept of positional heaviness, as introduced by Jordanus and revived by Tartaglia and Cardano, as well as some of the consequences drawn from it. As this criticism provides the background for many of his marginal notes to Benedetti's book, it shall be discussed in the following at some length.103 Even in the preface to his book, Guidobaldo stressed the fundamental importance of his criticism of Jordanus and his early modern followers Tartaglia and Cardano:
Verum quo facilius totius operis substructio ad fastigium suum per duceretur, nonnulla quoque de libra fuerunt pertractanda, et praesertim dum unico pondere alterum solum ipsius brachium penitus deprimitur: que in re mirum est quantas fecerint ruinas Iordanus (qui inter recentiores maximae fuit auctoritatis) et alii; qui hanc rem sibi discutiendam proposuerunt.
Now, in order that my whole work might be more easily built up from its foundation to its very top, certain properties of the balance had to be treated, particularly the case when one arm of the balance is depressed by a single weight. On this subject it is strange what disastrous errors were made by Jordanus (who had enjoyed the greatest authority among recent writers) and others who proposed this subject.104
Of particular importance to Guidobaldo was the claim that the balance, in any position also outside the horizontal, is in an indifferent equilibrium, in contrast to the opinion of Jordanus, Tartaglia, and Cardano, that it would return spontaneously to the horizontal position. The argument was of such importance to Guidobaldo that he spent the better part of some fifty pages of his book in dealing with it. In the Italian edition of 1581, he made the translator, Filippo Pigafetta, insert at the end of this discussion a lengthy comment,105 actually written by himself, referring both to the theoretical novelty of Guidobaldo's treatment and to the evidence he had been able to offer for it by actually constructing balances that displayed indifferent equilibrium:
Che questo autore è stato il primo a considerare esquisitamente la bilancia, ed intenderla dalla natura, e dal vero esser suo; però che egli il primiero di tutti ha manifestato chiaramente il modo del trattarla, e insegnarla, con proporre tre centri da essere considerati in questa speculatione; l'uno è il centro del mondo, l'altro il centro della bilancia, ed il terzo il centro della gravezza della bilancia, che in essa era un nascosto secreto di natura. Senza questi tre centri, chiara cosa è, che non si puote venire in conoscimento perfetto, ne dimostrare gli effetti varii della bilancia, i quali nascono dalla diversità del collocare il centro della bilancia in tre modi, cioè quando il centro della bilancia sta sopra il centro della gravezza di essa, overo quando è di sotto, o pure allhorche il centro della bilancia è nell'istesso centro della gravezza di lei;
si come l'autore insegna nelle tre precedenti dimostrationi, cioè nella seconda, nella terza, e nella quarta propositione: perochè nella seconda mostra quando la bilancia torna sempre egualmente distante dall'orizonte; nella terza quando non solo non ritorna, ma si move al contrario; nella quarta, che essendo la bilancia sostenuta nel suo centro dalla gravezza sta ferma dovunque ella si trova, il quale effetto in particolare non è più stato tocco, ne veduto, ne manco da niuno manifestato, fuor che dall'autore: anzi fin hora tenuto falso, ed impossibile da tutti gli predecessori nostri; i quali con molte ragioni si sono sforzati di provare non solamente il contrario, ma hanno etiandio affermato per certo, che la sperienza mostra la bilancia non dimorare già mai ferma se non quando ella è egualmente distante dall'orizonte.
La qual cosa in tutto è contraria alla ragione prima, per essere la dimostratione della sudetta quarta propositione tanto chiara, facile, e vera, che non so, come se le possa in modo alcuno contradire: e poi all'esperienza conciosia che l'autore habbia fatto sottilissimamente lavorare bilancie giuste a posta per chiarire questa verità, una delle quali ho io veduto in mano dell'Illustre Signor Gio. Vicenzo Pinello, mandatagli dall'istesso autore, la quale per essere sostenuta nel centro della su a gravezza, mossa dovunque si vuole, e poi lasciata, sta ferma in ogni sito dove ella vien lasciata. Ben è egli vero, che non bisogna, nel fare cotesta esperienza, correr così a furia, per essere cosa oltra modo difficile, come dice l'autore di sopra, il fare una bilancia, la quale sia nel mezo delle sue braccia sostenuta à punto, e nel centro proprio della sua gravezza.
Per la qual cosa egli è da por mente, che qual'hora alcuno si mettesse a far cotale esperienza, e non gli riuscisse, non perciò si deve sgomentare, anzi dica pur fermamente di non haver bene operato, ed un'altra volta ritorni a farne la sperienza, fin che la bilancia sia giusta, ed eguale, e venga sostenuta a punto nel centro della gravezza sua.
Et benche da altri siano state tocche le altre due predette speculationi, cioè quando la bilancia ritorna sempre egualmente distante dall'orizonte, e quando si move al contrario di questo sito, tuttavia non si è più intesa questa verità già mai apertamente, se non dall'autore nostro; peroche gli altri non hanno co'l senno penetrato in ciò tanto avanti, che habbiano saputo con distintione considerare il centro della bilancia in tre modi, come ho narrato.
Now our author is the first to have considered the balance in detail and to have understood its nature and true quality. For he is the first of all to have shown clearly the way of dealing with it and teaching about it, by propounding three centers to be considered in its theory: one is the center of the world, another the center of the balance, and finally the center of gravity of the balance: for in this was a hidden secret of nature. Without these three centers, it is clear that one could not come to a perfect knowledge or demonstrate the various effects of the balance which emerge from the diversity of placing the center of the balance in three ways, that is, when the center of the balance is above the center of gravity, or below, or when the center of the balance is in its very center of gravity.
These the author shows in the three preceding demonstrations, that is, in the second, third, and fourth propositions. In the second, he shows when the balance returns to a horizontal position, in the third when it not only does not return but moves in the contrary direction, and in the fourth that, when a balance is sustained at its center of gravity, it remains at rest wherever it is left. This last effect in particular has not been dealt with before, or seen, or even suggested by anybody besides this author. Indeed, until the present time it has been held to be false and impossible by all our predecessors, who not only have given many arguments attempting to prove the contrary, but have even assumed it to be certain that experience shows the balance never to remain fixed except when parallel to the horizon.
This is quite contrary to reason, first because the demonstration of the above fourth proposition is so clear, easy, and true that I do not know how it could be contradicted in any way; and second, their view is contrary to experience, inasmuch as our author has arranged for precise balances to be manufactured in a very sophisticated way for the purpose of showing this truth, one of which I saw in the hands of the illustrious Giovanni Vicenzo Pinelli,106 sent to him by the author himself, and, because it was sustained at its center of gravity, it could be moved to any position and would rest at any place where it was left. True it is that in performing this experiment one might not act hastily, for it is an extremely difficult thing (as the author says above) to make a balance which is sustained precisely at the center of its arms and at its precise center of gravity.
For this reason it is good to remember that, when anyone tries to perform such an experiment and does not succeed, he should not be discouraged, but rather should say that he had not been careful enough, and should try repeatedly until the balance is just and equal and is sustained precisely at its center of gravity.
And though others have touched on the other two propositions (that is, when the balance always returns to a horizontal position, and when it moves to the contrary side), yet the truth of this has never been understood except by this author, and others have not gone far enough to have made a distinct consideration of the center of the balance in three ways, as I have explained.107
This inserted text higlights the centrality of the reconcialiation of Aristotelian and Archimedean approaches for Guidobaldo's work, embodied in the relation between the three centers: the center of the world, the center of the balance, and the center of gravity of the balance.108 Inachievable as this synthesis was because of the impossibility of an indifferent equilibrium with gravitational forces acting toward a center, it did create a challenging problem driving the further development of mechanics, including experimental endeavors as described by Pigafetta.
Guidobaldo started the main part of his book with a long chapter on the balance. After some propositions about balances that are not suspended from the center of gravity, he turned with his fourth proposition to his major concern mentioned above, that is, the indifference of a balance suspended from the center of gravity against displacements. He actually gave a rather concise demonstration of the statement formulated in this proposition:
Libra horizonti aequidistans aequalia in extremitatibus, aequaliterque a centro in ipsa libra collocato, distantia habens pondera; sive inde moveatur, sive minus; ubicunque relicta, manebit.
A balance parallel to the horizon, having its center within the balance and with equal weights at its extremities, equally distant from the center of the balance, will remain stable in any position to which it is moved.109
The gist of his proof consists of a simple idea. The proof directly follows from his definition of the concept of center of gravity of a body, adopted from Commandino's Latin translation of Pappus' Collectiones:110
Centrum gravitatis uniuscuiusque corporis est punctum quoddam intra positum, a quo si grave appensum mente concipiatur, dum fertur, quiescit; et servat eam, quam in principio habebat positionem: neque in ipsa latione circumvertitur.
The center of gravity is a certain point within it, from which, if it is imagined to be suspended and carried, it remains stable and maintains the position which it had at the beginning, and is not set to rotating by that motion.111
If the balance is suspended from its center of gravity it must – according to this definition – remain stable in any position. From a modern point of view of the necessary rigor of demonstrations, this of course is a tautology rather than a proof. What is missing is a justification of the implicit assumption that a center of gravity meeting the requirements of Pappus' definition always exists.
Guidobaldo also gave another definition of the center of gravity which he adopted from Federico Commandino:
Centrum gravitatis uniuscuiusque solidae figurae est punctum illud intra positum, circa quod undique partes aequalium momentorum consistunt. si enim per tale centrum ducatur planum figuram quomodocunque secans semper in partes aequeponderantes ipsam dividet.
The center of gravity of any solid shape is that point within it around which are disposed on all sides parts of equal moments [partes aequalium momentorum], so that if a plane is passed through this point cutting the said shape, it will always be divided into parts that are in equilibrium [partes aequeponderantes].112
If the concept of moment is understood in a modern sense as describing the effect of a weight depending on its position, that is, the vector product of the weight and the lever arm, the definition is essentially correct (see section 1.4). It should be noted, however, that the concept of momento or momentum, later revived by Galileo,113 was employed by Guidobaldo neither here nor in any of his other demonstrations.
Guidobaldo must have felt that his proof of the indifference of a balance suspended from the center of gravity could not easily convince his contemporaries. Thus he noted:
Quoniam autem huic determinationi ultimae multa a nonnullis aliter sentientibus dicta officere videntur; idcirco in hac parte aliquantulum immorari oportebit; et pro viribus, non solum propriam sententiam, sed Archimedem ipsum, qui in hac eadem esse sententia videtur, defendere conabor.
But with regard to this last conclusion, many things are said by men who believe otherwise. Hence it will be well to dwell further on this; and according to my ability I shall endeavor to defend not only my own opinion but Archimedes too, who seems to have been of the same opinion.114
Continuing the proof of his fourth proposition he therefore started to address extensively the erroneous claim of his adversaries and their alleged proofs that a balance removed from the horizontal position will actually not remain indifferent to this displacement, but rather return to its original position.
3.8.1 Overview of Guidobaldo's criticism of the claims of his adversaries
The long, somewhat chaotic supplement of some fifty pages115 to Guidobaldo's fourth proposition of the chapter on the balance starts with a marginal note. This explicitly lists the treatises that were the subject of Guidobaldo's critique (see figure 3.16). In the first place he referred to Jordanus' De ponderibus, known to him from the commented edition of Apianus which he owned.116 In the second place he referred to Cardano's De subtilitate,117 and finally to Tartaglia's Quesiti.118 As we have discussed in the preceding sections, these treatises in fact all contain the claim that a balance in equilibrium, if it is moved out of the horizontal position, will spontaneously move back into the horizontal.119

Fig. 3.16: Marginal note listing the treatises Guidobaldo is criticizing.
Guidobaldo proceeded, over many pages, to derive assertions within the framework of Jordanus, Tartaglia, and Cardano, including his own opinion about the indifferent equilibrium of a balance, initially derived with the help of the concept of center of gravity. His motives are explained in the already mentioned comment inserted by Pigafetta (see page
ed affine che questa nova opinion sua, dimostrata a pieno nella predetta quarta propositione, resti totalmente chiara, non si è già contentato egli d'haverla dimostrata con vive ragioni, e certe solamente, ma come buon filosofo, procedente con via di reale dottrina, e di fondata scienza, (imitando Aristotele, il qual ne' principii de suoi libri, investigando dottrina migliore, ha datto contra la opinione de gli antichi, solvendo le ragioni addotte da loro:) ha ben voluto, essendo la verità una sola, proporre le opinioni de' suoi predecessori, ed esaminare le loro ragioni, le quali sembrano provar il contrario, e solverle, la loro fallenza dimostrando co'l presente discorso […]
Anzi di più per confermatione della verità soggiunge, che questi tali non hanno saputo fare le loro demostrationi; poi che co'l proprio modo di speculare usato da loro, e con le loro medesime ragioni prova la sua intentione, e sentenza essere verissima, appoggiando si alla dottrina di Aristotele sempre, e facendo toccar con mano, che egli con esso lui è d'accordo nelle questioni mechaniche.
And to the end that this new opinion of his, fully demonstrated in the aforesaid fourth proposition [about the indifferent equilibrium], should be completely clear, he has not been content to demonstrate it with vivid and certain reasoning alone, but, like a good philosopher, proceeding by the path of true doctrine and well-founded science (imitating Aristotle, who at the beginning of his books, in quest of the best doctrine, has given the contrary opinions of the ancients, analyzing the reasons which they accepted), he has wished, because there is but one truth, to propound the opinions of his predecessors and examine the reasons by which they prove the contrary, and to resolve these, showing their fallacy in the present argument […]
Moreover, as a confirmation of the truth, he adds that they did not know how to construct their proofs; for by their own mode of theorizing and their very own reasons, he proves his opinions to be most true, supporting them always on the doctrine of Aristotle and making it clear that he is in accord with him in the mechanical questions.120
Mentioning Aristotle here is significant. It shows that Guidobaldo could not easily dismiss a concept as closely related to Aristotelian dynamics as is positional heaviness. His faithfulness to Aristotle was evidently a major motive for his engagement in the equilibrium controversy, as also his marginal comments to the works of Jordanus and Benedetti show.
Guidobaldo's discussion of arguments in the treatises of his adversaries, which are related to his allegedly fundamental “discovery” of the indifferent equilibrium of a balance suspended from its center of gravity, is composed of several sections. Typically these sections begin with a paraphrase or reference to an argument of one of these treatises which Guidobaldo considered worthy of substantial rejection. He then presented opposing arguments or derived implicit consequences that justified his criticism. The result is a flow of meandering arguments and counterarguments. They extend the proof of his fourth proposition to an irritating web of inferences that cannot easily be disentangled. Given that the arguments of Guidobaldo's adversaries are themselves partly hybrids of various threads of implications, an adequate understanding of the disproportionate “proof” of his fourth proposition requires taking into account the context of the arguments in their treatises. A brief overview of the different sections of Guidobaldo's continuation of his proof may help to follow his arguments.
1 Guidobaldo first developed a general argument against the proposition that a balance in equilibrium if moved into an oblique position will return to the horizontal. He showed that the implications of this proposition are incompatible with the concept of the center of gravity upon which Archimedes' theory of equilibrium is based.121
2 Guidobaldo then paraphrased and extended a counterargument of Tartaglia's fictitious interlocutor Mendoza against his claim that the balance will return to the horizontal.122 This counterargument is based on the idea that it must be possible to compensate the alleged greater positional heaviness of the upper end of the balance in an oblique position by adding a weight to the lower end.123
3 Tartaglia rejected this counterargument by referring to an idea of Jordanus concerning the possibility of infinitely small differences between “mixed” angles which are composed of straight and curved legs.124 Guidobaldo paraphrased Tartaglia's rejection of Mendoza's counterargument, followed by an extensive argument against this rejection.125 At the end of this argument Guidobaldo introduced the condition that the directions to the center of the world for both ends of the beam of the balance are not parallel, attributing this assumption also to his adversaries although they did not make explicit use of it in their arguments. This condition later became a major concern in his reception of Benedetti's work. Contrary to the claim of Guidobaldo's adversaries, it follows that the lower end becomes positionally heavier than the upper end, a conclusion to which he returned in the sequel.
4 Next, Guidobaldo paraphrased three different arguments for dealing with the changing positional heaviness in dependence of the position of the beam of the balance. They differ in the measure of the positional heaviness, the first determining the positional heaviness by the horizontal distance of the weight from the vertical axis of support, the second by the vertical component of the actual trajectory, the third by the angle between the beam of the balance and the direction toward the center of the world. They have in common that they seem to determine somehow the effect of the obliquity by which the weights are hindered in descending directly to the center of the world.
Guidobaldo first reported Cardano's argument that the weight of a body attached to the beam of the balance is heavier the more distant it is from the support of the balance (see section 3.7).126 This distance is measured, as we have seen, by the horizontal distance of the suspended weight from the vertical through the center of the balance.127 Accordingly, a body suspended from a balance arm would be heaviest in the horizontal position of that arm, the position in which its motion would also be swifter than in any other position. This conceptualization of positional heaviness is close to the modern concept of torque, suggesting that the positional heaviness at the upper and the lower position must be the same (see section 1.4).
The second argument is based on taking the vertical distances of descent as a measure of the positional heaviness.128 Guidobaldo knew this argument from his copy of Apianus' edition of Jordanus' treatise Liber de ponderibus, where the argument forms the basis of the fourth and fifth postulates and is further elaborated in Apianus' commentary to Jordanus' second proposition.129 The argument also appears in Jordanus' treatise De ratione ponderis and is thus also contained in Tartaglia's edition (see section 3.5).130 As discussed above, an extensive version of the argument is furthermore contained in Tartaglia's Quesiti (see section 3.6).131 The argument is also appended by Cardano to his virtually correct conceptualization of the positional heaviness as representing – in modern terms – the torque. It seemed to imply the same conclusion as his first argument about the changing positional heaviness in dependence of the obliquity of the beam of the balance. This argument, however, provided a strong reason in favor of the erroneous conclusion that the balance must return to the horizontal position.
The third argument, which Guidobaldo again explicitly attributed to Cardano,132 involves the concept of meta and is based on taking as a measure the angle between the beam of the balance and the direction toward the center of the world.133 From the fact that the angle, thus defined, is greater in the upper than in the lower position, Cardano concluded that also the positional heaviness must be greater in the upper position.
5 Before detailing a refutation of his adversaries, Guidobaldo countered both Cardano's and Tartaglia's arguments in a general way by stressing that from the observation that a weight is swifter or its motion straighter, it does not follow that it will therefore also be heavier:
Neque enim intellectus quiescit, nisi alia huius ostendatur causa; cum potius signum, quam vera causa esse videatur.
Now the intellect is not satisfied unless this can be demonstrated from some other cause, for this appears to be merely a sign rather than a cause.134
He also noticed that all arguments referring to the swiftness of motion do not actually infer the positional heaviness of a body from its position, but only from its departure from that position.
Guidobaldo started his detailed account of the arguments of his adversaries with a discussion of Cardano's claim that the positional heaviness is determined by the distance from the vertical through the center of the lever, that is, the first argument he had introduced earlier.135 In the sequel he gave an account of the changing effect of the obliquity of the beam of a balance from his own perspective.136 His account included the cosmological context, in contrast to the tacit assumption of Cardano that the lines drawn from different points of the balance to the center of the world are parallel and thus cannot meet at this point. Guidobaldo's arguments are mainly based on physical reasons for his own claim that a weight (pondus) attached to the end of the beam of a balance is more or less heavy (gravius) according to the amount of support the beam gets from the center of the balance in dependence on the obliqueness of its position.
6 Guidobaldo continued with a critique of the second claim of his adversaries, in this case, as mentioned above, maintained by Jordanus, Tartaglia, and Cardano as well.137 All of them considered the vertical descent of a weight attached to the end of the beam of a balance, that is, the projection of the circular path of the end of the beam on the vertical direction to the center of the world, to be a measure of the obliquity of its path and thus of the weight's changing positional heaviness. Guidobaldo's refutation made use of two arguments. He first referred to the cosmological fact that the directions from different points of the circular path of the end of the beam toward the center of the world cannot be parallel and thus only approximately represent the positional heaviness. From the failure of his adversaries to take this fact into account, he concluded that all their demonstrations are false. His second argument conceded that the difference of the directions toward the center of the world is so small as to be imperceptible, and that their assumption that the straight descents of the weights are parallel was feasible. On this basis he then showed that their definition of positional heaviness was ambiguous and leads to contradictory results.
7 After demonstrating that the arguments of his three adversaries may lead to untenable conclusions, Guidobaldo added a sophisticated geometrical proof that on the basis of their assumptions about the relation between the vertical descent, the obliqueness of descent, and the positional heaviness, he could actually infer the opposite of their claim, namely that the positional heaviness at a position closer to the vertical is greater than the positional heaviness at a position more distant to the vertical, which is counter-intuitive.138
8 What follows is a short commentary on the origin of the errors of his adversaries. Guidobaldo argued that in general, inferences from false assumptions are false.139
9 After this general commentary, Guidobaldo once again returned to the dependence of the positional heaviness on the geometrical constellation of the inclined balance, now paying attention to the fact that both weights should be considered as being connected by the beam so that their motions cannot be considered independently.140 He tried to show that, even if the assumptions of his adversaries were accepted, that is, if the directions from the weights attached to the ends of the beam toward the center of the world were assumed to be parallel, and that the positional heaviness depended on how straight (rectus) their descent is, it does not necessarily follow from their arguments that the beam returns to the horizontal.
At this point Guidobaldo introduced the idea that one has to consider both weights not separately, but connected by the beam of the balance. From this perspective he reconsidered the arguments of his adversaries. He first discussed the dependence of the positional heaviness on the vertical descent of weights attached to the beam, as claimed by Jordanus, Tartaglia, and Cardano. He then discussed the dependence on the horizontal distance to the vertical through the point of suspension of the balance, as claimed by Cardano. In both cases Guidobaldo argued that the positional heaviness must be equal. In the first case he drew attention to the fact that one must not compare two descents, but rather a descent on one side with a rise on the other. In the second case the positional heaviness is equal by definition so that both measures lead to the same conclusion, in agreement with Guidobaldo's claim that the balance is in indifferent equilibrium. As an act of virtuosity Guidobaldo added the argument that if one compares ascents rather than descents, the balance will move, according to the logic of his adversaries, into a vertical and not a horizontal position.
10 Guidobaldo continued with an investigation of the situation in which the directions meet at the center of the world, instead of being parallel, and with a discussion of the meaning of obliqueness and straightness as criteria for the positional heaviness, offering his own reinterpretation of this concept.141 He concluded that, contrary to the opinion of his adversaries, the positional heaviness in the lower position must be greater and not smaller than the weight in the upper position.
11 This conclusion contradicts, of course, not only the claims of Guidobaldo's adversaries, but also his own claim that an equilibrated balance suspended at its center of gravity, if moved to an oblique position, will remain there. Therefore he now made use of his main argument, which he had introduced earlier, namely that the two weights on the balance have to be considered in conjunction.142 He criticized his adversaries for not taking this circumstance into account. His argument is implicitly based on the modern idea that the horizontal components of the directions toward the center of the world cancel each other out so that the remaining directions of gravity are parallel and the straightness of descent is the same for both weights.
12 So far Guidobaldo had extensively discussed and refuted all the inferences his adversaries had drawn from taking horizontal and vertical measures as defining the magnitude of the positional heaviness. At this point he moved on to the last claim of his initial overview.143 Cardano had argued that the angle between a beam supported from above and the meta, the direction toward the center of the world, determines the positional heaviness of a body attached to the end of the beam. He concluded that in this case the positional heaviness of the upper body exceeds that of the lower body. He further claimed that if the balance is supported from below, the positional heaviness of the lower body will exceed that of the upper body. Guidobaldo replied that there was no reason whatsoever for this assertion. Moreover, he argued that this assertion would lead to a contradiction if it were taken into account that a balance can be supported, at the same time, from above and below.
13 Guidobaldo finally discussed extensively the issue of a balance supported from above or from below144 as it had been treated in the Aristotelian Mechanical Problems, that is, with regard to a material beam in which the point of suspension of the balance does not necessarily lie on the line connecting the centers of gravity of the two weights. Cardano had indeed ascribed to Aristotle his assertion that the angle between the beam and the meta determines the heaviness of its weight (gravius pondus reddere).145 Cardano had further maintained, as discussed above, that Jordanus neither proved nor even understood this relation. In addition he had claimed that experience (experimentum) supports his assertion.146 Guidobaldo first discussed Cardano's misunderstanding of Aristotle's proposition. He conceded the difficulty in constructing a balance that is supported exactly at its center of gravity, but maintained that this is not a principal difficulty but only a question of practical precision. He then continued with his own interpretation of Aristotle's arguments, adding detailed proofs of his own of all possible constellations including equilibrated balances with unequal weights attached to them, compensated by corresponding unequal arms, and finally balances with a bent beam. The gist of this discussion is the support of his own claim from the Aristotelian treatment of the balance.
In summary, this long and somewhat chaotic supplement to Guidobal-
do's fourth proposition of the chapter on the balance is concerned with a number of basic ideas intimately related to the concept of positional heaviness. In the following, some of these ideas will be addressed in more detail, also in order to demonstrate how carefully Guidobaldo studied the contemporary literature and how he worked the fruits of these readings into his own line of reasoning. Our later discussion of the marginalia to Benedetti's work vividly illustrates how this process of reception actually worked.
3.8.2 Exploiting the concept of center of gravity
Guidobaldo began his discussion147 by generally refuting his adversaries' claim that a balance with equal weights attached at equal distances from its beam will, if the beam is moved from the horizontal position, not be indifferent to this displacement, but rather return to its original horizontal position. He pointed out a specific consequence of this claim:
Hanc eorum sententiam nullo modo consistere posse ostendam. Non enim, sed si quod aiunt, evenerit, vel ideo erit, quia pondus D pondere E gravius fuerit, vel si pondera sunt aequalia, distantiae, quibus sunt posita, non erunt aequales.
For if what they say is true, this result will occur because either the [upper] weight D is heavier than the [lower] weight E or the weights are equal but the distances at which they are placed are not equal.148
Guidobaldo argued that, since the weights are equal, the return to the horizontal position would involve a shift of the common center of gravity of the two weights at the arms of the balance. This, however, would be in conflict with the third proposition of Archimedes' On the Equilibrium of Planes149 and with Pappus' definition of the center of gravity he used in his own proof of the contrary statement:
Cum pondera eandem inter se se servent distantiam. Unius cuiusque enim corporis centrum gravitatis in eodem semper est situ respectu sui corporis.
For the weights remain the same distance apart, and the center of gravity of any body stays always in the same place with respect to that body.150
In the following part151 Guidobaldo turned to the other possibility, that is, to the claim that the balance might return to the horizontal position due to an increase of the weight152 of the ascending side of the balance. He used an indirect proof working with the counterargument of Tartaglia's interlocutor Mendoza that, if the two bodies on the arms of the balance should attain different weights, that difference could be compensated by placing an additional weight on the side that has become lighter. The latter conclusion then would lead to a contradiction.153 While on the one hand the center of gravity of the balance now in equilibrium must still be at the center of the balance, according to the law of the lever the addition of a weight would move the center of gravity out from the center of the balance. Guidobaldo argued that the existence of two centers of gravity contradicts Archimedes' theory, indirectly demonstrating that in the oblique position the balance would remain stationary (manebunt).
3.8.3 The intricacies of the concept of curvilinear angles
Fig. 3.17: Guidobaldo refuted the argument that the curvilinear angle MDG, which from a modern point of view is zero, is the smallest possible angle by inserting the curves QD and RD. According to the line of reasoning of his adversaries the angles MDQ and MDR must be smaller than MDG.
The objection put forward by Tartaglia's interlocutor Mendoza that a greater positional heaviness of the upper part of an inclined balance might be compensated by an additional weight on the lower part, had been refuted by Tartaglia using an argument going back to Jordanus.154 Tartaglia had argued that the difference in positional heaviness may just be infinitesimally small (not just minimal, but still less) so that it cannot be compensated by any finite weight. In his book Guidobaldo summarized this argument as follows:
Excessum enim ponderis D supra pondus E, cum quantitatis rationem habeat, non solum minimum esse, verum in infinitum dividi posse immaginabamur, quod quidem ipsi, non solum minimum, sed ne minimum quidem esse, cum reperiri non possit, hoc modo demonstrare nituntur.
For, the excess of weight D over weight E having some ratio and quantitative part, we imagined it to be not only minimal but also capable of infinite division. They seek in the following manner to prove that no such weight can be found, since it is not just minimal, but still less.155
Indeed, Tartaglia had argued that this is exactly what happens because the ratio of the mixed angles (angulus mixtus), as Guidobaldo called them, included between circumference and perpendicular at the two sides of the balance, that is, between the path of the weight and the direction to the center of the world, is supposedly smaller than any other ratio that exists between greater and smaller quantities.156 The term mixed angle designates angles with a curved leg. Guidobaldo reduced them to the special case of circles and a tangent touching each other. From a modern point of view the degree of such angles is zero, independent of the curvature of their legs. Guidobaldo, however, shared with Tartaglia the opinion that such angles differ from each other, although the difference is infinitely small.
In his response Guidobaldo first argued that it is easily possible, by considering circles of larger diameters, to construct situations in which the ratio between the two angles is even smaller so that the claim that the ratio is the smallest possible one is refuted (see figure 3.17). He then pointed to the fact that the lines connecting the weights to the center of the world are not parallel but must converge at that center. On this basis he argued that the lower weight actually becomes positionally heavier than the weight that has been raised,157 because the small but finite angle between perpendiculars and the directions to the center of the world outweighs any effect of infinitely small “angles” (see figure 3.18).
Fig. 3.18: According to Guidobaldo, if S represents the center of the world the mixed angle SEG between the circular path of the weight at E and the direction to the center of the world is less than the mixed angle SDG. Thus, contrary to what his adversaries claim, by their own suppositions the weight placed at E must be heavier than that at D.
As we shall discuss below (see section 3.9), Benedetti shared this conclusion but based this argument on entirely different assumptions.158 In contrast to Benedetti, Guidobaldo stayed entirely within Tartaglia's conceptual framework, comparing curvilinear angles as indicators of positional heaviness. It is thus also clear that Guidobaldo's insistence on the convergence of perpendiculars at the center of the world was not exaggerated precision, but rather a valid argument in a context in which infinitesimally small angles are being considered.159
3.8.4 Guidobaldo's reaction to Cardano's first argument
In responding to the arguments of his adversaries,160 Guidobaldo began with a general remark on their failure to offer physical reasons for the changing effect of the obliquity of the beam of a balance. He then adressed Cardano's claim that the closer a weight is to the vertical of the beam the less it weighs, offering his own account for this claim (see figure 3.19).
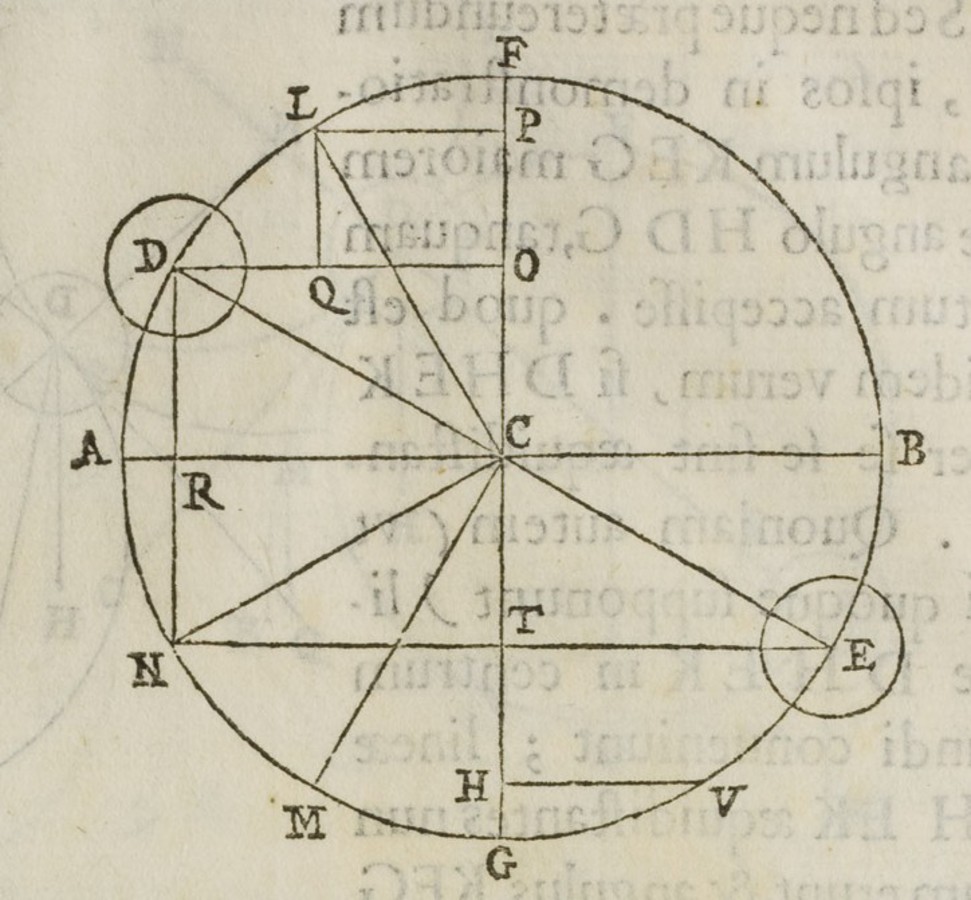
Fig. 3.19: Discussing Cardano's first measure of positional heaviness by the horizontal distances LP, DO, AC Guidobaldo explained the changing effect of the weight by the different extent to which the weight presses on the circumference of the circle traced by the balance.
In dealing with the varying distance of a weight from the vertical position of the beam, Guidobaldo reconstructed the whole line of reasoning by which the weight of a body on a balance arm has different effects according to the position of the arm from his own perspective, governed by attention to the relation between weight, support and center of the world. He summarized his own account stressing the physical reasons for the changing effect of a weight in different positions on the circle described by the beam of the balance:
Idem ergo pondus propter situum diversitatem gravius, leviusque erit. Non autem quia ratione situs interdum maiorem re vera acquirat gravitatem, interdum vero amittat, cum eiusdem sit semper gravitatis, ubicunque reperiatur; sed quia magis, minusque in circumferentia gravitat […]
Therefore the same weight, by diversity of position, will be heavier or lighter, and this not because by reason of its place it sometimes truly acquires greater heaviness and sometimes loses it, being always of the same heaviness wherever it is, but because it presses [grava] more or less on the circumference […]161
The proximity of the descent of a weight moving in constrained motion, on the one hand, and the natural motion of a weight to the center of the world, on the other, is determined by the angle of contact between the circular path of constrained descent and the straight line of direct descent to the center of the world. In this way Guidobaldo concluded, in particular, that it is not in the horizontal position of the balance arm that a body weighs most but at that point where a straight line drawn from the center of the world touches, as a tangent, the circle described by the balance arm. In the following we shall call that point for ease of reference the extreme point. At this point the lever arm forms a right angle with the path of direct descent to the center of the world. Accordingly, at this point the constrained descent of the weight along the circle will be closest to its natural descent along a straight line. It is also at the extreme point where the balance arm sustains the weight less than if it were at any other place on the circumference. The position of the balance arm at this point will be parallel to the horizontal, though not at the fulcrum of the balance but at the position of the center of gravity of the suspended body.
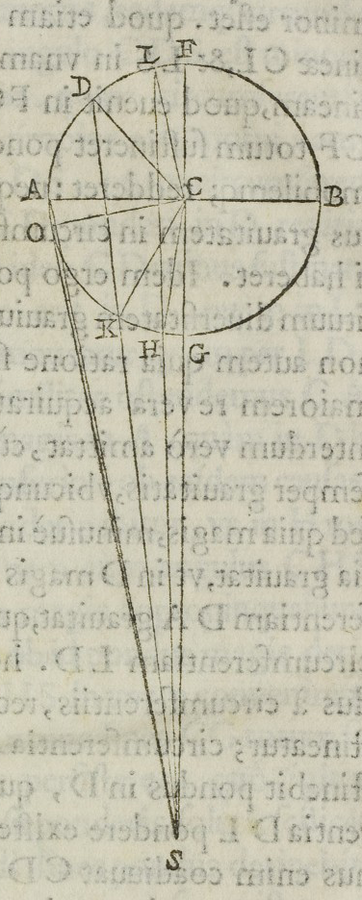
Fig. 3.20: Contrary to Cardano, Guidobaldo took into account that the directions from the two weights at the end of a balance cannot be parallel and that therefore the extreme point at which a weight is heaviest differs from point A.
Evidently, if the center of the world were infinitely distant and all lines of direction converging at it were perpendiculars and parallel to each other, then the extreme point would mark the horizontal position of the balance arm, also at the fulcrum. For a finite distance of the center of the world, the point where the weight is heaviest lies instead slightly below the horizontal through the fulcrum (see figure 3.20).
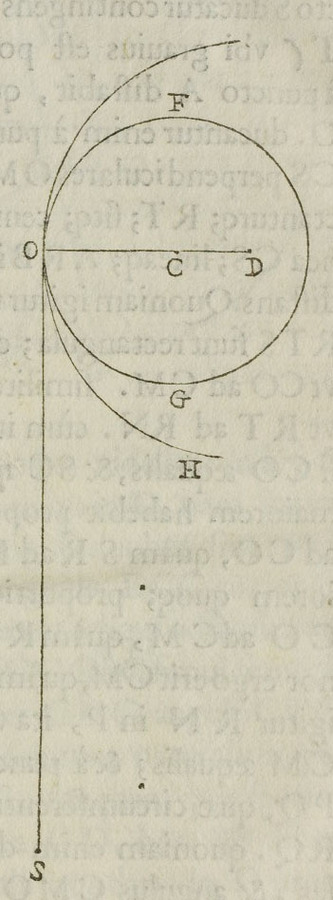
Fig. 3.21: Guidobaldo argued that the weight placed at O will be heavier along the arm DO than along the arm CO because the curvilinear “angle” SOH is less than the “angle” SOG.
Guidobaldo then showed that the same line of reasoning also allowed him to conclude that the weight at the extreme point is heavier the longer the balance arm, a crucial feature of any acceptable concept of positional heaviness (see figure 3.21). His argument is based on comparing curvilinear angles. In fact, the larger circle marked by the larger balance arm will make the smaller “angle” with the line of straight and natural descent to the center of the world. He then continued to consider the balance from a cosmological perspective, taking into account its finite distance from the center of the world (see figure 3.20). As we have discussed, this perspective was suggested to him by the attempt to set mechanical devices and processes into the context of an Aristotelian cosmos, a characteristic feature of preclassical mechanics. Guidobaldo demonstrated that the closer the balance is to the center of the world the farther the extreme point (where the weight is heaviest) will lie from the horizontal position of the balance arm (as seen from the fulcrum). He even proceeded to study cases in which the balance is located so that the center of the world lies either on or within the circle described by the balance arm. In his analysis Guidobaldo stuck to the principle that the positional heaviness (which he avoided to designate in this way) is determined by the closeness between constrained and direct descent to the center of the world, as given by the angle of contact between these two descents.
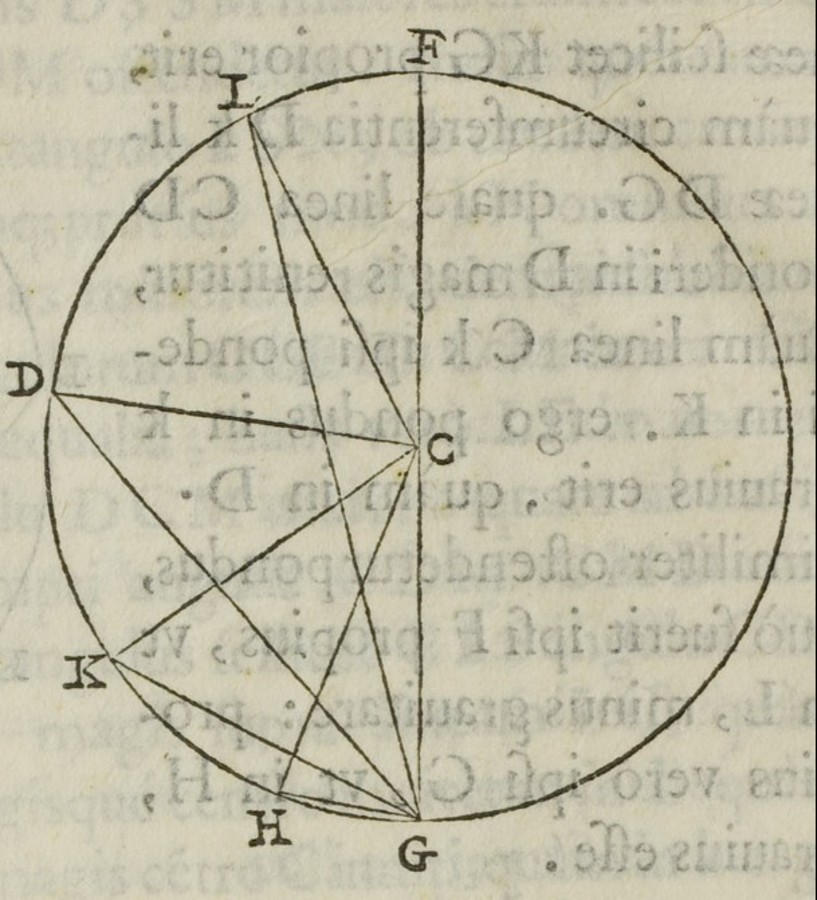
Fig. 3.22: Guidobaldo considered the extreme case in which the center of the world lies at the bottom of the circle described by the balance.
Particularly interesting is the case in which the balance is located so that the center of the world lies at the bottom of the circle described by the balance arm (see figure 3.22). For this case Guidobaldo showed that the closer the weight is to the bottom the heavier it becomes since, in any other position, it receives support from the balance arm and thus does not attain its full effect. The drawing accompanying the argument shows a circle with various chords connecting points on the circumference with the bottom of the circle; these points are also connected by radii to its center. Guidobaldo compared the constrained motion along the circumference with the direct motion along the corresponding chord to the center of the world located at the bottom of the circle. The exact same constellation of motions would later play a crucial role in Galileo's theory of motion, albeit with a different interpretation (see figure 3.23). It seems that Galileo simply transposed Guidobaldo's cosmological model to a terrestrial situation. The center of the world located at the bottom of the circle then simply becomes again the lowest point of the motion of the beam of a balance, while the various radii represent positions of the beam at different angles. But what about the chords? In a terrestrial setting they can only be interpreted as inclined planes connecting various points along the circumference with the bottom of the circle. Alternatively, the circle itself could also be conceived as representing the cross-section of a sphere or a cylinder constraining the motion. In any case, the motion of a weight left to itself along the circle, whether constrained by the beam of a balance or the surface of a sphere, would then be the motion of a pendulum.
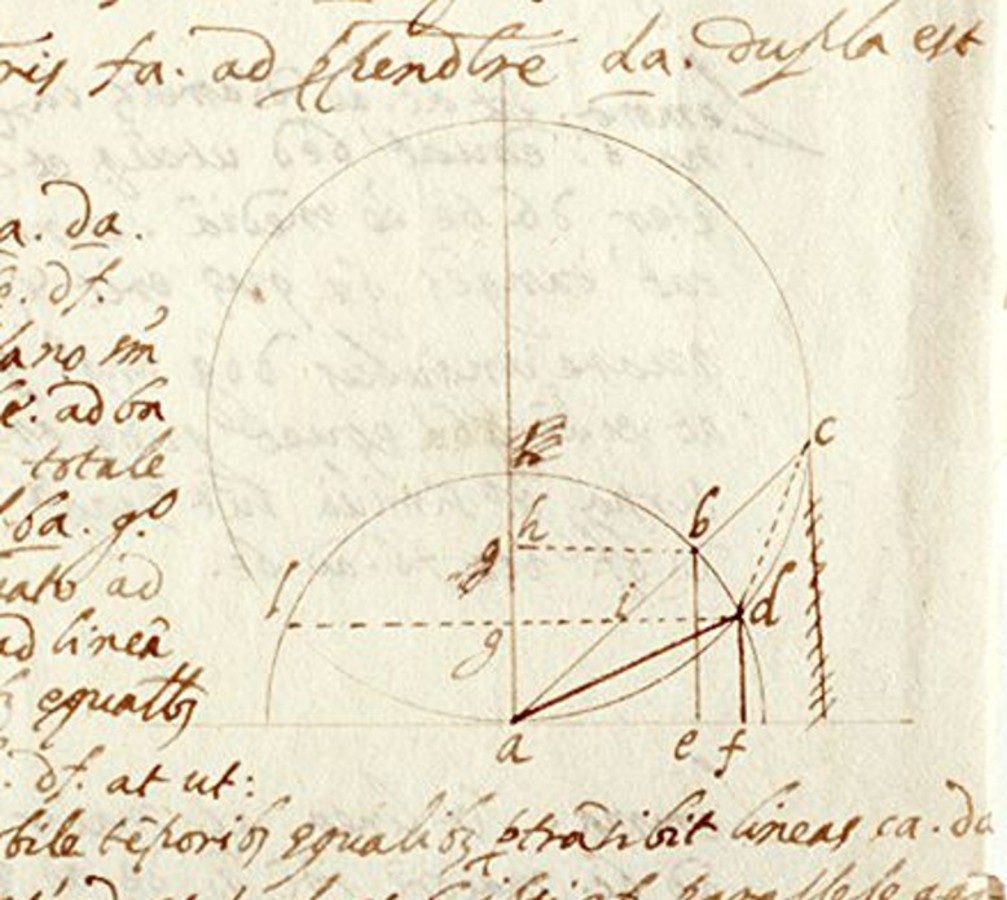
Fig. 3.23: Part of a page of Galileo's manuscript MS 72 Galilei 1602, fol. 172r related to theorem 6 of Galilei 1638 in Favaro 1968, vol. 8, the so-called “Theorem of Chords.” According to this theorem a falling body will require equal times to traverse the distances CA and DA.
Guidobaldo's cosmological model of a balance touching the center of the world could thus serve as the blueprint for a cornerstone of Galileo's new science of motion, the comparison of the motion of a pendulum along a certain arc with the motion along an inclined plane representing the chord of that arc. In 1602 the motion of a pendulum as well as the motion of fall along inclined planes representing the chords of a circle became the subject of a famous letter by Galileo to his patron Guidobaldo, who had been skeptical with regard to Galileo's claim about the isochronism of these motions.162 Indeed, Guidobaldo's analysis does not suggest any such isochronism. Its demonstration required a recognition of the laws of motion along differently inclined planes. This Galileo attained on a conceptual basis that was closer to Benedetti's mechanics than to Guidobaldo's theory (see section 3.10). Galileo's famous insights into the relation between the motion of a pendulum and the motion along inclined planes thus ultimately derived from integrating elements of both Guidobaldo's and Benedetti's work.
Guidobaldo finished his excursion on the question of how a balance behaves in the vicinity of the center of the world with a remark on the material beam of the balance which, of course, has weight itself. With the help of the concept of center of gravity he was able to quickly settle the issue. All that needed to be done was to find the center of gravity of the entire constellation of the arm of the balance and the weight attached to it. This constellation could then be treated as before as an idealized beam with a weight attached to it. Before going further, Guidobaldo summarized what he had identified so far as being the false assumptions of his adversaries, in particular, that a weight is heaviest in the horizontal position of the beam, which cannot be the case if the finite distance to the center of the world is taken into account.
3.8.5 Guidobaldo's reaction to the main argument of his adversaries
Having exhausted the issue of the distance of the balance beam from the vertical, Guidobaldo, as he had announced before, next entered a series of arguments shared by Jordanus, Tartaglia, and Cardano.163 These arguments concerned the determination of the positional heaviness by straightness and obliqueness in the sense of the amount to which a given descent partakes more or less in the direct descent to the center of the world. His adversaries took the horizontal projections of equal parts of the circular trajectory to the vertical as a measure of this partaking (see figure 3.24). Comparing the different descents along equal arcs of the upper and the lower weight, for geometrical reasons they thus came, as we have discussed, to the conclusion that the beam of the balance must return to the horizontal because the descent of the upper weight exceeds that of the lower.
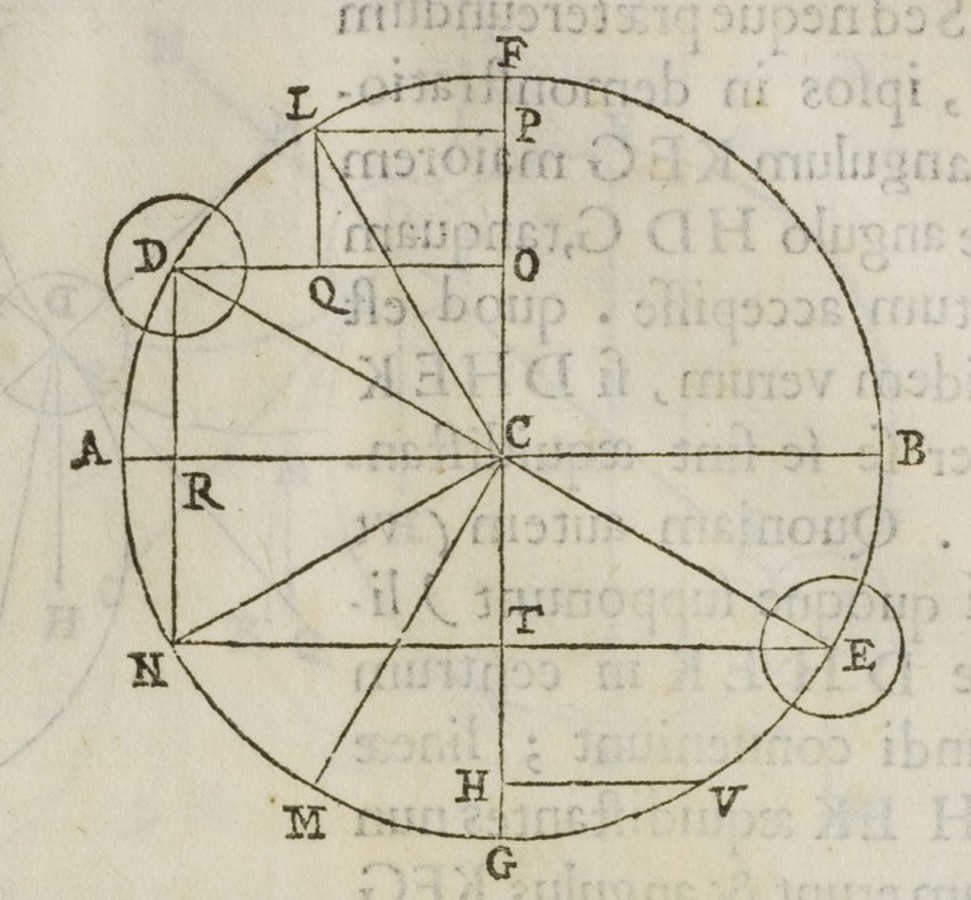
Fig. 3.24: According to Jordanus, Tartaglia, and Cardano, the vertical lines PO and OC represent the vertical descents of the starting points of the displacements along the equal arcs LD and DA. Therefore, the positional heaviness at point L must be smaller than at point D. Consequently, the balance must move spontaneously into the horizontal position.
Since Guidobaldo had earlier EOAemphasized that the lines connecting the weights with the center of the world cannot be parallel, he could now argue that the alleged proofs of his adversaries were altogether fallacious:
Ex quibus non solum suppositio illa, qua libram DE in AB redire demonstrant, verum etiam omnes fere ipsorum demonstrationes ruunt.
Thus they ruin not only the assumption from which they demonstrate that the balance DE returns to AB, but also almost all their demonstrations.164
Guidobaldo's response to his adversaries, however, left room for the counterargument that the deviations from the parallelism of the lines to the center of the world is negligibly small and that their arguments would work at least approximately. Therefore, Guidobaldo conceded this parallelism and proceeded to demonstrate that measuring positional heaviness by vertical projections leads to inconsistencies, even under these conditions.165 Jordanus, Tartaglia, and Cardano attempted to determine the magnitude of the positional heaviness by the vertical components of their further descent. They thus fell into the trap that they had to determine an attribute of a weight at a particular point by the length of a line, neglecting that this implicit definition did not sufficiently clarify how and in which direction the endpoint of this line had to be placed.
This is the tacit background of Guidobaldo's construction of counter-examples to their claim. He compared subsequent descents along equal arcs such as LA and AM corresponding to the equal vertical descents PC and CH. According to the implicit definition of his adversaries, the positional heaviness at points L and A should thus be equal (see figure 3.24). However, these subsequent descents in fact bring the beam into two different inclinations in which the endpoints of the beam are obviously of different positional heaviness.
Guidobaldo extended this discussion with further arguments, claiming in particular that when comparing the positional heaviness of descents on the two sides of the balance, their vertical components with regard to the horizontal position of the beam must be taken into account because otherwise further difficulties arise. He finally concluded that this definition of the magnitude of positional heaviness by vertical descents is inconsistent:
Ergo ex diversitate tantum modi considerandi, idem pondus, et gravius, et levius esse continget. Non autem ex ipsa natura rei. Insuper ipsorum suppositio non asserit, pondus secundum situm gravius esse, quanto in eodem situ minus obliquum est principium ipsius descensus. Suppositio igitur superius allata, hoc est, secundum situm pondus gravius esse, quanto in eodem situ minus obliquus est descensus; non solum ex his, quaediximus, ullo modo concedi potest; sed quoniam huius oppositum ostendere quoque non est difficile: scilicet idem pondus inaequalibus circumferentiis, quo minus obliquus est descensus, ibi minus gravitare.
Thus from a mere diversity in manner of consideration, and not from the nature of the thing, it would come about that the same weight was heavier or lighter. Moreover, their assumption does not affirm that the positional heaviness will be greater when at the same place the commencement of the descent is less oblique. Hence the postulate [they] adopted above, that is, that the weight is positionally heavier according as the descent from the same place is less oblique, is not to be conceded at all, for the reasons we have given; and not only that, but it is not difficult to show the exact opposite; that is, that the less oblique the descent of the same weight along equal arcs, the less it weighs.166
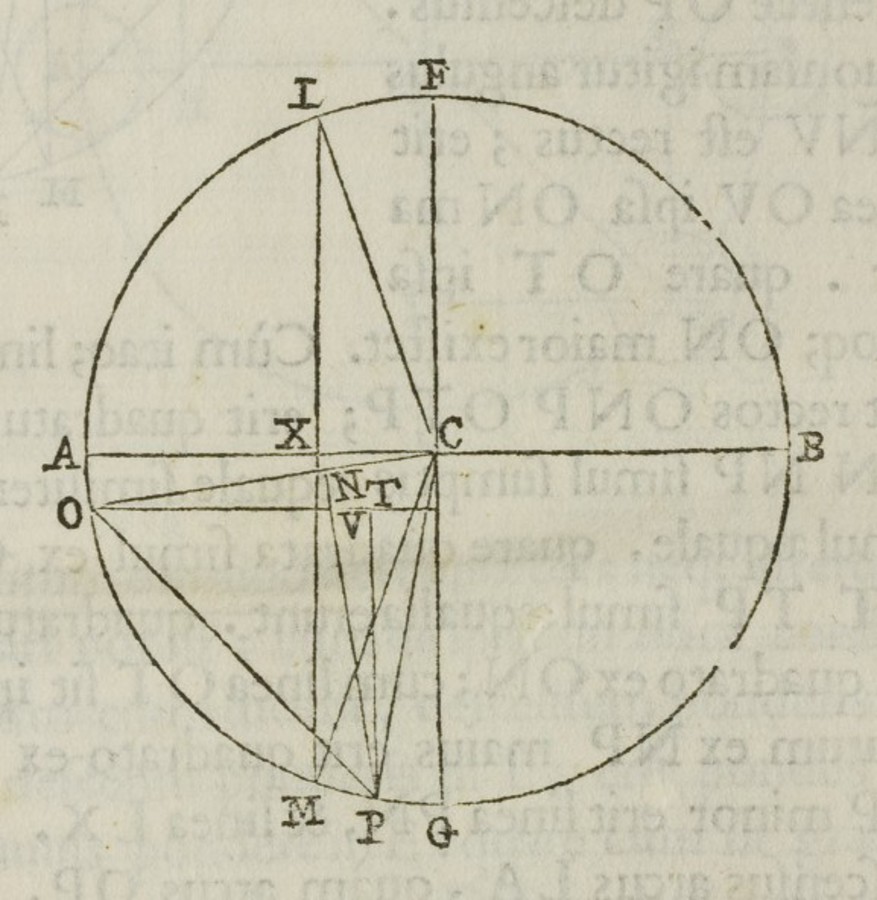
Fig. 3.25: Guidobaldo argued that according to the definition of his adversaries and contrary to their claims the positional heaviness in point L must be greater than in point O, since the vertical descent LX is longer than the descent TP.
Guidobaldo proceeded to consider equal arcs as before but now shifted the lower arc AM to result into the arc OP. By a rather involved geometrical proof he was now able to show that by applying the definition of his adversaries, the positional heaviness in the upper position L must be greater than the positional heaviness in the almost horizontal position O, which is absurd.
Guidobaldo concluded with a general methodological reflection:167
Non igitur ex rectiori, et obliquiori motu ita accepto colligi potest, secundum situm pondus gravius esse, quanto in eodem situ minus obliquus est descensus. atque hinc oritur omnis ferme ipsorum error in hac re, atque deceptio: nam quamuis per accidens interdum ex falsis sequatur verum, per se tamen ex falsis falsum sequitur, quemadmodum ex veris semper verum, nil idcirco mirum, si dum falsa accipiunt; illisque tanquam verissimis innituntur; falsissima omnino colligunt, atque concludunt. Decipiuntur quinetiam, dum librae contemplationem mathematice simpliciter assummunt; cum eius consideratio sit prorsus mechanica: nec ullo modo absque vero motu, ac ponderibus (entibus omnino naturalibus) de ipsa sermo haberi possit: sine quibus eorum, quae librae accidunt, verae caulae reperiri nullo modo possint.
Therefore it is not possible to deduce from the degree of straightness or bending of the motion (taken in their sense) that the weight is positionally heavier [secundum situm pondus gravius esse] according as, at a given place, the fall is less bent. And from this arises most of their error and delusion in this matter. And though at times the truth may accidentally follow from false assumptions, nevertheless it is the nature of things that from the false the false generally follows, just as from true things the truth always follows. So it is no wonder that, when they assume false things as true and use these as a basis, they deduce and conclude things that are quite false. These men are, moreover, deceived when they undertake to investigate the balance in a purely mathematical way, its theory being actually mechanical; nor can they reason successfully without the true movement of the balance and without its weights, these being completely physical things, neglecting which they simply cannot arrive at the true cause of events that take place with regard to the balance.168
3.8.6 The necessity of considering the weights in conjunction
Finally, Guidobaldo approached his goal of demonstrating with the help of a modified but still ambiguous concept of positional heaviness the indifferent equilibrium of a balance, assuming that the weight itself is changing.169 This rather tedious procedure is in stark contrast to his straightforward earlier proof which made use of the concept of the center of gravity. Now, at the beginning of the home stretch, he introduced the key idea that distinguishes his own approach from that of his adversaries, namely that the weights on a balance cannot be considered in isolation “as if now one and now the other were placed in the balance, but never both of them together.”170

Fig. 3.26: Guidobaldo's drawing on page 18r related to his proof of the indifferent equilibrium of a balance in an oblique position.
Neglecting the cosmological context for the time being, Guidobaldo first showed that the procedure of determining positional heaviness by the amount to which a given descent partakes more or less in the direct descent, a procedure he had just refuted with a reductio ad absurdum, allowed for the conclusion that a balance, when removed from the horizontal, would stay in its oblique position and not return to its original place (see figure 3.26). In his argument he used the key idea of the connection of the two weights, stressing that one should not compare the descents of the weights but rather the descent of one (from position D) with the simultaneous rise of the other weight (from position E):
Erit itaque descensus ponderis in D ascensui ponderis in E aequalis, et qualis erit propensio unius ad motum deorsum, talis etiam erit resistentia alterius ad motum sursum. Resistentia scilicet violentiae ponderis in E in ascensu naturali potentiae ponderis in D in descensu contra nitendo apponitur; cum sit ipsi aequalis. Quo enim pondus in D naturali potentia deorsum velocius descendit, eo tardius pondus in E violenter ascendit. Quare neutrum ipsorum alteri praeponderabit, cum ab aequali non proveniat actio. Non igitur pondus in D pondus in E sursum movebit. Si enim moveret; necesse esset, pondus in D maiorem habere virtutem descendendo, quam pondus in E ascendendo; sed haec sunt aequalia: ergo pondera manebunt. Et gravitas ponderis in D gravitati ponderis in E aequalis erit.
Therefore, the descent of the weight placed at D will be equal to the rise of the weight placed at E, and whatever the inclination of the one is to downward movement [propensio […] ad motum deorsum], such will also be the resistance of the other to upward motion [resistentia ad motum sursum]. That is, the resistance to the force of the weight [violentia ponderis] placed at E in its ascent opposes itself to the natural power [naturalis potentia ponderis] of the weight placed at D, because of their equality, so that by however much the weight placed at D goes with its natural power more swiftly downward, by so much the weight placed at E is more slowly forced upward. So that neither of the two will weigh more [praeponderare] than the other; there being no action that proceeds from equality, the weight [pondus] placed at D will not move the weight placed at E upward, because, if it did, it would be necessary that the weight placed at D should have stronger force [maior virtus] in descending than should the weight placed at E in rising. But these things are equal; therefore the weights [pondus] will remain at rest and the weighing down of the weight [gravitas ponderis] placed at D will be equal to the weighing down of the weight placed at E.171
Not leaving any doubt among his readers that he nevertheless considered the procedure applied to be worthless, Guidobaldo inserted another virtuoso-like reductio ad absurdum. He used the same procedure of determining positional heaviness by the amount to which a descent partakes in the vertical, to conclude that the balance would, when removed from its original horizontal position, ultimately assume a vertical position. The argument only works when the connection of the two weights on the balance is once again ignored. The trick of Guidobaldo's reductio ad absurdum is not to compare descents, as Jordanus and Tartaglia had done in order to show that the balance returns to its horizontal position, but to compare ascents instead. When previously the descent of the upper weight was straighter than that of the lower weight so that it acquired a greater positional heaviness, its rise is now more oblique than that of the lower weight so that it acquires a smaller positional heaviness. As a consequence, the lower weight which acquires a greater positional heaviness sinks to the bottom and the balance attains a vertical position.
Quae quidem suppositio, adeo manifesta esse videtur, veluti ipsorum altera.
This assumption seems as evident as theirs. […]172
Thus Guidobaldo commented and concluded that neither of these demonstrations is true.
3.8.7 Guidobaldo's reinterpretation of the concept of positional heaviness
It is at this point that Guidobaldo introduced his own interpretation of the changing effect of a weight attached to the end of a beam in dependence of its inclination.173 Following up on his earlier discussion,174 this interpretation takes the cosmological context into account, i.e., the finite distance to the center of the world. Furthermore, this interpretation determines obliquity in terms of the deviation of the actual path of the displacement from the closest route to this center. This deviation is measured by the curvilinear angle between both paths at the initial point of the displacement. In order to discriminate the weight pondus from its effect Guidobaldo qualified the way in which a weight acts under different circumstances using the term gravitare. He formulated his reinterpretation in the following way:
Praeterea si ipsorum suppositionem, eorumque verborum vim recte perpendamus; alium certe habere sensum conspiciemus. nam cum semper spatium, per quod naturaliter pondus movetur, a centro gravitatis ipsius ponderis ad centrum mundi, instar rectae lineae a centro gravitatis ad centrum mundi productae, sit sumendum; tanto huiusmodi ponderis descensus, magis, minusque obliquus dicetur; quanto secundum spatium instar praedictae lineae designatum, magis, aut minus (naturalem tamen locum petens, semperque magis ipsi appropinquans) movebitur; ita ut tanto obliquior descensus dicatur, quanto recedit ab eiusmodi spatio: rectior vero, quanto ad idem accedit. et in hoc sensu suppositio illa nemini difficultatem parere debet, adeo enim veritas eius conspicua est; rationique consentanea: ut nulla prosus manifestatione egere videatur.
In addition to this, if we shall examine their assumption, and the force of their argument, we shall certainly see that these have a different meaning. For since the space through which the weight moves naturally must be from the center of gravity of this weight toward the center of the world, along a straight line drawn from the center of gravity to the center of the world, it will be said that a descent of the weight made in this way will be more or less oblique according to the space designated, and that it will move more or less along the said line, always going to seek its natural place by the closest route. Thus the descent is said to be more oblique, the more it departs from that space, and straighter the more it approaches it. Now in this sense the assumption need not give rise to difficulty on the part of anyone, because this is so clear in its truth and its agreement with reason that it does not appear to need to be made evident in any way.175
Guidobaldo thus explained his understanding of the concept of positional heaviness, an understanding that he evidently no longer saw as being in conflict with his own line of reasoning, which EOAemphasized the concept of center of gravity and its relation to the center of the balance and the center of the world. The concept of positional heaviness was indeed an underdetermined concept, susceptible to various interpretations that were not necessarily in agreement with each other.176 These interpretations, moreover, could vary in conciseness. A more concise interpretation typically allows for more powerful conclusions, but is also more liable to conflict with other branches of the conceptual network in which it is employed. Guidobaldo's vaguer version of the concept avoided conflicts with his elaborate framework: it allowed for comparisons between weights of larger and smaller positional heaviness, it avoided the ambiguities that result from making the positional heaviness dependent on finitely extended descents, but it did not comprise a quantification as will be encountered in Benedetti's case. In other words, there was no quantitative measure for the positional heaviness of a given body under given circumstances.
Nevertheless, Guidobaldo's concept opened up a wide range of conclusions, in particular with regard to the cosmological behavior of balances and weights closer or more distant from the center of the world. With this Guidobaldo implicitly also left a challenge to his successors employing his achievements in their own work: For instance, how stable are these conclusions or what modifications do they require when reconsidered from the perspective of a modified interpretation of the concept of positional heaviness such as that of Benedetti or Galileo? As we have mentioned above, Galileo for instance turned Guidobaldo's statements about weights on a balance being closer or more distant from the center of the world into statements about weights on lesser or more steeply inclined planes.
3.8.8 From positional heaviness to indifferent equilibrium
After Guidobaldo had reinterpreted the notion of positional heaviness, he now approached the task of demonstrating the indifferent equilibrium of a balance. He had just shown that this reinterpretation would apparently even lead to the conclusion that the lower weight tends more to the center of the world than the upper weight. As a consequence, it seemed to follow that the balance would spontaneously move into a vertical position as soon its horizontal position is slightly disturbed, which is indeed a correct consequence from a modern point of view which Guidobaldo, however, could not accept. In order to show that, with the help of his reinterpretation of the positional effect of a weight, he could nevertheless derive the indifferent equilibrium of a balance, Guidobaldo now made crucial use of the fact that the two weights are connected. He thus complemented his reinterpretation with the idea to consider the balance as a system with an interaction of the two weights (see figure 3.27).177
His crucial argument was that if the two weights are joined together, one has to consider the descent not of each single weight, but of their center of gravity toward the center of the world. As a consequence, the natural motions of the two weights fixed to the balance will not be along straight lines converging at the center of the world, but along parallels to the straight line that connects their center of gravity with the center of the world. He argued that the connection of the two weights by the balance forces the weights into these parallel downward tendencies.
Si vero pondera in ED sibi invicem connexa, quatenusque sunt connexa consideraverimus; erit ponderis in E naturalis propensio per lineam MEK: gravitas enim alterius ponderis in D efficit, ne pondus in E per lineam ES gravitet, sed per EK.
But if the weights at E and D are joined together and we consider them with respect to their conjunction, the natural inclination of the weight placed at E will be along the line MEK, because the weighing down of the other weight [gravitas alterius ponderis] at D has the effect that the weight [pondus] placed at E must weigh down [gravitet] not along the line ES, but along EK.178
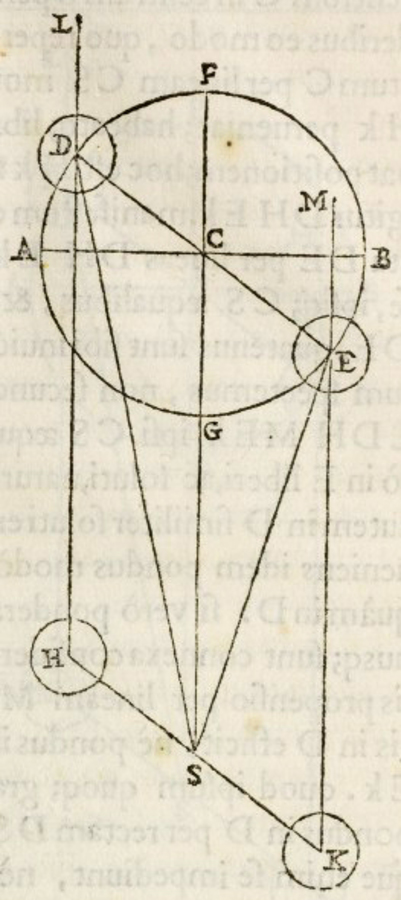
Fig. 3.27: Guidobaldo considered the weights in conjunction and argued that the balance resulting tendencies of the weights downward are parallel.
Having thus established the legitimacy of considering the natural descents of the two weights as being parallel, Guidobaldo could now use the same consideration as he had done before: comparing the rise of one weight with the decline of the other. The downward tendencies of the two weights were then identified by means of the closeness between constrained and natural descent (or rise) as measured by the angles of contact between these two paths:
Cum autem suppositio illa, quae ait, secundum situm pondus gravius esse, quanto in eodem situ minus obliquus est descensus; tanquam clara, atque conspicua admittatur; proculdubio haec quoque accipienda erit; nempe, secundum situm pondus gravius esse, quanto in eodem situ minus obliquus est ascensus. Cum non minus manifesta, rationique sit consentanea. Aequalis igitur erit descensus ponderis in E ascensui ponderis in D. eandem enim obliquitatem habet descensus ponderis in E, quam habet ascensus ponderis in D; et qualis erit propensio unius ad motum deorsum, talis quoque erit resistentia alterius ad motum sursum.
Now assuming that the weight is positionally heavier to the degree that its descent from a given place is less oblique, one will also admit without doubt that the weight will be positionally heavier according as its rise at a given point will be less oblique, since this is no less evident or agreeable to reason. Therefore the descent of the weight at E will be equal to the rise of the weight at D, because the descent of the weight at E has as much of the oblique as does the rise of the weight at D; and whatever may be the inclination of the one to downward movement, this likewise will be the resistance of the other to upward movement.179
Guidobaldo finally concluded:
Ex quibus sequitur pondera in D E, quatenus sunt sibi invicem connexa, aeque gravia esse.
From which it follows that the weights at D and E, considered in conjunction, are equally heavy.180
3.8.9 Guidobaldo's interpretation of Aristotle's balances
In agreement with his plan Guidobaldo next addressed the last argument in favor of the balance returning to the horizontal position, involving the idea of the meta of the balance.181 This meta is represented by the lower half of the perpendicular line through the fulcrum when the support is from above. He was quite aware of the obscure character of argument:
[…] nihil meo iudicio concludit. Figmentumque hoc de trutina, et meta potius omittendum, ac silentio praetereundum esset, quam verbum ullum in eius confutatione sumendum; cum sit prorsus voluntarium.
[…] in my opinion this [i.e. the return to the horizontal] does not follow, and this fiction about the support and the meta should just be left out and passed over in silence; for to say anything about it only confuses the issue, the whole thing being arbitrary.182
Nevertheless, Guidobaldo went to some length to reveal the illusionary character of the argument, apparently because the argument seemed to be supported by the Aristotelian Mechanical Problems as well as by empirical evidence.183 As to the role of empirical evidence, Guidobaldo stressed that the case in which the balance is supported at its center is particularly difficult to realize in practice, in contrast to the cases in which the support is either from above or from below:
Quocirca si centrum in ipsa libra esse consideraverimus, ad sensum confugiendum non est: cum artificilia ad summum illud perfectionis gradum ab artifice deduci minime possint.
Hence if we consider the center to be in the balance, one cannot have recourse to the senses, for artificial devices cannot be brought to such a degree of perfection.184
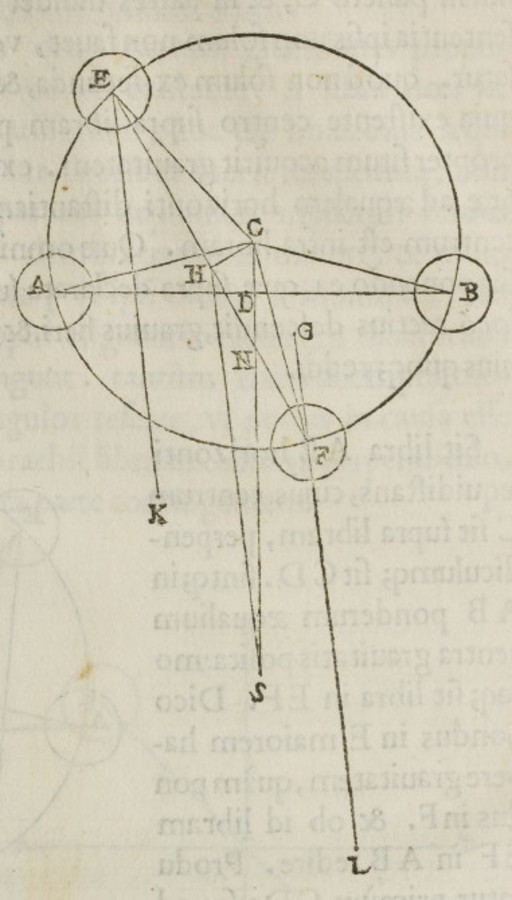
Fig. 3.28: In agreement with Aristotle, Guidobaldo argued that a balance supported from above when displaced from the horizontal position would return to the horizontal. His proof differs, however, from the proof of Aristotle. Guidobaldo argued that the upper weight E requires a greater heaviness than the lower weight F because the descent of the upper weight toward the center of the world S is less oblique than the rise of the lower weight.
This consideration may have provided a challenge and the starting point for Guidobaldo's efforts to actually produce such an indifferent balance, as it is described in Pigafetta's inserted letter quoted above (see page
The remainder of Guidobaldo's discussion of the Aristotelian Mechanical Problems deals mainly with the other two cases discussed by Aristotle, i.e., the cases when the support is either from above or from below (see figure 3.28). He had actually already dealt with these cases in the deductive part of his book, in propositions 2 and 3, on the basis of the concept of center of gravity. Now Guidobaldo re-expressed these conclusions with the help of his concept of the dependence of the heaviness (gravitas) on the positional circumstances:
Quod non solum ex secunda, et tertia huius liquet; verum quia existente centro supra libram pondus elevatum maiorem propter situm acquirit gravitatem. Ex quo contingit redditus librae ad aequalem horizonti distantiam. E contra vero, quando centrum est infra libram. Quae omnia hoc modo ostendentur; supponendo ea, quae supra declarata sunt. Scilicet pondus ex quo loco rectius descendit, gravius fieri. et ex quo rectius ascendit, gravius quoque reddi.
This [i.e. Aristotle's opinion that a balance supported from above will return to the horizontal, while a balance supported from below will move toward the lower side] is clear not only from the second and the third propositions of the present book, but also because, if the center is above the balance, the higher weight acquires a greater positional heaviness, considering the return of the balance to the position parallel to the horizon. The contrary happens when the center is below the balance. These things are demonstrated in the following manner, what has been said above being assumed: that is, that the weight will be heavier in that place from which its descent is straighter, and is likewise heavier at the place from which its rise would be straighter.185
Throughout the arguments that follow, Guidobaldo made use of defining that straightness in terms of angles of contact as he had done before. But he also occasionally employed Tartaglia's other definition of straightness, in terms of the descent partaking more or less in the vertical. The use of the latter definition, however, is prefaced by a note of caution on the intrinsic falsity of this approach:
Ex ipsorum quinetiam rationibus, ac falsis supositionibus iam declaratos librae effectus, ac motus deducere, ac manifestare libet; ut quanta sit veritatis efficacia appareat, quippe ex falsis etiam elucescere contendit.
Besides, we may use their logic and their false assumptions to produce the effects and motions of the balance already explained, so that from this one may see the power of truth and how it forces itself to shine forth even from false things.186
The excursion on Aristotle's balances ends with an extension of the previous arguments to the case in which an additional weight is placed on one arm of the balance, to the case in which the arms of the balance are of different lengths, and to the cases in which the arms are curved or form an angle.
3.8.10 Arguments in further propositions
This lengthy digression is followed in the Italian version by the comment of the editor Pigafetta (page
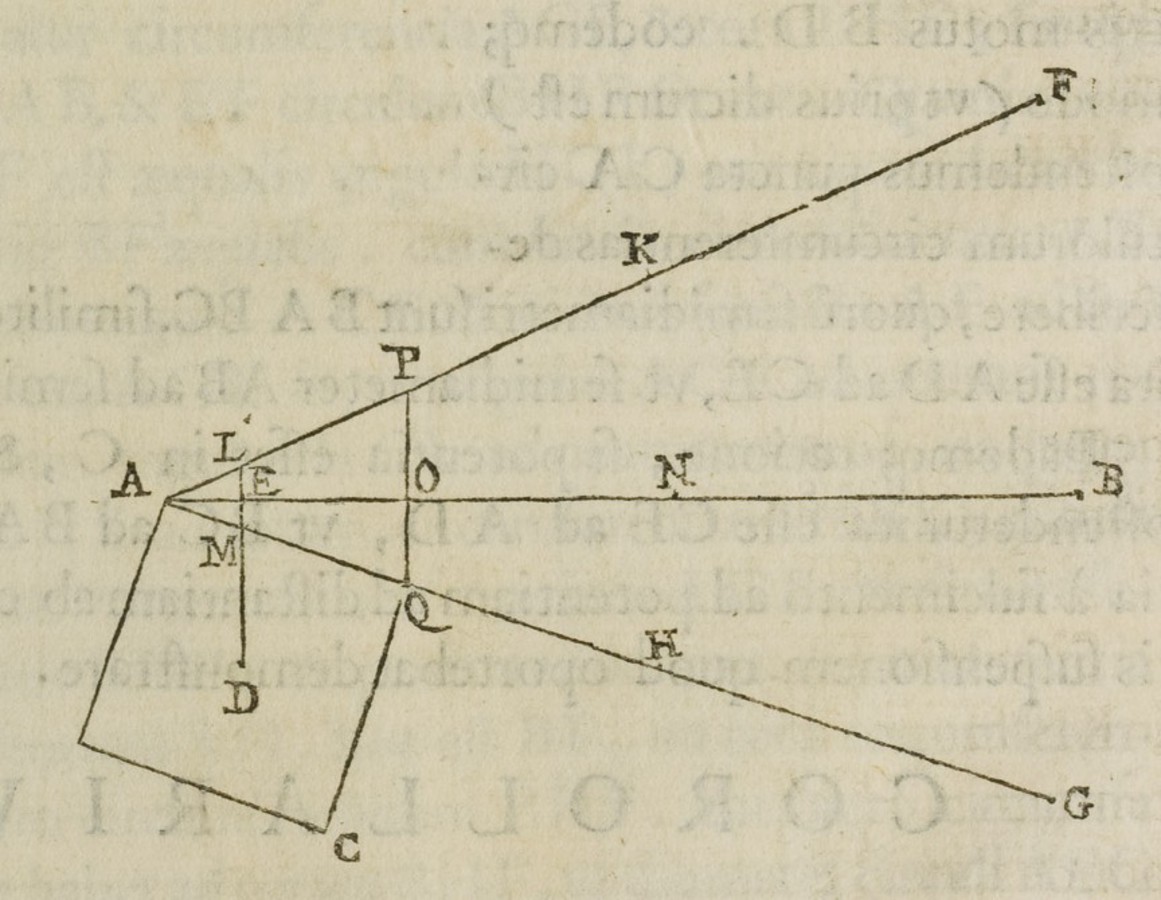
Fig. 3.29: Guidobaldo extended the vertical through the center of gravity of the weight to the beam of the lever in order to determine its effective heaviness, a conclusion that is not compatible with classical mechanics.
The crucial theorem is proposition 5 (see figure 3.29):
Potentia quomodocunque vecte pondus sustinens ad ipsum pondus eandem habebit proportionem, quam distantia a fulcimento ad punctum, ubi a centro gravitatis ponderis horizonti ducta perpendicularis vectem secat, intercepta, ad distantiam inter fulcimentum, et potentiam.
The power that sustains the weight in any way by means of the lever will have the same proportion to the weight as that of the distance from the fulcrum to the point on the lever, vertical to the center of gravity of the weight, to the distance between fulcrum and the power.187
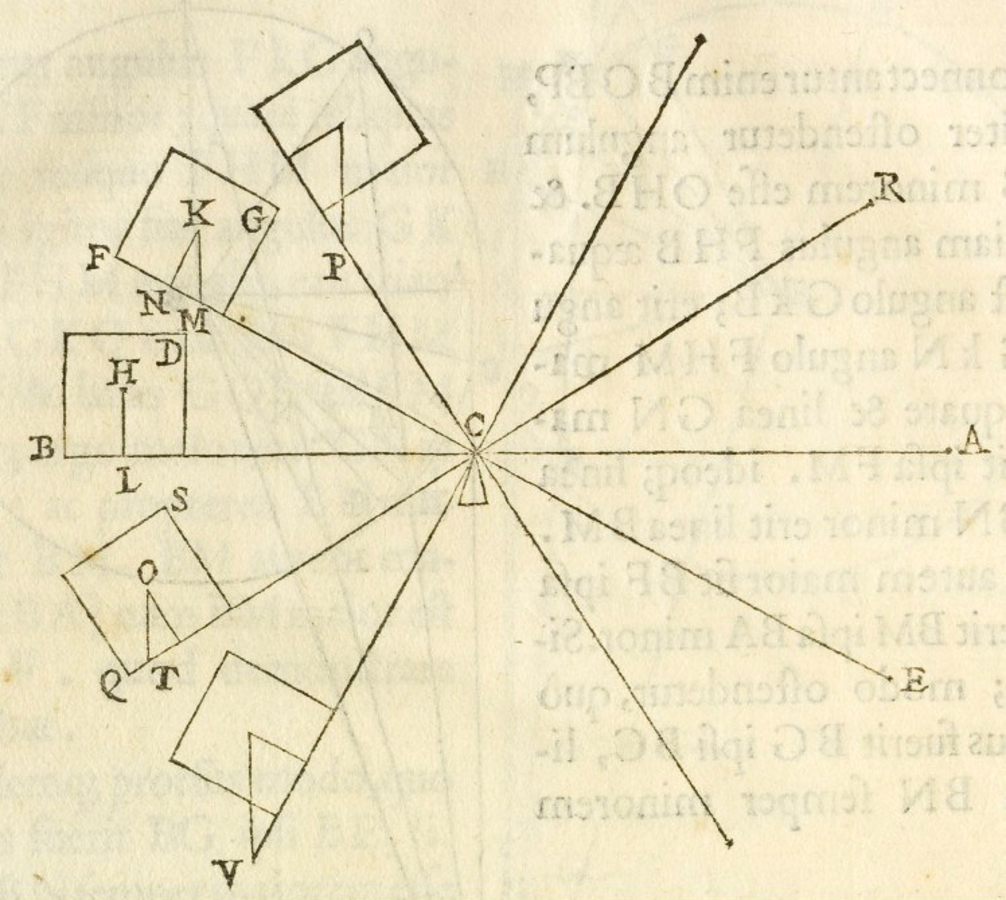
Fig. 3.30: Guidobaldo considered the lever in various positions, always determining the effective lever arm by vertically projecting the position of the center of gravity of the sustained weight upon the lever arm.
In order to fully appreciate the significance of what Guidobaldo had in mind, it is necessary to consider the ensuing applications of this theorem as well, for instance proposition 8 (see figure 3.30):
Potentia pondus sustinens centrum gravitatis supra vectem horizonti aequidistantem habens, quo magis pondus ab hoc situ vecte elevabitur; minori semper, ut sustineatur, egebit potentia: si vero deprimetur, maiori.
If the power sustaining the weight which has its center of gravity above a horizontal lever is given, then, the more the weight is raised from this position by means of the lever, the smaller the power required to sustain it. But if it shall be lowered, greater power is required.188
In other words, Guidobaldo attempted to address the variation of the force required to lift a weight placed from above on a lever, when that lever is either raised or lowered. Now while it does seem that in this analysis Guidobaldo made use of the projection on the horizontal, measuring the effective length of the lever arm of a weight appended or sustained at an angle, this is actually not the case. What he considered is merely the projection of the center of gravity of the sustained weight along the vertical upon the lever arm in an oblique or horizontal position. In the case of a weight placed from above on a lever arm, the base point of this projection on the lever is then taken as determining the effective length of the lever arm. This is different from the way in which the effective weight (or rather the torque) would have to be determined according to classical physics. From a modern perspective, it would be the point where the perpendicular through the center of gravity of the weight placed on the lever arm crosses the horizontal (and not the arm of the lever as Guidobaldo had it) that determines the effective length of the lever arm, namely the distance of this point from the fulcrum. The two procedures only coincide in the trivial case in which the lever is in a horizontal position. In summary, although Guidobaldo's approach is vexingly close to that of Benedetti and Galileo, it does not actually yield the same correct results.
Another instance in which Guidobaldo needed to take into account something like positional heaviness can be found in his book on the wheel and the axle (see figure 3.31). Proposition 1 of this book states that
Potentia pondus sustinens axe in peritrochio ad pondus eandem habet proportionem, quam semidiameter axis ad semidiametrum tympani una cum scytala.
The power sustaining the weight by means of the wheel and axle is in the same ratio to the weight as the radius of the axle to the radius of the wheel including the handle.189
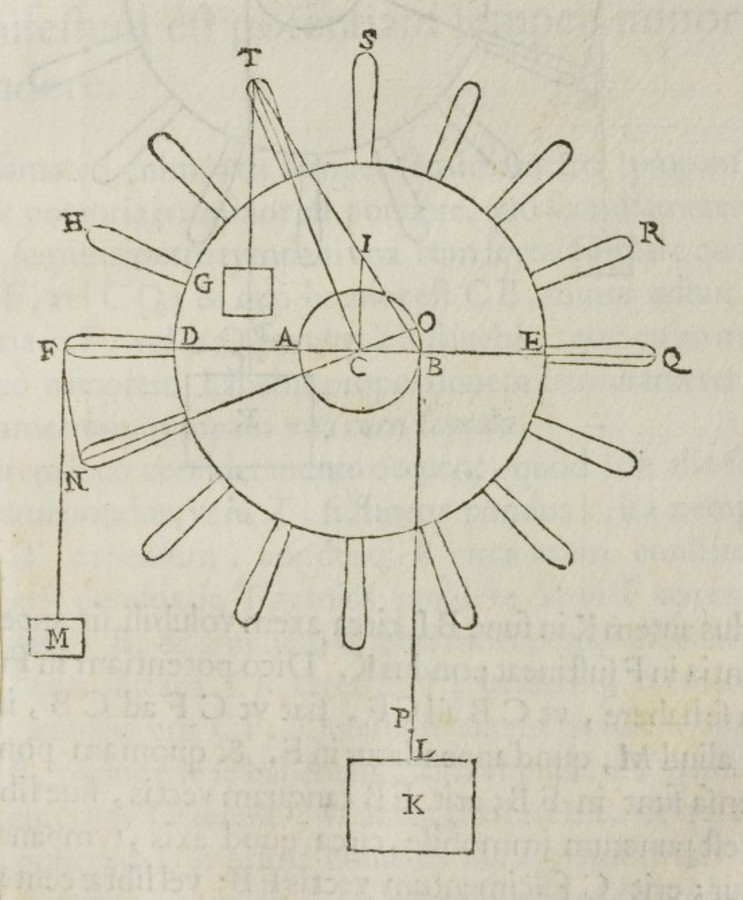
Fig. 3.31: Guidobaldo reduced the wheel to the case of a balance in which the power may act in a non-vertical direction. He did not offer a general procedure for determining the effective lever arm.
In the context of explaining this proposition Guidobaldo also considered the case in which the power is applied to a handle not in a horizontal but in an oblique position. He treats this case according to the model of a balance at the end points of which the weight to be moved and the moving weight (representing the power) are attached. This balance is in an oblique position, its fulcrum supposed to be at the center of gravity of the two weights (and not at the center of the wheel). The relation between those two weights, in case of equilibrium, can hence be derived from the law of the lever. Remarkably, Guidobaldo did not make use of the treatment of the bent lever according to the procedure of determining effective lever arms by horizontal projection, a procedure that would, in this case, have yielded the same result. His approach is indeed not a generic one at all, but depends entirely on the adequate identification of the lever problem at hand.
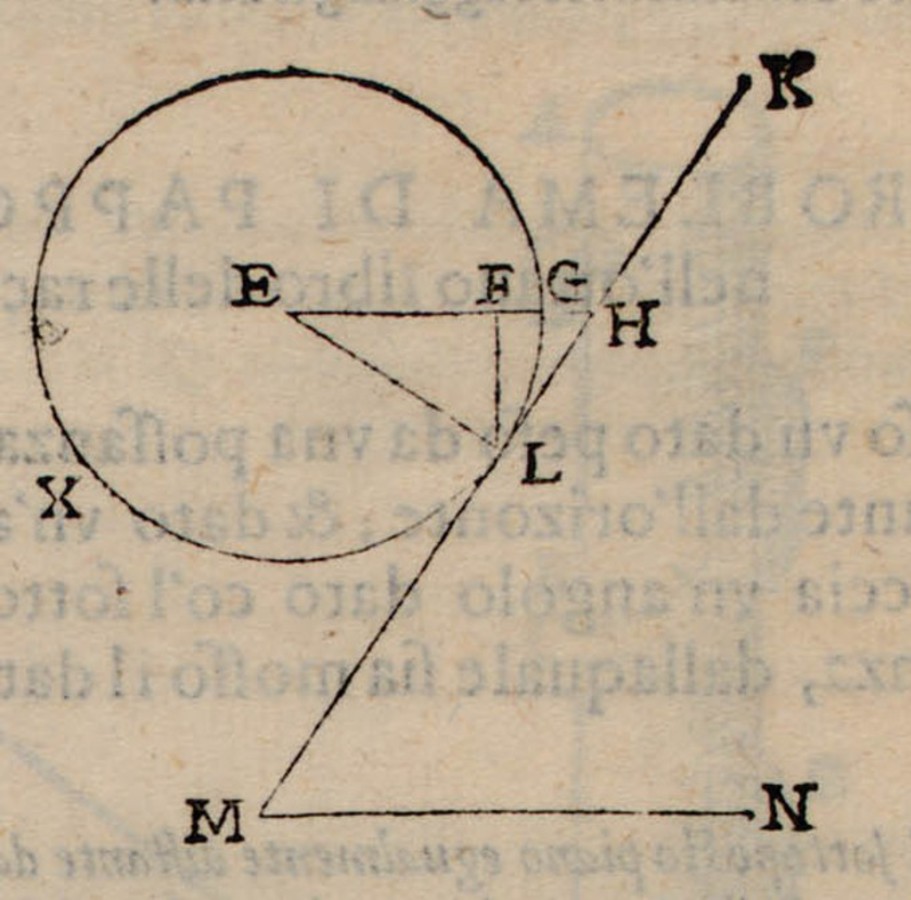
Fig. 3.32: Pigafetta, the translator of Guidobaldo's book, added Pappus' erroneous proof of the law of the inclined plane.
The risky character of this identification may be well illustrated by a third instance in which something like positional heaviness plays a role. In his book on the screw, Guidobaldo dealt with its reduction to the inclined plane which in turn is reduced to the balance. For the latter reduction he referred to Pappus. Pappus' analysis of the inclined plane has therefore at this point been inserted into the Italian edition by Pigafetta (see figure 3.32). It considers a spherical body placed on an inclined plane and imagines that the force needed to move its weight along the plane can be determined by imagining the whole situation being equivalent to that of an appropriately positioned balance. The procedure is indeed quite similar to the one we have just encountered in the discussion of wheel and axle, albeit much more problematical. A balance with unequal arms in horizontal position is erected from the point at which the sphere touches the inclined plane, its fulcrum being positioned vertically above it. At one side of the balance the body to be moved is attached, and on the other side, a weight, whose magnitude is to be determined, that balances the body to be moved. The length of this other side is given by the point at which the horizontal balance arm touches the plane. In other words, from the geometrical constellation the lengths of both lever arms are known so that the magnitude of the counter-balancing weight can be obtained, and from it, and some dynamical assumptions, the power needed to move the given weight along the inclined plane. Although the procedure reproduces correctly some qualitative features of the problem, such as the increase of power with steepness of the plane, it turns out to be incompatible with classical physics, implying that an infinitely large power would be required to lift a weight vertically.
In his 1588 book on Archimedes,190 Guidobaldo briefly returned to the issue of the distances at which weights act to form a center of gravity. But instead of entering a detailed discussion of the positional effect of a weight, he limited himself to EOAemphasizing that one should always consider weights arranged in a straight line (see figure 3.33):
Quare cum Archimedes tam in hoc postulato, quam in sequentibus, supponit pondera in distantiis esse collocata, intelligendum est distantias ex utraque parte in eadem recta linea existere. Nam si (ut in secunda figura) distantia AB fuerit aequalis distantiae BC, quae non in directum iaceant, sed angulum constituant; tunc pondera AB, quamvis sint aequalia, non aeque ponderabunt. nisi quando (ut in tertia figura) iuncta AC, bifariamque divisa in D, ductaque BD, fuerit haec horizonti perpendicularis, ut in eodem tractatu nostro exposuimus. Distantias igitur in eadem recta linea semper existere intelligendum est. ut ex demonstrationibus Archimedis perspicuum est.
For this reason, since Archimedes assumes in this postulate as well as in the following ones that the weights are placed at certain distances, it is to be understood that these distances exist on both sides in the same straight line. For if (as in the second figure) the distance AB were equal to the distance BC, which do not lie along a straight line, but constitute an angle, the weights AB, although they are equal, do not weight equally [non aeque ponderabunt], other than when (as in the third figure) AC is connected and divided in half at D and BD being drawn, the latter would be perpendicular to the horizon, as we have discussed in our treatise. Therefore the distances are always understood to be along the same straight line, as is evident from the demonstrations of Archimedes.191
Fig. 3.33: In his 1588 book on Archimedes, Guidobaldo stressed that the distances of weights have to be considered always along the same straight line, without giving a prescription for the case of a bent lever.
3.8.11 The flaws of Guidobaldo's understanding of the positional effect of heaviness
After this lengthy discussion, following Guidobaldo's meandering arguments, let us summarize his views on positional heaviness. He abandoned the framework of Jordanus and Tartaglia as he considered this to be incompatible with his own treatment based on the concept of center of gravity. He considered their exclusive focus on the straightness of descent as resulting from a purely mathematical perspective, neglecting the fact that the descent of a body is related, on the one hand, to the mechanical constraints of the motion of weights suspended from a balance, and, on the other, to the direction of the descent toward the center of the world.
In view of his extensive discussion of the concept as well as the arguments of his adversaries, which were based on it, one may ask if Guidobaldo himself believed in a concept of positional heaviness that may be freed from the contradictions he had revealed, or whether his use of that concept was exclusively polemical in character. At first glance one may be inclined to answer this question in favor of the merely polemical use, as indeed most interpreters have done.
On closer inspection, however, it has turned out that Guidobaldo did not reject the concept of positional heaviness altogether. He reinterpreted it using a conceptual differentiation between the weight (pondus) and its heaviness (gravitas) as a result of the positional circumstances of its descent. In his own treatment, Guidobaldo avoided the definition of a quantitative measure of the positional effect of a weight in a constrained situation so as not to run into the same ambiguities he himself had criticized. Instead, he limited himself to a consideration of the tendency of the center of gravity to join the center of the world along the most direct path possible, without having the mathematical means at his disposal to make such a procedure concise. He used ad-hoc suppositions to obtain the results he believed to be true. In this way, however, he exposed himself to the same kind of criticism that he had raised against his adversaries.
In summary, neither in the polemical nor in the deductive part of Guidobaldo's treatise on mechanics, a generic procedure for quantitatively determining positional or effective heaviness by a projection of the lever arm onto the horizontal can be found that corresponds to the modern procedure for determining the torque of a weight on a bent lever. Similarly, no treatment of this problem of forces not acting along the vertical was offered by Guidobaldo. Against this background, the question of how he might react to an analysis in which such procedures are employed becomes relevant as it must have constituted a foundational challenge for his mechanics. Pondering this question would have remained a matter of mere speculation were we not in the fortunate position of having Guidobaldo's extensive marginalia on Benedetti's book at our disposal.
3.9 Benedetti's approach to positional heaviness
For Benedetti's mechanics a specific way of determining positional heaviness, measured by the distance from the fulcrum to the line of inclination of a weight (linea inclinationis, the line connecting the center of gravity of the weight to the center of the elements) played a crucial and unambiguous role.192 Benedetti's situation was, in fact, somewhat different from that of his predecessors. Nothing speaks against the assumption that he was familiar with the preceding literature, in particular, with the works discussed above. He thus also knew the pitfalls and contradictions into which the discussion of the positional effect could lead. In the beginning of his treatise on mechanics he introduced the positional aspect of weight, without, however, explicitly introducing positional heaviness as a technical term.
Benedetti then carefully analyzed how a weight changes its effect in dependence on the position of a moveable arm of a balance.193 Following the tradition of his predecessors, he explained this change of effective weight in physical terms by claiming that a weight is impeded by the balance arm in following its straight path to the center of the region of the elements, as he expressed himself. As a consequence, it exerts a certain pressure on the arm which varies according to its inclination. This pressure will be greater the nearer the arm is to the vertical, while it would vanish in the horizontal position. Hence the weight will be positionally heavier when the moveable arm of the balance is along the horizontal than in any other position.
More specifically, Benedetti proposed a quantitative measure of a given weight or of a motive force according to its position. In contrast to Tartaglia's measure of positional heaviness, he determined the (positional) weight using a projection by means of perpendiculars drawn from the center of the balance to the line of inclination, corresponding to the effective length of the lever arm. This argument resembles Cardano's first argument, that is, to take the horizontal component of the distance to the support as a measure of the positional heaviness. However, going beyond Cardano who only considered the case of parallel directions to the center of the world, Benedetti also considered lines of directions not directed along the vertical. From the perspective of classical physics Tartaglia's (and Jordanus') concept of positional heaviness is closer to issues of energy conservation and the work principle, while that of Benedetti (and later of Galileo) is closer to the modern concept of torque (see section 1.4).
Benedetti may have taken his lead from Cardano's argument or even from its criticism by Guidobaldo. But he may also have turned a result that he could have found in Jordanus' De ratione ponderis, edited by Tartaglia,194 into a key principle of his mechanics. As we have discussed, proposition 8 of De ratione ponderis states in fact that when the arms of a balance form an angle, then if their ends are equidistant from the vertical line passing through the axis of support, equal weights suspended from them will be of equal heaviness (see figure 3.15).195 Jordanus' proof is a rather complex indirect proof that is based on showing that if such a balance were not in equilibrium, a weight by descending through a certain vertical distance would be able to lift an equal weight by a larger vertical distance, which is assumed to be impossible. If Jordanus was indeed Benedetti's starting point, which seems likely as he referred to Nemore 1565, then he must have dropped any consideration of such vertical descents and rather took the end result of Jordanus' analysis, namely the distance of a weight from the line of suspension, as a general criterion for its positional effect.196
Benedetti also made use of his method to determine the effectiveness of a force according to its position by treating a balance with a weight on one arm and a force acting on its other arm at an angle other than 90 degrees.197 The line of inclination is hence, in this case, not a perpendicular but given by the direction in which the force acts. Nevertheless, Benedetti's procedure is general enough to cover this case as well. Accordingly, a perpendicular is drawn from the center of the balance to the oblique line of inclination, and it is the length of that perpendicular which determines the effective lever arm of the force. This treatment happens to be in agreement with the way in which the torque of the force would be determined according to classical physics (see section 1.4).
Benedetti also dealt with the fact that the beam of a balance is not a mathematical line but a material body which he imagined as having a rectangular cross-section.198 Furthermore, he treated balances supported at one of their ends. His idea was to use his treatment of forces not acting along the vertical in order to reduce such a material balance to the simple case of a bent lever. For this purpose he first imagined a balance supported from below with two bodies attached to its arms that are conceived as exerting their weights from the top of the rectangular beam of the balance. Connecting the fulcrum of the balance with the places of the weights Benedetti thus obtained a triangle positioned on its top. He then argued that what determines the effectiveness of the weights are the distances of their lines of inclination from the center, i.e. the horizontal projections of the sides of that triangle. Next he generalized the treatment to the cases of balances supported at their center or at another point. Benedetti claimed that such an analysis of the material beam had never been achieved before in the literature.199
Benedetti further addressed alleged errors in Tartaglia's Quesiti.200 His main target, however, was Tartaglia's understanding of the concept of positional heaviness. He did agree with Tartaglia's general claim which has been quoted above (see section 3.7).
Dalle cose dette, et dimostrate di sopra, se manifesta qualmente un corpo grave in qual si voglia parte, che lui se parta, over removi dal sito della equalità lui si fa più leve, over leggiero secondo il sito, over luoco, et tanto più quanto più sara remosso da tal sito […]
From the things said and demonstrated above, it is manifest how a heavy body, whenever parted or removed from the position of equality, is made positionally lighter, and the more so, the more it is removed from that position.201
But he disagreed with the cause assigned by Jordanus and Tartaglia to this effect. According to Benedetti,
quia vera causa per se ab eo oritur, quod a centro librae dependeat ut primo cap. huius tractatus ostendi.
the true cause emerges by itself from the fact that the weight hangs down [in part] from the fulcrum of the balance, as I showed in the first chapter of this treatise.202
In other words, Benedetti stressed that by taking into account the distance from the fulcrum to the line of inclination his approach to the positional effect of a weight is distinct from and superior to Tartaglia's consideration in the Jordanus tradition of straightness of descent.
More specifically, Benedetti refuted several of Tartaglia's claims. In particular, he disputed the central claim in the equilibrium controversy that when a balance is moved from its horizontal position it will return to this position because the body that had been moved upward will attain greater positional heaviness than the body which had been moved downward.203 As we have seen above, Jordanus' and Tartaglia's argument was based on comparing the descents of the two weights. In other words, the balance would thus have to break in the middle in order to visualize these descents. Benedetti now pointed to the simple fact, already EOAemphasized by Guidobaldo, that, when one weight descends, the other must ascend, and that the corresponding arcs will always be similar to each other and placed in the same way. He concluded that no positional difference in heaviness can be produced in the way that Tartaglia argued.204
Nevertheless, Benedetti did not believe in an indifferent equilibrium of such a balance when considered in a cosmological context. In the continuation of his argument, he rather came to the from a modern viewpoint correct conclusion that, when such a balance in equilibrium is displaced from its original horizontal position, the weight that has been lowered will actually assume a greater positional heaviness than the one that has been lifted up:
Pondus igitur ipsius A in huiusmodi situ, pondere ipsius B gravius erit.
Therefore the weight of A in this [lower] position will be heavier than the weight of B.205
He reached this conclusion by taking into account that the lines of inclination of the two weights are not parallel to each other but must converge at the center of the elements. The effective lever arms of the two weights must hence be determined by perpendicular lines drawn from the center of the balance to these lines of inclination. It now turned out that the perpendicular line, corresponding to the weight that had been lowered, is larger than the line corresponding to the weight that had been lifted. Consequently, the lower weight had become heavier positionally so that one would expect the balance to tilt into a vertical position (see figure 1.4).
Benedetti added some more critical remarks on Tartaglia's way of considering positional heaviness. Tartaglia had argued in Quesiti, as we have seen, that the upper weight attains a greater positional heaviness than the lower one, but that this difference is arbitrarily small and can therefore not be compensated by any finite weight.206 This conclusion was reached by comparing curvilinear angles of contact on each side of the balance. In his analysis of this argument Benedetti again took into account that the lines of inclination are not parallel to each other but must converge toward the center of the elements, just has Guidobaldo had done before him. Clearly, since Tartaglia's argument hinges on angles of contact, which are infinitesimally small compared to ordinary angles, even that small deviation from being parallel must matter in this case. Taking this into account, Benedetti was able to construct a contradiction, thus refuting Tartaglia's argument. He concluded:
Omnis autem error in quem Tartalea, Iordanusque lapsi fuerunt ab eo, quod lineas inclinationum pro parallelis vicissim sumpserunt, emanuit.
Now the whole error into which Tartaglia and Jordanus fell arose from the fact that they took the lines of inclination as parallel to each other.207
Other propositions of Tartaglia, such as his demonstration using the concept of positional heaviness of basic properties of a balance with unequal arms in propositions 7 and 8 of the Quesiti, were dismissed as lacking in rigor when compared to the corresponding demonstrations of Archimedes. Concerning the inclined plane treated in Tartaglia's proposition 14, Benedetti interpreted it by reducing it to a balance in a position parallel to the plane. He did not consider the vertical displacements that are crucial to the analysis given by Jordanus and Tartaglia. Instead, he rather argued that Tartaglia's geometrical analysis was flawed by the neglect of the convergence of the lines of inclination at the center of the elements and that the same body which Tartaglia considered at different positions on the same inclined plane cannot have the same weight in these positions since, in Benedetti's interpretation, they correspond to places at different lengths along the arm of a balance.
In summary, Benedetti had introduced a way to determine the positional effect of a weight or a force that essentially gives, in the cases he considered, the same results as the application of the modern concept of torque. In particular, Benedetti had managed to go beyond the consideration of weights tending downward to include forces acting in an arbitrary direction. In this way, he was also able to take into account the fact that, on a spherical earth, the lines of inclination of weights on a balance are not parallel. He did not manage, however, to successfully apply his measure of positional heaviness to challenging objects such as the inclined plane.
3.10 Benedetti, Guidobaldo, and Galileo
Historians of science have always regarded Benedetti's Diversarum speculationum […] liber208 as remarkable because of the close similarity of some of its parts with Galileo's early writings. The range of themes and methods common to both authors is indeed astonishing. Both Benedetti and Galileo proposed a theory of the motion of fall based on Archimedean hydrostatics, both considered the acceleration of this motion and its causes, both formulated what in hindsight appear as proto-inertial principles, both dealt with the bent lever in a similar fashion, both analyzed the relation between vibrating strings and musical tones, both formulated similar views on the irradiation of surfaces, both expressed similar views on thermal and hydrostatic phenomena, and, last but not least, both embraced the Copernican world system.209 Many of these themes and ideas belonged to the shared knowledge of preclassical mechanics. Yet, in some respects the agreement of their approaches is so striking that one may wonder whether it is due to mere coincidence.
In the introduction to Mechanics in Sixteenth-Century Italy Stillman Drake writes:
The question of Benedetti's influence, particularly on the young Galileo, is one of great interest and importance in the history of mechanics in the sixteenth century.210
Still, in spite of many pages dedicated to the issue over more than one century, the question of Benedetti's direct impact on Galileo has remained unclear, in particular as Benedetti was never mentioned by him. Did Galileo ever consider Benedetti's mechanics, his theory of motion, and his cosmology in any detail? Did Benedetti's work shape Galilei's own views during his formative years, and, if so, why did he never refer to it?
There are a number of possible connections that have been considered in the past. For instance, Galileo's Pisan colleague Jacopo Mazzoni mentioned Benedetti in In universam Platonis et Aristotelis philosophiam praeludia from 1597.211 He also received a letter from Galileo, written on May 30, 1597 arguing for the Copernican world view. 212 In his book Mazzoni referred to Benedetti's discussion of the possibility that motion along a straight line can be continuous,213 a theme that was later taken up by Galileo in chapter 20 of De Motu, which also contains an explicit reference to Copernicus.214 Another potential intermediary was Galileo's friend Paolo Sarpi who discussed Benedetti's theory of fall in Pensieri naturali e metafisici.215 While earlier historians of science such as Caverni, Duhem, Wohlwill, and Mach stress Benedetti's role for the history of mechanics and his pivotal role for Galileo's subsequent achievements, the more recent historical literature tends to deny the possibility of an influence of Benedetti on Galileo.216
The present edition of the parts of Benedetti's book that deal with mechanics together with Guidobaldo's critical notes may help to provide a somewhat surprising answer to this question. It was most probably Guidobaldo, Benedetti's fervent opponent in matters of mechanics, who served as a conduit to Galileo and, at the same time, made it virtually impossible for Galileo to openly admit to this influence if did he not want to risk the protection of the most important patron of his early career.
Among the most striking and consequential similarities between the work of the young Galileo and that of Benedetti is the latter's theory of the motion of fall,217 with the treatment of the motion of fall as motion in a medium according to Archimedean principles, just as it was presented in Galileo's early work De motu.218 After carefully examining the issue, Drabkin arrived at the following conclusion:
While there may be some instances of the influence, direct or indirect, of the earlier author on the later, in many cases the similarities seem to be the reflection of a common heritage and tradition, the use of the same sources, or the concurrence of independent minds.219
Drake surmised, referring to a period extending at least up to 1596:
But of course it may be simply that Galileo had not yet heard of Benedetti.220
In line with this assessment, even recent, more careful studies of the emergence of Galileo's science have basically ignored a possible impact of Benedetti on its formative period.
There are, however, other perhaps less striking similarities between Galileo and Benedetti. One of them is the prominence of the bent lever in their writings on mechanics, which contrasts with the rather minor role it played for Guidobaldo.221 A related similarity is the analysis of the bent lever in terms of special concepts expressing the varying effect of a weight according to its position.
In his mechanical writings, most likely postdating his move to Padua, Galileo used such a term for expressing the varying effect of a weight, his famous concept of momento which he defined as follows:222
Momento è la propensione di andare al basso, cagionata non tanto dalla gravità del mobile, quanto dalla disposizione che abbino tra di loro diversi corpi gravi.
Moment is the tendency to move downward caused not so much by the heaviness of the movable body as by the arrangement which different bodies have among themselves.223
Galileo's concept of momento224 and his analysis of the bent lever, crucial to both his mechanics and his theory of motion, evidently emerged from the midst of the controversy about the concept of positional heaviness. In this controversy Galileo took a position much closer to Benedetti than to Guidobaldo. Instead of positional heaviness Galileo used the concept of momento or momentum that Guidobaldo had introduced in his book by quoting Commandino's definition of the center of gravity. But while Guidobaldo made no further use of it in his mechanics, Galileo took this concept with respectable lineage in the Urbino school, gave it a new meaning that was taken over from Benedetti and made it a pillar of his own framework, including, following Commandino, the definition of the center of gravity:
Centro della gravità si diffinisce essere in ogni corpo grave quel punto, intorno al quale consistono parti di eguali momenti.
Center of gravity is defined to be that point in every heavy body around which parts of equal moments are arranged.225
The evidence for our claim concerning Benedetti's legacy in Galileo's work comes from Guidobaldo's marginal notes on Benedetti's book, as well as from his entries in a research notebook, known under the title of Meditatiunculae,226 which contain traces of Galileo's intervention in this controversy.
According to Benedetti and Galileo (and in contrast to Tartaglia and Guidobaldo) the effective length of the lever arm, obtained by drawing a perpendicular from the fulcrum of the balance to the line of inclination determines the effectiveness of a weight or a mechanical constellation. As we have seen, the measure of positional heaviness used by Benedetti had already played a role in Cardano's treatment of the balance in De subtilitate where it occurs together with two other measures.227 While these measures in a similar way qualitatively determine the changing effect of a weight attached to a balance in dependence on the obliquity of the beam, they result in quantitatively different values. Cardano was either unaware of these differences, or he simply did not pay attention to the possibility of defining a quantitative measure of the magnitude of positional heaviness.
As we have also discussed, in contrast to Cardano, Benedetti unambiguously introduced a quantitive measure for the magnitude of a given weight or force in dependence of the positional circumstances (see section 3.9). His prescription is strikingly similar to that of Galileo:
Quod quantitas cuiuslibet ponderis, aut virtus movens respectu alterius quantitatis cognoscatur beneficio perpendicularium ductarum a centro librae ad lineam inclinationis.
That the magnitude of one given weight or the magnitude of one motive force in comparison with another can be found by means of perpendiculars drawn from the center of the balance to the line of inclination.228
Similarly Galileo wrote in his Mechanics:
Ma qui è d'avvertire, come tali distanze si devono misurare con linee perpendiculari, le quali dal punto della suspensione caschino sopra le linee rette, che dai centri della gravità delli due pesi si tirano al centro commune delle cose gravi.
But here it must be noted that such distances must be measured with perpendicular lines dropped from the point of suspension upon the straight lines drawn from the centers of gravity of the two weights to the common center of heavy bodies.229
In his Mechanics, Galileo later stressed once more how important it is to carefully define the effective distances of weights from their support:
Un'altra cosa, prima che più oltre si proceda, bisogna che sia considerata; e questa è intorno alle distanze, nelle quali i gravi vengono appesi: per ciò che molto importa il sapere come s'intendano distanze eguali e diseguali, ed in somma in qual maniera devono misurarsi.
There is one thing that must be considered before proceeding further, and this concerns the distances at which heavy bodies come to be weighed; for it is very important to know the sense in which equal and unequal distances are to be understood, and in what manner they must be measured.230
He also made it clear in his analysis of the inclined plane by means of the bent lever that this procedure is critical in determining the momento of a given weight.231 As discussed earlier, in his Diversarum speculationum […] liber Benedetti convincingly demonstrated the effectiveness of this method in determining the magnitude of a force or weight according to its position.
Another remarkable similarity between Benedetti's and Galileo's mechanics is the proof of the law of the lever. Both started by considering a uniform weight supported from its center of gravity which is then broken into unequal pieces sustained by strings from a support above the uniform weight. The proof then argues about the possibility to rearrange these strings without disturbing the equilibrium. Benedetti's somewhat obscure proof was critically annotated by Guidobaldo (see section 7.15). A similar proof is then much more clearly expressed in Galileo's mechanics.232 Finally, Benedetti's discussion of projectile motion may have stimulated Galileo and Guidobaldo's joint experiment using an inclined plane to trace the trajectory of a projectile (see page
The very existence of Guidobaldo's marginal notes on Benedetti's Diversarum speculationum […] liber provides one definitive answer to the question of who had actually read this book. The fact that Guidobaldo del Monte had read it, however, is not entirely new.233 Guidobaldo's notebook, the famous Meditatiunculae,234 contains a few entries referring to Benedetti's book which furthermore suggest that Guidobaldo must have studied this work at about the same time he began to correspond with Galileo.235 It has also been shown that other entries in the Meditatiunculae document common research and discussions by Guidobaldo and Galileo.236
This coincidence strongly suggests that Guidobaldo served as a conduit to his younger colleague Galileo, transmitting knowledge about some of Benedetti's methods that he himself rejected. A closer inspection of the Meditatiunculae reveals striking evidence for the likelihood of this scenario. Remarkably, the page of Guidobaldo's notebook facing the page with his most detailed critique of Benedetti shows Galileo's famous construction relating the bent lever to the inclined plane (see figure 3.34).237
Fig. 3.34: Galileo's construction relating the bent lever to the inclined plane in Guidobaldo's notebook.

Fig. 3.35: Guidobaldo's construction related to the inclined plane in his notebook. The construction was adapted from Pappus' erroneous solution.
This circumstance is all the more noteworthy as Guidobaldo's notebook also contains, on an earlier page, his own problematic adoption of Pappus' analysis of the inclined plane (see figure 3.35).238 In his writings Galileo had criticized this analysis,239 substituting it with his own solution of the problem which makes use of the bent lever conceptualized in the same way as Benedetti did. Guidobaldo therefore must have learned about this proof from Galileo, and he must also have seen the connection to Benedetti's methods. It is in any case most unlikely that the two scientists did not discuss this connection and it is quite plausible that Galileo became familiar with Benedetti's work through Guidobaldo. Galileo started corresponding with Guidobaldo in 1588, three years after the publication of Benedetti's book and shortly before he embarked on what later became known as his writings De Motu.240 First Galileo wrote a dialogue version and then an essay in twenty-three chapters. Only this second version contains his proof of the law of the inclined plane, the argument about continuity of motion along a straight line, and the mention of Copernicus. Most probably this version was written after Galileo became familiar with Benedetti's work. His treatise on mechanics, which for the first time explicitly discussed the problem of the effective lever arm, was only written much later, certainly after he had visited Guidobaldo in 1592 on his way to Padua (see section 2.3). It therefore seems most probable that Galileo was familiar with key ideas of Benedetti when he wrote these works.
A more detailed examination of Guidobaldo's argument in his notebook makes it evident that the discussion of Benedetti's work was not only a turning point for Galileo, but also for Guidobaldo himself. In fact, this discussion must have convinced him, at least to some extent, both of the legitimacy and the fertility of Benedetti's procedure for determining the positional effect of a weight. In fact, he was able to justify this procedure with the help of the concept of center of gravity central to his own mechanics.
In the approach to the bent lever problem that he took in his notebook, Guidobaldo considered an arrangement familiar from Benedetti's book, a balance with one deflected arm and with two weights that are in inverse proportion to the projections of their lever arms on the horizontal (see figure 3.36). He assumed this balance to be in equilibrium and determined the center of gravity of the two weights according to the principles of his own book on mechanics. He found that their center of gravity lies at the crossing point between a vertical line through the support and the line connecting the two weights, thus justifying the assumption that it is in equilibrium.
For geometrical reasons it is now clear that the distances of the weights from the center of gravity are in the same proportion as the projections on the horizontal, and inversely as the weights themselves. Guidobaldo had thus managed to relate Benedetti's procedure for determining positional heaviness to his own use of the concept of center of gravity, a typical example of how concepts become related by being applied to the same problem. At first he concluded that this is what was to be shown, but then continued the argument to include Galileo's consideration of inclined planes (see figure 3.36):
Libra ABD habeat AB horizonti aequidistans. Ponderaque in AD maneant. Primum ducta DC ad AB perpendiculari, dico pondus D ad pondus A esse, ut AB ad BC. Sit BK ipsi AB perpendicularis, et in centrum mundi tendat, iungaturque AGD. Et quod pondera manent, erit ex meis mechanicis punctum G centrum gravitatis, et ut pondus D ad pondus A, ita AG ad GD. Et quod BG DC sunt parallelae erit AB ad BC ut AG ad GD, hoc est ut pondus D ad A. Quod demonstrare oportebat.
Let the balance ABD have [the part] AB equidistant from the horizon. And let the weights in AD be at rest. If first DC is drawn perpendicularly to AB, I say that the weight D is to the weight A, as [is] AB to BC. Let BK be perpendicular to AB and tend toward the center of the world, and let AGD be joined. And since the weights are at rest, according to my [book on] mechanics the point G will be the center of gravity, and as the weight D is to the weight A, so is AG to GD. And since BG DC are parallel, AB will be to BC as AG to GD, that is, as the weight D to [the weight] A. Which was to be demonstrated.241

Fig. 3.36: Guidobaldo's analysis of Galileo's construction relatinginclined plane and bent lever.
Before the claim that this is what was to be demonstrated, Guidobaldo inserted a passage in which he prepared the argument concerning inclined planes by reformulating what he had found in terms of positional heaviness without actually using the term. What he nevertheless needed was a way to describe the changing effect of a weight with position in order to then argue about the powers capable of supporting weights on differently inclined planes. So he attempted to reformulate the equilibrium of two different weights on a bent lever in terms of the different effects of one and the same weight, which he introduced as a reference weight, on the two sides of the bent lever. Expressing himself in a rather cumbersome and confusing way, he argued, from what he had shown before, that these effects are proportional to the projections of the lever arms on the horizontal:
Ex hoc patet aequalia pondera in A D […] esse pondus A ad pondus D ut AG ad GD. Sit n[empe] ob evitandam confusionem pondus L, quod intelligatur in A aequale existens ipsi ponderi in D. Quod n[empe] pondus in D ad pondus in A cui aequeponderat est ut AG ad GD. Pondus vero in D eandem habet gravitatem ut pondus in A. Ergo pondus L ad pondus A et ad pondus in D est ut AG ad GD. et per consequens ut AB ad BC. Levius ergo est pondus in D quam pondus in B, quanto minor est BC quam BA.
From this it is evident that, equal weights [being] in A D […], that the weight A is to the weight D as is AG to GD. Let now, in order to avoid confusion, the weight L, which is understood to exist in A, be equal to the same weight at D. Because in fact the weight at D is to the weight at A, with which it is in equilibrium, as is AG to GD. But the weight at D has the same heaviness as the weight at A. Therefore the weight L is to the weight A and to the weight at D as is AG to GD, and in consequence as AB to BC. Hence the weight at D is lighter than the weight at B by as much as BC is smaller than BA.242
After this preparation, following Galileo's argument, Guidobaldo related the bent lever to the inclined plane, comparing the power supporting a weight in the vertical direction with the power supporting the same weight along the plane. He formulated the law of the inclined plane by stating that these powers are inversely as the length of the plane is to its height. He then proceeded to relate the inclined plane as well as the vertical to the balance or rather to the bent lever with different positions of its arm, by claiming that a weight on the plane is as if it were on an arm that is vertical to the plane. He could then apply the result previously derived for the bent lever to the inclined plane. For geometrical reasons his argument refers to an inclined plane formed by the intersection of the line representing the original inclined plane and the vertical line tangent to the circle formed by the possible positions of the deflected lever arm (see figure 3.36):
Sit deinde planum DE horizonti inclinatum, et per EF horizonti recta sitque DF horizonti aequidistans. Dico potentiam pondus sustinentem in EF ad potentiam idem pondus sustinentem super DE, ita esse, ut DE ad EF. Intelligatur idem pondus in N. Quoniam nempe pondus in N super NO est, ac si esset libra ABN essetque pondus in brachio BN, cum sit BNP angulus rectus. Similiter ob eandem causam pondus in D super DE est ac si esset in brachio BD, cum sit BDE quoque rectus. Hoc nempe modo pondera tangunt plana quod nempe similiter pondus in N super planum NPO est ac si esset in brachio BN pondus vero in N est aequegrave ut in A erit pondus in N ad pondus D ut AB hoc est BD ad BC. Et quod triangula CDE EDF PDO sunt similia, et CDE simile est ipsi BDC erit BD ad BC ut DE ad EF, hoc est ut DP ad PO.
Let then DE be a plane inclined to the horizon, and through EF, perpendicular to the horizon, let DF be equidistant to the horizon. I say that the power supporting the weight at EF is to the power supporting the weight over DE as is DE to EF. It is to be understood that the same weight is in N. Now evidently the weight at N is over NO, as if the balance were ABN and the weight on the arm BN, because BNP is a right angle. Similarly for the same reason the weight at D over DE is as if it were on the arm BD, because BDE is also a right [angle]. In this way namely the weights touch the planes since indeed the weight at N over the plane NPO is similarly as if it were on the arm BN. But the weight at N is equally heavy as at A. The weight at N will be to the weight D as AB, that is BD, is to BC. And since the triangles CDE EDF PDO are similar, and CDE is similar to BDC, BD will be to BC as DE is to EF, that is, as DP to PO.243
Guidobaldo returned to his introduction of a reference weight representing the power of supporting a weight in the vertical. This weight corresponds to the weight at the deflected arm of the balance and is to the weight on the horizontal arm as is the horizontal arm to the projection of the deflected arm. He could now conclude that the same proportion also holds for the powers supporting weights along the vertical and the inclined plane, respectively:
Pondus atque in N sustinetur a pondere L. Pondus vero D sustinetur a pondere in A, pondus vero in L ad ipsum in A, est ut AB hoc est BD ad BC. Ergo potentia sustinens pondus super NO ad potentiam pondus sustinens super DPE est ut BD ad BC.
And the weight at N is supported by the weight L. But the weight D is supported by the weight at A, but the weight at L is to the same in A, as is AB, that is BD, is to BC. Therefore the power supporting a weight over NO is to the power supporting the weight over DPE as BD is to BC.244
In a final step of his proof Guidobaldo then transferred the proportions he had found for the small triangle generated by his geometrical construction to the originally considered inclined plane:
Eodem atque modo sustinetur pondus super DP, veluti super DE, et super PO, ut super EF. Ergo potentia sustinens pondus super DE ad eam, quae sustinet pondus super EF est ut DE ad EF. Quod demonstrare oportebat.
And in the same way the weight is supported over DP, or over DE, and over PO, as over EF. Therefore the power supporting the weight over DE is to that which supports the weight over EF as is DE to EF. Which was to be demonstrated.245
Guidobaldo had thus recapitulated Galileo's proof of the inclined plane based on relating it to the bent lever. Since he had previously shown that Benedetti's treatment of the bent lever could be justified using the concept of center of gravity, he had reached a new understanding of the problem of the inclined plane within the framework of his own mechanics.
Let us summarize the situation with regard to the interaction between Guidobaldo, Galileo, and Benedetti:
At the beginning of 1588, Galileo and Guidobaldo exchanged their views on the technicalities of proofs in the Archimedean tradition. A more intensive and regular scientific exchange then developed, as we may conclude from the few surviving letters. Thus Guidobaldo had sent Galileo his commentary on Archimedes for commentary and criticism, as we know from a letter of May 28, 1588.246 From another letter to Galileo, dated December 8, 1590,247 we may conclude that Guidobaldo used to receive letters from Galileo on an almost daily basis and that Galileo sent his findings likewise to his mentor Guidobaldo. As mentioned above, recent research into Guidobaldo's biography has revealed evidence that Guidobaldo and Galileo must have met as early as 1589 in Tuscany.248 They might even have met jointly with Galileo's teacher Mazzoni who, as we have also seen, cited Benedetti in his work. Thus Guidobaldo, Mazzoni and Galileo may have discussed Benedetti's Diversarum speculationum … liber with the consequence that Galileo reconsidered his work in progress on motion and, in particular, his treatment of motion along inclined planes. This treatment essentially relies on Benedetti's theory of the bent lever and was included in Guidobaldo's notebook. But Benedetti's impact on Galileo probably went even further than that. Galileo may now have taken the Copernican hypothesis much more seriously than before, discussing this as well as other subjects with Mazzoni. In the above-mentioned letter of 1597 Galileo praised Mazzoni for his Praeludia and reminded him of the controversial issues on which they meanwhile had reached an agreement, trying now to also press him on the Copernican hypothesis (see page
It is in any case difficult to imagine that Guidobaldo did not discuss his views on Benedetti's mechanics with Galileo, views that he considered at the same time misguided as well as profoundly challenging, as his marginal notes make evident.
3.11 Theoretical excursus: mental models in the transmission of knowledge
3.11.1 The basic mental models of early mechanical knowledge
An analysis of the long-term development of mechanical knowledge requires an appropriate description of the architecture of this knowledge. As pointed out earlier (see section 1.2), one must take into account, in addition to the theoretical knowledge usually considered in the history of science, two further types of knowledge, intuitive physics and practical mechanical knowledge. In order to describe the interaction between these different layers, it has turned out to be useful to adopt the concept of mental model from cognitive science and to adapt it to the needs of historical analysis.250 Mental models are cognitive instruments for drawing conclusions from experiences in the context of given knowledge.
More specifically, mental models are knowledge representation structures which allow inferences to be drawn from prior experiences about complex objects and processes, even when only incomplete information on them is available. Furthermore, conclusions based on mental models can be corrected in light of new information. The concept of mental model is thus particularly suited to explain the long-term continuity of certain aspects of physical thinking. Mental models are also capable of mediating between existing theories and experiences which may or may not be difficult to subsume under these theories. They thus constitute a particularly important theoretical instrument for understanding what happened in the early modern period. It was indeed the period of preclassical mechanics that was characterized, as we have discussed, by the encounter between traditional theories and novel challenging objects that were difficult to subsume under the existing theories so that these objects became a stimulus for further developments (see section 3.3).
A mental model consists of a relatively stable network of possible inferences relating inputs that are variable. Cognitive science often uses the term slots to indicate the nodes in the structure which have to be filled with inputs satisfying specific constraints. Applying a mental model presupposes the assimilation of specific knowledge to its structure, that is, input information compatible with the constraints of the slots is mapped into them. Filling the slots is the crucial process that decides on the appropriateness and applicability of a mental model for a specific object or process. Once the mapping is successful – if the input information satisfies the constraints of the slots – the reasoning about the object or process is, to a large extent, determined by the mental model.
An example of fundamental importance of the history of mechanics is the motion-implies-force model which, when involved in the interpretation of a process of motion, yields the conclusion that the moved object is moved by a force exerted upon it by some mover. While this conclusion is incorrect from the perspective of classical physics, contradicting as it does Newton's principle of inertia, it is in agreement with Aristotelian dynamics (see section 3.4.1). What is more important in our context, the motion-implies-force model represents elementary human experiences. In fact, when observing some moving object, one usually presumes that there is some mover at work which drives the object by its force, even when the mover itself and its force cannot be directly observed. The missing information about the mover is simply added by the default setting of the model based on prior experiences. If, however, additional empirical information eventually becomes available, e.g. specifying the kind of mover, then this information replaces the original default setting without, however, challenging the model itself.
Mental models relevant to the history of mechanics either belong to generally shared knowledge or to the shared knowledge of specific groups. Accordingly, they can be related to the three types of knowledge mentioned above. First, there are the basic models of intuitive physics, such as the motion-implies-force model just described. Another group of mental models is part of the professional knowledge of more or less specialized practitioners. Their historical transmission is related to the transmission of the real instruments that embody them. And, finally, there are the mental models that belong to theoretical knowledge and that are communicated by an explicit description of their structure and of the conditions of their applications.
A foundational experience of practitioners' knowledge since ancient times has been the equivalence of the weight of a body and the force required to lift it up. This equivalence is prototypically embodied in a real model, namely that of the balance with equal arms. In fact, the force that keeps the balance in equilibrium is equal to the weight in the scale pan. Hence we call this model of compensation between force and weight the equilibrium model. However, the practical knowledge of the technicians and engineers of antiquity also involved other basic experiences, and, in particular, the experience of how one can free oneself from the constraint of the equivalence between weight and force. In fact, the art of the mechanician consisted precisely in overcoming the natural course of things with the help of instruments such as the lever. According to this understanding, a mechanical instrument serves to achieve, with a given force, an unnatural effect that could not have been achieved without the instrument. We therefore call the model underlying this understanding the mechanae model – according to the Greek word μηχανή which means both mechanical instrument and trick, and which is at the origin of the word mechanics.
A key mental model of theoretical knowledge resulted from an integration of the mechanae model with the equilibrium model in the context of a theoretical reflection on the practical knowledge related to the balance with unequal arms that occured in the context of Aristotelian physics, and in particular in the Aristotelian Mechanical Problems. We call this model the balance-lever model. It can be understood as a generalization of the equilibrium model, associated with the ordinary balance with equal arms. In the case of an equal-arms balance, weight differences are balanced by weights; in the case of an unequal-arms balance, they are balanced by changing the position of the counterweight along the scale or by fixing the counterweight at the end of the beam and changing the position of the suspension point. This necessarily generalized the equilibrium model: weights can be compensated not only by weights but also by distances. It was this practical knowledge related to balances with unequal arms, invented in Greek antiquity some time before Aristotle, which provided the empirical basis for the formulation of the law of the lever.251
Another key mental model of mechanical knowledge is the center of gravity model. It can be applied to any given heavy body, allowing one to mentally replace it by its total weight and its center of gravity. Its slots are therefore the heavy body itself, its total weight, and the center of gravity. The structure of the model is determined by noting that any axis through the center of gravity turns the body into a lever in equilibrium. In other words, the center of gravity model allows any body to be conceived as a generalized balance with a fulcrum and a distribution of weights around it in equilibrium. In contrast to the fulcrum, however, the center of gravity no longer has to be a physically distinguished point that can be identified by visual cues, but its identification is rather the result of the application of the model to a heavy body. In fact, the center of gravity model can be applied to any body, whether it physically resembles a balance or not. This is the step taken by Archimedes in his work on the equilibrium of plane figures.252
To what kind of knowledge does the center of gravity model belong? It is clearly rooted in practical knowledge dealing with balances as it is embodied in the equilibrium model and also in observations on the stability of bodies. On the other hand, understanding the center of gravity model actually requires an explicit or implicit description of its properties. In other words, neither the emergence nor the transmission of this mental model is conceivable without its representation by written language. The very fact that the model is applicable to all heavy bodies suggests that it could hardly have emerged in the context of practitioners' knowledge dealing with specialized domains, but that the model rather belongs to theoretical knowledge.
The center-of-gravity model resulted from a reflection on the applicability of the equilibrium model to all bodies. Indeed, the application of a mental model to different objects and processes and the outcome of such applications may themselves become the object of reasoning that produces new knowledge, provided that such knowledge is appropriately represented – in our case by written language. Knowledge about knowledge structures may then in turn change these knowledge structures. Thus, the application of a mental model may lead to changes – in our case to a generalization – of that model by a deliberate reorganization of its structure as the result of the accumulated meta-knowledge obtained by reflection. As an example for such a reorganization, take the transformation of the concept of fulcrum into that of the center of gravity. While in the equilibrium model the fulcrum is primarily characterized by its physical properties as the turning point of a balance, and only then by the functions it takes on as a consequence of the application of the model, in the more developed model these secondary properties now become the primary properties of the center of gravity.
Fig. 3.37: If a material beam of a balance is supported from above, and deflected from its horizontal position, it returns to this position according to the Aristotelian Mechanical Problems because the upper part of the balance, to the right of the plane indicated by the perpendicular line through the suspension point, is heavier than the lower part to the left of this plane.
A starting point for the development of the center-of-gravity model is found in the Aristotelian Mechanical Problems discussed above in section 3.4. There the Aristotelian author considered, as we have seen, an equal-arms balance with an extended, material beam and distinguished between the case in which the balance is suspended from above and the case in which it is supported from below. In these two cases the balance displays different behaviours when its equilibrium is disturbed, for instance by adding or removing a weight. The solution to the problem of why it rises again when supported from above is based on a consideration of the perpendicular line across the point of suspension, which represents a plane dividing the balance into two parts (see figure 3.37). The relation between the weights of these two parts of the balance now decides whether or not the balance rises again. In this way, the equilibrium model is generalized to apply to the suspended beam itself, without the weights usually attached to a balance. The criterion for whether it moves or remains at rest is now no longer the relation between such weights, but that between the two parts divided by the perpendicular plane across the point of suspension.
Although applied to the special case of the material beam of a balance either suspended from above or supported from below, this model works quite generally for all bodies and, if elaborated systematically, naturally singles out the case in which the two parts are always of equal weight. Indeed, if the suspension point across the beam is appropriately moved, a point is reached where the downwardly displaced side of the beam is neither greater nor lesser than the other side. For the material beam this happens if it is suspended from the middle rather than from above or below, in other words, if it is suspended from its center of gravity – a conclusion that the Aristotelian author does not actually draw. But a reflection on the Aristotelian argument could yield a first characterization of the center of gravity as the point from which a suspended body will remain at rest and preserve its position. In this way, the center-of-gravity model eventually resulted from a reflective abstraction of the equilibrium model rooted in practical knowledge, made possible because of the representation of this knowledge in terms of written language, in this case in the Aristotelian text.
Fig. 3.38: Archimedes' proof of the law of the lever is based on a redistribution of weights justified with the help of the concept of center of gravity. A constellation of unequal weights at unequal distances from the fulcrum may thus be replaced, as shown in the figure, by a set of equal weights evenly distributed with regard to the fulcrum. The two constellations are equivalent because the redistribution of weights leave the center of gravity invariant. The redistribution may be visualized by replacing the unequal weights by equilibrated balances, appended from the same suspension points and carrying evenly distributed weights. This illustrates how the concept of center of gravity makes it possible to conceive any given body as a balance and how this concept can be iteratively applied to justify such redistributions of weights.
The center-of-gravity model provided the backbone for Archimedes' proof of the law of the lever based on redistributing weights under the constraint that the equilibrium is maintained (see figure 3.38). The legitimacy of this argument, however, has often been disputed, in particular vividly and powerfully by the historian and philosopher of science Ernst Mach around the turn of the last century.253 He argued that Archimedes' proof actually presupposes what has to be shown, the law of the lever. In fact, he argued that the proof involves the assumption that equal displacements of a weight placed on a beam from and towards the point of support cancel each other. This assumes that the effect of a weight placed on a beam is a linear function of distance, a presupposition essentially equivalent to the law of the lever. A closer look at Archimedes' proof reveals, however, that he did not actually talk about such displacements of weights at all. This objection to Mach's analysis has been raised by several historians and has been masterfully elaborated in Dijksterhuis's book on Archimedes.254 In his analysis Dijksterhuis correctly EOAemphasized that, in the critical step of his proof, Archimedes made use of the concept of center of gravity in order to justify that the original weights keep the system in equilibrium. Indeed, Archimedes argued that these weights maintain the equilibrium because they are placed at the respective centers of gravity of the two groups of equally spaced weights which correspond to them and which, taken together, keep the beam in equilibrium because their overall center of gravity coincides with the point of support of the beam.
Archimedes' proof essentially presupposes three properties of the center of gravity: First, the center of gravity of a symmetric configuration as used in the proof will be at the middle point of the configuration. Second, if a body is supported at its center of gravity, it will be in equilibrium. And third, bodies of equal weight may be substituted for each other without changing the state of equilibrium as long as their centers of gravity coincide. The latter point is crucial for Archimedes' argument: Because of the new abstract quality which the concept of fulcrum assumes when generalized to the concept of center of gravity, it could now be applied iteratively, allowing, in particular, the point of suspension of a weight on a balance to be conceived as the fulcrum of another balance (see figure 3.38). The properties listed above are also used in the proofs of Benedetti and Galileo (see section 7.15). The iterative application of the concept of center of gravity is in fact the critical feature of these proofs, working with different constellations of weights on a balance, considered to be equivalent with regard to their center of gravity.
Against this background, it now becomes possible to characterize the concept of positional heaviness as resulting from a reflective abstraction following a route alternative to that which led to the center-of-gravity model. As our historical analysis has shown, the concept of positional heaviness emerged in a situation where the concept of center of gravity was not available and thus left room for this alternative conceptualization (see section 3.4).
3.11.2 The positional-heaviness model
The basic idea of the concept of positional heaviness was to express the equilibrium of two different weights on a balance with unequal arms, not as a statement of proportionality – equilibrium results when the lengths of the lever arms are inversely proportional to the weights – but as resulting from an equality. Equilibrium then results when the two different weights are nevertheless equal in positional heaviness, given that a weight acquires a larger or smaller positional heaviness the longer or shorter the lever arm is on which it acts. As we have seen, the concept of positional heaviness proved to be effective also in treating devices such as the bent lever and the inclined plane because it lent itself to dealing with the varying effect of a weight in dependence on the angle of inclination.
From a theoretical point of view the concept of positional heaviness is based on a special mental model. Like the center-of-gravity model, this mental model also resulted from a reflective abstraction based on generalizing the equilibrium model to all balances, including balances with unequal arms. But in contrast to the center-of-gravity model, the positional heaviness model did not lead to a generalization of the concept of fulcrum, but rather to a generalization of the concept of weight attached to a mechanical constellation such as a balance. The original positional heaviness model allowed for a differentiation between a weight and its effect without establishing any precise relation between them – other than requiring that equilibrium is associated with equal positional weights. The model thus paved the way for a number of theoretical attempts to specify such a relation under the condition that they are conformal with general properties of the model such as the monotonous relation between the magnitude of the observable effect and the magnitude of the positional heaviness which describes this effect. As we have discussed, several different and partly incompatible measures of positional heaviness were triggered in the framework of its underlying mental model which provided a coherence of qualitative knowledge, in spite of such alternatives.
Mental models are usually context-specific and not universally valid. Thus, the concept of positional heaviness made sense only against the background of the specific context of knowledge about mechanical devices used in medieval and early modern technology and of the body of available contemporary theories available to organize this knowledge. In particular, when the concept of positional heaviness was first coined by Jordanus, it was shaped by a context in which the Archimedean concept of center of gravity was not available, in which the perplexing differentiation between a weight and its effect under certain conditions could make reference to Aristotle's theory of fallacies, and in which a deductive organization of knowledge on the Euclidean model served as an epistemic ideal. The reflection on such theories and their function constituted a specific image of knowledge255 and thus another context-specific condition of the concept.
In the early modern period, the context for using, rejecting, or elaborating the positional-heaviness model changed. New technological devices and a broader program of mechanical explanation entered the scene. The possibility to reduce an effect such as the power-saving potential of a pulley or a complex machine to the paradigm of the balance from which the concept of positional heaviness had been derived now became a critical, context-specific condition of the applicability of the model. Another context-specific condition was the cosmological assumption that weights always tend to move toward the center of the world. This was an almost universally accepted Aristotelian premise of preclassical mechanics. Furthermore, the adherence to the Archimedean kind of deductive theories as a model for structuring the body of mechanical knowledge provided an image of knowledge characteristic for the Renaissance and early modern context. This explains the common mathematical framework of the attempts to render the meaning of the concept of positional heaviness in precise mathematical terms. And finally, the availability of Archimedean writings made it necessary to confront the consequences of interpreting a mechanical problem against the background of the positional-heaviness model with the implications of the center-of-gravity model.
Mental models can be adapted to new experiences attained, in particular, in the process of studying challenging objects. The example of an equilibrated balance deflected into an oblique position of its beam shows that this adaptation may be a multifaceted process. The analysis of the different approaches of Guidobaldo and his adversaries demonstrates, on the one hand, that these scholars and engineers shared a basic understanding of the difference between a weight and its effect. This common understanding was based on a shared mental model which reflected general experiences obtained from the practical handling of balances. We have shown, on the other hand, that the specific ways in which Guidobaldo and his adversaries applied the shared mental model to particular experiences such as those concerning the behavior of a deflected balance and to results of experiments dedicated to studying this behavior in detail challenged the application of the model and determined in various ways its more or less successful adaptation.
These adaptations were, however, limited by some common context-specific historical conditions. In particular, no concept of mathematical function existed that would have allowed experiences involving several physical dimensions such as space, time, and weight to be integrated into a single composite physical magnitude such as torque or work. In the case of the challenging object of a deflected balance, it was thus impossible to integrate the effect of geometrical properties of the deflected balance and the effect of physical properties of the attached weights into a composite magnitude representing all of these effects. The changing effect of a weight in dependence on the obliquity of the beam of a deflected balance could either be explained as resulting from circumstantial conditions that could not be assimilated to one theoretical framework, or the effect could be represented by a new concept of weight that would be determined by specific geometrical or mechanical aspects of the experiences with deflected balances. Realizing the latter possibility led to the specific problems of defining a precise concept of positional heaviness. The deficiency in adequately representing the interplay between various physical magnitudes was fundamental, to the effect that not even the equilibrium of a balance could be conceived of as an equality of values of a composite physical magnitude. The introduction of generalized composite mechanical properties such as the product of lengths and weights would have been, however, the precondition for a conceptual development leading to the concept of torque used in classical mechanics to define the equilibrium of a balance.
The historical development we have reviewed nevertheless did eventually lead to a certain reconciliation of the original alternative conceptualizations in terms of center of gravity and positional heaviness. This must be understood as the result of the extensive elaboration and controversial evaluation of the consequences of the application of the underlying shared mental models to an ever increasing array of challenging objects. It is thus no accident that this relative and preliminary stabilization of the conceptual structures of preclassical mechanics went along with a growing network of arguments connecting these mechanical problems and hence the mental models underlying their conceptualization. Galileo's proof of the inclined plane theorem with the help of the bent lever, analyzed with the help of his concept of momento, itself an adaptation of the concept of positional heaviness, may stand as a representative for this process of knowledge integration.
Mental models link past with present experiences and thus allow conclusions to be drawn from incomplete information. In the present case the knowledge about a challenging object such as the bent lever, the inclined plane or the equilibrated balance deflected by a force acting in an arbitrary direction, was too incomplete to determine a general theory covering all of this knowledge. Only mental models such as the positional-heaviness model made it possible to link this knowledge to prior experiences and to the tradition of theoretical mechanics based on the law of the lever, as well as to Aristotelian cosmology and the medieval science of weights. Among the relevant prior experiences was, in particular, the familiarity with balances in equilibrium which were normally conceived of as being in horizontal position, a default assumption which was even reflected in the designation of the equilibrium as the position in which the beam of the balance is parallel to the horizon.256
Mental models bridge various levels of knowledge that represent the same object in various forms. Early modern technology was based largely on the intuitive knowledge of practitioners and, in particular, on rules of thumb derived by engineers who organized their work. Early modern practitioners had ample experience with the dependency of forces and weights on geometrical and mechanical constellations. However, such knowledge was not usually written down and transmitted only by participation in its application in practical contexts. It was mental models such as the positional-heaviness model that allowed this practical knowledge to be combined with knowledge at the level of theoretical reflection based on theories of mechanics available at the time.
If one tries to confront the historical concept of positional heaviness with potential counterparts in classical physics, it becomes particularly evident that the effectiveness of the historical concept requires an explanation along the lines just sketched, rather than conceiving it in some sense as an ancestor of modern concepts (see section 1.4). For the cases of the equilibrium of a balance with unequal arms and that of a bent lever, the equality of positional heaviness corresponds, in modern terms, to the equality not of weights or forces but of torques. This translation, however, does not work in the case of equilibrium on an inclined plane. In this case the equality of positional heaviness for different weights placed on differently inclined planes has to be interpreted in terms of the changing component of the force of gravitation in the direction of the inclined plane and as a consequence of the principle of work. The equilibrium of two bodies of different weights placed on differently inclined planes and connected with each other by a weightless rope can then be explained by the compensation of weight and distance in the sense that the larger weight travels a shorter vertical distance along the less steeply inclined plane than the smaller weight hanging down along the more steeply inclined plane, when both are being moved in accordance with their constraints. In other words, the compensation between lengths and weights receives different explanations in the two cases, excluding the possibility of translating positional heaviness with a single modern term such as torque, vector component of force, or work.
In summary, both the concept of center of gravity and the concept of positional heaviness are reflective abstractions resulting from mental models rooted in practical experience, in particular, the equilibrium model and the balance-lever model. The representation of these models in the medium of written language constituted not only the basis for using these models far beyond the original extension of their range of applicability but also the presupposition for reflecting on the properties of the model as they are revealed by applying it to particular challenging objects. Whereas mental models such as the motion-implies-force model emerged from a reflection on the operations directly performed with a real object, secondary abstractions such as that yielding the concepts of center of gravity or of positional heaviness resulted from a reflection on mental operations represented by language and performed in order to explore the properties of the model and its application. Without the representation in terms of language, such concepts would have hardly emerged.
Against this background, we recognize that the proofs encountered in our historical sources presuppose not only the practical knowledge about balances with equal and unequal arms, which gave rise to the equilibrium and the balance-lever model, but also concepts of theoretical knowledge such as center of gravity and positional heaviness, which resulted as reflective abstractions from these models. These proofs involve, however, not only these abstract concepts but also, just like the proofs of Euclidean geometry after which they are often modelled, complex constructions corresponding to physical arrangements and the operations performed on them. While in Euclidean geometry the physical operations reflected in the written text are constructions performed with compass and ruler, here they typically correspond to operations with balances. In this way, the practical knowledge about balances continued to provide the empirical grounding that made these proofs convincing.
Footnotes
For a discussion of the parallelism between the emergence of mechanics in Greece and in China, see Renn and Schemmel 2006.
Leonardo da Vinci, 1452–1519.
For a still very helpful survey of different sixteenth-century knowledge traditions, see Drake and Drabkin 1969.
For the notion of borderline problem, see Renn 2007, 30.
See the discussion in section 1.3; compare also the approach developed in Beller 1999.
See the extensive discussion of the preclassical framework of Galileo's work in Renn et.al. 2001 and Damerow et.al. 2004.
For an argument that Archimedes only elaborated an already existing intuitive concept, see Dijksterhuis 1956, 298–313.
Aristotle 1980. See the discussion in Krafft 1970, Damerow et.al. 2002, and Renn and Damerow 2007.
The law of the lever is also contained in the Aristotelian Mechanical Problems. However, the answers to the problems in this treatise are not based on this law but – as far as they deal with the force-saving potential of mechanical devices which is the case for approximately half of the problems – on a basic explanatory principle discussed in the following section 3.4.1. Notwithstanding the debated attribution of the treatise to Aristotle, this principle can be considered as a precursor of the law of the lever. This law itself occurs in the whole treatise only once, pointlessly inserted into the answer to the third problem which is based on the basic principle as all other related problems Aristotle 1980, 352–353. It is therefore likely that the inserted phrase stating the law of the lever is a later addition based on the erroneous inclusion of a marginal note in a Byzantine manuscript from which all surviving copies are derived, see section 3.4.2 below.
Caverni 1972, vol. 4, 190 ff. discusses extensively the problem of the deflected balance and the opinions of Jordanus, Leonardo, Tartaglia, Cardano, Guidobaldo, and Benedetti, as well as the subsequent discussions of this issue in the seventeenth century. Duhem 1991 also refers frequently to the problem. In both accounts Leonardo is considered a pivotal figure for having found or identified the correct solution to this problem as well as to the related problem of the bent lever. Both authors essentially assume that the transmission of such insights was unproblematic, supposing in particular that Benedetti's treatment was based on knowledge of Leonardo's manuscripts. Clagett 1959, 159 assumes that Galileo knew the correct solution to the bent lever problem because he was familiar with Jordanus' De ratione ponderis in the Tartaglia edition. We will come back to the challenges of knowledge transmission below. The role of the equilibrium controversy for Galileo's Mechanics is also discussed in the introductory essay of Galilei 2002. The role of the controversy for Guidobaldo's work has been discussed extensively in Palmieri 2008. For a general survey of early modern mechanics, see also Laird 1986.
Tomeo 1525, 27r–27v. Translation in Aristotle 1980, 341–342.
See, for instance, how Tartaglia's virtual interlocutor reminds him in his Quesiti of the connection between the claim that the equilibrated balance deflected into an oblique position will return to the horizontal and the treatment of the balance in the Aristotelian Mechanical Problems; see Tartaglia 1546, 88v, cf. Drake and Drabkin 1969, 124.
The arguments for its availability are indeed rather weak, see Clagett 1957.
For an overview of Arabic science and technology, see Hill 1993, 59–70.
It is sometimes assumed that Jordanus must have been familiar with the Aristotelian Mechanical Problems. However, Jordanus wrote his works in the first half of the thirteenth century whereas there are no indications that any manuscript reached the Latin West at that early date.
One must assume that the actual number at the time was much higher, but due to their long and changeful history, not all manuscripts that had once existed came down to us. Rose and Drake 1971, 72–76 list twenty-nine manuscripts. The codices Ms. Vat. Gr. 2231 and Vat. Gr. 905 have to be added to this list while Ms. Phi 1,10 of the Biblioteca de El Escorial has to be dropped.
At the end of the fifteenth century, between 1495 and 1498, the Aristotelian corpus was printed for the first time by Aldus Manutius (1449–1515). The Mechanical Problems are contained in the second volume, printed in 1497.
All data on the manuscript tradition are based on unpublished work by Paul Weinig who joined the project on the history of mechanical knowledge at the Max Planck Institute for the History of Science for several years.
Georgios Pachymeres, 1242–ca.1310.
Thirteenth century: three copies; fourteenth century: three copies; fifteenth century: nine copies; sixteenth century: twenty copies, among them Ms. Phi 1,10 of the Biblioteca de El Escorial which was erroneously listed by Rose and Drake 1971, 73 as an original Greek copy; seventeenth century: one copy; eighteenth century: one copy.
This way of transmission, however, is untypical for the transmission of Greek manuscripts in general. Byzantine scholars tended to neglect sources of the mathematical science and natural philosophy; see Krumbacher 1897, 605–638 for an overview of the scarcity of technical literature.
Willem of Moerbeke, c.1215–1286.
Clagett 1964-1984, see the introduction to volume 1.
See Clagett 1959, 24–30. Here as in other passages we make use of a text written by the authors jointly with Peter McLaughlin Renn et.al. 2003.
Moody and Clagett 1960, 55–75; see also the discussion in Knorr 1982, 15–39.
Al-Muzaffar al-Isfizari, 1048–1116.
See Moody and Clagett 1960, 81–82 for the occurrence of such knowledge in a treatise of Thābit, and Abattouy 2001, 227 for its occurrence in a treatise of al–Isfizari.
For a discussion of the manuscript sources, see Knorr 1982, 75–87.
Abu al-Fath Khāzini, fl. 1115–1130).
Gerard of Cremona, 1114–1187.
Francesco Maurolico, 1494–1575.
See Maurolico 1685a.
For a discussion of this fallacy, see Überweg 1882, 418–422 and Schreiber 2003, 141–151.
Moody and Clagett 1960, 150, see also Apianus' edition of Nemore 1533, A iii verso, page 292 in the present edition. Translation adapted from Moody and Clagett 1960, 151.
Nemore 1533, A iv recto, page 293 in the present edition.
Nemore 1533, A iv verso, page 294 in the present edition. Translation in Moody and Clagett 1960, 155.
Nemore 1533, B ii recto, page 297 of the present edition. Translation by the authors, cf. Moody and Clagett 1960, 156–157.
The proposition is the same as the fourth proposition in Jordanus' Elementa and the third proposition in his De ratione ponderis.
Nemore 1533, B iii verso, page 300 in the present edition. Translation adapted from Moody and Clagett 1960, 157.
The proposition is the same as the eighth proposition in Jordanus' Elementa and the sixth proposition in De ratione ponderis.
Nemore 1533, C iv recto, page 309 in the present edition.
Nemore 1533, C ii verso, page 306 in the present edition, cf. Moody and Clagett 1960, 158–159.
Blasius of Parma, 1345–1416.
See Lücke 1953, 485 on Ms. 2038 Bib. Nat. 2 v. See also the discussion on pages
Tartaglia 1546, 92v. Translation in Drake and Drabkin 1969, 132–133.
Tartaglia 1546, 84v. Translation in Drake and Drabkin 1969, 118.
Tartaglia 1546, 83r. Translation in Drake and Drabkin 1969, 115.
Tartaglia 1546, 83r. Translation in Drake and Drabkin 1969, 115.
Tartaglia 1546, 84v–85r. Translation in Drake and Drabkin 1969, 118–119.
Nemore 1565, 3v–4r. Evidently, at the time Tartaglia wrote Quesiti, he must have been familiar with Jordanus' De ratione ponderis.
See Tartaglia 1546, 84v–85r, Drake and Drabkin 1969, 119. For a review of the contemporary controversial discussion of this mathematical concept, see Maierù 1992, see also Bordiga 1985, 627–628.
Nemore 1533, A iii verso, page 292 in the present edition.
Tartaglia 1546, 90r. Translation in Drake and Drabkin 1969, 127.
Nemore 1533, A iv recto, page 293 in the present edition. Translation in Moody and Clagett 1960, 175.
Tartaglia 1546, 83v. Translation in Drake and Drabkin 1969, 116.
Tartaglia 1546, 82v. Translation in Drake and Drabkin 1969, 114.
Tartaglia 1546, 83r. Translation in Drake and Drabkin 1969, 115.
See also the illuminating discussion of Guidobaldo's controversy on the same issue with the “Goto” in Gamba and Montebelli 1988. For a discussion of Guidobaldo's criticism of the concept of positional heaviness, see also Duhem 1991, 150–156.
The preface of DelMonte 1577 is printed without page numbers, see the facsimile reproduction in Renn and Damerow 2010, 54. Translation in Drake and Drabkin 1969, 246.
DelMonte 1581, 28v–29r. See the discussion in Micheli 1995, in particular, pp. 163–167.
Giovanni Vincenzo Pinelli, 1535–1601.
DelMonte 1581, 28v. Translation in Drake and Drabkin 1969, 294–295, with modifications.
For the role of this argument in Guidobaldo's work, see Dyck 2006a and Dyck 2006b; for the general role of cosmological considerations in preclassical mechanics, see Dyck 2006b.
DelMonte 1577, 5r, Renn and Damerow 2010, 65. Translation in Drake and Drabkin 1969, 261.
See Commandino's edition Alexandria 1660, 450, first published in 1588 Alexandria 1588.
DelMonte 1577, 1r, Renn and Damerow 2010, 57. Translation in Drake and Drabkin 1969, 259.
DelMonte 1577, 1r, Renn and Damerow 2010, 57. Translation in Drake and Drabkin 1969, 259. In the second part Guidobaldo clearly referred to the Latin translation aequeponderare of Archimedes' expression for being in equilibrium. The translation of Drake and Drabkin has been corrected here accordingly.
For a comprehensive study of Galileo's use of the term and its historical context, see Galluzzi 1979.
DelMonte 1577, 5v, Renn and Damerow 2010, 68. Translation in Drake and Drabkin 1969, 262.
Nemore 1533, see chapter 5 for the discussion of Guidobaldo's marginal notes in his copy of the treatise. It seems that this version of Jordanus' doctrine was the only one to which he explicitly referred, although he could have also seen the edition of De ratione ponderis by Tartaglia Nemore 1565. On the manuscript tradition and an English translation, see Moody and Clagett 1960, 169–227.
Cardano 1550, 16–20 and the corresponding part contained in Opera omnia Cardano 1966, vol. 3, 369–371.
Nemore 1533, page 297 in the present edition; Cardano 1550, 17, EOAemphasized by a marginal note; Tartaglia 1546, 88v, ; see also the corresponding proposition in Tartaglia's edition of Jordanus' De ratione ponderis Nemore 1565, 3v, .
DelMonte 1581, 29r. Translation in Drake and Drabkin 1969, 295–296, with slight modifications.
DelMonte 1577, 6r–6v, Renn and Damerow 2010, 69–70, for an English translation see Drake and Drabkin 1969, 262–263.
Tartaglia 1546, 90v–91r, for an English translation see Drake and Drabkin 1969, 128–129.
DelMonte 1577, 6v, Renn and Damerow 2010, 70, for an English translation see Drake and Drabkin 1969, 263.
Tartaglia 1546, Book 8, sixth proposition, 91r–92r, for an English translation see Drake and Drabkin 1969, 129–131. Tartaglia had evidently taken this argument from the manuscript he used in his later edition of Jordanus' De ratione ponderis, Nemore 1565, 4r, for an English translation see Moody and Clagett 1960, 179.
DelMonte 1577, 6v–8r, Renn and Damerow 2010, 71–73, for an English translation see Drake and Drabkin 1969, 263–265.
DelMonte 1577, 8v, Renn and Damerow 2010, 74, for an English translation see Drake and Drabkin 1969, 265–266. See also Cardano 1550, 16–20 and Cardano 1966, vol. 3, 369–371 which is discussed above.
DelMonte 1577, 8v added the marginal note: Cardanus primo de subtilitate. The note concerns Cardano 1550, 16–17. Drake and Drabkin 1969, 266, footnote 20 attribute misleadingly also Guidobaldo's following references to Jordanus and Tartaglia to this proof.
DelMonte 1577, 8v–9r, Renn and Damerow 2010, 74–75, for an English translation see Drake and Drabkin 1969, 266–267.
Nemore 1533, B ii recto–B ii verso, pages 297–298 in the present edition.
Nemore 1565, 3v, for an English translation see Moody and Clagett 1960, 176–179.
Tartaglia 1546, 89r–89v, for an English version see Drake and Drabkin 1969, 125–127.
Guidobaldo referred to Cardano 1550, 17–18.
DelMonte 1577, 9r, Renn and Damerow 2010, 75, for an English translation see Drake and Drabkin 1969, 267.
DelMonte 1577, 9v, Renn and Damerow 2010, 76. Translation in Drake and Drabkin 1969, 267–268.
DelMonte 1577, 9r–9v, Renn and Damerow 2010, 75–76, for an English translation see Drake and Drabkin 1969, 267–268.
DelMonte 1577, 9v–15r, Renn and Damerow 2010, 76–87, for an English translation see Drake and Drabkin 1969, 268–275.
DelMonte 1577, 15r–17r, Renn and Damerow 2010, 87–91, for an English translation see Drake and Drabkin 1969, 275–277.
DelMonte 1577, 17r–17v, Renn and Damerow 2010, 91–92, for an English translation see Drake and Drabkin 1969, 277–278.
DelMonte 1577, 17v–18r, Renn and Damerow 2010, 92–93, for an English translation see Drake and Drabkin 1969, 278–279.
DelMonte 1577, 18r–19r, Renn and Damerow 2010, 93–95, for an English translation see Drake and Drabkin 1969, 279–281.
DelMonte 1577, 19r–19v, Renn and Damerow 2010, 95–96, for an English translation see Drake and Drabkin 1969, 281.
DelMonte 1577, 19v–20v, Renn and Damerow 2010, 96–98, for an English translation see Drake and Drabkin 1969, 281–283.
DelMonte 1577, 20v–21v, Renn and Damerow 2010, 98–100, for an English translation see Drake and Drabkin 1969, 283–284.
DelMonte 1577, 21v–30r, Renn and Damerow 2010, 100–117, for an English translation see Drake and Drabkin 1969, 284–294.
The discussion concerns the second problem of the Aristotelian Mechanical Problems, see Aristotle 1980, 346–351.
DelMonte 1577, 6r, Renn and Damerow 2010, 69. Translation in Drake and Drabkin 1969, 262.
Archimedes 1953, 190, see also the first proposition in Tartaglia's edition Archimedes 1543b, 5.
DelMonte 1577, 6r, Renn and Damerow 2010, 69. Translation in Drake and Drabkin 1969, 263.
Guidobaldo avoided here as in other places the term positional heaviness used by his adversaries.
DelMonte 1577, 6v–7r, Renn and Damerow 2010, 70–71. Translation in Drake and Drabkin 1969, 263–264.
Tartaglia 1546, 130–131, thirty-third question, sixth proposition; for an English translation see Drake and Drabkin 1969, 128–132. See also the discussion on page
DelMonte 1577, 7r–8r, for an English translation see Drake and Drabkin 1969, 264–265.
Benedetti 1585, 148–149, pages 336–338 in the present edition, for an English translation see Drake and Drabkin 1969, 175–176.
See the discussion in Dyck 2006a.
DelMonte 1577, 9r–15r, Renn and Damerow 2010, 75–87, for an English translation see Drake and Drabkin 1969, 267–275. See point 5 of the overview, page
DelMonte 1577, 10v, Renn and Damerow 2010, 78. Translation in Drake and Drabkin 1969, 269.
Favaro 1968, vol. 10, 97–100. See also the discussion in Renn et.al. 2001 and in Büttner 2009.
Drake and Drabkin 1969, 279. Translated from DelMonte 1577, 18r, see Renn and Damerow 2010, 93.
DelMonte 1577, 18v, Renn and Damerow 2010, 94. Translation in Drake and Drabkin 1969, 279–280.
DelMonte 1577, 19r, Renn and Damerow 2010, 95. Translation in Drake and Drabkin 1969, 280.
DelMonte 1577, 19r, Renn and Damerow 2010, 95. Translation in Drake and Drabkin 1969, 281.
In the words of Yehuda Elkana, it was a “concept in flux,” Elkana 1970.
DelMonte 1577, 20r, Renn and Damerow 2010, 97. Translation in Drake and Drabkin 1969, 282.
DelMonte 1577, 20v, Renn and Damerow 2010, 98. Translation in Drake and Drabkin 1969, 283.
DelMonte 1577, 20v–21r, Renn and Damerow 2010, 98–99. Translation in Drake and Drabkin 1969, 283.
DelMonte 1577, 22r, Renn and Damerow 2010, 101. Translation in Drake and Drabkin 1969, 285, modified by the authors.
DelMonte 1577, 23r, Renn and Damerow 2010, 103. Translation in Drake and Drabkin 1969, 286.
DelMonte 1577, 25v, Renn and Damerow 2010, 108. Translation in Drake and Drabkin 1969, 289.
DelMonte 1577, 43v, Renn and Damerow 2010, 144. Translation in Drake and Drabkin 1969, 300.
DelMonte 1577, 49r, Renn and Damerow 2010, 155. Translation in Drake and Drabkin 1969, 301–302, with slight modifications.
DelMonte 1577, 107r, Renn and Damerow 2010, 271. Translation in Drake and Drabkin 1969, 318.
DelMonte 1588. For extensive historical discussion, see Frank 2007.
Moody and Clagett 1960, 185–187. See also the discussion in sections 2.1 and 3.5.
We have observed such a process of reinterpretation also in many other instances of conceptual development, see e.g. Damerow et.al. 2004, and referred to it as a Copernicus process.
Benedetti 1585, 143, page 326 in the present edition. See also sections 6.1 and 7.3.
Tartaglia 1546, 90r. Translation in Drake and Drabkin 1969, 127.
Benedetti 1585, 148, page 336 in the present edition. Translation in Drake and Drabkin 1969, 175.
Thirty-second question, fifth proposition; see Drake and Drabkin 1969, 124–127.
Benedetti 1585, 148, page 336 in the present edition. Translation in Drake and Drabkin 1969, 176.
Thirty-third question, sixth proposition; see Drake and Drabkin 1969, 130–131. See the discussion in section 3.6.
Benedetti 1585, 150, page 340 in the present edition. Translation in Drake and Drabkin 1969, 177.
For an overview, see Bordiga 1985.
See Benedetti 1585, 183–184. For a historical discussion of the context of this argument in contemporary technology, see Freudenthal 2005.
Mazzoni 1597, 193 and Galilei 1960b, 326. It is conceivable that such issues had been discussed, inspired by Benedetti's work, between Galileo, Mazzoni, and Guidobaldo during the latter's stay in Tuscany in 1589. We would like to thank Pier Daniele Napolitani for drawing our attention to this possibility and to the above-mentioned passages.
Cozzi and Sosio 1996. For an overview of such potential connections, see the discussion in Bordiga 1985, 732–736 who also mentions Mersenne, Clavius, and Cardinal Michelangelo Ricci as possible intermediaries.
See the discussion by Ventrice in Bordiga 1985, 732–736 who mentions Drake, Drabkin, Fredette, and Galluzzi among those who are skeptical about a concrete influence of Benedetti on Galileo. A notable exception are the commentaries by Carugo and Geymonat to their edition of Galileo's Discorsi Carugo and Geymonat 1958. Bertoloni Meli even discusses the possibility of Guidobaldo and Galileo discussing Benedetti, but nevertheless rejects any substantial influence by the latter on Galileo's thinking because that influence would have supposedly arrived too late, see Bertoloni Meli 2006, 61–65.
This topic was the first subject in the letter of dedication in Resolutio Benedetti 1553. It was taken up again with different arguments in the two editions of Demonstratio Benedetti 1553. Finally it became the subject of a chapter on the Aristotelian theory of motion in Diversarum speculationum […] liber Benedetti 1585, 168–197 which remained without any marginal notes by Guidobaldo.
Benedetti's achievements in this regard have been recognized in the history of mechanics since Mersenne's French edition, Galilei 1634; see the discussion in Bordiga 1985, 184–187. For a more recent assessment, see Benvenuto 1987.
Remarkably, the concept of momento is also used in Stigliola's treatise from 1597, see Stelliola 1597 and, for historical discussion, Gatto 2006.
Favaro 1968, vol. 2, 159. Translation in Galilei 1960a, 151. See also Galilei 2002.
See the extensive discussion in Galluzzi 1979.
Favaro 1968, vol. 2, 159. Translation in Galilei 1960a, 151. See also Galilei 2002.
Cardano 1550, 16–20, see section 3.7.
Benedetti 1585, 143, page 326 in the present edition. Translation in Drake and Drabkin 1969, 169.
Favaro 1968, vol. 2, 160. Translation in Galilei 1960a, 152.
Favaro 1968, vol. 2, 164. Translation in Galilei 1960a, 156–157.
See Renn et.al. 2001, 74.
DelMonte 1587. For a historical discussion and a transcription, see Tassora 2001.
See, in particular, DelMonte 1587, 145–146, extensively discussed in sections 5.2 and 7.3 below.
See Renn et.al. 2001.
DelMonte 1587, 145bis, this page may have been inserted.
Galilei 1960b. For a thorough discussion of the chronology of these writings, see Giusti 1998.
This scenario was developed in a joint discussion with Pier Daniele Napolitani.
On the concept of mental model, see Renn and Damerow 2007. In the following we also make use of Renn et.al. 2003.
See the discussion in Damerow et.al. 2002 and Renn and Damerow 2007.
Mach 1988, 10–24. Mach also reports other criticisms.
See Elkana 1978.
See, for instance, the term parallelum epipedo orizontis in the Liber de canonio, the expression equatur linea super equidistantiam orizontis in the Liber karatonis, and the expression situm equalitatis esse equidistantiam super superficiei orizontis in the Liber de ponderibus; for reference see Moody and Clagett 1960, passim.
