Facsimile of Benedetti's Chapter on Mechanics
Image Transcription
Transcription
quetur dictum pondus gravius futurum pro parte .F.C. quam pro ea, quae est .A.F. &
minus supra centrum .B. pro dicta parte .F.C. quam pro parte .A.F. quieturum; &
dictum brachium quanto magis orizontale erit a situ .B.F. tanto minus-ſupra dictum
centrum .B. quiescet, & hac ratione gravius quoque erit, & quanto magis vicinum
erit ipsi .A. a dicto .F. tanto magis super centrum .B. quoque quiescet, unde tanto quo-
que levius existet. Idem dico de omni situ brachii per girum inferiorem .C.Q. ubi
pondus pendebit a centro .B. dictum centrum attrahendo, quemadmodum superius
illud impellebat. Haec vero omnia cap. sequenti melius percipientur.
minus supra centrum .B. pro dicta parte .F.C. quam pro parte .A.F. quieturum; &
dictum brachium quanto magis orizontale erit a situ .B.F. tanto minus-ſupra dictum
centrum .B. quiescet, & hac ratione gravius quoque erit, & quanto magis vicinum
erit ipsi .A. a dicto .F. tanto magis super centrum .B. quoque quiescet, unde tanto quo-
que levius existet. Idem dico de omni situ brachii per girum inferiorem .C.Q. ubi
pondus pendebit a centro .B. dictum centrum attrahendo, quemadmodum superius
illud impellebat. Haec vero omnia cap. sequenti melius percipientur.
De proportione ponderis extremitatis brachii libr &
in diverso situ ab orizontali.
CAP. II.
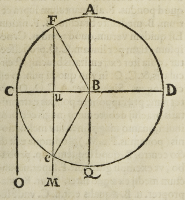
PRoportio ponderis in .C. ad idem pondus in F. erit quemadmodum totius
brachii .B.C. ad partem .B.u. positam inter centrum & lineam .F.u.M. inclinatio-
nis, quam pondus ab extremitate .F. liberum versus mundi centrum conficeret. Quod
ut facilius intelligamus imaginemur alterum brachium librae .B.D. & in extremo .D.
locatum aliquod pondus minus pondere .C. ut .B.u. pars .B.C.m. nor est .B.D. cla-
re cognoscetur ex .6. lib. primi de ponderibus Archimedis, quod si in puncto .u. col-
locatum erit pondus ipsius .C. libra nihil penitus a situ orizontali dimovebitur. Sed
perinde est quod pondus .F. aequale .C. sit in extremo .F. in situ brachii .B.F. quam ut sit
in puncto .u. in situ ipsius .B.u. orizontali. Ad cuius rei evidentiam imaginemur filum .
F.u. perpendiculare, & in cuius extremo .u. pendere pondus, quod erat in .F. unde cla
rum erit quod eundem effectum gignet, ac si fuisset in .F. quod, ut iam diximus re-
manens affixum puncto .u. brachii .B.u. tanto minus grave est situ ipsius .C. quanto .u.
B. minus est ipso .B.C. Idem assero si brachium esset in situ .e.B. quod facile cogno-
scere poterimus, si imaginemur filum appensum ipsi .u. brachii .B.C. & usque ad .e.
perpendicularem, in quo extremo appensum esset pondus aequale ponderi .C. & liberum
ab .e. brachii .B.e. unde libra orizontalis manebit. Sed si brachium .B.e. consolida-
tum fuisset in tali situ cum orizontali .B.D.
& appenso pondere .C. in .e. libero a filo, nec
ascenderet, neq; descenderet. quia tantum
est quod ipsum sit appensum filo, quod pendet
ab .u. quantum quod ab ipso liberum appem
nsum fuisset .e. brachii .B.e. & hoc procede
ret ab eo quod partim pendereta centro .
B. & si brachium esset in situ .B.Q. totum pon
dus centro .B. remaneret appensum, quem-
admodũ in situ .B.A. totum dicto centro an-
niteretur. unde fit ut hoc modo pondus
magis aut minus sit grave, quo magis
aut minus a centro pendet, aut eidem niti-
tur: atq; haec est causa proxima, & per se,
[Handwritten]
qua fit ut unum idemq; pondus in uno eo-
demque; medio magis aut minus grave exi-
brachii .B.C. ad partem .B.u. positam inter centrum & lineam .F.u.M. inclinatio-
nis, quam pondus ab extremitate .F. liberum versus mundi centrum conficeret. Quod
ut facilius intelligamus imaginemur alterum brachium librae .B.D. & in extremo .D.
locatum aliquod pondus minus pondere .C. ut .B.u. pars .B.C.m. nor est .B.D. cla-
re cognoscetur ex .6. lib. primi de ponderibus Archimedis, quod si in puncto .u. col-
locatum erit pondus ipsius .C. libra nihil penitus a situ orizontali dimovebitur. Sed
perinde est quod pondus .F. aequale .C. sit in extremo .F. in situ brachii .B.F. quam ut sit
in puncto .u. in situ ipsius .B.u. orizontali. Ad cuius rei evidentiam imaginemur filum .
F.u. perpendiculare, & in cuius extremo .u. pendere pondus, quod erat in .F. unde cla
rum erit quod eundem effectum gignet, ac si fuisset in .F. quod, ut iam diximus re-
manens affixum puncto .u. brachii .B.u. tanto minus grave est situ ipsius .C. quanto .u.
B. minus est ipso .B.C. Idem assero si brachium esset in situ .e.B. quod facile cogno-
scere poterimus, si imaginemur filum appensum ipsi .u. brachii .B.C. & usque ad .e.
perpendicularem, in quo extremo appensum esset pondus aequale ponderi .C. & liberum
ab .e. brachii .B.e. unde libra orizontalis manebit. Sed si brachium .B.e. consolida-
tum fuisset in tali situ cum orizontali .B.D.
& appenso pondere .C. in .e. libero a filo, nec
ascenderet, neq; descenderet. quia tantum
est quod ipsum sit appensum filo, quod pendet
ab .u. quantum quod ab ipso liberum appem
nsum fuisset .e. brachii .B.e. & hoc procede
ret ab eo quod partim pendereta centro .
B. & si brachium esset in situ .B.Q. totum pon
dus centro .B. remaneret appensum, quem-
admodũ in situ .B.A. totum dicto centro an-
niteretur. unde fit ut hoc modo pondus
magis aut minus sit grave, quo magis
aut minus a centro pendet, aut eidem niti-
tur: atq; haec est causa proxima, & per se,
[Handwritten]
demque; medio magis aut minus grave exi-