Facsimile of Benedetti's Chapter on Mechanics
Image Transcription
Transcription
stat. Et quamuis appellem latus .B.C. orizontale, supponens illud angulum rectum
cum .C.O. facere, unde angulus .C.B.Q. fit ut minor sit recto, ob quantitatem unius
anguli aequalis ei, quem duae .C.O. et .B.Q. in centro regionis elementaris constituunt,
hoc tamen nihil refert, cum dictus angulus insensibilis sit magnitudinis. Ab istis au-
tem rationibus elicere possumus, quod si punctus .u. erit ex aequo medius inter cen-
trum .B. & extremum .C. pondus .F. aut .M. pendebit, aut nitetur pro medietate dicto
centro .B. & si dictum .u. erit propius .B. quam puncto .C. pendebit ab ipso, aut nitetur
ipsi amplius quam exmedietate, & si magis versus .C. minus quam ex medietate nitetur.
cum .C.O. facere, unde angulus .C.B.Q. fit ut minor sit recto, ob quantitatem unius
anguli aequalis ei, quem duae .C.O. et .B.Q. in centro regionis elementaris constituunt,
hoc tamen nihil refert, cum dictus angulus insensibilis sit magnitudinis. Ab istis au-
tem rationibus elicere possumus, quod si punctus .u. erit ex aequo medius inter cen-
trum .B. & extremum .C. pondus .F. aut .M. pendebit, aut nitetur pro medietate dicto
centro .B. & si dictum .u. erit propius .B. quam puncto .C. pendebit ab ipso, aut nitetur
ipsi amplius quam exmedietate, & si magis versus .C. minus quam ex medietate nitetur.
Quod quantit as cuiuslibet ponderis, aut virtus movens re-
spectu alterius quantitatis cognoscatur beneficio
perpendicularium ductarum a centro
libr & ad line am inclinationis.
CAP. III.
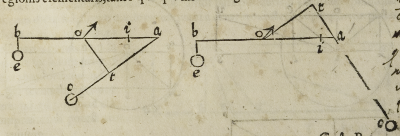
EX iis, quae a nobis hucusque sunt dicta, facile intelligi potest, quod quantitas .B.u.
quae fere perpendicularis est a centro .B. ad lineam .F.u. inclinationis, ea est,
[Handwritten]
quæ nos ducit in cognitionem quantitatis virtutis ipsius .F. in huiusmodi situ, consti
tuens videlicet linea .F.u. cum brachio .F.B. angulum acutum .B.F.u. Ut hoc tamen
melius intelligamus, imaginemur libram .b.o.a. fixam in centro .o. ad. cuius etrema
sint appensa duo pondera, aut duae virtutes moventes .e. et .c. ita tamen quod linea incli-
nationis .e. idest .b.e. faciat angulum rectum cum .o.b. in puncto .b. linea vero inclina
tionis .c. idest .a.c. faciat angulum acutum, aut obtusum cum .o.a. in puncto .a. Imagi-
nemur ergo lineam .o.t. perpendicularem lineae .c.a. inclinationis, unde .o.t. minor
erit .o.a. ex .18. primi Euclidis. secetur deinde imaginatione o.a. in puncto .i. ita ut
o.i. aequalis. sit .o.t. & puncto .i. appensum sit pondus aequale ipsi .c. cuius inclinationis
linea parallela sit lineae inclinationis ponderis .e. supponendo tamen pondus aut vir
tutem .c. ea ratione maiorem esse ea, quae est .e. qua .b.o. maior est .o.t. absque dubio
ex .6. lib. primi Archi. de ponderibus .b.o.i. non movebitur situ, sed si loco .o.i. imagi
nabimur .o.t. consolidatam cum .o.b. & per lineam .t.c. attractam virtute .c. similiter
quoque continget ut b.o. t; communi quadam scientia, non moveatur si tu. Est ergo
[Handwritten]
quod proposuimus verum quantitatem alicuius ponderis respectu ad eam, quae est
alterius debere depraehendi a perpendicularibus, quae a centro librae ad lineas incli
nationis exiliunt. Hinc autem innotescit facillime, quantum vigoris, & vis pondus,
aut virtus .c. ad angulum rectum cum .o.a. minime trahens, amitttat. Hinc quoque co
rollarium quoddam sequetur, quo d quanto propinquius erit centrum .o. librae cen-
tro regionis elementaris, tanto quo que minus erit grave.
quae fere perpendicularis est a centro .B. ad lineam .F.u. inclinationis, ea est,
[Handwritten]
tuens videlicet linea .F.u. cum brachio .F.B. angulum acutum .B.F.u. Ut hoc tamen
melius intelligamus, imaginemur libram .b.o.a. fixam in centro .o. ad. cuius etrema
sint appensa duo pondera, aut duae virtutes moventes .e. et .c. ita tamen quod linea incli-
nationis .e. idest .b.e. faciat angulum rectum cum .o.b. in puncto .b. linea vero inclina
tionis .c. idest .a.c. faciat angulum acutum, aut obtusum cum .o.a. in puncto .a. Imagi-
nemur ergo lineam .o.t. perpendicularem lineae .c.a. inclinationis, unde .o.t. minor
erit .o.a. ex .18. primi Euclidis. secetur deinde imaginatione o.a. in puncto .i. ita ut
o.i. aequalis. sit .o.t. & puncto .i. appensum sit pondus aequale ipsi .c. cuius inclinationis
linea parallela sit lineae inclinationis ponderis .e. supponendo tamen pondus aut vir
tutem .c. ea ratione maiorem esse ea, quae est .e. qua .b.o. maior est .o.t. absque dubio
ex .6. lib. primi Archi. de ponderibus .b.o.i. non movebitur situ, sed si loco .o.i. imagi
nabimur .o.t. consolidatam cum .o.b. & per lineam .t.c. attractam virtute .c. similiter
quoque continget ut b.o. t; communi quadam scientia, non moveatur si tu. Est ergo
[Handwritten]
alterius debere depraehendi a perpendicularibus, quae a centro librae ad lineas incli
nationis exiliunt. Hinc autem innotescit facillime, quantum vigoris, & vis pondus,
aut virtus .c. ad angulum rectum cum .o.a. minime trahens, amitttat. Hinc quoque co
rollarium quoddam sequetur, quo d quanto propinquius erit centrum .o. librae cen-
tro regionis elementaris, tanto quo que minus erit grave.