Facsimile of Benedetti's Chapter on Mechanics
Image Transcription
Transcription
Quemadmodum exsupradictis causis omnes staterarum &
vectium causae dependeant.
CAP. IIII.
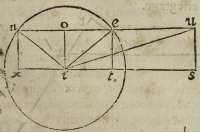
VIs brachii longioris alicuius staterae, aut vectis, maior brevioris, ab iis, quae in su
perioribus capitibus diximus, idest quod nitatur pendeatuem magis aut minus a
centro pondus in extremitate brachii maioris positum, oboritur. Quamobrem illud
a nobis primo est cognoscendum, stateras, aut vectes, puras mathematicas li-
neas non esse, sed naturales, hincque existere corpora cum materia coniuncta. Nunc
igitur imaginemur .n.s. eam superficiem esse, quae secundum longitudinem axem sta
terae scindit. & supponamus ipsius centrum esse primum in .i. & maius brachium esse
.i.u: minus autem .i.n. & lineam verticalem .i.o. quae tanta sit, quanta est spissitu-
do, aut crassities ipsius staterae a superiori latere ad inferius, ad faciliorem intelligen-
tiam, supponendo .n.s. parallelogrammam. Positis igitur duobus ponderibus aequali-
[Handwritten]
bus in extremitatibus brachiorum, experientia innotescit, quod pondus ad .u.s. appen-
sum, viol entiam faciet ponderi appenso ad .n.x. sed nos volumus inuestigare causam
huius effectus, quae a nemine unquam literarum monumentis, quod sciam, consignata
[Handwritten]
fuit. Iam diximus stateram, aut vectem materialem esse & .n.s. eius superficiem me-
diam, supponendo .i. esse centrum quo nititur dicta statera aut vectis; Cum hocer-
go ita se habeat, sint .u.s. et .n.x. lineae inclinationum ponderum, & imaginemur, quod
dicta pondera pendeant a punctis .u. et .n. ut revera pendent, etiam si appensa essent
sub .s. et .x. quia punctum .u. & punctum .n. ita coniuncta sunt cum .s. et .x. ut qui unum
trahit alterum quoque trahat. Imaginemur quoque duas lineas .i.u: i.n. et .i.e. quae
i.e. faciat angulum .o.i.e. aequalem angulo .o.i.n. Hinc clare nobis patebit, si quis ipsi
e. pondus ipsius .u. (quod aequale est ponderi .n.) appenderet, id eandem plane vim habe
ret, quam pondus ipsius .n. habet, & stateram neque sursum, neque deorsum move-
ret, quia ambo pondera ad centrum .i. mediantibus lineis .e.i. et .n.i. exaequo annite-
rentur, sed dicto pondere posito in .u: linea .u.i. per quam pondus centro annititur,
magis orizontalis quam .e.i. fit, & linea .u.s. inclinationis longius distans a centro .i.
[Handwritten]
quàm linea .e.t. unde huiusmodi pondus magis quoque liberum a centro .i. resultat.
magisque ponderosum, quam cum erat in .e. ratione eorum, quae primo & secundo
capitibus diximus, & ob hanc causam superat pondus positum in .n. Sed si centrum
fuerit .in .o. imaginabimur duas lineas .o.s. et .o.x. & supponemus quod pondera po-
sita sint in .s. et .x. unde existente magis orizontali linea .o.s. quam erit .o.x. & linea
u.s. inclinationis longius distante a centro .o. quam linea .e.t. eius pondus erit quoq;
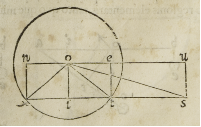
perioribus capitibus diximus, idest quod nitatur pendeatuem magis aut minus a
centro pondus in extremitate brachii maioris positum, oboritur. Quamobrem illud
a nobis primo est cognoscendum, stateras, aut vectes, puras mathematicas li-
neas non esse, sed naturales, hincque existere corpora cum materia coniuncta. Nunc
igitur imaginemur .n.s. eam superficiem esse, quae secundum longitudinem axem sta
terae scindit. & supponamus ipsius centrum esse primum in .i. & maius brachium esse
.i.u: minus autem .i.n. & lineam verticalem .i.o. quae tanta sit, quanta est spissitu-
do, aut crassities ipsius staterae a superiori latere ad inferius, ad faciliorem intelligen-
tiam, supponendo .n.s. parallelogrammam. Positis igitur duobus ponderibus aequali-
[Handwritten]
sum, viol entiam faciet ponderi appenso ad .n.x. sed nos volumus inuestigare causam
huius effectus, quae a nemine unquam literarum monumentis, quod sciam, consignata
[Handwritten]
diam, supponendo .i. esse centrum quo nititur dicta statera aut vectis; Cum hocer-
go ita se habeat, sint .u.s. et .n.x. lineae inclinationum ponderum, & imaginemur, quod
dicta pondera pendeant a punctis .u. et .n. ut revera pendent, etiam si appensa essent
sub .s. et .x. quia punctum .u. & punctum .n. ita coniuncta sunt cum .s. et .x. ut qui unum
trahit alterum quoque trahat. Imaginemur quoque duas lineas .i.u: i.n. et .i.e. quae
i.e. faciat angulum .o.i.e. aequalem angulo .o.i.n. Hinc clare nobis patebit, si quis ipsi
e. pondus ipsius .u. (quod aequale est ponderi .n.) appenderet, id eandem plane vim habe
ret, quam pondus ipsius .n. habet, & stateram neque sursum, neque deorsum move-
ret, quia ambo pondera ad centrum .i. mediantibus lineis .e.i. et .n.i. exaequo annite-
rentur, sed dicto pondere posito in .u: linea .u.i. per quam pondus centro annititur,
magis orizontalis quam .e.i. fit, & linea .u.s. inclinationis longius distans a centro .i.
[Handwritten]
magisque ponderosum, quam cum erat in .e. ratione eorum, quae primo & secundo
capitibus diximus, & ob hanc causam superat pondus positum in .n. Sed si centrum
fuerit .in .o. imaginabimur duas lineas .o.s. et .o.x. & supponemus quod pondera po-
sita sint in .s. et .x. unde existente magis orizontali linea .o.s. quam erit .o.x. & linea
u.s. inclinationis longius distante a centro .o. quam linea .e.t. eius pondus erit quoq;