Facsimile of Benedetti's Chapter on Mechanics
Image Transcription
Transcription
gravius, quia tanto minus pendebit a centro .o. & ratiocinando, ut superius dixi-
mus, inueniemus eundem effectum verum esse. In stateris, recte & proprie appella
ri potest .x.i.s. aut .n.o.u. orizontalis, sed in omni vectium specie, hoc tantum per quan
dam similitudinem dicetur. Idem contemplari licet supponendo centrum in medio
inter .o. et .i. quod unusquisque ex se absque alterius auxilio facile praestare poterit.
mus, inueniemus eundem effectum verum esse. In stateris, recte & proprie appella
ri potest .x.i.s. aut .n.o.u. orizontalis, sed in omni vectium specie, hoc tantum per quan
dam similitudinem dicetur. Idem contemplari licet supponendo centrum in medio
inter .o. et .i. quod unusquisque ex se absque alterius auxilio facile praestare poterit.
De quibusdam rebus animaduersione dignis.
CAP.V.
NOn omittenda mihi videntur quaedam, quae ad tractationem vectium admodum
sunt necessaria. Quod autem quaerimus, in eo consistit, quod aliqui vectes
adhibeantur ad opus, quorum centrum, quod Graeci hypomochlion appellant unum
est ex extremis ipsius vectis, & pondus, quod sursum elevari debet, inter ipsa-
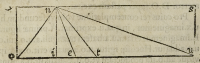
met extrema iacet, propinquum tamen hypomochlio, ut exempli gratia, si vectis
esset infrascripta figura .o.s.u.x. cuius hypomochlion esset in puncto .o. & pondus in
puncto .n. clarum erit, quod cum elevari debeat .n. oportebit quoque opera manus ele-
vari .u. Nunc considerandum est quomodo pondus .n. annitatur ad .u. Hanc ob cau
sam imaginabimur rectas lineas .n.o: n.i: n.e: n.t. et .n.u. quarum .n.i. versus mundi cen
trum sit posita, et .n.t. faciat angulum .i.n.t. aequalem angulo .i.n.o. Nunc ponendo ali
quam virtutem in .i. aequali inclinatione ad superius constante, ut .n. ad inferius (re-
mota tamen gravitate materiae vectis) huiusmodi virtus, totum pondus ipsius .n. com
muni quadam scientiae notione sustinebit. & si pondus ipsius .n. esset in .x. e directo su-
per .o. totum pondus super hypomochlio se haberet, & tanta virtus ipsius hypomo-
chlii sufficeret ad resistendum pro sustinendo, quanta est gravitas ipsius ponderis,
sed ipsum iterum ponamus in .n. ibi clarum erit, quod si alia virtus a parte inseriori
ad superiorem vectis non opponitur, excepto tamen hypomochlio, oportebit virtu
te cuiusdam partis ponderis .n. (absque consideratione tamen, ut iam dixi, ponderis
materiae vectis) ut vectis a parte .s.u. deprimatur, & dixi unius cuiusdam partis pon-
deris .n. quia alia eiusdem ponderis pars annititur ipsi hypomochlio .o. mediante linea
o.n. quae angulos rectos cum .o.x. non facit. Si autem a puncto .t. opponet sese huius-
modi resistentia, ut vectis non deprimatur, clarum erit communi scientia, quod virtus
ponderis .n. divisa erit per medium aequaliter, cuius una medietas super .o. quiescet,
& alia super .t. mediantibus duabus lineis .n.o. et .n.t. Imaginemur nunc resistentiam
t. ablatam esse, positamq; in .e. clarum quoque erit, quod maior pars ponderis .n. ipsi .e.
annitetur beneficio lineae .n.e. quam ipsi .o. cum linea .n.i. inclinationis ipsi .e. sit pro
pinquior quam .o. quia omnis resistentia aut in .i. aut in .e. aut in .t. aut in .u. est loco
centri, quemadmodum est .o. & alter alterius opera ivvatur. Si vero eadem resisten
tia posita erit in .u. clarum quoque erit, quod minor pars ponderis .n. annitetur ipsi .u. quam
ipsi .o. cum dicta .n.i. a centro .u. longius quam a centro .o. dister, & proportio partis
ponderis .n. in .o. ad propor-
tionem partis ponderis .n. in
u. non erit secundum propor
tionem angulorum .u.n.i. et
o.n.i. sed secundum propor
tionem .u.i. ad .i.o. quod cla
re compraehendi potest ab
sunt necessaria. Quod autem quaerimus, in eo consistit, quod aliqui vectes
adhibeantur ad opus, quorum centrum, quod Graeci hypomochlion appellant unum
est ex extremis ipsius vectis, & pondus, quod sursum elevari debet, inter ipsa-
met extrema iacet, propinquum tamen hypomochlio, ut exempli gratia, si vectis
esset infrascripta figura .o.s.u.x. cuius hypomochlion esset in puncto .o. & pondus in
puncto .n. clarum erit, quod cum elevari debeat .n. oportebit quoque opera manus ele-
vari .u. Nunc considerandum est quomodo pondus .n. annitatur ad .u. Hanc ob cau
sam imaginabimur rectas lineas .n.o: n.i: n.e: n.t. et .n.u. quarum .n.i. versus mundi cen
trum sit posita, et .n.t. faciat angulum .i.n.t. aequalem angulo .i.n.o. Nunc ponendo ali
quam virtutem in .i. aequali inclinatione ad superius constante, ut .n. ad inferius (re-
mota tamen gravitate materiae vectis) huiusmodi virtus, totum pondus ipsius .n. com
muni quadam scientiae notione sustinebit. & si pondus ipsius .n. esset in .x. e directo su-
per .o. totum pondus super hypomochlio se haberet, & tanta virtus ipsius hypomo-
chlii sufficeret ad resistendum pro sustinendo, quanta est gravitas ipsius ponderis,
sed ipsum iterum ponamus in .n. ibi clarum erit, quod si alia virtus a parte inseriori
ad superiorem vectis non opponitur, excepto tamen hypomochlio, oportebit virtu
te cuiusdam partis ponderis .n. (absque consideratione tamen, ut iam dixi, ponderis
materiae vectis) ut vectis a parte .s.u. deprimatur, & dixi unius cuiusdam partis pon-
deris .n. quia alia eiusdem ponderis pars annititur ipsi hypomochlio .o. mediante linea
o.n. quae angulos rectos cum .o.x. non facit. Si autem a puncto .t. opponet sese huius-
modi resistentia, ut vectis non deprimatur, clarum erit communi scientia, quod virtus
ponderis .n. divisa erit per medium aequaliter, cuius una medietas super .o. quiescet,
& alia super .t. mediantibus duabus lineis .n.o. et .n.t. Imaginemur nunc resistentiam
t. ablatam esse, positamq; in .e. clarum quoque erit, quod maior pars ponderis .n. ipsi .e.
annitetur beneficio lineae .n.e. quam ipsi .o. cum linea .n.i. inclinationis ipsi .e. sit pro
pinquior quam .o. quia omnis resistentia aut in .i. aut in .e. aut in .t. aut in .u. est loco
centri, quemadmodum est .o. & alter alterius opera ivvatur. Si vero eadem resisten
tia posita erit in .u. clarum quoque erit, quod minor pars ponderis .n. annitetur ipsi .u. quam
ipsi .o. cum dicta .n.i. a centro .u. longius quam a centro .o. dister, & proportio partis
ponderis .n. in .o. ad propor-
tionem partis ponderis .n. in
u. non erit secundum propor
tionem angulorum .u.n.i. et
o.n.i. sed secundum propor
tionem .u.i. ad .i.o. quod cla
re compraehendi potest ab