DE MECHANICIS.
SCripservnt multi multa, & quidem scitissime, de mechn-
nicis, at cum natura ususq; aliquid semper vel novum, vel
Latens in apertum emittere soleant, nec ingenui aut grati sit
animi, posteris inuidere, si quid ei contigerit comperuisse prius
tenebris inuolutum: cum tam multa ipse ex aliorum diligentia
sit consequut us. Paucula quaedam futùra, ut reor, non ingrata his
qui in bisce mechanicis versantur, nusquam ante bac tentata,
aut satis exaste explicata in medium proferre volui: quo vel ivvandi desiderium, vel
saltem non ociosi ingenioli argumentum aliquod exbiberem: at que vel boc uno modo me
inter bumanos vixisse testatum relinquerem.
De differentia situs brachiorum libra.
CAP.I.
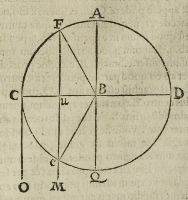
OMne pondus positum in extremitate alicuius brachii librae maiorem, aut mi-
[Handwritten]
norem gravitatem habet, pro diversa ratione situs ipsius brachii. sit exempli
gratia .B. centrum, aut, quod dividit brachia alicuius librae, & .A.B.Q. vertica-
lis linea, aut, ut rectius dicam, axis orizontis, & .B.C. unum brachium dictae li-
brae, & in .C. sit pondus, & .C.O. linea inclinationis, sevicineris .C. versus cen-
trum mundi, cum qua .B.C. angulum rectum constituat in puncto .C. Existente
igitur in huiusmodi situ brachio .B.C. dico pondus .C. gravius futurum, quam
in alio quolibet situ. quia supra centrum .B. omnino non quiescet, quemadmodum
in quovis alio situ faceret. Ad quod intelligendum, sit dictum brachium, in situ .B.
F. cum eodem pondere in puncto .F. & linea itineris seu inclinationis dicti ponderis
sit .F.u.M. per quam lineam dictum pondus progredi non potest, nisi brachium .B.F.
brevius redderetur. Unde clarum erit
[Figure 209]
trum .B. mediante brachio .B.F. nititur.
Est quidem verum, quod pondus .C. nec
ipsum etiam per lineam .C.O. proficisce-
tur, quia iter extremitatis brachii est cir-
cularis, & .C.O. in uno quodam puncto est
contingens. Sit hociter .A.C.Q. Opor-
tet nunc praesupponere pondus extremi-
tatis brachii deberetanto magis centro .B.
inniti, quanto magis linea suae inclinatio-
nis (ponamus .F.u.M.) propinqua erit di
cto centro .B. quod sequenti cap. proba-
bo, ut exempli gratia, sit .F. super .u. pun-
ctum medii ex aequo inter .C. et .B. qua-
propter .u.B. aequalis erit .u.C. vndeſe- 
