Chapter structure
- 5.1 Second theorem: rejecting Jordanus' stance in the equilibrium controversy
- 5.2 Fourth theorem: the neglect of the cosmological context
- 5.3 Fifth theorem: failure to recognize the authority of Archimedes in mechanics
- 5.4 Seventh theorem: on the erroneous treatment of an equilibrium problem
- 5.5 Eighth theorem: rejecting Jordanus' proof of the law of the lever
- 5.6 Ninth theorem: the problematic attribution to Euclid
- Footnotes
Guidobaldo evidently owned a copy of Apianus' edition of Jordanus.1 This copy survived and is annotated in Guidobaldo's hand. These marginal notes are presented here not with the aim to offer an exhaustive philological analysis, but in order to gain insight into the equilibrium controversy, in particular with regard to the concept of positional heaviness. The presentation of the notes comprises a short characterization of the relevant passages in Jordanus' text, including quotations of the passages to which Guidobaldo referred – if these passages could be identified, then the marginalia themselves are presented and interpreted.
5.1 Second theorem: rejecting Jordanus' stance in the equilibrium controversy
Guidobaldo left several notes on this theorem and its commentaries, some of them very minor. The second theorem deals, as mentioned above, with the equilibrium position of a balance, claiming that a balance always returns to its horizontal position when it is displaced from it. Guidobaldo in contrast was, as we have also discussed extensively, convinced that the balance remains in whatever position it has and does not return to the horizontal.
Guidobaldo's first note refers to Jordanus' statement of the theorem:
Cum fuerit aequilibris positio aequalis, aequis ponderibus appensis, ab aequalitate non discedet, etsi ab aequidistantia separetur, ad aequalitatis situm revertetur.
If an equilibrated [balance] is in horizontal position [positio aequalis], with equal weights suspended, it will not leave the horizontal position [aequalitate]; and if it is removed from the horizontal position [aequidistantia], it will return to the horizontal position [aequalitatis situm].2

Fig. 5.1: First marginal note to the second proposition.
In his first short marginal note Guidobaldo simply rejects this claim. He noted:
haec propositio falsa e[st]
this proposition is false
Guidobaldo's second note, on the next page, refers to the detailed argument in the second commentary, in particular to the following statement:
Non enim ulterius descendet B, eo quod descensus eius versus D magis obliquus est, quam ascensus C ad aequalitatem, B enim et C iam equaliter distant a situ aequalitatis […]
In fact B does not descend further because its descent toward D is more oblique than the ascent of C to the horizontal position since B and C have the same distance from the horizontal position […]3
The argument compares, as usual, the obliquity of descents in order to establish which weight is positionally heavier. In the present case it is argued that the descent of the [lower] weight B is more oblique than that of [upper] weight C so that weight B is positionally lighter than weight C, with the effect that the balance returns to its horizontal position. Guidobaldo has underlined the word “ascensus” in the sentence quoted above and noted in the margin that it has to be replaced by “descensus” to make the argument work following the logic of Jordanus who compared descents on both sides of the balance:
descensus
descent

Fig. 5.2: Second marginal note to the second proposition.
In a third marginal note on the same page, still related to the second theorem, Guidobaldo remarks:
[ha]ec demonstratio inutilis est [pr]orsus ut in nostro Mechanicorum libro patet. [s]equens vero recte concludit
this demonstration is completely useless as is clear from our book on mechanics, but in the following he reasons correctly

Fig. 5.3: Third marginal note to the second proposition.
Guidobaldo claimed here, not that Jordanus' proof is wrong, because geometrically it is correct, but that it is useless. In fact the geometrical reasoning of the commentator about arcs and what they capture from the vertical is mathematically correct.
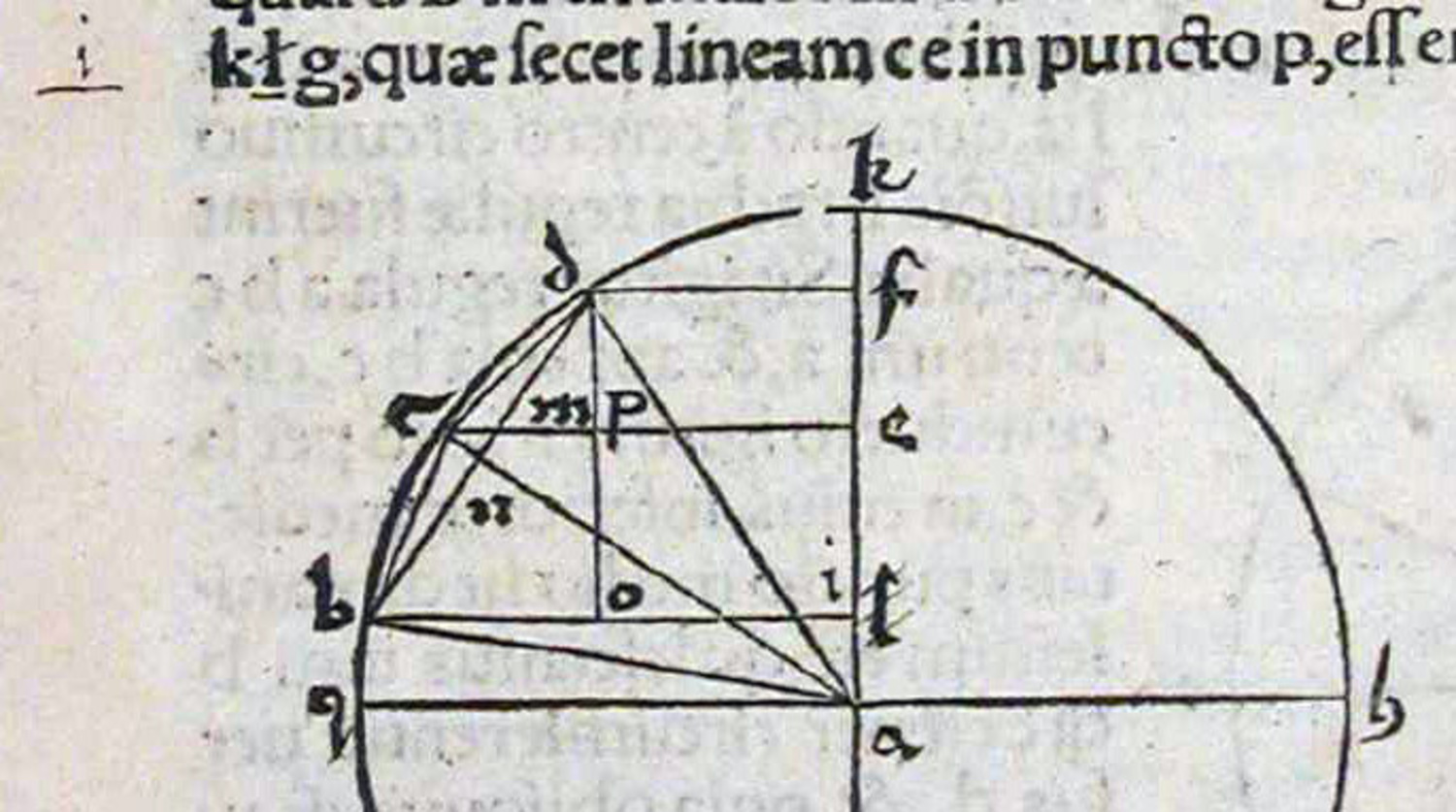
On the same page there is a very brief fourth marginal note and a correction in the lettering of a figure. The letter i replaces the letter l in the text which is crossed out. The same is done in the drawing. This just corrects a sloppy designation of a point in the diagram.

Fig. 5.5: Correction of another typographical error.
A similar error in the same paragraph is also corrected by Guidobaldo. The word in in the text is crossed out and replaced by the letter m.
This shows that Guidobaldo worked carefully through Apianus' edition, even correcting typographical errors, and that he followed, equally carefully, the intrinsic logic of Jordanus' arguments.
5.2 Fourth theorem: the neglect of the cosmological context
The next marginal note refers to the fourth theorem which claims that a weight becomes positionally lighter when it is removed from the horizontal position:
Quodlibet pondus in quamcumque partem discedat secundum situm fit levius.
In whichever direction a weights descends, it becomes positionally lighter.4
Guidobaldo's comment may address either this claim or the first statement of the commentary to this theorem which refers to the fourth postulate, the definition of positional heaviness by the obliqueness of descent:
Manifestum est hoc per suppositionem quartam.
This is evident by the fourth postulate.5

Fig. 5.6: Marginal note to the fourth proposition.
Guidobaldo noted in the margin, close to both of these statements, in large script:
Falsa
False
Most probably, this comment refers to Guidobaldo's claim, discussed extensively in his book (see section 3.8.4), that, when one takes into account the cosmological context, it is not the horizontal position but a different one, in dependence on the distance of the balance from the center of the world, in which a weight reaches its maximal positional heaviness.
5.3 Fifth theorem: failure to recognize the authority of Archimedes in mechanics
The fifth theorem claims, as we have discussed, that a balance with equal weights but unequal arms will descend on the side of the longer arm. In the middle of the extensive second commentary justifying this proposition, which, as we have also discussed, contains many technical references, Guidobaldo just underlined the word Archimedes:
[…] sed sicut circumferentia ad circumferentiam, ita semidiameter ad semidiametrum per quintam Archimedis de curvis superficiebus.
[…] but as circumference to circumference such is diameter to diameter by the fifth proposition of Archimedes' De curvis superficiebus.6
Possibly this underlining simply meant that Guidobaldo found it remarkable that Archimedes is just quoted as an authority in mathematics but not in mechanics by the author.

Fig. 5.7: Underlining a word in the proof of the fifth proposition.
5.4 Seventh theorem: on the erroneous treatment of an equilibrium problem
The seventh theorem is one of the problematic theorems concerning the bent lever, the other being theorem 6 on which Guidobaldo left no annotation. Theorem 7 concerns the balance with one fixed and one freely moving suspension, claiming that the freely swinging weight is positionally heavier.
Guidobaldo's first note is written in the margin of the beginning of the commentary to this theorem, but it may also refer to the theorem as a whole. Indeed, as we have discussed above, the first part of the commentary is hardly illuminating, while the enunciation of the theorem offers itself to criticism from the viewpoint of Guidobaldo's mechanics. Guidobaldo's approach crucially involves the concept of center of gravity, as we have discussed above. Now the question raised by the present theorem, namely what happens to such a balance when it is displaced from the horizontal position, can be addressed with the help of this concept, leading to the conclusion that the balance is in stable equilibrium. But Guidobaldo may have also focused on a statement in the commentary which is obviously problematic:
[…] tunc illud quod est circumvolubile, maiorem circulum constituit in causa [should be casu] quia plus declinat propter circumvolutionem, et sic pondus ibi gravius est secundum situm cum eius descensus sit rectior.
Then the arm which can swing freely will describe a greater circle in its descent, because it has a greater declination on account of the rotation; and thus the weight there is positionally heavier, since its path of descent is straighter.7
In any case, Guidobaldo wrote:
falsa [i]mmo sequitur oppositum [s]i per principia vera fiat demonstratio
false; in fact the opposite follows if the demonstration is performed according to true principles
The next marginal note simply corrects a typographical error at the end of the commentary to theorem 7, replacing ho in the text which is underlined by the correct word hoc.

Fig. 5.9: Correction of a typographical error near the end of the commentary to Jordanus' seventh theorem.
5.5 Eighth theorem: rejecting Jordanus' proof of the law of the lever
Theorem 8 constitutes, as we have discussed, a proof of the law of the lever. Guidobaldo left two marginal notes to this theorem and its discussion in the commentaries. The first note refers to the statement of the theorem, expressed in terms of an equality of positional heaviness:
Si fuerint brachia librae proportionalia ponderibus appensorum, ita, ut in breviori gravius appendatur, aeque gravia erunt secundum situm.
If the arms of the balance are proportional to the weights suspended, in such manner that the heavier weight is suspended on the shorter arm, then the suspended weights will be of equal positional heaviness.8
Guidobaldo wrote:
propositio quidem vera. Demonstrationum vero sequentium nulla ex necessitate concludit
the proposition is true indeed, but he derives nothing of the following demonstrations by necessity
While the claim – the law of the lever – is evidently correct, Guidobaldo questioned the method of proof based on Aristotelian principles rather than on the concept of center of gravity.
Guidobaldo's second marginal note to this theorem on the same page refers to the proof given in the second commentary which he evidently worked through. It refers, in particular, to the following statement (see figure 5.11):
Dico, quod non faciet motum in aliquam partem regula recta, ascendat primo B et descendat C, ita ut DAE sit quasi regula, et D quasi pondus C, sint DM et EF perpendiculares super BC palam est igitur […], quod triangulia ADM et AEF sunt similes.
I say that, without the balance moving in any direction, let first B rise and C descend so that DAE becomes like the balance and D like the weight C, and let DM and EF be perpendicular lines on BC then it is obvious […] that the triangles ADM and AEF are similar.9
Here the words “D quasi pondus C” (“D like the weight C”) are underlined.
In the margin next to it Guidobaldo wrote:
DE quasi pondera [BC]
DE like the weights [BC]
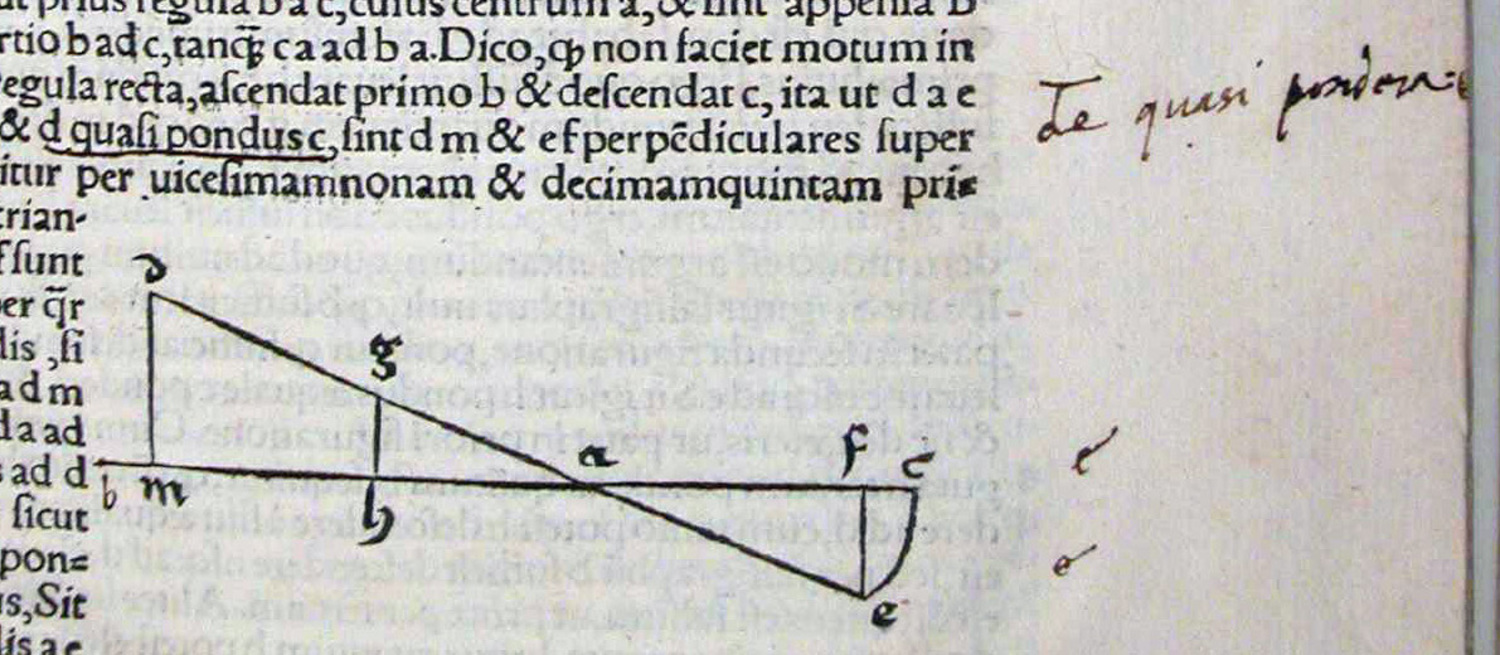
Fig. 5.11: Guidobaldo clarifies a sentence of Jordanus' proof.
Furthermore, he added labels to the diagram. Evidently, Guidobaldo attempted to follow the proof concerning imaginary displacements of weights that allow the application of Aristotelian dynamical principles. In particular, the weight D corresponds to the weight originally labelled B but then designated as C in the text quoted above. The lettering of the text and of the diagram was apparently so confusing to Guidobaldo that he strove for greater clarity by correcting labels both in the diagram and in the text.
5.6 Ninth theorem: the problematic attribution to Euclid
The last sentence of the commentary to the ninth theorem ascribes the first nine theorems not to Jordanus but to Euclid. Guidobaldo evidently found this remarkable and underlined the statement that here the book of Euclids ends:
Hic explicit secundum aliquos liber Euclidis de ponderibus.
Here ends, according to some, Euclid's book on weights.10
Footnotes
Nemore 1533, B ii recto, page 297 of the present edition. Translation by the authors, cf. Moody and Clagett 1960, 156–157.
Nemore 1533, B ii verso, page 298 of the present edition.
Nemore 1533, B iii verso, page 300 in the present edition. Translation in Moody and Clagett 1960, 156–157.
Nemore 1533, B iii verso, page 300 in the present edition. Translation in Moody and Clagett 1960, 156–157.
Nemore 1533, C i recto, page 303 in the present edition. Translation by the authors, cf. Moody and Clagett 1960, 158.
Nemore 1533, C iii verso, page 308 in the present edition. Translation in Moody and Clagett 1960, 158–159.
Nemore 1533, C iv recto, page 309 in the present edition. Translation adapted from Moody and Clagett 1960, 160–161.
Nemore 1533, D i verso, page 312 in the present edition.