Um die Rezeption der Sphaera, die als Werk des Proklos gilt, in der Renaissance zu verstehen, muss auch geklärt werden, was für ein Autor Proklos in dieser Zeit ist, basierend auf der Proklos-Rezeption im Mittelalter. Dabei spielt eine Rolle, an welchen seiner Werke die Humanisten am meisten interessiert sind bzw. welche Proklos-Werke bereits vor der editio princeps der Sphaera in Westeuropa bekannt sind und welche später, möglicherweise zeitgleich mit der Sphaera übersetzt und gedruckt werden. Auch ist von Bedeutung, mit welchen anderen Werken (nicht nur des Proklos) die Sphaera herausgegeben wird. Francesco Petrarca beklagt, dass im Mittelalter aus Ablehnung der Antike als Traditionsstifterin viele Texte verloren gegangen sind – eine Haltung, die sich in der Renaissance wandelt. Eine Schrift aus den Lieblingsbüchern des Petrarca mit dem Titel Sphaera mag die des Pseudo-Proklos gewesen sein. Sie wurde angeblich von Marsilio Ficino (1433–1499) übersetzt, was aber nicht belegt ist.1 Allerdings lässt sich Pseudo-Proklos’ Sphaera, wie im Kapitel über die Autorschaft erläutert, frühestens auf das späte 15. Jahrhundert datieren, während Petrarca aus dem 14. Jahrhundert stammt. Es kann sich bei dieser Erwähnung auch um die Sphaera des Sacrobosco handeln, die das Standardlehrbuch zur Kosmologie seit dem 13. Jahrhundert war.
In Mittelalter und Renaissance ist der Neoplatoniker Proklos, dem die Sphaera zugeschrieben wird, neben der Elementatio theologica v. a. durch seine Kommentare, klaren Zusammenfassungen und Bearbeitungen traditioneller Werke bekannt;2 hier fügt sich die Sphaera als kurzer Lehrbuchtext gut ein. Über lange Zeit steht die Rezeption der metaphysisch-theologischen Werke im Mittelpunkt, während die eher naturwissenschaftlichen Werke des Proklos kaum Beachtung finden. Proklos wird ab dem 12. Jahrhundert im lateinischen Europa einem kleinen Kreis als „Physiker“, „als Metaphysiker“ und ab dem 13. Jahrhundert einem relativ großen Kreis bekannt. Ab dem 15. Jahrhundert erfährt das Interesse am Metaphysiker Proklos einen neuen Aufschwung und das Interesse an Proklos wächst zunehmend über den Bereich der Metaphysik hinaus. Das ab den Moerbeke-Übersetzungen (13. Jahrhundert)3 fast ausschließlich philosophische Interesse an Proklos wird zu astronomisch-philologisch-hermeneutischem Interesse.4
Proklos gilt in der Renaissance als Vermittler des Neoplatonikers Plotin (205–270, indirekt), des Platon, des Ptolemaios und des Euklid. Er dient der Verteidigung der Astronomie als Disziplin, z. B. bei Simon Grynaeus (1493–1541), Francesco Barozzi,5 und der Versöhnung mit Aristoteles.6 Ein wichtiger Schritt in diese Richtung kann die neue, intensive Beschäftigung mit dem platonischen Timaeus (365 v. Chr.) und dessen proklischem Kommentar (439 n. Chr.) sein. Schon im frühen Mittelalter ist Platons Timaeus der Inbegriff platonischer Weisheit. Gott als Schöpfer und Ordner des Kosmos wird als Inspiration für die Suche nach den Ursachen des Kosmos angesehen.7 Aber während sowohl bei den Original-Proklos-Texten als auch dem Proklos zugeschriebenen Texten im Mittelalter und in der Renaissance hauptsächlich die theologisch-humanistische Auslegung im Vordergrund steht, findet um die Mitte des 16. Jahrhunderts eine Wende zur praktischen Verwendung der Sphaera als Begleitung oder sogar Vorlage einer Instrumentenbeschreibung statt. Dennoch bleibt das literarische Interesse lebendig: So behalten die Übersetzungen den Anspruch auf dichterische Originalität bei, wie sich u. a. darin zeigt, dass sie die in der Sphaera zitierten Arat-Verse in eigener Versübersetzung wiedergeben.
5.1 Renaissanceblick auf Proklos und die ihm als authentisch zugeschriebenen Werke
Um Proklos in der Renaissance zu verstehen, muss man auch seine Rezeption im Mittelalter bis früher Neuzeit kennen. Im Mittelalter ist Proklos v. a. durch seine theologisch-metaphysischen Texte bekannt. Dabei ist die Zuschreibung falscher Werke zu Proklos kein Einzelfall, sondern ein häufiges Phänomen in dieser Zeit. Proklos gilt als letzter Universalgelehrter der Antike und als einer der bedeutendsten Vertreter des Neoplatonismus. Seine Werke sind nicht innovativ, aber in Mittelalter und Renaissance durch seine intelligenten Zusammenfassungen und seine Kritik traditioneller Ansichten berühmt.8 Auch wird er als vom vorgeblichen Paulusschüler (Pseudo-)Dionysios Areopagita (6. Jh. n. Chr.) beeinflusst aufgefasst. Im 16. Jahrhundert herrscht die Meinung vor, wie bereits im Kapitel über die Autorschaft erwähnt, dass Proklos aus dem 2. Jahrhundert n. Chr. stamme. Die Renaissance-Gelehrten Johannes Stöffler, Jakob Ziegler, Francesco Barozzi, Petrus Ramus und Johannes Hagius übernehmen diese falsche Datierung (vgl. die Einleitung).9
Eine indirekte Übertragung des Proklos ins „Christliche“ entsteht durch die um 500, kurz nach Proklos’ Tod verfassten Werke, die dem Apostelschüler Dionysios vom Areopag (Areopagus), auch „Areopagit“ genannt (1. Jh. n. Chr.), zugeschrieben werden. Tatsächlich stammen sie aber von einem unbekannten christlichen Autor, der für seine theologischen Texte proklisches Gedankengut aus den Elementen der Theologie verwendet (Corpus Dionysiacum). Im 9. Jahrhundert wird Pseudo-Dionysios im lateinischen Westen bekannt und sogleich wirksam (Johannes Scottus Eriugena). Die größte Wirksamkeit entfaltet das sog. Corpus Dionysiacum10 im 12. und 13. Jahrhundert. Zentrale Denker wie Albertus Magnus (1200–1280), Thomas von Aquin (1225–1274) und viele andere verfassen Kommentare zu einzelnen Werken des Proklos. Bis ins 15. Jahrhundert bleibt der Areopagit eine zentrale Figur der Philosophie und Theologie des Abendlandes. Dabei ist (nach anfänglichem Zweifeln im Moment des Erscheinens der Werke kurz nach 500) die Authentizität des Corpus und die Abhängigkeit des Proklos von Dionysios unumstritten. Proklos gilt noch für Cusanus als Nachfolger des Dionysios, welchen er für den Apostelschüler hält.11 Erst Lorenzo Valla (ca. 1406–1457) stellt das Gegenteil fest, dass nämlich Dionysios von Proklos abhängig sein muss, v. a. in seiner Himmlischen Hierarchie, und nicht der Apostelschüler sein kann.12
Eine weitere indirekte Proklos-Überlieferung stellt der anonyme Liber de causis dar, der wohl im 9. Jahrhundert in Bagdad entstanden ist und ca. 1167 von Gerhard von Cremona (1114–1187) aus dem Arabischen ins Lateinische übersetzt wird.13 Zuerst wird dieser Text in der ersten Hälfte des 13. Jahrhunderts dem Aristoteles zugeschrieben und in den Pariser Lehrplan der Artistenfakultät integriert. Der Liber de causis ist eine Verarbeitung des Anfangs von Proklos’ Stoicheiosis theologike, was aber erst durch den Liber de causis-Kommentar des Thomas von Aquin (1272) bekannt wird.14 Thomas verwendet die 1268 durch Wilhelm von Moerbeke übersetzte Stoicheiosis theologike, um Vergleiche zwischen diesem Text und dem Liber de causis anzustellen.15 Möglich werden die direkten Übersetzungen von proklischen Texten durch den vierten Kreuzzug, der 1204 zur Eroberung Konstantinopels durch die Kreuzfahrer führt. Im Gefolge dieser Ereignisse kommt es zu einer Flut direkter Übersetzungen zahlreicher wichtiger Schriften aus dem Griechischen, die bislang entweder nur über den Umweg arabischer Texte oder noch gar nicht bekannt sind. Zu den bis dahin kaum namentlich bekannten Autoren gehört Proklos. Das Liber de causis ist dem ganzen Mittelalter ein zentraler philosophischer Text und auch noch Cusanus (Ms. Kues. 195, Bl. 1–34v.), Ficino und Pico bekannt.16 Seine Prominenz nimmt ab, als Proklos’ Elementatio theologica (Stoicheiosis Theologike) zugänglich wird.17
Pseudo-Proklos’ Sphaera wird dagegen noch übersetzt, nachdem ihre Zugehörigkeit zu Geminos bekannt ist. Michael Psellos fügt im 11. Jahrhundert in seinen Schriften mehrere Proklos-Werke oder Exzerpte aus Proklos’ Schriften ein, darunter De sacrificio et magia, De philosophia Chaldaica und den Kommentar zu Plotinus.18 De sacrificio et magia, auch Heilkunst genannt, entnimmt Psellos aus einem größeren Werk des Proklos namens Orpheus, Pythagoras und Platon über die chaldäischen Orakel, das heute verloren ist.19 Im 16. Jahrhundert wird Psellos an Proklos herangerückt: Die Sphaera-Übersetzung des Élie Vinet wird mit dem Quadrivium des Psellos gedruckt, einer Zusammenfassung der Arithmetik, Geometrie und Musik, wobei die Sphaera den Teil für Astronomie einnimmt; heute gilt dieser Text als pseudepigraphische Schrift.20 In seinem Programm für das Collège de Guyenne in Bordeaux Schola Aquitanica (Bordeaux, 1583)21 schreibt Vinet, dass aufbauend auf Psellos’ Quadrivium die Elementa Euklids und sphärische Astronomie (Sphaerica) unterrichtet werden.22 Mit dem letzten Werk muss Vinet die Sphaera des Sacrobosco meinen,23 weil Pseudo-Proklos’ Sphaera ja schon in den vier Disziplinen (Quadrivium) enthalten ist.
Schon im Mittelalter ist Proklos als Autor kurzer und übersichtlicher Kommentare bekannt, wofür im 16. Jahrhundert auch die Sphaera gelobt wird. Im 12. Jahrhundert wird Proklos’ Elementatio Physica oder De motu von einem anonymen Übersetzer, der in Salerno Medizin studiert hat, am sizilianischen Hof aus dem Griechischen ins Lateinische übersetzt.24 De motu enthält Propositionen und Beweise nach dem Vorbild Euklids und behandelt die aristotelische Bewegungslehre.25 Von dieser Übersetzung sind sieben Handschriften vor dem 14. Jahrhundert erhalten, eine davon aus dem Besitz von Berthold von Moosburg (†1361).26 Berthold erklärt in seiner Expositio der Elementatio theologica, Propositio 50, dass in Aristoteles’ Physik, Buch VI und in Proklos’ Elementatio physica dieselbe Art von Bewegung dargestellt würde, nämlich die Bewegung des primum mobile bzw. der Himmelskörper.27 Der Hauptverdienst von Proklos’ Version des Aristoteles liegt in seiner Kürze und seiner übersichtlichen Zusammenfassung von Aristoteles’ Physik, Buch VI und VII, und von De Caelo in 52 Propositionen.28 Proklos’ De motu besitzt also durch seine Übersichtlichkeit eine Parallele zur kurzen Schrift Pseudo-Proklos’ Sphaera.
In der Renaissance sind die Hauptrezipienten des Proklos der deutsche Universalgelehrte Nikolaus von Kues oder Nicolaus Cusanus (1401–1464) und der italienische Humanist Marsilio Ficino an der Akademie von Florenz. Auch nehmen Proklos’ Werke Einfluss auf Johannes Kepler.
Das früheste Werk, in welchem Cusanus den Proklos zitiert, ist De beryllo (1459) über das optische Instrument „Beryll“ („Brille“), das als Analogie für Gegensätze dient.29 Auch im Kommentar zu Pseudo-Proklos’ Sphaera von Johannes Stöffler (Tübingen, 1534) wird der „Beryll“ erwähnt, allerdings hier in der Bezeichnung eines Edelsteins, mit dem das Sphaera-Werk wegen seiner geringen Größe verglichen wird. Cusanus stellt, beeinflusst von Proklos, das „Eine“ als Prinzip dar, das dem anderen „Vielfalt hervorbringenden Einen“ übergeordnet ist: die „absolute Negation“.30 In Cusanus’ Besitz ist auch Sacroboscos Sphaera, die ohne Autorangabe im Katalog des Cusanusstifts in Bernkastel-Kues erwähnt wird. Allerdings wird Pseudo-Proklos’ Sphaera nicht genannt.31 Im 15. Jahrhundert beginnt Ambrogio Traversari (1386–1439) im Auftrag des Cusanus eine Übersetzung von Proklos’ Theologia Platonis ins Lateinische, die er aber wegen seines Todes nicht vollendet.32 Eine vollständige Übersetzung fertigt im Jahre 1462 Petrus Balbus Piscanus (1399–1479) an, Bischof von Tropea33 und Georg von Trebizund (1395–ca. 1484) übersetzt in Cusanus’ Auftrag Proklos’ metaphysischen Parmenides-Kommentar.34
In den postum herausgegebenen Opera (Basel, 1576)35 sind Ficinos Übersetzungen der philosophischen Schriften De re publica mit Kommentar (ms. Chisian. R VIII 58, 13. Jahrhundert),36 De sacrificio et magia37 und des Alkibiades-Kommentars38 enthalten. Die letzten beiden Übersetzungen werden mit Jamblichs’ (um 245–um 325) De mysteriis (3./4. Jh. n. Chr.) 1497 bei Aldus Manutius in Venedig gedruckt, der auch zwei Jahre später Pseudo-Proklos’ Sphaera herausgibt.
Ficino ist der Gründer der „Platonischen Akademie“ (der Begriff stammt erst aus dem 17. Jahrhundert), die ab 1463 ihren Sitz in einem Landhaus in Careggi (Florenz) hat, ein Geschenk des Cosimo de’ Medici (1389–1464). Ihre Mitglieder sind nicht nur neoplatonisierende Philosophen, sondern auch Dichter. Ficino selbst strebt danach, durch Kommentare die Texte Platons und der Neoplatoniker in christlicher Weise auszulegen und ins Lateinische zu übersetzen.39 Um 1464 übersetzt Ficino den Kommentar des Proklos zu Platons Parmenides, versieht ihn mit einer Einführung und verfasst nach 1492 selbst einen Parmenides-Kommentar unter Verwendung des Proklos in Moerbekes Übersetzung.40 Auch verwendet Ficino Proklos’ Timaios-Kommentar für seinen eigenen Timaios-Kommentar und für seine Theologia Platonis.41
In der Renaissance gilt Proklos allgemein als Verteidiger Platons gegenüber Aristoteles.42 Die Kontroverse um Platon und Aristoteles prägt das 15. Jahrhundert. Georgios Gemistos Plethon aus Konstantinopel
In der Kunst spielt Platons Timaeus in Raffael von Urbinos
Der italienische Philosoph Pico della Mirandola verwendet Proklos’ Elementatio theologica in seinen Conclusiones nongentae („900 Thesen“).51 Dieses Werk stellt eine Versöhnung aller bekannten Philosophien dar, darunter mit platonischen Thesen, dem Liber de causis und u. a. mit mathematischen Fragen und magischen Thesen.52
Keplers Konzept der harmonikalen Kosmologie ist hauptsächlich von Proklos’ Euklid-Kommentar geprägt. In seinem Werk In Harmonice Mundi („Weltharmonie“, 1619) verweist Kepler auf Proklos’ Hymne an die Sonne, wenn er schreibt, dass die Sonne der Sitz des Nous und des Schöpfers sei. Im ersten Buch von In Harmonice Mundi erwähnt Kepler Proklos’ Prinzipien „Begrenzung“ (Form) und „Unbegrenztes“ (Materie) der geometrischen Dinge.53 Proklos hält hier das wirkliche Sein der Dinge für den Gegenstand der Astronomie statt fiktiver geometrischer Konstruktionen wie die Epizykel-Konstruktion der Spätantike. Dazu passt Pseudo-Proklos’ Hinweis in der Sphaera, dass Kreise nur durch den Verstand, nicht durch die Sinne wahrnehmbar seien.
Im Streit um die Beziehung zwischen Mathematik und materiellem Sein kommt der Italiener Pietro Catena, der eine italienische Übersetzung mit Kommentar von Pseudo-Proklos’ Sphaera verfasst hat (Padua, 1565), zu dem Schluss, dass sich die mathematische Wissenschaft nach Euklid (und nach Proklos’ Kommentar zu Euklid) von der aristotelischen grundlegend unterscheide, und definiert sie in seiner Oratio pro idea methodi (Padua, 1563) als autonome Wissenschaft.54
Mit den frühen Drucken tritt eine weitere Facette des Proklos in den Vordergrund: Im Jahre 1497 erscheinen bei Aldus Manutius in Venedig Proklos’ De sacrificio et magia und sein Kommentar zum Alkibiades in Marsilio Ficinos Übersetzung mit anderen philosophischen Schriften. Proklos’ Hymnen werden mit Johannes Lascaris’ Orphica Argonautica in Florenz gedruckt (1500). In dieser Zeit scheint sich auch das allgemeine Interesse vom „metaphysischen Proklos“ zum im weitesten Sinne „naturbetrachtenden Proklos“ zu verschieben, denn kurz nachdem die frühesten Handschriften der Sphaera Ende des 15. Jahrhunderts erschienen sind, wird um 1499 in Venedig sogleich der erste Druck sofort auf Griechisch-Latein mit der Übersetzung Linacres und mit dem ebenfalls griechisch-sprachigen Arat-Text herausgegeben.
Die Sphaera ist also um 1499 nicht das erste gedruckte, dem Proklos zugeschriebene Werk, wohl aber das erste seiner mathematisch-astronomischen Werke (vgl. Tabelle 5.1). Wie aus dieser Tabelle hervorgeht, werden Proklos’ andere Schriften hauptsächlich in Basel gedruckt. Bei Simon Grynaeus erscheint Proklos’ zweibändiges Werk De motu oder Institutio physica (1531). Im Jahre 1533 wird der Euklid-Kommentar auf Griechisch bei dem deutschen Humanisten Grynaeus herausgegeben, auf Latein im Jahre 1560 bei Francesco Barozzi in Padua. Ebenfalls in Basel erscheinen Proklos’ Kommentar zum Timaeus und zur Politeia bei Johann Walder (1534) und Proklos’ Hypotyposis (die auch in der ältesten Handschrift Mut. mit der Sphaera in Vallas Besitz war) in Giorgio Vallas Übersetzung mit Ptolemaios’ Geographie, herausgegeben von Erasmus Oswald Schreckenfuchs bei Heinrich Petri (1551). Proklos’ Paraphrasis in quattuor Ptolemaei libros de siderum effectionibus wird mit einem Vorwort Philipp Melanchthons bei Johann Oporinus (1507–1568; 1554) gedruckt. Die Paraphrase ist nicht zu verwechseln mit dem anonymen Kommentar zu Ptolemaios’ Tetrabiblos, der in der Renaissance dem Proklos zugeschrieben und 1591 bei Heinrich Petri in Basel gedruckt wird.55 Der letzte ist anonym und zitiert einzelne Worte aus Ptolemaios’ Text mit Erklärungen, während die Paraphrase einen zusammenhängenden Traktat darstellt; inhaltlich sind die beiden Texte aber fast identisch.
Im späten 16. und im 17. Jahrhundert erscheinen Proklos’ Schriften auch in anderen Städten. In Ferrara wird Proklos’ Elementa theologica et physica (Dominicus Mamarellus, 1583) gedruckt, in Bremen De significationibus eclipsium (bei Bernhard Peters, 1592), in Hamburg und Frankfurt die Theologia Platonica (Rulandius, 1618) und in Leiden Proklos’ Paraphrase von Ptolemaios’ Tetrabiblon (Elzevir, 1635).
| Jahr | Ort, Drucker | Titel | Sprache |
|---|---|---|---|
| 1497 | Venedig: Aldus Manutius |
In Platonis Alcibiadem | Latein, übers. v. Marsilio Ficino |
| 1528 | Basel: Thomas Wolff |
De fide, in: Antidotum contra haereses, S. 176–181 | Griech.-Lat., übers. v. Dionysius Exiguus |
| 1531 | Basel: Johann Bebel |
De motu | Griechisch |
| 1532 | Basel: Michael Isengrin |
In Alcibiadem. De sacrificio et magia | Latein, übers. v. Marsilio Ficino |
| 1533 | Basel: Simon Grynaeus |
In Euclidis elementorum librum I | Griechisch |
| 1534 | Basel: Johann Walder |
In Timaeum. In rem publicam | Griechisch |
| 1537 | – | Scholia in Homerum | – |
| 1541 | Basel: Heinrich Petri |
Hypotyposis astronomicarum positionum. Ptolemaei Geographia | Griechisch |
| 1542 | Paris: Jakob Bogard |
De motu | Griechisch |
| 1551 | Basel: Heinrich Petri |
Hypotyposis. Ptolemaei Geographia | Latein, übers. v. Giorgio Valla |
| 1554 | Basel: Johann Oporinus |
Paraphrasis in quattuor Ptolemaei libros de siderum effectionibus | Griechisch |
| 1560 | Paris: Guilelmus Morelius |
De liturgia | Griechisch, hg. v. Claudio de Sainctes |
| 1560 | Padua: Percacino |
In Euclidis elementorum librum I | Latein, übers. v. Francesco Barozzi |
| 1562 | Basel: Perna |
De motu | Latein, übers. v. Josef Waldanius |
| 1576 | Basel: Henricpetri |
Opera | Latein, übers. v. Marsilio Ficino |
| 1577 | Paris: Federicus Morellus |
De conscribendis epistolis | Griechisch |
| 1583 | Ferrara: Dominicus Mamarellus |
Elementa Theologica et Physica | Latein, übers. v. Francesco Patrizi |
| 1591 | Basel: Heinrich Petri |
Commentaria in Tetrabiblon | Griechisch |
| 1592 | Bremen: Bernhard Peters |
De significationibus eclipsium | Griechisch |
| 1496 | Florenz: Lorenzo d’Alopa |
Timaeus | Latein, übers. v. Marsilio Ficino |
| 1497 | Venedig: Aldus Manutius |
In Alcibiadem; De sacrificio et magia | Latein, übers. v. Marsilio Ficino |
| 1590 | Frankfurt: apud Andreae Wecheli haeredes Claudium, Marnium et Iohannem Aubrium |
Chrestomathia | Griech.-Lat., übers. v. Andrea Schotto, Komm. v. Petri Johann Nunnesius |
| 1618 | Hamburg/Frankfurt: Aemilius Portus |
Procli In Platonis Theologiam libri sex | Griechisch, Hg. Aemilius Portus |
| 1635 | Leiden: Elzevir |
Paraphrasis in Ptolemaei Tetrabiblion | Griechisch |
| 1565 | Paris: Charles Perier |
Deux livres de Proclus du mouvement | Französisch, übers. v. Pierre Forcadel de Beziés |
Tab. 5.1: Die Erstausgaben von Proklos’ Werken im 15. und 16. Jahrhundert (vgl. Hoffmann 1845).
Tab. 5.1: Die Erstausgaben von Proklos’ Werken im 15. und 16. Jahrhundert (vgl. Hoffmann 1845).
5.2 Andere Werke des Proklos in der Renaissance im Vergleich zu Pseudo-Proklos’ Sphaera
Nachdem der Inhalt der Sphaera nicht eindeutig als „proklisch“ gedeutet werden kann (vgl. das Kapitel zum Inhalt der Sphaera), soll dieses Kapitel zeigen, ob die Autorität des Proklos für die Verbreitung des Sphaera-Werkes eine Rolle gespielt hat. Dazu gehört die Frage, ob die Sphaera mit den Proklos-Werken Überschneidungen aufweist und als Vorbereitung auf komplexere Prokloswerke dienen kann. Inhaltlich gehört die Sphaera weniger zu Proklos’ metaphysischen als zu dessen mathematischen und physikalischen Werken wie der Hypotyposis und der Elementatio Physica, mit denen sie aber in der frühen Neuzeit nie gedruckt oder gelehrt wird (Ausnahme: die Handschrift Mut.).
Neben seinen Platonkommentaren schreibt Proklos philosophische Werke wie die Elemente der Theologie (στοιχείωσις θεολογική) und die Platonische Theologie (Περὶ τῆς κατὰ Πλάτωνα θεολογίας), außerdem mathematische und astronomische Werke: einen Kommentar zum ersten Buch der Elemente Euklids (Εἰς τὸ α’ τῶν Εὐκλείδου στοιχείων), die kurze Darstellung der astronomischen Hypothesen (῾Υποτύπωσις τῶν ἀστρονομικῶν), eine Paraphrase zu Ptolemaios’ astrologischer Tetrabiblos, ein astrologisches Werk über die Eklipsen (De Eclipsibus) und eine Einführung in die Physik (Στοιχείωσις φυσική), die eine Zusammenfassung von Aristoteles’ Physik und dem ersten Buch von Aristoteles’ De Caelo darstellt. Außerdem schreibt Proklos ein Werk Über die Vorsehung (Περὶ τῆς προνοίας), Über die Existenz des Bösen (Περὶ τῆς τῶν κακῶν ὑποστάσεως) sowie weitere Abhandlungen und Hymnen. Der Suda zufolge soll Proklos auch einen Kommentar zu Homers Epen und zu Hesiods Werken und Tagen,56 grammatische Schriften und den Angriff über die Ewigkeit der Welt gegen die Christen (Epicheiremata) geschrieben haben, der nur teilweise erhalten ist.57
Die astronomischen Werke des Proklos (wie auch in gewissem Maße der Euklid-Kommentar) behandeln alle die parallelen Kreise der Sphaera, die Himmelsachse und die Himmelspole, weshalb man die Sphaera für Proklos’ Werk halten kann (aber nicht zwangsläufig). Im Euklid-Kommentar definiert Proklos z. B. die Achse, die auch in der Sphaera vorkommt: „Der Durchmesser der Sphäre wird ,Achse‘ genannt“ (S. 124, Definition XVII, 156). In seinem Vorwort stellt Euklid den nördlichen Himmelspol und die allgemeinen Kreise auf der Himmelsphäre dar, die auch in der Sphaera vorkommen, nämlich die Parallelkreise, die Ekliptik, den Horizont und die Milchstraße. Auch stellt er, wie in der Sphaera erläutert, die arktischen und antarktischen Kreise relativ zu ihrer gegebenen Lokalität vor und erläutert die Teilung der Sterne in jene, die nie aufgehen, jene, die auf- und untergehen, und jene, die nie untergehen.58 Ferner beschreibt Proklos im Euklid-Kommentar den Kosmos sowohl geometrisch als auch philosophisch: „Die Sphären sind Gleichnisse der vollkommenen Gottheiten, die das Beginnen und Enden verbinden und alle anderen Figuren in Einfachheit, Gleichförmigkeit und Vollkommenheit übertreffen“ (Definition I, 90–91). Stöffler unterscheidet die Sphaera von Proklos’ Fabrica astrolabii darin, dass letztere eine Fläche bzw. ein Planisphaerium beschreibe, während die Sphaera eine Kugel darstelle.59 Pseudo-Proklos’ Sphaera wird hier also mit einer anderen Instrumentenbeschreibung des authentischen Proklos verglichen bzw. von ihr abgegrenzt.
Die Hypotyposis ist eine Auseinandersetzung mit Ptolemaios’ Almagest60 und behandelt das System der Exzenter und Epizykel des Ptolemaios, der eine mathematische Erklärung für die Anomalien in den Bewegungen der Himmelskörper geben will. Proklos bestätigt die Motive, die zu ihrer Konstruktion führen, und gibt dieses Wissen an seine Studenten weiter; das letzte Kapitel der Hypotyposis heißt De astrolabio. Auch einige Kommentare zur Sphaera werden als Konstruktion der Armillarsphäre aufgebaut (z. B. Stöffler, Ziegler, Anonymus Hauniensis). Die ältesten Handschriften der Hypotyposis stammen aus dem 15. Jahrhundert. Der erste vollständige Druck erscheint 1540 bei Johann Walder in Basel. Zuvor übersetzt schon Giorgio Valla Teile der Hypotyposis in seinem De expetendis et fugiendis rebus (Venedig, 1501).61 Die Paraphrase zu Ptolemaios’ Tetrabiblos stellt eine Umformulierung von Ptolemaios’ Tetrabiblos durch Proklos dar und behandelt im Gegensatz zur Sphaera die Aspekte der Planeten und ihre Auswirkungen auf irdische Dinge, ihre Eigenschaften (Geburt, Reichtum, Krankheit) sowie ihre Korrelation zwischen den Erdzonen und den Sternen. Auch die Sphaera behandelt die Konstellationen und die Erdzonen und kann dadurch als eine Einführung zur Tetrabiblos fungieren. In einer anderen Schrift des Proklos De Eclipsibus kommen die Sternzeichen vor, welche die Sphaera behandelt: das Werk diskutiert die Bedeutungen der Sonnen- und Mondfinsternisse für menschliche und irdische Belange, wenn sie in den Zeichen des Tierkreises auftauchen. Proklos’ Schrift Uranodromos („Himmelslauf“), von der nur zwei Fragmente in byzantinischen Handschriften (also vor Pseudo-Proklos’ Sphaera) erhalten sind, ähnelt der Sphaera als ein Traktat über die Sterne und den Tierkreis.62
In der Sphaera werden die „Sphären“, wie schon im Kapitel zum Inhalt gesagt, nicht näher definiert. In Proklos’ Kommentaren zum Timaeus und zur Re publica gelten sie als physikalische Regionen, in denen die Planeten sich bewegen. Aus metaphysischer Sicht werden sie bei Proklos von ihrer herrschenden Macht (δύναμις κρατική) bewegt, also vom Intellekt (νοήσεις) der Sterne.63 Wo die Sphäre sichtbar ist, wird sie σφαιροειδής genannt. Dieser Begriff kommt auch in Pseudo-Proklos’ Kap. 14 vor, bezogen auf die Erdsphäre.64 Im Timaios-Kommentar nennt Proklos außerdem die drei Argumente Platons dafür, dass der Kosmos eine Sphäre sei: 1. das Eine oder Eins (ἕν), 2. das Schöne (καλλόν) und 3. das Verwandte (συγγενές, Tim. 33b). Das Gute sei Eins und da der Kosmos gut sei, müsse auch er Eins sein. Die Sphäre sei die schönste und vollständigste aller Formen, weil sie alle anderen Formen enthalte. Nur diese Form könne dem vollkommenen Kosmos entsprechen. Der Kosmos sei sich selbst ähnlich und mit seinem Vorbild (παράδειγμα) verwandt. Dieses Vorbild sei die Charakteristik des Kosmos, d.h. die Kreisform, die der Kosmos mit der Planetenbewegung wieder und wieder produziere. In der Planetenbewegung um einen Punkt liege ein anderer Beweis des kreisförmigen Kosmos. Die Kreisbewegung der Sonne z. B. sei durch den Wechsel von Tag und Nacht und die Bewegung der Schatten erkennbar. Aus physikalischer Sicht (φυσικῶς) würde es Leerstellen geben (κενόν), wenn die Sphären Ecken hätten, was nicht möglich sei.
Durch diese philosophische Beschreibung des Kosmos, des Demiurgs, des Weltkörpers, der Weltseele und der Seelenwanderung ist der Timaios-Kommentar ein grundlegend anderes Werk als die Sphaera. Ferner kommt dem Timaios eine metaphysische Komponente zu, mit der Proklos die Lehre Platons von den vollkommenen Kreisbewegungen des Himmels gegen die beobachtbaren unregelmäßigen Bewegungen der Planeten zu verteidigen versucht.65 Methodisch kommen Etymologien wie in der Sphaera auch in Proklos’ Kommentaren zum Cratylus und zum Timaeus vor. Im Cratylus beschreibt Proklos die Etymologien: Der Name Cratylus stamme von dem Verb κρατεῖν („befehlen“), weil er über Heraklits Lehre „befehle“. „Sokrates“ sei ein Retter (σωτήρ), weil er die Macht der Seele bewahre.66 Etymologien der Götter Zeus, Kronos, Uranos und von „Gott“ allgemein nennt Proklos mit dem Ziel, Aristoteles’ Sprachtheorie durch eine platonische zu ersetzen.67
Abschließend lässt sich sagen, dass die Sphaera keinen Gegensatz zu Proklos’ anderen Werken bildet, sondern sich in sein mathematisch-astronomisches Repertoire einfügt, das die komplexen Werke Platons und Euklids vereinfacht. Ferner bildet die Sphaera aus Sicht der Gelehrten in der Renaissance speziell Proklos’ geometrisch-astronomische Interessen ab.
5.3 Die Sphaera
5.3.1 Die Lehre der Astronomie
Das Fach Astronomie gehört zum Quadrivium, die Fächer Griechisch (ab 1387 in Florenz) und Latein zum Grammatikunterricht innerhalb des Triviums der septem artes liberales, die als Grundstudium für die weiterführenden Studiengänge Theologie, Jurisprudenz und Medizin dienen (wie schon in der Einleitung erwähnt). Das Wissen über den sphärenförmigen Kosmos gehört also zum kanonischen Allgemeinwissen eines studierten Menschen und wird auch für Zeitrechnung und Messungen benötigt, die besonders in der Theologie zur Bestimmung des Osterdatums und in der Medizin zur Behandlung von Patienten dient. Im Grammatikunterricht der Renaissance werden neu entdeckte griechische Autoren wie Pseudo-Proklos übersetzt (vgl. das Kapitel Kapitelnamen und Begriffe).
Was die Astrologie angeht, so ist sie ab der Mitte des 15. Jahrhunderts, v. a. aber im 16. Jahrhundert im Kanon des Quadriviums der artes liberales verankert. Die Astrologie hat lange Zeit vor der Astronomie Vorrang, bzw. gilt letztere als Hilfswissenschaft der Astrologie. Denn die Astrologie spielt bis in die zweite Hälfte des 16. Jahrhunderts eine wichtige Rolle innerhalb des universitären Fächerkanons, wie z. B. in der Medizin (Iatromathematik). Zur Zeit Johannes Keplers aber wird die Astrologie zunehmend aus der akademischen Naturwissenschaft ausgegliedert, bis sie mit der Aufklärung im 18. Jahrhundert nicht mehr als wissenschaftliches Fach vertreten wird. Ein bedeutender Vertreter der Naturwissenschaft im 16. Jahrhundert ist Nikolaus Kopernikus, ein Mathematiker, Astronom und Doktor der Medizin in Italien, der Dank seiner theologischen Ausbildung auch des Lateinischen und Griechischen mächtig ist.68
Zwar steht die humanistische Bewegung ursprünglich abseits von den Universitäten, doch sind Humanisten akademische Lehrer.69 Aus Italien kommend ist der Humanismus im Nordeuropa des 15. Jahrhunderts nur partiell vorhanden. Zuerst werden in Wien um die Mitte des 15. Jahrhunderts an der Artistenfakultät Vorlesungen über lateinische Klassiker wie Terenz oder Pseudo-Ciceros Rhetorica ad Herennium gehalten, und über Renaissancegelehrte wie Philipp Mautter aus Stockerau
An den Universitäten werden die studia humanitatis zuerst von Grammatik- und Rhetorikprofessoren gelehrt, die zu den Grundfächern der artes Geschichte, Dichtung und Moralphilosophie hinzufügen.71 Grammatik ist Grundlagenfach der artes und enthält Logik, Rhetorik und Literatur (Poesie). Bis ins 12. Jahrhundert werden Priscians Institutiones (um 500 n. Chr.) und Donats Ars minor (320–380 n. Chr.) unterrichtet.72 Im 13. Jahrhundert lehrt man, besonders in Paris, im Fach Grammatik über die neu übersetzten Schriften des Aristoteles, darunter die Analytica posteriora, De anima und die Metaphysik.73 Im 15. Jahrhundert gewinnt die von Moerbeke bereits 1278 übersetzte Poetik an Bedeutung.74 An norditalienischen Schulen werden um 1450 innerhalb der studia humanitatis, in Rhetorik Ciceros Epistulae ad familiares, in Poesie Vergils Aeneis und in Geschichte Caesars (100–44 v. Chr.) De bello Gallico gelesen.75
Im mathematischen Unterricht der Renaissance mag die Sphaera als Einführung zu Proklos’ Stoicheiosis physike undHypotyposis gedient haben, die sich mit den Planetenbewegungen beschäftigen. Dafür spricht, dass die Sphaera in der ältesten griechischen Handschrift (Ende 15. Jahrhundert) mit Proklos’ Hypotyposis kombiniert wird (Modena, Biblioteca Estense, Gr. 24).76 An nordeuropäischen Universitäten dienen im Spätmittelalter Mathematik, Astronomie und Grammatik als Grundlage der Logik, Physik und Metaphysik. Auch Sacroboscos’ Sphaera wird als Lernhilfe für die Physik verwendet,77 vielleicht so auch Pseudo-Proklos’ Sphaera. Pietro Catena oder Élie Vinet lehren über Pseudo-Proklos’ Sphaera und über Euklids Elementa, weshalb nicht auch über Proklos’ Kommentar zu Euklid?78 Weitere Lernorte der Sphaera in Astronomie sind Paris (Vinet), Augsburg (Henisch), Wien (Georg Tannstetter), Wittenberg (Rheticus), Freiburg und Basel (Schreckenfuchs).79 Daneben wird Pseudo-Proklos’ Sphaera im 16. Jahrhundert aber auch als Griechisch- und Lateinlehrbuch verwendet (vgl. Abbildung 5.1).
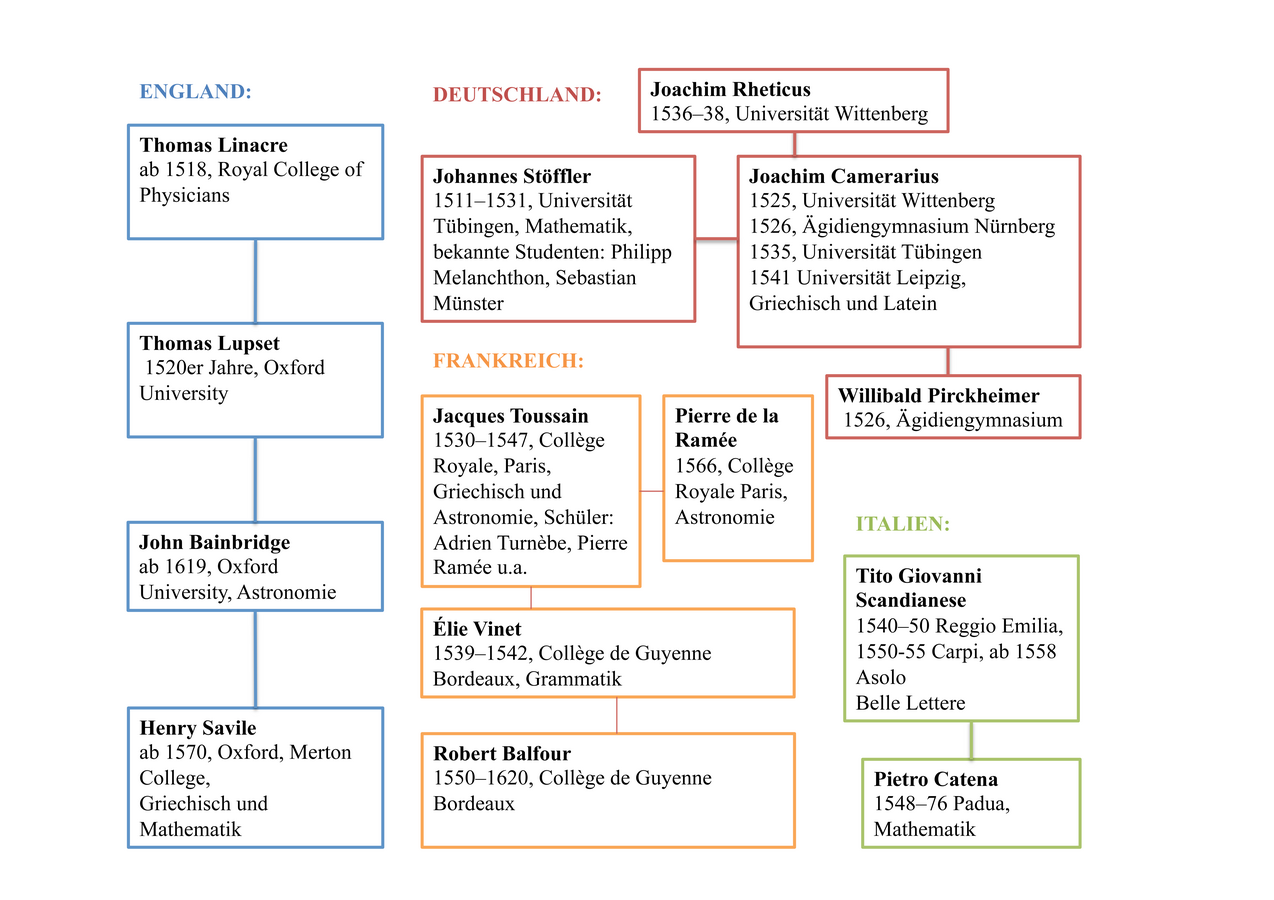
Um 1536–38 lehrt der Wittenberger Kopernikusschüler Rheticus zur Einführung in Astronomie (für Bakkalaureanden) über Sacroboscos Sphaera und über den Computus ecclesiasticus (kirchliche Kalenderrechnung).80 Für fortgeschrittene Magistranden ist Erasmus Reinhold (1511–1553) zuständig, der über Proklos’ Kommentar zu Euklids Elementa, Johannes de Muris’ (um 1300–um 1360) Arithmetik und Speculum Musicale oder Georg Peuerbachs Theorica Planetarum lehrt.81 Aus seiner Vorlesung über Al-Farghani geht hervor, dass Rheticus abwechselnd über Pseudo-Proklos und über Al-Farghani lehrt.82 In seine Interpretation von Pseudo-Proklos’ Sphaera lässt Rheticus zwar nicht die kopernikanische Lehre einfließen, weil sie in Wittenberg verboten ist. Jedoch umgeht Rheticus im Jahre 1541 das Verbot durch eine Vorlesung über Ptolemaios’ Megale syntaxis, die viele Anknüpfungspunkte zu Kopernikus’ Werk bietet.83 Dantis Lehre teilt sich nach dem Vorbild von Pisa in drei Jahre :84 Im ersten Jahr lehrt er die Grundlagen der Kosmographie (Pseudo-Proklos’ Sphaera), also die Sphären der Planeten und Konstellationen, im zweiten und dritten Jahr die „Anwendungen der Mathematik“ bzw. die scientiae mediae. Die letzten diskutiert Danti im Proöm des Trattato del radio latino (Rom, 1583), ein Nachschlagewerk für Studenten.85 86 Auch im Vorwort seines Trattato della sfera ridotto in sette tavole (S. 18) zitiert Ziegler mehrmals Proklos’ Einteilung der mathematischen Disziplinen aus seinem Euklid-Kommentar und die Milchstraße aus Proklos’ Sphaera.
Außerdem wird Pseudo-Proklos’ Sphaera in der Sammlung von Astronomielehrbüchern (Lyon, 1531) des flämischen Lehrbuchautors Joachim Fortius Ringelbergius (Joachim Sterck van Ringelbergh
In De ratione studii bemerkt Ringelbergius, dass mathematisches Wissen nützlich sei für den Stil, wie man bei Cicero, Quintilian, Vergil, Ovid und Lukan sehen könne.89 Ringelbergius betrachtet also Astronomie sowohl als literarische als auch als mathematische Tätigkeit. Astronomie helfe, die Wegbeschreibungen der Sterne und Planeten in klassischen Werken zu verstehen und diese in den eigenen Werken nachzuahmen. Dabei sei jedes Buch wichtig wegen seiner Aussagen, Anekdoten und Verse.90 Um Firmicus zu verstehen, solle man vorher ein Bild von den Häusern des Horoskops aus den Ephemeriden zeichnen und die Grundlagen der „barbarischen Autoren“ lernen, am besten bei Alcabitius (al-Aziz ibn Uthman, † 967 n. Chr.). In Kosmographie solle man Ptolemaios, in Geographie Pomponius Mela (15–45 n. Chr.), in Geometrie Euklid lesen.91 Ringelbergius geht es um Vollständigkeit, denn selbst das beste Lehrbuch benötigt Ergänzungen.92 Außerdem erwähnt Ringelbergius Pseudo-Proklos’ Sphaera in dem Abschnitt Institutiones Astronomicarum, Buch 2, mit dem Fehler, dass der Stern Canopus in Alexandria ganz unsichtbar sei, wie Plinius und Proklos schreiben. In Buch 3 zitiert Ringelbergius Proklos’ Definition des arktischen Kreises durch seine Berührung in Griechenland mit dem vorderen Fuß der Bärin.93
Der französische Mathematiker Oronce Finé verwendet Vallas Enzyklopädie De expetendis et fugiendis rebus für seine Lehre am Collège Royale in Paris (1531–1555).
Wegen seiner antiken griechischen Sprache bietet sich Pseudo-Proklos’ Sphaera auch als Sprachlehrbuch an. Den Griechischlehrstuhl am Collège de Royal in Paris besetzt auf Geheiß von König Franz I. (1494–1547) im Jahre 1529 der französische Gelehrte Jacques Toussain,94 der dort als „lecteur royal“ bis 1547 Griechisch lehrt. Als Lehrbücher verwendet er Drucke von Christian Wechel, neben Pseudo-Proklos’ Sphaera (griechische Ausgaben in Paris: Wechel, 1531, 1536, 1542) auch Drucke literarischer Werke wie Musaeus’ Hero und Leander (Paris: Wechel, 1538),95 Dionysios Periegetes’ De mundo (Paris: Jean Loys, 1538), Hesiods Werke und Tage (Paris: Simon de Collies, 1538) und Xenophons Kyropädie, Buch II (Paris: Wechel, 1539).96 Wechel druckt auch andere Ausgaben von Pseudo-Proklos’ Sphaera in Paris. Der Kommentar des Toussain zur Sphaera ist seinen Griechischvorlesungen entnommen (ex Praelectionibus Iacobi Tusani Regii Graecarum literarum professoris, exceptae; Titel der Ausgabe von 1543). Die veröffentlichten 38 Anmerkungen scheinen wegen ihrer Knappheit nur eine Auswahl (ex praelectionibus) der Originalvorlesungen zu sein. Toussains Kommentar zu Pseudo-Proklos’ Sphaera wird 1543 und 1547 von Jacques Bogard gedruckt, für den Toussain selbst als Korrektor arbeitet. Die späteren Ausgaben werden durch Bilder bereichert (1560, 1562), um ein besseres Verständnis des Textes zu erzielen. Seine Kenntnisse aus der Sphaera verwendet Toussain für sein Lexicon graecolatinum (Paris, 1552).97 Über das Wort „schief“ (λοξός) schreibt er: „daher kommt ,ein schiefer Kreis wird der Tierkreis genannt‘, wie Proklos in seinem Traktat über die Sphäre schreibt“ (unde λοξὸς κύκλος ὁ ζωδιακὸς λεγόμενος, ut scribit Proclus in tractatu de sphaera). „Sphärisch“ (σφαιρικός, globosus), „kugelförmig“ wird für „Sitz der Sphäre“ (σφαιρικὴ θήκη) verwendet und zu „Pol“ (πόλος) „siehe nach in der Sphäre des Proklos“ (de quibus [...] vide in sphaera Procli).
Vinets Lehre über Euklids Elementa am Collège de Guyenne in Bordeaux bildet einen Gegensatz zur Lehre des Jesuiten Christopher Clavius (gedruckt in Rom, 1574) 98 am Collège Royale in Rom. Während Clavius an einer mathematischen Akademie für Spezialisten lehrt und dafür einen umfangreichen Euklid-Kommentar von 483 Seiten verfasst, schreibt Vinet kürzere Kommentare für ein breites Publikum (Bordeaux, 1575) und wählt kurze Originaltexte aus wie Pseudo-Proklos’ Sphaera mit sieben Seiten. In einem Brief an den Gelehrten Pierre Pithou (1539–1596) von 1583 (Bordeaux) äußert Vinet seine Meinung über den römischen Kollegen: „Clavius [...] verfasst Kommentare über das kleine Buch des Sacrobosco, länger als ein Tag ohne Brot [zu ertragen wäre]“.99 Bereits früher kritisiert Vinet im Vorwort zur revidierten französischen Übersetzung von Pseudo-Proklos’ Sphaera die Länge des Kommentars von Johannes Stöffler: „Stoefler, qui a fait sur ceste Sphaire des commentaires que trop grandes, cuide, que ce soit le Proclus de Lucie“ (Paris, 1573). Vinets Befürwortung kurzer Lehrtexte kann als Plädoyer für Pseudo-Proklos (und Vinets Kommentar zu diesem) gegen Clavius’ Sacrobosco gelesen werden. Vinets eigener Kommentar zu Sacrobosco, gedruckt 1552 bei Guillaume Cavellat in Paris mit Melanchthons Vorwort und mit Proklos’ De eclipsibus in Vinets Übersetzung, umfasst nur 104 Seiten. Möglicherweise soll die Zusammenstellung der Proklos-Psellos-Texte sogar die Sphaera des Sacrobosco in der mathematischen Geometrie der Ausgabe Tournon, 1592 ersetzen100 oder auch nur vorbereiten. In einer späteren Ausgabe von Vinets lateinischer Übersetzung der Sphaera (Bordeaux, 1553) wird auch das Quadrivium des (Pseudo-)Psellos abgedruckt, dessen astronomischer Teil von Pseudo-Proklos’ Sphaera ersetzt wird. Zumindest stellt Vinet in seinem Lehrplan Schola Aquitanica (1583) für das Collège de Guyenne in Bordeaux Psellos’ Quadrivium als Vorbereitung auf Sacroboscos Sphaera und Euklids Elementa dar.101 Am Collège de Guyenne fehlen elementare Traktate über Mathematik, weshalb Vinet neue antike Texte wie Pseudo-Proklos’ Sphaera übersetzt,102 die anscheinend als elementarer eingestuft werden als die gleichnamige Schrift des Sacrobosco.
Auch Vinets jüngerer Kollege Robert Balfour (ca. 1550–ca. 1625) verwendet Pseudo-Proklos’ Sphaera für seine Astronomievorlesungen vor 1605 am Collège de Guyenne in Bordeaux; z. B. zitiert er in seinem Kleomedes-Kommentar (Bordeaux, 1605) Pseudo-Proklos’ Definitionen der Parallelkreise, der Meridiane und des Sterns Canopus.103 Der Engländer Robert Recorde ist der Schatzmeister von Edward VI. (1537–1553) und Mary I. Tudor. Er ist Arzt, der griechischen Sprache mächtig, Historiker. Hauptsächlich lehrt er Mathematik in Oxford und Cambridge und gilt als Übermittler der praktischen Mathematik nach England.104 Recorde schreibt eine Reihe von Lehrbüchern, die Studenten nacheinander lesen sollen: The Grounde of Artes, teachyng the perfect worke and practise of Arithmetike (1542), Pathway to Knowledge (1551), Gate of Knowledge (1556), das verloren ist und wahrscheinlich von Messungen handelte, und The Castle of Knowledge (London, 1556). In seinen Lehrbüchern erklärt Recorde einfache Fakten ohne nähere Beweise, da er sich an Anfänger richtet. In The Castle105 erwähnt Recorde wiederholt, dass der Schüler die früheren Lehrbücher lesen muss, bevor er schwierigere Themen meistern kann.106 Im Inhaltsverzeichnis zu The Castle stellt Recorde fest, dass die Himmels- und die materielle Sphäre noch in keiner volkssprachlichen Literatur behandelt worden sind, obwohl Salisbury sechs Jahre zuvor seine englische Übersetzung von Pseudo-Proklos’ Sphaera herausgegeben hat (Salisbury 1550: not written before in any vulgare woorkes). The Castle besteht aus vier Abhandlungen (treatise), wovon die erste die Teile der materiellen- und der Himmelssphäre behandelt (S. 1–34), die zweite die Konstruktion der Sphäre, d.h. sowohl die massive Sphäre (Globus) als auch die beringte Sphäre (Armillarsphäre; S. 35–60), die dritte die Verwendung der Sphäre (S. 61–96) und die vierte Beweise und Tabellen enthält (S. 97–286). In diesem Werk erwähnt Recorde auch Ringelbergius’ Abhandlung über die Sphäre (S. 9).
The Castle ist ein Dialog zwischen einem Lehrer und seinem Schüler. Um die Sphaera zu verstehen, rät der Lehrer dem Schüler, folgende Werke zu lesen:
Cleomedes the greeke authour, is very woorthye to bee often readde: but beste in hys owne tongue, for the latine booke is muche corrupted. Also Euclide his booke entituled Phaenomena, and Stoffler his commentaries uppon Proclus Sphere: shyche booke I wishe were well recognised (as it hathe greate neede) then mythe it serve in steede of a greate numbre of other bookes. Dyuers Englyshe menne have written right well in that argument: as Grostehed, Michell Scotte, Batecombe, Baconthorpe, and other dyuers, but fewe of their bookes are printed as yet, therefore I will staye at those three for this tyme. As for Plinye, Hyginius, Aratus, and a greate manye other, are to bee readde onlye of masters in suche arte, that can iudge the chasse from the corne. And Ptolemye that worthye writer and myracle in nature, is to harde for younge schollars, except they be fyrste instructed not onlye in the principles of the Sphere, but also well traded in Euclides his Geometrye, and also well exercised in the Theorykes of the Planetes. But nowe let me see the table that you have collected. (Recorde 1556, 98–99).
Recorde empfiehlt also Stöfflers Kommentar zur Sphaera zusammen mit Kleomedes und Euklid als Einführung zum mathematischen Werk des Ptolemaios zu lesen.107 Auch lobt er den Autor Proklos: „die besten Autoren von ihnen für meine Studien waren Proklos, Johannes de Sacrobosco und Orontius [Orontius Finaeus oder Oronce Finé] der Franzose“ (the best writers of them for my study, were Proclus, Iannes de Sacrobosco, and Orontius the Frencheman, Recorde 1556, 98. Recorde ignoriert antike Autoritäten wie Aristoteles und folgt eher der englischen anti-aristotelischen Bewegung, basierend auf Erasmus’ und Melanchthons Linie.108 Gleichzeitig übt Recorde Kritik an Pseudo-Proklos, wenn er schreibt, es könne nicht sein, dass die arktischen Kreise die immer sichtbaren und die immer unsichtbaren Kreise begrenzen, und gleichzeitig als Projektion auf der Erde die Grenzen zwischen den Zonen darstellten, denn dann würden die Zonen sich mit dem Breitengrad des Beobachters verändern.109
In Oxford dient Pseudo-Proklos’ Sphaera als Einführungswerk für komplexere Schriften. Der erste Astronomieprofessor auf dem von Sir Henry Savile 1619 eingerichteten Lehrstuhl ist John Bainbridge, der für seine lateinische Übersetzung von Pseudo-Proklos’ Sphaera eine Handschrift aus Henry Saviles Besitz verwendet (Savile 10 in der Bodleian Library, Oxford; enthält auch Stöfflers Sphaera-Kommentar).110 Viele Studenten in Oxford nutzten später ihre Griechischkenntnisse im Theologiestudium, um traditionelle aristotelische Texte sowie das Neue Testament im Original lesen zu können.111
Die Lehre von Pietro Catena zeigt, dass die Sphaera-Texte des Pseudo-Proklos und des Sacrobosco alternativ oder additiv unterrichtet werden. Pietro Catena, 1547 ernannt zum „lettore di mathematiche“, lehrt an der Universität Padua über die pseudo-aristotelische Mechanik, Euklids Elementa, Proklos’ Euklid-Kommentar, Sacroboscos Sphaera sowie seinen eigenen von Sacrobosco beeinflussten Sphaera-Traktat (1574),112 und wohl auch Pseudo-Proklos’ Sphaera ab 1548 bis zu seinem Tod.113
Egnazio Danti unterrichtet ab 1562 an der Akademie Mathematik und Naturwissenschaften und wird 1575 als Professor nach Bologna berufen.114 Im Jahre 1583 wird er Kosmograph bei Papst Georg XIII. (1502–1585). Florenz ist das von Cosimo de Medici geförderte Zentrum der Gelehrtenkreise von Literaten und Dichtern um Marsilio Ficino, dem großen Proklos-Übersetzer, gefördert von Cosimo de’ Medici. Die Lektüre neuer, gerade platonischer Texte, findet im Landhaus in Careggi statt, das Cosimo dem Ficino im Jahre 1463 schenkt; ab dem 17. Jahrhundert trägt es nach antikem Vorbild den Namen „Platonische Akademie“.115
Der Lehrer für Literatur, Tito Giovanni Scandianese, schreibt in der Einleitung zu seiner italienischen Übersetzung von Pseudo-Proklos, dass er öffentliche und private Lesungen hält und für die Schüler von Carpi nützliche griechische Autoren („ad util loro traducendo“) ins Italienische übersetzt,116 wozu auch Pseudo-Proklos’ Sphaera gehört. In der Widmung erwähnt er seine Ernennung zum publico lettore und maestro de figliuoli suoi („Schulmeister“) durch die Stadt Carpi, Provinz Modena, wo er sich 1550–1555 aufhält; zuvor hat er in Reggio 1540–1550 gelehrt. Scandianeses Reisen gehen 1558 weiter nach Asolo, Provinz Modena, und 1581 nach Conegliano in der Provinz Treviso und Padua.117
Bei Philipp Apian (1531–1589) dient Pseudo-Proklos’ Sphaera in seinen Tübinger Vorlesungen der 1570er Jahre als Einführung zu Peuerbachs Theoricae Planetarum und der Cosmographia seines Vaters Peter Apian.118 Im Titel von Schreckenfuchs’ Kommentar zu Pseudo-Proklos’ Sphaera (Basel, 1561) steht, dass die Ausgabe für Studenten gedacht sei, die Latein und Griechisch beherrschen, damit sie das Original mit der Übersetzung vergleichen können (Omnia Graece et Latine coniuncta, ut conferri ab utriusque linguae studiosis possint). Diese Verwendung ist auch in Catenas lateinisch-italienischer Ausgabe (Padua, 1565) und in den griechisch-lateinischen Ausgaben von Linacres Übersetzung (25 Ausgaben zwischen 1499 und 1591) und Vinets Übersetzung mit Kommentar (Paris, 1543; Paris, 1553; Leiden, 1593; Wittenberg, 1597) erkennbar.
Die Verbreitung von Pseudo-Proklos’ Sphaera zeigt sich in den Inventaren englischer Gelehrter, z. B. in der Bibliothek von Richard Secol (†1577), der seinen Bachelor 1574 am New College in Oxford macht. Er besitzt die Sphaera zusammen mit Werken des Gemma Frisius
Einige Autoren erwähnen einzelne Passagen aus Pseudo-Proklos’ Sphaera zur Erklärung ihrer eigenen Lehrbücher und geben teilweise auch an, mit welchen Texten die Sphaera gelehrt werden soll. Der italienische Astronomielehrer und Neffe des Entdeckers Amerigo Vespucci, Bartolomeo Vespucci, zitiert die Definition der Koluren aus Linacres Übersetzung von Pseudo-Proklos’ Sphaera (Venedig, 1499ff.) in seinen Glossulae im Compendium Spherae Tractatus (des Sacrobosco), herausgegeben von Luca Gaurico (1476–1558) und 1531 in Venedig von Iunta.125 Dabei erwähnt er Linacre nicht: Die wahre Etymologie von „Kolur“, schreibt Vespucci, sei „kurz und gestutzt“, wie Boethius in Buch 2, Kap. 24 seiner Arithmetik über die Pyramide schreibt: „Wie wenn die Einheit das erste Quadrat war, nennen die Griechen sie kurz ,Kolur‘“.126 Proklos ist in seiner Sphäre auch dieser Meinung, wenn er sagt: „Es gibt durch die Pole geführte Kreise, die einige ,Koluren‘ nennen. Diesen kommt es zu, dass sie in ihren Umgebungen die Pole der Welt annehmen. Koluren aber werden sie genannt, weil sie einige Teile in sich haben, die kaum sichtbar sind. Die übrigen Kreise nämlich werden ganz in der Umdrehung der Welt wahrgenommen. Aber irgendwelche Teile der Koluren [gibt es], die offensichtlich vom Antarktischen Kreis [sichtbar sind]. Unter dem Horizont verbergen sie sich und können nicht gesehen werden.“127 Ferner zitiert Recorde in seinem Buch Pseudo-Proklos’ Definition der Achse, der Pole und des Horizonts128 und erwähnt den Fehler, dass der Canopus in Alexandria nicht unsichtbar, sondern sichtbar sei, sowie das Sternzeichen Thyrsolochos und das Haar der Berenike.129
Der Tübinger Mathematikprofessor Michael Mästlin zitiert in seiner Epitome Astronomiae (Tübingen, 1597) Pseudo-Proklos’ Bezeichnung des Horizonts als „Grenze des Sichtfeldes“: διορίζων ἡμῖν τότε φανερὸν καὶ τὸ ἀφανὲς μέρος τοῦ κόσμου („er trennt den für uns sichtbaren vom unsichtbaren Teil des Kosmos“).130 Der spanische Humanist Juan Luis Vives macht in seinem Werk De disciplinis (Antwerpen: Hillen, 1531), Buch IV, Kap. 5 die interessante Äußerung, dass man Sacroboscos Sphaera durch Pseudo-Proklos’ Sphaera ersetzen könne. 131
In ergänzender, nicht kontrastierender Weise schreibt Clavius in seinem Kommentar zu Sacrobosco von 1606, dass Pseudo-Proklos’ Begriff „Durchmesser“ (diameter) in der Sphaera genauer sei als Euklids Definition der „Linie“ (linea).132 Auch zitiert Clavius Pseudo-Proklos’ Einteilung der Himmelskreise in parallele, schiefe und solche, die durch die Pole gehen.133 Zum Thema „Horizont“ fragt sich Clavius, warum der Horizont auf eine Distanz von 400 Stadien sichtbar derselbe bleiben solle, der Meridian aber nur auf eine Distanz von 300 Stadien, wenn sie doch denselben Durchmesser haben müssten.134 Zur Begründung der Milchstraße verweist Clavius auch auf Proklos, definiert sie aber nach Ptolemaios, Kap. 8.135
Der deutsche Mathematiker Johannes Kepler scheint in seiner Widmung zur Epitome Astronomiae Copernicanae (1618) auf Pseudo-Proklos’ Sphaera hinzuweisen, deren erste drei Bücher die Doctrina Sphaerica behandeln. Hier wird Proklos in einer Reihe antiker Autoren, darunter Geminos und Sacrobosco, und frühneuzeitlicher Autoren, darunter Schreckenfuchs, erwähnt, die über die Sphäre geschrieben haben. Kepler behauptet, dass diese alle nichts Neues entdeckten, aber trotzdem immer wieder Einführungen in die sphärische Astronomie verfasst haben, weil nicht jeder Stil oder jede Methode für jeden Studenten geeignet sei.136 Kepler nimmt an, dass Proklos selbst in der Antike die Sphaera aus Geminos’ Werk entnommen habe, eine Ansicht, die auch Marcus Hopper (1561), Edo Hilderich (1590) und John Bainbridge (1620) teilen.137 Auch verwendet Kepler Pseudo-Proklos für sein Traktat über Optik, Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur (Frankfurt, 1604),138 wenn er schreibt, dass der Stern Canopus in Rhodos kaum von den höchsten Bergen aus sichtbar sei.139
5.3.2 Die Drucker
Einige Übersetzer, Kommentatoren und Drucker bilden Arbeitsgemeinschaften und geben auch andere Werke zusammen heraus. Aufgrund ihrer philologischen Kenntnisse (besonders des Griechischen) und Handschriftensammlungen sind die Drucker auf die Übersetzer und Kommentatoren angewiesen. Linacre und Valla helfen dem Drucker Manutius bei seiner Aristoteles-Ausgabe, Toussain und Wechel drucken klassische griechische Werke und Vinet und Cavellat geben Lehrbücher heraus. Auch die Beziehungen der Drucker und Autoren zu adeligen Geldgebern sind elementar wie für Thomas Linacre zu Arthur Tudor, für Aldus Manutius zu Alberto Pio und für Egnazio Danti zu Isabella de Medici. Unter den Druckern verschiedener Städte und verschiedener Werke von Pseudo-Proklos’ Sphaera und Sacroboscos Sphaera werden Ausgaben und Titelbilder in verschiedenen Städten weitergereicht und erneut gedruckt.140
So sind die Titelbilder einiger Ausgaben von Pseudo-Proklos’ Sphaera identisch mit Titelbildern der Ausgaben von Sacroboscos Sphaera (und mit anderen astronomischen Werken, vgl. Abbildung 5.2).141 Der erste Typus des Titelblatts stammt aus Venedig, Paris und London, der zweite spätere Typus ausschließlich aus Wittenberg. Somit zeigt sich, dass die Titelbilder auch mit Druckort und -zeit korrelieren. Die Titelbilder spiegeln den Inhalt der Sphaera wider, nämlich die Armillarsphäre. Der Autor ist dabei irrelevant.
Die Beschreibung astronomischer Instrumente in Drucken der Sphaera wird durch Abbildungen von Globen142 und geometrische Abbildungen der Himmelskreise veranschaulicht (vgl. das Kapitel zur Sphaera).143 So enthält der Druck von Stöfflers Kommentar Abbildungen zur Konstruktion einer Armillarsphäre und ihrer Bestandteile, z. B. vom Äquatorring und den beiden Wendekreisen (Abbildung 5.3).
Auf der Schlussseite enthält Stöfflers Kommentar ein bewegliches Astrolabium, wohl als Übung astronomischer Rechnungen für die Studenten (vgl. Abbildung 5.4). Ein weiteres Indiz für die Verwendung der Sphaera als Instrumentenanleitung (Himmelsglobus oder Armillarsphäre) ist, dass einige Übersetzer, nämlich Valla, Vinet, Anonymus Monacensis, Salisbury, Thuroczi, Henisch und Bainbridge, in ihren Übersetzungen das Wort σφαῖρα mit „Globus“ übersetzen, Danti bezeichnet es als sfera armillare.

Abb. 5.2: Zwei Typen von Titelblättern: Typus I: 1. Reihe. Typus II: 2.–4. Reihe. Die Titelbilder sind Hamel 2014, 34–65 entnommen, außer: Londini, 1522: EEBO British Library, London; Vitebergae, 1531: Österreichische Nationalbibliothek, Wien; Lutetiae, 1560, Biblioteca Nacional de España, Madrid.

Abb. 5.3: Die Konstruktion einer Armillarsphäre: Aus dem lateinischen Kommentar des Johannes Stöffler zu Pseudo-Proklos’ Sphaera, Bl. 56r, digitalisiert von der Bayerischen Staatsbibliothek München, aus: http://www.mdz-nbn-resolving.de/urn/resolver.pl?urn=urn:nbn:de:bvb:12-bsb11057858-3, besucht am 2.08.2019.
Danti schreibt, dass seine Tabelle XVI Della Sfera delle principali operazioni sue zusammen mit seiner Übersetzung von Pseudo-Proklos’ Sphaera eine Anleitung für die Messoperationen der Armillarsphäre bilde. Die Armillarsphäre sei nützlicher als das Astrolabium, weil sie den sphärenförmigen Aufbau des Kosmos besser nachahme. Astrolabien, die von den Gelehrten selbst gebaut werden, dienen zur Zeitmessung wie auch die feste oder tragbare zylinderförmige Sonnenuhr. Wahrscheinlich werden Quadranten, Astrolabien und Armillarsphären im Unterricht verwendet.144In der Tabelle XVI listet Danti auf, welche Messungen die Armillarsphäre erlaubt: die Mittagsstunde, die Höhe des Pols, den Beobachterstandpunkt, die Position der Sonne im Tierkreis u. a.

Abb. 5.4: Bewegliches Astrolabium. Aus dem lateinischen Kommentar des Johannes Stöffler zu Pseudo-Proklos’ Sphaera, hinteres Titelblatt, digitalisiert von der Bayerischen Staatsbibliothek München, aus: http://www.mdz-nbn-resolving.de/urn/resolver.pl?urn=urn:nbn:de:bvb:12-bsb11057858-3, besucht am 2.08.2019.
Oft wird dieselbe Ausgabe von Pseudo-Proklos’ Sphaera in denselben Ländern und Städten nachgedruckt; in Venedig um 1499 und 1503, in Basel um 1523 und 1534 (1. Ausgabe), um 1547, 1561 und 1585 (2. Ausgabe), in Basel um 1549 und 1582 (3. Ausgabe), in Wittenberg um 1538 und 1543, in Bordeaux um 1553 und 1557. Hierdurch wird klar, dass die Drucker derselben Orte zusammenarbeiten und ihre Drucklizenzen austauschen. Wenn ein Thema in einem Sphaera-Traktat der Sacrobosco-Tradition aufgenommen wird, erscheint es oft in späteren Ausgaben, unabhängig von Druckort und Herausgeber.145 Zwar wird Sacrobosco nicht wie Pseudo-Proklos in Holland (Leiden) gedruckt, aber an Navigationsschulen in Spanien und Portugal gelehrt, wo Pseudo-Proklos nicht herausgegeben wird. Eine Erklärung dürfte sein, dass die katholische Tradition in Spanien mit ihrer gegenreformatorischen Gesinnung eher das scholastische Lehrbuch des Sacrobosco befürwortet als die griechische Sphaera des Neoplatonikers Proklos, der offenbar eher in reformierten oder erasmischen Kreisen zirkuliert. Auch ist Spaniern der Besuch nicht-spanischer Universitäten verboten.146
Die Hauptdrucker von Pseudo-Proklos sind Christian Wechel, Guillaume Cavellat und Johann Herwagen. Diese haben klassische und zeitgenössische mathematische Werke herausgegeben. Die Druckerhäuser Cavellat in Paris, Giunti oder Giunta (1477–1658)
Cavellat druckt Sacroboscos Sphaera schon 1551 zusammen mit Pedro Nuñes’
Als Korrektor unterstützt Jacques Toussain den Drucker Jacques Bogard (Jacobus Bogardus), der in Paris 1543 und 1547 seinen Kommentar zu Pseudo-Proklos’ Sphaera druckt.149 Nach Toussains Tod lebt die Sphaera in seinem Schüler Petrus Ramus fort: 1566 schreibt Petrus Ramus, Professor am Collège Royale in Paris um 1551–1555, dass Pseudo-Proklos’ Sphaera am Collège Royal zusammen mit Aristoteles’ De caelo alternativ (gleichwertig, ou bien) zu Sacroboscos Sphaera mit Euklids Elementa gelesen werde.150 Aber auch Sacroboscos Sphaera wird als Vorbereitung auf Aristoteles’ De caelo gelesen.151 Außerdem stellt Petrus Ramus die Sphaera in seinen Scholarum mathematicarum libri unus et triginta in die Reihe von Proklos’ mathematischen Werken (vgl. das Kapitel Inhalte und Quellen): „Die [Abhandlungen] über ,sphärische Astronomie‘ [also die Sphaera], ,das Astrolabium‘ und die ,astronomischen Hypothesen‘ werden in die Hände der Menschen gegeben. So ein großer Mathematiker war Proklos also (Basel, 1569).“152
Vinet, der 1534–1539 bei Jacques Toussain in Paris studiert, hat vielleicht von Toussains Vorlesungen über die Sphaera gehört und sie für seinen Kommentar zu Pseudo-Proklos verwendet.153 Hier ist Pseudo-Proklos ab 1539 Teil der ersten mathematischen Lehre am Collège de Guyenne in Bordeaux, wo Vinet bis zu seinem Tod unterrichtet.154 Neben seinem Unterricht erstellt Vinet Lehrbuchausgaben, die für den lateinisch-französischen Unterricht vorgesehen sind.155 Er innoviert die Pädagogik seiner Zeit durch humanistische Lehrmethoden.156 Zu Élie Vinets Lehrbuchausgaben gehören neben Pseudo-Proklos’ Sphaera (Erstausgabe: Paris, 1543, letzte Ausgabe: Wittenberg, 1597) auch Theognis’ Sententiae elegice (Paris und Basel, ab 1543) und Senecas (1–65 n. Chr.) Formulae vitae honestae (Poitiers, 1544). Vinet schreibt nur gelegentlich über praktische Themen und meistens auf Latein, nicht auf Französisch. Mit dem Drucker G. Cavellat gibt er 1556 in Paris seine (Vinets) Übersetzung von Sacroboscos Sphaera heraus. Cavellat beeinflusst mit seinen Beziehungen zu Professoren das Wissensnetzwerk in Paris.157 Zusammen entscheiden Cavellat und Vinet, dass nur mathematische Demonstrationen in die Wissensstruktur von Sacroboscos Sphaera integriert werden sollen, aber im Fall von Pseudo-Proklos wohl auch Dichterzitate.
5.3.3 Die Drucke in Raum und Zeit
Die Diagramme basieren auf einer Zahl von 61 Drucken von Pseudo-Proklos’ Sphaera im 16. Jahrhundert (vgl. die Tabelle in der Bibliographie), deren bibliographische Daten durch erhaltene Exemplare nachgewiesen sind und somit eine valide Auswertung ermöglichen. Insgesamt sind ca. 92 Drucke und 22 Handschriften vom 15. bis zum 19. Jahrhundert entstanden, von Sacroboscos Sphaera 376 Ausgaben zwischen 1472 und 1697.158 Also wird Pseudo-Proklos’ Sphaera in kürzerer Zeit verbreitet als Sacroboscos Sphaera.
Die Zahl der Drucke von Pseudo-Proklos’ Sphaera überwiegt leicht in der zweiten Hälfte des 16. Jahrhunderts (vgl. Abbildung 5.5). Fast die Hälfte der Drucke erscheint in Frankreich, gefolgt von Deutschland und den großen Städten London, Wien und Basel. Die wenigsten Drucke werden in Italien, Niederlande und Polen herausgegeben (vgl. Abbildung 5.6). Starke Druckjahre sind mit drei bis vier Drucken 1534, 1543, 1547, 1553, 1554 und 1556, also die Jahre um die Jahrhunderthälfte.
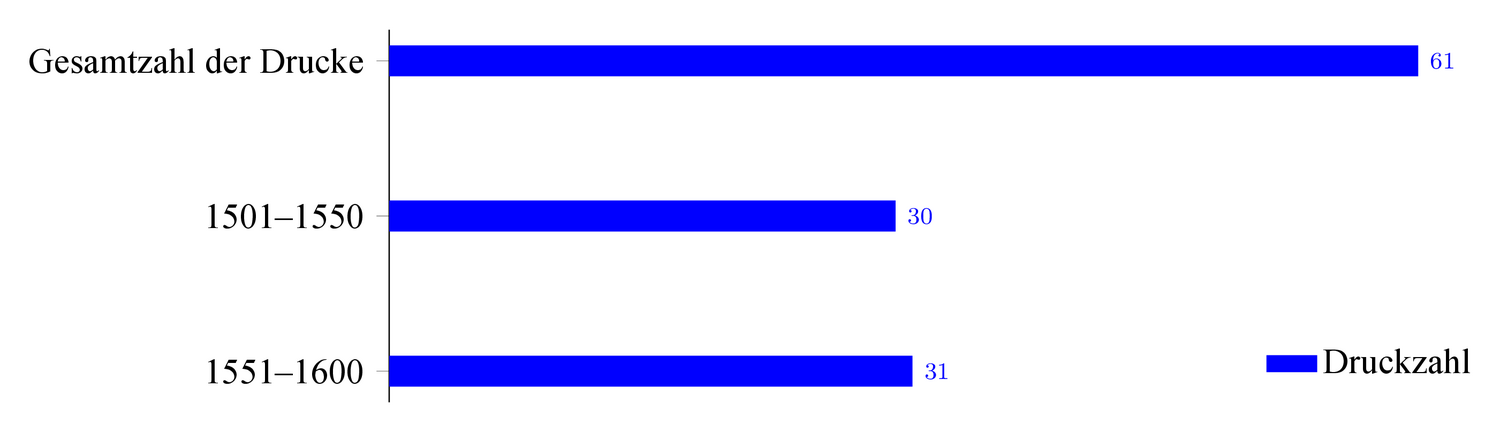
Abb. 5.5: Die Zahl der Drucke von Pseudo-Proklos’ Sphaera in zwei Zeiträumen.

Abb. 5.6: Die Druckorte von Pseudo-Proklos’ Sphaera.
Auch von Sacroboscos Sphaera erscheinen die meisten Publikationen in Nordeuropa, Italien und Zentraleuropa in der ersten Hälfte des 16. Jahrhunderts, dann in der entgegengesetzten Reihenfolge in der zweiten Jahrhunderthälfte. Die stärksten Druckstädte für Sacrobosco sind Wittenberg, Venedig und Paris in der ersten Hälfte des 16. Jahrhunderts sowie Lyons und die Hafenstadt Antwerpen in der zweiten Jahrhunderthälfte. Die Küstenstädte erreichen ihre Spitze der Drucke mit 43 Prozent in Paris und Venedig in der ersten Hälfte des 16. Jahrhunderts.159
Spitzendruckjahre in der Sacrobosco-Tradition sind 1494, 1518, 1550 und 1560. Diese Spitzen beziehen sich auf mehrere Orte, z. B. erscheinen zwischen 1493–1501 25 Drucke, davon sieben in Paris, acht in Venedig, Bologna, Leipzig, Lissabon und Köln.160 1531 ist ein starkes Jahr der Rezeption von Pseudo-Proklos’ Sphaera, da Vespucci (Venedig), Vives (Antwerpen) und Ringelbergius (Lyon) sie in diesem Jahr erwähnen. Alle drei Städte sind große Handelszentren des 16. Jahrhunderts, die über den europäischen Finanzplatz „Nürnberger Börse“ im Austausch stehen.161
Die Druckorte zeigen also, dass Pseudo-Proklos’ Sphaera und Sacroboscos Sphaera beide in Wittenberg und Paris gedruckt werden. Andere Druckzentren für Sacrobosco sind Küstenstädte wie Venedig und Lissabon, während Pseudo-Proklos niemals im katholischen Spanien, sondern in der reformatorischen Stadt Basel gedruckt wird. Tendenzen, Sacrobosco gegen Pseudo-Proklos zu bevorzugen sind v. a. in Frankreich aufgrund des dortigen Zentrums griechischer Lehre nachweisbar (Vives in Antwerpen und Vinet in Paris). Besonders zum Ende des 16. Jh. wird Sacrobosco in der protestantischen Astronomieausbildung weniger gelesen. In Wittenberg wird Sacrobosco durch die Schriften des Hartmann Beyer
5.3.4 Die Einzeldrucke und Sammlungen und deren Inhalte
Über die Hälfte der Drucke von Pseudo-Proklos’ Sphaera erscheint als Einzeldruck, wobei sich ihre Zahl in der zweiten Hälfte des 16. Jahrhunderts noch erhöht, weil die Wertschätzung der Sphaera als eigenständiges Werk steigt (vgl. Abbildung 5.7).
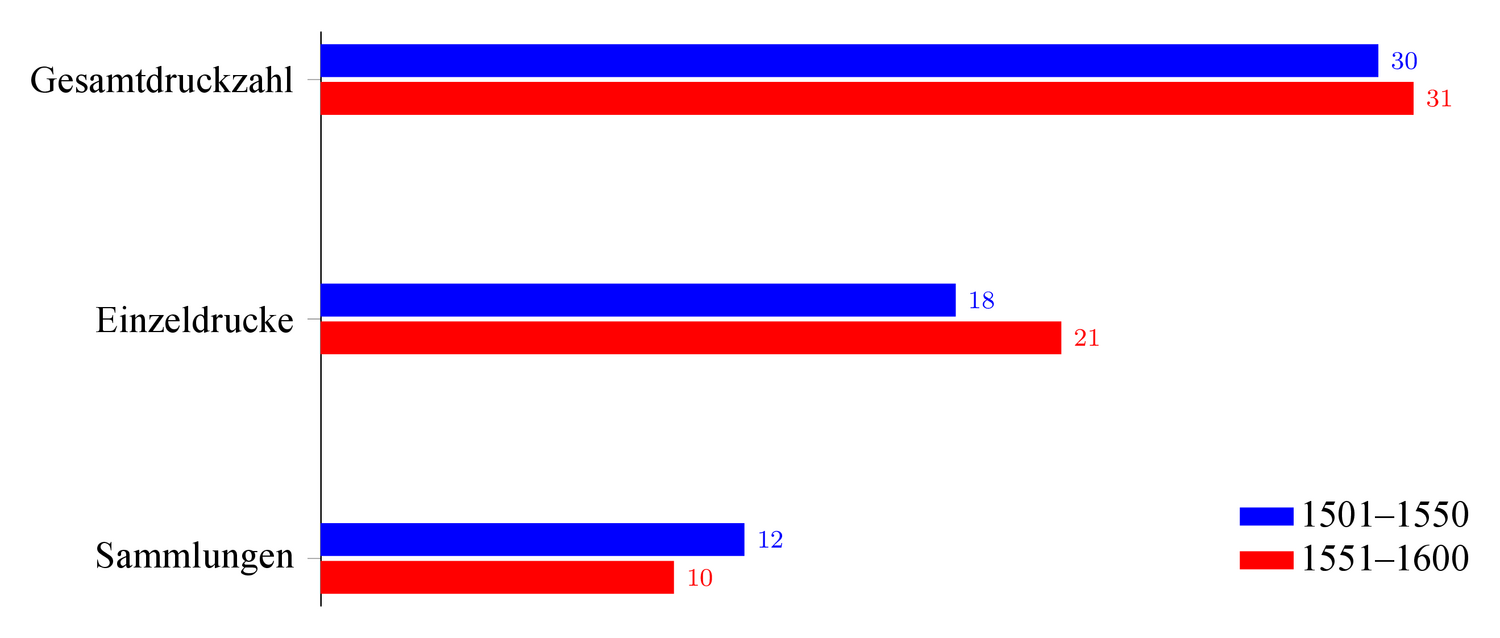
Abb. 5.7: Einzeldrucke und Sammlungen mit Pseudo-Proklos’ Sphaera.
Dabei werden die Übersetzungen und Kommentare von Pseudo-Proklos’ Sphaera z. T. mit antiken bis mittelalterlichen astronomischen Texten, frühneuzeitlichen Instrumentenbeschreibungen oder antiken Gedichten und mythologischen Texten zusammengedruckt. Sacroboscos Sphaera dagegen erscheint in Sammlungen v. a. in Paris oder Venedig, z. B. mit Werken des Peuerbach und des Regiomontanus.163
Die klare Trennung von humanistischer (Arat, Hygin, Plinius) und mathematischer Lehrtradition (Kleomedes’ Caelestia, Euklids Phaenomena) der Sphaera, die Todd (2003, 13) aufgestellt, lässt sich also nicht in den Drucken und Handschriften nachweisen. So besitzt auch Dantis Kommentar zu Pseudo-Proklos’ Sphaera mathematischeren Charakter als sein Kommentar zu Sacroboscos Sphaera.164 Vielmehr zeigt sich eine Vermischung beider Traditionen durch antike Parallelstellen, philologische Methoden und geometrische Abbildungen bzw. Tabellen in den Kommentaren zu Pseudo-Proklos’ Sphaera. Wie zahlreiche Bilder und Bezeichnungen belegen, wird die Sphaera als Beschreibung eines Himmelsglobus oder einer Armillarsphäre verstanden.Technischere Autoren wie Kleomedes und Ptolemaios werden in Kombination mit Arats Gedichten gedruckt. Die Sphaera ist beliebt, weil sie mit Gedichten und Bildern kombiniert wird, während Sacrobosco nicht zusammen mit Gedichten herausgegeben wird. Diese Vermischung zeigt sich v. a. in Drucken aus der Schweiz, Italien, Frankreich, weniger in Deutschland und England und geht mit der zweiten Hälfte des 16. Jahrhunderts zurück, da die Sphaera als Einzeltext an Bedeutung gewinnt (vgl. Abbildung 5.8).
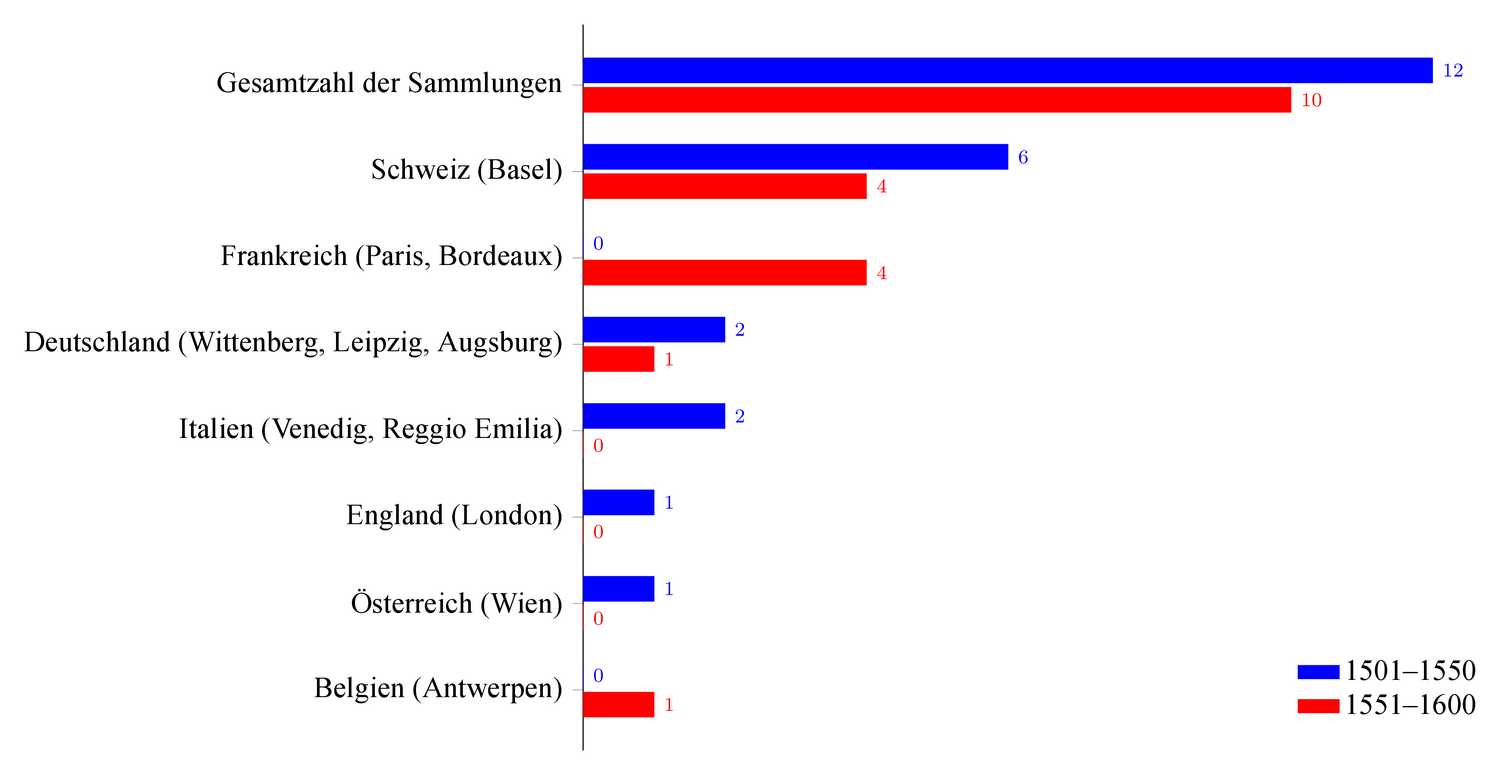
Abb. 5.8: Geographische Verteilung der Sammlungen mit Pseudo-Proklos’ Sphaera in den beiden Hälften des 16. Jahrhunderts.
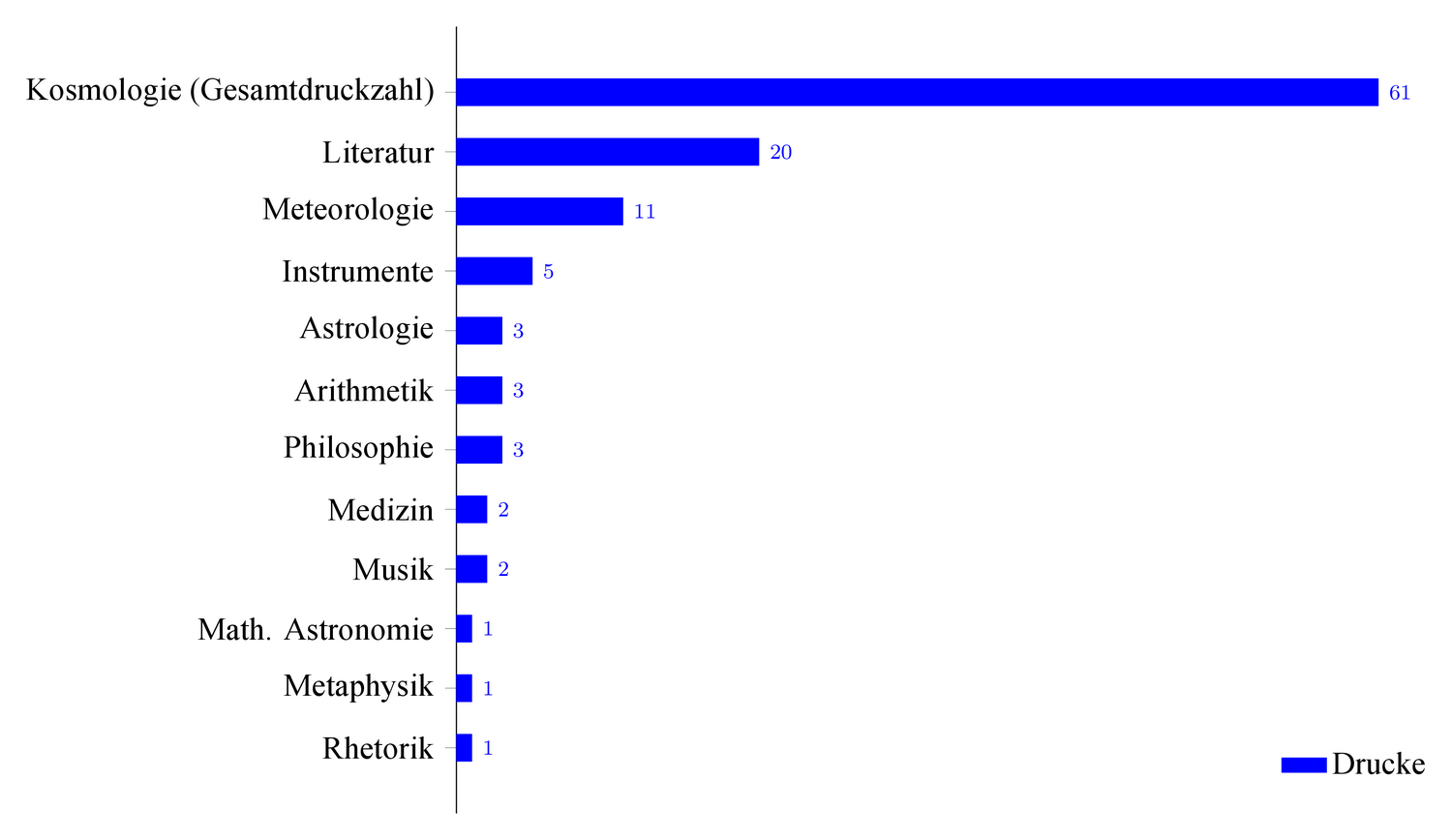
Abb. 5.9: Die Inhalte in den Kommentaren zu und Sammlungen mit Pseudo-Proklos’ Sphaera.
Die von Todd als „literarisch“ deklarierten Kommentare des Élie Vinet und des Jacques Toussain enthalten geometrische Instrumentenabbildungen. Auch ist der Stil in Linacres und Thuroczis Übersetzungen von Pseudo-Proklos’ Sphaera poetischer als das Latein von Sacroboscos Sphaera, wobei Linacres Übersetzung den Schwerpunkt der Pseudo-Proklos-Rezeption darstellt. Wo Linacre Vorlage ist, gibt es auch starke Ähnlichkeiten mit seinem Text, der sich um Nähe zum Griechischen bzw. Verständlichkeit bemüht. Die volkssprachlichen Übersetzungen neigen zu Umschreibungen und Vereinfachungen, v. a. gegenüber Linacre.
Häufig werden Verse zitiert, um den Text aufzulockern. Selbst die von Todd als „literarisch-humanistisch“ charakterisierten Kommentare des Toussain und Vinet zitieren verschiedene Textgattungen neben der Dichtung: Vinet zitiert Sacrobosco, Plinius und Kleomedes, Toussain nennt Aristoteles, Macrobius und Euklid. Bei unklaren Formulierungen im Pseudo-Proklos-Text wird häufig Sacrobosco als Ergänzung herangezogen. Auch zeitgenössische Autoren wie Erasmus (bei Toussain) und Kopernikus (bei Anonymus Hauniensis) dienen zur Erklärung. Längere Ausschnitte von antiken Dichtern zitieren Stöffler und Toussain wie z. B. Ovid, Lukan und Manilius. Generell wird Pseudo-Proklos’ Sphaera mehr mit literarischen Texten und Zitaten gedruckt als Sacroboscos Sphaera.165
Die Sphaera wird in Sammlungen mit Kommentaren verschiedenen Inhalts gedruckt. Die meisten Drucke enthalten neben dem kosmologischen Text literarische Inhalte, da Pseudo-Proklos’ Sphaera auch als Sprachlehrbuch verwendet wird, d.h. Giorgio Vallas Enzyklopädie De expetendis, Gedichte wie jene des Aratos Solensis (Phaenomena) und des Marcus Manilius (Astronomica), Dionysios’ mythologisch-geographische Abhandlung Orbis descriptio; außerdem Hygins Erzählungen (Fabulae) und Lilius G. Gyraldus’ (Lilio Gregorio Giraldi
Dem Sphaera-Text des Sacrobosco werden über die Jahrhunderte mehr und mehr Themen in den Kommentaren und Bearbeitungen hinzugefügt, z. B. Navigationswissen und die Verwendung astronomischer Instrumente zur Zeitmessung und Messgeographie, Astrologie bzw. die Einflüsse der Planeten auf das menschliche Leben, Kalenderrechnung, Optik bzw. Messung durch Sicht,166 während Navigationstechniken und optische Themen bei Pseudo-Proklos weniger vorkommen. Beiden Texten gemeinsam ist, dass sie die Konstruktion astronomischer Instrumente und die geometrische Beschreibung der Sphäre zum Verstehen von Geographie und Kartographie enthalten.
Zur Verwendung der Sphäre bzw. des Globus lässt Recorde den Schüler sagen, dass er zum Verständnis des Aufbaus des Kosmos beiträgt: „All this seemeth easy to me, as longe as I beholde this materiall sphere: but when I doo not conferre it wyth your woordes, then your saynges appeare the more doubtefull.“ Und der Lehrer antwortet: „For that cause did I teach you the making of it, before I instructed you in the use of it, knowing how greate a helpe the sighte of the eye doth minister to the righte and speedye understandyng of that which the eare doth heare“ (Castle, S. 66). Recorde lehrt also erst die Konstruktion, dann den Gebrauch des Globus oder der Armillarsphäre für ein besseres Verständnis des Schülers. Pseudo-Proklos’ Sphaera muss dennoch auch durch Kommentare über den Gebrauch und die Konstruktion der Armillarsphäre ergänzt werden.
Die Sphaera ist also ein elementarer Grundlagentext, der verschiedenen Disziplinen oder Werken als Vorbereitung dient. Der Text ermöglicht es, griechische Autoren wie Arat und Aristoteles zu lesen. Auch bietet Pseudo-Proklos’ Sphaera eine Basis für angewandte Astronomie, also Messungen und Geometrie. Im Falle von Vallas Enzyklopädie, Vives’ De disciplinis und Henischs Tabellen hat sie den Charakter eines „Nachschlagewerkes“. Die genannten Enzyklopädien zeigen die Tendenz dieser Gattung seit dem Spätmittelalter, sich weniger auf das Christentum, sondern auf Naturwissenschaften zu berufen und damit einen wissenschaftlicheren Charakter anzunehmen. Somit ist Pseudo-Proklos’ Sphaera nicht nur ein Teil der Sphaera-Gattung, sondern auch der Enzyklopädien-Gattung.167
Pseudo-Proklos’ Sphaera wird v. a. von Mathematikern und Rhetorikern rezipiert. Valla z. B. übersetzt Proklos’ Paraphrase der Armillarsphäre des Ptolemaios (De astrolabo; Venedig 1498). Zu seinen Übersetzungen aus dem Griechischen in De expetendis schreibt Valla: „Ich habe schon alle mathematischen Schriften in meinen Sammelbänden übersetzt“,168 und „ich habe hinzugefügt, was von den herausragendsten griechischen Autoren verborgen aufbewahrt und entnommen wurde durch irgendeine göttliche Fügung“.169 Valla liegt also daran, einen vollständigen Überblick der antiken, v. a. griechischen mathematisch-astronomischen Werke zu geben, wozu Pseudo-Proklos’ Sphaera gehört. Er übersetzt den für den Humanismus wichtigen Text, die Poetik des Aristoteles, ins Lateinische (Venedig 1498).
Jakob Ziegler veröffentlicht vorwiegend Schriften zur Kosmographie und Astronomie, darunter den Kommentar zu Plinius’ zweitem Buch der Naturgeschichte (Naturalis historia, Basel: Heinrich Petri, 1531). Im Kommentar zu Pseudo-Proklos schreibt Ziegler, dass er einige astronomische Fragen in seinem Plinius-Kommentar behandelt, die er nicht im Kommentar zu Pseudo-Proklos’ Sphaera erwähnen will (S. 84), was zeigt, dass er die beiden Kommentare als Einheit betrachtet. Beide Kommentare beweisen Zieglers Interesse an philologischen, aber auch mathematischen Fragen.170 Auch Giorgio Valla lehrt über Plinius in Venedig, Rheticus dagegen gibt 1540 die erste Nachricht von Kopernikus’ Werk De libris revolutionum narratio prima (Danzig 1540) heraus. 1542 bereitet er mit Johannes Petreius, Drucker in Nürnberg, die Herausgabe von Kopernikus’ Hauptwerk Narratio Prima mit einer Einleitung vor.171 1550 erscheinen seine von Kopernikus beeinflussten Ephemerides Novae (Leipzig, 1550).
Obwohl Bainbridge der heliozentrischen Perspektive gewogen ist,172 übersetzt er die geozentrischen Werke Pseudo-Proklos’ Sphaera und Ptolemaios’ Hypotyposis (London, 1620). Sein größtes astronomisches Werk ist die Beobachtung des Kometen von 1618 mit dem Teleskop (An Astronomical Description, 1619), in welchem Bainbridge das ptolemäische System kritisiert. In seinem letzten Werk Antiprognosticon (1642) widerlegt Bainbridge die Gültigkeit astrologischer Prognostik. Über 20 Jahre nach Bainbridges Tod (1663) wird sein Diskurs über den Längengrad De meridianorum sive longitudinum differentiis inveniendis entdeckt.173
5.3.5 Die Sprachen
Unter den Sprachen dominiert in der zweiten Jahrhunderthälfte die Zahl der griechisch-lateinischen Drucke, wohl wegen der Möglichkeit des Sprachenvergleichs und des Griechisch-Latein-Erwerbs, gefolgt von der Zahl der lateinischen Drucke, die das ganze 16. Jahrhundert über relativ konstant bleibt. Die Minderheiten bilden Ausgaben mit nur dem griechischen Originaltext und volkssprachliche Übersetzungen. Die Zahl der griechischen Drucke nimmt in der zweiten Jahrhunderthälfte ab, da im Zuge der Popularisierung antiker Schriften diese in volkssprachliche Übersetzungen übertragen werden, während die französischen Drucke konstant bleiben. Auf Englisch wird Pseudo-Proklos’ Sphaera in der ersten Jahrhunderthälfte übersetzt, auf Italienisch in der zweiten Jahrhunderthälfte (vgl. Abbildung 5.10). Auf Deutsch erscheint Pseudo-Proklos’ Sphaera vor 1830 nicht, wird aber anders als Sacroboscos’ Sphaera in deutschen Städten gedruckt.
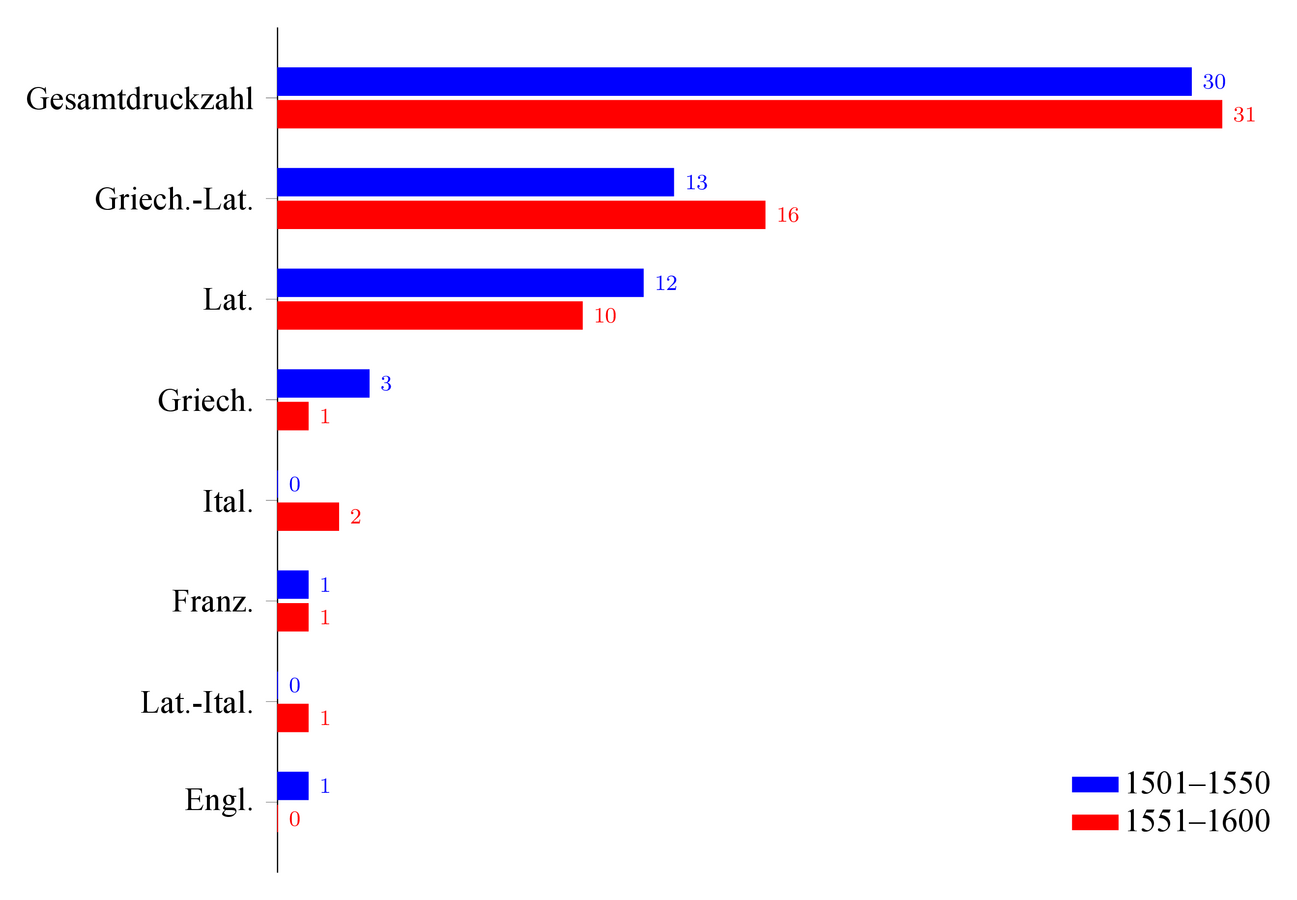
Abb. 5.10: Die Sprachenverteilung in Drucken von Pseudo-Proklos’ Sphaera.
Vinet übersetzt auch Pedro Nuñes’ Kommentar zu Sacroboscos Kapitel über Klimazonen (1556). Diese Übersetzung zeigt, dass Mathematik eine Übersetzung von der Volkssprache ins Lateinische rechtfertigt, während alle anderen großen Innovationen, die Nuñes in den 1560er Jahren einführt, das Thema von Traktaten in Volkssprache bleiben.174 Von Vinets französischer Übersetzung der proklischen Sphaera mit Kommentar ist die Erstausgabe (Poitiers, 1544) verloren, die vielleicht bereits den französischen Kommentar enthielt, und nur der Nachdruck (Paris, 1573) erhalten.175 Der Kommentar in der französischen Ausgabe von 1573 steht direkt neben dem Haupttext und ist somit leichter zu lesen, wohingegen die lateinischen Ausgaben den Kommentar am Ende der Übersetzung enthalten. Auch weist die Ausgabe von 1573 viele vereinfachte Darstellungen der Kreise auf; von den lateinischen Ausgaben zeigen nur jene von 1592 geometrische Abbildungen. Für seine Übersetzung von Pseudo-Proklos’ Sphaera verwendet Vinet den zu seiner Zeit besten griechischen Text aus der Pariser Edition von 1531.176 Vinets einzige andere französische Übersetzung sind Euklids Elementa (Urbino, 1575), die er zuvor auf Griechisch herausgegeben hat (Basel: J. Herwagen, 1546).
Der walisisch-protestantische Gelehrte William Salisbury oder Salesbury177 ist Protestant und Befürworter der Volkssprache und schreibt vorwiegend lexikalische, liturgische und medizinische Werke auf Walisisch, darunter A Dictionary in Englyshe and Welshe (1547) und eine Übersetzung des Neuen Testaments Testament Newydd ein Arglwydd Iesu Christ (1567). Die Sphaera-Übersetzung ist Teil seines Bestrebens, die walisische Sprache zu fördern. Der astrologische Appendix zur Sphaera spiegelt Salisburys medizinisches Interesse wider, wie auch seine medizinischen Werke: „Llysieulyfr“ (ca. 1569), eine Paraphrase der zeitgenössischen Kräuterkunde, und die Handschrift eines anderen medizinischen Werkes, Prifysgol Cymru, die 1916 von E. Stanton Roberts transkribiert und ediert wird.178
Auch Tito Giovanni Scandianese, eigentlich Tito Giovanni Ganzarini,179 ist ein Vertreter der Volkssprache. Er schreibt Komödien und Kommentare zu klassischen Werken in italienischer Sprache.180
Der österreichische Humanist Erasmus Oswald Schreckenfuchs kommentiert auch Sacroboscos Sphaera (Basel: H. Petri, 1569) und gibt mit Sebastian Münster zwei hebräische Werke über Kosmologie und Arithmetik aus dem 14. Jahrhundert heraus.181
Catenas italienische Übersetzung der Sphaera wird 1565 in Padua bei Gabriel Giolito
Fußnoten
Vgl. Rüdiger 1961, 536f.. Mit Dank an Dr. Matthias Vollet für diese Referenz.
Francesco Barozzi lehrt über Proklos’ Euklid-Kommentar an der Universität Padua.
Vgl. Klibansky 1939, 76–77.
Vgl. Kristeller1987, 192–193; Dillon 2014.
Vgl. Klibansky 1939, 46; Kieszkowski 1973, 73–74.
Vgl. Rosán 1949, 42–43.
Cui [curriculo] subjungit Pselli Mathematicum breviarium: quo summam quattuor Mathematicarum adolescentes primum cognoscant, tum Euclidis Elementa ac postea Sphaerica, vgl. Vinet 1886, 26.
Vgl. Massebieau 1886, 73–74, Nr. 59.
Vgl. Kristeller 1987, 196–197.
Zu Moosburgs Übersetzung der Elementatio physica vgl. Böse 1958, 20–21; diese wird auch in der sechsbändigen Ausgabe von Moosburgs Elementatio theologica-Übersetzung erwähnt: Moosburg 1984–2011.
Zum Inhalt der Elementatio Physica vgl. Rosán 1949, 50–51.
Vgl. Gersh 2014b, 336–337.
Vgl. Marx [1905] 1966.
Vgl. Ficino 1576, 937–943.
Vgl. Ficino 1576, 1928–1929; Allen 2015, 184.
Vgl. Ficino 1576, 1908–1928. Zur Standardausgabe von Proklos’ Alkibiades vgl. Segonds 1985–1986.
Die Antwort des Plethon ist zu lesen bei Bass 1844, 54–116.
Vgl. Bessarion 1960; Proklos 1968, CLIX–CLX.
Vgl. Prins 2015b, 263.
Vgl. Prins 2015a, 408.
Vgl. Fricker 1963, 181–183, Nr. 68; Kristeller 1987, 210.
Vgl. die Ausgabe von 1973, 44–48.
Vgl. Claessens 2011, 52; 67; 81–82. Zu Kepler und Proklos vgl. auch Bialas 2004.
Zur Debatte über die Mathematik vgl. Giacobbe 1979; De Pace 1993, 187–260.
Vgl. Rosán 1949, 49–50.
Vgl. die deutsche Übersetzung des ersten Arguments in Philoponos’ Zitat bei Baltes 1978, 134–164.
Zu den Inhalten der Proklos-Werke vgl. im Folgenden Rosán 1949, 36–59.
Vgl. Manitius’ Geminos-Ausgabe, Manitius 1974, III–XVI.
In Rep. 2.215.17–19; 2.215.24; 2.216.4; In Tim. 3.133.6–7
„Die sphärenhafte Oberfläche, die der ganzen [Erde] zugrunde liegt, wird in fünf Zonen geteilt.“
Vgl. Proklos 2007, 15, Nr. 18.
Vgl. Grössing 2012, 40f..
Vgl. Grössing 2012, 40–41.
Vgl. Schöner 1999, 91–92.
Vgl. die Referenzen hierzu im Kapitel über die Kommentare.
Kraai widerlegt die Annahme, dass die Sacrobosco-Vorlesung nicht von Rheticus stamme; vgl. Kraai 2003, 30–31.
Vgl. Burmeister 2015, 31–39.
Vgl. Rheticus 1536, 73v: Interim legit magister Ioahim spheram Procli. finito Proclo incepit iterum al Fraganum.
Zu den scientiae mediae zählt Danti Kosmographie, Astronomie, Geographie, Geometrie, militärisches Ingenieurwesen, Architektur, Optik, Malen und künstlerische Perspektive; vgl. Fiorani 2005, 44, Anm. 26.
In Astronomia legendi Proclus et Aratus, nam apud Latinos pauci de dea docte scripsere. Si altiora spectes, adiungere potes Ptolemaeum. In Astrologia Firmicus Maternus, qui caeteris elegantius et verius artem tradidit, vgl. Ringelbergius 1531, 21.
Vgl. Grafton 2008, 27–28.
Nunc qui in his potissimum legendi sint auctores. In Grammatica Diomedes, Perottus, Valla: in Dialectica, Aristoteles: in Rhetorica, Cicero et Fabius praecipui. In Astronomia legendi Proclus et Aratus, nam apud Latinos pauci de ea docte scripsere. Si altiora spectes, adiungere potes Ptolemaeum. In Astrologia Firmicus Maternus, qui caeteris elegantius et verius artem tradidit. Is tamen nihil profuerit, nisi composita prius ex Ephemeriduum libris pictura domorum, et nisi habitis rudimentis e barbaris scriptoribus, quorum Alcabitius princeps. In Cosmographia Ptolemaeum: in Geographia Pomponium Melam: in Geometria Euclidem censeo perdiscendos, vgl. Ringelbergius 1531, 21.
Vgl. Ringelbergius 1531, 365, 412.
Ein Exemplar dieser Ausgabe trägt Jacques Toussains handschriftliche Anmerkungen; vgl. Renouard 1991, 77.
Vgl. Irigoin 2006, 238–249.
„Clavius faict commentaires sur le petit livre de Sacrobosco plus long qu’un iour sans pain“, transkribiert in Desgraves 1977, 148–149.
Cui [curriculo] subjungit Pselli Mathematicum breviarium: quo summam quattuor Mathematicarum adolescentes primum cognoscant, tum Euclidis Elementa ac postea Sphaerica, vgl. Vinet 1886, 26.
Balfours Astronomievorlesungen sind erhalten in: Bordeaux, Bibliothèque Municipale, ms. 1588, mit einem Prokloszitat auf Bl. 10v; Todd 2003, 14; zu den Sphaera-Zitaten vgl. Balfour 1605, 148, 215–216.
Vgl. Johnson 1935, 60–86.
Im Folgenden wird The Castle of Knowledge mit The Castle abgekürzt.
Vgl. Johnson und Larkey 1935, 62–64.
Vgl. Johnson und Larkey 1935, 77–78.
Vgl. Todd 2003, 14, Anm. 49.
Vgl. Fletcher (Fletcher 1986, 196).
Vgl. Drake 1999, 152. Catenas Vorlesungen über Proklos’ Euklid-Kommentar als Quelle des platonischen meta-mathematischen Denkens sind in der Bibliothèque Nationale, Paris, MS Latin 7218, Bl. 44–98v erhalten; vgl. De Pace 1993, 340–341.
„Giudicai, che con opera e con effetto giovare a tutti li gioveni Carpeggiani, e questo non solo con publiche, e private lettioni, anzi ad util loro traducendo questo e quell’altro Greco autore in Italiano idioma“, vgl. Scandianese 1556b.
Vgl. Westman 1975b, 330.
Vgl. Feingold 1984, 116–118.
Vgl. Westman 1975b, 324.
Vgl. Westman 1975b, 323–324.
Die Bibliothek des Geographen Gerhard Mercator (1512–1594) enthält Pseudo-Proklos’ Sphaera nicht; vgl. Watelet 1994, 403–418.
Diese Stelle bei Vespucci verdanke ich dem Hinweis von Dr. Angela Axworthy.
Vera igitur coluri ethimologia est quod curtum et truncatum significet, quod Boe. lib. ii. arith. c. xxiiii. de piramide curta loquens sic aut, ut si unitas defuerit primus quadratus, curtam quam graeci coluron vocant, vgl. Vives 1531, 28r.
Proclus in sua quoque sphaera huius sententiae fuit dicens. Sunt et per polos ducti circuli, quos nonnulli coluros vocant. iis accidit, ut in ambitus suos mundi polos recipiant. Coluri autem dicti sunt, quod partes aliquas in se minime conspectas habent. Reliqui enim circuli in mundi circumactu integri cernuntur. Sed colurorum partes quaepiam, quae videlicet ab antarctico. Sub orizonte latent cerni non possunt, vgl. Vives 1531, 28r.
Vgl. Recorde 1556, 24f., 181.
Vgl. Recorde 1556, 269–271.
Vgl. Mästlin 1597, 132–133.
Spheram quoque conscripsit ad eam, quae extat Ioannis a Sacrobusco, quam item enarrari auditoribus conueniet, nisi quis eam malit, quae aedita est a Proclo Diadocho, vgl. Vives 1531, 120r; bemerkt bei Todd 2003, 13.
Vgl. Clavius 1606, 258–259.
Non debet autem inutilis vel otiosa videri repetitio ista Doctrinae Sphaericae; quasi post veterum, Euclidis, Arati, Cleomedis, Gemini, Procli, Theonis, conceptiones, aut post recentiorum, Sacrobosci nimirum, et infinitorum eius commentatorum, interque eos doctissimi et copiosissimi Christophori Clavii, Hartmann etiam, et Virdungi, Wurstisii, et Peuceri, Schreckenfuxii, et Piccolhominei, Brucaei, Winshemii, Moestlini, et novissimi omnium Metii Repetitionen, post Peurbachii, Reinholdi, et Simi Theoricas, causa nulla restet, cur haec doctrina compendiaria denuo tradatur. Nam primo etsi nihil accessisset novi ad doctrinam Veterum, tamen illam ipsam expedit a variis authoribus tradi, cum sint ingenia discentium varia, nec eidem omnes magistro apti discipuli, nec idem omnibus discentibus stilus, nec eadem methodus commoda, vgl. Kepler 1618; zur kritischen Ausgabe vgl. Kepler 1991, 7. Vielen Dank für diese Textstelle an Dr. Jonathan Regier.
Zu den Stellennachweisen vgl. in dieser Arbeit das Kapitel über die Autorschaft von Pseudo-Proklos’ Sphaera.
Vgl. Kepler 1939, 135–136.
Canopus, qui in Rhodos vix a summis montibus est conspicuus, teste Proclo, vgl. Kepler 1939, 149.
Zur Bedeutung der Bilder in Drucken zur Tradition von Sacroboscos Sphaera vgl. Crowther und Barker 2013.
Die Titelblätter der Ausgaben Paris, 1498, Wittenberg, 1549, Ingolstadt, 1526, Antwerpen, 1547, Wittenberg, 1550 sind Hamel 2014, 34, 43, 44, 49, 52 entnommen.
Vgl. Bainbridge 1620, Toussain 1560.
Vgl. Schreckenfuchs 1561 und 1585, Vinet 1573 und 1592 und Toussain 1560.
Vgl. North 1993, 303–314.
Vgl. Valleriani 2017b, 440.
Vgl. Valleriani 2017b, 450. Für weitere Informationen zu Cavellat vgl. Pantin 1988.
Vgl. Pantin 1988, 241, 246.
Vgl. Renouard 1991, 75–81.
„Dedans trois mois il [= le lecteur du Roy] commencera à lire Aristote au livre De Coelo, le livre de la Sphère de Proclus, ou bien les Eléments d’ Euclide et de Sacrobosco“, vgl. Waddington 1855, 178–179.
Vgl. Valleriani (2017b, 427).
Astronomica de sphaera, de astrolabo, de hypothesibus astronomicis in manibus hominum versantur. Tantus igitur mathematicus Proclus fuit, vgl. Ramus 1569, 37.
Vgl. Norton 1984, 140–142; Todd 1995, 106, Anm. 6.
Vgl. http://www.lycee-elie-vinet.fr/index.php?id_menu=14, besucht am 2.08.2019.
Vgl. Valleriani 2017b, 441.
Vgl. Valleriani 2017b, 442f..
Vgl. Valleriani 2017b, 446f..
Vgl. Hack 1995, 31–33; Denzel 1996, 66–67.
Vgl. Krayer 1991, 111–113.
Vgl. Valleriani 2017b, 447.
Vgl. Thorndike 1949, 412ff..
Vgl. Valleriani 2017a, 14–15.
Vgl. Noreña 1970, 247–248; Schneider 2006, 11.
Me iam mathematicas omnes coniectaneis meis in volumina transtulisse, vgl. Heiberg 1896, 64–65, Brief 7.
Recondita et abstrusa de Graecis eminentissimis sumpta autoribus et quae nos quoque duce deo addidimus, vgl. Heiberg 1896, 89–90, Brief 38.
Vgl. Westman 1975a, 184.
Vgl. Catt 2014, 143–149,161–165, hier: 143.
Vgl. Valleriani 2017b, 451.
Vgl. Crocioni 1910, 25, 73; Crocioni 1907, 3, 8.
Vgl. Worth 1988, 79–80; Todd 1995, 106.
