For the following list of calculations and problems in al-Hawārī’s book, we have adopted our transcription of the Arabic notation. This is explained in our commentary, especially at 219.1. We had introduced the algebraic notation in our commentary at 211.2, and notation for fractions is explained in our commentary in the chapter on fractions, beginning at 135.1. Here is a quick guide to the notation:
The notation is a transcription of how it appears, or in some cases would have appeared, in the manuscripts. With the exception of the figures for double false position, we put the notation in red, as it is in many Arabic manuscripts. It should be read right to left.
The reversed letter “
![\scalebox {-1}[1]{\ell }](../../../media/sources/14/6/EOAineq_6_1.png) ” stands for “less”, and indicates that the number to its left is removed from the number to its right. So, an apotome that we would write as
” stands for “less”, and indicates that the number to its left is removed from the number to its right. So, an apotome that we would write as
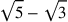 is shown as
is shown as
![\leavevmode {\color {red}\sqrt{3}~\scalebox {-1}[1]{\ell }~\sqrt{5}}](../../../media/sources/14/6/EOAineq_6_3.png) . See our commentary at 86.1. Binomials have no sign for “+”, so the modern
. See our commentary at 86.1. Binomials have no sign for “+”, so the modern
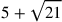 is shown as
is shown as
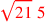 .
.
Instead of the letter jīm above a number to indicate square root, we use the modern “
 ” which functions similarly.
” which functions similarly.
We write “=” for the “equals” in algebraic equations, and for no other purpose. This sign functions like the elongated lām, its counterpart in Arabic manuscripts.
Because the transcribed notation for algebra is entirely different from our notation, we include the versions of the calculations in modern notation as well, even if it sometimes makes little sense (as in the calculations from through 222.1).
An “L” is placed after the reference for examples taken from Ibn al-Bannāʾ’s Lifting the Veil.
Part 1. On known numbers
Chapter 1. On whole numbers
| Passage | Example |
|---|---|
| 65.2 | Examples of whole numbers: 15, 18, etc. |
| 65.2 | Examples of fractions:
 , ,
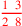 , ,
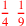 , ,
 , ,
![\leavevmode {\color {red}{1\over 9}~\scalebox {-1}[1]{\ell }~{5\over 6}}](../../../media/sources/14/6/EOAineq_6_11.png) |
| 65.6,10,17, 66.1 | Even: 10, 50; evenly-even: 32; evenly-odd: 14; |
| 66.7 | Odd prime: 11, 29; Oddly-odd: 15, composed of 3 by 5 |
| 66.17 | Even square: 36 is 6 by 6 |
| 67.3 | Even, composed of two unequal numbers (a surface): |
| 67.3 | Even, composed of three unequal numbers (a surface): |
| 67.12 | Even cube: 64 is 4 by 4 by 4 |
| 67.19 | Odd square: 25 is 5 by 5 |
| 68.1 | Odd, composed of two unequal numbers (a surface): |
| 68.8 | Odd cube: 27 is composed of 3 by 3 by 3 |
| 70.8, 70.23 | Sample figures for numbers: 9367184225 and 84725 |
| 71.6 | 143 has three places |
| 71.16 | The rank of 10000000 is 8 |
| 72.4 | The name of 1000000000 is thousands thousands of thousands |
| 74.17 | Adding from the units place: add 4043 to 2685 to get 6728 |
| 75.9 | Adding from the highest place: add 978 to 456 to get 1434 |
| 75.20 | The most one can get by adding is one extra place: |
| 76.15 | Chessboard: add the first sixteen squares to get 65535 |
| 77.11 | Chessboard: add the first eight squares with 4 as the first square to get 1020 |
| 78.4 | Adding five numbers with a ratio of
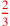 : : |
| 79.4 | Adding six numbers starting at 10, with a difference of three: |
| 79.13 | Add 1, 2, 3, …, 10 to get 55 |
| 79.18 | Add the squares of 1, 2, 3, …, 10 to get 385 |
| 80.1 | Add the cubes of 1, 2, 3, …, 10 to get 3025 |
| 80.5 | Add 1, 3, 5, 7, 9 to get 25 |
| 80.10 | Add the squares of 1, 3, 5, 7, 9 to get 165 |
| 80.15 | Add the cubes of 1, 3, 5, 7, 9 to get 1225 |
| 80.20 | Add 2, 4, 6, 8, 10 to get 30 |
| 81.4 | Add the squares of 2, 4, 6, 8, 10 to get 220 |
| 81.9 | Add the squares of 2, 4, 6, 8, 10, 12 to get 364 |
| 81.15 | Add the cubes of 2, 4, 6, 8, 10 to get 1800 |
| 83.16 | Subtracting from the highest place: |
| 84.13 | Subtracting from the units place: |
| 85.8 | The most one can get by subtracting is one fewer place: |
| 86.9 L | ![\leavevmode {\color {red}2~\scalebox {-1}[1]{\ell }~5~\scalebox {-1}[1]{\ell }~7~\scalebox {-1}[1]{\ell }~8~\scalebox {-1}[1]{\ell }~10}](../../../media/sources/14/6/EOAineq_6_13.png) is 6 is 6 |
| 87.19 | Casting out nines from 6435 gives nothing |
| 88.5 | Casting out eights from 5393 gives 1 |
| 89.4 | Casting out sevens from 23786435 gives 1 |
| 90.7 | Casting out sevens from 58064 gives 6 |
| 91.4 | Add 43 to 64 to get 107 |
| 91.16 | Subtract 74 from 96 to get 22 |
| 92.10 | Multiply 12 by 16 to get 192 |
| 92.17 L | Multiply
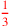 by by
 to get to get
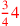  by by
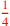 to get to get
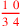 |
| 93.10 | Divide 1488 by 12 to get 124 |
| 93.15 L | Divide
 by by
 to get to get
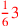 . Cast out sevens to check: multiply . Cast out sevens to check: multiply
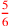 by by
 , then convert to 4ths of 6ths to get , then convert to 4ths of 6ths to get
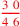 |
| 94.1 | Denominate 11 with 15 to get
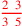 . Cast out sevens to check: multiply 4 by 1 to get 4 . Cast out sevens to check: multiply 4 by 1 to get 4 |
| 94.5 L | Denominate
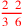 with with
 to get to get
 . Cast out sevens to check: multiply 2 by 2, adjust for the denominators to get 3 . Cast out sevens to check: multiply 2 by 2, adjust for the denominators to get 3 |
| 95.10 L | Meanings of multiplication: 3 men, each has 5 dirhams; 5 dirhams, how many thirds? |
| 96.3 | Multiplication by shifting: multiply 43 by 54 to get 2322 |
| 97.4 | Vertical multiplication: multiply 42 by 37 to get 1554 |
| 98.15 | Multiplication by half-shifting: |
| 100.5 | Lattice multiplication: multiply 435 by 287 to get 124845 |
| 102.1 | Vertical multiplication (no shifting): |
| 104.10 | Sleeper multiplication (no shifting): |
| 107.6 | Multiply 444 by 333 to get 147852 |
| 108.13 | Multiplication by excess: multiply 12 by 15 to get 180 |
| 109.1 | Multiply 13 by 17 to get 221 |
| 109.10 | Multiplication by denomination: multiply 6 by 12 to get 72 |
| 110.6 | Another method of multiplication by denomination: |
| 110.12 | Multiply 12 by 15 to get 180 |
| 111.1 | Multiply 3 by 15 to get 45 |
| 111.15 | Multiplication by nines: multiply 444 by 999 to get 443556 |
| 112.10 | Another method of multiplication by nines: |
| 113.1 | Multiplication by squaring: multiply 17 by 19 to get 323 |
| 113.9 | Another squaring method: multiply 25 by 15 to get 375 |
| 113.19 | Another squaring method: multiply 36 by 14 to get 504 |
| 114.8 | Multiplication with zeros: multiply 30 by 140 to get 4200 |
| 117.16 L, 118.1 L | Meanings of division: Divide 15 dirhams among 3 men; |
| 119.1 | Divide 245 by 12 to get
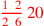 |
| 120.5 | Divide 44 among 11 men to get 4 |
| 120.10 | Divide 96 by 12 to get 8 |
| 120.16 | Divide 35 by 15 to get
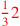 |
| 121.4 | Apportionment. Wealth of donors: 4, 5, 6 dinars, |
| 122.5 | Apportionment. Wealth of donors:
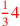 , ,
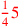 , ,
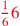 dinars, dinars, |
| 123.22 | Common denomination: denominate 11 with 15 to get
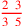 |
| 124.12,14,17 | Other denominations: denominate 4 with 12 to get
 ; ;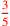 ; denominate 10 with 16 to get ; denominate 10 with 16 to get
 |
| 124.20ff | Finding divisors: 50, 36, 66, 42, 64, 68, 14, 26, 81, 39, 123, 77, 221 |
| 129.6 | Restore 8 to 19; reduce 50 to 6 |
| 129.8 | Restore 3 to 6: divide 6 by 3 to get 2 |
| 129.12 | Reduce 8 to 3. Denominate 3 with 8 to get
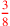 |
Part 1, Chapter 2. On fractions
| Passage | Example |
|---|---|
| 134.2 L | Language of parts:
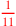 , ,
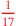 |
| 134.8 | Numerator
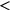 denominator: denominator:
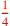 , ,
 , ,
 ; and ; and
 through through
 |
| 135.1 | Fractions with two or more names:
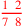 ; ;
 |
| 135.10 L | A related fraction:
 |
| 136.8 L | A distinct fraction:
 |
| 137.1 L | A portioned fraction:
 |
| 137.13 | The numerator of
 is 1 is 1 |
| 138.5 | The numerator of
 is 596 is 596 |
| 139.2 | The numerator of
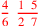 is 122 is 122 |
| 139.11 | The numerator of
 is 105 is 105 |
| 140.8 | The numerator of
![\leavevmode {\color {red}{1\over 9}~\scalebox {-1}[1]{\ell }~{6\over 8}}](../../../media/sources/14/6/EOAineq_6_57.png) is 46 is 46 |
| 141.1 | The numerator of
![\leavevmode {\color {red}{1\over 3}~\scalebox {-1}[1]{\ell }~{1~\,6\over 2~\,7}}](../../../media/sources/14/6/EOAineq_6_58.png) is 26 is 26 |
| 141.11 | The numerator of the connected fraction
![\leavevmode {\color {red}{1\over 5}~\scalebox {-1}[1]{\ell }~{1\over 7}~\scalebox {-1}[1]{\ell }~{1\over 4}~\scalebox {-1}[1]{\ell }~{1\over 3}\,5}](../../../media/sources/14/6/EOAineq_6_59.png) , ,![\leavevmode {\color {red}{1\over 5}\,{1\over 7}\,{1\over 4}\,\scalebox {-1}[1]{\ell }\,{1\over 3}\,5}](../../../media/sources/14/6/EOAineq_6_60.png) , is 912 , is 912 |
| 142.6 | The numerator of the distinct fractions
![\leavevmode {\color {red}{1\over 5}~\scalebox {-1}[1]{\ell }~{1\over 7}~\scalebox {-1}[1]{\ell }~{1\over 4}~\scalebox {-1}[1]{\ell }~{1\over 3}\,5}](../../../media/sources/14/6/EOAineq_6_61.png) is 1991 is 1991 |
| 143.5 | The numerator of
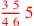 is 143 is 143 |
| 143.13 | The numerator of
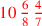 is 740 is 740 |
| 144.10 | The numerator of
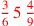 is 147 is 147 |
| 145.4 | The numerator of
 is 106 is 106 |
| 147.4 | Add
 to to
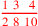 to get to get
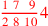 |
| 147.15 | Subtract
![\leavevmode {\color {red}{1\over 3}~\scalebox {-1}[1]{\ell }~2\,{7\over 10}}](../../../media/sources/14/6/EOAineq_6_69.png) from from
 to get to get
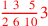 |
| 149.8 | Multiply
 by by
 to get to get
 |
| 150.2 | Multiply
 by by
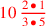 to get to get
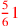 |
| 151.4 | Divide
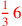 by by
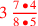 to get to get
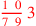 |
| 151.14 | Denominate
![\leavevmode {\color {red}{2\over 9}~\scalebox {-1}[1]{\ell }~{1\over 4}\,3}](../../../media/sources/14/6/EOAineq_6_81.png) with with
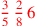 to get to get
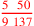 |
| 152.11 | Divide
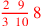 by by
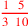 to get to get
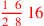 |
| 153.3 | Denominate
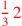 with with
 to get to get
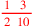 |
| 153.12 L | Divide 5 by
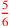 to get 6; denominate to get 6; denominate
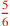 with 5 to get with 5 to get
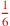 |
| 154.6ff | Restore
 to to
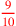 ; ;
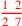 to to
 ; ;
 to 10; 5 to to 10; 5 to
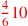 ; ;
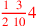 to 8; to 8;
![\leavevmode {\color {red}{1\over 3}~\scalebox {-1}[1]{\ell }~{3\over 5}3}](../../../media/sources/14/6/EOAineq_6_100.png) to to
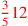 |
| 155.11ff | Reduce
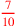 to to
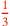 ; 8 to ; 8 to
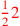 ; 10 to ; 10 to
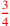 ; ;
 to to
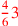 ; ;
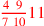 to 5; to 5;
 to to
 |
| 157.2 L | Convert
 to tenths. Answer: to tenths. Answer:
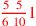 |
| 157.12 L | How many tenths are in
 ? Again, it is ? Again, it is
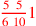 |
| 158.1 L | How many tenths are in 5? Answer: 50 |
| 158.11 | How many ninths are in
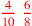 ? Answer: ? Answer:
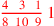 |
Part 1, Chapter 3. On roots
| Passage | Example |
|---|---|
| 163.4 L | Examples:
 , ,
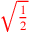 , ,
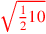 , ,
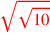 |
| 166.13 |  is 25 is 25 |
| 167.8 |  is approximately is approximately
 |
| 167.14 |  is approximately is approximately
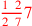 |
| 168.1 | 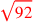 is approximately is approximately
 |
| 168.16 | 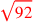 is approximately is approximately
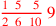 |
| 169.4 | 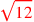 is approximately is approximately
 |
| 169.10,17 L | 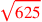 is 25; is 25;
 is 27 is 27 |
| 170.6 |  is 10 is 10 |
| 170.16 |  is is
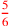 |
| 171.1 | 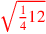 is is
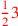 |
| 171.6 | 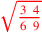 is is
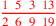 |
| 171.15 |  is approximately is approximately
 |
| 172.6 | 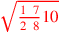 is approximately is approximately
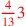 |
| 172.12 | 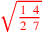 is approximately is approximately
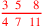 |
| 173.13 L | Binomials:
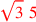 ; ;
 |
| 173.16 L | Apotomes:
![\leavevmode {\color {red}\sqrt{3}~\scalebox {-1}[1]{\ell }~5}](../../../media/sources/14/6/EOAineq_6_149.png) ; ;
![\leavevmode {\color {red}\sqrt{3}~\scalebox {-1}[1]{\ell }~\sqrt{5}}](../../../media/sources/14/6/EOAineq_6_150.png) |
| 174.5 | 1st & 4th binomials:
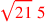 , ,
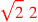 |
| 174.8 | 2nd & 5th binomials:
 , ,
 |
| 174.11 | 3rd & 6th binomials:
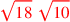 , ,
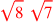 |
| 175.11 |  is is
 |
| 175.19 | ![\leavevmode {\color {red}\sqrt{\sqrt{60}~\scalebox {-1}[1]{\ell }~8}}](../../../media/sources/14/6/EOAineq_6_159.png) is is
![\leavevmode {\color {red}\sqrt{3}~\scalebox {-1}[1]{\ell }~\sqrt{5}}](../../../media/sources/14/6/EOAineq_6_160.png) |
| 176.6 |  is is
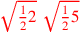 ; ;
![\leavevmode {\color {red}\sqrt{\sqrt{55}~\scalebox {-1}[1]{\ell }~8}}](../../../media/sources/14/6/EOAineq_6_163.png) is is
![\leavevmode {\color {red}\sqrt{{1\over 2}2}~\scalebox {-1}[1]{\ell }~\sqrt{{1\over 2}5}}](../../../media/sources/14/6/EOAineq_6_164.png) |
| 176.10 |  is is
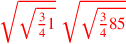 ; ;![\leavevmode {\color {red}\sqrt{\sqrt{112}~\scalebox {-1}[1]{\ell }~7}}](../../../media/sources/14/6/EOAineq_6_167.png) is is
![\leavevmode {\color {red}\sqrt{\sqrt{{3\over 4}1}}~\scalebox {-1}[1]{\ell }~\sqrt{\sqrt{{3\over 4}85}}}](../../../media/sources/14/6/EOAineq_6_168.png) |
| 176.15 | 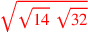 is is
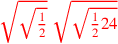 ; ;![\leavevmode {\color {red}\sqrt{\sqrt{14}~\scalebox {-1}[1]{\ell }~\sqrt{32}}}](../../../media/sources/14/6/EOAineq_6_171.png) is is
![\leavevmode {\color {red}\sqrt{\sqrt{1\over 2}}~\scalebox {-1}[1]{\ell }~\sqrt{\sqrt{{1\over 2}24}}}](../../../media/sources/14/6/EOAineq_6_172.png) |
| 176.20 |  is is
![\leavevmode {\color {red}\sqrt{\sqrt{{3\over 4}4}~\scalebox {-1}[1]{\ell }~{1\over 2}3}~\sqrt{\sqrt{{3\over 4}4}~{1\over 2}3}}](../../../media/sources/14/6/EOAineq_6_174.png) ; ;![\leavevmode {\color {red}\sqrt{\sqrt{30}~\scalebox {-1}[1]{\ell }~7}}](../../../media/sources/14/6/EOAineq_6_175.png) is is
![\leavevmode {\color {red}\sqrt{\sqrt{{3\over 4}4}~\scalebox {-1}[1]{\ell }~{1\over 2}3}~\scalebox {-1}[1]{\ell }~\sqrt{\sqrt{{3\over 4}4}~{1\over 2}3}}](../../../media/sources/14/6/EOAineq_6_176.png) |
| 177.5 |  is is
![\leavevmode {\color {red}\sqrt{\sqrt{{1\over 4}~{1\over 2}2}~\scalebox {-1}[1]{\ell }~\sqrt{5}}~\sqrt{\sqrt{{1\over 4}~{1\over 2}2}~\sqrt{5}}}](../../../media/sources/14/6/EOAineq_6_178.png) ; ;![\leavevmode {\color {red}\sqrt{3~\scalebox {-1}[1]{\ell }~\sqrt{20}}}](../../../media/sources/14/6/EOAineq_6_179.png) is is
![\leavevmode {\color {red}\sqrt{\sqrt{{1\over 4}~{1\over 2}2}~\scalebox {-1}[1]{\ell }~\sqrt{5}}~\scalebox {-1}[1]{\ell }~\sqrt{\sqrt{{1\over 4}~{1\over 2}2}~\sqrt{5}}}](../../../media/sources/14/6/EOAineq_6_180.png) |
| 177.11 |  is is
![\leavevmode {\color {red}\sqrt{{1\over 2}~\scalebox {-1}[1]{\ell }~\sqrt{{3\over 4}2}}~\sqrt{\sqrt{{3\over 4}2}~{1\over 2}}}](../../../media/sources/14/6/EOAineq_6_182.png) ; ;![\leavevmode {\color {red}\sqrt{\sqrt{10}~\scalebox {-1}[1]{\ell }~\sqrt{11}}}](../../../media/sources/14/6/EOAineq_6_183.png) is is
![\leavevmode {\color {red}\sqrt{{1\over 2}~\scalebox {-1}[1]{\ell }~\sqrt{{3\over 4}2}}~\scalebox {-1}[1]{\ell }~\sqrt{\sqrt{{3\over 4}2}~{1\over 2}}}](../../../media/sources/14/6/EOAineq_6_184.png) |
| 179.7,11 | Add
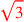 to to
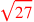 to get to get
 |
| 179.16 | Add
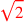 to to
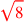 to get to get
 |
| 179.20 | Add half of
 to two to two
 s to get s to get
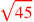 |
| 180.10 | Add
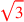 to to
 to get to get
 |
| 180.15 | Add half of
 to to
 of of
 to get to get
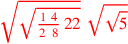 |
| 181.6 | Subtract
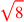 from from
 to get to get
 |
| 181.12,16 | Subtract
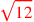 from from
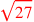 to get to get
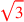 |
| 182.4 | Subtract
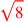 from from
 to get to get
![\leavevmode {\color {red}\sqrt{8}~\scalebox {-1}[1]{\ell }~\sqrt{10}}](../../../media/sources/14/6/EOAineq_6_209.png) |
| 183.4 | Multiply
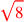 by by
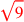 to get to get
 |
| 183.7 | Multiply
 by by
 to get to get
 |
| 183.11 | Multiply
 by by
 to get to get
 |
| 183.15 | Multiply 3 by
![\leavevmode {\color {red}2~\scalebox {-1}[1]{\ell }~\sqrt{7}}](../../../media/sources/14/6/EOAineq_6_219.png) to get to get
![\leavevmode {\color {red}6~\scalebox {-1}[1]{\ell }~\sqrt{63}}](../../../media/sources/14/6/EOAineq_6_220.png) |
| 184.1 | Multiply 3 by
 to get to get
 |
| 184.4 | Multiply 2 by
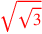 to get to get
 |
| 184.11 | Multiply 2 by two
 s to get s to get
 |
| 184.18 | Multiply 5 by three
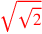 s to get s to get
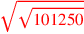 |
| 185.6 | Multiply
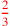 by half of by half of
 to get to get
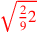 |
| 185.12 | Multiply
 by half of by half of
 to get to get
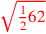 |
| 186.1 | Duplicate
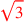 twice to get twice to get
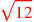 |
| 186.4 | Duplicate
 five times to get five times to get
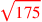 |
| 186.8 | Half of
 is is
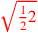 |
| 186.11 |  of of
 is is
 |
| 187.4 | Divide
 by by
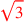 to get to get
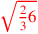 |
| 187.7 | Denominate
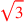 with with
 to get to get
 |
| 187.10 | Divide
 by by
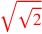 to get to get
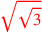 |
| 187.14 | Denominate
 with with
 to get to get
 |
| 188.6 | Divide
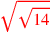 by by
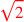 to get to get
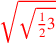 |
| 188.11 | Divide two
 s by 2 to get s by 2 to get
 |
| 188.15 | Divide half of
 by by
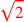 to get to get
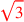 |
| 189.1 | Divide 12 by
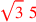 to get to get
![\leavevmode {\color {red}\sqrt{9~~9\over 11~\,11}~\scalebox {-1}[1]{\ell }~{8\over 11}2}](../../../media/sources/14/6/EOAineq_6_265.png) |
| 189.11 | Divide 10 by
![\leavevmode {\color {red}\sqrt{7}~\scalebox {-1}[1]{\ell }~ 3}](../../../media/sources/14/6/EOAineq_6_266.png) to get to get
 |
Part 2. Finding unknown numbers
Chapter 1. Solving problems by proportion
| Passage | Example |
|---|---|
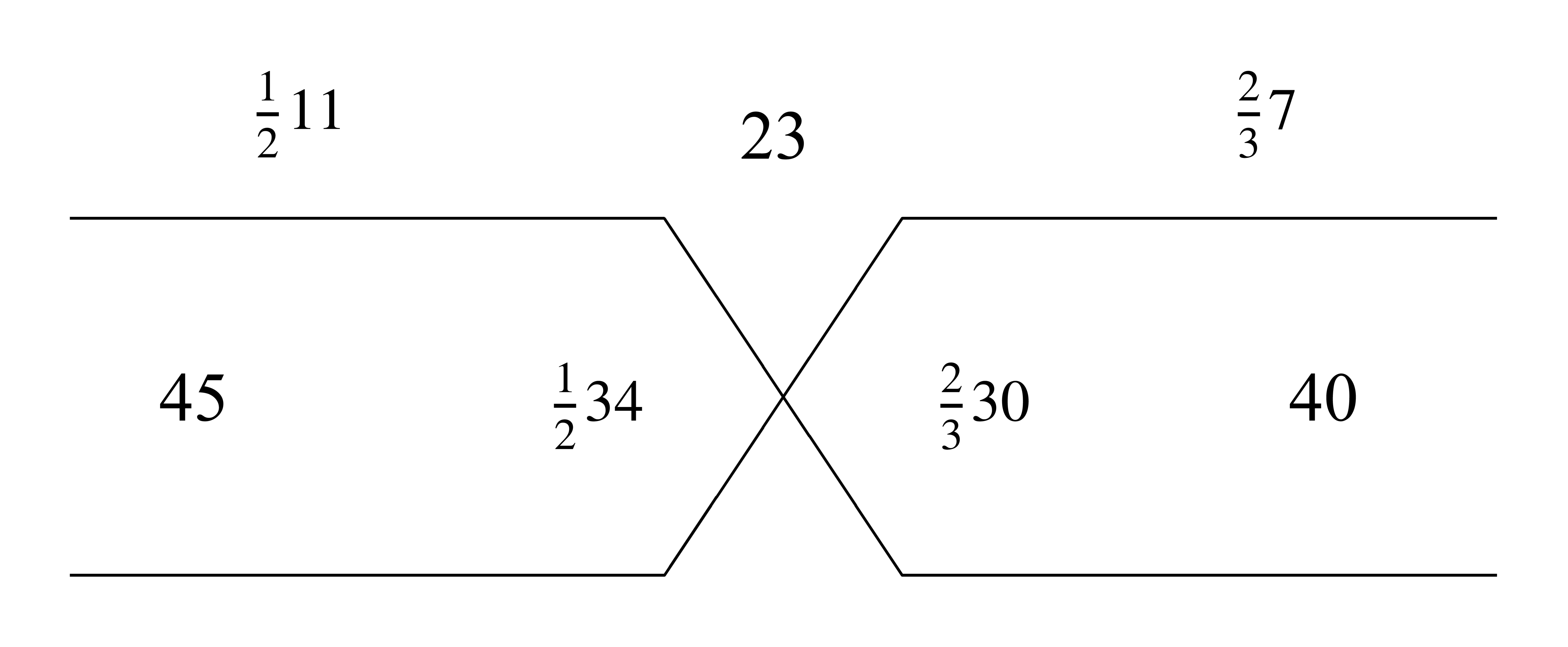
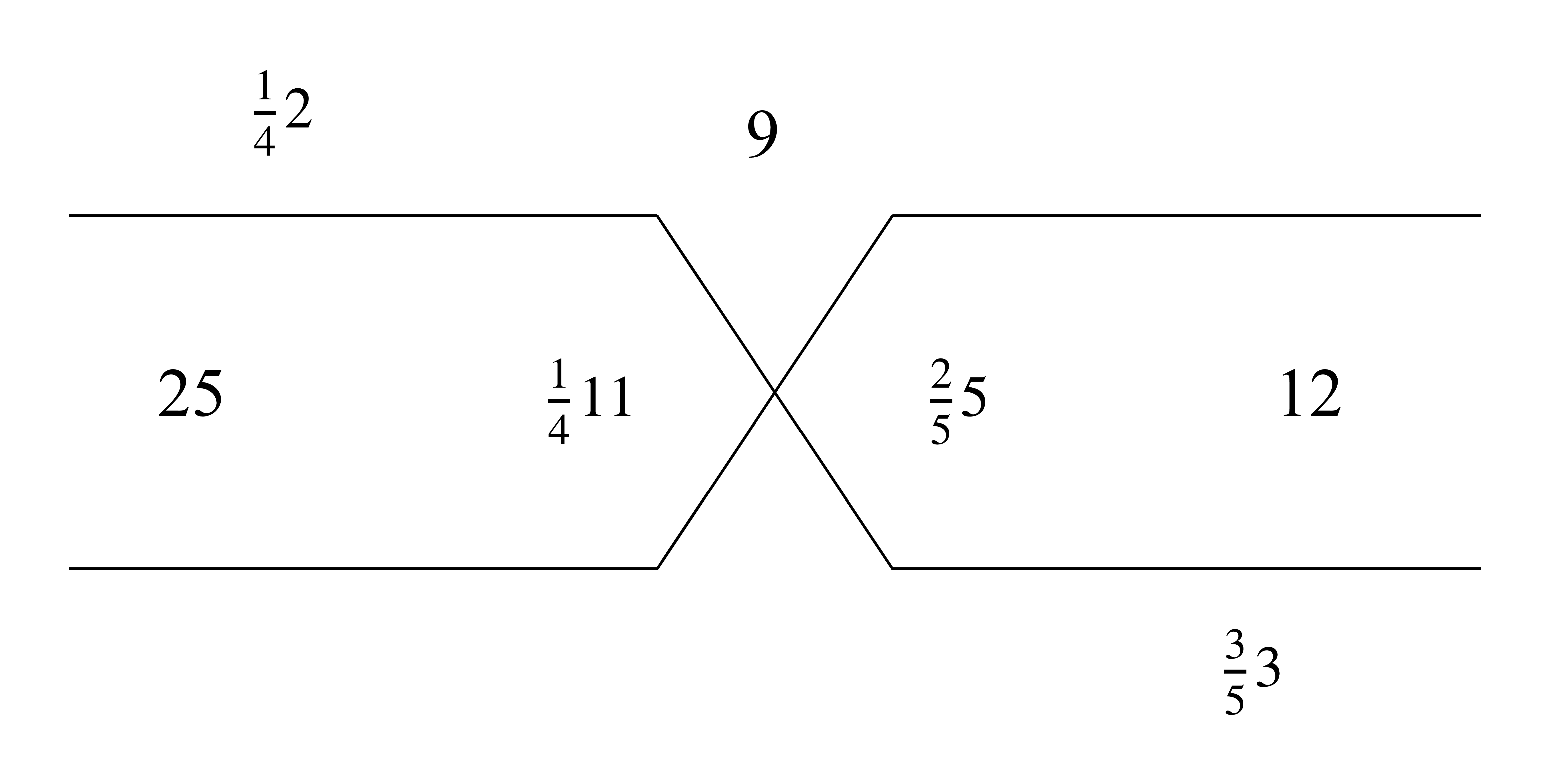
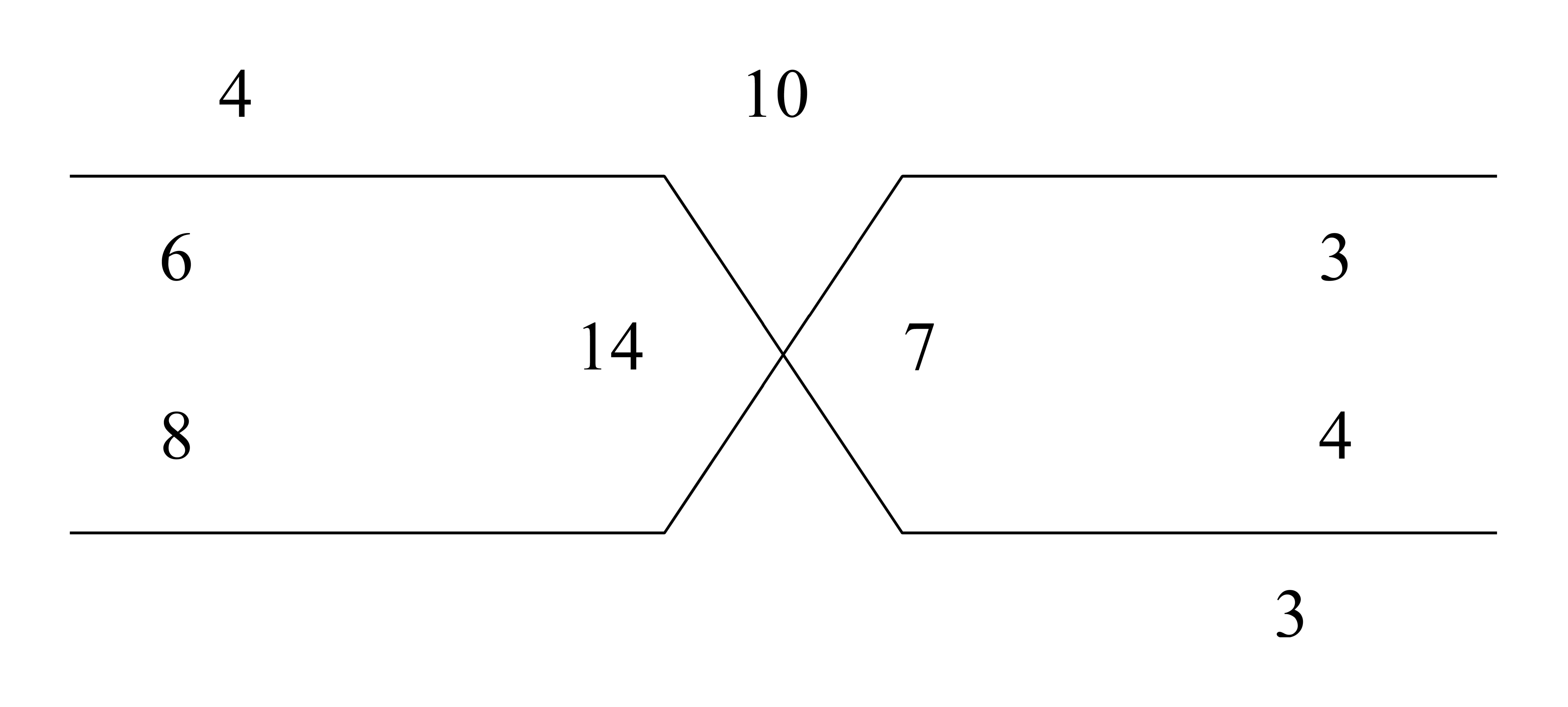
| 195.16 | Example of four proportional numbers:
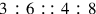 |
 |
|
 |
|
 |
|
 |
|
 |
|
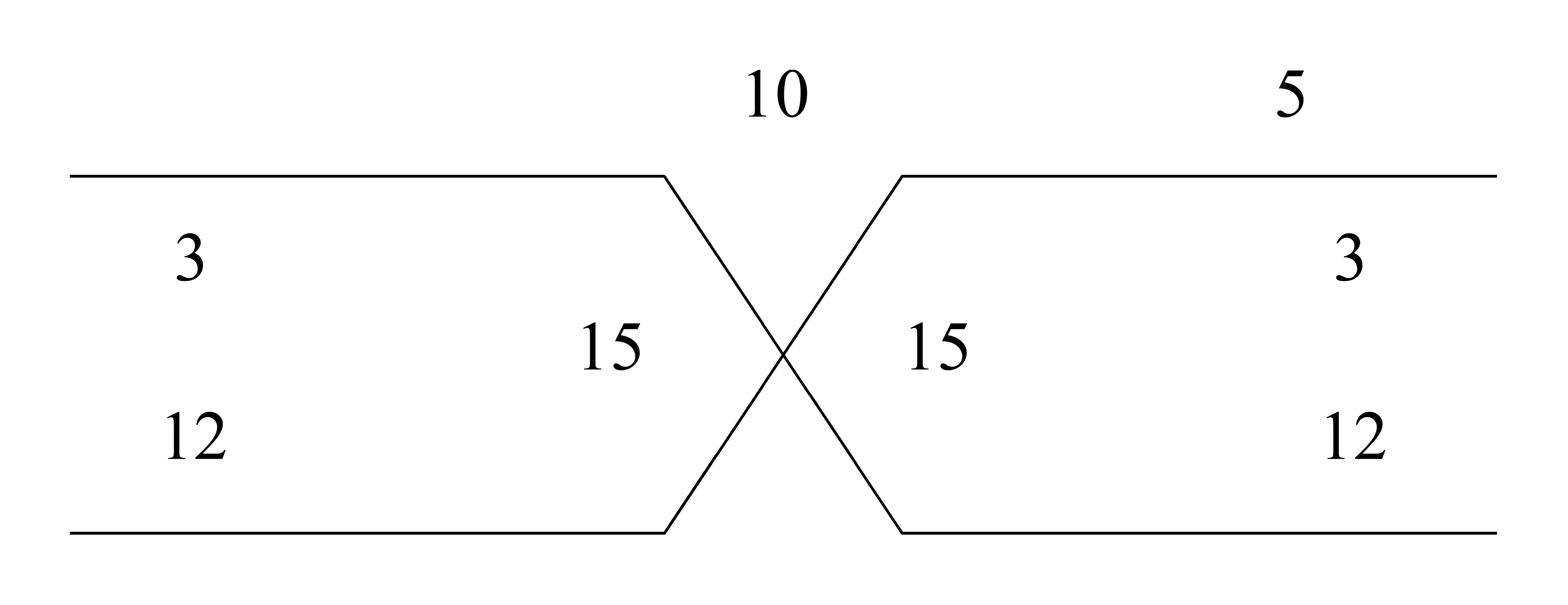 |
|
 |
|
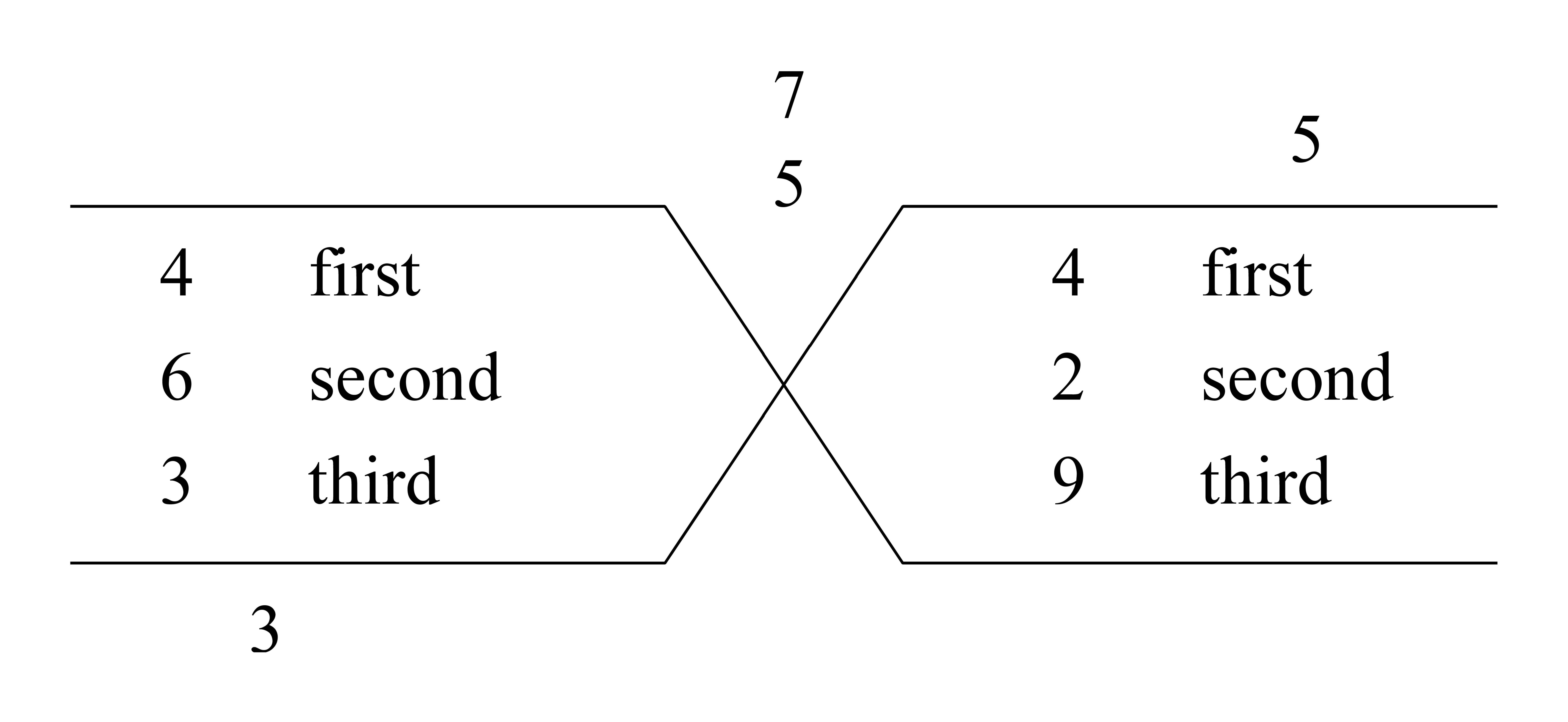 |
|
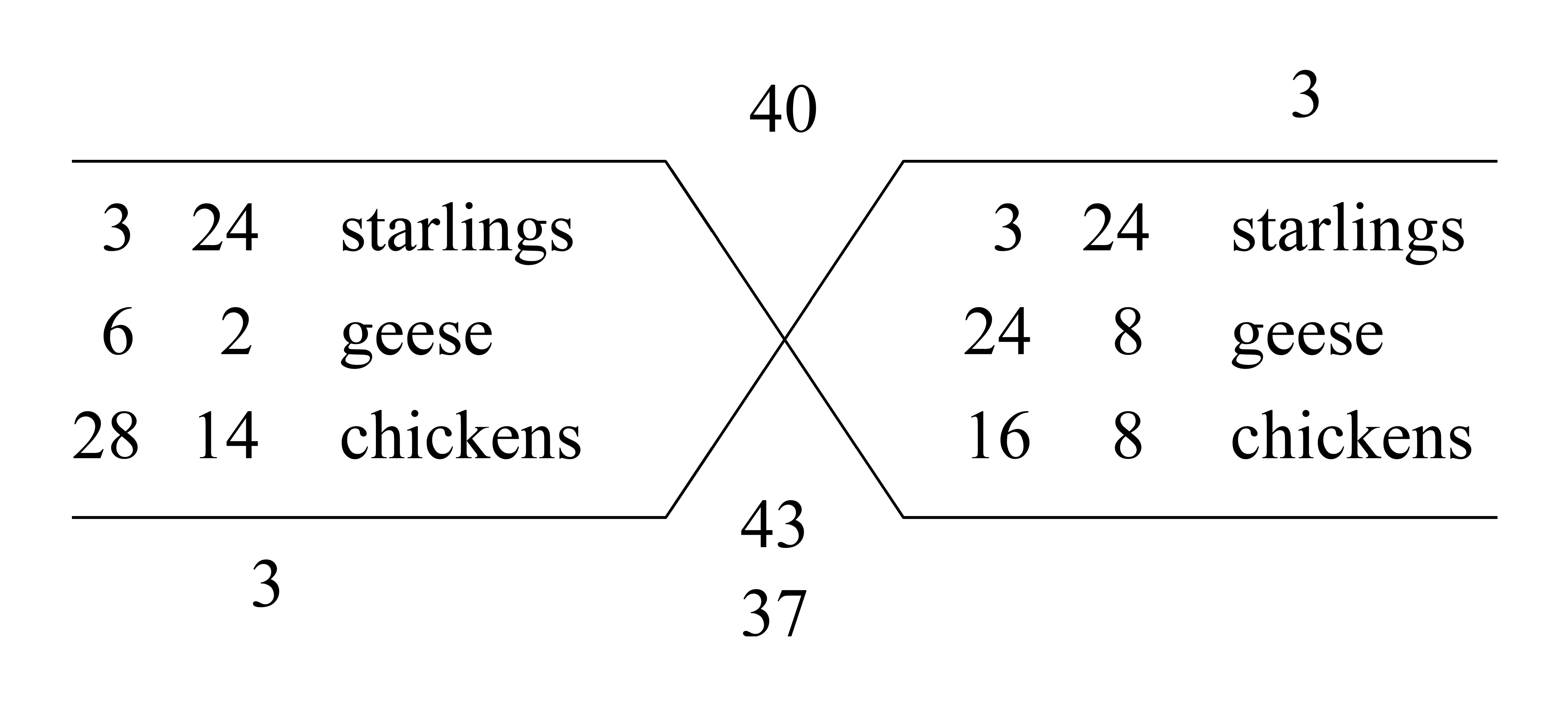 |
Part 2, Chapter 2. Solving problems by algebra
| Passage | Example |
|---|---|
| 211.15 | Simple equations:
 ; ;
 ; ;
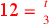 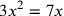 ; ;
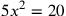 ; ;
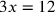 ) ) |
| 212.6 | Composite equations:
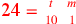 ; ;
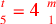 ; ;
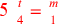 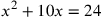 ; ;
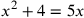 ; ;
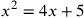 ) ) |
| 213.7 | Solve
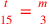 to get to get
 is 5 and is 5 and
 is 25 is 25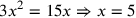 , ,
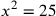 ) ) |
| 213.13 | Solve
 to get to get
 is 9 and is 9 and
 is 3 is 3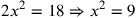 , ,
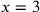 ) ) |
| 214.1 | Solve
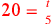 to get to get
 is 4 and is 4 and
 is 16 is 16 , ,
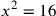 ) ) |
| 214.9 | Solve
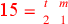 to get to get
 is 3 and is 3 and
 is 9 is 9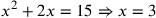 , ,
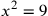 ) ) |
| 215.6 | Solve
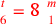 to get to get
 is 4 and is 4 and
 is 16, or is 16, or
 is 2 and is 2 and
 is 4 is 4 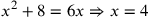 , ,
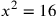 or or
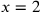 , ,
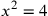 ) ) |
| 215.14 | Solve
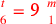 to get to get
 is 9 and is 9 and
 is 3 is 3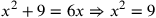 , ,
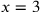 ) ) |
| 216.13 | Solve
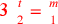 to get to get
 is 3 and is 3 and
 is 9 is 9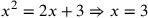 , ,
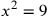 ) ) |
| 217.10 | 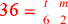 simplifies to simplifies to
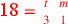 ( (
 ) ) |
| 218.1 |  simplifies to simplifies to
 ( (
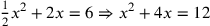 ) ) |
| 219.2 | Add
 , ,
 , and , and
 to get to get
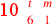 ( (
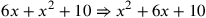 ) ) |
| 219.5 L | Add
![\leavevmode {\color {red}{t\atop 1}~\scalebox {-1}[1]{\ell }~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_331.png) to to
 to get to get
![\leavevmode {\color {red}{t\atop 1}~\scalebox {-1}[1]{\ell }~\hbox{10}~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_333.png) ( (
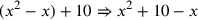 ) ) |
| 219.7 L | Add
![\leavevmode {\color {red}{m\atop 1}~\scalebox {-1}[1]{\ell }~{m\atop 2}}](../../../media/sources/14/6/EOAineq_6_335.png) to to
 to get to get
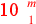 ( (
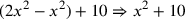 ) ) |
| 219.10 L | Add
![\leavevmode {\color {red}{t\atop 2}~\scalebox {-1}[1]{\ell }~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_339.png) to to
 to get to get
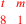 ( (
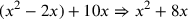 ) ) |
| 219.12 L | Add
![\leavevmode {\color {red}{t\atop 5}~\scalebox {-1}[1]{\ell }~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_343.png) to to
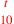 to get to get
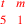 ( (
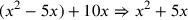 ) ) |
| 220.1 | Subtract
 from from
 to get to get
![\leavevmode {\color {red}{t\atop 1}~\scalebox {-1}[1]{\ell }~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_349.png) ( (
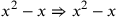 ) ) |
| 220.3 | Subtract
 from from
 to get to get
![\leavevmode {\color {red}\hbox{10}~\scalebox {-1}[1]{\ell }~{t\atop 3}~{m\atop 2}}](../../../media/sources/14/6/EOAineq_6_353.png) 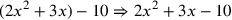 ) ) |
| 220.9 | Subtract
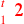 from from
![\leavevmode {\color {red}{t\atop 3}~\scalebox {-1}[1]{\ell }~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_356.png) to get to get
![\leavevmode {\color {red}\hbox{2}~\scalebox {-1}[1]{\ell }~{t\atop 4}~\scalebox {-1}[1]{\ell }~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_357.png) 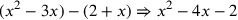 ) ) |
| 221.1 | Subtract
![\leavevmode {\color {red}{t\atop 5}~\scalebox {-1}[1]{\ell }~\hbox{52}}](../../../media/sources/14/6/EOAineq_6_359.png) from from
 to get to get
![\leavevmode {\color {red}{t\atop 22}~\scalebox {-1}[1]{\ell }~{t\atop 5}~{c\atop 2}}](../../../media/sources/14/6/EOAineq_6_361.png) 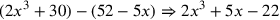 ) ) |
| 221.13 | Subtract
![\leavevmode {\color {red}{t\atop 4}~\scalebox {-1}[1]{\ell }~\hbox{12}}](../../../media/sources/14/6/EOAineq_6_363.png) from from
![\leavevmode {\color {red}{t\atop 2}~\scalebox {-1}[1]{\ell }~{m\atop 3}}](../../../media/sources/14/6/EOAineq_6_364.png) to get to get
![\leavevmode {\color {red}\hbox{12}~\scalebox {-1}[1]{\ell }~{t\atop 2}~{m\atop 3}}](../../../media/sources/14/6/EOAineq_6_365.png) 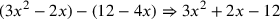 ) ) |
| 222.1 | Subtract
![\leavevmode {\color {red}{m\atop 2}~\scalebox {-1}[1]{\ell }~{c\atop 1}}](../../../media/sources/14/6/EOAineq_6_367.png) from from
![\leavevmode {\color {red}{t\atop 4}~\scalebox {-1}[1]{\ell }~\hbox{30}}](../../../media/sources/14/6/EOAineq_6_368.png) to get to get
![\leavevmode {\color {red}{t\atop 4}~\scalebox {-1}[1]{\ell }~{c\atop 1}~\scalebox {-1}[1]{\ell }~{m\atop 2}~\hbox{30}}](../../../media/sources/14/6/EOAineq_6_369.png) 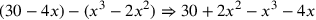 ) ) |
| 223.2 | ![\leavevmode {\color {red}{t\atop 1}~\hbox{2}={t\atop 3}~\scalebox {-1}[1]{\ell }~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_371.png) simplifies to simplifies to
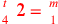 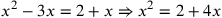 ) ) |
| 223.7 | ![\leavevmode {\color {red}{t\atop 5}~\scalebox {-1}[1]{\ell }~\hbox{24}={t\atop 3}~\scalebox {-1}[1]{\ell }~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_374.png) simplifies to simplifies to
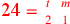 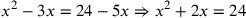 ) ) |
| 223.14 | ![\leavevmode {\color {red}{t\atop {1\over 2}2}~\scalebox {-1}[1]{\ell }~{m\atop 1}=\hbox{10}~\scalebox {-1}[1]{\ell }~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_377.png) simplifies to simplifies to
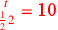 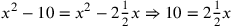 ) ) |
| 223.17 | ![\leavevmode {\color {red}{t\atop 4}~\scalebox {-1}[1]{\ell }~\hbox{51}=\hbox{10}~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_380.png) simplifies to simplifies to
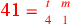 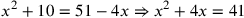 ) ) |
| 224.1 | ![\leavevmode {\color {red}{t\atop 1}~\scalebox {-1}[1]{\ell }~{m\atop 2}~\hbox{10}={t\atop 5}~{m\atop 1}}](../../../media/sources/14/6/EOAineq_6_383.png) simplifies to simplifies to
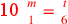 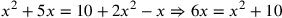 ) ) |
| 224.4 | ![\leavevmode {\color {red}{t\atop 7}~\scalebox {-1}[1]{\ell }~\hbox{7}~{m\atop 3}={t\atop 2}~\scalebox {-1}[1]{\ell }~\hbox{10}~{m\atop 2}}](../../../media/sources/14/6/EOAineq_6_386.png) simplifies to simplifies to
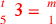 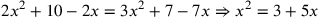 ) ) |
| 225.8 | The power of the māl māl is 4; of the māl cube is 5; |
| 225.13 | The power of the māl cube māl māl is 9; |
| 226.1 | A term for 4 is a māl māl; for 7 is a cube māl māl; |
| 226.3 | A term for 8 is a māl māl māl māl or a cube māl cube, |
| 226.7 | A term for 9 is a cube cube cube or a cube māl māl māl, etc. |
| 226.12 | Multiply
 by by
 to get to get
 ( (
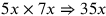 ) ) |
| 226.17 | Multiply
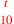 by by
 to get to get
 ( (
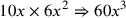 ) ) |
| 227.4 | Multiply
 by by
 to get to get
 ( (
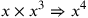 ) ) |
| 227.7 | Multiply 6 by
 to get to get
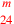 ( (
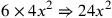 ) ) |
| 227.10 | Multiply 7 by
 to get to get
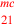 ( (
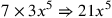 ) ) |
| 227.17 | 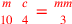 simplifies to simplifies to
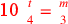 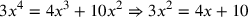 ) ) |
| 228.1 |  simplifies to simplifies to
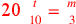 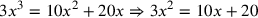 ) ) |
| 228.4 | 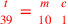 simplifies to simplifies to
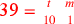 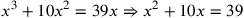 ) ) |
| 228.11 | Multiply
 by by
![\leavevmode {\color {red}{t\atop 4}~\scalebox {-1}[1]{\ell }~\hbox{13}}](../../../media/sources/14/6/EOAineq_6_417.png) to get to get
![\leavevmode {\color {red}{m\atop 20}~\scalebox {-1}[1]{\ell }~{t\atop 65}}](../../../media/sources/14/6/EOAineq_6_418.png) ( (
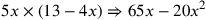 ) ) |
| 228.15 | Multiply
![\leavevmode {\color {red}{t\atop 2}~\scalebox {-1}[1]{\ell }~\hbox{8}}](../../../media/sources/14/6/EOAineq_6_420.png) by by
![\leavevmode {\color {red}{m\atop 4}~\scalebox {-1}[1]{\ell }~\hbox{7}}](../../../media/sources/14/6/EOAineq_6_421.png) to get to get
![\leavevmode {\color {red}{m\atop 32}~\scalebox {-1}[1]{\ell }~{t\atop 14}~\scalebox {-1}[1]{\ell }~\hbox{56}~{c\atop 8}}](../../../media/sources/14/6/EOAineq_6_422.png)  ) ) |
| 229.4 | Divide
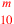 by by
 to get to get
 ( (
 ) ) |
| 229.8 | Divide
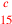 by by
 to get to get
 ( (
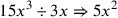 ) ) |
| 229.13 | Divide
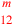 by by
 to get 4 ( to get 4 (
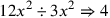 ) ) |
| 229.17 | Divide
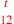 by 4 to get by 4 to get
 ( (
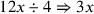 ) ) |
| 230.4 | Divide
![\leavevmode {\color {red}{m\atop 3}~\scalebox {-1}[1]{\ell }~{c\atop 12}}](../../../media/sources/14/6/EOAineq_6_438.png) by by
 to get to get
![\leavevmode {\color {red}{t\atop {1\over 2}1}~\scalebox {-1}[1]{\ell }~{m\atop 6}}](../../../media/sources/14/6/EOAineq_6_440.png) ( (
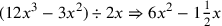 ) ) |
| 230.8 | Divide
![\leavevmode {\color {red}{t\atop 3}~\scalebox {-1}[1]{\ell }~{m\atop 10}}](../../../media/sources/14/6/EOAineq_6_442.png) by 2 to get by 2 to get
![\leavevmode {\color {red}{t\atop {1\over 2}1}~\scalebox {-1}[1]{\ell }~ {m\atop 5}}](../../../media/sources/14/6/EOAineq_6_443.png) ( (
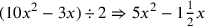 ) ) |
| 230.13 | Divide
 by by
 to get to get
 ( (
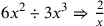 ) ) |
| 230.17 | Divide
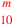 by by
![\leavevmode {\color {red}{t\atop 1}~\scalebox {-1}[1]{\ell }~\hbox{3}}](../../../media/sources/14/6/EOAineq_6_450.png) to get to get
![\leavevmode {\color {red}{m\atop 10}\over {{t\atop 1}~\scalebox {-1}[1]{\ell }~\hbox{3}}}](../../../media/sources/14/6/EOAineq_6_451.png) ( (
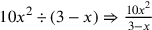 ) ) |
