1.1 Ibn al-Bannāʾ and al-Hawārī
1.1.1 Ibn al-Bannāʾ’s textbook and al-Hawārī’s commentary
Shortly before the year 1301 CE, in the western part of North Africa, the celebrated mathematician and astronomer Ibn al-Bannāʾ (1256-1321) wrote what was to become a very popular arithmetic textbook. His Condensed [Book] on the Operations of Arithmetic (Talkhīṣ aʿmāl al-ḥisāb) describes rules for operating with Arabic numerals and methods of arithmetical problem-solving. One factor that made the book appealing was that it is brief. Condensed expositions were popular because students then were often expected to memorize textbooks, and this one covered just the right amount of material.
But brevity is also a drawback. Ibn al-Bannāʾ’s little book contained no numerical examples to illustrate how the calculations were to be performed, and his concise exposition left no room for proofs or supplementary remarks. So, over the course of the next three centuries, the Condensed Book inspired a number of people to write commentaries elaborating on its contents in various ways. Ibn al-Bannāʾ himself became the first to write such a commentary in 1301 CE (701H). In Lifting the Veil from the Face of the Operations of Arithmetic (Raf ʿ al-ḥijāb ʿan wujūh aʿmāl al-ḥisāb) he expounds on his short work by providing philosophical remarks, proofs, numerical examples, and expanded explanations.
Al-Hawārī was among Ibn al-Bannāʾ’s students in Marrakesh early in 1305 (704H). Ibn al-Bannāʾ was teaching his Condensed Book, and already during the course of the lectures al-Hawārī was writing his own commentary. As he tells us in his introduction, al-Hawārī’s specific purpose was to provide numerical examples for Ibn al-Bannāʾ’s rules. The present book contains our edition, translation, and commentary of his Essential Commentary on the Condensed [Book] on the Operations of Arithmetic (al-Lubāb fī sharḥ Talkhīṣ aʿmāl al-ḥisāb), which he completed June 12, 1305. In it, al-Hawārī reproduces passage by passage the entire text of the Condensed Book. After each of Ibn al-Bannāʾ’s rules he gives his own numerical examples, and, where he finds it necessary, he supplements Ibn al-Bannāʾ’s explanations with further remarks often extracted from his teacher’s Lifting the Veil.
1.1.2 The authors and their works
Ibn al-Bannāʾ’s full name is Abū al-ʿAbbās Aḥmad ibn Muḥammad ibn ʿUthmān al-Azdī al-Marrākushī. For those not familiar with the forms of Arabic names, we will dissect this one. His given name is Aḥmad, and he gained the sobriquet Abū al-ʿAbbās when his wife gave birth to a son they named al-ʿAbbās (Abū means “father”). The word ibn means “son”, so he was the son of Muḥammad, who in turn was the son of ʿUthmān al-Azdī. The designation al-Marrākushī indicates that he was from Marrakesh, a city now in modern Morocco. He is best known today by the nickname Ibn al-Bannāʾ, which means “son of the builder”.
Ibn al-Bannāʾ was a renowned scholar known to have written nearly 120 works on topics ranging from the rational sciences (mathematics, astronomy, logic) to religion (including law), language (rhetoric and prosody), the occult sciences (including astrology), agronomy, philosophy, and medicine.1 He was born in Marrakesh and remained in Morocco his whole life.
Four of his books are relevant to us, and the Arabic text of each has been published:
Condensed [Book] on the Operations of Arithmetic (Talkhīṣ aʿmāl al-ḥisāb, [M1]).2
This is Ibn al-Bannāʾ’s brief introduction to calculation with Indian (i.e. Arabic) numerals, including methods for finding unknown numbers. Because it does not include examples, the book does not show the numerals. It was completed before 1301. Souissi’s 1964 edition also contains a French translation.
Lifting the Veil from the Face of the Operations of Arithmetic (Raf ʿ al-ḥijāb ʿan wujūh aʿmāl al-ḥisāb, [M8]).3
Ibn al-Bannāʾ’s own commentary to his Condensed Book was completed in 1301. Although it contains many numerical examples that would be of help to students, the theoretical and philosophical nature of many of his remarks suggest it was written for a more sophisticated audience. Al-Hawārī copied many passages from this commentary into his own book, mainly those giving further explanations of the rules.
Essays on Arithmetic (Maqālāt fī l-ḥisāb, [M2]).4
This is another arithmetic book that covers much of the same material as the Condensed Book. In it, Ibn al-Bannāʾ sparingly shows the Indian numerals. He does not cover algebra or double false position, but he does include a collection of problems solved by single false position and proportion. Problems [1] and [2] in Appendix B are translated from this book.
Book on the Fundamentals and Preliminaries in Algebra (Kitāb al-uṣūl wa l-muqaddimāt fī l-jabr wa l-muqābala, [M6]).5
Ibn al-Bannāʾ’s book on algebra, dating from the late thirteenth century, builds on Abū Kāmil’s
Al-Hawārī’s full name is ʿAbd al-ʿAzīz ibn ʿAlī ibn Dāwud al-Hawārī al-Miṣrātī. The designation “al-Miṣrātī” indicates that he was descended from the Libyan tribe of Miṣrāta. The “al-Hawārī” tells us that he hailed from the Berber tribe named Hawārī, which we know emigrated from Libya to Morocco in the ninth century.6
The only secure dates we have on al-Hawārī are found in his book. The earliest extant manuscript, that of Medina (described below), reports that he completed it on Saturday, 18 Dhū al-Qaʿda, 704H, which is the Julian date 12 June 1305. Also, at line 204.3 he relates that Ibn al-Bannāʾ was dictating to him on Wednesday, the 28th of the month of Rajab. This can only be in 704H, which corresponds to 24 February 1305. Because we know that Ibn al-Bannāʾ was in Marrakesh at that time, it places al-Hawārī there as well. We know nothing else about his dates, his locations, or his career. His commentary on the Condensed Book is his only known work: Essential Commentary on the Condensed [Book] on the Operations of Arithmetic (al-Lubāb fī sharḥ Talkhīṣ aʿmāl al-ḥisāb, [M1]).7
Al-Hawārī delivered just what he said he would in his introduction: a book supplementing each of Ibn al-Bannāʾ’s rules with numerical examples. There is nothing innovative or theoretical about it. Like the Condensed Book, al-Hawārī’s commentary makes no advances in either ideas or techniques. He gives no proofs, and he generally avoids philosophical discussions. And yet, the very lack of innovation in this book makes it a good source for learning about the nature of arithmetic in the epoch of its author, especially when it is compared with other Arabic arithmetic books. By reading how these authors worked with and expressed numbers and equations, we gain insights into the concepts underlying their arithmetic. Furthermore, the apparent lack of interest of both Ibn al-Bannāʾ and al-Hawārī in prior mathematical traditions, when coupled again with an examination of other books, allows us to identify influences from Greece, the Middle East, and India on the practical arithmetical tradition in Arabic.
1.1.3 Manuscripts of al-Hawārī’s Essential Commentary
The fourteen known surviving manuscripts of al-Hawārī’s book were copied between the fourteenth and nineteenth centuries CE. We published our Arabic edition based on the following five manuscripts:
Medina, MS Ḥikmat 21 ḥisāb. 63 ff, 16 lines per page, 16 × 21 cm. The copyist completed it on 18 Rabīʿ I, 746H (Julian 18 July 1345). This manuscript does not distinguish between Ibn al-Bannāʾ’s and al-Hawārī’s words.
Oxford, MS Marsh 378/3, fols. 109a-162a. Copied in 1444 according to Woepcke.8 In this manuscript a word or two is written in red ink to denote the beginning of a new idea, or what we might consider as a new paragraph. This often corresponds to a shift in author (Ibn al-Bannāʾ to al-Hawārī, or vice-versa), but many times it does not.
Istanbul, Süleymaniye Library, MS Şehit Ali Paşa 1977/2 (Türkiye Yazma Eserler Kurumu Başkanlığı Süleymaniye Yazma Eser Kütüphanesi, Şehit Ali Paşa Collection 01977), fols. 54a-103b. Copied 20 Ramaḍān 880H/Julian 16 January 1476 in Constantinople. The copyist distinguished Ibn al-Bannāʾ’s text from al-Hawārī’s comments by placing in front of Ibn al-Bannāʾ’s extracts the letter “ ” (ṣād), which stands for muṣannif (“Author”), while passages from al-Hawārī are preceded by the letter “
” (ṣād), which stands for muṣannif (“Author”), while passages from al-Hawārī are preceded by the letter “ ” (shīn), which is the first letter of the word sharḥ (“commentary”).
” (shīn), which is the first letter of the word sharḥ (“commentary”).
Tehran, Library of Parliament MS 2672/2, fols. 10a-56b, copied before 972H/1564. Red ink is employed here like in the Oxford manuscript.
Tunis, National Library of Tunis MS 9940. 32 ff., 22 × 26 cm, 29 lines per page. Copied 4 Jumādā II, 1082H/Julian 28 September 1671 in Damascus. In this manuscript Ibn al-Bannāʾ’s passages are preceded by the letter “ ” (mīm), which either stands for matn or muʾallif, both of which mean “[original] text”, and al-Hawārī’s comments start with a “
” (mīm), which either stands for matn or muʾallif, both of which mean “[original] text”, and al-Hawārī’s comments start with a “ ” (shīn) for sharḥ (“commentary”).
” (shīn) for sharḥ (“commentary”).
For those not familiar with the notation, the Tehran manuscript is number 2672 in the collection, and the “/2” indicates that al-Hawārī’s treatise is the second treatise contained in that manuscript. In this manuscript, al-Hawārī’s treatise begins on the front (a) of folio (sheet) 10 and ends on the back (b) of folio 56. The Tunis manuscript 9940 contains only al-Hawārī’s treatise, and it is 32 folios long.
As is common with manuscripts, there are variations from one copy to another. In the case of al-Hawārī’s commentary, these differences are all minor. Some are clearly errors, while for others it is not easy to tell which variation the author originally wrote. When in doubt we have sided with the oldest manuscript, that of Medina, copied only four decades after the book was finished. There are, however, greater differences between the figures drawn in the manuscripts. We discuss them below.
On the following pages are samples from each of the five manuscripts. We have chosen the page that contains the double false position diagram just before 208.8. (Double false position is described below in chapter 1.5.)

Fig. 1.1: Medina Manuscript fol. 55b, covering the text from 207.16 to 209.2.

Fig. 1.2: Oxford manuscript fol. 154b, covering the text from 208.6 to 211.15. The scan is in black and white. Lighter shaded portions, which can be seen in the text in the middle of the page, in the lines of the diagram, and as bars over some words, are in red ink.

Fig. 1.3: Istanbul manuscript fol. 97b, covering the text from 208.2 to 211.15. This manuscript does not show the diagram.

Fig. 1.4: Tehran manuscript fol. 50b, covering the text from 207.1 to 208.9.

Fig. 1.5: Tunis manuscript fol 28a, covering the text from 208.2 to 213.5. This scan is in black and white, so it is difficult to tell if there is anything written in red ink.
1.2 Historical setting
Even a quick look over the translation reveals that al-Hawārī’s arithmetic textbook differs from its modern counterparts in format, contents, and methods. These differences run deeper than what might be seen as accidental variations. Medieval Islam was an intellectual melting-pot of ideas from the various cultures it was in contact with, and al-Hawārī’s book exhibits these different influences, each with qualities of its own, and which were not always amenable to merging. Further, medieval people conceived of numbers differently than we do today, and their system of education and their very attitude toward books affected the way they presented their calculations. These historical, mathematical, and conceptual issues warrant a few words to put the Essential Commentary in context, and we begin in this section with history.
When the prophet Muḥammad died in 632 CE, his empire already covered most of the Arabian peninsula. The military push by his successors resulted in rapid conquests both east and west, so that by the time the Umayyad dynasty fell to the ʿAbbāsids in 750 CE the empire stretched from the Iberian peninsula in Western Europe all the way to the Indus River. The Arab conquerors found themselves ruling over territory once controlled by Greece to the west, Persia in the Middle East, and bordering India to the east.
One remarkable cultural phenomenon that arose from this expansion is known as the Arabic translation movement. From roughly the middle of the eighth century until the end of the tenth, the ruling class and other wealthy patrons subsidized the large-scale collection, translation, and study of scientific and other knowledge. Books were sought out from any available source, whether in Greek, Sanskrit, Persian, or Syriac. Topics included the mathematical sciences (arithmetic, geometry, optics, mathematical astronomy, etc.) as well as philosophy, astrology, geography, mechanics, medicine, agriculture, alchemy, and assorted other topics. Concurrent with this translation activity, several authors wrote down in books the arithmetic (including algebra), mensuration, and folk astronomy that had previously been transmitted orally among people working in the trades in the Middle East.
The causes of the Arabic translation movement are complex and are still being debated. We will only note that it appears to have been spurred by the demands of managing such a large empire combined with the demands of political expediency involving Persian influence.9 The causes of its demise around the latter tenth century are necessarily equally complex, but one factor seems to have been that they had just about run out of relevant books to translate, and most of those that were left had been surpassed by original works in Arabic.
In conjunction with the translation movement, scholars composed original works in various branches of mathematics. The circulation in this singular environment of books originating from different cultures naturally gave rise to the mixing of ideas and techniques. To pick just a few examples: in astronomy, Indian trigonometry was adopted in books based on Greek planetary theory; in geometry, definitions and constructions from Greek texts were introduced to books on practical mensuration; and we find applications of algebra to Greek geometry and of Greek geometry to algebra. This combining of elements from different traditions was a lasting characteristic of Arabic mathematics and science, despite their occasional incompatibility.
The prevalence of the word “Greek” in this last paragraph is not accidental. The majority of works translated and studied by Arabic scholars were originally written in that language. And, just as important, Arabic authors consciously structured their mathematical works, at least the more theoretical ones, on Greek models. Arabic scholars were drawn in particular to the logical-deductive structures that guided Euclid’s
After the translation movement had run its course, the production of new books continued unabated. Innovative work continued in algebra, geometry, optics, mechanics, and various aspects of astronomy that included planetary models, trigonometry, and numerical interpolation. In some branches of learning this momentum persisted longer than in others. After the thirteenth century, for example, we see little advancement in algebra from a theoretical perspective (including the algebra in al-Hawārī’s book), while new and innovative books on planetary theory continued to appear at least to the middle of the sixteenth century.11
Even if Arabic scholars distinguished between practical (ʿamalī) and theoretical (naẓarī) mathematics,12 it was common for the two to appear together in the same book. A good example in which the two approaches mingle is the Completion of Arithmetic of al-Baghdādī
Ibn al-Bannāʾ states his practical intent when he writes that his Condensed Book “is useful for inheritance and business transactions and other [purposes]”.16 The commentaries it spawned, however, frequently take it in philosophical and theoretical directions. For example, Ibn al-Bannāʾ ensured that the nature of the unit would become a source for philosophical debate by the elaboration he gave the issue in his Lifting the Veil.17 And many commentators, Ibn al-Bannāʾ included, provided proofs to many of the rules in the Condensed Book. Al-Hawārī’s commentary, on the other hand, retains the practical orientation by focusing almost exclusively on numerical examples.
Like many Arabic mathematics books, Ibn al-Bannāʾ’s Condensed Book is a kind of hybrid, exhibiting techniques originating from Indian, Greek, and Middle Eastern sources. Part I of the book is devoted to calculation with Indian numerals (we call them Arabic numerals), which originated in India. Certain chapters contain material extracted ultimately from Greek sources, like Euclid’s
1.3 Arabic arithmetic
The two common notations for writing numbers in medieval Arabic were jummal and Indian. Jummal notation is sometimes called abjad, after the first four letters in the traditional ordering of the Arabic alphabet: alif, bā, jīm, and dāl. In this system, the 28 letters of the alphabet are assigned values 1, 2, 3,…, 9, 10, 20, 30,…, 90, 100, 200, 300,…, 900, and 1000.18 It is an additive system, so to express the number 542, for example, one writes the letters whose values are 500 ( ), 40 (
), 40 ( ), and 2 (
), and 2 ( ):
):  . Jummal notation makes its appearance in al-Hawārī’s book only in the rule for casting out sevens, in the figures just before 89.10 and 90.1 (see our commentary at 88.10). Jummal numerals were associated with two forms of calculation, finger reckoning and sexagesimal arithmetic, which will be described below.
. Jummal notation makes its appearance in al-Hawārī’s book only in the rule for casting out sevens, in the figures just before 89.10 and 90.1 (see our commentary at 88.10). Jummal numerals were associated with two forms of calculation, finger reckoning and sexagesimal arithmetic, which will be described below.
We acquired our “Arabic” numerals from Arabic sources, but Arab-speaking people called them “Indian” (al-hindī) numerals because they learned them from Indian sources. Indian numerals consist of the signs for 1, 2, 3, …, 9, together with a 0 for the empty place. This is the system taught in Ibn al-Bannāʾ’s textbook and illustrated by al-Hawārī’s examples. The shapes of the numerals have varied greatly over time and place, even among the manuscripts of al-Hawārī’s book. See our commentary at 69.2 for some of the forms.
There was another way of writing numbers that was practiced mainly in the far western part of the Islamic world. The earliest extant mention of rūmī (“Roman”) signs is a brief description in the Chapters on Indian Arithmetic by al-Uqlīdisī,
The three main methods of calculation in medieval Islam were finger reckoning, sexagesimal arithmetic, and Indian arithmetic. Sexagesimal arithmetic and finger reckoning had already been in use in the Middle East prior to the rise of Islam. And although Indian numerals are attested in Syria by the mid-seventh century CE, it seems that rules for calculating with them became known to Muslims about a century later through direct contact with Indian scholars, at the start of the translation movement. The three systems remained popular throughout the medieval period, and were often described together in the same book.
Finger reckoning was a method popular among merchants, government secretaries, and surveyors. Calculations were preformed mentally in base ten, with intermediate results “stored” by positioning the fingers in particular ways. It was called ḥisāb al-yadd (hand arithmetic), al-ḥisāb al-hawāʾī (aerial calculation), al-ḥisāb al-maftūḥ (open calculation), or sometimes ḥisāb al-rūm wa l-ʿarab (calculation of the Romans (i.e., Byzantines) and Arabs). In one of many examples, Abū l-Wafāʾ
We begin by multiplying forty by twenty, to get eight hundred, and by eight to get three hundred twenty. Hold them. Then we multiply the six by twenty to get one hundred twenty, and by eight to get forty-eight . Then we add them all to get one thousand, two hundred eighty-eight.21
The command “hold them” means “store the intermediate sum” 1,120 by positioning the fingers. Then, after the next sum 168 is calculated, the two can be added to get the answer. When the result of such a calculation was recorded on paper, jummal notation was used. Finger reckoning and jummal numerals played roles similar to the abacus (counters manipulated on tabletops) and Roman numerals in the West: the first was for calculating and the second for recording the numbers.22
Most Arabic arithmetic books covering mental calculation do not address the actual positioning of the fingers. One that does is ʿAlī ibn al-Maghribī’s
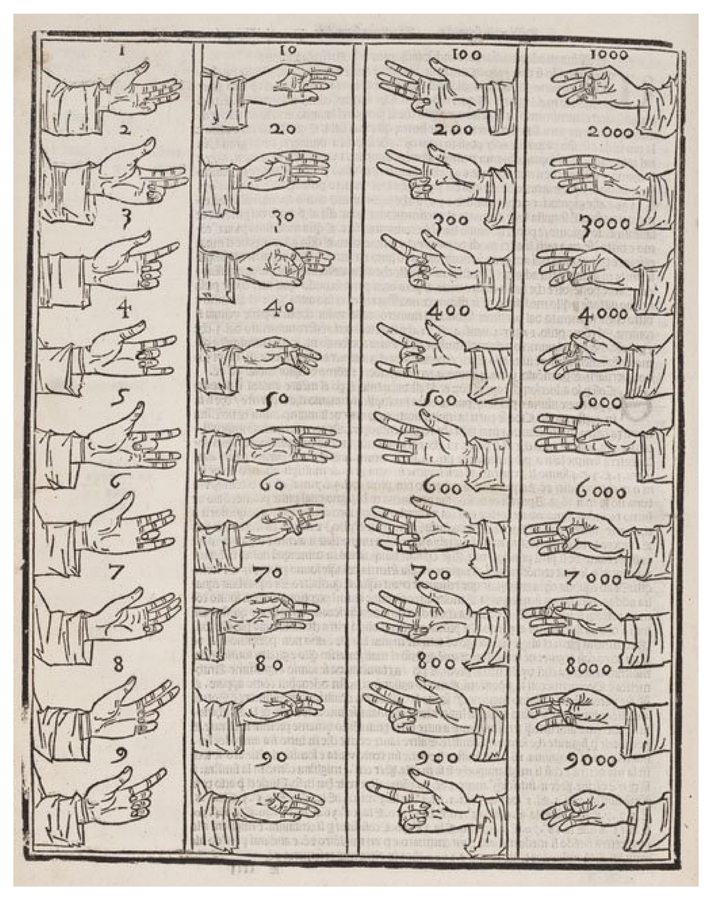
Fig. 1.6: Finger positions in Luca Pacioli’s
We know from literary references that finger reckoning had been practiced by the ancient Greeks and Romans, and it was probably known in other parts of the ancient world as well.25 The passage from Abū l-Wafāʾ
Sexagesimal arithmetic is calculation in base sixty. This place-value system is like our base ten system, with sixty taking the place of ten. Where, for example, our 9062 is
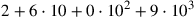 , the sexagesimal number 12,0,45,1 is
, the sexagesimal number 12,0,45,1 is
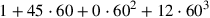 or, in base ten, 2,594,701. Sexagesimal arithmetic dates back to late third millennium BC Mesopotamia, where the numbers were recorded in cuneiform on clay tablets. It became the standard system for Babylonian astronomers, and later it was adopted by astronomers writing in Greek, Arabic, Sanskrit, and other languages. It is because of sexagesimal arithmetic that today we still have sixty seconds in a minute and sixty minutes in an hour. In Arabic the numbers 1 through 59 were written in jummal form so, reversing our 12,0,45,1, the number would have looked like
or, in base ten, 2,594,701. Sexagesimal arithmetic dates back to late third millennium BC Mesopotamia, where the numbers were recorded in cuneiform on clay tablets. It became the standard system for Babylonian astronomers, and later it was adopted by astronomers writing in Greek, Arabic, Sanskrit, and other languages. It is because of sexagesimal arithmetic that today we still have sixty seconds in a minute and sixty minutes in an hour. In Arabic the numbers 1 through 59 were written in jummal form so, reversing our 12,0,45,1, the number would have looked like
 ō
ō . The “ō” is the sexagesimal zero, or empty place. Sexagesimal arithmetic is not covered in al-Hawārī’s book.
. The “ō” is the sexagesimal zero, or empty place. Sexagesimal arithmetic is not covered in al-Hawārī’s book.
Indian arithmetic is calculation in our base-ten place-value system using the nine figures 1, 2, …, 9 and the zero (0). This system originated in India probably around the first century CE, though the earliest Indian text showing the numerals dates from the late sixth century. The numerals had reached Syria by 662 CE when the bishop Severus Sebokht
The earliest known Arabic treatise on Indian numerals is the Book on Indian Calculation,27 written by Muḥammad ibn Mūsā al-Khwārazmī
Al-Khwārazmī’s
The earliest extant Arabic book on Indian reckoning is al-Uqlīdisī’s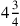 . Al-Uqlīdisī also gave rules for working out the computations with pen and paper, without any erasing. He famously explains that one advantage of switching to ink and paper is because the dust board is associated with “the misbehaved who earn their living by astrology on the streets”.30
. Al-Uqlīdisī also gave rules for working out the computations with pen and paper, without any erasing. He famously explains that one advantage of switching to ink and paper is because the dust board is associated with “the misbehaved who earn their living by astrology on the streets”.30
Al-Uqlīdisī’s
1.4 Greek mathematics and Arabic arithmetic
1.4.1 Greek and Arabic concepts of number
Some Arabic arithmeticians gave their subject the semblance of a rigorous foundation by adding definitions from Greek number theory. This might have been a good way to merge different approaches to arithmetic were it not for the incongruity of their number concepts. The numbers of the Arabic arithmeticians (ḥussāb) include any positive quantity that arises in calculation, including fractions and irrational roots. But numbers in Euclid’s
Aristotle’s
Although the relevant Greek works had been translated into Arabic by the end of the first quarter of the ninth century, the Greek notions of unit and number took some time to make their way into practical Arabic arithmetic books. The earliest books we consulted give no definition of number, and instead begin with instructions on how to perform operations.35 Philosophical treatments of arithmetic could not ignore the issue, however. Two early books whose chapters on arithmetic depend heavily on Nicomachus
Evidence of Greek influence on practical arithmetic in Western Islam appears in the earliest extant texts from the late 1100s. Al-Ḥaṣṣār,
Number is a multitude composed of units…Its origin emerges from the arithmetical one. And the arithmetical one is by its essence not a number, since it is the cause and number is the effect.39
Ibn al-Bannāʾ took a different approach in the Condensed Book by condensing the definitions of Euclid
The incompatibility problem was solved by the Persian mathematician and poet ʿUmar al-Khayyām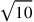 can be the length of a line, the area of a planar figure, or the volume of a body. Consequently there are two different units, the indivisible arithmetical unit and the divisible geometric unit.
can be the length of a line, the area of a planar figure, or the volume of a body. Consequently there are two different units, the indivisible arithmetical unit and the divisible geometric unit.
1.4.2 Greek number theory and geometry in Arabic arithmetic
Books VII to IX of Euclid’s
Ibn al-Bannāʾ’s Condensed Book covers the classification of even numbers (65.10) and the sieve of Eratosthenes
Rules for summing finite series were known in both India and Greece before the advent of Islam, and probably in other parts of the old world as well.41 The rules we read in Arabic books ultimately derive from Greek sources, with some innovations introduced by the Arabic authors.42 Ibn al-Bannāʾ likely took his rules (starting at 79.13) from another Arabic source.
It is largely because numbers could take only integer values that geometric magnitudes in Euclid,
By contrast, Arabic practitioners held a concept of number deriving as much from measurement as from counting, allowing them to work freely with fractions and irrationals. By routinely assigning numerical values to geometric magnitudes in surveying work and in architecture, they were able to foster the intimate connection between arithmetical and geometrical calculation. So when Euclid’s
Euclid’s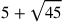 . Ibn al-Bannāʾ briefly presents the arithmetical version of the theory of quadratic irrationals in his Condensed Book, and al-Hawārī gives it a thorough review with the help of some passages from Lifting the Veil (starting at 173.4). Al-Hawārī also copied from Lifting the Veil the manipulations of geometric proportion that Ibn al-Bannāʾ took, once again directly or indirectly, from definitions 12-15 in Book V of an Arabic translation of Euclid’s Elements (196.16).
. Ibn al-Bannāʾ briefly presents the arithmetical version of the theory of quadratic irrationals in his Condensed Book, and al-Hawārī gives it a thorough review with the help of some passages from Lifting the Veil (starting at 173.4). Al-Hawārī also copied from Lifting the Veil the manipulations of geometric proportion that Ibn al-Bannāʾ took, once again directly or indirectly, from definitions 12-15 in Book V of an Arabic translation of Euclid’s Elements (196.16).
1.5 Arithmetical problem solving
Part II of the Condensed Book covers arithmetical problem-solving techniques that were originally associated with finger reckoning. Here, instead of solving problems that ask for the result of a calculation on given numbers, Ibn al-Bannāʾ explains methods for finding unknown numbers. For instance, instead of working out a calculation like “divide thirty-five by fifteen” (at 120.16), al-Hawārī poses the problem “a quantity: taking away its third and its fourth leaves ten. How much is the quantity?” (at 199.1).
Today, a problem asking for an unknown number is typically viewed as an algebra problem. We would solve the problem just mentioned by naming the quantity
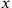 , and then setting up and solving the equation
, and then setting up and solving the equation
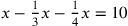 . But problems like this were regarded by medieval mathematicians as belonging to arithmetic, since algebra was just one of several methods available to solve them. In fact, al-Hawārī works out this particular problem not by algebra, but by double false position (described below). The independence of problems from the methods of solution is most evident in other books that show the same problem solved by two or three different methods. One example is a problem of al-Ḥaṣṣār
. But problems like this were regarded by medieval mathematicians as belonging to arithmetic, since algebra was just one of several methods available to solve them. In fact, al-Hawārī works out this particular problem not by algebra, but by double false position (described below). The independence of problems from the methods of solution is most evident in other books that show the same problem solved by two or three different methods. One example is a problem of al-Ḥaṣṣār
Here is a brief list of the problem solving methods covered by Ibn al-Bannāʾ. These are the most common among the methods described in Arabic arithmetic books:
The method Arabic authors called “the four proportional numbers” is known to us also as “the rule of three”. Given a proportion
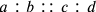 , this method shows how to find one of the values given the other three. It is explained starting at 195.9. Al-Hawārī does not solve any problems by this method, so we translate one from Ibn al-Bannāʾ’s Essays on Arithmetic in Appendix B, problem [1].
, this method shows how to find one of the values given the other three. It is explained starting at 195.9. Al-Hawārī does not solve any problems by this method, so we translate one from Ibn al-Bannāʾ’s Essays on Arithmetic in Appendix B, problem [1].
Single false position is a method that directly applies the rule of three. One posits a convenient, but probably incorrect, value for the solution to a problem, then the answer is calculated from the value and the error via proportion. This method is not taught in Ibn al-Bannāʾ’s Condensed Book, but it was very common in Arabic arithmetic. Problems [2] and [7] translated in Appendix B are solved by single false position. The first of these is from Ibn al-Bannāʾ’s Essays on Arithmetic.
Double false position. Two (false) values are posited for the solution to a problem, and the correct answer is found from the values and their respective errors. This method is also based on proportion, and is explained beginning at 198.2 with examples at 199.1, 200.1, 201.1, 202.3, 203.1, 205.5, 207.6, and Appendix B, problem [7].
Algebra. In Arabic algebra the powers of the unknown are assigned particular names corresponding to our
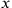 ,
,
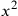 ,
,
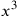 , etc. To solve a problem an unknown is assigned one of these names, or sometimes a combination of them. The conditions of the enunciation are worked out to set up an equation, which is then simplified and solved. The basic rules of algebra are explained starting at 209.1, though no sample problems are provided. Examples worked out by algebra from other books are given in problems [3] through [7] in Appendix B.
, etc. To solve a problem an unknown is assigned one of these names, or sometimes a combination of them. The conditions of the enunciation are worked out to set up an equation, which is then simplified and solved. The basic rules of algebra are explained starting at 209.1, though no sample problems are provided. Examples worked out by algebra from other books are given in problems [3] through [7] in Appendix B.
The rule of three was practiced across the Old World in antiquity, from Europe to China. As mentioned, it is the basis for the method of single false position, which dates back at least to a problem solved in the Rhind Papyrus
Double false position also circulated among people who solve problems on the job. The only evidence we have of its use before the ninth century comes from a few problems in a single ancient Chinese text, the Nine Chapters on Mathematical Procedures,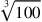 (ca. 100 CE), nor has it been found in Babylonian or Sanskrit sources.50 This does not mean that it was not practiced in those places. We just have no positive evidence that it was.
(ca. 100 CE), nor has it been found in Babylonian or Sanskrit sources.50 This does not mean that it was not practiced in those places. We just have no positive evidence that it was.
Because of confusion in many modern accounts, algebra will require a bit more explanation. Algebra in medieval Arabic was called al-jabr wa l-muqābala, literally “restoration and confrontation”.51 The phrase was often shortened to just al-jabr, and transliterations into Latin and Italian eventually led to our word “algebra”. But algebra then was quite different from algebra now. Many of the various meanings we impart to the word “algebra” today are due to modern developments and to the disappearance of other problem-solving methods. Today, people often apply the words “algebra” and “algebraic” to any kind of formal, abstract reasoning, or to any technique of finding unknown numbers. Two current definitions of “algebra” in the Oxford English dictionary support the former view:
2a. As a mass noun: (originally) the branch of mathematics in which letters are used to represent numbers in formulae and equations; (in later use more widely) that in which symbols are used to represent quantities, relations, operations, and other concepts, and operations may be applied only a finite number of times.
3. In extended use and fig. Something, esp. a system or process, that resembles algebra in substituting one thing for another, or in using symbols, signs, etc., to represent ideas and concepts.52
Neither of these characterizations apply to Arabic algebra. Letters and other symbols are only incidentally employed in Maghrebi texts (see below), and in any case they represent kinds of numbers and not numbers themselves.53 Further, there is no abstract reasoning that would take the art beyond arithmetic. These modern views of algebra have muddled the attempts of some historians to properly identify just what al-jabr wa l-muqābala is, and to distinguish it from other techniques and modes of reasoning in Arabic and other premodern mathematics.
By “Arabic algebra” we mean the art of al-jabr wa l-muqābala as it was understood by those who practiced it. This was a specific technique of numerical problem-solving, with it own vocabulary and rules. As Ibn al-Bannāʾ and al-Hawārī explain, the powers of the unknown are given names. The first power of the unknown is called a “thing” or a “root”, akin to our
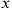 . The second power is called a “māl ”, an Arabic word which ordinarily means “sum of money” or “wealth”, and which corresponds to our
. The second power is called a “māl ”, an Arabic word which ordinarily means “sum of money” or “wealth”, and which corresponds to our
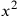 .54 The cube of the thing, our
.54 The cube of the thing, our
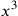 , is called a “cube”, and higher powers are expressed by combinations of māl and cube, such as māl māl for the fourth power and māl cube for the fifth.
, is called a “cube”, and higher powers are expressed by combinations of māl and cube, such as māl māl for the fourth power and māl cube for the fifth.
In most problems solved by al-jabr wa l-muqābala an unknown number is named “a thing”, though sometimes it is named as one of the other powers or some combination of them. The conditions of the problem are then applied to set up a polynomial equation expressed in terms of the names of the powers, and the equation is then simplified and solved. One important distinction between al-jabr and other methods like single and double false position is that, in the latter, operations are performed only on known numbers, while in algebra calculations can be performed on the names of the powers. In other words, in algebra one operates on the unknown.
The earliest known Arabic books on algebra are the Book of Algebra by al-Khwārazmī
With a clear idea that al-jabr must predate the time of al-Khwārazmī,
Diophantus’s
We also know from two passages in Ibn al-Nadīm’s
1.6 Education, books, and notation
One peculiar feature of medieval mathematics books, at least to modern readers, is their general lack of notation. Ibn al-Bannāʾ wrote all numbers in his Condensed Book in words, even if he was teaching the use of Indian numerals! And al-Hawārī, whose purpose was to give numerical examples, still writes the numbers and operations in words before showing the notation. This is perhaps the most glaring of the many differences between medieval and modern arithmetic books. The causes of these differences have to do largely with how the material was taught, and more generally with how people in al-Hawārī’s time related to books.
1.6.1 Education in medieval Islam
Where today education is structured around institutions, curricula, and degrees, in medieval Islamicate societies it was structured around individual teachers, books, and licenses (ijāzāt).64 Schools did exist and provided support for both teachers and students, and from what we can gather they often had curricula; but throughout the medieval period education remained centered on the student-teacher relationship. To learn a topic, a student chose a teacher (shaykh) with a good reputation to study a particular book. Once the student had learned the book to the satisfaction of the shaykh, he (or rarely, she) received an ijāza, or license, granting him authority over the text. The ijāza not only certified mastery of the contents of the book, it gave its possessor authorization to teach it himself. The ijāza recorded the names in the chain of transmission of that particular text, listing the student, his teacher, his teacher’s teacher, ideally all the way back to the author of the book.
Instruction was centered around dictation and memorization. The shaykh read the book to the student, who memorized it and dictated it back to the shaykh. This emphasis on speaking and listening reflects the notion that books properly reside in the minds of those who had memorized them, and not in manuscript copies. Students recited aloud even when studying alone after the lecture, “for what the ear hears becomes firmly established in the heart”.65 Manuscripts played an essential role in this oral environment. Copying the words of a teacher on paper aided memorization, and written books gave the student access to the text when studying alone. But true learning was thought to take place in the presence of the teacher, who possessed an understanding of the book that manuscripts lacked.
Instruction was not restricted to dictation of the book under study. The shaykh would often supplement it with examples, illustrative remarks, and material from other sources. Al-Hawārī cites additional procedures for double false position that Ibn al-Bannāʾ dictated to him at 204.3, and he signals other added material at 163.11 and 232.9. Many other passages are attributed in the manuscripts to Ibn al-Bannāʾ that are not in the Condensed Book, and most likely they were dictated to al-Hawārī as well.66 Whatever a textbook lacked in examples and explanations would have been covered somehow by the shaykh teaching it.
Many authors wrote their books concisely to make memorization easier, which is certainly the case for Ibn al-Bannāʾ’s Condensed Book. Some authors even put down the mathematical ideas in verse, since poetry is easier to memorize than prose. Ibn al-Yāsamīn’s
1.6.2 The role of notation
Because of the oral nature of learning in medieval Islam, books read like transcriptions of lectures.71 Notation serves no purpose to the student listening to a lecture, so there is no advantage in including it in the running text of a book. This is why Ibn al-Bannāʾ wrote his book entirely in words, and why the notation for the calculations in al-Hawārī’s book only appear as figures or illustrations. These figures play a role much like geometric diagrams or other illustrations, and were intended to show the student what is to be put down on the dust-board or other surface. For example, he begins this calculation in the chapter on addition, at 75.9:
Suppose we want to add nine hundred seventy-eight to four hundred fifty-six. We put them down on two lines, as mentioned, as in this figure:.
The visual notation (here
![\begin{matrix}978\\[-.5mm]456\end{matrix}](../../../media/sources/14/2/EOAineq_2_17.png) ) is always set apart from the audible text in al-Hawārī’s book with some phrase like “and its figure is” or “so we write it down like this”.
) is always set apart from the audible text in al-Hawārī’s book with some phrase like “and its figure is” or “so we write it down like this”.
Some Arabic authors included the Indian notation in the spoken parts of their arithmetic books, but there the numbers were still meant to be recited aloud like the words that surround them. Naṣīr al-Dīn al-Ṭūsī,
For example, we want to multiply 123 by 456. We write them in two lines like this:.
Here the 123 and 456 are still intended to be spoken, while the same numbers shown in columns form a figure that was to be apprehended visually, like any illustration.
There were thus two ways of writing arithmetic. To solve a problem, one wrote in notation on a dust-board or other temporary surface. Then, if one wished to communicate the result to others, a rhetorical version was composed. For this reason, the numerals tend to appear in arithmetic books only to show students what is to be put down on the board.
Because board calculations were for personal, immediate use, the notation can tolerate ambiguities. For example, the notation for excluded fractions of both connected and disconnected types were often represented the same way in notation. But this does not matter, because the person working out the calculation knows which is which while doing so (see our commentary at 140.14). Ambiguity would only be a problem if one wanted to consult the book later or have others read it. Dust does not permit the former, and for the latter a rhetorical version in unambiguous prose was composed.
1.6.3 Developments in Indian notation: fractions, roots, and algebra
Arabic practitioners devised notations to extend Indian numerals to show fractions and roots in arithmetic and polynomials and equations in algebra.73 There are differences in these notations that can usually be ascribed to geography, mainly between east and west. The Persian mathematician al-Fārisī,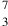 , for example.74 By contrast, al-Kāshī,
, for example.74 By contrast, al-Kāshī,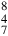 .75 The earliest known book from the Maghreb showing fractions in notation is al-Ḥaṣṣār’s
.75 The earliest known book from the Maghreb showing fractions in notation is al-Ḥaṣṣār’s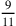 from a manuscript copied in 1194 CE:
from a manuscript copied in 1194 CE: 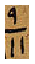 .76 Other books from the west, including al-Hawārī’s commentary, also show fractions this way.
.76 Other books from the west, including al-Hawārī’s commentary, also show fractions this way.
Ibn al-Yāsamīn’s ) above the affected numbers, much like the way we use our elastic sign “
) above the affected numbers, much like the way we use our elastic sign “
Initially, there seems to have been no notation specific to Arabic algebra. The little evidence we have indicates that polynomials were written on a board as a list of coefficients. In the early eleventh century, al-Karajī,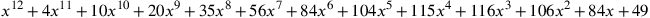 , and then wrote “you put it down in this figure: 1 4 10 20 35 56 84 104 115 116 106 84 49”.77 A century and a half later al-Samawʾal,
, and then wrote “you put it down in this figure: 1 4 10 20 35 56 84 104 115 116 106 84 49”.77 A century and a half later al-Samawʾal, . We can transcribe this as “
. We can transcribe this as “
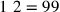 ”, and in modern notation we write it as
”, and in modern notation we write it as
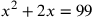 .79
.79
Later, in the western part of the Islamic world, a notation came into common use in which the first letter of the name of the power was placed above the coefficient. Our earliest glimpses are two brief figures in Ibn al-Yāsamīn’s . Algebraic notation is neither mentioned nor shown in more advanced books on algebra, like Ibn al-Hāʾim’s
. Algebraic notation is neither mentioned nor shown in more advanced books on algebra, like Ibn al-Hāʾim’s
1.6.4 Nesselmann’s stages revisited
Addressing Nesselmann
Although historians of mathematics in the past few decades have moved beyond Nesselmann’s
1.6.5 The figures in al-Hawārī’s book
One consequence of the distinction between visual figure and audible text is that in European languages we read numbers expressed with Indian numerals backwards. Arabic is written right-to-left, so when reading a number like “214” in that language one starts from the 4 in the units place. When Europeans translated Arabic texts on arithmetic into Latin in the Middle Ages they preserved the orientation of figures. This is why “214” did not become “412”. Because European languages are written left-to-right, we read the number 214 starting from 2 in the hundreds place.
Like the Latin translators, we have preserved the orientation of the Arabic figures in our translation. We could not reverse figures showing numbers horizontally, like
![\begin{matrix}4043\\[0mm]2685\end{matrix}](../../../media/sources/14/2/EOAineq_2_26.png) (at 74.17), or else the “four thousand forty-three” would look like 3404. It would not make sense to reverse some figures and not others, so we kept the orientation of all figures as they appear in the manuscripts. Keep in mind when reading the translation that figures would have been viewed right to left.
(at 74.17), or else the “four thousand forty-three” would look like 3404. It would not make sense to reverse some figures and not others, so we kept the orientation of all figures as they appear in the manuscripts. Keep in mind when reading the translation that figures would have been viewed right to left.
Although copyists of al-Hawārī’s book transcribed his words more or less faithfully, the same cannot be said for the figures. For example, the figure we typeset for the passage after 103.3 is shown below, followed by the figures from the Tehran, Oxford, and Tunis manuscripts.
We deem our translation to be correct because it agrees with the verbal description of the operations in the text. Of the five manuscripts we consulted, only the Tehran manuscript shows this figure correctly. The Oxford and Medina manuscripts leave off the last round of calculations, and although not incorrect, the Oxford manuscript is the only one that crosses off numbers. Most of the numbers in the Tunis manuscript are wrong, and in the Istanbul manuscript (not shown here) the numbers between the lines are shifted up one row. All five manuscripts, including the Tehran manuscript, have errors in many figures, and it is rare to find a mistake that is common to all manuscripts. In our translation we show figures in the style found in the manuscripts which agree with the calculations described in the text.
1.7 The legacies of the Condensed Book and al-Hawārī’s commentary
The popularity of Ibn al-Bannāʾ’s Condensed Book is evident in the number of commentaries, poems, and abridgments it inspired. After his own Lifting the Veil and al-Hawārī’s Essential Commentary, we know of ten people who wrote commentaries on the Condensed Book between the fourteenth and sixteenth centuries.86 In the other direction, Ibn al-Hāʾim
Although by no means as well known as his professor’s Condensed Book, the number of surviving manuscripts of al-Hawārī’s Essential Commentary is testimony to its popularity across several centuries. We have found four later works that reference or copy from al-Hawārī. ʿIzz al-Dīn al-Ḥanbalī
We last hear of al-Hawārī in 1875, in connection with the proposed mathematics curriculum for the Zaytūna mosque school in Tunis. Until then, mathematics instruction at the mosque had been limited to five stylistic commentaries of a poem on inheritance and arithmetic. In an attempt to modernize instruction, Prime Minister Hayreddin Pasha oversaw the creation of an entirely new curriculum made public on December 25, 1875. Although a great improvement over the dismal curriculum in place at the time, the ten recommended texts on mathematics were themselves already hopelessly out of date. They included al-Hawārī’s Essential Commentary in the upper division, even though it was already over 500 years old! The proposed curriculum received harsh resistance from the ulama, the religious authorities, and it was likely never implemented.
Footnotes
Published in (Ibn al-Bannāʾ 1969).
Published in (Ibn al-Bannāʾ 1994).
Published in (Ibn al-Bannāʾ 1984).
Published in (Saidan 1986, vol. 2).
Published in (al-Hawārī 2013) and in the present volume.
(Gutas 1998); (Saliba 2007).
The classic work on Greek influence is (Rosenthal 1975). For mathematics and philosophy, see (Endress 2003).
See (Saliba 2007); (Ragep 2007); (Brentjes 2007).
As, for example, al-Fārābī does in his Enumeration of the Sciences (first half of 10th c.) (al-Fārābī 1953, 54.7).
Al-Takmila fī l-ḥisāb. Saidan published the Arabic text in (al-Baghdādī 1985). See also (Saidan 1987).
(Oaks 2011a). Al-Khayyām himself used algebra this way to solve a particular problem of cutting a quadrant of a circle to produce a particular ratio.
A German translation is published in (Suter 1908–1909).
There were minor differences between east and west in the Islamic world in the schemes used.
(al-Uqlīdisī 1978, 310); (al-Uqlīdisī 1984, 386). The signs are likely related in some way with special signs appearing on Roman coins minted in Siscia in the period 348-350 CE (Kent 1981, 343, 359, 364-67).
Al-Ḥaṣṣār (d. before 1194), writing in the Maghreb, mentions them in his Complete [Book] on the Art of Number (Guergour 2000, 68). The signs, which varied between east and west, are also mentioned in the writings of Mozarabs (Christians writing in Arabic) in Toledo around the same time (Colin 1933, 204).
For the Roman and later European abacus, see (Pullan 1968).
Saidan describes the poem and translates the relevant parts in (Saidan 1968). Pellat gives an edition and French translation of a similar poem from the previous century, by Abū ʿAbd Allāh Muḥammad ibn Aḥmad al-Mawṣilī al-Ḥanbalī (#768), in (Pellat 1977, 52-59).
The illustration is in (Pacioli 1494, fol. 36b). We reproduce a scan from the 1523 printing from the Columbia University Library copy. This illustration is identical to that in the 1494 printing.
Edited in (Saidan 1971). See (Saidan 1974) for a description of the contents.
Kitāb al-ḥisāb al-hindī. Following (Saidan 1987, 44), we attribute this and some other books listed in Ibn al-Nadīm’s Fihrist under Sanad ibn ʿAlī (#48) to al-Khwārazmī. This is our source for the Arabic title of the book.
For more on the dust-board, and on the transmission of Arabic numerals generally, see (Kunitzsch 2003).
The Arabic text is published in (al-Uqlīdisī 1984), and Saidan’s English translation is published in (al-Uqlīdisī 1978).
Saidan’s translation, from (al-Uqlīdisī 1978, 247).
(Djebbar 2004). There was no single Greek concept of number. Diophantus’s Arithmetica (ca. fourth century CE) shows many fractions, and the works of Hero of Alexandria (first century CE) give many rational approximations to irrational numbers. Also, because number concepts, whether in Greek or Arabic, were based in counting or measuring, it would not have occurred to ancient or medieval mathematicians that negative or complex numbers could exist.
Categories 4b20-24, translated in (Aristotle 1963, 12). Language is discrete because it consists of indivisible syllables.
For these ideas in Aristotle, see (Cleary 1995, 345ff).
We checked the arithmetic books of al-Khwārazmī (Latin redaction), al-Uqlīdisī, Abū l-Wafāʾ, Kūshyār ibn Labbān, al-Karajī, al-Baghdādī, Ibn al-Samḥ, and Ibn al-Haytham.
The Brethren of Purity write “The ‘one’ is said in two ways: in its proper usage, and by way of metaphor. In its proper usage it is a thing that cannot be partitioned or divided…As for ‘one’ in metaphor, it is every aggregate that is considered a unity. So, for example, ten is called a ‘unit’, and a hundred is called a ‘unit’, and a thousand is called a ‘unit’” (translated in (El-Bizri 2012, 67). See also (Goldstein 1964, 136)). Al-Bīrūnī writes “Although ‘one’ is in reality indivisible, nevertheless the unit, one as a technical expression, employed in dealing with sense-objects, whether by weighing, measuring by bulk, or length or number, or merely in thought, is obviously capable of sub-division” (translated in (al-Bīrūnī 1934, 24)). Al-Baghdādī tacks onto his Completion of Arithmetic a chapter on number theory based in Nicomachus (Chapter 6), but he does not address the nature of the unit.
(al-Fārisī 1994, 71.8). Sibṭ al-Māridīnī (died 1506), working in Egypt, similarly contrasted Euclid’s definition with that of the “Arithmeticians” (Sibṭ al-Māridīnī 2004, 73.5). See also (Djebbar 2004, 315-318).
Two Indian books containing such rules are the Āryabhaṭīya of Āryabhaṭa (ca. 500 CE) and the Pāṭī-gaṇita of Śrīdhara (8th or 9th c.) (Plofker 2009, 131-132); (Sridhara Acarya 1959).
Proposition I.47.
Even Greek geometers in late antiquity had begun to assign numbers to magnitudes.
(al-Khwārizmī 2009, 34-42). We deliberately cited the same author in this paragraph and the last. For Thābit ibn Qurra, a proposition in the tradition of Greek geometry should be free of any arithmetizations, but for algebra this rigor is relaxed. It is the setting, not the mathematician, that determined which approach is appropriate.
For Egypt: (Imhausen 2003, 37, 51); (Gillings 1972, Chapter 14). For Babylonia: (Høyrup 2002, 59-60, 102, 311-313). For Sanskrit: (Hayashi 1995, 396-399).
(Chemla 1997).
http://www.oed.com/, accessed August 26, 2018.
There is no good English translation of māl, so we leave it transliterated.
Rashed’s edition of al-Khwārazmī’s book, with an English translation, is published in (al-Khwārizmī 2009). Only a portion of Ibn Turk’s book survives. It is edited with an English translation in (Sayili 1962). In his tenth-century Kitāb al-Fihrist, Ibn al-Nadīm reports a book on algebra by Sanad ibn ʿAlī (#48), a contemporary of al-Khwārazmī and Ibn Turk. This attribution is probably an error, and the book belongs instead to al-Khwārazmī. See (Saidan 1987, 439-440).
For evidence of oral transmission, see (Oaks 2012b); (Saidan 1974, 369); (King 1988).
Kitāb al-burhān ʿalā ʿamal ḥisāb al-khaṭaʿān. Suter published a German translation in (Suter 1908–1909). We have also consulted the British Library, Oxford, and Cairo manuscripts. Abū Kāmil (late ninth century) is also reported to have written a book on double false position about the same time, but it is not extant.
Léon Rodet made a detailed analysis of these differences in (Rodet 1878).
(Høyrup 2002).
The four surviving books of the Arabic translation have been edited and translated twice, in (Sesiano 1982) and (Diophantus 1984).
(Ibn al-Nadīm 1871–1872, 269, 283); (Ibn al-Nadīm 1970, 642, 668). Both references mention Abū l-Wafāʾ’s commentary on Hipparchus’s “book on the art of algebra (al-jabr)”. In addition, Abū l-Wafāʾ himself mentions this commentary in his Book of What is Necessary for Scribes, Businessmen, and Others in the Science of Arithmetic (Saidan 1971, 126.7).
For Islamic education, see (Makdisi 1981), (Berkey 1992), and (Chamberlain 1994).
Abū l-Hilāl al-Ḥasan al-ʿAskarī, quoted in (Berkey 1992, 27).
These passages are shown in small caps in the translation.
Published in (Abdeljaouad 2005a). Ibn al-Yāsamīn also wrote a 55-line poem on root extraction and an 8-line poem on double false position.
The commentary is titled Aim of the Students in Commentary on Desire of Reckoners (Ibn Ghāzī 1983).
(Chamberlain 1994); (Berkey 1992).
(Saidan 1967, 125). Some other books that show notation in the spoken parts of the text include al-Uqlīdisī’s Chapters on Indian Arithmetic (952/3 CE), Ibn Munʿim’s Understanding Calculation (12th-13th c.), and al-Fārisī’s Foundation of Rules on Elements of Benefits (early 14th c.).
For algebraic notation, see (Abdeljaouad 2005a) and (Oaks 2012a).
(al-Kāshī 1969, 89). Al-Baghdādī writes fractions the same way (al-Baghdādī 1985, 102ff).
(al-Karajī 1964, 52). The same polynomial is written similarly by al-Samawʾal (al-Samawʾal 1972, 67).
(al-Samawʾal 1972, 45ff). Here al-Samawʾal is performing operations on the coefficients in tables.
(Ibn Ghāzī manuscript, fol. 108b). It appears that the Eastern marginal annotator felt the need to clarify the final calculations shown in the manuscript, which were written sloppily in Western notation.
Albrecht Heeffer, in particular, has recently criticized Nesselmann (Heeffer 2009).
Ibn Ghāzī’s page showing an entire problem worked out in notation is the one example we have of what must have been commonly written on a board. See (Oaks 2012a, 62).
Al-Ghurbī (M158, 2nd half 14th c.), al-Mawāḥidī (M176, ca. 1382), Ibn Zakariyyā (A336, #793, died 1403-4), Ibn Qunfudh (died 1407-8), al-ʿUqbānī (died 1408), Ibn Haydūr (M196, died 1413), Ibn Majdī (#815, died 1447), al-Ḥabbāk (M219, #831, died 1463), al-Qalaṣādī (died 1486), and Muḥammad al-Ghazzī (#998, 16th c.).
The others are Ibn Marzūq (M205, died 1438), al-Wansharīsī (M257, died 1548-9), and Ibn al-Qāḍī (M315, died 1616).
(Abdeljaouad 2011); (Abdeljaouad and Oaks 2013). Ibn al-Hāʾim’s Contents of Calculation is his abridgment of the Condensed Book mentioned above. Incidentally, Şeker Zāde’s figure for the passage after 103.3 is shown correctly.

